> Техника, страница 96 > Равновесие химическое

Равновесие химическое

Равновесие химическое. Расчет равновесий газовых реакций по термохимическим и спектроскопическим данным. Расчет равновесия (смотрите Равновесие химическое, т. XVIII) основан на применении тепловой теоремы Нернста или квантово-статистич. методов для подсчета термодинамич. величин, определяющих состояние равновесия. Гетерогенные равновесия характеризуются равенством термодинамич. потенциалов (смотрите Потенциал термодинамический) сосуществующих фаз. Равновесие в газовой фазе или растворе определяется константой равновесия К_р (смотрите Действующих масс закон), связанной с термодинамич. потенциалами реагирующих веществ“ следующим соотношением:

Д1п“,=АФ=--^-; (1)

здесь АФ и ΔΖ — разности между суммой соответствующих термодинамич. потенциалов для веществ, образующихся при реакции, и суммой термодинамич. потенциалов для веществ, вступающих в реакцию, взятых при t° реакции и давлении, равном 1 atm. Термодинамич. потенциал Z определяется выражением

* ζ=η

-TS=U + pV-TS

(2)

и потенциал

С a Q U + pV.

s _т s _т,

(2)

здесь U — внутренняя энергия, р — давление, V — объём, Т — абсолютная темп-pa, Н — энтальпия и S — энтропия. Изменение потенциалов Ф и Z при реакции определяется выражением

АФ=— ψ=Δ6· — -ψ, (3)

где АН — изменение энтальпии, равное тепловому эффекту реакции при постоянном давлении, и AS — изменение энтропии при реакции. Очевидно, что при гетерогенном равновесии системы газ — твердые фазы в виду равенства термодинамич. потенциалов сосуществующих фаз условием равновесия будет

АН=TAS, (4)

где АН и AS — изменения Н и S при переходе одной фазы в другую. Из ур-ий (1), (3) и (4) видно, что задача нахождения условий равновесия в гетерогенной системе и вычисление константы равновесия для определения состояний равновесия в газовой системе сводятся к нахождению теплового эффекта реакций и энтр (или термодинамич. потенциалов) веществ, принимающих участие в реакции. Тепловые эффекты

АН м. б. достаточно точно определены только с помощью методов термохимии (смотрите). Другие методы, как то: подсчет из энергий диссоциации, находимых по спектроскопия, данным, расчет на основании температурной зависимости состояний равновесия и прочие, в настоящее время еще не могут дать достаточно точных данных. Поэтому необходимые для расчета равновесия величины АН определяются с помощью закона Гесса из термохимических величин. Зависимость теплового эффекта от t°, необходимую для получения развернутой формы ур-ий (1) и (4), получают с помощью ур-ия Кирхгофа где АС_р — изменение теплоемкости при реакции, вычисляемое аналогично ΔΖ. Основной и наиболее трудной частью расчета равновесия является нахождение энтр *5* (или термодинамич. потенциалов Z и Ф) для участвующих в реакции веществ.

Термодинамический метод расчета энтр основан на применении экспериментальных данных для теплоемкостей и теплот превращения различных агрегатных состояний для определения изменения энтропии при нагревании вещества от 0° К до интересующей нас темп-ры. Изменение энтропии при нагревании (при постоянном давлении) вещества, не меняющего своего агрегатного состояния, равно аг₂

AS=S — S_Tl=J C_p JlL·. (6)

В точке перехода изменение энтропии (на 1 моль) выражается равенством

- S,== ±, (7)

где АН=λ — теплота превращения одного агрегатного состояния в другое. С помощью выражений {6) и (7) на основании экспериментальных данных по теплоемкостям легко подсчитать изменения энтропии. Обычно интегрирование проводят графин. путем; откладывают по абсциссе Т и по ординате площадь между двумя ординатами

Т_г и Т₂, осью абсцисс и кривой численно равна приросту энтропии при нагревании от Т_г до Т₂ при постоянном давлении. Для вычисления энтропии необходимо знание теплоемкостей до темп-p порядка 10° К. Расчет теплоемкостей при более низких темп-pax м. б. произведен с помощью закона Дебая, требующего, чтобы теплоемкость при низких темп-pax была пропорциональ-

на кубу абсолютной темп-ры (закон куба темп-ры для большинства веществ справедлив до темп-р порядка 15—40° К, точнее до темп-p, при которых теплоемкость достигнет 0,3° cal на 1 трамматом):

C_v=аТК (8)

Найденные вышеописанным путем изменения энтропии при нагревании м. б. использованы для подсчета равновесий в случае, если известны нулевые энтропии твердых веществ. На основании предложенного Планком обобщения закона, открытого Нернстом (так называемым третьего теплового закона), энтропии твердых тел при 0° К равны нулю. По Планку задача сводится только к нахождению изменения энтр при нагревании от 0° К до нужной темп-ры. Эти изменения м. б. приравнены энтропиям *5* и послужить основой для подсчета по ур-иям (1), (2) и (4). Но проверка этого метода подсчета Эйкеном (Eucken) показала, что равенство нулевой энтропии нулю является свойством лишь очень ограниченного числа кристаллич. веществ. В настоящее время мы можем считать, что при абсолютном нуле энтропия равна нулю только для немногих идеальных кристаллич. веществ. Появление нулевой энтропии, отличной от нуля, м. б. вызвано наличием изомерных форм молекул (аналогично орто- и параводороду), наличием расщепления низшего энергетич. уровня молекул в кристалле, различной ориентации несимметричных молекул в кристалле и другими причинами. Только для ограниченного числа веществ мы можем с достаточной точностью вычислить нулевую энтропию. Поэтому термодинамич. метод ограничен в своем применении; применение же его без точного учета нулевых энтр приводит к значительным погрешностям и позволяет получить лишь весьма грубое приближение.

Квантово-статистический метод расчета термодинамических величин для газов основан на применении методов статистики к изучению распределения энергии между различными степенями свободы и уровнями энергии молекул газа. В основе метода лежат: 1) Ур-ие Больцмана, связывающее энтропию S и вероятность,

S — к In w_t (9)

где к — постоянная Больцмана, a w — термодинамич. вероятность. Термодинамич. вероятность данного макроскопического состояния полагается равной числу различных возможностей его осуществления. 2) Ур-ие термодинамики, связывающее изменения внутренней энергии и энтропии при обратимом изотермич. процессе:

dS 1 /. _Λ.

<¹⁰)

Термодинамич. величины S, С_р (теплоемкость), Ζ, Ф, U и Я связаны простыми соотношениями с суммой состояний Q:

Ф=R In Q - U₀/T₉z=и₀ - RT in Q,

Н =U + pv=RT* + ϋ₀ + RT, S=RlnQ + RT^®, c — n ^{d d} i" Q

P dT dT—i

(11a)

(lib)

(11c)

(lid)

(lie)

Сумма состояний определяется распределением энергии между различными молекулами. Ее обычно разбивают на два множителя:

<?=<?<·

Qt-

Q_t — сумма, или интеграл, состояний поступательного движения молекул, a Q_{ — сумма внутримолекулярных состояний. Квантовая статистика для Q_t дает следующее выражение:

₀_ψψγι,ν. _{Щ

здесь m — масса молекулы, h — постоянная Планка, V — объём, занимаемый молем газа, и N — число Авогадро. Величина определяется на основании законов распределения энергии между следующими формами энергий молекул:

1) вращательной^, 2) колебательной E_Vi 3) электронной Е_е и наконец зависит от распределения направлений вектора спина ядер в молекулах. В общем случае

Qi=Po+Pi exp (— ·§γ) +. +

+ Л^ехp (- w) + - ’ <¹⁴)

здесь E_l9 ., E_i9 ., — уровни энергии молекул, выраженные как разности между энергией молекулы в известном состоянии и нулевой энергией молекулы; р₁₉ ., .,—соответствующие этим уровням статистич. веса. Необходимые для подсчета величины р и Е получают из анализа молекулярных спектров. Для расчета р необходимо глубокое знание структуры молекулярных термов. В общем случае расчет Q_i сводится к почленному суммированию суммы (14); такого рода подсчет требует весьма много времени. В различных случаях оказывается возможным применение упрощенных приближенных методов расчета. Упрощенные методы основаны на сведении суммы (14) к произведению более простых рядов, которые либо сводятся к конечному выражению либо подсчитываются с применением интегрирования вместо суммирования.

Упрощенные методы определения Qi. Одноатомные молекулы. Сумму состояний одноатомной молекулы можно выразить как произведение сумм состояний электронной энергии (Q.=G_p) и ориентаций спина ядра (Q_s=G_s):

Qi=· G_s. (15)

G_x определяется просто как

O_s — 2 s -f- 1 (16)

(s — спиновое число; вектор спина равен s --),

то есть как число возможных направлений вектора спина в силовом поле.

Значения s для различных атомов следующие:

Элементы	S	Gs
О¹⁸; С¹²; Не..		1
H¹; F¹⁹. ν¹⁴η².	,. 1/₂	2
H¹; F¹⁹. ν¹⁴η².		S
As..	³/2	4

Значение электронной суммы состояний G_e определяется уровнями энергии электронов и их квантовыми чи следующим выражением:

G_e=(2и + 1) + (2/j + 1) exp (- ^-)+. (17)

Двухатомные молекулы. Для большинства изученных молекул в интервале температур до 5 000° К удается получить достаточную точность, приняв независимость друг от друга электронных, ядерных и вращательно колебательных сумм состояний. Тогда

Qi=Q„_r G_e G„ (18)

где Q_v,_r — вращательно-колебательная сумма состояний. В ряде случаев взаимное действие

(12)

колебаний и вращений также невелико, и тогда мы можем принять -

Qi=<?. · Q_r · G* · <?.· (»)

Мы остановимся только на разборе последнего случая. 1) Q_t — колебательная сумма состояния: а) В первом приближении двухатомную молекулу по отношению к колебаниям можно рассматривать как гармония, двухмерный осциллятор. Тогда

Е„=hcoj₀ (* + -f) “ У *«»·. (²⁰)

где ео₀ — характеристич. частота осциллятора в обратных сантиметрах, h — постоянная Планка, с — скорость света и v — колебательное квантовое число, принимающее значения 0, 1, 2,. Для всех уровней статистич. вес р=1. В этом случае согласно (13)

Qv — 2 e~^EvlhT=[i — exp (— )Γ· (21)

б) Более точно будет принять молекулу за ангар-монич. осциллятор. Тогда

Ε_ν=he |ω₀ (ν + у) “ (^ν + τ)^{2 +}

+ 3>₀ (^ν τ) ^ο^ωο ~

- τ *>.]; (22)

Υ₀ — факторы ангармоничности. Для большинства расчетов достаточную точность дает использование одного лишь первого поправочного члена. В этом случае подсчет ведут суммированием или с помощью таблиц, составленных Gordon и Barnes. 2) Q_r—вращательная сумма состояний. В первом приближении, принимая молекулу за твердый ротатор, для величины уровня вращательной энергии находим

Е_г =

8n*J

(/+!)/>

(23)

где J — момент инерции молекулы, a j — квантовое число вращения (могущее принимать любое целое значение, большее 0). а) Для несимметричной молекулы с основным состоянием ^г2 стайгстич. веса равны ру=2 + 1. Для большинства случаев подсчет Q_r м. б. с достаточной точностью выполнен путем интегрирования уравнения (14) после подстановки значений р и Е_г по /:

оо

Qr=2 (2 + 1) exp [- aj (j + 1)]=0

ОО

= J (2j + 1) exp [— aj (j + 1)] dj=o

__ 1 __ 8π2 JkT

σ hP

Где —

__ h2

^σ WJkT *

(24)

б) Для симметричной молекулы в 27-состоянии, атомы которой не обладают спином ядер,- выпадает половина вращательных уровней, вследствие чего приближенное выражение Q_r принимает вид

П _ 8n2JkT Vr=№σ*

(25)

где σ* — 2, т. н. число симметрии, в) Для симметричной молекулы в состоянии ^ΧΣ, атомы которой обладают спином ядра (Н₂, Ν₂ и др.), мы не можем разделить просто сумм состояний Q_rи Q_s. В этом случае молекулы с нечетной суммой состояний Q% могут обладать только нечетными /, а молекулы с четной QI — четными или наоборот. Таким образом например

= 2 (2 + 1) Gf exp [ —or/( + 1)] +

j-0,2,.

ОО

+ 2 (2 + 1) G? exp [ — aj(j + 1)] ., (26)

ΐ=ι,3

где Gf=s (2s + 1) и G%=(s + 1) (2s + 1); инте-грируя это выражение по /, мы получаем приближенно

Qrs=Gs

8π2 JkT

где

№о“ >

G₈= (2s-M)²=G“+G?.

(27)

г) Для молекул в основном состоянии ²П (без исключения состоящих из разных ядер) основной уровень состоит из двух электронных компонент, различающихся на ΔΕ. Молекулы с низшей энергией обладают квантовыми чи вращения=¹/₂, ³/₂, ⁵/₂ и т. д., а находящиеся на уровне ΔΕ могут находиться в состояниях с квантовыми чи=³/₂, ^б/₂. Здесь суммы состояний вращения и электронных неразделимы. Приближенно

Qe,_r=2 (2 + 1) exp [ oi ( + 1)] +

i=Чг, ³lt,.

+ 2 (2 + ¹) exp [— jy — oj ( +1)]. (28) ³li, »/»,.

Здесь, заменяя суммирование интегрированием, находим

Qe>r

8π2 JkT №

[l+exp (-§)]

(29)

Для большинства молекул с Л расщеплением (Л-дублеты) вращательных уровней ур-ие (29) при высокой t° (выше комнатной) переходит в

О ^ 9 —=2 -^^л2^^т.

3) Сумма состояний спина ядер, а) Для молекул с двумя одинаковыми атомами образуются два вида молекул (аналогично орто- и параводороду) с симметричной и антисимметричной ф-ией спина G_s (см.- случай 2в). б) Для молекулы, состоящей из атомов с различными спинами ядер *1 ^{и 5}2>

G_s=(2s, + 1)(2*_а + 1). (30Х

4) Электронная сумма состояний. В большинстве случаев высшие уровни электронной энергии возбуждаются только при очень высоких температурах, поэтому для расчета равновесия их не приходится принимать во внимание. При-ходится считаться только с расщеплением низшего электронного уровня, к-рое имеет место для ряда молекул. Значение G_e (мультиплетность нулевого электронного уровня) для ряда молекул видно из следующего:

Молекулы. СО CN 0₂, NH N0. ОН,

СН, SiH

Уровень----1£ 3Σ 2 п

G_e.1 2 3 2

В этом случае G_e=pi=целому числу, указывающему мультиплетность уровня; при значительных расщеплениях (ΔΕ велико), как при Л расщеплении ²П уровня, приходится при невысоких темп-pax учитывать это расщепление более точно. В общем виде приближенное значение суммы состояний внутренних степеней свободы двухатомной молекулы м. б. выражено следующей ф-лой

Qi=Qr Qv ^Ge * =

“^ [⁴ - ^exP (·- tf)]. <³¹>

справедливой приближенно для всех приведенных случаев.

Многоатомные молекулы. Для приближенного расчета, дающего в большинстве случаев достаточную точность, мы можем считать независимыми внутренние степени свободы и общую сумму состояний (ф-ию распределения) определять как произведение ряда отдельных ф-ий распределения.

Ф-ия электронной энергии G_ei так же как и для двухатомных молекул, для темп-p от 300° К до 5 000° К выразится целым числом, указывающим мультиплетность низшего электронного уровня.

Ф-ия спина G_s м. б. с достаточной точностью выражена ур-ием

G₈=(2_Sl + l)(2s_a + I).··, (32)

где s_lf s₂ — спиновые числа отдельных ядер.

Функция Q_v колебательных уровней в первом приближении4,достаточно точно м. б. найдена на основу предположения, что молекула состоит из I независимых гармоничных осцилляторов. Для каждого из осцилляторов ф-ия распределения определится согласно ур-ию (21), и общая ф-ия распределения будет равна

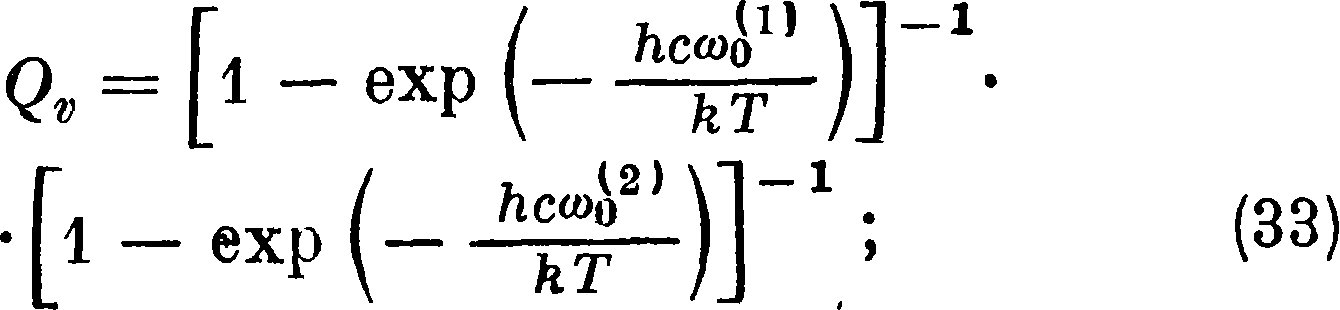
здесь ω₀^α ω₀^ί8) — характеристич. частоты различных колебаний молекулы. Число колебаний Молекулы определяется для прямолинейной молекулы (С0₂, Ν₂0, С₂Н₂) как

= Зп —5, (34)

а для молекул более сложной формы — как

= 3п—б, (35)

где п — число атомов в молекуле. Для молекул, в которых различные части могут совершать свободные вращательные движения (С₂Н₆ и др.), число колебаний меньше на число типов возможных внутримолекулярных вращений. Более точный подсчет требует учета ангармоничности колебаний и взаимного влияния одних колебаний на другие и представляется очень сложной задачей, в каждом отдельном случае являющейся предме том специального исследования.

Функция состояний вращательных уровней Q_r. Для приближенного расчета можно применить следующие выражения: 1) для линейных молекул (С₂Н₄, С₂Н₂, Н₂0₂ и др.) приближенное выражение, определяющее Q_rt тождественно таковому для двухатомных молекул:

г ^ Sn^JkT /ОА

(36)

2) Молекулы формы простой пирамиды или бипирамиды можно рассматривать как симметричный волчок. Для таких молекул (NH₃, NG1₃, НСС1₃ и др.), обладающих тремя моментами инерции, два из которых равны между собой (Jj), справедливо приближенное равенство

_п _ ieVTnVtj_AV7_B(hT)^a!* ₍₃₇₎

"r — h&o* * ^{1 У}

и др.), могут рассматриваться как шаровые волчки. Для них приближенно

16 YTnVt j³/2(feT)³/a

Vr=№_σ* · що;

4) Для несимметричных молекул, обладающих тремя неравными моментами «инерции,

^ _16 1^2"пУ2 УТШГс (feT)³/2

™ — ЬЗо“

5) В случае молекулы типа этана — симметричной бипирамиды, обладающей свободным вращением группы СН₃ вокруг одной оси симметрии, мы имеем молекулу с четырьмя моментами инерции (попарно равными). Здесь

<?_ras

64ПЬ (ftг)2 J_A - J_B

h*a* (³⁹)

В случаях 2, 3, 4, 5 число симметрии σ* зависит от строения молекулы. Оно определяется числом возможных пространственных совмещений молекулы (в предположении тождественности атомов одного и того же элемента).

Учет взаимного влияния энергетич. уровней друг на друга очень сложен. Современные методы анализа спектров не позволяют его провести однозначно. Более точное решение вопроса о подсчете Q_г· и тем самым термодинамич. ф-ий для многоатомных молекул в настоящее время возможно только для очень незначительного числа примеров (Н₂0, С0₂). Ниже приведены развернутые приближенные выражения термодинамич. функций для ряда частных примеров. Ф-ии даны для газов в идеальном состоянии (подчиняющихся закону ρν — nRT при р == 1* atm).

Одноатомные газы:

Ф=-=-|Л1пГ + -|-Л1пМ +

+ Л1пб₍. в, — 7,267,

5=4^1n7^, + -i-RlnM+_JRln G_eG_s -

- 2,999 + RT

d In G_edT

RT + RT²

d In G_e

^{: E}° 2 “ dT

r* ^ 7? jjd/dln G_e

^CP ~ 2 ^R ^ dT di/T ) * Двухатомные газы и газы с молекулами в форме палочки:

Ф’=-I R In Т + — R In М + R In +

+ Д In <?, + 168,42,

G_SJ

S=1 R nT + -| R nM + Д In -ί^_— + R In <?„ + RT^d-^§+ 175,38.

Нелинейные инерции:

моментами молекулы с тремя

Ф’=4Д In Т + R In М + у R In J_AJ_BJ_C + + R In ^Qv--?i ^Gs + 257,40,

S=4Λ In T + -f- R In M + 4 R In J_A · J_B J_c +

+ Д1п

Ge · Gs

+ RT

din Q₀ · dT

¹ + 265,35.

Молекулы типа этана:

Ф’=R In T + A R In Μ + R In J_A · J_B

Ge *

+ 346,38,

S=Φ’ 4- 8,94 -f RT-

3) Молекулы, обладающие тремя равными моментами инерции (тетраэдрические СН₄, СС1₄

Приведенные ур-ия позволяют на основании полностью расшифрованных молекулярных спектров получить достаточно точные данные для энтр, теплоемкостей и термодинамич. потенциалов. Все величины, полученные этим путем, рассчитываются, как легко видеть, без учета взаимодействия между молекулами. Поэтому найденные величины относятся к идеальному газу, подчиняющемуся закону pv — nRT. В случае если в условиях, для которых производится расчет, изучаемые газы не подчиняются с желаемой точностью идеальным законам, необходимо ввести поправки на отступления от законов идеальных газов. Эти поправки получают интегрированием термодинамич. ур-ий

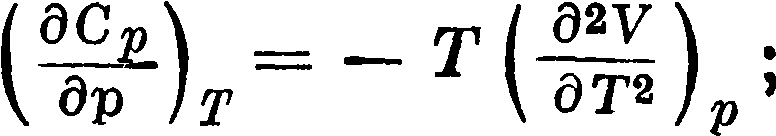
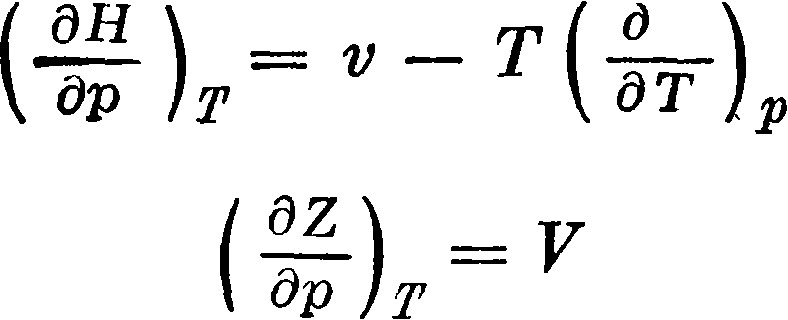
по р от 1 atm до 0, по ур-ию pV=RT и от 0 до 1 aim по ур-ию состояния соответствующего газа. Обычно с помощью найденных величин S,

Ф=— ^Ζ ~_τ~ и АН, относящихся к газу в иде альном газовом состоянии, рассчитывают значения констант равновесия, а поправки на уклонения от идеальных газов вносят уже при расчете равновесных концентраций.

Лит.: У л и х Г., Химическая термодинамика, пер. с нем., Л., 1933; Алексеев Д., Физическая химия, -т. 1, Л., 1934; Lewis G., Randall М., Thermodynamics, N. Y., 1923; Parks C., Huffman H., The Free Energies of Some Organic Compounds, N. Y., 1932; •Фрост, Расчет равновесий газовых реакпий, «Успехи химии», 1933, т. 2, стр. 445—474; G i a u q и e W., «Journal of the American Chemical Society», Wsh., 1930, v. 52, p. 4808 (Вычисление свободной энергии из спектроскопических данных); Z e i s e H., «Ztschr. fur Elek-trochemie», Lpz., 1933, В. 39, p. 758—773 u. 895—909, В. 40, p. 662—669 u. 885—890 (Спектроскопия и термодинамика); Clusius К., ibid., 1934, В. 40, p. 98— 101 (Замечания по поводу реферата Цейзе); Gordon A., Barnes К., Evaluation of the Series which Arise in the Calculation of Thermodynamic Quantities from Spectroskopic Data, «Journ. Chemical Physics», 1933, v. 1, p. 297—307; Vi liars O., «Chemical Reviews», Baltimore, 1932, v. 11, p. 369—436 (Уровни энергии и статистические веса многоатомных молекул). А. Фрост.