> Техника, страница 76 > Разряд электрический

Разряд электрический

Разряд электрический, процесс прохождения тока через газовые, жидкие и твердые диэлектрики и их пробой (смотрите). Все явления электрич. разряда разбиваются на две области: несамостоятельного и самостоятельного разряда. Первая из них характеризуется тем, что носители тока (ионы и электроны) образуются в среде вследствие внешних причин (фотоэффектом, процессами тепловой диссоциации в твердых и жидких диэлектриках, ионизации γ- и α-лучами в газах). Вторая—характеризуется образованием носителей тока под действием приложенного электрического поля. В дальнейшем речь будет идти только о газовом разряде в самостоятельной области (о разряде в твердых и жидких средах см. Диэлектрики). Переход к самостоятельному разряду в случае всех газов и независимо от давления проявляется в виде сильного возрастания тока при неизменном напряжении на электродах. Это возрастание объясняется резким увеличением числа электронов и ионов в результате ударной ионизации в среде. Молекулы газа характеризуются со стороны прочности связей электронов в них значением ионизационной энергии, той энергии, которую необходимо затратить для отрывания о г молекул одного из электронов. Под действием приложенного электрического поля первоначальные электроны газа ускоряются и, пройдя нек-рый путь, накапливают энергию, равную ионизационной. При столкновении таких электронов с молекулами газа последняя теряет электрон, в газе образуются новые добавочные носители тока. В виду того, что последние в свою очередь вызывают ионизацию, число ионов в газе резко возрастает: он становится проводником электричества. Может случиться, что при столкновении с молекулой электрон еще не накопит ионизационной энергии, но будет двигаться уже достаточно быстро. В этом случае ионизации не произойдет, но расположение электронов в молекуле все же изменится; при восстановлении нормального расположения молекула будет излучать свет. Эти соображения позволяют понять наличие свечения в самостоятельном разряде.

Развитые выше соображения позволяют легко ориентироваться в многообразии форм самостоятельного Р. э. В основном нужно различать три такие формы: 1) Тоунсенд-разряд,

2) тлеющий разряд (смотрите Гейслера трубка),

3) дуговой разряд (смотрите Дуговая лампа), В первой из этих форм поле мало искажается развивающейся в газе ударной иопизаци и (с.м.), во втором и третьем случаях, наоборот, это искажение очень велико; отличие же дугового Р. э. от тлеющего сводится к высокой (порядка нескольких тысяч градусов) температуре катода в дуге. Искажение поля связано с движением больших масс ионов (продуктов ионизации) и образованием вдоль пути Р. э. объёмиыт зарядов (смотрите). Так как объёмные заряды образуются очень быстро вслед за ионизацией, устойчивы лишь тлеющий и дуго-

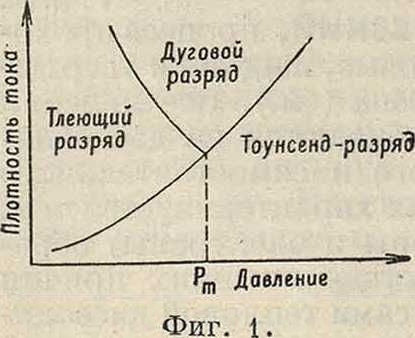
вой Р. э. Тоунсенд-форма только предшествует каждому из них, но не может длительное время существовать в газе. На фигуре 1 приведена диаграмма областей существования различных форм разряда по Зеелигеру. Координатами выбраны сила тока и давление газа. Из диаграммы видно, что при больших давлениях Тоунсенд-разряд переходит в дугу, причем этот переход определяет-. ся плотностью протекающего через газ тока; чем выше давление,тем при большей плотности тока возможно возникновение дуги. Если мощность источника ограничена и дуга возникнуть не может, в газе периодически загорается и тухнет Тоунсенд-разряд (в форме искры). Начиная с давления Р_т, возможно уже существование всех трех форм электрического разряда. Как видно из диаграммы на фигуре 1, возникновение дуги при этом давлении возможно при минимальной плотности тока; понижение, равно как и увеличение давления, требует для зажигания дуги больших токов.

Тоунсенд-разряд Г¹]. Свечение при Тоунсенд-разряде должно было бы быть одинаковым вдоль всего пути, но в такой простой форме явление наблюдается только в совершенно однородном поле. Большую сложность наблюдающегося на опыте Тоунсенд-разряда следует отнести именно к неоднородности поля между обычно употребляющимися в практике электродами. Только в тех случаях, когда расстояние между электродами мало по сравнению с их кривизной, разряд остается одинаковым вдоль всего пути. В случае наир, шаровых электродов и небольших расстояний менаду ними, газ остается непроводящим вплоть до тех пор, пока разность потенциалов не достигает нек-рого значения Е„ (начальный потенциал), при котором между шарами проскакивает искра. Явление протекает также и при увеличении расстояния d, но лишь до некоторого критич. значения d₀; последнее зависит от диаметра!)

шаров и связано с ним соотношением ~==5,5, если оба шара симметрично заряжены по отношению· к земле. При бблыдих расстояниях, чем d₀, поле уже становится заметно неоднородным, и при увеличении разности потенциалов при Е₀ свечение появляется только у поверхности шаров; здесь градиент поля выше, чем в окружающей среде, и в газе появляется местная ионизация. Это значение потенциала называется начальным. Далее, при повышении разности потенциалов, при значении Е_к (потенциал кистевого раз-• ряда) появляется Р. э. в виде кистей, к-рый затем уже при искровом потенциале Е_и переходит в искру. Между расстоянием d₀ и Zd₀ лежит переходная область; искровое напряжение здесь неопределенно, и искра может проскочить в газе при любых значениях, лежащих в заштрихованной области фигура 2, где графически представлена зависимость Е₀, Е_к и Е_и от расстояния d менаду шарами. Аналогичные соотношения получаются для двух цилиндрич. электродов и в других случаях неоднородного поля. Исследования Кауфмана позволили определить электрическое сопротивление искры. Под этим следует понимать такое омич, сопротивление, что при замене им искрового промежутка количество теплоты, выделяемое в этом сопротивлении, будет тем же, что и в искре. В виду того,

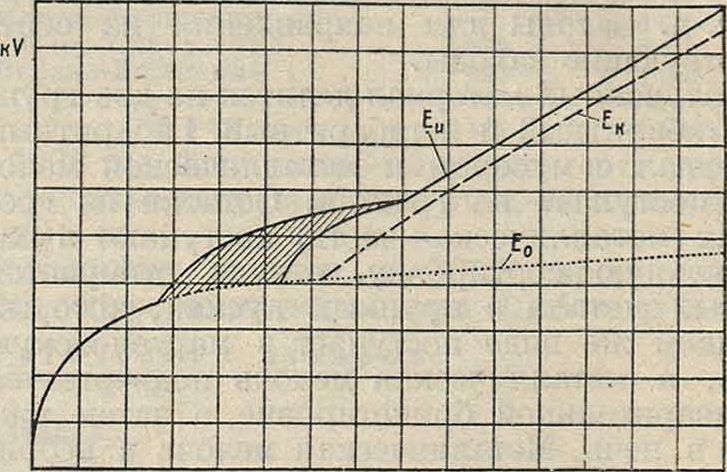
Фигура 2.

что количество теплоты, выделяющейся в искре, пропорционально третьей степени приложенной разности потенциалов, электрическое сопротивление ее оказывается величиной переменной. Оно зависит от приложенной разности потенциалов, емкости системы и сопротивления подводящих к электродам ток проводов. В табл. 1 приведены значения этого сопротивления г_и при разных значениях искрового потенциала Е„ и двух сопротивлениях подводящих проводов R.

Таблица 1 .—3 н а ч е н п я г„ в а.

Дня Ен в kV	При #i=0,85 2	При 1?2=М S
6,9	0,022	0.046
9,1	0,034	0,062
15,6	0,043	0,078

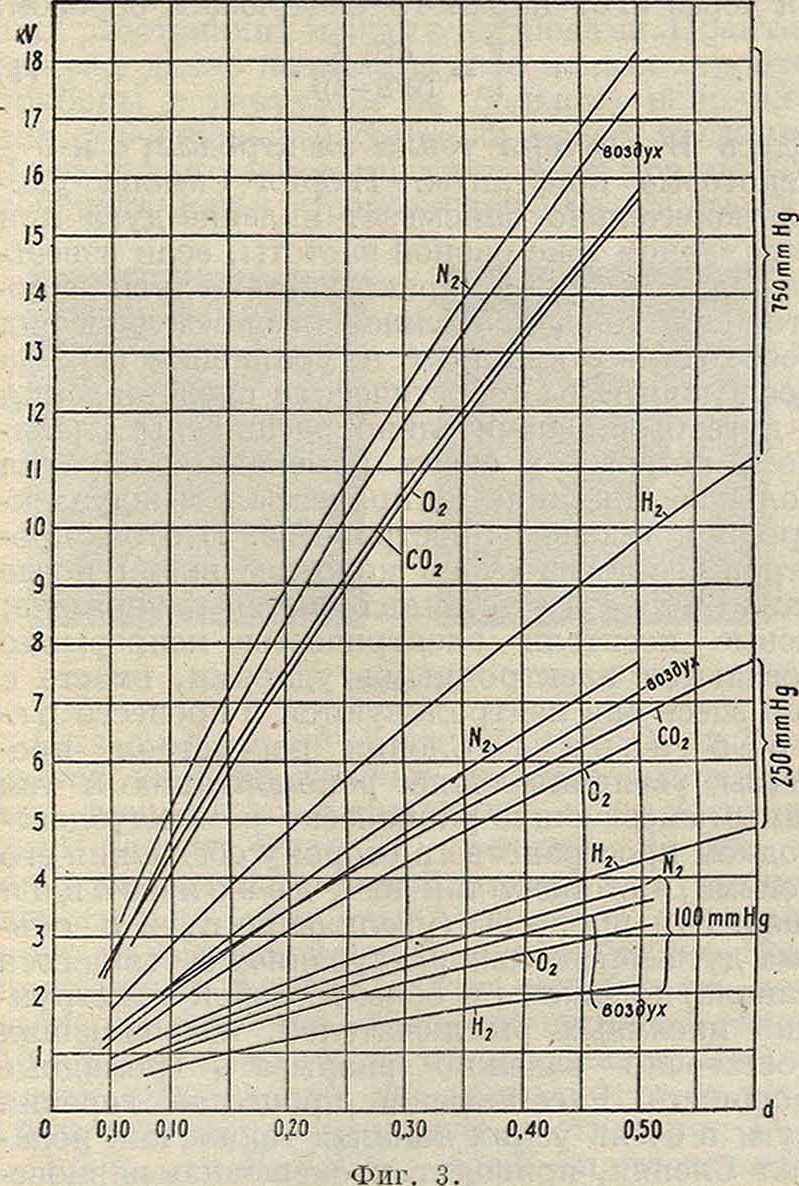
Начальные и искровые напряжения меняются в зависимости от природы и давления газа. По отношению к последней зависимости Па-шеном был установлен закон, по которому Е_и является однозначной функцией произведения pd. Так как в общем случае уменьшается при изменении расстояния а менаду электродами, оно будет уменьшаться и при понижении давления р. На фигуре 3 даны значения Е_и для разных газов в зависимости от расстояния d между шарами (в см) при давлении в 750, 250 и 100 миллиметров ртутного столба.

Целый ряд исследований показал, что сжатые газы, следуя в больших пределах закону Пашена, обладают чрезвычайно большим сопротивлением пробою. Так например, воздух, при нормальном давлении имеющий прочность -30 kV/еж,при увеличении давления до 10atm упрочняется в 10 раз; пробивное напряжение его оказывается равным 300 kV/еж; при 15 atm эта величина уже достигает 450 kV/сж и т. д. Бути предложил след, формулу зависимости от давления для областей с давлением >1 atm:

гг „, afe

V=ара + —;

здесь а и &—константы, d—расстояние между электродами. С количественной стороны Тоунсенд-разряд в основном подчиняется теории Тоунсенда, на случай неоднородного поля подробно развитой Шуманом. Для силы тока 1

при ударной ионизации Тоунсенд дает ф-лу:

1=пе

(,_αχ-β_χ)^^αχ-^βχ)ά

α_χ-β_χβ^(αχ~^βχ)ί

где п—число пар электронов и ионов, созданных внешним ионизатором, е—элементарный заряд, равный 4,77 · 10¹⁰ CGSE, d—расстояние между электродами, а_х и β_χ— коэф-ты, равные числу ионов, к-рое при силе поля х образуется в газе при ионизации одним электроном (а_х) и положительным ионом (β_χ) на 1 ом пути. При расстоянии d между электродами пробой наступает в том случае, если а_х= β_χβ^(α*-^βχ^)ά,

так как 1 здесь обращается в бесконечность. Функциональные зависимости а_х и β_χ от силы поля, а также и других условий не могут быть выведены теоретически при настоящем

состоянии науки и задаются графически па основании специальных измерений при не особенно высоких давлениях. В последнее время теория Тоунсенда встретила ряд возражений со стороны немецких ученых в связи с большими затруднениями объяснения пробоя при ударных напряжениях. Опыт показывает, что при импульсах длительностью КГ⁶ ск. пробой происходит при тех же напряжениях, как и в случае постоянного напряжения. Из этого следует, что процесс нарастания ударной ионизации должен успеть завершиться за 10"^в ск. Может быть доказано, что это требование находится в противоречии с теорией Тоунсенда. Роговский, обративший внимание на эти затруднения, дал новую теорию

* В формуле через одну и ту же букву е обозначены заряд электрона и основание натуральных логарифмов. явления, которая однако даже после очень инте-ресных изысканий Франка и Хиппеля не дает количественных закономерностей устойчивого характера.

Еще более неопределенно теоретическое состояние вопроса при Тоунсенд-разряде в неоднократном поле в условиях частичного разряда, при так называемой короне. Исследования показали, что радиус короны а (то есть радиус чехла, охватывающего например цилиндрический проводник) растет пропорционально разности между приложенным Е и начальным Е₀ потенциалом, при котором возникает разряд:

α= г₀ β (Е — В₀);

здесь г„ —радиус проводника, β—константа. Исходя из этих предположений, можно найти следующее теоретическое выражение для силы тока через цилиндрический конденсатор с радиусами обкладок R и г₀ для напряжения постоянного тока:

2kE (E — Eq).

i?² In — го здесь Jc—подвижность иона того знака, которым заряжена обкладка с меньшим радиусом. Эта формула хорошо объясняет тот факт, что во влажном воздухе ток утечки в короне сильно уменьшается, что очевидно связано с убыванием подвижности во влажном воздухе. Для короны переменного тока все явления протекают очень сложным образом; теоретическому разбору их посвящено несколько работ Хольма. Для величины энергии, которая затрачивается в короне, Хольм дает следующее выражение в случае двух параллельно натянутых проводников:

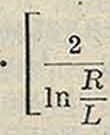
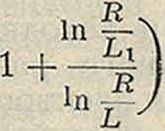
i

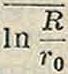
kW/ки,

где

L=In - · 42,3 f 1 + --di kV;

*« V V r₀l

1?=0,85 · 10^s cos 0,3 a ·. JL см-2;

V;=V- ( l

In

1

я/3,

2a β cos 0,3a

¥

cosa ,8=2,12; /?!= 1,63; /—частота;

^афф.

R и r₀—радиусы проводников в см. Эта формула дает очень хорошее согласие с опытом. Худшее соответствие с опытом дает эмпирическая формула для потерь на корону при переменном напряжении, хорошо известная в технике формула Пика; в данном случае она представляется соотношением (W в kW/тш):

W =

1,22 103

(/-

• 25) ]

Го+р +0,04

(Е_афф, — E,)²

где все обозначения те же, что и в ф-лах Хольма. Аналогичные соотношения даны Хольмом для трех одинаковых цилиндрических проводников, расположенных по вершинам равностороннего треугольника, в случае трехфазного переменного тока; им же разобраны и некоторые другие расположения.

Тлеющий и дуговой разряд [*]. Эти формы 1азового разряда являются стационарными, ток может длительное время проходить через газ, не меняя своего значения. Нетрудно сформулировать требования стационарности разряда. Около поверхности отрицательного электрода (катода) ионизации нет, т. к. агенты ионизации—электроны—именно отсюда начинают двигаться и способны достигнуть ионизационной энергии, только пройдя "нек-рое расстояние d. В области от катода до этого d газ остается так. обр. непроводником. В первые моменты по наложении напряжения ток может проходить через газ емкостным образом в непроводящем слое и путем переноса зарядов в остальной части междуэлектродного пространства; длительное же существование разряда возможно очевидно только при наличии переноса зарядов также и в непроводящем слое. Было показано, что источником носителей тока в этом слое являются электроны, сорванные с катода. Процесс развивается след, образом: при включении напряжения равномерное распределение потенциала между электродами быстро искажается таким образом, что у катода образуется большое падение на непроводящем слое. Положительные ионы разгоняются в этом слое и, попадая на поверхность катода, вырывают оттуда электроны. В виду того что этот акт сильно зависит от металла катода, характеристики тлеющего разряда определяются не одним только газом, как в Тоунсенд-фэрме, но и материалом катода. Замечательной особенностью тлеющего разряда является постоянство катодного падения потенциала в очень значительных пределах изменения, приложенного извне к трубке. Сила тока через газ при тлеющем разряде может быть представлена соотношением

, V-Vtr

1=- -_R - ; V и V_K — соответственно -приложенный потенциал и катодное падение, R— сопротивление газового разряда. Чем легче теряет катод свои электроны, тем меньшая необходима энергия ударяющих в него ионов для того, чтобы обеспечить хорошую проводимость прикатодного слоя, т. ё. тем меньше катодное падение. В табл. 2 приведены значения V„ в зависимости от металла катода и природы газа. Со стороны физики явление влияния газа сводится к различию в природе рдирующих ионов.

Таблица 2,—Значения V* я вольтах.

Металл	Воздух	н2	N„	Не	А
К.	_	94	170	64	64
Си.	252	214	208	177	131
Ag.	279	247	233	162	132
Pt.	277	276	216	160	132
AI.	229	171	179	141	100
Ре.	269	198	215	160	131

Дуговой разряд по существу повторяет все характеристики тлеющего, но только катодное падение здесь оказывается очень малым. При больших плотностях тока, которые характерны для этой формы, происходит сильное нагревание катода; последний по этой причине дает интенсивное электронное излучение, которое обеспечивает хорошую электропроводность прикатодного слоя. В отличие от тлеющего разряда, где V_K достигает всегда многих десятков, а иногда и сотен V, при дуговом разряде оно не превосходит обычно 2—3 V, и таким образом дуга может существовать при значительно меньших разностях потенциалов, чем тлеющий разряд.

Теоретические представления о дуговом разряде не дают еще в данный момент законченной теории этого явления. До самого последнего времени интерес исследователей был направлен гл. обр. на процессы у электродов, учет теплового баланса которых в основном определяет электронное излучение и всю характеристику дуги. На этой почве развилась известная теория Сныона; если считать темп-ру катода равной Т, а площадь раскаленного пятна F, то произведение этих двух величин S=FT является по Симону основным параметром дуги. Ур-ие, связывающее разность потенциалов V на электродах дуги с силой протекающего через нее тока г, выражается через этот параметр следующим образом:

IV a‘WS _m

i ⁼ |(1VS— 6)2 *

Здесь W—потеря тепла электродом, а и Ь— некоторые константы. Теория Симона удовлетворительно описывает явление дуги при переменном токе разной частоты, если известна вольт-амперная характеристика дуги на постоянном токе, позволяющая определить ряд необходимых констант в уравнении (1). За последние годы теоретические представления о дуге были значительно расширены Слепя-ном, который в своих изысканиях обратил большое внимание на процессы в междуэлек-тродном газовом пространстве. В этом пространстве через очень короткое время после зажигания дуги устанавливается равновесие; новые носители электричества непрерывно создаются электронными ударами, вместе с тем здесь они нейтрализуются в процессе р е-комбинации; Слепян рассмотрел процессы, увеличивающие рекомбинацию и тем самым смещающие равновесие в междуэлект-родном пространстве в сторону обеднения его ионами, в сторону так называемым деионизации газа. Эти процессы (увеличение пути и объёма дуги магнитным раздуванием светящегося канала) положены в основу особой конструкции масляных выключателей, позволяющих достаточно надежно разрывать громадные мощности. Рассмотрение процессов горения дуги в очень узких каналах также, как показал Слепян, приводит к смещению равновесия и к совершенно особой вольт-амперной характеристике дугового разряда; эти исследования привели к новой системе защитных коронных разрядников, которые в последнее время приобрели большое значение в американской высоковольтной технике.

Разряд в вакууме. Теоретически легко показать, что разряд в вакууме может происходить только путем вырывания электронов из металла силами электрического поля. Потребный для этого градиент будет порядка ΙΟ⁸ Y/см. На практике же, где идеальный вакуум не достигается, процесс идет по совершенно отличному от предсказываемого теоретически пути. Так как такой разряд очень своеобразен, то его молено условно назвать разрядом в вакууме. В пространство между электродами иногда влетает ион, где-нибудь случайно образовавшийся в трубке. Под действием приложенной разности потенциалов этот ион, двигаясь между электродами и не встречая нигде на своем пути препятствий (в виде столкновения с газовыми молекулами), развивает колоссальную скорость. При ударе об электрод ион дает-сильное местное нагревание, из металла выделяется окклюдированный в нем газ, давление в приборе повышается, и далее процесс идет так же, как и в уже описанных нами случаях. Энергия свободно движущегося в вакууме иона по основным уравнениям механики определяется соотношением=eV и задается приложен-

а ной разностью потенциалов I—-кинетич. энергия). Так как величинойэнергии будет обусловлен нагрев электрода, то очевидно, что независимо от расстояния между вводами в трубке пробой будет происходить при одной и той же разности потенциалов. Вакуум оказывается более прочным при небольших расстояниях; между электродами. Практика уже давно подметила, что нельзя строить приборы с вакуумом на большие напряжения, увеличивая" расстояние между вводами. Предельная разность потенциалов при любых конструкциях не превосходит 300—350 тыс. V.

Фигура 4.

Скользящий разряд" [⁸]. Он наблюдается на поверхностях твердых диэлектриков, лучше всего в том случае, когда электродами служат острие и пластина. На фигуре 4 представлен скользящий разряд в случае положительно (а) и отрицательно (б) заряженного но отношению к пластине острия. Разница получающейся фигуры тем больше, чем выше напряжение, и для напряжений выше 10 kV линейно зависит от последнего. По Тендеру справедливо, вне зависимости от толщины твердого диэлектрика, соотношение V==11,5Л_отр. и F=5,9 Кпол., где V—приложенная разность потенциалов, a R_omp. и R_mJl.—соответственно радиусы отрицательной и положительной фигуры. Эта формула верна только при сравнительно больших длительностях приложения напряжения, бблыиих, нежели 10~⁷ск. Для меньших промежутков времени радиусы получаются меньшими,чем вычисленные по ф-лам Теллера. Последнее обстоятельство связано с тем, что скорость распространения фигур относительно невелика и при атмосферном давлении достигает 2-ЬЗ -10⁷ см/гк. При уменьшении давления и остальных неизменных условиях разница фигур возрастает. Согласно Микола это возрастание задается

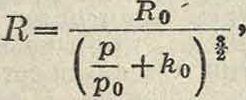
где fc₀—постоянная. Наконец определенным образом меняются данные для скользящего разряда при изменении твердого диэлектрика. Было установлено, что R ε=Const; здесь R—радиус фигуры, ε—диэлектрическая постоянная изолирующей прослойки. В силу этого соотношения на кристаллических пластинках получаются уже не круговые, а эл-липтич. фигуры. Очевидно все особенности скользящего разряда связаны не с принципиально новыми соотношениями в механизме явления, а только со специфич. особенностями строения поля.

Лит.: 1) Schumann W. О., Durchbruchfeld-stdrke von Gasen, Berlin, 1923; Rogowsky W., «Ат-chiv fiir Elektrotechnik», Berlin, 1926, B. 16, p. 496; 1928, B. 20, p-. 99 u. 625: Hippelu. Franck, «Zeil-scluift liir Physik», Berlin, 193U, B. 57, p. 696; 2) See-liger R., Einfiilirung In die Physik der Gasentla-dungen, Leipzig, 1927; з) Przi bram It., Die elektri-sche Figuren, Handb. der Physik, hrsg. v. H. Geiger u. It. Scheel, B. 14, p. 391—404, B., 1927.—Б p а г и н С. М., Вальтер А. Ф. иСеменовН. Н., Теория и практика пробоя диэлектриков, Москва — Ленинград, 1929. И. Курчатов.