> Техника, страница 76 > Рассеяние света

Рассеяние света

Рассеяние света, нарушение правильности светового потока при прохождении через материальную среду. Параллельный пучок света (плоская волна), входя в материальную среду, частично уклоняется во все стороны. Явление отчетливо заметно в так называемым мутных средах, то есть средах, плотность которых меняется от участка к участку. Примером мутной среды может служить туман (мелкие капли воды в воздухе) или различные взвеси (твердые частицы в жидкости или газе) или эмульсии (капельки жидкости в жидкости).

1. Явление Тиндаля. Если размеры частиц, нарушающих однородность среды, малы сравнительно с длиной волны падающего света, то законы рассеяния просты и не зависят от размера и формы частиц (Тиндаль, 1868 г.). Теория явления, предложенная Ре-- леем (1871 г., с электромагнитной точки зрения—1897 г.), сводится к следующему. Под действием электрического поля световой волны E sin 2πνί (ν—частота света) частицы приобретают электрический момент, величина которого зависит от поля волны, диэлектрич. постоянной среды е₀ и частицы в:

f=VE sin Ζπνΐ, (1)

где V—объём частицы.

Т. к. зависит от времени, то частица представляет собой электромагнитный осциллятор и излучает (во все стороны) электромагнитные волны. Складываясь между собой, эти волны и дают рассеянный свет. Интенсивность излучаемых осциллятором волн пропорциональна квадрату второй производной элек-

л ^с4

трич. момента, то есть пропорциональна ^=если с—скорость света, Я—длина волны. Итак, интенсивность излучаемого света обратно пропорциональна четвертой степени длины волны, чем и объясняется голубой тон рассеянно-• го света. Предполагая, что расстояние между частицами сравнимо с длиной световой волны, а сами частицы значительно меньше длины волны, получим, что начальные фазы колебаний отдельных частиц будут иметь всевозможные значения и изучения отдельных частиц некогерентны между собой. Т. о. общее излучение, рассеиваемое средой, получается как сумма излучений, даваемых отдельными частицами. Расчет Релея показывает, что интенсивность света, рассеиваемого под углом Θ к первоначальному пучку, пропорциональна 1 +cos² Θ, то есть распределяется симметрично относительно первоначального направления (симметричная полярная диаграмма, фигура 1). Если первичный пучок естественного (неполя-ризованного) света идет вдоль оси X, то электрич. поле световой волны лежит в плоскости ΥΖ; в этой же плоскости располагается и электрич. момент частиц, если они изотропны, то есть не обладают никакой асимметрией свойств в зависимости от направления. Поэтому в световой вол- г не, испускаемой частицами в направлении

&

Фигура 1.

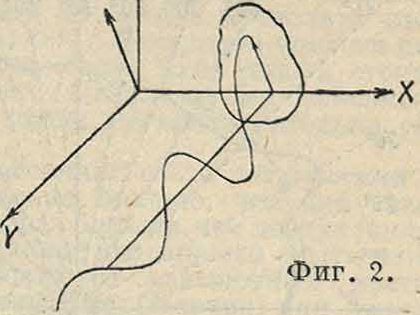
оси Υ, электрич. поле должен быть направлено вдоль Ζ, то есть рассеянный свет, наблюдаемый под углом Θ=”,

должен быть нацело поляризован в плоскости ХГ (фигура 2). Все три вывода Релея (~ -закон, симметрия и поляризация) подтверждаются в наблюдениях над явлением Тиндаля.

2. Я в л е н и е М и. Если рассеивающие частицы сравнимы с длиной световой волны, то теория становится сложнее и сводится к разбору диффракционных явлений на частицах (Ми, 1908 г.; Ганс, 1912 г.; Блюмер, 1925 г.). Результаты зависят от величины и формы частиц. С увеличением размеров частиц полярная диаграмма, изображенная на фигуре 1, теряет свою симметрию (эффект Ми) и может давать ряд вторичных максимумов (фигура 3 и 4). Вид диаграммы определяется размером частиц, их формой и диэлектрической постоянной вещества частицы и среды. Если частицы

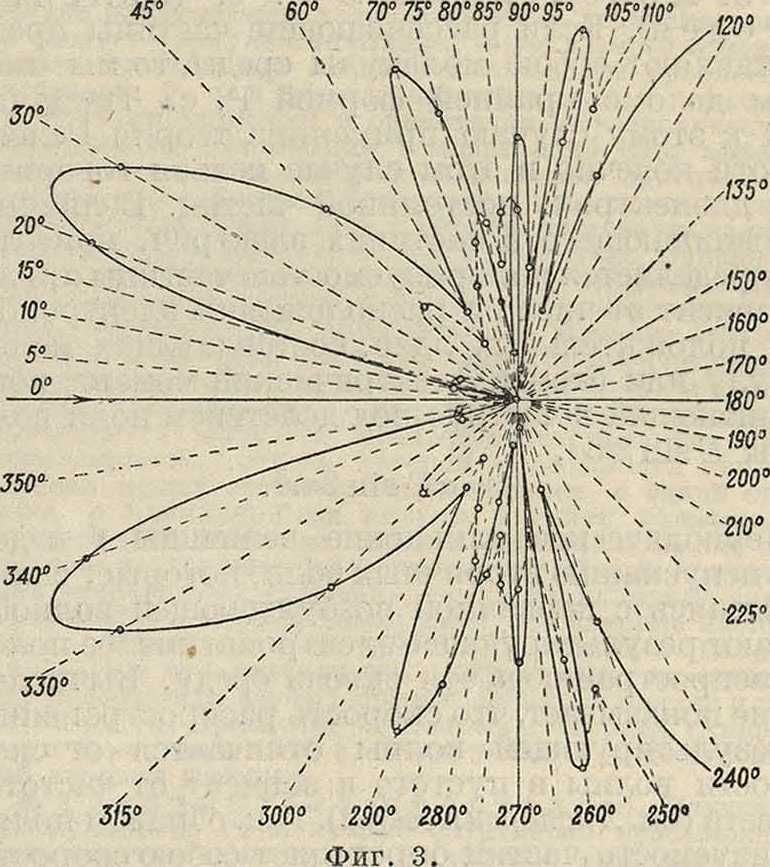
одного размера (центрифугированы), то по виду диаграммы можно сделать некоторые заключения о размерах и форме частиц. Степень λ в законе Р. с. понижается по мере увеличения размеров частиц (рассеянный свет становится белесоватым). Если форма частиц отступает от сферической, то рассеянный свет становится частично деполяризованным и притом тем значительнее, чем более вытянуты частицы. Т.к. деполяризация может вызываться большими концентрациями частиц (влияние электрич. моментов, наведенных в соседних частицах, друг на друга), то заключения

т. э. m. XIX.

о форме частиц по деполяризации можно делать только из наблюдений над слабыми растворами (Ганс, 1920 г.). Выводы теории Ми и других также хорошо подтверждены на опыте. Наблюдение над интенсивностью и поляризацией света, рассеянного такими мутными

45’ 60’ 70° SO’ 90’ 100’ 110’ 100’ 135’

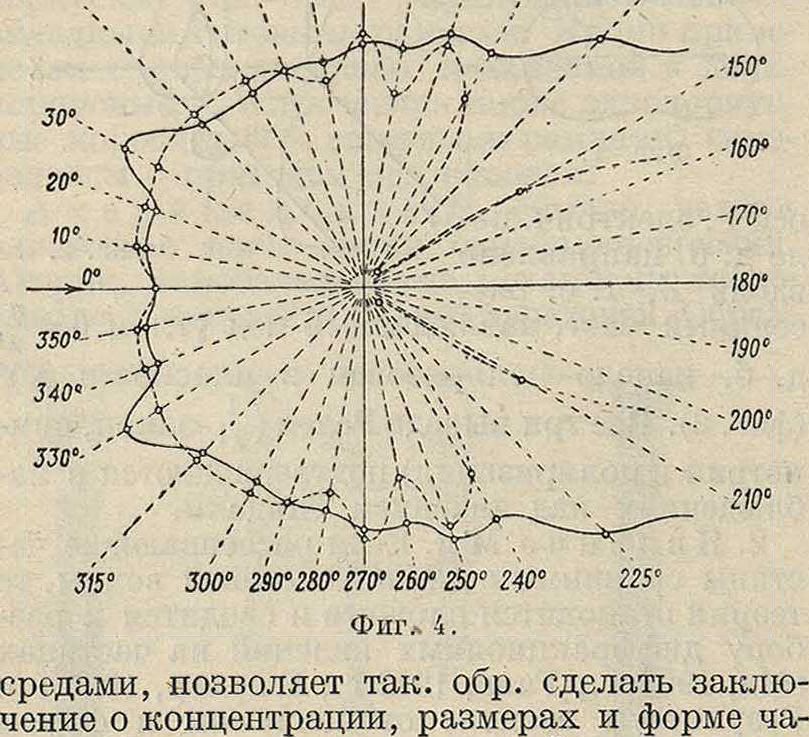
стиц. На этом основано устройство мутно-меров (тиндалеметров или нефелометров), находящих себе применение в геофизике, коллоидной химии, биологии ит. д. (смотрите Нефелометрия). Р. с. частицами, взвешенными в воде, играет известную роль в определении цвета моря и озер (Раман, 1922 г.; Шулейкин, 1923 г.).

3. Молекулярное Р. с. (явление Ре лея). Если рассеивающие частицы представляют собою молекулы среды, то мы имеем дело с крайней формой Р. с. Тиндаля. И к этому случаю применима теория Редея, хотя конечно в этом случае нельзя говорить о диэлектрич. постоянной частиц. Величина возникающего в частицах электрич. момента определяется поляризуемостью частицы а, т.е. зависит от числа и расположения электронов и положительных ядер, составляющих молекулу или атомы. Электрический момент, возникающий в частице под действием поля волны Esin Znvi,

f=аЕ sin 2πνί.

Периодическое изменение величины ведет к испусканию вторичных волн, которые, складываясь с первичной возбуждающей волной, дают результирующее электромагнитное поле, распространяющееся сквозь среду. Вычисление показывает, что скорость распространения результирующей волны отличается от скорости волны в пустоте и зависит от частоты света (смотрите Дисперсия света). Так. образом поляризуемость частиц определяет собою скорость света в среде, то есть показатель преломления среды, составленной из этих частиц. В то же время поляризуемость определяет собою и интенсивность рассеянного света, так что проблема Р. с. представляет собою один из вопросов теории дисперсии света. Для газа интенсивность света, рассеянного единицей объёма, выражается ф-лой Редея

I=Е‘ ^2д3(п^-¹-⁾² (1 + cos² Θ), (2)

где Е—амплитуда первичной (неполяризован-ной) световой волны, λ—длина волны, μ—по- ; казатель преломления газа, п—число частиц,

содержащихся в 1 см³, и Θ, как и раньше,— угол между направлением первичного пучка и направлением наблюдения. Все выводы π. 1 относительно зависимости от λ, симметрии распределения и поляризации остаются в силе· и для рассмотренного случая.

4. Флюкту ационная теория молекулярного Р. с. Приведенные рассуждения нуждаются в существенном дополнении. При суммировании действия вторичных волн, распространяющихся во все стороны от рассеивающих частиц, надо принять во внимание их способность к взаимной интерференции. Предположим, что распределение частиц таково, что в любом элементе объёма, линейные размеры которого малы по сравнению с длиной волны, но велики по сравнению с расстоянием между частицами и размером самих частиц, заключается число частиц, пропорциональное выбранному объёму. Тогда, как показывает расчет, все вторичные волны, идущие в направлениях, не совпадающих с направлением первичного пучка, взаимно уничтожаются вследствие интерференции^ Среда, удовлетворяющая поставленному выше условию (число частиц пропорционально объёму), называется оптически однородной. Итак, оптически однородная среда не рассеивает света. Мутные среды Тиндаля—пример грубого· нарушения однородности. Но и во всякой среде, построенной из молекул, оптическая однородность нарушается вследствие молекулярного движения, ведущего к образованию малых участков, плотность которых отступает от среднего значения (ф л ю к т у а ц и и плотности). Примером оптически однородной среды мог бы явиться совершенный кристалл при абсолютном нуле темп-ры: силы молекулярного взаимодействия расположили бы молекулы кристалла в правильную решетку, оптически однородную для волн, длина которых значительно превосходит межмолекуляриые расстояния (видимый или ультрафиолетовый свет). Для коротких (рентгеновских) волн такой кристалл представлял бы собою не однородную среду, но правильную решетку. Поэтому рентгеновские лучи должны.испытать правильную диффрак-цию при прохождении через такой кристалл (Лауэ, 1912 г.). Газ при абсолютном нуле может представлять, оптически однородную среду, но вследствие отсутствия сил молекулярного взаимодействия возможно и иное (не равномерное) распределение частиц, причем вероятность неравномерного распределения значительно больше. При темп-ре, отличной от абсолютного нуля, равномерное распределение частиц неминуемо нарушается. В случае длинных волн это нарушение приводит к появлению рассеянного света; в случае рентгеновских волн такое нарушение правильности диффрак-ционной решетки ведет к некоторому размытью резной диффракционной картины (Дебай, 1914 г.). Принципиальная необходимость нарушения однородности среды для явления Р. с. была выяснена Л. И. Мандельштамом (1907 год), а явление флюктуации, как физическая причина этого нарушения, указана Смолу-ховским (1908 год). Смолуховский применил флюктуа-ционную теорию к объяснению весьма сильного Р. с., наблюдаемого при критической темп-ре газа. Причипа этой интенсивной критической опалесценции в том, что при критич. температуре сжимаемость среды становится безгранично большой, т. ч. флюктуации плотности достигают значительных размеров. Эйнштейн (1910 год) вычислил, исходя из идеи флюктуаций, интенсивность рассеянного света для .газов и жидкостей, далеких от критической температуры. Согласно Эйпштейну интенсивность рассеянного света должна зависеть от сжимаемости среды, ибо чем больше коэф-т сжимаемости β, тем значительнее флюктуационные изменения плотности среды s; далее в· формулу входит зависимость ПОКаза-

15 μ

теля преломления среды μ от плотности, то есть ^ > ибо нарушение оптической однородности среды влечет нарушение постоянства показателя преломления. В формулу входят также молекулярные константы (R—газовая постоянная и N—число Авогадро) и абсолютная температура Т, с возрастанием которой увеличивается энергия молекулярных движений, способных вызывать флюктуации плотности. Формула Эйнштейна для интенсивности света, рассеянного единицей объёма среды, имеет вид:

I=^Ег fi · ^ ^{β 82}(fis)²⁽¹ + ^{0082 e)}’ <^S>

где E—амплитуда первичного (естественного) света и О—угол между направлением первичного пучка и направлением наблюдения. Для газов формула Эйнштейна переходит в формулу Релея.

5. Деполяризация рассеянного с в е т а. А н и з о т р о п ия молекул. Рассуждения, приведенные выше (π. 1), объясняют полную поляризацию света, рассеянного под углом 0=90° к первичному пучку.

Опыт показал однако, что рассеянный свет в б. или м. степени деполяризован (Стрэтт, 1918 г.)· Релей (1918 год) объяснил эту частичную деполяризацию допущением анизотропии молекул. Электрический момент, возникающий в анизотропной молекуле под действием световой волны, не совпадает с направлением электрического поля волны. В этом случае рассуждения, аналогичные приведенным в π. 1, приводят к выводу о необходимости частичной деполяризации рассеянного света, величина которого зависит от степени анизотропии молекулы. Сточки зренияфлюктуаци-онной теории наличие анизотропных молекул ведет к нарушению оптической однородности среды не только вследствие флюктуаций плотности, учтенных Эйнштейном, но и вследствие флюктуации ориентаций анизотропных молекул. Случайное образование участков среды, где анизотропные молекулы имеют более или менее правильное расположение, влияет на интенсивность рассеянного света. Поправка эта указана Кабанном (1920 год) и выражается множителем, где фактор де поляризации

_ интенс. света, поляризованного в плоскости ZY интенс. света, поляризованного в плоскости ХУ’

как и выше, направление первичного пучка— вдоль оси X; направление наблюдения—вдоль оси У. Фактор у может достигать значительной величины (для бензола 0,42, для сероуглерода даже 0,685), т. ч. поправочный множитель Кабанна достигает для сероуглерода 8,2. Для других веществ он значительно меньше, например для четыреххлористого углерода ρ =0,056, т. ч. множитель Кабанна равен всего лишь 1,12. Для газов и паров ρ значительно меньше. Так, для паров сероуглерода q =0,115, для водорода ρ =0,017, для аргона ρ =0,005. В соответствии с этим уменьшается и поправочный множитель Кабанна, который для аргона равен 1,01, то есть поправка достигает всего лишь 1%. Ганс (1921 год) указал на связь между фактором деполяризации ρ и постоянной Керра (смотрите Электрооптика), ибо эффект Керра также связан с анизотропией молекул. Вычисления Ганса подтверждаются экспериментальными данными.

6.Эксперимента л ь п ы е да п н ы е, к а-с а ю щ и е с я Р. с. а) Газы и пары. Первые наблюдения Р. с. в газах в лабораторной обстановке принадлежат Кабанну (1915 год). Им выработай метод очистки газа (от пыли) п изменена интенсивность рассеянного света (вкл. лист, 1). Кабанн подверг экспериментальной проверке теоретическую формулу Релея— Эйнштейна и определил по интенсивности света, рассеянного аргоном, постоянную Авогадро JV=(6,90± ±0,25)·10²³. Наблюдения Дора (1925 год) над хлористым этилом дали для N значение (6,50±0,65)-10²³. Измерения Ивинга (1926 год) над парами пяти органических веществ дали iV=(5,96±0,25)· 10²³ (эти последние измерения менее надежны). Значения ιΥ, найденные из рассеяния газами, довольно близки к истинному значению iV=6,06 · 10²³. Необходимы однако более точные измерения, чтобы решить, объясняется ли указанное расхождение ошибками опыта или недостатками теории. Первые наблюдения над деполяризацией спета, рассеянного газами, принадлежат Стрэтту (Ре-лею-младшему, 1918 г.). В настоящее время исследована деполяризация 89 газов и паров (Стрэтт, Кабанн, Гапс, Раман с сотрудниками). Одноатомные газы (нулевая группа) дают для в малую величину—ок. 0,01, что стоит в хорошем согласии с симметричным строепиед! атомов благородных газов. Исключение составляет Не, для которого е=0,065 и к-рый и по теоретическим соображениям далек от симметрии. Значительно больше е для некоторых трехатомных молекул (для СО_а—0,08, χ₂0—0,14, CS₂—0,12), что указывает на сильно удлиненную структуру этих молекул. Вообще же говоря, деполяризация у паров и газов не очень велика, редко встречается о >0,10 (вкладной лист, 2). Рассея ние света в атмосфере также позволяет проверить теорию Релея; на это указывал еще сам Релей (1899 г.), давший на основании теории Р. с. объяснение синеве неба

^закон “j. Более поздние измеренпя прозрачности атмосферы, выполненные Абботом (1906 год) п особенно Фоулем (1910—1912 гг.) на Маунт-Вильсон и Дембером (1916 год) на пике Тенериф, позволили вычислить число Авогадро [2V=(6,52±0,18).10²³].Измерения яркости неба и характера, поляризации света неба также стоят в согласии с теорией Релея, хотя и не все особенности поляризации небесного свода удовлетворительно объясняются теорией. б) Ж п д к о с т и. Рассеяние света жидкостями на единицу объёма значительно больше, чем для газов: бензол рассеивает в 2 700 раз больше, чем воздух (вкладной, лист, 3). Важное условие успешности опыта—тщательная очистка жидкости от взвешенных частиц: медленная перегонка в вакууме (Мартин) или ультрафильтрация (Леблан и Вольский). Абсолютные измерения интенсивности рассеянного света выполнены для трех жидкостей: воды, эфира и бензола. Интерпретация измерений по формуле Эйнштейна с поправкой на анизотропию молекул дает для числа Авогадро iVsi й8 · 10», то есть явно преувеличенную величину. Причина расхождения лежит очевидно в недостатках теории. Многочисленные попытки усовершенствовать теорию (Кинг, Раманатан, Кабанн, Рокар, Ганс) не могут считаться окончательными. Относительные измерения интенсивностей охватывают очень большое количество жидкостей. Зависимость интенсивности от показателя преломления не вполне укладывается в формулу Эйнштейна, равно как и в другие предложенные формулы. Измерение деполяризации дает в среднем значительно бблыние значения, чем для газов (вкладной лист, 4), что стоит в связи с сравнительно сильным взаимодействием молекул жидкости друг на друга. Большие значения фактора деполяризации д ведут к весьма большим значениям поправочного множителя Кабанна. Несовершенство теории заключается быть может в недостаточно точной оценке этого множителя. Интенсивность света, рассеянного жидкостями, сильно зависит от температуры (Раман с сотрудниками), как того и требует теория Эйнштейна. Интенсивность возрастает при приближении к критической температуре для эфира в 60 раз, изопентана в 75,5 раз и т. д. Однако наблюдаемый ход зависимости не вполне точно следует формуле Эйнштейна, которая и в этом отношении оказывается для жидкостей не вполне удовлетворительной. Р. с. в смесях жидкостей кроме эффекта флюктуации плотности и ориентации обусловливается еще эффектом флюктуации концентраций. Этот эффект может стать весьма значительным вблизи критической температуры смешения. Тщательные исследования смеси фенол-вода (Фюрт, 1915 г.) показали полную применимость теории Эйнштейна и в этом случае. Однако и здесь количественные совпадения не совершенны. Для числа Авогадро найдено 7,7 · 10²³. Видоизменепия теории, предложенные Орнштейном и Цернпке (1915— 1926 гг.) и Рокаром (1928 год), также не окончательны. Рассеяние света на поверхности жидкостей интерпретируется в духе идей Смолуховского следующим образом. Поверхность жидкости обнаруживает молекулярную шероховатость, степень которой определяется конкуренцией между термическим движением, с одной стороны, и капиллярными силами п силой тяжести,— с другой (Мандельштам, 1913 г.). Явление особенно отчетливо на границе двух жидкостей вблизи критической температуры смешения, когда капиллярные силы стремятся к нулю. В таком виде оно впервые наблюдалось Мандельштамом (1913 год). Раман и Рамдос (1924—1925 гг.) изучали его количественно на свободной поверхности мпогих органических жидкостей и даже на ртути. Сравнение их данных с теорией (Андронов и Леонтович, 1926 г.) обнаружило в ряде отношений хорошее согласие. в) Твердые тела (кристаллы). Изучение молекулярного Р. с. крайне затруднено невозможностью очистки кристаллов. Надежным критерием, позволяющим отличить молекулярное Р. с. от Р. с. па включениях, служат наблюдения при возрастающей температуре (Ландсберг, 1927 г.). Этим методом были изучены кварц (вкладной лист, 5) и каменная соль, дающие для интенсивности рассеянного света величину, близкую к теоретической, но все же отличающуюся от нее на 20—30 %. Теория учитывает не только изменения показателя преломления при изменениях плотности, но и влияние сдвигов при неизменном объёме (Ганс, 1925 г.). Тем не менее теория, так же как и в случае жидкостей, кажется недостаточной.

7. Комбинационное Р. с. При спектроскопия, изучении рассеянного света обнаруяшлось (Раман и Кришнан, Ландсберг и Мандельштам, 1928 г.), что в нем наряду с спектральными линиями, имевшимися в первичном пучке, наблюдаются новые ли-

нии (сателиты), частота которых определяется равенством

ν =v±v_it (4)

_Гд_е —частота рассеянного света, v—частота падающего и v_t—собственная частота инфракрасных колебаний, характерная для рассеивающего вещества (вкладной лист, 6 и 7). Линии, соответствующие частоте v—v_{, носят название красных сателитов, линии.частоты ν + -т-т_г· — фиолетовых. Образование сателитов может быть истолковано следующим образом. Квант падающего света hv при взаимодействии с молекулами рассеивающего вещества может отдать им энергию, необходимую для возбуждения собственных колебаний молекулы (то есть квант hv,), или же, если взаимодействие происходит с уже возбужденной молекулой, заимствовать от нее соответствующую порцию энергии. Закон сохранения энергии ведет к соотношению

hv=hv ± hv_it т. e. v=v ± ν_{.

Отсюда следует, что интенсивности фиолетовых (1„) и красных (I,.) сателитов относятся приблизительно, как число молекул ^ вещества в данном состоянии (с добавочной энергией hv,) к числу молекул в нормальном состоянии, то есть

hv;

где к—постоянная Больцмана, h — постоян" ная Планка и Т — абсолютная температура. Приведенная формула хорошо оправдывается на опыте и может служить для экспериментального определения j‘. Она показывает между прочим, что относительная интенсивность фиолетовых сателитов тем больше, чем меньше v_it то есть чем ближе расположен сателит к главной линии (вкладной лист, б) и чем выше температура рассеивающего вещества (вкладной лист, 7). Формула (4) показывает, что комбинационное рассеяние дает сравнительно простой и точный метод определения собственных частот молекул (г_г). Однако сопоставление частот колебаний, определенных по методам комбинационного рассеяния и инфракрасных лучей, показывает, что оба метода не только не исключают, но, наоборот, удачно дополняют друг друга. Таблица 1 показывает, что одни собственные колебания хорошо проявляются в явлении комбинационного рассеяния, другие—в явлении поглощения инфракрасных лучей.

Таблица 1. — Собственные частоты (v*) кварца.

Инфра красные лучи **•1018	Комбина-цион. рассеяние Vf-lO™	Инфра красные лучи ν^-1012	Комбина-цион. рассеяние V/-1012
3,85	3,80	14,6 *3	14,0 *4
—	6,25 *3	—	20,8
7,80 *4	7,81 *2	24,0	24,0
	10,7	33,4 *4	32,5 *1
11,5	12,2	35,8 *4	35,0 *1

*ι Очень слабое. *² Слабое. *з Сильное. ** Очень сильное.

Появление той или -иной линии как в спектре абсорбции, так и в комбинационном рассеянии объясняется формой колебания. Линии, не появляющиеся при инфракрас ном методе, соответствуют таким колебаниям, при которых электрический момент системы остается неизменным (неактивные колебания); линии, не появляющиеся при комбинационном рассеянии (или очень слабые), отвечают колебаниям, при которых ядра смещаются симметрично по отношению к электронной оболочке. Сопоставляя данные обоих методов, легко установить основные колебания системы; все остальные наблюдающиеся в ней колебания оказываются суммовыми или разностными (табл. 2). Возможность удобного оп-

Таблица 2. — С о б с тв е нн ы е частоты четыреххлористого кремния (vio-²).

(Λ—инфракрасные лучи, В—комбинационное рассеяние.)

риабл. ·	10-12	я о ;? 3 »	Истолкование *1	j v,hq6a.^ 12		T 0 тЧ 1 » A	1 - o-K* PJ <D О s и a К p
А	В			A	В
	4,56		vL	30,9		30,8	V3+V4
6,30	6,30	—	V2	! 36,6	—	36,0	2v4
—	12,75	—		40,5		40,6	2v4 + Vi
18,0	18,0	—	v4	i 46,2	—	43,5	2v3+r4
22,5	—	22,6	vl + vi	j 50,1	—	48,7	V3 + 2”4
24,6		24,3	"i+Vi	54,3		54,0	3V4

* Если четыре первых из приведенных частот принять за основные, то любая другая частота может быть получена из основных, как показано в таблице. ределения собственных частот молекул делает комбинационное Р. с. надежной базой для заключений о строении молекул. Особенно обширный «фактический материал собран для органических соединений (Дадье и Кольрауш и др.). На основании его установлены собственные частоты колебаний, характеризующие различные группы и радикалы, частоты, соответствующие простым, двойным и тройным связям, и т. д. Имеются попытки анализа промежуточных соединений, образующихся при смешивании (Трумпи), равно как и решения других физико-химич. проблем.

8. Рассеяние рентгеновских лучей. Соображения п. 3 сохраняют свою силу и для чрезвычайно коротких волн (рентгеновские), которым соответствует высокая частота колебаний. При этом надо иметь в виду, что частота колебаний, вынужденных рентгеновскими лучами, обыкновенно значительно превосходит собственную частоту электронов (по крайней мере для легких атомов). При этих условиях наличие связей, удержи-вающих электрон внутри атома, может не приниматься в расчет и явление можно рассматривать как вынужденное рентгеновской волной колебание свободных электронов. Теория явления (Дж. Дж. Томсон, 1903 г.) предполагает, что расстояния между этими электронами достаточно велики по сравнению с длиной волны, так что начальные фазы колебаний отдельных электронов не согласованы между собою (вторичные волны некогерентны). При этих предположениях интенсивность рассеянного единицей объёма вещества должна быть пропорциональна числу электронов Ζ в единице объёма. Так как число электронов в атоме (порядковое число атома) приблизительно пропорционально его атомно-.му весу (особенно для легких элементов кроме водорода), то число электронов в единице объёма рассеивающего тела можно считать пропорциональным плотности вещества. В со-

Рассеяние света

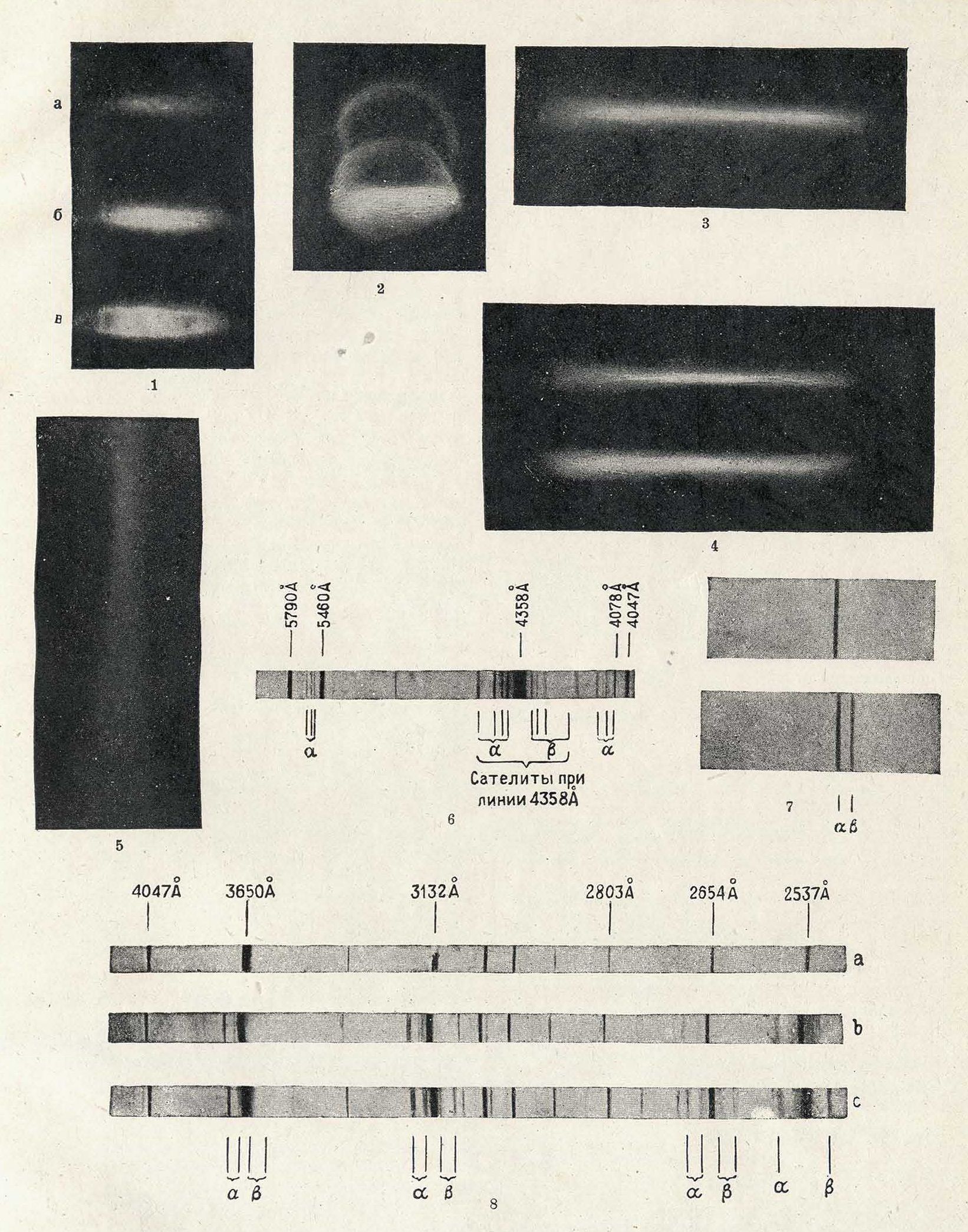
1. Свет, рассеянный газами (а—водород, 6—воздух, в—углекислота). 2. Поляризация света, рассеянного аргоном; туманные кольца—следы света, отраженного сосудом; полоска в нижнем кольце—свет, поляризованный в плоскости XY (смотрите текст); отсутствие полоски в верхнем кольце показывает, что свет, поляризованный в плоскости ZY, отсутствует, то есть в случае аргона поляризация при рассеянии полная, з. Свет, рассеянный бензолом. 4. Поляризация света, рассеянного бензолом: нижняя полоска соответствует свету, поляризованному в плоскости XY, верхняя—в плоскости ZY; деполяризация 42%. 6. Свет, рассеянный кристаллич. кварцем. 6. Комбинационное рассеяние в четыреххлористом углероде (СС1₄); спектр света, рассеянного CCJ,: а—красные сателиты; β—фиолетовыесателиты. 7. Явление Комптона в алюминии:вверху— спектр первичных рентгеновых лучей; внизу—спектр рассеянных алюминием рентгеновых лучей (а—несмещенная линия, р—смещенная линия). 8. Комбинационное рассеяние в кристаллич. кварце; а—спектр сравнения (ртутная дуга); Ь—спектр света, рассеянного кварцем при 20°; с—спектр света, рассеянного кварцем при 210° (α-красные сателиты, р-фиолетовые сателиты).

ответствии с этим правило Томсона приводит к утверждению, что коэфициент рассеяния а, то есть доля энергии первичного пучка, подвергшаяся рассеянию, пропорционален плотности вещества s. Другими словами,

-X —т. н. массовый коэф-т рассеяния—должен быть постоянным. По теории Томсона он равен 0,2. С другой стороны, некогерент-ность вторичных волн ведет (как и в теории Релея) к симметричному распределению лучей около первичного пучка: зависимость от угла наблюдения выражается фактором l+cos²6>. Оба эти вывода были подтверждены измерениями (Баркла, 1908 г.; Краузсер, 1911 г.) рассеяния рентгеновских лучей средней жесткости на легких элементах. При переходе к тяжелым атомам или рентгеновским лучам большей длины волны обнаруживаются значительные отступления от законов Томсона: нарушается симметрия в распределении (силь-¹ ный перевес в сторону первичного пучка) и заметно возрастает коэфициент рассеяния. Причина отступлений лежит в следующем. При новых условиях расстояния между отдельными электронами (внутри тяжелых элементов) оказываются сравнимыми с длиной волны (особенно при применении более мягких лучей). Колебания отдельных электронов становятся когерентными, а испускаемые ими вторичные волны—способными к интерференции. При этом складываются амплитуды волн, т. ч. амплитуда становится пропорциональной Z, а результирующая интенсивность— Z² (Z—число электронов в атоме). Т. о. интенсивность рассеянного света делается большей, чем по теории Томсона. Учет интерференции объясняет также и нарушение симметрии распределения (сравни эффект Ми: роль сравнительно крупных частиц играют тяжелые атомы с их плотным распределением электронов). Отступления от теории Томсона, обусловленные интерференцией вторичных волн, могут наблюдаться и на легких атомах и при жестких рентгеновских лучах в области узкого конуса, описанного около продолжения пучка первичных лучей (Фридрих, 1913 г.; Дебай, 1915 г.). С возрастающей мягкостью лучей конус этот расширяется, так что отступления от теории Томсона становятся весьма заметными. Совсем иного характера отступления от теории Томсона, обнаруживающиеся в области очень коротких волн (жесткие рентгеновские лучи или у-лучи): здесь коэфициент рассеяния гораздо меньше, чем следует п“о Томсону, и наблюдается резкий перевес интенсивности рассеянных лучей в направлении первичного пучка (Кольрауш, 1920 г.; А. Комптон, 1921 г.). В этом случае «дело идет о принципиальном отклонении от волновой оптики, связанном с величиной кванта энергии очень жестких лучей» (Зоммерфельд). Явление действительно получило свое объяснение в связи с открытием эффекта Комптона. Эффект Комптона состоит в увеличении длины волны, наблюдаемом при рассеянии жестких рентгеновских лучей. Явление было обнаружено А. Комптоном (1929 г.) при тщательном анализе длины волны рассеянных в графите монохроматич. рентгеновских лучей. Измерения производились по

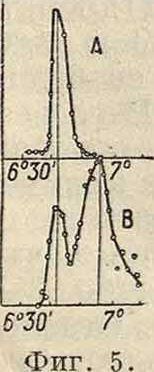
ионизационному методу и обнаружили, что наряду с длиной волны первичного пучка А в рассеянном свете присутствует и новая, большая длина волны В (фигура 5). Явление можно наблюдать и фотографически (вкладной лист, 8). В дальнейшем было установлено, что изменение длины волны зависит от направления, в к-ром наблюдается Р. с. и не зависит от длины волны первичного света и рассеивающего вещества (табл. 3 и 4).

Таблица 3,—3 а в и си м о с т ь ΔΛ от угла рас-сеяния 0.

0	Δλиабл.у-Δ-	Мвыч-*1	0	^иабл.г^·	Δλвыч-*1
30°	0,004	0,0032	120°	0,033	0,0363
60°	0,013	0,0121	135°	0,038	0,0413
90°	0,025	0,0242	165°	0,042	0,0476

Вычислено по формуле — · sin² — · тс 2

Таблица 4.—Н е з а в и с и м о с т ь ΔΛ от вещества рассеивателя (0=90°).

Вещество	Ζ	Αλ	Вещество	Ζ	ΔΑ
Графит. Алюминий. Сера.	6 13 16	0,0236 0,0244 0,0240	Медь. Серебро. Свинец.	29 47 82	0,0244 0,0238 0,0240

Удовлетворительная теория эффекта Комптона м. б. получена из представлений, диктуемых гипотезой световых квантов (А. Комптон, 1923 г.; Дебай, 1923 г.).

Рассеяние рентгеновских лучей электронами рассматривается какстолкновение кванта с электроном. Электроны, участвующие в этом процессе, можно считать свободными (об учете связи электронов с атомами см. нише) и неподвижными (тепловое движение настолько слабо, что им можно пренебречь). Квант

hv

частоты V имеет энергию hv, массу т — “ импульс

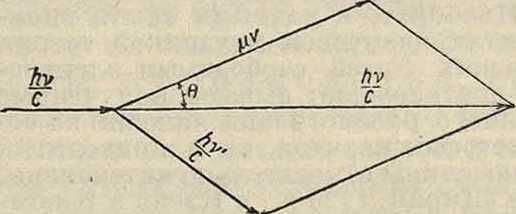
Фигура 6.

С2

hv

(8)

р=—. Масса электрона μ, его скорость до столкновения—нуль, после столкновения—ν. Столкновение происходит по закону упругих шаров, то есть подчиняется закону сохранения энергии и закону сохранения импульсов (схема взаимного расположения векторов импульсов приведена на фигуре 6):

hv=hv (ур-ие сохранения энергии), (6)

—^ ^

—=·^— -μυ (ур-ие сохранения импульса). (7)

Решая совместно эти два уравнения, определим изменение частоты Αν=ν- ν или изменение длины волны

Αλ——— —=являющееся следствием описанного

ν ν νV

процесса. Вычисление дает

Αλ=— · 2 sin² -. μθ 2

где 0—угол, показанный на фигуре 6. Таблица^ 3 показывает, в какой степени удовлетворяется найденное со-

отношение. —=А„=0,0242 А — константа, характе-

ризующая эффект. Она определяет собою величину Αλ при наблюдении под прямым углом к первичному пучку. Спектрограммы явления Комптона показывают, что наряду со смещенной линией в спектре рассеяния имеется также и несмещенная линия, соответствующая неизменной длине волны первичного света. Точное определение соотношения интенсивностен этих линий весьма затруднительно. Качественно, во всяком случае, установлено, что смещенная линия по отношению к несмещенной тем сильнее, чем больше угол рассеяния, чем меньше порядковое число рассеивающего вещества и чем больше частота первичного света ν. Сверх того обнаружено, что смещенная линия характеризуется несколько большей неоднородностью в лине волны (размытость). Объяснение. всех этих особенностей лежит в учете связей, удерживающих электроны в атоме. При легких атомах (малое Z) и жестких лучах (большое ίιτ) связи относительно слабы и все электроны, рассеивающие свет, могут считаться евободпыми. Развитая выше теория объясняет появление лишь смещенной линии: интенсивность несмещенной должна равняться нулю. При тяжелых атомах или мягких лучах „повышается вероятность рассеяния таким прочно связанным электроном, который не потеряет связи с ядром при воздействии рентгеновского кванта. В таком случае энергия кванта должна передаваться всему атому: в формуле (7) μ будет означать массу атома, то есть смещение АД будет в сотни тысяч раз меньше и линия практически будет не смещена. Соотношение интенсивностей смещенной и несмещенной части определяется следовательно относительными вероятностями рассеяния на свободных и связанных электронах, то есть должно зависеть от перечисленных выше факторов в согласии с опытными данными.

По теории эффекта Комптона одновременно с рассеянием кванта должно иметь место и отбрасывание электрона со скоростью ν (электрон отдачи). Действительно такие электроны удалось наблюдать по методу камеры Вильсона, так как скорость этих электронов достаточна, чтобы вызвать ионизацию воздуха. Комптон и Саймон (1925 год), пользуясь этим методом, изучили распределение направлений первичных и рассеянных квантов и электронов отдачи. Результаты оказались в полиом согласии с приведенной теорией столкновения, расхождение между опытным и теоретическим определением направления полета электрона лежало в пределах 0—20°, что следует считать весьма удовлетворительным для этого трудного опыта. Описанный опыт, так же как и специальный опыт Боте (1925 год) показали, что акт рассеяния и акт электронной отдачи локализованы и в пространстве и во времени, как два совпадающие акта, что заставляет признать описываемый процесс элементарным, а не статистическим. На основании этих уже опытных данных следует считать неудовлетворительным классическое истолкование изменения длины волпы при рассеянии, как результат явления Допплера, то есть рассеяние электронами, приведенными в достаточно быстрое движение. Наоборот, с данными опыта вполне согласуется развитая квантовой механикой теория рассеяния рентгеновских лучей свободными электронами. Онапе только подтверждает выводы, полученные при помощи упрощенного рассмотрения явлений на основании гипотезы световых квантов, но и приводит к количественным заключениям относительно интенсивности рассеянного света (Дирак, 1926 г., и Клейн и Ншии-на, 1929 г., применившие новую релятивистскую квантовую механику Дирака). Установленная этими теориями зависимость коэфициента рассеяния от направления наблюдения и длины волны хорошо подтверждается измерениями в весьма широком интервале частот, вплоть до очень жестких у-лучей. В области наиболее коротких волн (смотрите Космические лучи) формула Дирака-Клейн—Нишина дает пока единственно применимый, хотя и не вполне падежный, метод определения длины волны (Милликен, 1927 г.).

Поляризация рассеянных лучей. Применяя соображения π. 1, заключаем, что и рентгеновские лучи, рассеянные в направлении Θ =90° к первичному пучку, должен быть нацело поляризованы. Баркла (1906 год) доказал это экспериментально, применив в качестве метода анализа вторичное рассеяние в куске угля (также под углом 90°). В зависимости от направления наблюдения вторично рассеянный пучок имел разную интенсивность. Полная поляризация однако не была наблюдена, ибо лучи, рассеянные более глубокими слоями угля, частично деполяризовались при прохождении через слой вещества. А. Комптон и Хагенау (1924 год) получили вполне поляризованные лучи (с точностью до 1—2%). Ими же было показано, что поляризация рентгеновских лучей при рассеянии не зависит от вещества рассеивателя (применялся уголь, алюминий, сера). При явлении Комптона обе линии — смещенная и несмещенная—оказываются поляризованными в одинаковой степени (Кальман и Марк, 1926 г.).

Лит.: Ландсберг Г. С., Новое в явлении рассеяния света, «УФН», 1929, т. 9; К э й, Рентгеновские лучи, пер. с англ., М.—Л., 1928; Cabannes, La diffusion moieculaire de la lumidre, P., 1929; G a n s R., Liehtzerstreuung, Handb. d. Experimentalphysik, hrsg. ν. W. Wien u. F. Harms, B. 19, Lpz., 1926;

К oh Ira us ch F., Der Ramaneffekt, Berlin, 1931; Compton A. H., A-Rays a. Electrons, L., 1927; Kirschner E., Allgemeine Physik d. Rontgen-schallen, Handb. d. Exper Physik, hrsg. v. W. Wien u. F. Harms, B. 24, T. 1, Lpz., 1930. Г. Лан;сберг.