> Техника, страница 76 > Растворы

Растворы

Растворы. Обыкновенным, или настоящим, Р. с термодинамической точки зрения (макроскопической) называется однородная (гомогенная) фаза переменного состава; число веществ, составляющих Р., равно или больше двух. С кинетической (микроскопической) точки зрения настоящие Р. являются молекулярно-дисперсными системами (смотрите Коллоиды)·. высоко- (но не молекулярно-) дисперсные системы называются коллоидными Р. В настоящих Р. размеры молекул веществ, составляющих Р., одного порядка и колеблются в пределах 0,1-р1,5 т/л. В зависимости от агрегатного состояния различают 1) газообразные, 2) жидкие и 3) твердые Р.

1. Газообразные Р. К этим системам термин «раствор» применяется не всегда, обычно их называют смесями газов (паров); газы мы имем возможность изучать в предельном состоянии, называемом идеальным, и т. о. установить простые закономерности, лежащие в основе учения о газообразных Р. В теории таких Р. (смесей) исходят из определения, по которому свободная энергия смеси идеальных газов при данной t° и объёме равна сумме свободных энергий компонентов смеси, взятых в объёме смеси при той же ί°. Из этого определения и ур-ия состояния идеальных газов

pv=RT I

вытекает, что при смешении двух идеальных газов свободная энергия их уменьшается, а энтропия увеличивается. Пусть дано 1-го газа щ молей в объёме v_lt 2-го газа м₂ молей в объёме г>₂, при одинаковых давлении и t°, и. пусть их свободные энергии до смешения F_t HP’s (на моль); тогда сумма их свободных энергий до смешения F=n₁F₁ + №₂Р₂.

После смешения каждый газ будет занимать при прежнем давлении и той же <° объём «!+ «;₂; пусть их свободные энергии после смешения F[ и F₂, тогда по определе-лию смеси ее свободная энергия

F=«Л + w₂F₂.

Можно показать, что разность AF=F— F=—ЕТ(и._х1 + Щ Ш^-),

и следовательно F>F Отсюда возрастание энтропии в результате смешения

AS=S — S=Ii (те, In + те₂ In -"² ),

V ¹ П1+ГС2 ^Δ Щ + п_г!

т. e. S < £>. Этот результат известен под названием теоремы или парадокса Гиббса; парадокс здесь в том, что возрастание энтропии при смешении газов не зависит от их природы, а определяется только числом молей. Теорема Гиббса играет видную роль в химич. термодинамике.

В случае реальных газов в ур-ие состояния входят величины, характеризующие природу каждого из них, например в ур-ии Ван-дер-Ваальса

{р Ί" fi) (v —b)=RT

такими величинами являются а и b. Ур-ие смеси (Р.) газов м. б. представлено тем же ур-ием

(р+£р^ад-дт,

но постоянные смеси а_х и b_х—функции концентрации х—не м. б. сведены к постоянным а и Ь отдельных газов; по Ван-дер-Вааяьсу [«*=<*! (1 - ж)² +2а₁₂х (1 - ж) + а₂х где % и (1 — х)—постоянная и концентрация первого газа, а₂ и ж — те же величины для второго газа; аналогичное уравнение имеет силу и для постоянной Ь_х. В ур-ие входит также новая постоянная а₁₂, характеризующая смесь (Р.) как таковую. Т. о. даже в простейшем случае (газы) свойства Р. не могут быть сведены к функции только свойств компонентов. Особенности смесей реальных газов сказываются в ряде их свойств, особенно в кри-тич. области (смотрите Критическое состояние).

2. Жидкие Р., в которых по крайней мере один из компонентов—жидкость,являются Р.в узком смысле слова и могут быть разделены на следующие три группы: растворы газов, жидкостей и твердых веществ. Особо важным понятием здесь является понятие о насыщенности Р. Газы и твердые вещества как правило, а жидкости во многих случаях, не смешиваются с данной жидкостью во всех отношениях: имеется предел растворимости. Пусть имеется жидкость А и вещество В; если вещество В в данных условиях тоже жидкость, то м. б. два случая: А и В смешиваются во всех отношениях (вода и ) или только частично (вода и эфир). Мы говорим о растворе Вв1, если количество А значительно больше количества В, и о растворах 1 в В в обратном случае; если же количество А и В одного порядка, то говорят просто о их смесях. В случае частично смешивающихся жидкостей А и В имеются 2 предела растворимости: А в В и В в А; между этими пределами лежит гетерогенная область равновесия 2 жидких слоев.

Р. называется насыщенным, если его концентрация при данной ί° не изменяется в присутствии излишка растворенного вещества, т: е. он находится в равновесии с другой фазой, газовой, жидкой или твердой. Р., содер жащие вещества В меньше, чем в состоянии насыщения, называются ненасыщенными. В ряде случаев Р. в отсутствии второй фазы (состоящей из вещества В) могут содержать вещества В больше, чем в состоянии насыщения; такие Р. называются пересыщенными; их состояние метастабильиое, легко нарушаемое или самопроизвольно, или путем сотрясения, или путем прибавки кристалликов растворенного вещества.

Многие авторы в основу учения о Р. кладут их особое свойство — осмотическое давя е н и е—и, исходя из него, пытаются найти зависимости между ним и другими свойствами Р. Этот исторически важный путь в настоящее время должен быть оставлен, во-первых, потому, что осмотич. давление Р. проявляется только в искусственно создаваемых условиях неравновесных двухфазных систем и с трудом поддается точному количественному учету, и во-вторых, потому, что этим путем мы не можем дать полной картины свойств Р.

Р. жидкостей в жидкостях. В оскову эмпирического охвата области Р. следует положить закон Рауля и изучение Р. начинать с Р. жидкостей в жидкостях. Рассмотрим в качестве исходного общий случай двух летучих жидкостей А и Вымешивающихся во всех отношениях. Пусть в жидком Р. (жидкой фазе) первой жидкости щ, второй— те₂ молей, тогда молярная концентрация компонента А равна N,=—, компонента В — N_t=Пусть упругость пара жидкости А

при данной t° равна pj; после растворения в ней п_г молей компонента В упругость пара первой жидкости понизится до р₁₍ тогда выражение ^p „^Pl даст т. н. относительное

Pi

понижение· упругости пара первой жидкости. По найденному эмпирически закону Рауля это относительное понижение упругости пара в предельных (идеальных) условиях не зависит от природы компонентов А и В, но определяется чи их молей:

Ρ?-Ρι _ п₂

откуда	г>$>	ni+n.2’
	Pi 4,	——— — N.
следовательно	pf	П1+П2

р,=ад. (Г)

То же самое справедливо и для упругостей пара второго компонента, то есть

(1")

Этот закон м. б. обобщен на какое угодно число компонентов, тогда

^г П1- -П2+. + П_т

Vi=NiPi · (1")

Из (IQ и (lO полная упругость пара Р.

Ра + Р₂=P?tf i + pgW,=к_г (р? - р© + р§. (2) Следовательно парциальные упругости и общая упругость Р. изменяются с составом его линейно. Р., строго подчиняющиеся этим закономерностям, называются идеальными; в случае бинарных смесей им отвечает фигура 1, где на оси абсцисс отложены молярные концентрации обоих компонентов в жидкой фазе. на оси ординат—упругости паров; примером таких соотношений могут служить смеси бензола и э.тиленхлорида. В Р. летучих жидкостей состав пара и жидкой фазы, находящихся в равновесии, различны; на фигуре 1 прямые р

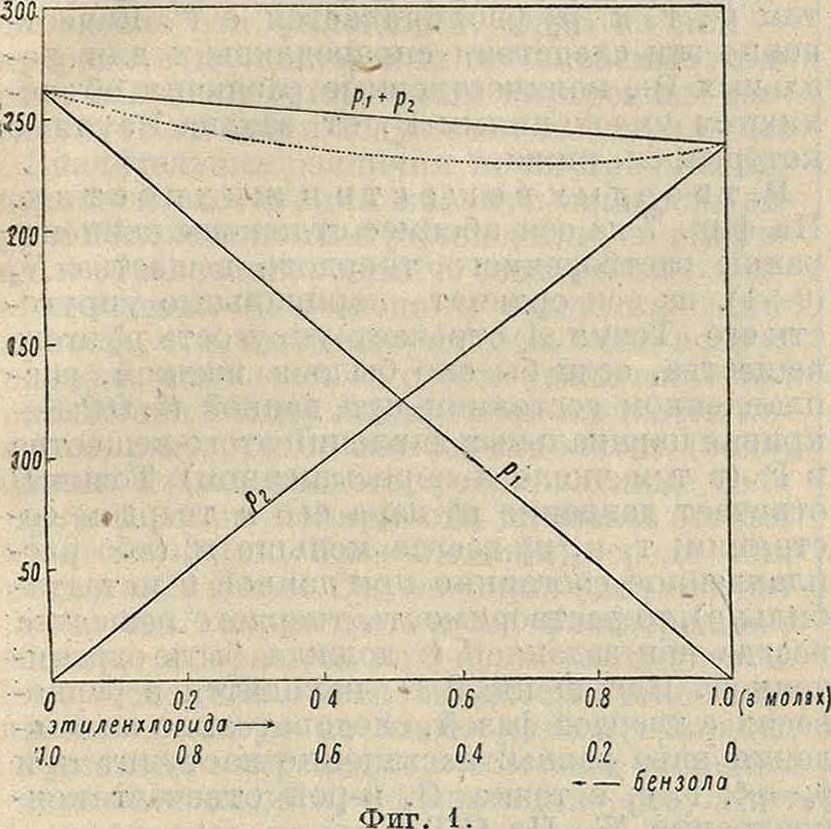
линии указывают упругости паров как функции от состава жидкой фазы; пунктирная кривая (гипербола) показывает полную упругость как функцию состава пара. Обычно реальные Р. уклоняются от закона Рауля, и можно различать два типа уклонений: положительные и отрицательные. На фигуре 2 показаны отношения между упругостями паров и составом жидкой фазы (сплошные кривые) и парообразной (пунктирная кривая для полного давления) для случая положительных уклонений.

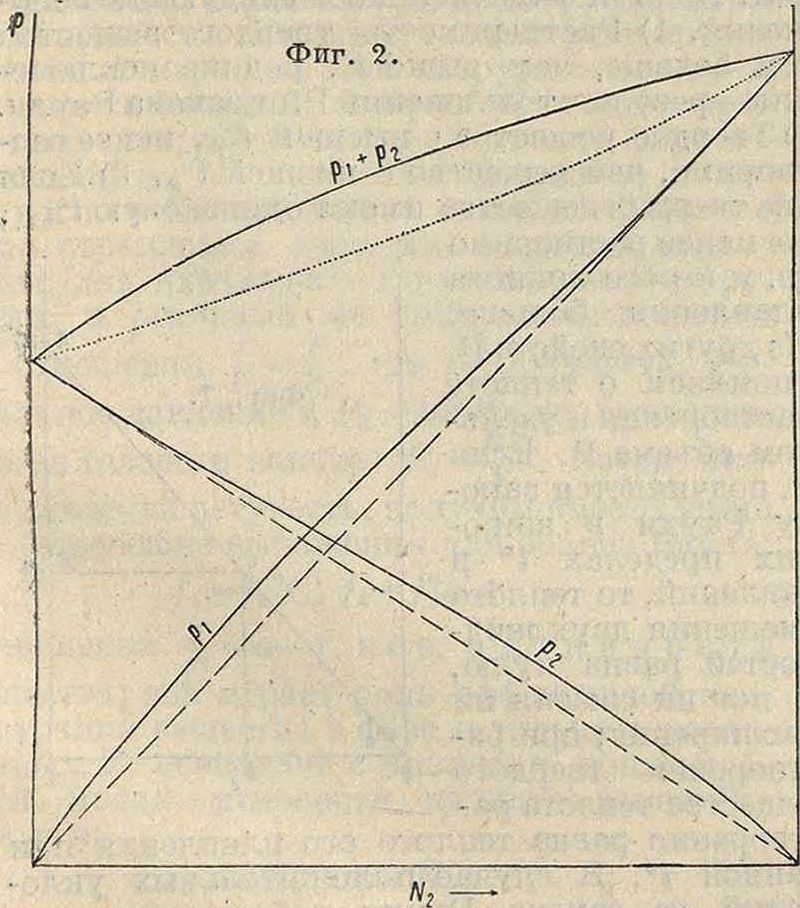
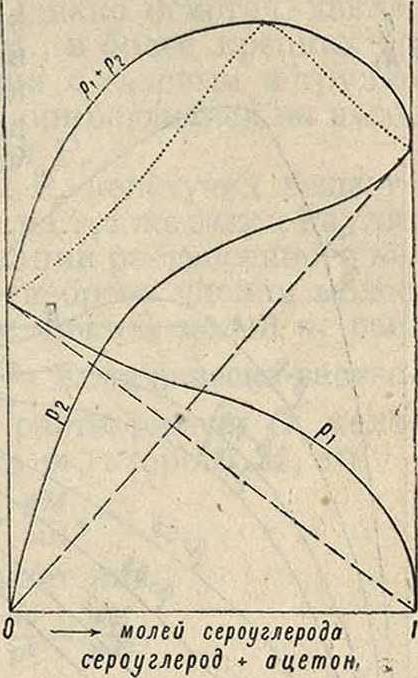
Таких Р. много; примерами могут служить -бензол + четыреххлористый углерод + этил-ацетат и многие др. На фигуре 3 приведен случай того же типа (сероуглерод и ацетон), но с такими уклонениями парциальных упругостей, что кривая полной упругости проходит через максимум (и здесь пунктирная кривая представляет полную упругость паров как функцию от состава пара). Весьма характерно совпадение максимумов обеих кривых полной упругости, что означает тождество " состава пара и жидкости в этой точке (закон Ги б б с а-Коновалова).

Р., отвечающий точке максимума,ведет себя при перегонке как индивидуальное вещество, однако и в этой точке мы имеем Р., а не химич. соединение, т. к. с изменением ί° положение максимума непрерывно изменяется. Очень характерно течение кривых парциальных давлений в верхней части (линейная часть), свойственное только неэлектролитам. Фиг.4, относящаяся к смесям ацетона и хлороформа, отвечает случаю отрицательных уклонений от закона Рауля; кривые общего давления проходят через минимум, и в этом экстремуме состав пара и жидкости одинаков. Для учета

фигура з.

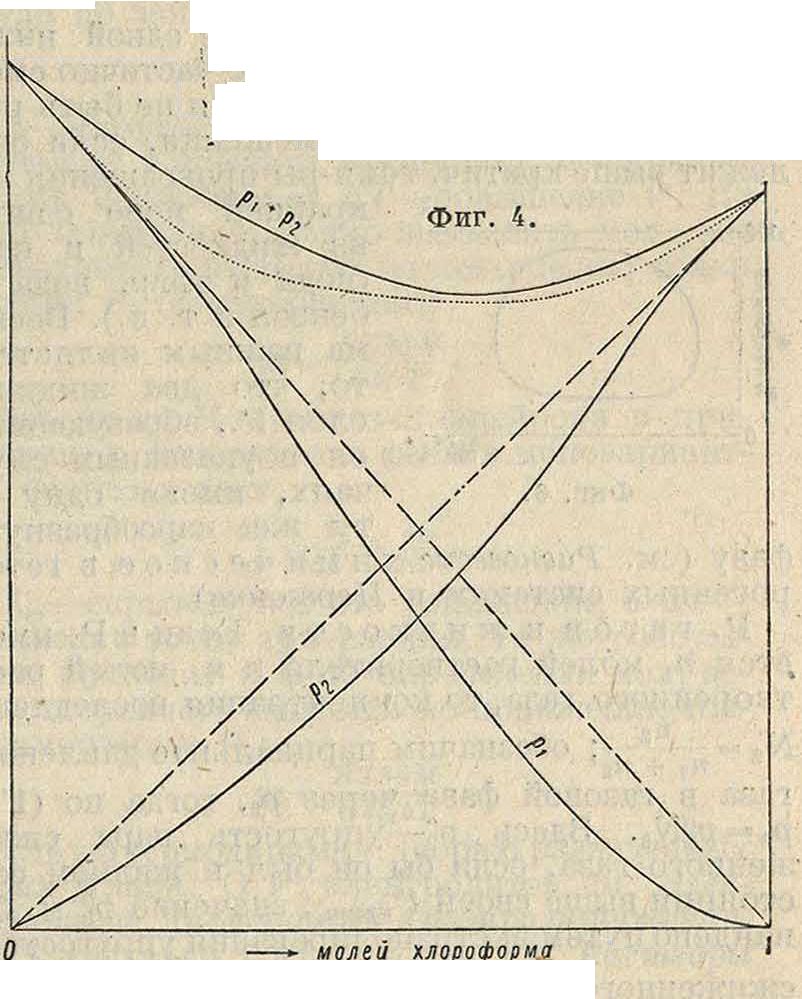
уклонений берут In -р-, разлагают в ряд и связывают с термодина.мич. ур-ием Дгогема, ш результате чего вытекает ряд важных положений. В выражении для уклонений Р. от закона Рауля имеется коэф. β.

ацетон * хлороформ

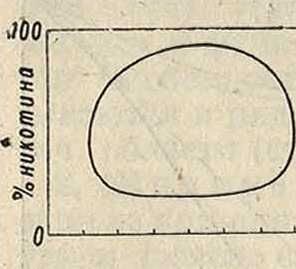
На фигуре 5 показан ход кривых парциального давления с изменением значения β, откуда видно, что при высших значениях β кривые проходят через максимум и минимум; физически это означает расслоение смеси на два слоя А и С (фигура 5). Среди лежащих ниже кривых имеется кривая с горизонтальной касательной, что отвечает наличию критической температуры смешения двух жидкостей. Общий случай расслоения смесей показан на фигуре 6 (никотин и вода) с нижней (60°) и верхней (210°) критич. темп-рами смешения: ниже 60° и выше 210° никотин и вода смешиваются во всех отношениях, но между этими 7° обра-

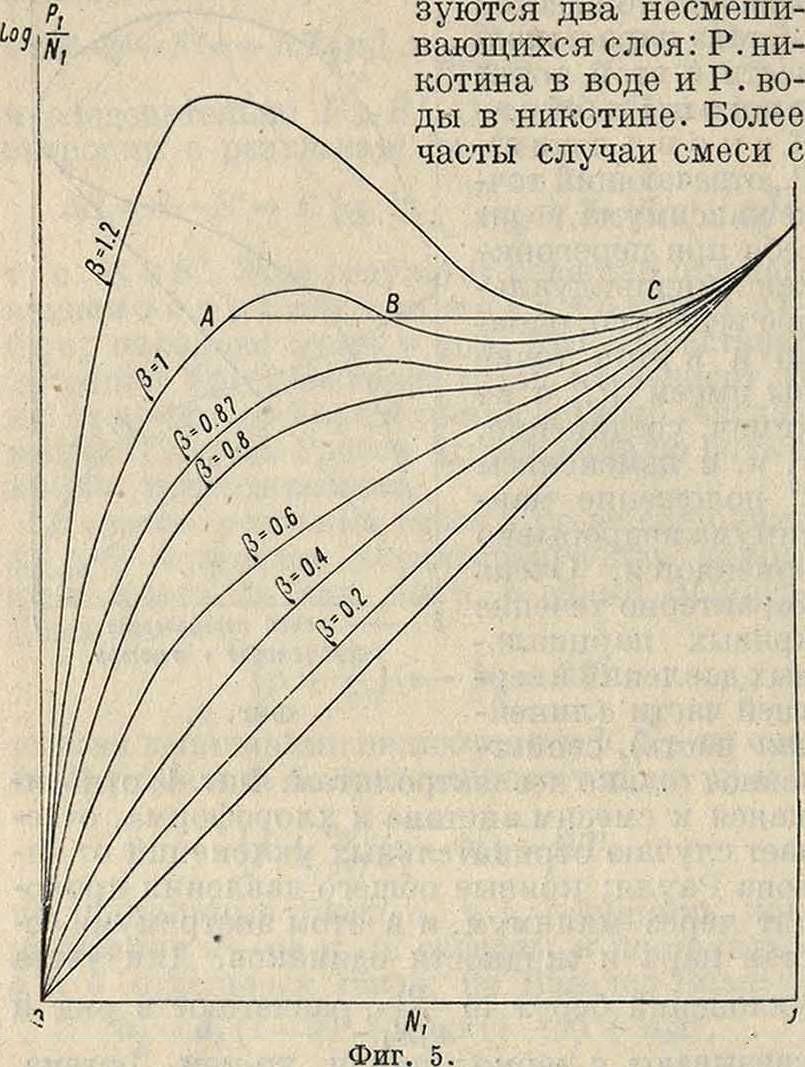
одной верхней, затем случаи с одной нижней критич. темп-рой. У двух частично смешивающихся жидкостей может и не быть реальной критич. темп-ры смешения, если она лежит выше критич. темп-ры превращения по — крайней мере одной из жидкостей в пар (вода и эфир, вода и бензол и тому подобное.). Весьма важным является то, что два жидких

, слоя Р., образующих-ягоР ся в указанных слу-Фигура 6. чаях, имеют одну и ту же парообразную фазу (смотрите Равновесие химическое в гетерогенных системах и Перегонка).

Р. газов в жидкости. Если в Р. имеется щ молей растворителя и п_г молей растворенного газа, то концентрация последнего

Н2=_п-~+_п;₂’ обозначим парциальное давление газа в газовой фазе через р?.> тогда по (1") p₂=p§iV₂. Здесь р5—упругость пара сжиженного газа, если бы он был в жидком состоянии выше своей t°_Kpum/, значение р" м. б. найдено путем экстраполирования упругостей

сжиженного газа. Из выражения N₂ =

i

обозначив -₆ через 7с, получим У₂=7ср₂—за-

кон Генри: «растворимость газа в жидкости при данной 7° пропорциональна давлению».

Из точного выражения У₂=вытекают

Р2

для идеальныхР. следующие следствия: 1) закон Генри; 2) одинаковая растворимость газа во всех растворителях при данном пар циальном давлении. Пример: метан при 25°, Рз=370 atm; при 1 atm ^{* 1}/_зт=0,0027; найдено в гексане 0,0031, в ксилоле 0,0026;

3) большая растворимость газов с высшей 7° ит.> чем с низшей, т. к. р5 в первом случае меньше; 4) падение растворимости газа с ростом 7°, т. к. р§ увеличивается с 7°. Качественно эти следствия справедливы и для реальных Р., количественные различия объясняются уклонениями Р. от закона Рауля, о которых смотрите ниже.

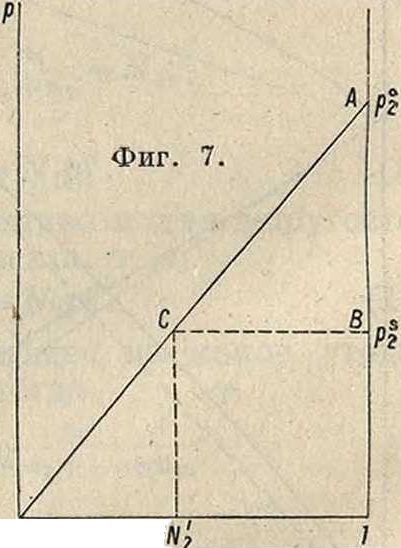
Р. твердыхвеществв жидкостях. На фигуре 7 на оси абсцисс отложены концентрации растворенного твердого вещества N₂(0-р1), на оси ординат—парциальные упругости его. Точке А отвечает упругость 2)2 этого вещества, если бы оно было в жидком, расплавленном состоянии при данной 7°. ОСА— кривая парциальных давлений этого вещества в Р. (в том числе и пересыщенном). Точке В отвечает давление р% пара его в твердом состоянии; т. к. р₂ всегда меньше р?₂ (ибо расплавленное состояние при данной 7° метастабильно), то растворимость твердого вещества всегда при заданной 7° должна быть ограниченной. Насыщенный Р. находится в равновесии с твердой фазой, следовательно их давления пара равны: насыщение наступит при р_а=р|, то есть в точке С, которой отвечает концентрация Щ. По (1")

приложив к данному случаю теорему Клаузиуса - Клапейрона, найдем замечательную формулу:

Ш(г-г,,)’

где L—теплота плавления растворенного вещества, Т_т—абс. темп-pa его плавления, Т— заданная абс. темп-pa и R—газовая постоянная. Из этой ф-лы вытекают следующие положения. 1) Растворимость твердого вещества тем больше, чем выше 7°; редкие исключения·—результат уклонений Р. от закона Рауля. 2) Твердое вещество с высшей 7°_я,. менее растворимо, чем вещество с низшей 7°_ял. 3) Если два твердых вещества имеют одинаковую 7°_и,., то менее растворимо то, у которого полнота плавления больше.

*Из других свойств Р. упомянем о теплоте растворения и удельном объёме Р. Если Р. подчиняется закону Рауля в широких пределах t° и давлений, то теплота смешения двух жидкостей равна нулю, и нет ни сжатия ни расширения; при растворении твердого о вещества теплота pa- ^Νι -створения равна теплоте его плавления при данной 7°. В случае положительных уклонений от закона Рауля наблюдается расширение Р., а теплота смешения двух жидкостей сопровождается поглощением теплоты, в случае же твердого вещества поглощение теплоты больше теплоты плавления; при отрицательных уклонениях—обратно. Уклонения от закона Рауля обусловливают и

величины растворимости: у газов и твердых веществ положительные уклонения отвечают меньшей растворимости, а отрицательные — большей, чем в случае идеального поведения. Два типа уклонений Р. от закона Рауля указывают на различные явления в них, обусловливающие эти уклонения. Одно из них — внутреннее давление; если смешиваемые жидкости обладают одинаковым внутренним давлением, то их смеси ведут себя как идеальные Р. Значительные различия во внутренних давлениях и ассоциация молекул жидкости ведут к положительным уклонениям, а тенденция к образованию химич. соединений—к отрицательным. К последним ведет также полярность, то есть несимметричность поля вокруг молекул, что влечет за собою увеличение сил притяжения между ними; такие жидкости являются растворителями электролитов (вода, аммиак, серная кислота, расплавленные соли и др.). Наличие полярности вызывает особый ряд явлений (смотрите Электролиты), среди них сольватацию. Сольватация (смотрите) состоит в том, что вокруг молекулы растворенного вещества собираются молекулы растворителя более тесно, чем в массе жидкости; такое ску-чивание молекул не имеет резкой границы, а постепенно переходит к обычным условиям в данной жидкости. Сольватация—результат ненормального притяжения между разными молекулами—влечет за собою отрицательные уклонения от закона Рауля. Если в качеств^ растворителя взята вода, то вместо общего термина сольватация применяют частный термин—гидратация. Это учение берет начало в трудах Д. И. Менделеева, рассматривавшего Р. как определенные гидраты в состоянии диссоциации. Сольватация и ионизация вместе, особенно если к ним присоединяется различие в химич. характере растворителя и растворенного вещества (кислотный и основной), вызывают сильное увеличение растворимости. Количественный учет наблюдаемых явлений весьма затруднителен из-за сложности явлений; нек-рое облегчение можно получить, вводя вместо упругости пара новые понятия летучести (Fugacity) и ак-тивности компонентов смеси. Летучесть— мера стремления вещества уйти из данной фазы; для идеального газа она равна упругости, в реальных же случаях вычисляется из отношения ц-=-б-. > ^гД^е /—летучесть, Р— ·* * 1

реальное давление и Р*·—давление, вычислен-ное из газового закона: Р₂-. Введя вме сто давлений летучесть, получим вместо ур-ий (1) следующие выражения для закона Рауля:

h=№x, /₂=№.

Отношение ~=а—т. наз. активность вещества; она играет роль эффективной концентрации вещества в фазе и только в разведенных Р. совпадает с аналитич. концентрацией. Введя активности, напишем закон Рауля так:

G&1 — -W,; а%=-NgJ ., ₄

откуда особенно ясно виден предельный характер этого закона.

Осмотическое давление Р. исторически было выдвинуто как важнейшее свойство их, исходя из которого можно вывести закономерности у Р. При изучении разведенных растворов Вант-Гофф пришел к численному равенству осмотического давления с газовым и показал приложимость к растворам уравнения nV=n₂RT,

где π—осмотич. давление, на чем он и построил свою теорию Р. Однако осмотич. давление, одно из свойств Р., в более крепких Р. уклоняется от аналогии с газовым и трудно определимо, а теория, опирающаяся на него, не может охватить всех Р.

Теория разведенных Р. нелетучих веществ по существу опирается на тот же закон Рауля; очень слабые концентрации растворенного вещества позволяют пренебречь числом молей его п г по сравнению с числом молей щ растворителя, тогдаЛ^т2= ~ · Если навеска растворенного вещества д, а растворителя G, молекулярные веса первого т, второго М, то

Па _ дм «i тG ’

и закон Рауля принимает вид рЧ-р _ Др дМ рО рО mG ’

откуда можно вычислить мол.в. растворенного вещества по понижению упругости пара растворителя. Ур-ие Клаузиуса-Клапейрона для моновариантных систем имеет следующий вид:

d In р Λ ~df HT2^-’

где Λ—скрытая теплота испарения или возгонки, и в первом приближении м. б. заменено выражением

Л In р 1 dp Др 1 i dT ~~ р * ~dT р * ΔΓ ~ ЛТ2 ’

откуда по закону Рауля для разведенных Р.

Δρ _ ΛΔΤ _ дМ •р ~~ ii Г 2 ~ тG ’

где р—упругость пара чистого растворителя (равная р° в прежних формулах), Я—скрытая теплота испарения и ДТ—повышение К Из этого выражения можно вычислить мол. вес растворенного вещества по повышению точки кипения Р. (эбулиоскопия):

_ птгдм

^m G/.ДГ

То же ур-ие Клаузиуса-Клапейрона, в применении к замерзанию фазы в моновариантных системах дает

Др i. р ‘ дг яг“’

где А_от—скрытая теплота плавления, а АТ— понижение точки замерзания. Те же рассуждения приводят к формуле определения мол. веса растворенного вещества по понижению точки замерзания Р.:

т =

RTtqM G>._mbT ‘

Полную термодинамич. теорию разведенных Р. дал Планк. О Р. электролитов см. Электролиты и Диссоциация электролитическая.

3. Твердые растворы, см. Растворы твердые.

Лит.: J e i 1 i n e k К., Lebrbuch d. physikaliseben Chemie, 2 Aufl., B. 2, Stg., 1928; KohnstammPh., Thermodvnamik d. Gemische, Handb. d. Physik, hrsg. v. H. Geiger u. K. Scheel, B. 10, B., 1926; Drucker С.» Thermodynamik d. Losungen, ibid.; Hildebrand J. H., Solubility, N. Y., 1924. А. Раковский.