> Техника, страница 76 > Регуляторы центробежные

Регуляторы центробежные

Регуляторы центробежные, механизмы, служащие для поддержания постоянства скорости вращения машин вообще и машин-двигателей в особенности. Маховое колесо выравнивает только периодические несоответствия между движущей силой и сопротивлением;

остановку машины, выравниваются автоматич. регуляторами, некоторых распространение получили только Р. ц. Автоматич. Р. ц. должен состоять по крайней мере из двух частей: 1) тахометра, то есть прибора, отмечающего отклонения скорости вращения машины от за- данной величины, причем указатель устойчивого тахометра должен перемещаться тем значительнее, чем больше это отклонение;

2) регулирующего прибора, воздействующего на приток энергии к двигателю т. о., чтобы противодействовать изменению скорости. Простейшим регулирующим прибором паровых машин, паровых турбин и прочие является дроссельный клапан, тормозящий приток пара к двигателю и понижающий давление рабочего пара; более экономично регулирование посредством изменения отсечки (смотрите Паровые машины); в двигателях внутреннего сгорания регулирующий прибор изменяет количество горючего, поступающего во время рабочего хода в цилиндр (смотрите Двигатели внутреннего сгорания). Если для перемещения регулирующего прибора требуется не большая сила (несколько кг), то тахометр связывается с регулирующим прибором системой рычагов, и получается Р. ц. п р я м о г о действ и я. Если же перестановочная сила велика, то тахометр приводит в действие только пусковой прибор (цилиндрич. золотник) особого вспомогательного двигателя, называемого сервомотором (обычно —· масляный пресс с давлением до 20 atm). Тахометр, сервомотор и регулирующий прибор составляют Р. ц. непрямого действия (смотрите Двигатели гидравлические).

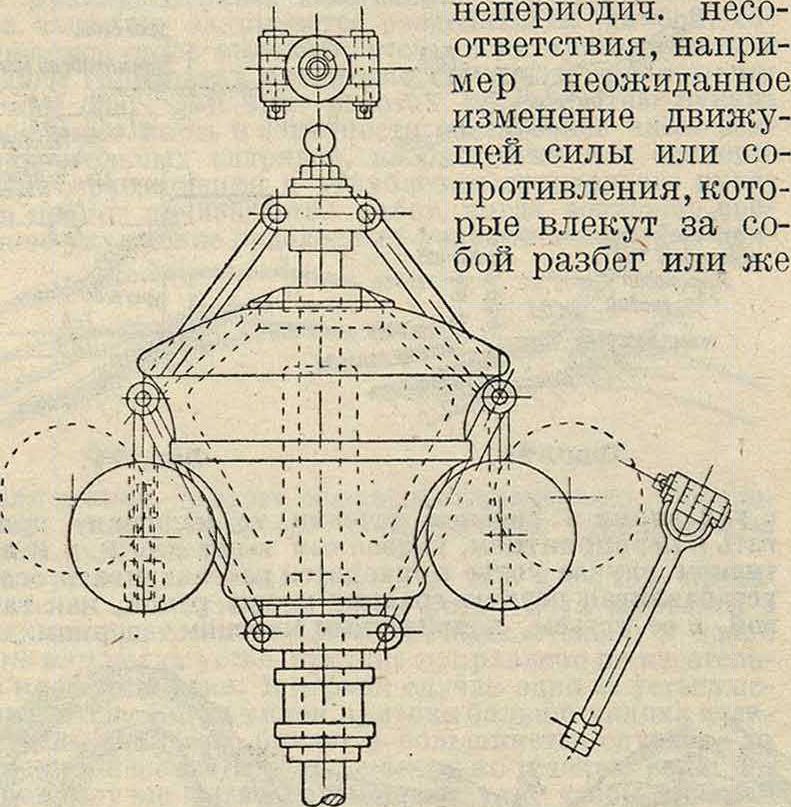
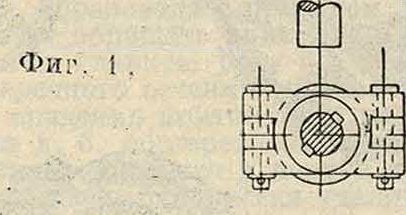
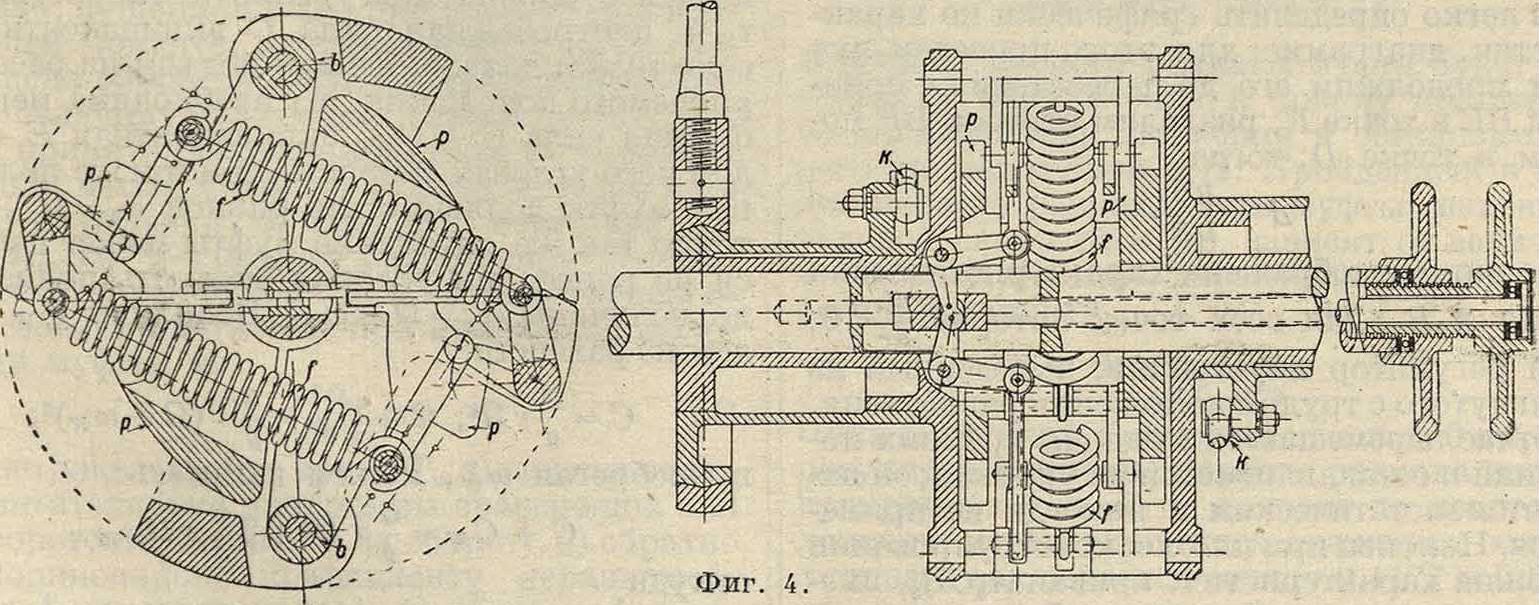
Устройство и действие регулирующих приборов так тесно связано с устройством двигателя, что мы не будем на них здесь останавливаться и повторять то, что уже было сказано о соответственных двигателях. Для расчета регулятора необходимо знать:· 1) рабочий ход регулирующего прибора, например положение муфты регулятора, при котором двигатель работает вхолостую, и положение муфты при наибольшей нагрузке; 2) перестановочную силу регулирующего прибора W_m, то есть ту силу для каждого из положений муфты, которая необходима для преодоления всех сопротивлений регулирующего прибора при его перемещении; 3) приведенную массу регулирующего прибора т_т для учета сил инерции при его перемещении. Т. о. теория Р. ц. прямого действия сводится к теории тахометра и к исследованию процесса регулирования. Старейшим типом тахометра является ромбический грузовой тахометр, носящий имя Уатта (1784 г.), известный однако в мельничном деле и описанный в литературе ранее применения его Уаттом к паровой машине. В настоящее время этот тип тахометра почти не встречается. Крупным этапом в построении тахометров было прибавление к регулятору Уатта тяжелой муфты, предложенное инж. Портером (1850 г.) и позволившее повысить число об/м. машин с 15—30 до 200. На фигуре 1 изображен совре

менный тип грузового регулятора сист. проф. М. Толле (1895 г.), состоящий из вертикального шпинделя, приводимого во вращение посредством системы зубчатых колес (ременная передача нежелательна) от коренного вала двигателя. В верхнем конце на шпинделе за-

клинена головка, несущая два шарнира для присоединения двух маятников; маятник представляет собой изогнутый стержень с шарообразной гирей и двумя шарнирами; верхний шарнир служит для сочленения маятника с головкой, так что при вращении шпинделя с той же скоростью вращаются и гири, а средний шарнир служит для сочленения маятника посредством прямой тяги с тяжелой муфтой, могущей перемещаться вверх и вниз по

шпинделю вдоль двух направляющих шпонок. Здесь изображе-

Фиг.

I на чугунная пу-I стотелая муфта, I заливаемая в ме-I ру необходимо-rtli сти свинцом; в ~Г нижн. части му ф-

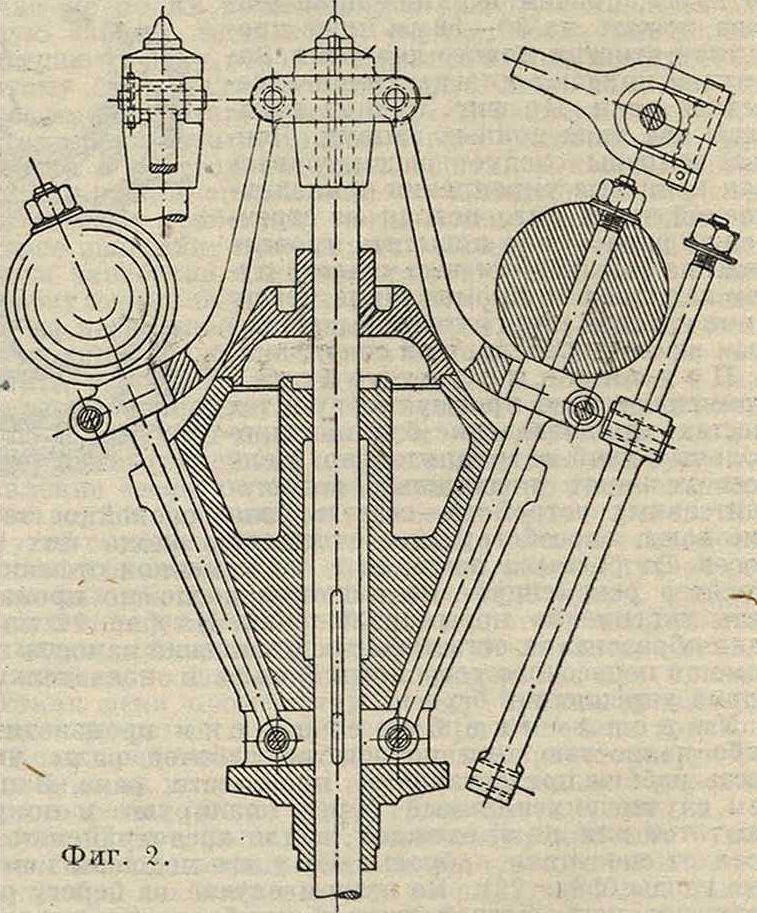
ты имеется ци-линдрич. часть, на к-рую свободно надевается невращающееся кольцо; цилиндрич. часть ограничена сверху и снизу буртиками, так что кольцо принуждено перемещаться вверх и вниз вместе с муфтой. Система рычагов передает эти перемещения кольца регулирующему прибору. На фигуре 2 изображен шпиндельный грузовой регулятор системы Прёлля, от-

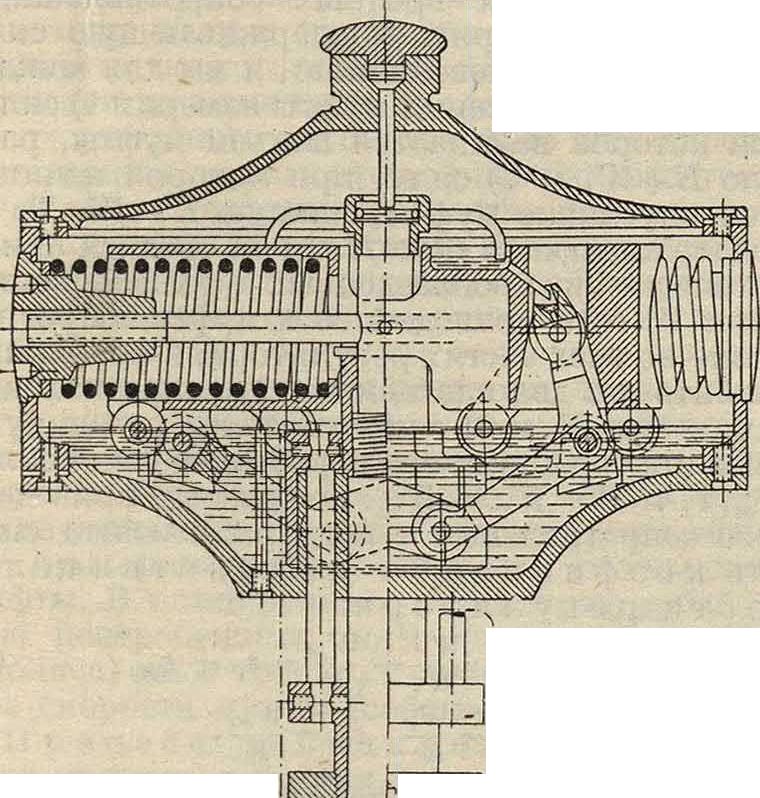
силы гирь посредством сжимаемой винтовой закаленной пружины, расположенной по линии-действия центробежной силы; силы трения, вызываются только весом гирь и перестановочной силой. На фигуре 4 в двух разрезах изображен плоский регулятор с приспособлением для изменения числа оборотов на ходу машины ; две гири р вращаются вместе с кожухом горизонтального вала; под действием центробежных сил гирь, с одной стороны, и винтовых закаленных пружин f, с другой стороны, гири могут поворачиваться вокруг шарниров b и поворачивают вместе с тем при помощи тяг к эксцентрик, изменяя его эксцентриситет и угол опережения; системой рычагов, задерживая тот или иной маховичок на конце вала, можно изменять положение точки воздействия пружины на гири и неподвижной точки каждой пружины.

Основания аиалитич. теории грузовых тахометров были впервые даны известным франц. ученым Ыавье; в настоящее время условия равновесия находятся посредством графических построений, предложенных в 1895 г. проф. М. Толле. Если заданы вес гирь G и вес муфты Q (вместе с весом рычагов регулирующего прибора), то, основываясь на общеизвестных теоремах статики механизмов, нетрудно найти такую величину С центробежной силы гирь, которая уравновешивала бы эти веса; удобнее отдельно найти величину С_д, уравновешивающую вес обеих гирь G, и величину C_q, уравновешивающую вес муфты Q; тогда С== Сд+Сд. Если г ом—расстояние ц. т. гирь от оси шпинделя и Ω ск.~³—равновесная угловая скорость шпинделя, то для определения ее по-заранее найденному С будем иметь равенство

С=-гй², я где д= 981 сж/ек². Толле предложил откладывать величину С как ординату и соответственную величину г как абсциссу для построения характеристической диаграммы

личающийся от вышеописанного только тем, что гири присоединены не к маятникам, а к продолжениям тяг. Грузовые тахометры с тяжелой муфтой в настоящее время почти не строятся вследствие значительной инертности. Современный тахометр — пружинный с возможно высоким числом оборотов шпинделя (до 500). На фигуре 3 изображена современная конструкция пружинного тахометра системы Гартунг завода Янс в Оффенбахе на Майне. Отличительной особенностью системы Гартун-га является уравновешивание центробежной

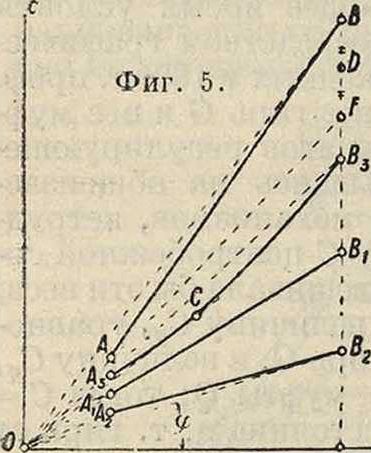
(фигура 5) исследуемого тахометра. Полученная кривая названа характеристической потому, что она наглядно характеризует квадрат равновесной угловой скорости. В самом деле иа последнего ур-ия находим: Я^а=~ ~=a tg φ.

здесь »=-|—постоянная для данного тахометра, а φ—угол между осью абсцисс и лучом из начала координат к рассматриваемой точке характеристической диаграммы с ордина-

Г)

той С и абсциссой г, так что tg.

На фигуре 5 изображено несколько типичных характеристич. кривых; первая из них А₁В₁представляет собой прямую, проходящую через начало координат; для каждой точки линии А₁В₁ угол φ будет один и тот же, откуда заключаем, что тахометр с этой характеристич. кривой имеет одинаковую равновесную угловую скорость Ω=Const для всех положений муфты; такой тахометр называется астатическим, или изохронны м; позже мы увидим,что такой тахометр непригоден для регулирования. Характеристич. диаграмма АВ типична для нормального статического, или неизохронного, тахометра; на всем протяжении АВ производная ^ > 0, то есть, чем больше г, чем выше поднимается муфта, тем больше равновесная угловая скорость Ω, т. ч. при наивысшем положении муфты равновесная угловая скорость Ω₀ больше, нежели Ω_Η при наинизшем положении ее, обыкновенно на 4—5%. Разность Ω₀—Ω_η характеризует статичность или неизохронность тахометра. Коэфициентом неравномерности, или коэф^том неизохрон-ности, Δ тахометра (центробежного регулятора) называется отношение разности равновесных угловых скоростей при наивысшем положении муфты (при г холостом ходе двигателя) и при наинизшем ее положении (при наибольшей нагрузке) к средней угловой скорости Ω,„

Δ=^н, (1)

где В_т=*/₂ (Ω₀ + Ω„). Если вывести такой тахометр из положения равновесия, то он сам возвратится обратно после нескольких колебаний или без колебаний. Коэф. неизохрон-ности легко определить графически по характеристич. диаграмме; для этого проведем луч О А и продолжим его до пересечения с ординатой BE в точке F; разделим отрезок BF пополам в точке D; тогда

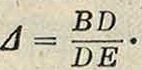
Далее внизу изображена характеристическая кривая А₂В₂, для всех точек которой ^<0;

такой регулятор неустойчив; выведенный из достигнутого с трудом положения равновесия, он тотчас перемещается в одно из крайних положений и останавливается на упорках; он называется астатическим и никогда не применяется. Наконец при плохом конструировании возможна характеристич. кривая А₃СВ_г, имеющая такую точку С, у которой касательная проходит через начало координат О. Точка С называется астатической точкой, т. к. вблизи ее равновесные угловые скорости одинаковы; кроме того участок А₃С неустойчив. Если при неподвижном невращающемся шпинделе поднимать муфту, то можно измерить ту силу Е кг, с которой действует муфта. Назовем ее поддерживающей с и jf о и или силой давления муфты регулятора {встречаются неправильны¹³ термины, как энергия или энергичность). Поддерживающая сила Е должна уравновешивать все внешние

силы, действующие в тахометре при данном положении его муфты; но равновесная центробежная сила С также должна уравновешивать эти силы, откуда заключаем, что поддерживающая сила Е и равновесная центробежная сила С эквивалентны (второе определение силы Е).

До сих пор при рассмотрении условий равновесия сил в тахометре и регулирующем приборе мы совершенно не упоминали о силах трения и других вредных сопротивлениях. Между тем измерить поддерживающую силу без сил трения невозможно, и мы для каждого данного положения муфты измерим 1) силу, при которой начинается подъем муфты, равную E + W, и 2) силу, при которой начинается опускание муфты, равную E—W. Т. о. поддерживающая сила Е равна средней арифметической из произведенных двух измерений. Сила W есть приведенное к муфте сопротивление во всех частях регулятора, к-рое можно разбить на два слагаемых: 1) сопротивление тахометра W и 2) сопротивление регулирующего прибора, или его перестановочная сила, W_m, т. ч. W= W,. + W_m. Отношение приведенного сопротивления к поддерживающей силе есть коэфициент ε нечувствительности регулятора:

5Р Ζ=Ζ?·+Ζ* -*+ (2)

E

W_r

E

W*

где e_r и — коэф-ты нечувствительности тахометра и регулирующего прибора. Обыкновенно общий коэфициент нечувствительности выбирают несколько меньше коэф-та неизо-хронности; частный коэф. нечувствительности грузовых тахометров (Толле, Прёлля, Клея и др.) бывает 1—1,5%, а пружинных системы Гартунга до 0,4% (без пружинных весов для изменения числа оборотов на ходу). Второе определение для коэф-та нечувствительности получим, представив себе тахометр вращающимся с равновесной угловой скоростью Ω. т. ч. центробежная сила С эквивалентна Е; если муфта должна начать подъем из рассматриваемого положения, то необходима центробежная сила С + С w, эквивалентная E + W, для чего угловая скорость при том же положении муфты должна стать равной ω₁=Ω + со^·; точно так же опускание муфты может начаться не ранее, чем угловая скорость понизится до величины ω₂=Ω — a>_w. Величину ω _w найдем из равенств:

0=£ г a·; c + c_w=f-r(0 + »_ж)·;

пренебрегая а>%, можем написать:

C + C_w=~ г Ω ^ζ- -2 ~ г Ωω _w,

откуда или

r=_i<JO-₅-

с w. и

2 ω γ Ω ⁼

со J - СО 2

Т. к. при данном положении муфты С эквивалентно Е, то также эквивалентны Сцг и W, откуда заключаем

W_} г, · e>j - а>2 1

t fc O Е ¹ - Ω

(3)

то есть коэф-т нечувствительности есть отношение разности той угловой скорости ω_χ, при которой муфта начинает подниматься, и той о>₂,

при которой она начинает опускаться, к равновесной угловой скорости Ω соответствующего положения муфты; различным положениям муфты соответствуют различные коэф-ты нечувствительности,’ обыкновенно в нижних положениях побольше, в верхних—поменьше.

В плоских регуляторах рабочим ходом муфты надо считать полное перемещение центра эксцентрика от его положения холостого хода до положения наибольшего наполнения. Поддерживающую силу, приведенную перестановочную силу и прочие надо в этом случае направлять по касательной к кривой вершин. Наконец для динамич. исследования плоского инерционного тахометра надо еще определить приведенную к кривой вершин касательную силу инерции; при этом обыкновенно предполагают, что тахометр получает угловое ускорение, равное 1 радиану в ск.², определяют касательные силы инерции гирь и специальных маховых масс и на основании законов статики механизмов определяют эквивалентную силу, действующую по касательной к кривой вершин. Если тахометр снабжен жидкостным тормозом—катарактом, то необходимо изучить сопротивление этого тормоза, обычно пропорциональное скорости скольжения муфты. В шпиндельных тахометрах добавочные центробежные силы (от ускорения Кориолиса) дают трение, также пропорциональное скорости муфты (собственный катаракт).

Процесс регулирования регулятора прямого действия определяется четырьмя параметрами, которые будем предполагать постоянными для всего рабочего хода муфты. Два из них уже знакомы нам: 1) коэф. неизо-хронности А и 2) коэф. нечувствительности ε; в случае плоского инерционного регулятора коэф. неизохронности надо брать динамический, равный сумме статического и инерционного, зависящего от эквивалентной касательной силы инерции. Третий параметр Т_т—время разбега двигателя или количество секунд, необходимое для того, чтобы неподвижная машина, пущенная в ход при наибольшем вращающем моменте, достигла нормального своего числа оборотов; этот параметр характеризует величину махового колеса двигателя. Если принять обозначение: I кгм ск²—момент инерции массы махового колеса, а также всех масс, вращающихся вместе с коренным валом; Ω,_η ск.¹—средняя равновесная угловая скорость коренного вала и М_и кгм—вращающий момент двигателя при наинизшем положении муфты, то

Тш-^сн. (4)

Молено доказать, что времяТ_та)зависит от типа двигателя (вид диаграммы вращающих сил за оборот, числа циклов за оборот), б) обратно пропорционально коэфициенту неравномерности δ махового колеса, в) обратно пропорционально нормальному числу оборотов п. Наконец четвертый параметр Τ_ν—время падения муфты регулятора век.—характеризует инертность масс тахометра и регулирующего прибора при быстрых перемещениях муфты. Если обозначить: т кгм^-1 ск² приведенную к муфте массу частей тахометра и регулировочного механизма; Е кг—поддерживающую силу и Н м—рабочий ход муфты тахометра, то

Г,-К¥». (5)

Чем больше приведенная масса этих органов,

тем больше Τ_ν грузовые тахометры оставлены отчасти потому, что в них приведенная масса слишком велика по сравнению с поддерживающей силой; наоборот, в пружинных тахометрах приведенная масса тем меньше по сравнению с поддерживающей силой, чем выше число оборотов шпинделя, и потому время падения Т_р мало. Исследование процесса регулирования основывается на следующих допущениях: а) величина вращающего момента двигателя является линейной функцией положения муфты регулятора; наивысшему положению муфты соответствует холостой ход двигателя и вращающий момент на коренном валу М — 0; наинизшему ее положению соответствует наибольший вращающий момент М, двигателя; для промежуточных положений муфты закон изменения вращающего момента—по прямой линии; б) равновесная угловая скорость для различных положений" муфты также имеет прямолинейную диаграмму, причем холостому ходу соответствует й₀, а наинизшему положению муфты—й_к; в) коэф. нечувствительности е, приведенная масса m и поддерживающая сила Е—постоянны для всех положений муфты. Когда установившееся движение машины будет нарушено, наир, изменением вращающего момента на х₀ долей от наибольшего момента двигателя, то процесс регулирования не начнется тотчас, т. к. трение не позволяет муфте двинуться; протечет f,=ск., пока муфта регулятора сдви-

нется и совершит первый размах. Расстояние муфты от нового положения установившегося движения не изменяется за это время и равно х₀Н; угловая скорость в момент изменения нагрузки была равна Ω_α и отличалась от равновесной угловой скорости нового положения установившегося движения Ω_ζ согласно уравнению

Ω _а=Ω.(1 Ах о), а по прошествии ск.

Ωά=Ω_ζ(ί — Ах₀ + I) ·

В течение первого размаха муфта будет двигаться по направлению к новому положению установившегося движения и остановится от него на расстоянии а Н. Пройденный в течение первого размаха путь муфты, изменение угловой скорости и прочие зависят от величины к—сводной динамич. характеристики процесса регулирования:

fc=—Чг· (в)

4 r_m4^3/2

Пока величина к заключается между 0 и 0,1177, регулятор в течение первого размаха недоре-гулировывает, то есть не доходит до нового положения установившегося движения; если величина к заключается между 0,1177 и 0,3439, то регулятор перерегулирует, то есть переходит за новое положение установившегося движения; если к > 0,3439, то расстояние муфты от нозого положения установившегося движения в конце размаха будет больше, чем в начале, т. ч. после каждого размаха муфта будет удаляться все больше от этого положения. Поэтому при к>0,3439 процесс регулирования неустойчив, он никогда не кончится. При fc= =0,1177 будем иметь наивыгоднейший процесс регулирования, т. к. муфта после первого же размаха приходит в новое положение установившегося движения.

После первого размаха может последовать остановка на некоторое время, если коэф. нечувствительности удовлетворяет неравенству ε>Αχ^α, где А—коэф. неизохронности, х₀— доля изменения нагрузки, а—множитель нечувствительности—функция от к (столбец 2 табл. 1). Если ε меньше этого наименьшего

Таблица 1, —Процесс регулирования с остановками.

h	а	Ь	С	d
0,0100	0,0278	0,8826	0,1138	0,9104
0,0200	0,0328	0,7741	0,2187	0,8069
0,0404	0,0894	0,5717	0,4151	0,6611
0,0612	0,1594	0,3956	0,6026	0,5551
0,0829	0,2401	0,2307	0,7864	0,4708
0,1057	0,3314	0,0755	0,9704	0,4069
0,1177	0,3811	о,оосо	1,0635	0,3814
0,1300	0.4059	0,0735	1,1579	0,3325
0,1563	0.5477	- 0,2186	1,3519	0,3292
0,1850	0,6759	- 0,3603	1,5557	0,3156
0,2166	0,8196	- 0,5043	1,7717	0,3153
0,2520	0,9730	- 0,6519	2,0041	0,3210
0,2918	1,1680	- 0,7935	2,2568	0,3745
0,3439	1,4536	- 1,СС00	2,5833	0,4537

допустимого коэф-та нечувствительности, то остановки не будет, и второй размах начнется тотчас же, причем направление движениямуфты будет непременно противоположно; условия устойчивого процесса регулирования в этом случае несколько сложнее. Если же ε>Αχ₀α, то после непродолжительной остановки начинается второй размах. К концу первого размаха отклонение муфты равно о И; величина ж, также является ф-ией динамич. характеристики к и определяется из равенства х_г=х₀6, где Ь—множитель отклонения муфты от нового положения равновесия (указанный в столбце 3 табл. 1). Из таблицы видно, что с увеличением к величина b все уменьшается, при fc=0,1177 равна нулю (наивыгоднейший процесс), а затем становится отрицательной (перерегулирование). В конце второго размаха расстояние муфты от нового равновесного положения составляет такую же долю от х_хН, как и во время первого размаха, то есть х_г=х_уb. В табл. 1 (ст. 3) указаны эти отношения b расстояний в конце и в начале каждого из размахов; если для начала первого размаха оно приблизительно равно ж₀ (диаграмма вращающих моментов двигателя в зависимости от положс-“° ния муфты предполагается- прямо-Фигура 6. линейной), то в конце первого^ размаха оно равно Ь-х₀, в конце второго размаха Ь²х₀ и т. д., в конце и-го размаха Ь^п-х₀, то есть в этом случае амплитуды убывают в геометрич. прогрессии до тех пор, пока отклонение угловой скорости не станет менее коэф-та нечувствительности.

Продолжительность каждого из размахов определяется из ф-лы

Т= АТ_т · с,

где с—множитель продолжительности размаха (в ф-ии от характеристики к) указан в 4-м столбце табл. 1. Величина угловой скорости ω_η двигателя к концу я-го размаха м. б. определена из ур-ия:

си_и=й_г(1 + |-^ж₀й&““¹);

здесь Ц,—равновесная угловая скорость но

вого установившегося движения, остальные величины уже знакомы, a d—множитель изменения угловой скорости, указанный в δ-м столбце табл. 1. Зная величину динамич. характеристики к, при которой процесс регулирования наивыгоднейший, можно подобрать коэф. неизохронности А=А_д так, чтобы он был осуществлен; решая ур-ие (6) относительно А, найдем наивыгоднейший коэф. неизохронности

4= 1,652 1/^. (7)

Проф. Толле дает

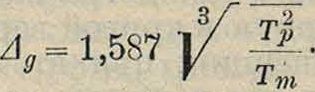
Наименьший допустимый коэф. неизохронности A_min по нашим исследованиям

А_тЫ=0,7903 у |f. (8)

⁷ 1 т

Проф. Толле дает

^тгп ~ 0,7937

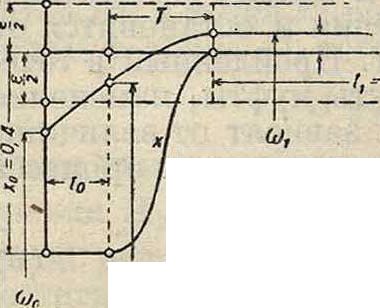
Поясним применение табл. 1 следующими примерами. 1) Наивыгоднейший процесс (смотрите фигура 6). Пусть ж₀=0,4; ε=0,02; Т_т=10 ск.; Т_р=0,03768 ск. Требуется подобрать наивыгоднейшее значение А по уравнению (7)

А_д=1,652 f(0,003768)²=0,04.

В начальный момент ж₀=0,4 Я, где Я—рабочий ходмуфты; е»₀=Ω_ζ(1-Αχ_Β)=й₂(1-0,016). Муфта начинает двигаться по прошествии вре-

мени ί₀== 0,25 ск. За это время угловая

AXq

скорость станет равна соо=fl,(l + I - Δχο)=Ω,(ί - 0,006).

Первый размах будет длиться Т=АТ_тс== 0,4252 ск.,; муфта за это время станет как-раз в свое новое равновесное положение ж,=х_яЬ== 0; угловая скорость к концу размаха будет со,=β„(ΐ + 2 - Δχ₀(ή=Ω_ζ(1 + 0,0039).

Отклонение от равновесной угловой скорости Ω_ζ менее половины коэф-та нечувствительности. В этом положении муфта и остановится; процесс регулирования ограничивается одним размахом.

2) Процесс с недоре гулирова-н и е м (фигура 7). Пусть при прежних данных и А=0,04 величина Т_р=0,024 ск.; по ур-ию (6) к=0,075. Интерполированием из табл. 1 находим: α=0,2107; 5=0,2907; с =0,7195; d== 0,5015. Неравенство ε>Αχ₀α соблюдено. Предварительная стоянка муфты длится в

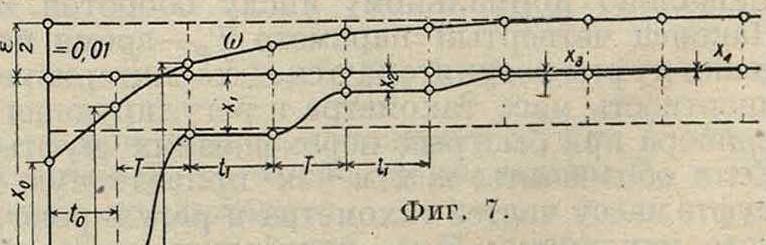
J течение ί„=0,25 секунд. Попреж-ю “< нему начальная угловая скорость ω» οι, ω₀=Ω_ζ( —0,016); к концу стоянки β>ή=#>(1 — 0,006). Каждый размах длится Т= 0,04 -10 - 0, 7195=0,2878 ск. К концу первого размаха a"i=bx₀=0,2907-0,4= 0,1163 от величины II:

ω_λ=ίλ(ΐ + - Δχ_ύ<ή=Ω_ζ( + 0.00198).

Муфта стоит неподвижно: ί₁=ΔΤ_Μ·— =

= 0,3235 ск.; за это время угловая скорость станет ω=й₂(1 + 0,00535). К концу второго размаха х₂=b²х₀= 0,03677 и

ω₂= Ω₈(ΐ + ^-ΔχΜ)=й_г(1 + 0,007667).

Вторая остановка такой же продолжительности, как и первая: t_z— (,=0,3235 ск.; к ее концу о>₂=Ω_ζ(ΐ + -Δχ₀ϋή=Ω_ζ(1 + 0,008648).

Третий размах: х₃=b³х_и=0,01069 и

. ω₃=Ω₂(ΐ + ^ε- - Δχ^ή=й,(1 + 0,009322).

Третья остановка: ί₃= + к ее концу

⁴ с«з=Ω_ζ(ί + ^ε-~Δ ж₀6³)=Ω.(1 + 0,003607).

Четвертый размах: ж₄=bх₀ и т. д. Муфта все ближе и ближе к новому равновесному положению ш=0. Угловая скорость все ближе к угловой скорости

«>_г=As(i +1)=Аг(1 + 0,01).

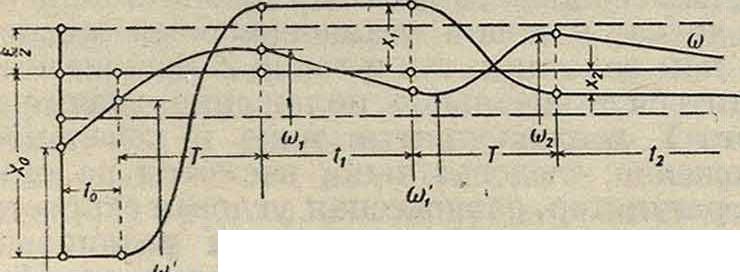
. 3)^Дроцесс с перерегулирование м (фигура 8). Прежние данные, но Т_р== 0,0592 ск. По ур-ию (6) /с=0,185 имеется

Фигура 8.

выше в таблице 1. Предварительная остановка: ί₀=0,25 ск. Начальная угловая скорость из <о₀=Ω_ζ(1 — 0 016) становится равной ω’„ =Ω_Ζ(1 — —0,006). Продолжительность каждого размаха Т=0,6223 ск. После первого размаха х_х== 0,3603+,= - 0,1441 и

ω,=β,(ΐ + - Δχβ)=Ω_ζ(1 + 0,00493);

первая остановка длится t_x= — ΔΙ

= 0,638 ск. (под Ь в дальнейшем понимаем абсолютную величину b=0,3603; знак минус во всех дальнейших ф-лах уже учтен); к концу первой остановки:

ω=0,(1 - + Ах_аъ) -0,(1-0,00424.). Второй размах: ж₂=(0,3603)^а+=+ 0,05166 и ®,=0,(ΐ+ |- Ax_abd )=0,(1 + 0,00818);

, ε T_WI, Ь -f- cl

вторая остановка длится ί₂=ь»х~^m ~ТГ ⁼ = 3,100 ск.; к ее концу со;=О, (l — I + Δχφ*)=0,(1 - 0,017922). Третий размах: х₃=— b³х₀=— 0,00187 и со₃=Ω_ζ(ΐ + 2 — Δχ₀№(1^;

i εΤ jji _л m b -Ь d

третья остановка длится t_z=^₃— — Δ1 _m —==9,94 ск. и со;=0,(1 -| + Лх₀b*)=0,(1-0,00928).

Итак, в случае процесса с перерегулированием муфта после каждого размаха становится все ближе и ближе к новому равновесному положению х=0; уменьшение расстояний идет в геометрия, прогрессии с знаменателем Ь; при каждом размахе муфта переходит через равновесное положение; между размахами муфта стоит некоторое время неподвижно, причем продолжительность остановок все удлиняется; угловая скорость все время то больше то меньше Ω, и постепенно приблиэкается то к

-О. (l + * ε) то к Ω, (l— При этом предполагается, что регулятор не имеет жидкостного тормоза (катаракта), а воздействие муфты регулятора на двизкущую силу машины непрерывно. В двигателях внутреннего сгорания и в паровых машинах с переменной отсечкой это последнее предполозкение не выполняется, т. к. только в момент подачи горючего или в момент отсечки полозкение муфты регулятора влияет на средний вращающий момент в течение последующего рабочего цикла. Такой процесс регулирования называется прерывным; начало его исследованию было положено Карглем (1781 г.); проф. Η. Е. Жуковский (1909 год) доказал, что для очень быстроходных машин условия устойчивости прерывного процесса такие же, как и для непрерывного.

В исследовании прерывного процесса автором были вычислены (1928 год) отклонения к концу первого размаха для тех же самых динамических характеристик, для которых был ранее исследован непрерывный процесс; отклонения зависят от особого параметра а. называемого мерой тихоходности машины:

__ 120J л. ~ ПШТр

(9)

где п—число об./м. коренного вала, a m— число рабочих циклов машины в течение одного оборота (например для однокривошипной паровой машины двойного действия или тендем т= 2; для двукривошипной, с углами 90°, паровой машины т=4; для одноцилиндрового четырехтактного двигателя внутреннего сгорания простого действия· т=0.5 и т. д.). В исследовании величины а изменялись от 0 до 6,283 (= 2 π) через 30°. Случай α= 0 есть предельный случай столь быстроходной машины, для которой прерывный процесс то-зкдествен с непрерывным. Не приводя здесь полного табличного материала, иллюстрируем влияние меры тихоходности а на наивыгоднейший коэфициент неизохронности Δ₃, определявшийся для непрерывного процесса уравнением (7) с множителем перед корнем к=1.652; при а>0 А возрастает и может быть определен интерполированием из следующей табл. 2.

Таблица 2.—3 а в и сим ость коэфициепта А от меры тихоходности а.

а.	0	0,1745	0,5230	1,0472	1,5708	2.0944 2,6180 1
А.	1,652	1,685	1,742	1,813	1,866	1,892	1,307
а.	3,1416	3,6652	4,1888	4,7124 5,2360 1		5,7596 6,2832 1
А.	1,947	2,009	2,069	2,111	2,134	2,145	2,145

Вторым, невыполняемым обыкновенно предположением является прямолинейность диаграммы вращающих моментов в ф-ии положения муфты; вследствие невыполнения этого предположения многие регуляторы при одних нагрузках работают удовлетворительно, а при других—неустойчивы.

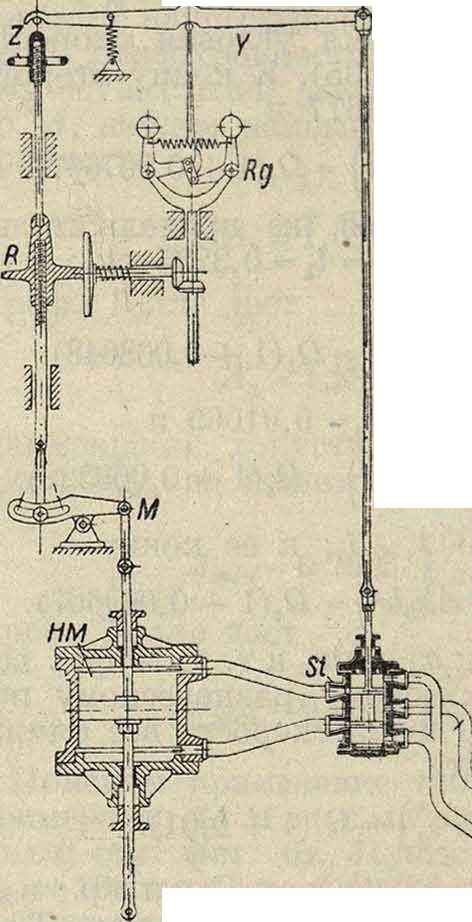
Регулятор непрямого действия простейшего типа схематически изображен на фигуре 9. Он состоит из тахометра R_g с муфтой Y, масляного пресса (сервомотора) НМ с пусковым прибором S_t (цилиндрич. золотник) и простого дроссельного регулирующего прибора, приводимого в движение от поршня масляного пресса через посредство рычага и зубчатых секторов. Новой и необходимой частью является

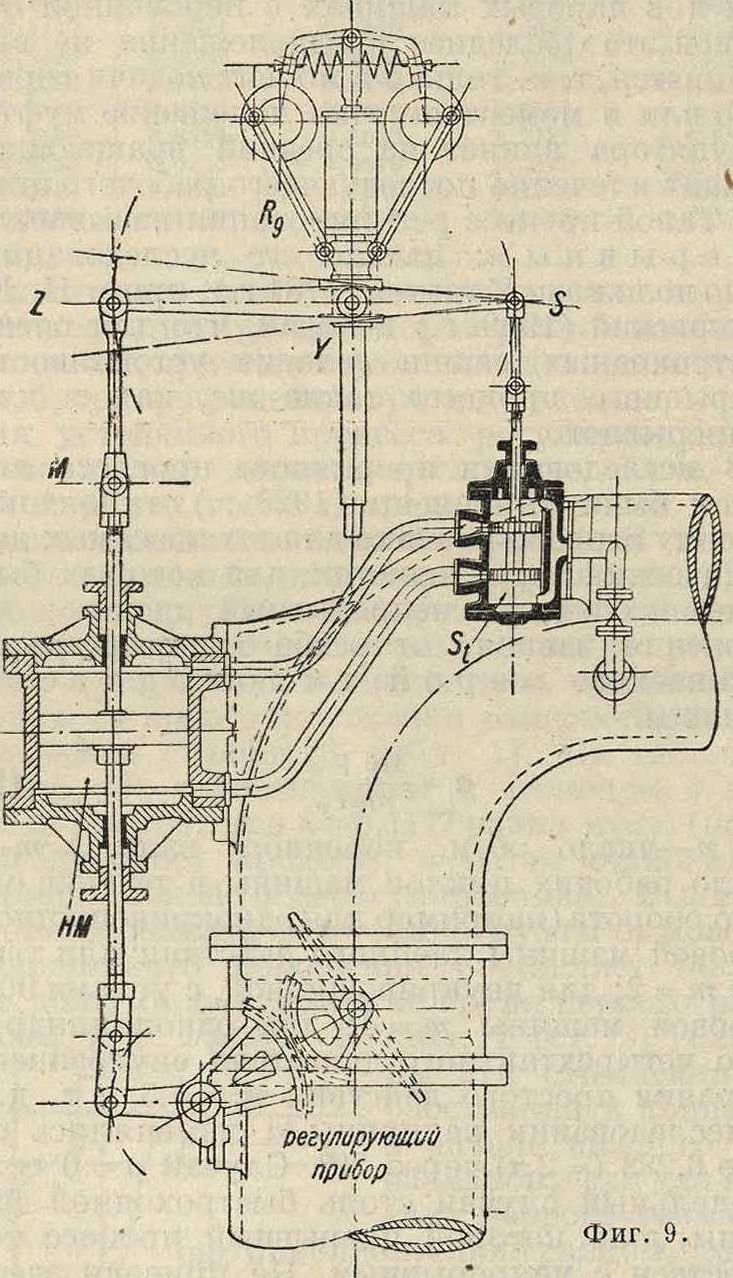
выключатель, сочленяющий точку М пресса с пусковым прибором S_t. При повышении числа оборотов муфта У поднимается и, пока М неподвижно, поднимает посредством рычага ZYS золотник S,-жидкость под напором устремляется в нижнюю половину цилиндра пресса, а из верхней выпускается в атмосферу; поршень поднимается, приток напорной жидкости к двигателю закрывается дроссельным клапаном; одновременно с поднятием точек М и Z золотник закрывает приток напорной жидкости в пресс и этим предотвращает перерегулирование.

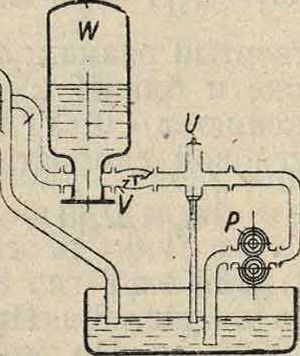
На фигуре 10 изображена схема более сложного, изодромного регулятора, причем одноименные с фигура 9 части схемы обозначены теми же буквами; здесь показан зубчатый насос Р, подающий под давлением до 20 atm масло в резервуар с воздушным колпаком W через обратный клапан V; через предохранительный клапан U масло возвращается в спускной резервуар в случае, когда давление в W превзойдет определенный предел. Главным отличием изодромного регулятора является податливый выключатель; гайка R снабжена фрикционной передачей к постоянно вращаемому от регулятора диску;по ка соприкасание происходит у центра диска, гайка не вращается ни в одну сторону, но стоит только поршню сдвинуть точку М, фрикционная передача начнет нави н-чивать или свинчивать гайку до тех

Фигура 10.

нор, пока соприкасание не оудет опять на центре диска; в новом установившемся движении как золотник, так и точка Z должны возвратиться в начальное положение, значит и муфта У должна прийти тоже в начальное положение; следовательно, несмотря на ега-тич. регулятор, равновесная угловая скорость установившегося движения при различных нагрузках двигателя будет одна и та же. Незначительные ее изменения м. б. произведены вручную посредством поворота маховичка Z.

К динамич. характеристикам регулятора прямого действия в регуляторах непрямого действия прибавляется еще время Т_а закрытия прессом регулирующего прибора в ск., равное рабочему ходу поршня, деленному на максимальную скорость поршня при полном открытии золотника. Условие устойчивого процесса регулирования при жестком выключателе в случае оченьбыстроходноготахометра с ничтожно малым временем падения Т_р приближенно выражается неравенством ΔТ_т > 4Т_а.

Изодромный регулятор с быстроходным тахометром всегда дает устойчивый процесс регулирования.

* Лит.: Вышнеградский И. А., О регуляторах прямого действия, Известия С.-Петербургского Технология, института, СПБ, 1877; его же, О регуляторах непрямого действия, там же, 1877; Сидоров А., Плоские регуляторы быстроходных машин, М., 1895; Линен В., Расчет центробежных регуляторов, пер. с нем., СПБ, 1900; Кондратьев А., Центробежные регуляторы, СПБ, 1901; Николаи Е.Л., Регулирование машин, Ленинград, 1930; Жуковский Η. Е., Теория регулирования хода машин, ч. 1, М., 1909 (литогр.); Рерих К., Влияние трения на процесс регулирования центробежных регуляторов прямого действия, «Известия Екатеринбургского горного института», Екатеринбург, 1924, т 14; его ж е, Влияние быстроходности двигателя на прерывный процесс регулирования, Известия Днепропетровского горного ин-та·, Днепропетровск, 1928, т. 15; М а к е-е в, Работа регуляторов первичных двигателей истребования, предъявляемые к ним при параллельной работе, «Тепло и сила>, Москва, 1929, 3; Сонги H,JPe-

гуляторы водяных турбин Ленинградского металлического завода, там же, 1930, 8—9; Тиме, К расчету регулятора водяной турбины е механическим фрикционным изодромом, там же, 1930, 11; Tolle М., Rege-lung d. Kraftmaschinen, Berechming u. Konstruktion d. Schwungrader des Massenausgleichs u. der Kraftmaschi-nenregler in elementarer Behandlung. 3 Auflage, Berlin, 1921; H о r t, Die Entwicklung des Problems d. stetigen Kraitmaschinenregulierung nebst einem Versuehe d. Theorie unsteliger Regelungsvorgange, «Ztschr. f.JIathematik u. Physik», Lpz., 1904, p. 233—280. K. P.p^x.