Резонанс

Резонанс в физике, явление, заключающееся в том, что амплитуда вынужденных колебаний в колебательной системе, обладающей не слишком большим затуханием, достигает отчетливо выраженного максимума при определенных соотношениях между параметрами системы и какой-либо из частот гармо-нич. колебаний, содержащихся в действующей на систему внешней возмущающей силе, причем при уменьшении затухания системы значение максимума беспредельно возрастает. В большинстве случаев это соотношение между гармонии. частотами внешней силы и параметрами системы сводится к тому, что какая-либо из этих частот приближается к одной из частот собственных колебаний, свойственных данной колебательной системе. Явление Р. в одинаковой степени типично как для механических, так и для электрических (или «смешанных»—электромеханических) колебательных систем и поэтому играет весьма важную роль в самых разнообразных отделах физики и техники. В нек-рых случаях явление Р. играет положительную роль (например в радиотехнике для целей радиоприема), в других случаях, наоборот, возникает вопрос об устранении явления Р., т. к. наступающее при этом нарастание амплитуды колебаний в системе является нежелательным или даже опасным для данной системы (например в механич. сооружениях, находящихся под действием переменной нагрузки или подвергающихся действию повторяющихся толчков). Характер Р. зависит от свойств как самой колебательной системы, в которой происходит явление, так и от свойств внешней возмущающей силы, действующей на систему, однако явление протекает совершенно одинаково как в механических, так и в электрич. колебательных системах, и поэтому анализ явления электрич. Р., приводимый низке для случая электрич. колебательных систем, м. б. путем замены параметров и координат электрич. системы (самоиндукция, сопротивление, емкость, заряд, сила тока) соответствующими параметрами и координатами механич. системы (масса, коэф. трения, упругость, смещение и скорость) перенесен полностью на механич. Р.

Р. в линейной системе с одной степенью свободы. Наиболее простой характер имеет явление Р. в случае системы с одной степенью свободы, с постоянными параметрами и гармонической, то есть изменяющейся _R по закону синуса, внешней си-

g^vwvw-1 лой. Системы с постоянными па-

I j раметрами, не зависящими от

Ii -Lf координат и скоростей, будем в дальнейшем называть линей-I ^ ными колебательными

Cyj_c системами. Такой линейной

_фш, [ системой является обычный ко лебательный контур (смотрите Колебания электрические), состоящий из емкости С, сопротивления В. и самоиндукции L (фигура 1.) Внешнюю эдс мы будем для простоты считать введенной непосредственно в электрич. контур (в случае если внешняя эдс введена иначе, например путем индуктивной связи с какой-либо электрич. цепью, характер явления остается неизменным и лишь несколько видоизменяются количественные соотношения). Для рассматриваемого случая, пользуясь законом Кирхгофа, получают следующее линейное диференциалыгое ур-ие второго порядка:

d²q

ΊΠ2

aq d t

_c=K₀sin cui,

(1)

где q—заряд на оокладках конденсатора π следовательно ^—сила тока в контуре. Общий интеграл этого ур-ия состоит из двух частей—общего интеграла ур-ия (1), но без правой части, и частного соответствующего периодическому решению интеграла этого ур-ия с правой частью—и имеет следующий вид (смотрите Колебательное движение):

q=q„e~^at sin (<u— qp) -(-

E о

sin(coi — ψ), (2)

В 2

где α= ₂у- — показатель затухания, ω_λ =

= [А»² - Cl²=£с~^а2

бодных колебаний в системе, со₀ =

-угловая частота сво-

Ylc

- угло вая частота «собственных» колебаний при отсутствии затухания и ψ—сдвиг фазы между напряжением внешней силы Е и напряжением, возникающим на обкладках конденсатора С вследствие наличия вынужденных колебаний в контуре. Этот сдвиг фазы определяется соотношением:

2αω

Ο)

Величины q₀ и φ в формуле (2)—константы интеграции, определяемые начальными условиями. Полученное выражение (2) вполне характеризует как само явление Р., так и процесс установления этого явления. Сначала в системе существуют два колебания—одно собственное, затухающее с частотой свободных колебаний системы ω₁ и убывающей по времени амплитудой (затухающее и поэтому не-периодич. колебание), и другое—вынужденное, с частотой вынуждающей силы со и постоянной амплитудой (периодич. колебание). Через достаточно долгое время собственные колебания с частотой а>₁ затухнут, и в системе установится чисто периодич. процесс, причем заряд на обкладках конденсатора будет определяться выражением:

q=г- ¹, ==— sin (ωί - ψ). (4)

Сила тока в контуре г=и следовательно в рассматриваемом случае, диферепцируя выражение (4), получим:

" ^Е0 .cos (ω t — ψ). (Б)

/1

Наконец эдс самоиндукции e_L, возникающая на зажимах катушки самоиндукции, есть

_Т di

¹=ΊΠ’^Τ· ^е·

«ζ =

-Е ₀α>

V^r[^Lu>~k]^i+R2

: Sin (ωί — ψ).

(С)

Легко видеть, что как амплитуда переменного заряда на обкладках конденсатора, так и амплитуда силы тока в контуре и амплитуда эдс самоиндукции—функции частоты внешней силы и параметров системы L, С я R. При известных соотношениях между со и параметрами системы амплитуды эти достигают максимума—в этом случае имеет место явление Р. Если достаточно медленно изменять частоту внешней силы, оставляя параметры контура неизменными, то амплитуды q, г и е/, будут изменяться по законам, определяемым выражениями (4), (5) и (6). Графич. изображение этих изменений, то есть кривые, характеризующие зависимость амплитуд q, г и e_L от частоты со, носят название кривых резонанса. Т. к. кривые Р. для заряда конденсатора, силы тока в контуре и эдс самоиндукции несколько отличаются по своим свойствам, то мы рассмотрим эти кривые отдельно.

Кривая Р. для заряда конденсатора (а вместе с тем и для напряжения па обкладках конденсатора V, т. к. между ними существует прямая пропорциональность: V=определяется ф-лой:

п —^{Ео 1}

чо —

/[«-•-и

(?)

Максимум этой ф-ии от си мы найдем, диферен-цируя выражение (7) по си:

9<7о до)

^2L2J

Е₀

/г

Χ,ω²

_μ--·]*₊*.}{

Это выражение обращается в нуль, если

[--£Ι+£-ο.

или если си² — ^ω?> ~ 2а²,

или наконец (т. к. (uf=co§—а²), если а)²=сиу —а².

Следовательно Р. для амплитуды заряда конденсатора, а значит и для амплитуды напряжений на обкладках конденсатора наступает при частоте си,., меньшей, чем частота свободных колебаний системы ω_1: а значит и меньшей, чем частота собственных колебаний си„, которой обладал бы контур при отсутствии затухания, но различие между си,. и ω₀ тем мепь-Ф) ше, чем меньше затухание. Для того чтобы выяснить свойства рассматриваемой кривой Р., определим значения q_a при предельных значениях си=со и со=0. При си->оо величина у,-> 0, а при со->0 величина <7., стремится к определенному значению Е,С. Это есть статич. заряд на обкладках конденсато-17 tu ю 15 г “* р_а> созданный посто-Фнг. 2. янным напряжением,

равным Ε_ί. Таким образом основные черты резонансной кривой для амплитуды заряда на обкладках конденсатора или, что то же самое, для амплитуды напряжений на конденсаторе следующие (фигура 2). Максимума эти

*14

амплитуды достигают при внешней частоте со?=<»3 — 2 a=а>1 — а². При малом затухании, т. к. со,=со₀, значение этого максимума

^Ко КдСлУ.

Чтах — фЩ _а

то есть амплитуда напряжения при Р. примерно в ” раз больше статического напряжения

(с5—логарифмический декремент затухания). При убывании ω от значения со, эти амплитуды падают, стремясь однако к определенному конечному значению. При возрастании со после значения со“ амплитуды снова падают, но уже стремясь к нулю.

Кривая Р. для силы тока определяется следующей ф-лой:

i, · - "^а (8)

И 2

Максимума эта кривая достигает при условии ^ω}=Ζδ или ο)₍=ω₀,

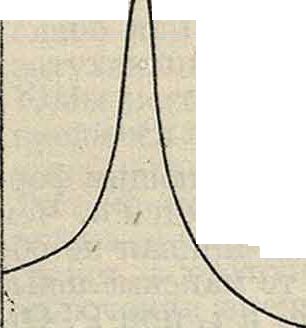
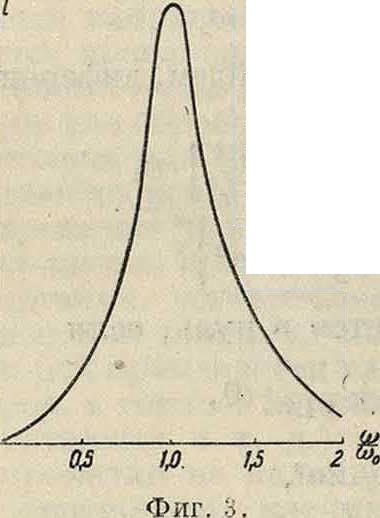
то есть когда частота внешней эдс совпадает с собственной частотой контура со₀, то есть частотой, которой обладал бы контур при отсутствии сопротивления. При крайних значениях со -* 0 и со -* оо кривая стремится в обоих случаях к нулю, то есть по обе стороны от Р. сила тока уменьшается и спадает до нуля (фигура 3).

В этом и заключаются основные различия между кривой Р. для амплитуды силы тока и кривой Р. для амплитуды напряжения на обкладках конденсатора. Положения Р. для амплитуды заряда и амплитуды тока сдвинуты друг относительно друга тем меньше, чем меньше затухание а. Скорость спадания кривой Р. по обе стороны от максимума, то есть «острота» кривой Р. или «ширина» кривой Р., а вместе с тем и значение той максимальной амплитуды напряжений или силы тока, которых достигают вынужденные колебания при данной амплитуде внешней силы it данной собственной частоте контура су₀, целиком определяется отношением -£, то есть показателем затухания α= ~. Действительно выражения

(7) и (8) мы можем привести к виду:

2.1 ⁼ -Ео "

г₀=Ε₀ω

°!.У: -,	(Г)
‘ [ с«2 - ω,²,]² -г 4α²ω²
и²С	(80
j/[ со² - ] ² + 4а²«²

Параметром, существенно определяющим форму кривой Р. при данном су₀, является а. Чем меньше а, тем быстрее спадает кривая по обе стороны от Р. и тем больше те максимальные значения, которых достигают </₀ и г₀ при Р. Отличаются обе кривые друг от друга только множителем со. Если затухание системы невелико, то область Р. достаточно узка и в пределах этой области со мало меняется. Следовательно обе резонансные кривые мало отличаются друг от друга по форме. Кроме того, т. к. при малых а сближаются положения макси мумов со,- и су“,т.к. со“=со, — 2а²,то при малых а обе резонансные кривые для q-, и для г_э в области, близкой к Р., практически совпадают (но только в этой области, так как различие в их ходе при су. стремящейся к 0 конечно сохраняется всегда).

Наконец кривая Р. для амплитуды эдс самоиндукции в смысле положения максимума и хода при предельных значениях ω отличается как от той, так и от другой из рассмотренных кривых Р. для напряжения и тока. Действительно кривая Р. для эдс самоиндукции определяется выражением:

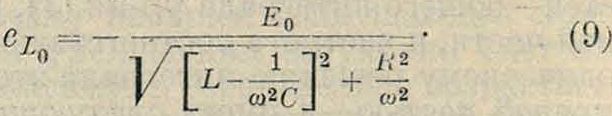
Максимума эта кривая достигает при следующих соотношениях параметров контура и частоты су:

г.с "Г

то есть максимум эдс самоиндукции наступает при частоте су_х, большей, чем со₀, причем" расстояние между ω_£ и су₀ тем меньше, чем меньше затухание. Кривая Р. для эдс самоиндукции при крайних значениях су стремится к нулю при су^-0 и к конечному значению Е, при су->ао. Выведенные свойства резонансных кривых можно подтвердить простыми физич. соображениями. Прежде всего максимумы всех трех величин q₀, г, и е_£ должен быть сдвинуты друг относительно друга в направлении возрастающих су. Действительно, если q=q,_t sin суt. то i=q,co cos cyi π ei=ι₀ω sin суt и если q„ при каком-то значении су достигает максимума, то благодаря тому, что ω продолжает возрастать. величина q.,су достигает максимума позднее, при больших значениях ω; по этой же причине максимум г₀су должен быть сдвинут в сторону больших со по отношению к максимуму г„. Точно так же легко выяснить из физич. соображений поведение резонансных кривых при крайних значениях су. При а>->0 бесконечно возрастает емкостное сопротивление, и поэтому ток стремится к нулю, при этом стремится к нулю и падение напряжения на сопротивлении. Вместе с тем при со 0 падает до нуля индуктивное сопротивление, а значит и напряжение, расходуемое на преодоление эдс самоиндукции. Следовательно все напряжение внешней эдс падает на емкости. При со -> оо бесконечно возрастает индуктивное сопротивление,и поэтому ток снова стремится к нулю. Вместе с тем падает до нуля емкостное сопротивление, и все напряжение внешней эдс падает на самоиндукции. Рассмотрение показывает, что явление Р. во Есех трех случаях наступает вовсе не при совпадении частоты внешней силы со с частотой свободных, колебаний в системе су_х, а при частотах, отличающихся от частоты о>_г, правда, отличающихся тем меньше, чем меньше затухание системы и совпадающих с частотой системы су₀ при затухании, равном нулю. Т. о. явление Р. наступает не при изохронизме (то есть равенстве частот вынуждающей силы и свободных колебаний системы), и эти два явления не следует смешивать друг с другом. При Р. амплитуды тока, когда сул=су_с, изохронизм также не имеет места, т. к. со не есть реальная физич. частота; реальное физич. значение имеет только частота свободных колебаний со_х У суд — а²,

0,5

t 15

Фигура 4.

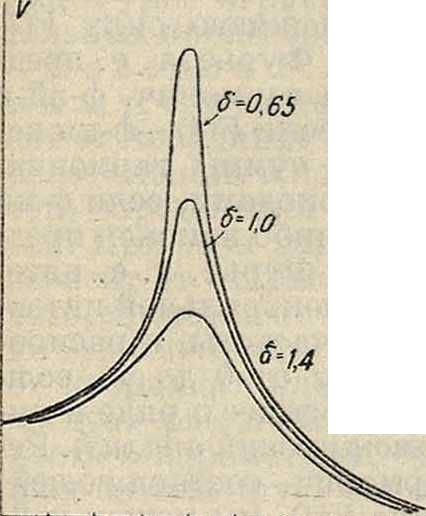
но она ни для одного из трех случаев Р. не равна частоте внешней силы. Только в идеализированной системе без трения Р. наступает при изохронизме. Форма кривой Р.,ее острота, как уже сказано, зависит от затухания того колебательного контура, в котором возникают вынуждаемые колебания. Чеммейь-ine-j (то есть чем меньше затухание контура),

тем больше, с одной стороны, те максимальные значения, которых достигают амплитуды вынужденных колебаний при Р., и тем быстрее, сдругой стороны, спадает резонансная кривая по обе стороны от положения Р. (фигура 4).

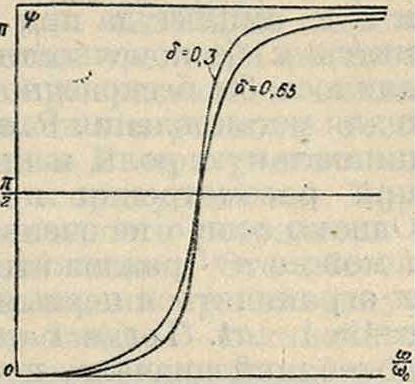
Однако при всех значениях частоты внешней силы со амплитуды вынужденных колебаний в контуре с малым затуханием по абсолютной величине будут больше, чем амплитуды в контуре с большим затуханием, другимисловами— вся кривая Р. для случая малого затухания будет расположена над кривой, соответствующей большому затуханию. Но отно-ё₀ сительная величина амплитуды, то есть отношение амплитуды при данной «расстройке» к амплитуде при Р., будет тем меньше, чем меньше затухание контура. Относительная величина амплитуды характеризует способность контура сильно отзываться на определенную частоту и выделять частоту, на которую он настроен, из целого спектра частот, то есть характеризует избирательность (смотрите) колебательного контура. Поэтому для характеристики колебательного контура как резонато-р а, то есть прибора, отзывающегося на определенные частоты сильнее, чем на все другие, вее кривые Р. приводятся обычно к одному и тому же максимальному значению, к-рое принимается за единицу (то есть по оси ординат от-• кладывается отношение данной амплитуды к амплитуде при Р.). В этом случае кривые Р. для малого затухания лежат, наоборот, во всех точках (конечно кроме максимума, где они все касаются в одной точке) ниже кривых для большого затухания. Т. к. форма кривой Р. определяется только затуханием контура, то показатель затухания, а значит и логариф-мич. декремент затухания контура м. б. определен непосредственно из кривой Р. (смотрите Затухание). В области Р. при изменении частоты внешней силы одновременно с изменением амплитуды колебаний происходит изменение и сдвига фаз между внешней силой и напряжением на обкладках конденсатора. Этот сдвиг фаз определяется приведенным выше соотношением (3). Из этого соотношения видно, что вблизи Р. сдвиг фаз быстро изменяется; когда частота со внешней силы проходит через а>, значение tg ψ становится равным со и меняет знак, то есть угол сдвига фаз у> проходит через значение ~. При крайних значениях со (со -»О

и ω -> со) tg ψ стремится соответственно к значениям + 0 и —0, то есть ψ стремится к значениям 0 и π. Кривая, изображающая сдвиг фаз как ф-ию со, т. н. ф а з о в а я кривая

Р., имеет вид, приведенный на фигуре 5. Из соотношения (3) следует также, что фаза изменяется в области Р. тем резче, чем меньше показатель затухания а и логарифмич. декремент <5 (фигура 5).

Все сказанное относительно явления элек-трич. Р. может быть целиком перенесено на явление механич. Р. для соответствующего случая, то есть действия синусоидальной внешней силы на «линейную» механич. колебательную систему с трением, обладающую одной степенью свободы, например груз, подвешенный на пружинке и движущийся в среде, сопротивление которой пропорционально скорости (фигура 6). Ур-ие движения груза для этого случая совершенно аналогично ур-ию (1):

ш j^ +h~ + lc^x~ Р sin wt, (Г)

где т—масса груза, h—коэф. трения и к— упругость пружины. Зависимость амплитуд смещения х, скорости — и сдвига фаз от частоты ω такова же, как и зависимость q, i я ψ от ω в случае электрич. Р. Если бы в рассмотренных случаях Р. мы пренебрегли затуханием системы (то есть пренебрегли бы сопротивлением в электрич. контуре или трением в механич. системе), то для положения Р., который в этом случае наступает при ω=со₀, мы получили бы бесконечно возрастающие амплитуды вынужденных колебаний. Поэтому такая идеализация колебательных систем (пренебрежение затуханием), целесообразная при. решении вопроса о частоте свободных колебаний слабо затухающей системы, является непригодной для рассмотрения установившегося явления Р. и вообще для определения амплитуды установившихся вынужден-ных колебаний в области, где ω близко Κίΐ,τ. к. в этих случаях затухание играет принципиальную роль; с другой стороны, при очень больших затуханиях, когда система приближается к апериодической (смотрите Колебания электрические), явление Р. становит-

Фигура 6.

ся мало заметным, теряет все типичные черты, к-рыми характеризуются явления в системах, слабо или во всяком случае не очень сильно затухающих.

Мы рассматривали явление Р. как установившееся явление, то есть рассматривали тот процесс, который установится в колебательной системе по прошествии достаточного промежутка времени, когда первый член в формуле (2) станет достаточно малым. Сразу же после включения внешней силы колебания в системе будут иметь характер, существенно отличный отт ого, какой имеют установившиеся колебания. Действительно сначала в системе будут существовать два колебания, вообще говоря, имеющие различные частоты со, и со. Эти колебания, складываясь, будут давать биения, причем амплитуда («глубина») биений будет уменьшаться благодаря затуханию колебаний частоты co^ Если же ω₁=ω, то биений в системе очевидно не будет, но процесс установления колебаний будет происходить по закону (1 - то есть установившаяся амплитуда вынужденных колебаний будет достигнута все же не сразу. Если бы затухания в системе не было, то нарастание амплитуды происходило бы пропорционально времени, и т. к. амплитуда при Р. в этом случае стремится к бесконечности, то установление Р. длилось бы бесконечно долго. В этом случае · и для установления Р. затухание играет принципиальную роль, и пренебрегать им нельзя при рассмотрении процесса установления. Однако если а не очень велико, то при малых t можно е-“* разложить в ряд по степеням at и ограничиться первым членом, то есть принять е-^п> =1 - at. Тогда 1 — e-^atmat и нарастание колебаний вначале, пока амплитуды колебаний, а значит и потери энергии в системе малы, и при наличии затухания будет происходить примерно пропорционально времени, т.е. в начале процесса установления затухание не изменяет существенно картины, и иногда целесообразно при определении характера установления в самом начале процесса пренебрегать затуханием системы. Чем меньше затухание системы, тем больше времени потребуется на установление процесса, на то, чтобы амплитуда вынуждаемых колебаний достигла например 0,99 от того предельного значения, к к-рому она стремится при ί-^οο. Поэтому все приведенное выше рассмотрение явления Р. имеет смысл только в том случае, если внешняя сила соответствует достаточно длинному «отрезку синусоиды» (строго говоря—бесконечной синусоиде). Длина этого отрезка должен быть такова, чтобы за это время процесс в колебательном контуре успел установиться, то есть должна быть тем больше, чем меньше затухание системы. Другими словами, за время г, к-рое определяется условием е-^ат«1, никаких заметных изменений в амплитуде и частоте внешней силы не должно происходить. Если это условие не будет соблюдено, то явления, происходящие в колебательной системе, будут существенно отличаться от рассмотренных выше, например если при снятии кривой Р. изменять частоту ω внешней силы очень быстро

. 5

(то есть так, чтооы например за время т=частота успела заметно измениться), то мы не получим тех кривых Р., которые выведены выше из рассмотрения установившегося процесса. Т. о. явление Р. со всеми его характерными чертами нужно рассматривать как явление, наступающее не мгновенно, а устанавливающееся с известной скоростью, причем это установление требует тем большего времени, чем меньше затухание системы.

Выше рассмотрен простейший случай Р. при действии гармонии. внешней силы на линейную колебательную систему. Однако часто приходится рассматривать более сложные случаи как в смысле характера внешней силы, так и в смысле свойств самой колебательной системы. Прежде всего внешняя сила часто представляет собой не гармоническую, а более сложного вида силу -чисто периодическую, почти периодическую или совсем непериодическую. Почти периодической является например ф-ия, представляющая собой сумму рядагармонич. ф-ий с несоизмеримыми периодами. Физически однако существенна не не соизмеримость в матенатич. смысле, а отсутствие между частотами отдельных гармонич. ф-ий простых кратных отношений. Эта задача хотя и сложнее рассмотренной нами выше, но в случае линейной колебательной системы легко м. б. к ней сведена благодаря тому, что в линейных системах имеет место принцип суперпозиции. Этот принцип заключается в следующем: решение, соответствующее случаю действия суммы нескольких сил, равно сумме решений, каждое из которых соответствует случаю действия одной из составляющих сил. Т. о. применимость принципа суперпозиции обусловлена линейностью самой системы, то есть тем, что параметры системы суть величины постоянные. Негармонич. внешнюю силу F(t) мы можем разложить в ряд Фурье, то есть представить либо в виде суммы гармонич. ф-ий с соизмеримыми периодами, если F(t)—ф-ия периодическая, либо в виде суммы гармонич. ф-ий с несоизмеримыми периодами, если ф-ия F(t) почти периодическая, либо наконец представить в виде интеграла Фурье, то есть интеграла гармонич. ф-ии со «спектральной интенсивностью», зависящей от частоты, и распространенного на все частоты от 0 до оо, если ф-ия непериодическая (подробнее о ряде и интеграле Фурье см. Гармонический анализ). Решение для каждой гармонич. составляющей, на которые разложена сила F(t), мы можем найти по предыдущему, и благодаря линейности системы общее решение (общий характер колебаний) определится суммой всех найденных решений. Резонансные явления будут наступать в системе очевидно всякий раз, когда одна из частот гармонич. составляющих внешней силы будет приближаться к собственной частоте колебательной системы. Для наступления Р. необходима т. о. не близость частоты самой внешней силы, а близость частоты какой-либо из ее гармонич. составляющих к собственной частоте системы. Действительно пусть внешняя сила состоит из двух гармонич. со-

т т ставляющих с периодами— и то есть

Fit)=a sin 2оЛ + b sin 3ωί.

Т. к. периоды соизмеримы, то F(t) есть ф-ия чисто периодическая с периодом, равным наименьшему кратному периодов составляющих ф-ий, то есть есть ф-ия с периодом Т и угловой частотой со. Резонансные явления будут однако наступать только тогда, когда собственная частота системы будет близка к частоте 2ω или Зсо. При собственной же частоте системы, близкой к частоте внешней силы ю, никаких резонансных явлений наступать не будет. Тем более недостаточным для наступления Р. является условие, что частота внешней силы в целое число раз меньше, чем собственная частота системы (а период внешней силы в целое число раз больше, чем период системы). И в этом случае необходимым условием для наступления Р. является наличие во внешней силе гармонич. составляющей, частота которой близка к собственной частоте системы. Так, если внешняя сила представляет собой перио-

со дич. ф-ию с периодом ₂, но содержащую только нечетные гармоники, то есть гармонич. частоты^, γ, -₀- ит. д., то при частоте системы,

близкой к со, никаких резонансных явлений наблюдаться не будет. Эта особая роль, к-рую играют гармонич. составляющие внешней си-

лы при Р. в линейных системах, и придает особое значение и особый физич. смысл представлению ф-ий в виде ряда или интеграла Фурье. Вообще говоря, всякую ф-ию можно представить в виде ряда самых разнообразных ф-ий, однако при рассмотрении действия внешней силы на линейную колебательную систему именно разложение на гармонические ф-ии, как мы видели, приобретает особый смысл и представляет особые удобства. И т. к. в большинстве случаев мы имеем дело с линейными колебательными системами—линейными резонаторами (по крайней мере в первом приближении),—то разложение именно в ряд Фурье играет при рассмотрении колебательных процессов весьма существенную роль.

Явления Р. в нелинейных систе-м а х, то есть в системах, параметры которых зависят от координат или скоростей, несравненно более сложны и подчас даже выходят из рамок того определения Р., к-рое дано в начале статьи. При этом характер явлений существенно зависит от «характера нелинейности», то есть от того, какие именно параметры системы не остаются величинами постоянными и зависят например от координат или скоростей. В этом смысле следует различать два случая. 1) Нелинейность в параметрах, существенно определяющих собственную частоту системы (то есть зависимость этих параметров от координат или скоростей) в емкости и самоиндукции для электрич. систем или в упругости и массе (или моменте инерции) для механич. систем. Такие системы нередко встречаются на практике. Примером емкости, величина которой зависит от заряда, может служить конденсатор с диэлектриком из сегнетовой соли, а самоиндукции, величина которой зависит от силы тока,—катушка с железным сердечником. В механич. системах особенно часто встречаются случаи переменной упругости, вообще переменной восстанавливающей силы. Примером этого могут служить обычный маятник при больших амплитудах, пружина при столь больших отклонениях, при которых нарушается закон Гука, и т. д. Во всех этих случаях частота собственных колебаний системы зависит от амплитуды колебаний, и термин «собственная частота системы» теряет свою определенность. Вместе с тем и явления Р. приобретают совершенно иной характер. В некоторых случаях явлений Р., в смысле наступления резкого максимума амплитуды вынужденных колебаний при определенной частоте внешней силы, вообще не наступает. Зато, с другой стороны, наступают новые явления—неустойчивые положения, срывы, резкое скачкообразное изменение амплитуды и фазы вынужденного колебания. 2) Переменное сопротивление в электрич. системах («неомические» проводники) и переменное трение в механических системах. Примером таких систем могут служить колебательный контур, в к-рый включена нить, накаливаемая током (Г, а значит и сопротивление нити, зависит от силы тока), регенератор (смотрите), то есть колебательный контур с электронной лампой и обратной связью, механич. колебательная система с трением (например в подшипнике), зависящим от скорости, и т. д. В этих случаях, если трение не достигает слишком больших значений, т. ч. система не слишком сильно затухает при всех значениях амплитуд выну-, жденных колебаний, явление Р. качественно в общих чертах сохраняет свой характер, но количественные соотношения существенно изменяются. Прежде всего, т. к. трение и затухание переменное, то понятия о показателе затухания и логарифмич. декременте затухания теряют смысл. Вместе с тем искажается и форма кривых Р.—она уже не соответствует той теоретич. форме резонансных кривых, которая была получена для линейных систем. Обычно в таких системах трение, а значит и затухание, возрастает с возрастанием амплитуд. При этом уменьшается и резкость резонансных явлений, кривые Р. при увеличении амплитуды внешней силы притупляются. Другими словами, избирательность резонатора с увеличением амплитуды падает. Это обстоятельство играет часто весьма существенную роль (смотрите Избирательность). В нелинейных системах, создающих незатухающие колебания, также происходят явления, имеющие в нек-рых случаях много общего с Р., однако под строгое определение Р. эти явления во всяком случае не подходят. Вообще же исследование явления Р. в нелинейных системах представляет большие математич. трудности даже для случая гармонич. внешней силы. В случае же негармонич. внешней силы эти трудности еще более возрастают, т. к. принцип суперпозиции не имеет места в нелинейных системах. Вследствие этого исследовать строго явления Р. в нелинейных системах удается только в наиболее простых случаях.

Р.в связанных системах. Резонансные явления существуют не только в случае систем с одной степенью свободы, но и в системах, обладающих многими степенями свободы, в частности в связанных системах (смотрите). Однако строгое решение задачи не только о вынужденных колебаниях, но даже и о собственных колебаниях связанных систем встречает большие трудности, если учитывать затухание системы. Поэтому при рассмотрении явления Р. обычно идеализируют задачу, пренебрегая затуханием системы". При этом надо иметь в виду, что в случае точного Р. вследствие пренебрежения затуханием системы амплитуды вынужденных колебаний стремятся коои установившихся решений не существует. Поэтому, пренебрегая трением, мы отказываемся от ответа на вопрос об амплитуде вынужденных колебаний и характере установления процесса. Но если затухание в системе достаточно мало, то установить общий характер явления и положения, при которых наступает Р., можно с достаточной степенью точности, рассматривая идеализированную задачу, то есть пренебрегая трением; при этом мы рассматриваем установившийся процесс, то есть полагаем, что явление в системе устанавливается за ко-4 нечный промежуток времени и что собственные колебания e, sin ωΐ 4 sin ап в системе все же за-Фнг. 7 тухают. Для двух связанных систем, например двух индуктивно связанных электрич. контуров, настроенных каждый в отдельности. вообще говоря, на разные частоты, наиболее общим случаем действия внешней силы является случай, когда внешняя сила действует на обе связанные системы (фигура 7), причем амплитуда эдс, создаваемой внешней силой в

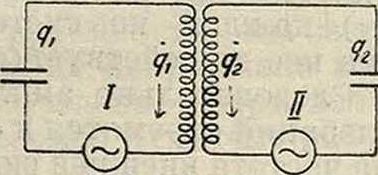
обоих контурах, м.б.различна. Обозначим эти амплитуды соответственно через Е_х и Е_г. Тогда на основании закона Кирхгофа ур-ия для рассматриваемой системы напишутся след. обр.

1) Lili + Mq.₂=Е_г sin eoi, (10)

2) L₂q₂ + Mq_x +=E₂ sin coi. (11)

Установившиеся решения этих ур-ий мы ищем в виде

q_x=α_Ί sin coi п cj₂=α₂ sin coi.

Подставляя эти решения в (10) и (11), получим характеристические ур-ия:

[i - Ι^ω*] - Moj²a₂=E_x, (12)

Μω²0-ι -f- ^2 ⁼ •^-2* (13)

Определяя из этих ур-ий значения а_х и а₂, мы получим их в виде отношения детерминантов:

Б,	- Μω 2
	- - ωί I
	ΙΛ 2 J

|^—— /. _χ - Мо)!

- М</)2 [—-

(14)

[± - L,«	μ
- Μω2	Е_г
[-i- - Litu² ] -	Μ 0)2 j
Ul J 1 - Μω2 Г— - LC-2
Ul J 1 - Μω2 Г— - LC-2	Li»2j

(15)

причем детерминант, стоящий в знаменателе выражений (14) и (15), должен быть отличен от нуля [если он равен нулю, то ур-ия (12) и (13) не имеют решений, то есть ур-ия (10) и (11) не имеют установившихся решений]. Если детерминант, стоящий в знаменателе выражений (14) и (15), стремится к нулю, то амплитуды вынужденных колебаний стремятся к бесконечности (если числители не обращаются в нуль). В этом случае и наступает явление Р. Но, приравнивая нулю детерминант, стоящий в знаменателе, получаем ур-ие:

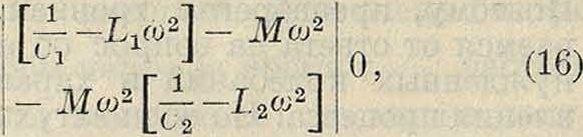
к-рое представляет собой характеристич. уравнение системы ур-ий (10) и (11) для случая Е_х^Е₂=0, то есть для случая свободных колебаний связанных систем. Это ур-ие («вековое» ур-ие) определяет частоты связанных («нормальных») колебаний в двух связанных системах, которые отличаются от собственных частот («парциальных») каждой из систем, когда другая система на нее не действует (смотрите Связанные колебания). Следовательно амплитуды вынужденных колебаний стремятся к ос, т“ e. Р. наступает, когда частота внешней силы совпадает с одной из частот связанных колебаний (нормальных частот), а не с одной из собственных (парциальных) частот, свойственных каждой из систем при отсутствии воздействия на нее другой системы.

Конечно вследствие наличия затухания амплитуды возрастают только до некоторой конечной величины, и кроме того положение Р. несколько смещается. Но при малом затухании практически можно считать, что Р. на ступает при совпадении частоты внешней силы с каждой из частот связанных колебаний. Частота же, которой обладает одна система при отсутствии воздействия на нее другой системы, то есть парциальная частота системы, не играет в этом случае никакой физич. роли; при совпадении частоты внешней силы с одной из этих парциальных частот Р. и вообще никаких особых явлений не наступает, кроме одного специального случая, когда знаменатель не обращается в нуль, но зато обращается в нуль числитель какого-либо из выражений для амплитуды, то есть (14) или (15). Этого можно достигнуть, если одна из амплитуд, наир. Е._г, равна нулю (то есть эдс создается только в одном контуре I). Если при этом подобрать такие условия, чтобы или_Σ~-=ω»,

то есть настроить контур II на частоту внешней эдс, то числитель в выражении для а обратится в нуль, и следовательно вынужденные колебания в контуре 1 будут отсутствовать. При этом в контуре II будут происходить колебания, амплитуду которых мы можем определить из условий: ,Ζ?₂=0 и £-!—Ιι«>²]=0. Подставляя эти соотношения в выражение (15), получим :

Е,

^— Мт 2 ‘

Таким образом, если настроить два связанных контура на разные парциальные частоты и действовать на контур I внешней эдс с частотой, на которую настроен контур II, то есть с парциальной частотой этого контура, то в контуре I колебаний не будет, а в контуре II амплитуда будет иметь конечную величину, несмотря на отсутствие затухания в системе. В этом специальном случае особые явления наступают при совпадении частоты внешней эдс с собственной «парциальной» частотой одного из контуров. Однако это явление нельзя называть Р., т. к. оно не подходит под наше определение. Это—своеобразное явление «обратного» Р. при к-ром амплитуда вынужденных колебаний не возрастает до бесконечности, а, наоборот, спадает до нуля в контуре I. Физически совершенно ясно, почему это происходит. Мы выбрали такие специальные условия, при которых вынужденные колебания, происходящие в контуре II, действуя обратно на контур I, как-раз компенсируют воздействие внешней эдс на этот контур. Только в этом специальном случае физич. роль играет не частота связанных «нормальных» колебаний, а собственная «парциальная» частота одного из контуров. Конечно вследствие затухания резкость этого явления притупляется.Амплитуда в контуре I не обращается в нуль, но лишь становится очень малой, причем для этого необходимо, чтобы разница в частотах контуров I и II была не слишком кала. Этот ссобый случай, к-рый не следует называть Р., находит весьма широкое применение в технике. Он используется в элек-трич. фильтрах, стопорных и отсасывающих, в механич. успокоителях разного типа, например в танке Фрама, применяемом для уменьшения качки кораблей, и т. д. В связанных системах возможен и другой специальный случай, когда, несмотря на совпадение частоты внешней эдс с одной из частот, связанных колебаний, Р. вообще не наступает. Это

Имеет место в том случае, когда одновременно с знаменателем обращается в нуль и числитель в обоих выражениях (14) и (15). Достигнуть этого можно путем соответствующего подбора например величины Е_г, если величина Е_х дана заранее (подбор этот надо производить для каждого значения ω). Т. о. при воздействии внешней силы на одну из систем можно избегнуть Р., подбирая известным образом характер воздействия внешней силы на вторую систему. Условия, которые при этом должен быть соблюдены,—это условия ортогональности вектора внешней силы и вектора собственных колебаний в системе. Физически это значит, что воздействие внешней силы на один контур компенсируется воздействием на этот контур со стороны другого контура, то есть что энергия источника внешней эдс не может переходить в систему. Этот последний случай является специфичным для систем, обладающих более чем одной степенью свободы. Здесь существенно новым является вопрос о точке приложения, или «законе распределения», внешней силы. В системах с одной степенью свободы такой вопрос вообще возникнуть не может.

Благодаря тому, что в рассматриваемом нами случае связанных линейных систем принцип суперпозиции имеет место, рассмотрение явления Р. в связанных системах при действии негармонич. внешней силы м. б. произведено таким же образом, как и в системе с одной степенью свободы, то есть разложением внешней силы в ряд Фурье. При увеличении числа связанных систем явление Р“. еще более усложняется. Практически важный случай применения большого числа связанных контуров представляют собой т. н. многоячеечные резонансные фильтры (смотрите Избирательность). Происходящие в них резонансные явления принципиально не отличаются от рассмотренных выше, с тою лишь разницей, что в многоячеечном фильтре с п степенями свободы существует и нормальных частот, и Р. наступает всякий раз при приближении гармонической частоты внешней силы к одной из нормальных частот.

Р.в сплошных системах. В сплошных системах (системах с распределенными параметрами), например антенна, струна, явления Р. сохраняют все свои типичные черты, однако к этим чертам прибавляются существенно новые. Система с распределенными параметрами обладает бесконечным числом собственных частот, и явление Р. может наступить всякий раз, когда одна из гармония, частот, содержащихся во внешней силе, приближается к одной из этих собственных частот системы. Кроме того в системах с распределенными постоянными существенную роль играет вопрос, возникающий в более простой форме уже в двух связанных системах, о распределении внешней силы или о точке приложения внешней силы, если возбуждение колебаний происходит в одной точке. Так, в случае возбуждения колебаний в одной точке Р. не наступает, если точка приложения внешней силы расположена в узле того из собственных колебаний системы, с частотой которого совпадает частота гармония. внешней силы. Р. также не наступает, если внешняя сила ортогональна к собственному колебанию, частота которого совпадает с частотой внешней силы. Вопрос о- резонансных явлениях в сплошной системе под действием негармонич. внешней силы в случае линейности системы решается так же, как и в линейных системах с сосредоточенными параметрами, то есть разложением внешней силы в ряд.

Р. часто называют также случай совпадения собственных парциальных частот в связанных системах. При собственных свободных колебаниях в связанных системах действительно в этом случае наступают явления, имеющие много общего с явлением Р. Однако в точности под определение Р. случай свободных колебаний при совпадении парциальных частот не подходит. По существу он представляет собой лишь особый случай свободных колебаний в связанных системах.

Лит.: Э Й х е и в а л ь д А. А., Теоретич. физика, ч. 2, М.—Л., 1930; его же, Теоретич. физика, ч. 6, М.—Л., 1931; Тимошенко С. П., Теория колебаний в инженерном деле, пер. е англ., М.—Л., 1931; Френкель А., Теория переменных токов, М., 1928; Rayleigh, The Theory of Sound, 3 ed., v. 2, L., 1929; Η о r t W., Technische Schwingungslehre, 2 Aufl., B., 1922; О 1 1 e n d о r f F., Die Grundlagen d. Hochfre-quenztechnik, B., 1926. С. Хайкин.

P. параметрический (параметрическое возбуждение, гетера- и автопара метрическое возбуждение, Р. 2-г о рода), возбуждение электрич. колебаний при помощи периодич. изменения параметров в контуре, в котором эти колебания происходят. Если в колебательной системе (электрическая колебательная цепь, маятник, струна и тому подобное.) происходит периодич. изменение параметров (электрич. емкости, самоиндукции, длины маятника, силы тяжести, натяжения струны), то при соблюдении некоторых ниже рассмотренных условий колебания системы, которые при постоянных параметрах были бы затухающими или незначительными по величине незатухающими, становятся нарастающими и стремятся к некоторому стационарному состоянию. Такое явление целесообразно (хотя еще и не общепринято) назвать параметрическим возбуждением. Для выяснения сущности этого явления рассмотрим электрич. колебательную систему, состоящую из емкости С и самоиндукции. В тот момент, когда ток в контуре нуль, увеличим несколько (на ΔС) емкость конденсаторов. При этом мы совершим работу Через jjj/₄ периода, когда Q=0,

вернемся к первоначальному значению С, что возможно сделать, нс совершая никакой работы. Эти операции повторим опять через Vs и периода. Мы т. о. за время одного колебания (цикла) системы затратили определенную работу, за счет которой очевидно должна увеличиться амплитуда колебаний. Продолжая такое периодич. изменение параметра (емкости), мы заставляем амплитуду колебаний непрерывно возрастать (параметрич. возбуждение). При наличии затухания вкладываемая в систему работа должен быть больше потерь в ней, то есть

АС

2С²

Q² > ЕР ;

где R есть активное сопротивление системы, или т. к. 1= Οω

АС

20’ ^> 2 ’

где д есть логарифмический декремент:

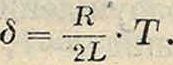
Так обр. характерными чертами процесса являются: 1) двукратное изменение параметра в течение одного полного колебания—п а р а-.метрический резонанс, 2)определенное соотношение между относительным изменением параметра и логарифмич. декрементом свободных колебаний возбуждаемой системы. Совершенно аналогичное явление—непрерывное нарастание колебаний—мы получаем в маятнике, изменяя периодически его длину. На том же основано раскачивание качели самим качающимся (периодич. изменение момента инерции и момента вращения). Во всех этих случаях имеем дело с возбуждением колебаний при помощи периодического изменения параметров, причем это изменение производится внешним, чуждым системе агентом. Поэтому такое возбуждение колебаний, в отличие от рассматриваемого ниже, целесообразно назвать гетеропар а метр и-ч е с к и м. Явление параметрич. Р. в физике известно уже давно. Как показал Мельде в 1880 г., можно, изменяя периодически натяжение струны с периодом, равным половине периода собственных колебаний струны, привести ее в интенсивные поперечные колебания. Теория явления гетеропараметрич. возбуждения приводит к диференциальному уравнению с периодич. коэф-тами. Напр. в случае периодич. изменения емкости электрич. колебательной системы по закону

Q Со_

1+ ?COS2»)i

это диференциальное ур-ие имеет вид:

_r di _п. 1+ grcos2a>t t>. ₇, , ^Ldt + ^Rl+ со Ι*^α(-0·		(2)
Подстановкой уе ^αί=	jidt, х=wt это	ур-ие
приводится к виду:
j- + ,«² (1 + т cos 2 ж) у=0,		(3)

где т=у 2α=-

“б + “².

μ =

“о.

ml + а²

L’ LCo

Решение этого ур-ия, называемого ур-ием Матье и соответствующего колебательной системе без затухания (а=0), может быть представлено в зависимости от значений μ и т либо в виде:

у=A cos βχ · у>! (ж) + В sin βχ у>., (ж) (4)

либо в виде:

у=Ае <р(х) + Ве ψ(-χ), (5)

где у>_х (ж), у>_г (ж), φ (ж)—периодические ф-ии с периодом π (или 2π), β и к—нек-рые ф-ии от μ я т, а А к В—константы интегрирования, определяемые начальными условиями. В то время как решения типа "(4) приводят к колебаниям конечной величины (стабильные решения), решения вида (5) благодаря наличию члена Βα^φί—χ) дают значения, возрастающие с. увеличением ж (т. e. ί). Такие решения называются нестабильными. Совокупность значений μ и т, при которых получаются нестабильные решения, можно графически представить на плоскости (μ, тонн) в виде областей,-обведенных пунктиром (фигура 8). Для т малых возбуждение наступает только вблизи значений д=1, 2, 3,. (пара метрический Р.). Исходя из этих свойств ур-ия Матье и зависимости

J idt=уе “ _>

получаем, что ур-ие (2) может иметь решения, возрастающие с ж (что соответствует возбуждению колебаний) только для типа (δ). В этом случае:

-(* + —

fidt=Ae ^ω° φ (х) +

+ Ве ^{1 0 У} φ(-χ),

то есть имеем нестабильные решения только при к— — > 0. Т. о. наличие затухания (α Ф 0)

а>0

уменьшает области нестабильности (фигура 8, где эти области заштрихованы). Границы пер

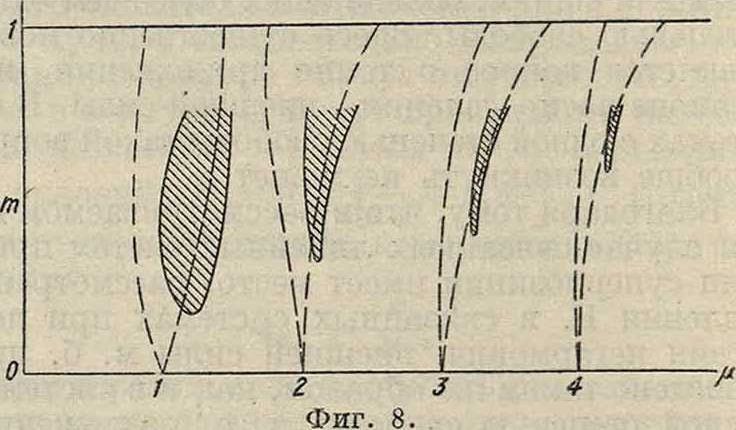
вой области нестабильности, практически наиболее важной, определяются соотношением:

(6)

μ·

= 1±Кт-

откуда вытекает как условие возоуждения при синусоидальном изменении параметра:

т > — (7)

Передавая существенные стороны процесса возникновения колебаний при параметрцч. возбуждении, линейное диференциальное ур-ие с периодич. киэф-тами не может однако полностью описать всего явления, например определить величину стационарной амплитуды колебаний. Для этого необходима более углубленная теория, основанная па рассмотрении нелинейных обыкновенных диференциальных ур-ий е периодич. коэф-тами. Особое значение приобрели явления параметрич. возбуждения в электрич. системах в связи с возможностью легко изменять параметры этих систем, а также осуществлять системы с малым затуханием, необходимым для выполнения условия (7). Относящиеся сюда работы произведены гл. обр. в Центральной радиолаборатории Всесоюзного электротехнич. объединения под руководством Л. И. Мандельштама и Н. Д. Папалекси.

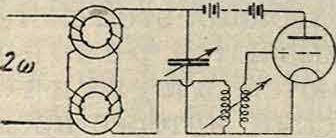
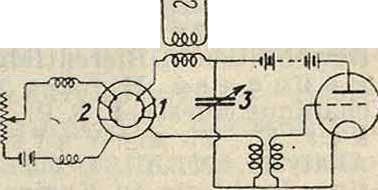
Примером осуществления гетеропараметрич. возбуждения в электрич.системе может служить схема фигура 9. Здесь, изменение самоиндукции контура достигается пропусканием тока частоты со через первичные обмотки 1_Х и ί₂ двух последовательно соединенных тождественных трансформаторов—с железными сердечниками (из тонко подразделенного железа для высокой частоты), вторичные обмотки 2_Х и 2._г которых включены в контур друг против друга. При таком включении в контуре не наводятся эдс, и действие первичного переменного тока выражается только в обусловленном изменением намагничивания сердеч-

	I
		г,

_L		2_г
	ж	3
	Фигура 9.

ника периодич. (с частотой 2 со) изменении эффективного коэф-та самоиндукции колебательной системы, которая при настройке на частоту со или близкую к ней приходит в пара-метрич. Р. Для соответствующей подгонки ко-эфициента затухания согласно условию (7) целесообразно применять (фигура 10) принцип обратной связи (смотрите). Величина стационарной амплитуды колебаний обусловливается здесь зависимостью самоиндукции (железо) и величины регенерации от амплитуды. Кривые зависимости амплитуды параметрически возбужденных колебаний от расстройки контура (кривые гете-ропараметрич. Р.—фигура 11 и 12) существенно отличаются от обычных резонансных кривых. Главной особенностью их является помимо формы возбуждение колебаний только в вполне определенном интервале частот, coot-1,

=, °->0!

Фигура 11. Фигура 12.

петствующем интервалу нестабильности, на границах которого амплитуда внезапно резко, иногда скачком, увеличивается (фигура 12).

В последнее время в Гос. физнко-технич. институте (1931 г.) удалось возбудить в колебательной системе в отсутствии каких-либо эдс одним механич. периодич. изменением самоиндукции мощные электрнч. колебания (порядка kW) и т. о. осуществить новый род генератора переменного тока. Такое механич. возбуждение элек-трич. колебаний представляет физический интерес, между прочим потому, что для самовозбуждения принципиально достаточно наличия только т. н. самопроизвольных флуктуаций токов и напряжений.

Кроме рассмотренного явления гетеропа-раметрнч. возбуждения, в тесной связи с ним находится другой род параметрич. возбуждения, вызываемый действием внешних периодич. эдс на колебательные системы, параметры которых зависят от амплитуды тока или напряжения (сопротивления, образованные электронными лампами, самоиндукции с железом, емкости с диэлектриком, диэлектрич. постоянная к-рых, как у кристаллов сегне-товой соли, зависит от напряжения, и т. д.). Если например, как в случае недовозбужденного регенеративного приемника, зависимость сопротивления колебательного контура от тока выразится через

R₀(l + βί-γίη,

то тогда при действии на контур эдс E sin 2 ωί и настройке на частоту ω в нем возникают незатухающие колебания частоты ω. Краткая теория этого явления для установившегося состояния заключается в следующем: дифе-ренциальное ур-ие, управляющее процессом, имеет вид:

L -jj + Л о (* + β i²—yi^r) -f — f i dt=E sin 2 <ot.

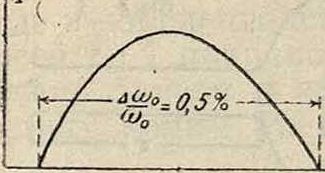
Фигура io.

После подстановки:

где a>g=j-p, и диференцирования по ур-ие принимает вид:

d*i

Зт2

• г=— 2 (1

2βί~3 уР)|| +

с, 2Е

f + cos 2т.

(8)

Согласно свойствам диференциальных ур-ий, развитых Пуанкаре, справедливо следующее. Если диференниальное ур-ие типа (8), зависящее от малого параметра (в данном случае #₀и ξ), допускает при #₀=0 и f=0 периодич. решение или семейство периодич. решений, то, вообще говоря, и при #₀=£0 и ξφ 0 (но достаточно малых) это уравнение также имеет периодич. решение с тем же периодом, соседнее одному из этих решений. Можно показать, что эти выводы применимы к данному ур-ию

(8). И т. к. при #о=0 и |=0 ур-ие (8) переходит в

2 Е,

ап ,.

d^ ^{+ l =}

Lot

cos 2т,

ж-рое имеет периодич. решение

2 Е

i —a sin т — b cos т — -ф. cos 2т,

3 Loi

то и решение ур-ия (8), соседнее с этим, м. б. представлено в виде гармония, ряда, основной период которого в два раза больше периода действующей эдс, то есть является субгармоникой ее. Такое явление возбуждения колебаний в электрической колебательной цепи гармония. эдс при настройке цепи на субгармонику этой эдс имеет место только вблизи этой настройки, причем область возбуждения тем шире, чем больше амплитуда эдс. Этот результат можно распространить на случай более сложной зависимости параметра от тока или напряжения, причем, смотря по роду этой зависимости, можно получить ту или иную субгармонику действующей эдс. Т. к. сущность этого явления несомненно заключается в изменении параметра цепи, обусловливаемом собственными токами или напряжениями цепи, то такой род параметрического возбуждения колебаний целесообразно назвать а в т о и а-ра метрическим в отличие от гетеропа-раметрич. возбуждения. Рассматривая весь процесс в целом и учитывая наступление сильного эффекта при настройке на половинную (вообще * часть) частоты действующей эдс, явление автопараметрич. возбуждения иногда называют также Р. 2-г о р о д а (вообще и-го). Очень эффективной схемой для получения автопараметрич. колебаний является схема недовозбужденного _2шрегенеративного приемника, обратная связь которого устанавливается меньше критической. Другим примером может служить схема, представленная на фигуре 13. ^фиг- ¹³·

Здесь необходимая для требуемого эффекта зависимость параметра от тока достигается самоиндукцией с железным сердечником, нужная степень подмагничивания которого устанавливается постоянным током через обмотку 2. При соответствующей настройке контура (2,

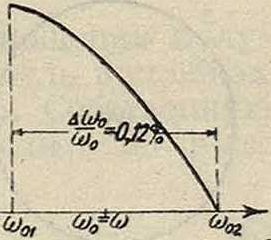
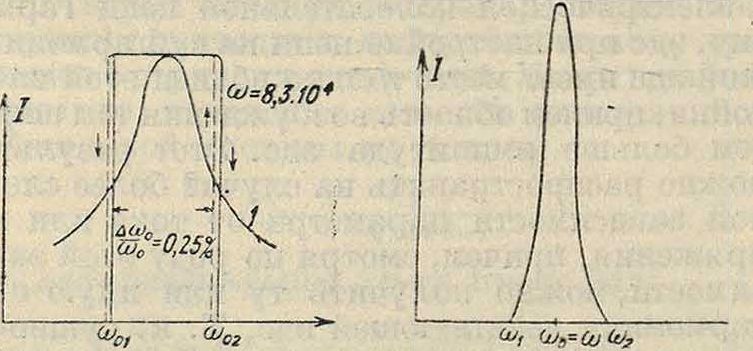
3) и правильной подгонке коэф-та затухания, что достигается и здесь использованием принципа обратной связи, в контуре возникают интенсивные колебания частоты а>. На фигуре 14— 17 изображены различные типы кривых зависимости амплитуды, получающихся при автопараметрич. возбуждении колебаний (I) от расстройки (кривые Р. 2-го рода). Здесь мы также имеем возбуждение в строго ограни-

ченных интервалах частот ок. ω₀=ω, причем на границах этих интервалов происходит быстрое возрастание амплитуды колебаний (фигура 17), к-рое в нек-рых случаях

и
	-%Ё°^Ж0,25%

Ч, ^ω<τ^ω Чг

Фигура 14.

рТР)] I I I!

-М&,

•vi—

• i

W’t, tS. to¹

Фигура 15.

превращается в резкий скачок (фигура14,15, 16). В последних случаях кривая возбуждения имеет П-образыую форму, резко отличаясь от обычной резонансной кривой (фигура 16, кривая J). Следует особо отметить, что в отличие от обычного Р. при изменении амплитуды действующей эдс в широких пределах изменяется лишь величина области возбуждения, амплитуда нее автопараметрич. колебаний остается почти неизменной (фигура 15; амплитуда эдс для кривой 1 почти вдвое больше, чем для кривой 2). Явления гетеро-автопараметрич.

Флг, 13.

Ф.!Г. 17.

возбуждения допускают различные практич. применения, из которых можно указать на параметрич. генератор переменного тока, деление частоты и освобождение от атмосфер ных помех при радиоприеме.

Лит.: Ляпунов А., Общая задача об устойчивости движения, Харьков, 1892; Гурса Э., Курс теоретич. анализа, т. 2, ч. 1—2, М.—П., 1923; Андронов и Л е о н т о в и ч, Колебания систем с меняющимися параметрами, «ЖРФХО», часть физич., 1927, е-гр. 429—442; Папалекс и II., О некоторых современных проблемах в области колебаний, «Успехи физич. наук», М.—Л., 1931; Мандельшта м Л., Некоторые современные проблемы теории колебаний, Доклад на конференции по колебаниям, М., 1931; Напал е-к си II., Воздействие на авто- и потенциально-автоколебательные системы, Доклад на конференции по колебаниям. Труды конференции, М., 1931; Horn W., Gewohnliche Dilferentialgleichungen, 2 Aufl., В., 1927; PoincarP H., Les methode? nouvelles de la md-chaniejue celeste, t. 2, P., 1894, t. 3, P., 1899; Whittaker E. T. a. Watson G. N., Course ol Modern Analysis, N. Y., 1927; Timoshenko S., Vibration Problems in Engineering, p. 87—108, N. Y., 1928; Rayleigh, OnMaintained Vibrations,«ThePhilosophi-cal Magazine», L., 1883, v. 15,p. 229—235; Rayleigh, On the Maintainance of Vibrations by Forces of Double Frequency, ibid., 1887, v. 24, p. 145— 1 59; Rayleigh, Theory of Sound, 3 ed., v. 1, L., 1929; H e e g-n er K., Selbsterregungserscheinungen bei Systemen mit gestorter Superposition, «Ztschr. f. Physik», Berlin, 1924, B. 29, p. 91, 1926, В 33, p. 85; Van der Pol a. Strutt M„ On the Stability of Solutions of Ma-thiew’s Equations, «The Philosophical Magazine», L. 1928; Koga L., A New Frequency Transformer or Frequency Changer, «Proceedings of the Institute of Radio Engin.», New York, 1927, v. 15, p. 669; Winter-0 ϋ л t h e r, Cher selbsterregte Schwingungeu in Kreisen mit Eisenkernspulen, «jahrbuch d. drahtlosen Telegrapliie u. Telephoiiie», v. 34, Berlin, 1929, p. 42; Croszkowski I„ Frequency Division, «Proceedings of the Institute of Radio Engin.», N. Y., 1930, v. 18, p. 1960; Mandelstam L. u. P a p a 1 e-x i N., Ober Resonanzerscheinungen bei Frequenz-teilung, «Ztschr. f. Physik», Brschw.—B., 1931, B. 73, p. 223—248. H. Пгпаленси.