> Техника, страница 77 > Релаксационные колебания

Релаксационные колебания

Релаксационные колебания, незатухающие колебания, по форме существенно отличные даже при весьма малых амплитудах от синусоидальных и возникающие при известных условиях в системах, не обладающих свойствами колебательной системы в обычном смысле, то есть в системах, не способных совершать свободные затухающие колебания с определенными собственными частотами. Р. к. нашли себе широкое применение в технике, гл. обр. в технике измерения частоты высокочастотных электрич. колебаний. Возможность применения Р. к. для этой цели обусловливается именно сильно выраженной их несину-соидальностыо и следовательно богатством их •обертонами вплоть до весьма высоких: в Р. к. легко м. б. обнаружены обертоны выше десятого. Так как Р. к. в обычных схемах практически вполне периодичны, то, зная частоту основного колебания и порядок обертона, можно с большой точностью определить частоту, соответствующую каждому обертону, и тем самым свести задачу измерения высоких частот к измерению частот гораздо более низких, путем сравнения частоты данного высокого обертона с частотой измеряемой.

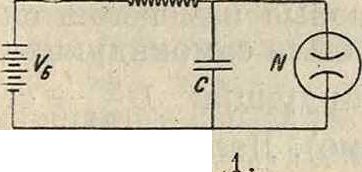
Наиболее простым примером генератора Р. к. является схема с неоновой лампой N (фигура 1). Неоновая лампа обладает следующими свойствами, которые и делают возможным при-_я менение ее для получе ния Р. к.: пока напряжение на зажимах лампы не достигло определенной величины Fi,t.h. напряжения зажигания, лампа не горит и не пропускает тока. Когда напряжение на зажимах достигло V_lt лампа вспыхивает и в ней сразу появляется нек-рый ток конечной величины ij. При дальнейшем возрастании напряжения сила тока влампе возрастает примерно по линейному закону. В обратном направлении при уменьшении напряжения лампа не гаснет при V_x, а продолжает гореть, пока напряжение не упадет до некоторой величины F₂<F, (напряжению V₂ соответствует некоторая определенная сила тока г₂), после чего лампа гаснет и ток в ней прекращается скачком—· падает от г₂ до 0 (фигура 2).

Условия,при которых лампа, обладающая такими свой-1, ствами, будет создавать ко- ί> лебания, следующие. Если напряжение батареи больше F_1; то через нек-рое время после включения напряжение на зажимах лампы достигнет величины F_t, и лампа вспыхнет (участок 1—2 на кривой фигура 3). Если сопротивление R достаточно велико, то напряженке на конденсаторе начнет уменьшаться, т. к. разряд конденсатора через лампу будет происходить быстрее, чем его заряд через сопротивление. Если это сопротивление так велико, что зарядный ток будет меньше, чем г₂

Фиг.

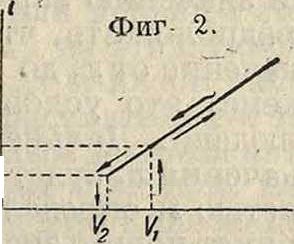
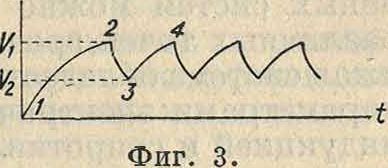
(минимальный ток, при котором лампа еще горит), то конденсатор разрядится ниже напряжения V₂, и лампа погаснет. Этой части процесса соответствует участок 2—3 на кривой фигура 3. После этого конденсатор снова начнет заряжаться, и лампа снова вспыхнет (участок 3—4). В схеме будут происходить колебания, форма которых соответствует фигура 3 и существенно отличается от синусоидальной. Частота колебаний зависит от скорости заряда конденсатора, к-рый определяется временной постоянной цепи Сй; кроме того она зависит от характеристики лампы (величин V_x и F₂) и напряжения батареи. В схеме нет никаких контуров, в которых могли бы происходить свободные колебания при отсутствии лампы и которым была бы свойственна какая-либо определенная собственная частота. В этом существенное отличие Р. к. от обычных «томсоновских» колебаний, частота которых во всяком случае в первом приближении определяется ф-лой Томсона

t

(0=,—=,

V LC

то есть задается параметрами колебательного контура. Рассмотренный процесс представляет собой периодически повторяющийся процесс с периодом, определяемым временем заряда и разряда конденсатора, к-рое в электротехнике по аналогии с временем запаздывания или ослабления упругих натяжений называют временем релаксации (смотрите).

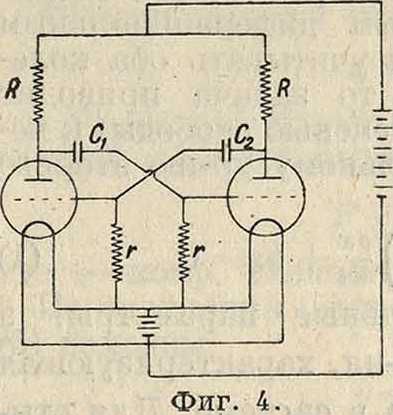
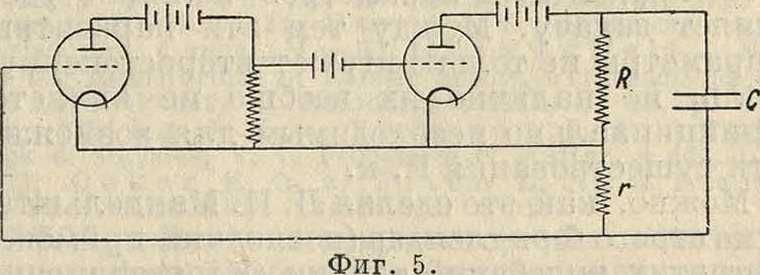
Р. к. могут возникать в целом ряде весьма разнообразных схем. Они возникают обычно в системах, к-рые, с одной стороны, не имеют устойчивых положений равновесия (неустойчивость м. б. достигнута путем применения приборов типа электронной или неоновой лампы), а с другой, не обладают колебательными свойствами (не имеют колебательных контуров, состоящих из сосредоточенной емкости и сосредото-ченной самоиндукции). Таковы например схемы мультивибратора Абрагама-Блоха (фигура 4) или схема, приведенная на фигуре 5. Обе они при достаточно больших сопротивлениях не имеют устойчивых положений равновесия и создают Р. к.

Релаксационные колебания возможны не только в электрических, но и в механических системах. Если механическая система обладает например большой упругостью и большим тре

нием, то это трение может лишить, систему колебательных свойств. С другой стороны, вследствие того, что характеристика трения, то есть кривая, характеризующая зависимость тре ния от скорости, в нек-рых областях представляет собой падающую кривую, положение равновесия оказывается неустойчивым, и система начинает совершать типичные Р. к., существенно отличные от синусоидальных, причем период этих колебаний определяется не массой и упругостью, как при обычных ме-ханич. колебаниях, а упругостью и характеристикой трения. Такие колебания могут возникать повидимому во многих случаях, когда в механич. системах трение играет преобладающую роль.

Теоретич. рассмотрение Р. к. и релаксационных систем можно вести, исходя из двух различных точек зрения. Вообще говоря, каждая система обладает всеми тремя основными параметрами: электрическая—емкостью, самоиндукцией и сопротивлением (если не в сосредоточенном виде, то в распределенной форме «паразитных параметров»), а механическая— массой, упругостью и трением. В тех случаях, когда система обладает колебательными свойствами, в ней сопротивление должен быть мало, и преобладают следовательно два колебательных параметра—емкость и самоиндукция или упругость и масса. В тех же случаях, когда система не обладает колебательными свойствами, то есть именно в системах, в которых возможны Р. к., это всегда обусловлено тем, что сопротивление (трение) преобладает над каким-либо из двух, других параметров—самоиндукцией (массой) или емкостью (упругостью) и один из этих двух параметров играет второстепенную роль. При рассмотрении таких систем конечно можно было бы учитывать все три параметра и попытаться решить задачу с учетом всех параметров, в том числе и «паразитных». (Так именно поступал Ван-дер-Поль.) Однако системы, создающие незатухающие колебания (автоколебания), всегда обладают нелинейным сопротивлением, и рассмотрение этих систем приводит к нелинейным диференциальным ур-иям. Если при этом учитывать оба колебательных параметра, то задача приводит (для системы с одной степенью свободы) к нелинейному диференциальному ур-ию второго порядка, например:

‘Ш + г(ъ)т,+ *-<> <»

где а и, b—колебательные параметры, а F (^) — нелинейная ф-ия, характеризующая сопротивление (трение) в системе. Для отыскания периодич. решений этого ур-ия, существенно отличных от синусоидальных, не существует регулярных методов; графич. же методы требуют много времени. Кроме того учесть точно все паразитные параметры, например самоиндукцию или емкость соединительных проводов, все равно невозможно, т. к. точно их значения никогда неизвестны. Поэтому учет паразитных параметров излишне усложняет задачу. Между тем эти паразитные параметры не только играют второстепенную роль, но наличие их вообще не является принципиально необходимым для возможности существования Р. к.

Можно, как это сделал Л. И. Мандельштам и не строго Фридлендер (последний применял для этих колебаний термин «Kippschwmgun-gen», то есть колебания опрокидывания), поставить вопрос о существовании периодич. решений, вовсе не учитывая паразитных параметров, но предполагая, что решения эти р а з-

р ы в н ы. Напр. в приведенных нами схемазс нет сосредоточенных самоиндукций; самоиндукция присутствует лишь в виде паразитного параметра. Пренебрегая этой паразитной самоиндукцией, мы для схемы фигура 5 получим например ур-ие вида:

F(x)f_t=X, ; (2)

где F(x)—нелинейная ф-ия от ж,имеющая вид, изображенный на фигуре 6, то есть нелинейное ди-ференциальное ур-ие первого порядка (х— сила тока). Вообще говоря, нелинейное ди-ференциалыгое ур-ие 1-го порядка не допу

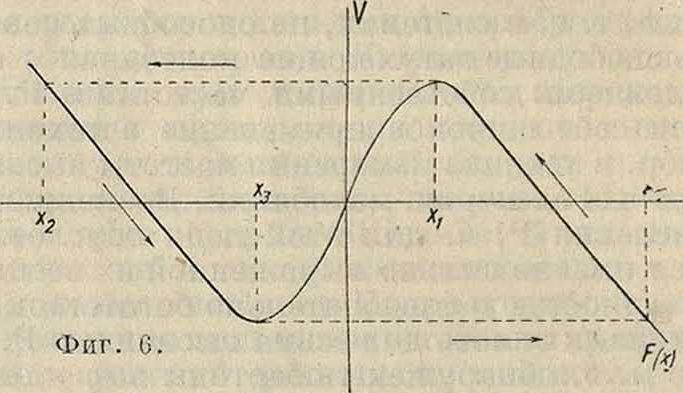
скает непрерывных периодич. решений, но «разрывные» периодич. решения этого ур-ия могут существовать, и отыскание их представляет собой несравненно более простую задачу, чем отыскание периодич. решений ур-ия (1). Если положение ж=0 равновесия неустойчиво, то система уйдет из этого положения. Далее, если при каком-то значении х_гФО

F(x)=0, то Αγ обращается в бесконечность,

то есть сила тока х может измениться скачком. Этот результат нужно считать вполне естественным, поскольку мы пренебрегли самоиндукцией, т. к. в цепи без самоиндукции вполне допустимы скачкообразные изменения силы тока (если бы в цепи была самоиндукция,

то ггри^=со, эдс самоиндукции L^==cc. что физически недопустимо). Дальнейшее поведение системы при=с» неопределенно, т. к. х может принять любые значения. Но можно ввести новое условие, к-рое определяло бы дальнейшее поведение системы; именно, исходя из физич. соображений, нужно потребовать, чтобы энергия системы (в нашей схеме энергия заряда конденсатора) не изменялась скачком, то есть чтобы при скачкообразном изменении энергия (заряд конденсатора) оставалась неизменной. Если существует второе такое значение ж₂, к-рое соответствует тому же значению заряда конденсатора, то нужно· предположить, что ток скачком изменит свое значение от х_г до ж₂. В рассматриваемых нами схемах это условие скачка как-раз м. б. соблюдено. Дальнейшее движение системы от значения сс₂ будет происходить с конечной скоростью и определяться ур-ием (2), пока х не примет нового значения ж₃, при к-ром F(x₃)=0. Тогда снова система пойдет скачком в положение *₄, удовлетворяющее условию скачка для значения ж₃. Дальнейшее движение снова будет происходить непрерывно. Если при этом система попадет снова в положение х_г, то весь процесс начнется сначала—система будет совершать разрывные периодич. колебания. Теоретич. форма этих колебаний примерно изображена на фигуре 7. Конечно в действительности изменения силы тока от х_г до ж₂ и отж₃

до x_t происходят не мгновенно, ибо в системе всегда присутствуют паразитные емкости и самоиндукции, препятствующие этим скачкам. Но если эти паразитные параметры малы, то скачки совершаются очень быстро по сравнению с движениями от х.₂ до ж, и ж₄ до ау, и несмотря на наличие паразитных параметров колебания примерно сохраняют частоту и форму, полученную из «разрывной» трактовки. Отказываясь от учета паразитных параметров, мы отказываемся т. о. от рассмотрения самого процесса скачка, но пока этот сказок происхо

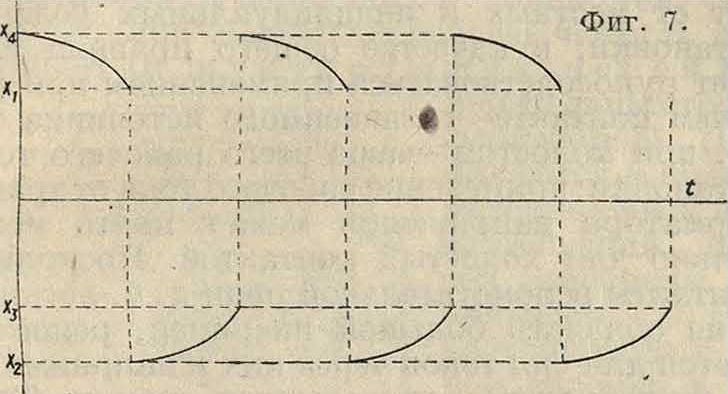
дит достаточно быстро, мы можем получить удовлетворительный ответ на вопрос об амплитуде, частоте и форме колебаний. Вместе с тем «разрывная» трактовка весьма упрощает решение задачи. Эта же трактовка м. б. применена к электрич. схемам с самоиндукцией и сопротивлением, но без емкости. В этом случае мы не можем допустить скачкообразного изменения силы тока в цепи с самоиндукцией, но зато допустимы скачкообразные изменения производной силы тока, то есть скачки эдс самоиндукции, а вместе с тем скачки напряжения на концах сопротивлений. Наконец эта же трактовка м. б. применена и к меха-нич. системам, в которых масса играет второстепенную роль по сравнению с упругостью и трением. В такой системе, пренебрегая массой, мы можем допустить скачкообразные изменения скорости. Условия скачка сведутся к тому, что потенциальная энергия системы, то естьупругая деформация, при этом скачке должна оставаться неизменной. Р. к. не являются каким-то резко ограниченным классом колебаний. Изменяя соотношение параметров в системе, всегда можно перейти от колебаний том-соновских к Р. к. и наоборот. По существу мы имеем целую область колебаний разного типа, ограниченную с двух сторон двумя идеализированными типами—синусоидальных колебаний и «разрывных» колебаний. И только эти два идеализированных случая легко поддаются теоретич. исследованию. Реальные же колебания лишь в большей или меньшей степени приближаются к одному из этих типов. В том случае, когда они лежат ближе к началу области, целесообразно рассматривать их как близкие к синусоидальным и применять те методы исследования, которые пригодны для синусоидальных и близких к ним колебаний. Кбгда же реальные колебания лежат ближе к концу области, целесообразно рассматривать их как релаксационные колебания и применять к ним «разрывную» трактовку.

Лит.: Андронов А. и Витт А., Разрывные периодич. решения, Доклады Академии наук СССР, Л., 1930, стр. 189; Хай кин С., Непрерывные и «разрывные» колебания, «Журнал прикладной физики», М., 1930, т. 7, вып. 6; Barkhausen H.,Das Problem d. Schwingungserzeugung, Lpz., 1907; LeCorbeiller Pb., Les systemes autoentretenus et Ies oscillations de relaxation, P., 193d; FriedldnderE., Ober Kipp-chwingungen in besondere bei Elektronenrohren, «Ar-

chiv f. Elektrotechmk», B., 1926, B. 16; V an der P о 1 B., Ober Relaxation Schwingungen, «Jahrbuclt d. draht. Telegr. u. Teleph.», B., 1926, B. 28, p. 178, 1927, Band 29, p. 114; Van der Pol B., Oscillations sinusoidales et de relaxation, «L’onde dlectrique», P., 1930, p. 245; Van der Pol B. u. van der Mark J., Quelques experiences avec des triodes et les-oscillations de relaxation, ibid., 1927, p. 461. С. Хайкин.