> Техника, страница 77 > Рентгенографический анализ

Рентгенографический анализ

Рентгенографический анализ, наука, возникшая в 1913 году после открытия интерференции рентгеновых лучей (Лауэ, Фридрих и Книппинг), занимающаяся изучением строения вещества методами, основанными на интерференции рассеянных рентгеновых лучей. При освещении вещества рентгеновыми лучами электроны, из которых построены атомы данного вещества, становятся сами центрами излучения колебаний той же длины волны. Происходит рассеяние рентгеновых лучей. Освещенный образец становится следовательно сам источником излучения. Колебания, идущие от отдельных электронов, складываются. Суммарная интенсивность определяется фазовыми соотношениями между колебаниями, испускаемыми отдельными центрами, которые в свою очередь зависят от расположения рассеивающих центров данной системы и от пололгения по отношению к ней направления первичного пучка и направления, в котором рассматривается рассеянный (вторичный) пучок. Т. о. распределение интенсивности рассеянных лучей по направлениям является функцией расположения рассеивающих центров. Методы Р. а. сводятся к изучению этого распределения и к определению расположения рассеивающих центров или систем центров (атомов, молекул) на основании этого распределения.

Рассеивание рентгеновых лучей кристаллами. Вследствие правильного расположения атомов в кристалле (смотрите) рассеянные ими лучи, интерферируя, имеют значительную интенсивность только по вполне определенным направлениям. Брагги показали, что эти интерференционные максимумы можно рассматривать как простые отражения от граней кристаллов. При этом отражения могут произойти только при определенных углах φ_η, которые данная грань составляет с направлением первичного пучка и которые определяются ур-ием Брагга:

2d sin φ_η=ηλ. (1)

Отражения могут происходить и в том случае, когда угол ψ весьма мало отличается от ψ_η. Величина Αφ„ очень мала и практически мол-сет быть наблюдена при специальных условиях. Одним из существенных факторов, определяющих величину Δφ_η, является число рассеивающих центров, то есть величина кристалла: она увеличивается с уменьшением размеров кристалла. Практически заметной φ_ηделается при размерах порядка 1(Н⁶ сантиметров и ниже. Формула (1) является основной для изучения строения кристаллов. Величины d связаны определенным образом с размерами элементарной ячейки кристалла и миллеровскими индексами данной грани. Под последними понимают 3 целые числа ft, h₂, h_a, которые обозначают, что ближайшая к началу координат плоскость, параллельная данной грани,

отсекает на осях отрезки Ϊγ,τγ,Ρ, где a_L,

Ml Alg М3

α₂, «з — ребра элементарной ячейки. Величины определяются следующей ф-ией, имеющей для общего случая (триклинная система) вид:

⁼ + ^22^2 + ^33^3 + +

-}- 27f₂₃7i₂7i₃ -)- 27c₃₃/i₃/?.₃, (2)

хде величины к зависят от a_lt я₂, а₃ и углов между ними а, β, γ. Для прямоугольных систем А)_1а=7c_2S=7с₃₁=0, например для ромбич. системы:

1

d*

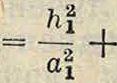
ч

Ч

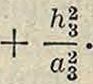
(3)

Интенсивность отражений для различных граней неодинакова и зависит от ряда факторов, вытекающих как из природы самого рассеяния, так и из строения кристалла и условий опыта. Изучение соотношения интенсивностей отдельных отражений играет весьма важную роль при определении структуры, о чем будет сказано ниже.

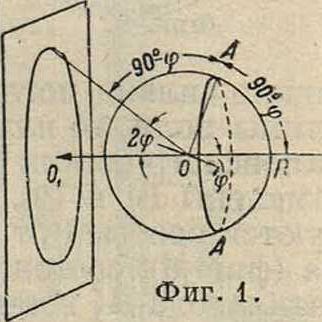
Методы а н а л и з а строения кристаллов. При рассмотрении связи между структурой кристалла и рентгенограммой, полученной тем или другим методом, удобно пользоватьсят. н. шаровой проекцией кристалла. Такую проекцию получим, окружив кристалл сферой и проведя из центра нормали ко всем граням. Точки пересечения нормалей с поверхностью шара называются полюсами граней и представляют шаровую проекцию. Если RO — направление пучка

(фигура 1) лучей длины волны Я, то какая-либо грань (7i_t h₂ h₃) отразит лишь в том случае, если нормаль к ней составляет с осью пучка угол 90° — φ (φ—угол Брагга), то есть нормаль лежит на конусе с осью НО и раствором 90°—φ, иначе говоря, если полюс этой грани лежит на круге А А (отражающий круг полюсов). Для каждой грани условием отражения будет нахождение полюса на соответствующем круге. При произвольном положении пучка по отношению к осям кристалла вероятность положения какой-либо грани н а отражающем круге весьма мала, и в общем случае мы отражения не получаем. Для того чтобы иметь полюсы на отражающем круге, необходимо иметь переменными или ориентацию кристалла по отношению к пучку или длину волны. В первом случае или вращают кристалл (метод вращения) или берут образец мелкокристаллический (метод пор о ш к о в). Во втором случае пользуются сплошным спектром (метод Лауэ). Эти три метода являются основными методами изучения строения кристаллов.

Метод Дебая-Шеррера-Хёлла (метод порошков). Образец для исследования является мелкокристаллич. агрегатом. При достаточной малости величины кристалликов последние имеют какую угодно ориентацию, то есть полюсы любой грани лежат во всех точках сферы, а следовательно и на отражающем круге. Т. о. для каждой грани мы получим отраженные лучи. Tax как весь отражающий круг для данной грани в этом случае заполнен полюсами, то все отраженные от этой грани лучи идут по образующим конуса с осью ROi и углом 2<р (фигура 1). Каждой грани (7ι₃ Тг₂ 7i₃) с расстоянием между плоскостями d_hl ь₃ соответствует свой конус отраженных лучей с углом На пластинке,

поставленной перпендикулярно первичному пучку, получится ряд кругов. Если расстояние пластинки от образца D и радиусы кругов г, то

tg2<p=^· (4>

Обычно же образец устанавливают на оси ци-линдрич. камеры; на цилиндре помещается фотографии, пленка. На пленке получается, ряд линий (пересечение ьонусов с цилиндром), симметрично расположенных относительно плоскости, проходящей через направление пуч

Фигура 2.

ка и ось цилиндра (фигура 2). По расстояниям между симметричными линиями I определяют углы отражений:

4?> =

360,

(5)

где R — радиус цилиндра. Рентгенограмма Дебая позволяет следовательно определить углы отражений для всех граней (у которых

< 1) и по формуле Брагга вычислить расстоя-

ния между плоскостями. Неизвестными остаются индексы соответствующих граней. Для определения симметрии и размеров элементарной ячейки на основании расстояний между плоскостями или же по углу φ пользуются квадратичной ф-ией. Ф-ла Брагга переписывается так:

sin² ?>=Д Ji · (6)

Подставив ~ из (2), получаем:

sin² φ=~f(a_lt α₂, α₃, α, β, γ, h_lt h₂, h₃). (7)

Вид квадратичной функции определяется формой элементарной ячейки, то есть кристаллографической системой; для кубической системы:

sin² ?>=^ (&? + &! +hi); (8)

для тетрагональной системы:

зт“<р=(Щ+Щ) + ~Щ; (9)

для гексагональной системы:

sin² Ψ=,**- (h + hl + М₂) + ~ Щ- (10)

Если параметры заданы, то, подставляя различные комбинации чисел ft, h₂, h_s, получим всевозможные углы отражений.

Расчет рентгенограмм Дебая сводится к определению такой квадратичной функции от hi, /гг, ii₃, в к-рую укладываются все найденные углы φ. Подыскание квадратичной ф-ии довольно легко для кубич. системы, не очень сложно для тетрагональной, гексагональной и ромбоэдрической, где в квадратичную ф-ию входят два коэфициента, и весьма сложно для остальных систем. Кубическая система легко узнается потому, что по (8) отношение sin² 93 должен быть отношением целых чисел 1 : 2 : 3 :4 :5. Определение квадратичной функции связано с индицированием рентгенограммы, то есть приписыванием каждой линии (каждому углу φ) определенного триплета h_lh₂ h₃. Индици-рование рентгенограмм для систем с двумя параметрами (тетрагональной, гексагональной и ромбоэдрической) упрощается применением графич. метода Хёлла, Если рентгенограмма проиндицирована и квадратичная ф-ия найдена, то вопрос о кристаллографии, системе и о размерах элементарной ячейки (из коэф-та к) решен. В случае простой решетки, то есть в случае, когда на элементарную ячейку приходится только один атом, этим задача и исчерпывается. В случае сложной решетки для решения вопроса о расположении атомов элементарной ячейки пользуются соотношением интенсивности между линиями. Интенсивность линий на дебаевских рентгенограммах определяется ф-лой:

^J=^|SPniS^TE(7>). (И)

Величина 1 + cos² 2 ψ учитывает зависимость рассеивания отдельным электроном от направления; фактор ψ² называется атомным и определяется распределением электронов

^{в атоме}; ϋ_η2 До, _φ — Фактор Лоренца, учитывающий отражение от какой-либо грани рентгеновых лучей, падающих под углом, несколько отличным от брагговского угла; увеличение интенсивности, происходящее при этом, различно в зависимости от угла φ. Фак тор W (Т, φ) называется тепловым. Он возникает вследствие того,что атомы не сидят точно· в узлах решетки, а находятся в тепловом дви-.жении, колеблясь около узлов как центров равновесия. Его действие сводится к уменьшению интенсивности с увеличением ^гла φ. Все перечисленные факторы дают непрерывную зависимость от угла φ. Характерными для структуры кристалла являются факторы |5Ί² и п; |S|² называется структурным фактором. Он определяется расположением атомов в элементарной ячейке и равен квадрату модуля комплексного выражения:

g _ у _{4 i}i2^i(a,_/:f_h + d_zf-h₂ + α₃*Λ₃). (12)

ft, hq, h₃—индексы грани, a_lk, a_2k,a_3i—координаты к-το атома, А_к—число электронов в атоме. Для центрированной решетки,координаты узлов которой 0 0 0 и он равен

8=1 + _eⁿⁱ(^hi + ^h* + ^h* (13)

откуда видно, что для случая, когда 1ι, + /ι₂ + + h₃—нечетное число, S= 0, то есть для таких граней отражения нет. Для решеток с центрированными гранями выпадают отражения для граней, у которых индексы смешанные, то есть которые в триплете ft, h₂ h₃—четные и нечетные числа, п—фактор повторяемости грани и равен числу комбинаций чисел h_lt h₂, fe₃, для которых квадратичная ф-ия (а также и структурный множитель) неизменны. Все такие грани дают одну и ту же линию. В кубической решетке для грани куба п=6, для грани октаэдра 8, для грани додекаэдра 12 и т. д. Расположение атомов в ячейке можно считать установленным, если вычисленное соотношение интенсивностей между линиями согласуется с найденными экспериментально. При расчете весьма существенно значение плотности исследуемого вещества ρ, которая позволяет вычислить число атомов или молекул в элементарной ячейке из ф-лы:

где S—число атомов в элементарной ячейке, М—ат. вес, V— объём элементарной ячейки, выраженной в A³, ili х 1,649 х 10“³ —вес атома в а. Основной ход расчета следующий: 1) определение углов отражений квадратичной ф-ии и индицирование; 2) вычисление размеров элементарной ячейки; 3) определение числа атомов (молекул) в ячейке из (14); 4) определение центрированности (трансляционной группы) на основании выпадающих отражений; 5) определение координат атомов на основании изучения интенсивностей.

Метод вращения.

Образцом для исследования служит монокристалл. На фигуре 3 АА—отражающий круг для какой-либо грани, нормаль к которой составляет с осью вращения угол д( При вращении полюс этой грани описывает круги ВВ. Очевидно, что грань может отражать при четырех положениях, соответствующих пересечениям кругов АА и ВВ. Если перпендикулярно пучку поставить пластинку для каждой грани,

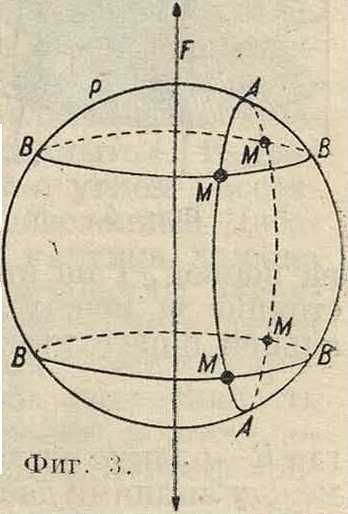
мы в общем случае получим 4 пятна, лежащих на дебаевском круге для данной грани. Пятна характеризуются углом <5 и расстоянием пятна до центрального пятна (радиус дебаевского круга). Последний определяет угол φ. Зная φ и <5, находим о из ф-лы:

COS ρ=С03 φ COS δ, (15)

к-рая становится понятной из фигура 4. Так. обр. есливращать кристалл вокруг какого-либо направления, то легко определить угол любой грани с осью вращения, чем пользуются для

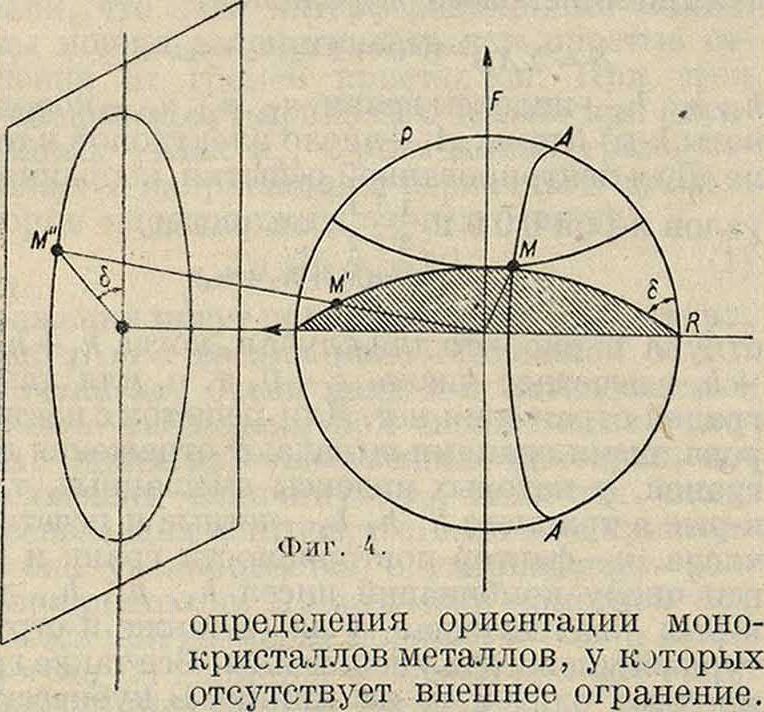
Если M—шаровая проекция отраженного луча (фигура 4) и FM — μ есть угол, к-рый отраженный луч составляет с осью вращения, если I есть индекс данной грани, отнесенный к оси вращения, то оказывается, что

COS μ=^l_g > (16)

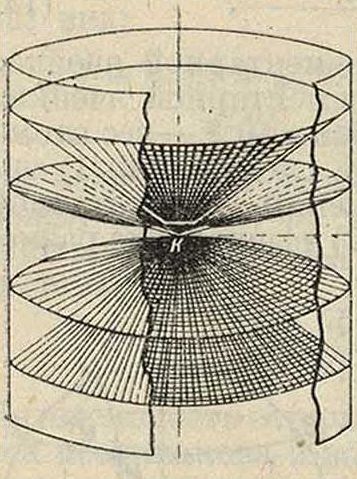
где η—расстояние между атомами (период идентичности) по оси вращения. Это значит, что все отражения от граней, у которых индекс по оси вращения один и тот же, лежат на конусе, ось которого совпа-• лает с осью вращения (фигура 5). Если снимок сделать на цилиндрич. пленку, то на ней мы получим пятна (фигура 6), расположенные по линиям. Пятна, лежащие на одной линии, согласно (16) имеют один и тот же индекс к оси вращения. Индекс на экваториальной линии пятен (и=90°) есть нуль на первой, 1 на второй и т. д. (фигура 6); расстояние »м,_: между линиями пятен и экваториальной определяет угол:

ctg μ i — ф (Π)

где R—радиус цилиндра. Так. обр. расстояние между линиями дает непосредственно (16) расстояние между атомами по оси вращения.

В том случае, когда по внешней форме кристалла (размеры его м. б. около V* лш) можно узнать основные кристаллографии, направления, определение структуры можно вести след.обр. Сделав 3 рентгенограммы с вращением вокруг (100), (010) и (001), определяем параметры по трем осям. Далее определяем транс ляционную группу, что легко делается с по-мощыо добавочных рентгенограмм с вращением вокруг нек-рых направлений, наир, в случае кубич. решетки соотношения между периодами идентичности по направлению (100), (110) и (111) являются характерными для той или

иной центрированности:	(100)	(110)	(Ш)
Простая кубич. решетка.	а	аУ2	а Уз
Центрированная решетка.	а	a VF	УГ а " 2
С центрирован, гранями.	а	ΫΪ	а УЗ

Дальнейшее индицирование рентгенограммы не представляет затруднений, т. к., зная размер элементарной ячейки (углы можно определить с помощью гониометра) .получаем квадратичную функцию. Для случая, когда кристаллографии. измерения нельзя произвести и нельзя так просто определить размеры элементарной ячейки, определение квадратичной ф-ии и индицированце рентгенограммы вращения упрощаются тем обстоятельством, что для каждой линии пятен один из индексов определяется номером линии пятен. Для экватора он нуль, вследствие чего квадратичная ф-ия для пятен, лежащих на экваторе, даже для триклинной системы имеет простой вид:

sin² ψ=(]с^Щ + + 2Л_1аг А);

при этом период идентичности по третьему направлению мы уже имеем.

Фигура 6.

При изучении сложных решеток после ин-д> цирования рентгенограмм выявляются те грани (h₁ h₂ h₃), которые не дали отражений. Затем в таблицах выбирают те пространственные группы, относящиеся к данной трансляционной группе, для которых характерно найденное выпадение отражений. Это упрощает отыскание координат атомов в элементарной ячейке, которое производится на основании соотношения интенсивностей отдельных отражений.

Дальнейшее развитие метода вращения дал Вейсенберг. Прибор, сконструированный им, называется гониометром Вейсенбер-г а. Сущность метода заключается в следующем. Из всех линий пятен выделяется с помощью диафрагмы только одна (наир, экваториальная). Во время съемки цилиндр с пленкой двигается вдоль оси, причем его движение связано с вращением кристалла. В результате мы получаем рентгенограмму, все пятна которой можно расположить на двух системах кривых. На каждой кривой один из индексов постоянен. При переходе от одной кривой к другой (той же системы) индексы грани изменяются на 1. Т. к. третий индекс известен (номер выбранной линии пятен), то индицирование такой рентгенограммы весьма несложно. Метод Вейсенберга позволяет непосредственно определить положение каждой отражающей грани по отношению к трем направлениям в пространстве, т. к. кроме угла с осью вращения (15) он дает еще и азимуталь-

Фигура О.

ный угол. Методы вращения являются наиболее мощными методами анализа. С их помощью определены весьма сложные структуры.

Метод Лауэ. Кристалл освещается сплошным спектром и во время экспозиции неподвижен. На пластинке, поставленной перпендикулярно к первичному пучку, мы получим отражение от какой-либо грани, составляющей с пучком угол Брагга лишь в том случае, если в спектре имеется длина волны,удовлетворяющая условию:

2d sin φ=ηλ.

Т. о. расположение пятен на рентгенограмме будет зависеть только от взаимного расположения граней, а не от расстояний между плоскостями граней. Тогда при совпадении первичного пучка с какой-либо кристаллографии. осью расположение пятен будет иметь симметрию, соответствующую этой оси (фигура 7). Для индицирования рентгенограмм пользуются тем _ьобстоятельством, что лучи, отраженные от всех граней, принадлежащие одной и той же зоне [Mj, г<₂, м₃], пойдут по образующим конуса, ось которого совпадает с направлением [%, м₂, щ], а угол раствора равен углу между [м, и_г, и_а] и направлением пучка. Поэтому пятна, принадлежащие определенной зоне, лежат на эллипсе, близком к окружности и проходящем через первичное пятно. Если пятна (направления отраженных лучей) перенести на стереографии. проекцию, то_они расположатся на кругах; центры этих_кругов дают направления [%, м₂, м₃].

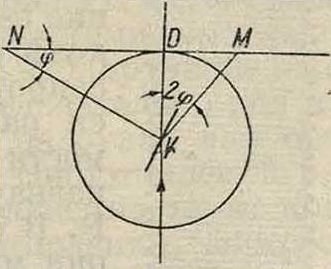
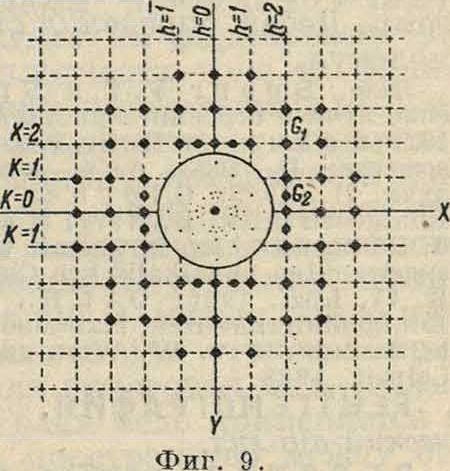
Более просто индицировать рентгенограммы построением на основании рентгенограмм Лауэ гно-монич. проекции кристалла. Связь между положением на рентгенограмме отражения от данной грани и ее точкой на плоскости проекции видна из фигура 8; DM определяет положение пятна на рентгенограмме, ΏΝ— положение проекции соответствующей грани: Ш=кп Ctg<p.

Грани, принадлежащие одной зоне, дают на проекции точки, лежащие на одной прямой. Если пучок лучей совпадает с кристаллографии. направлением, то построенная проекция должна иметь вид сетки. Все точки проекции располагаются на двух системах прямых. Номера прямых дают индексы граней (фигура 9). Если по внешней форме кристалла нельзя узнать основных кристаллографии, направлений, то устанавливают кристалл с помощью светящегося экрана, меняя положение его до тех пор, пока не получают симметричного расположения пятен. Метод Лауэ непосредственно дает только взаимное расположение граней вследствие того, что длина волны для каждого отражения неизвестна. Этим методом пользуются гл. обр. для определения симметрии кристалла. При этом метод позволяет из 32 классов различать только 11 групп. Классы,

различающиеся между собой наличием центра инверсии, дают одну и ту же картину.

Применения Р. а. Возможность определения взаимного расположения атомов в крист сделала Р. а. весьма мощным орудием для изучения как структуры твердого тела, так и процессов, происходящих в нем. Весьма плодотворно оказалось применение Р. а. в металлографии. Возможность каждую фазу характеризовать определенной решеткой, возможность замечать весьма малые изменения параметров, происходящие наприм. при образовании твердых растворов, обеспечивали широкое поле деятельности для методов Р. а. при изучении строения сплавов и тех изменений в их строении, которые возникают при термической обработке сплава. В этой области применяется гл. обр. метод Дебая-Шеррера, а в последнее время, с развитием выращивания монокристаллов металлов и твердых растворов, и др. уже методы. Большие возможности открыл Р. а. для изучения пластич. деформации, позволив определять без труда плоскости и направление скольжения при деформации монокристаллов, определять ориентацию (текстуру) кристаллитов, возникающую при волочении проволок или прокатке металла и т. и. Для изучения волокнистой структуры, образующейся примехаиич. обработке металла (протяжка, вальцовка), а также волокнистых структур органич. веществ (целлюлозы) методы Р. а., описанные выше, были видоизменены в соответствующем направлении. Зависимость ширины интерференционных максимумов от величины кристаллов позволила определить величину кристалликов субмикроскопич. размеров, что нашло себе применение в коллоидной химии.

Рассеяние рентгеновых лучей аморфными телами, жидкостями и газами. Интерференционные явления получаются не только при рассеянии лучей кри-сталлич. телами. Для случая некристаллич. веществ на пластинке, поставленной перпендикулярно первичному пучку, образуются кольца, подобные кольцами от мелкокристаллического вещества, но весьма размытые. Интенсивность их быстро убывает с углом рассеяния. Теоретич. расчет, произведенный Дебаем, показал, что подобная картина должна обусловливаться строением молекулы. Именно, если осветить пучком рентгеновых лучей вещество, в к-ром имеются беспорядочно ориентированные молекулы, то интенсивность рассеянных лучей в направлении, составляющем с первичным угол &, определяется ф-лой:

J-

1 + cos² 9

Sin X/Is ^xik

(18)

Величины x_ik связаны с расстоянием между атомами в молекуле _ik и углом # след, обр.:

Ел ” у sin з; (19)

ψ—рассеивающая способность атомов. В слу-

чае жидкостей и аморфных тел, как показали детальные исследования, картина усложняется вследствие интерференции лучей, рассеянных целыми молекулами. Образуются добавочные кольца, которые соответствуют среднему расстоянию между молекулами. В чистом виде интерференция от молекул была получена при освещении газов, для которых расстояния между молекулами достаточно велики по сравнению с размерами самих молекул. Пользуясь рассеянием рентгеновых лучей газами, Дебай определил структуру некоторых молекул.

Лит.: Брэгг У. Г. и Брэгг У. Л., Рептгенов-счие лучи п строение кристаллов, пер. с нем., М.—Л., 1929; Беляков Н. Я., Рентгеновы лучи и структура вещества, П., 1923; его же, Техника к рентгеновы лучи. Л., 1925; Glocker R., Materialpriifung mit Rontgenstrahlen, В., 1927; Mark II., Die Verwcndung d. Rontgenstrahlen in Chemie u. Technick, Ilandbuch d. angcwamiten physikalischen Chemie, hrsg. v. G. Bredig, B. 14, Lpz., 1926; Ott H., Strukturbestimmung mit Rontgeninterferenzen, Ilandbuch d. Experimentalphvsik,. herausgegei en v. W. Wien und F. Harms, B. 7, f. 2, Leipzig, 1928. Г. Курдюмов.