> Техника, страница 77 > Рефракция

Рефракция

Рефракция, преломление лучей света в земной атмосфере. Лучи света при прохождении через атмосферу благодаря ее неоднородности преломляются, вследствие чего видимое направление на светило или на земной предмет отличается от истинного направления. Различают Р. астрономическую и земную (атмосферную).

Р. астрономическая. При рассмотрении астрономических Р. достаточно принимать землю за шар и считать, что земная атмосфера состоит из бесконечно большого числа бесконечно тонких концентрических сферических слоев с общим центром в центре земного шара. При этом принимается, что плотность воздуха, оставаясь постоянной в каждом отдельном слое, постепенно увеличивается по какому-нибудь, закону от слоя к слою от нуля на границе атмосферы до некоторой величины <5., около поверхности земли. Луч света, идущий от какой-нибудь звезды, внутри земной атмосферы, переходя от одного слоя, более удаленного от поверхности земли и потому имеющего меньшую плотность, в соседний, более близкий к поверхности земли и обладающий большей плотностью, будет преломляться.

Луч bb_L (фигура 1), переходя из менее плотного слоя в более плотный слой, приближается к нормали b_vC к поверхности, разделяющей эти слои: падающий луч bb_lrпреломленный луч Ь^Ьу и нормаль Ь|С лежат в одной плоскости, и синус угла падения г относится к синусу угла преломления как показатель преломления μ_ι слоя, в к-.рый луч переходит, к показателю преломления μ слоя, из которого луч выходит. Т. о. путь луча, идущего от звезды S, после вступления в земную атмосферу в точке В представляется в дальнейшем некоторой ломаной линией, которая в пределе при бесконечном увеличении числа слоев и бесконечном уменьшении каждого из них обращается в кривую липию, обращенную своей вогнутостью к поверхности земли. Из законов преломления следует, что эта кривая есть плоская кривая, и следовательно астрономическая рефракция влияет только на высоту светила, не изменяя его азимута. По свойству нашего глаза наблюдатель А увидит звезду по направлению касательной AS’ к последнему элементу криволинейного пути луча. Т. о. рефракция повышает звезду или вообще небесное тело. Т.к.расстояние от земли до звезды практически можно считать бесконечно большим по сравнению с высотой земной атмосферы, то в случае отсутствия атмосферы наблюдатель увидел бы звезду по направлению AS параллельному направлению SB луча до вступления в атмосферу и изображенному на чертеже пунктирной линией. Угол ZAS, где Z—зенит наблюдателя, называется истинным зенитным расстоянием, угол ZAS—видимым зенитным расстоянием. Разность этих углов, выражающаяся углом S’AS, есть Р. Истинное зенитное расстояние получается из видимого прибавлением к этому последнему влияния Р.

Величина Р. меняется с зенитным расстоянием. В зените, где луч проходит перпендикулярно к слоям атмосферы, Р. равна нулю, на высоте 45° над горизонтом она составляет ~1, наибольшего значения Р. достигает на

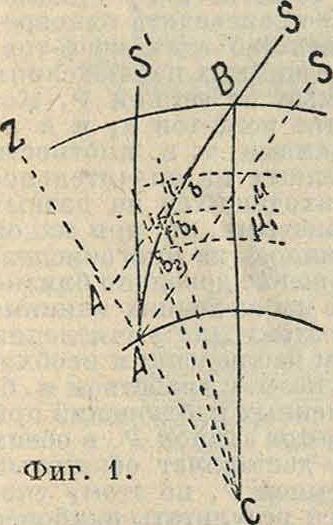
горизонте, где она равна ~35.

На основании законов преломления элементарная Р. dr при переходе луча из какого-нибудь бесконечно тонкого слоя в соседний, более близкий к поверхности земли, представляется ф-лой

В этой формуле du — бесконечно малое увеличение показателя преломления второго из рассматриваемых слоев по сравнению с первым.

Полное влияние Р. получается путем суммирования всех элементарных Р., то есть в пределе путем интегрирования. Но т. к. μ= + 2ей, где δ плотность воздуха в нек-ром бесконечно тонком слое, а с—коэф. его преломляющей способности, то ясно, что решение задачи о точном вычислении Р. требует знания закона, распределения плотностей в земной атмосфере. Но т. к. этот закон, как и закон уменьшения t° воздуха с высотой, от которого должен зависеть и первый закон, неизвестен, то приходится устанавливать различные гипотезы о-строении земной атмосферы, стремясь к тому чтобы вычисленная Р. возможно лучше согласовалась с наблюденной. Простейшей гипотезой являлась бы гипотеза уменьшения плотностей воздушных слоев с высотой над поверхностью земли в арифметич. прогрессии. Потакая гипотеза дает для Р. в горизонте лишь 28,5 вместо 35 и является явно неудовлетворительной. Ближе к действительности подходит гипотеза уменьшения плотностей с высотой в геометрия, прогрессии. Однако величины Р. для больших зенитных расстояний по· этой гипотезе выходят слишком большими, например для горизонта 38,5 вместо 35. Поэтому многие ученые или вводили нек-рые коррективы в эту гипотезу или представляли зависимость между плотностью воздушного слоя и его высотой под поверхностью земли более сложными математич. выражениями. Теоретическими изысканиями в области Р. занимались Айвори, Лёббок, Бессель, Лаплас, Опольцер, Гюльден, Радо, Ковальский и др. Так как при очень больших зенитных расстояниях точное значение Р. вследствие различных не подвергающихся учету атмосферных влияний не-м. б. получено, то астрономы редко наблюдают светила ниже 10—15° высоты над горизонтом. Для зенитных же .расстояний, не превосходящих 75—80°, все теории дают результаты, согласные между собою и с наблюдениями. Это усматривается из приведенной ниже· таблицы, которая дает также представление о расхождении различных теорий для более значительных зенитных расстояний.

Видимое зенит- Ополь- Вес- Лап- Поль-

ное расстояние •4^<*^в“^ш дер сель лас ден

-5°. В34" 334" 334" 334" 334"

85°. 950" 950" 951" 9’51" 9’50"

87°. 1421" 1422" 1423" 1423" 1421"

88°. 1В 17" 18Ί8" 1823" 1820" 18Ί4"

89°. 2436" 2430" 2450" 2435" 24Ί7"

90°. 356" 359" 3623" 35С" 3427"

Дтя зепитных расстояний, не очень близких к горизонту, удобно выражать Р. в виде ряда членов с нечетными степенями tg 2, а именно:

г=A tg z-В tg³ z+C tg у z-D tg⁷ z+ ., где z—видимое зенитное расстояние, а А, В, C, D,.— числовые коэф-ты. Этот ряд получается через интегрирование приведенного выше диференциального ур-ия Р.

Т. к. плотность воздуха изменяется с давле-. кием и (°, то и значение Р. для любого зенитного расстояния также зависит от этих факторов. Поэтому ясно, что для вычисления Р. необходимо записывать при наблюдениях показания барометра и термометра. Р. для нормальных показаний барометра и термометра, каковыми являются 760 миллиметров и +10°, называется среднейР. Коэф. первого члена вышеприведенного ряда при нормальных давлении и F называется постоянной Р.

Эта постоянная м. б. определена из наблюдения око-лополярных звезд в верхней и нижней кульмипациях.

Б настоящее время обычно ищут по способу наименьших квадратов поправку к некоторому принятому значению иостоянной Р. из обширного наблюдательного материала, так чтобы паилучшим образом удовлетворить всем этим наблюдениям. Т. к. значение Р. в горизонте, вычисленное по той или другой теории, дает возможность судить -о пригодности этой теории, то необходимо показать, как :мошно определить Р. в горизонте из наблюдений. Для этой цели наблюдают солнце или звезды с хорошо известными склонениями около их восхода или захода. Зная прямое восхождение светила и звездное время наблюдения, вычисляют часовой угол светила. Затем по этому часовому углу, склонению светила и география, широте места наблюдения вычисляют высоту светила, которая и будет истинной. Разность между этой и наблюденной высотой и даст Р., соответствующую измеренной высоте. Таким способом определяли Р. в горизонте Аргеландер в Кенигсберге, Гендерсен на Мысе Доброй Надежды и Фу с в Пулкове. При больших рядах наблюдений вычислять Р. для каждого отдельного наблюдения по формуле неудобно. Поэтому для практич. применений составляют таблицы Р., основывая их на той или иной теории Р. Вообще Р_г можно представить в виде

r=a tg z (ΒΤ)·^Αγ^λ}

где В зависит от показания барометра, Т—от показания термометра при барометре, у—от 1° внешнего воздуха, а—коэф., медленно изменяющийся с зенитным расстоянием, А и Я величины, вообще близкие к единице и -заметно от нее отличающиеся только при больших зе-нитпых расстояниях. Все эти величины даются в таблицах Р. по аргументу «зенитное расстояние». В предыдущей формуле множитель a tg z дает среднюю Р., а остальные множители служат для учета влияния давления и t° на Р. Т. о. составлены основанные на теории Гюльдена Пулковские таблицы Р., недавно вышедшие 3-м изданием. Из других отметим таблицы Билля и Гарцера.

Помимо преломления лучей в свободной атмосфере имеет место еще преломление внутри лого помещения, в к-ром установлен инструмент, в особенности на границе внутреннего, •обычно более теплого, воздуха и наружного, более холодного. Это преломление, называемое зальной Р. (Saalrefraction), вообще •очень мало, но может иметь заметное влияние при точных астрономии, работах. С целью избежать влияния зальной Р. в 1929 г. в Пулкове один из основных инструментов, именно вертикальный круг, служащий для определения склонений, был перенесен из главного здания в особый павильон, раскрывающийся при наблюдениях так, что весь инструмент оказывается на открытом воздухе. При относительных определениях положения светил, например при микрометрии, измерениях, при измерениях фотографии, пластинок, влияет разность Р. для измеряемых объектов, называемая диференциальной Р.

Р. земная имеет значение в геодезии при производстве нивелировок. На триангуляциях для определения разности высот двух точек земной поверхности применяется тригонометрии, нивелирование, основанное на измерении зенитных расстояний. Кроме зенитных расстояний при этом требуется еще знать горизонтальное расстояние между наблюдаемой точкой и точкой наблюдения, к-рое для точек триангуляций всегдаизвестно.

I

I

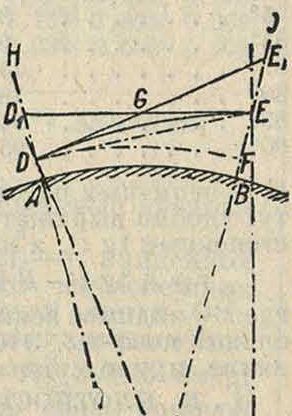
Вследствие существования земной атмосферы луч света от одной точки Е к другой D идет ие по прямой, а по кривой •линии, обращенной к поверхности земли своей вогнутостью (фигура 2). Наблюдатель в D видит точку Е не по направлению этой хорды, а по направлению касательной DGEi, к последнему элементу кривой JJE. Как и при астрономии, наблюдениях угол HDE называется истинным, а угол ¹

IIDE_l—видимым зенитным расстоянием.

При нормальном распределении плотно- Фигура 2. •стейвземной атмосфере видимое зенитное расстояние всегда меньше истинного. Разность между истинным и видимым зенитными расстояниями, т.е.угол EiDE, и есть земная Р. Величина земной Р. не поддает ся точному определению п зависит не только от расстояния между точками, но также от их абсолютных высот, вида и свойств местности между ними, Г и давления воздуха, высоты луча зрения над почвою и других причин. Обыкновенно принимают, что луч света, идущий от одной точки к другой, представляет дугу круга. Т. о. земная Р., как угол между касательной и хордой, пропорциональна половине дуги DE. Но дуга DE почти равна горизонтальному расстоянию между точками D и Е, или расстоянию AB=S по уровенной поверхности. Следовательно земная Р. пропорциональна половине дуги АВ или половине соответствующего этой дуге угла С между отвесными линиями АС и ВС. Поэтому для земной Р. получается простая формула

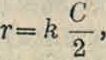
в которой k называется коэф-том земной Р. Чтобы определить разность высот точек D и Е, можно измерить или одно зенитное расстояние z—Z.HL1E1 точки Е, наблюдаемое из точки D, или кроме этого зенитного расстояния еще зенитное расстояние z₁=^JED₁ точки В, наблюдаемое из точки Е. Когда измеряется одно зенитное расстояние, наблюдения называются односторонними. При измерении двух зенитных расстояний наблюдения называются двусторонними, или взаимными. Разность высот двух точек при односторонних наблюдениях определяется по формуле

h^Sctgz+Sa¹—,

а при взаимных наблюдениях по формуле

k₁-k 4 R

В их ф-лах R—радиус кривизны уровенной поверхности в вертикальном сечении точек D и Е, к-рый вместе с горизонтальным расстоянием S между этими точками вошел в члены, выражающие влияние земной Р., через посредство угла С. В ф-ле, определяющей h при взаимных наблюдениях, введены различные коэф-ты и k земной Р. при наблюдениях из точек Е и D. Однако, если наблюдения в точках Е и D производить одновременно, то можно допустить равенство этих коэф-тов, то есть принять kj=k, и тогда при взаимных наблюдениях результат получается независимым от земной Р. Конечно предположение о равенстве коэф-тов и k не всегда может оказаться справедливым, т. к. плотности воздуха в точках D и Е, удаленных на значительное расстояние одна отдругой и находящихся на разных высотах, могут и не быть одинаковыми, но при мах ой разности высот точек, как выяснилось из многочисленных наблюдений, такое предположение довольно близко к истине. При односторонних же наблюдениях влияние земной Р. входит полностью. Поэтому для вычисления разности высот по односторонним наблюдениям необходимо знать коэф. земной Р. Этот коэф. с удобством м. б. определен из взаимных одновременных наблюдений при предположении о равенстве коэф-тов земной Р. в обеих точках. Каждая триангуляция доставляет обширный материал для вывода коэф-та земной Р. по этому способу. Ниже в таблице приводятся результаты наиболее тщательных исследований.

Триангуляция	Исследо ватель	Коэф. земной Р.
		наи боль ший	наи мень ший	сред ний
Французская. Английская. Прусская. Прусская. Зап.-русская. Лифляндская.	Деламбр. Кларк. Бессель. Байер. Теннер. Струве.	0,595 0,212 0.154 0,888 0,207 0,144	-0,007 +0,064 0,126 0,096 0,079 0,031	0,168 0,158 0,137 0,145 0,145 0,124

Приведенные в этой таблице наибольшие и наименьшие значения коэф-та земной Р. показывают, какую трудность представляет определение этого коэф-та. Коэф. земной Р. подвержен суточному ходу. На рассвете Р. имеет наибольшую величину, затем утром до 8 час. она быстро уменьшается, от 8 до 10 час. уменьшение продолжается, но гораздо медленнее, а от 10 час. до 3 час. дня Р. почти не меняется, проходя через свое наименьшее значение, время которого почти совпадает со временем наибольшей ί°. После 3 час. Р. увеличивается сперва медленно, потом быстрее и быстрее и к закату солнца опять приобретает значительную величину, но меньшую чем на рассвете. Ночью Р. продолжает увеличиваться и наибольшей величины достигает на рассвете, около времени наименьшей темп-ры. На рассвете, когдаР.имеет наибольшую величину, отдаленные земные предметы настолько приподнимаются, что кажутся как бы висящими в воздухе и этими моментами следует пользоваться для отыскания отдаленных тригонометрия. сигяа-лов. Наименьшее значение Р. равно—0,09, наибольшее

~ 0,20. Для измерения зенитных расстояний лучше всего выбирать время от 11 ч. утра до 2 ч. дня и притом в такие дни, когда небо бывает или сплошь ясное или сплошь ^пасмурное, то есть когда погода обладает устойчивостью, т. к. при неустойчивой погоде коэф. Р. подвержен наибольшим колебаниям. При тригонометрич. нивелировке надо избегать случаев, когда луч проходит ппзко над поверхностью земли, т. к. в этих случаях коэф. Р. может меняться скачками. В среднем коэф. земной Р. можно принять равным ~0,14. Вообще метод тригонометрич. нивелирования не может давать очень благонадежных

^_ii

результатов. Поправка S2, принятая выше вметоде тригонометрич. нивелирования при односторонних наблюдениях, должна иметь место также при определении высот кипрегелем в мензульной съемке, равно как и при точной геометрич. нивелировке. Но т. к. в этом случае •S всегда бывает достаточно малым по сравнению с ii и кроме того точность определения высот при мензульной

1 — и. съемке невысока, то в поправке S* —— обыкновенно бе-

2 к рут для ft нек-рую постоянную величину, именно, принимая ft=0,16, получают для указанной поправки выражение 0,42 ;. Необходимо заметить, что в поправке 1-Л S2

член — представляет поправку на кривизну или сферичность земли, а член ft есть собственно поправка иа земную Р. Т. к. при точной геометрич. никелировке отсчеты по рейкам делаются нивелиром, уста-

Harzer Р., Gebrauchstabellen zur Berechnung d. Ablenkungen der Lichtstrahlen in d. Atmosphare, Pub-likationen d. Sternwarte in Kiel, Kiel, 1924; Jordan W., Handbuch d. Vermessungskunde, B. 2,8 Aufl., Stg., 1923; Pertrer J. u. Exner F., Meteorologiscbe Optik, 2 Aufl., Lpz., 1922. А. Иванов.