> Техника, страница 78 > Ротор

Ротор

Ротор, основная часть быстровращающихся двигателей и рабочих машин, несущая на себе органы для восприятия энергии рабочего тела у первых и органы для отдачи энергии рабочему телу—у вторых и непосредственно связанная с ведущим валом (у первых) и приводным (у вторых). Основные формы Р. представляют собой барабаны, диски и колеса. Конструктивные выполнения Р. см. Турбины и Насосы.

При расчете быстровращающихся барабанов и дисков на прочность обыкновенно принимают во внимание лишь центробежную силу, развиваемую как ими самими, так и расположенным на их периферии венцом из лопаток, полюсов или других рабочих органов, пренебрегая напряжением от действия окружного усилия, вызываемого рабочим телом“ как незначительной величиной по сравнению с полным напряжением. Для упрощения расчета делается допущение, что вся масса, составляющая венец, равномерно распределена по всей внешней поверхности барабана или диска. Вычисленное таким образом напряжение конечно тем меньше действительного, чем в меньшем числе мест сосредоточена масса венца.

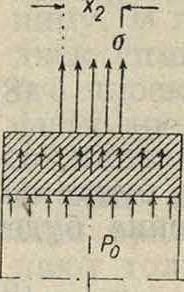
Напряжения в барабанах. Полые барабаны скрепляются с валами при помощи спиц или дисков на концах, но при расчете рассматривают барабан как свободно вращающееся кольцо, что соответствует во всяком случае средней части барабана. Если на поверхности барабана сделаны канавки для укрепления лопаток турбины, то определяют прежде всего среднюю толщину стенки <5 и соответствующий ей внешний радиус барабана R_x(фигура 1). Выделенный из барабана элементов длиной I (фигура 2) испытывает напряжение от действия центробежной силы, вызываемой его собственной массой и равной

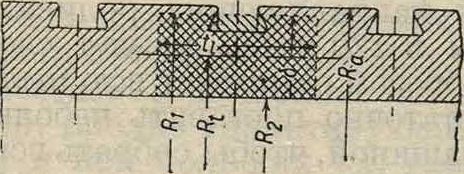
Фигура 1.

dF=^SlR_td<p)R_tu>

где у—вес 1 см³ материала в килограммах, д—ускорение силы тяжести, равное 981 вм/ск², и ω—угловая скорость вращения. Касательное напря-

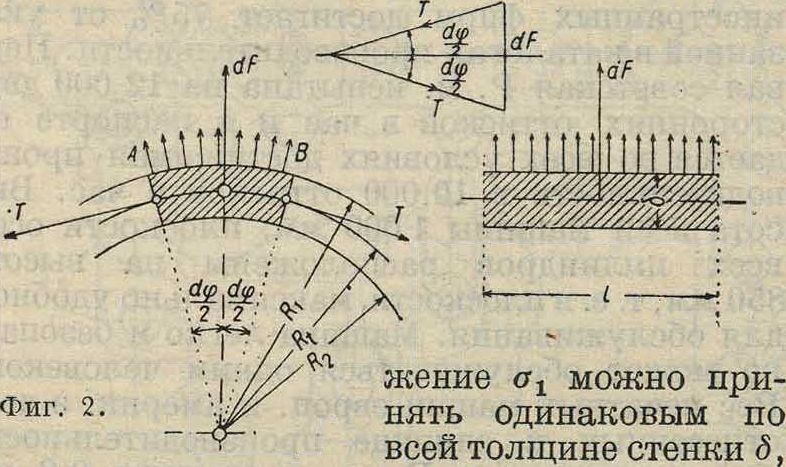
если она незначительна по сравнению с радиусом. Тогда на ограничивающих элемент площадках Ιδ действуют силы

Ιδσ_χ.

Эти силы должны уравновешиваться с центробежной силой. Следовательно откуда

σ_χ=^γ- ₌ у „з

9 ^г 9 *

кг/см²,

(1)

где V выражено в м/ск. Из этой ф-лы получаем, что при у=0,00785 килограмм/см³ уже при ν= 100 м/ск напряжение достигает 800 килограмм/см², что определяет пределы применимости барабанов. Напряжение от центробежной силы венца Р. определяется из условия равновесия сил, действующих в вертикальном направлении (фигура 3):

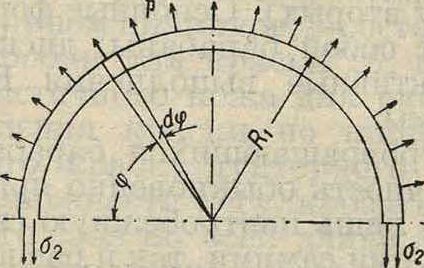
Фигура з.

2 σ.₂1δ=J* plR-^Ιφ sin ψ=2 plR_lt

откуда

pR,

(2)

T. о. полное касательное напряжение г»

^σ=од + σ₂ =

(3)

i

Я

Кроме того по основаниям зубцов на повер-хности барабана возникает радиальное на пряжение от центробежной силы, вызываемой как венцом Р., так и массой самих зубцов, но лишь при необычайно узких зубцах оно превышает касательное напряжение и только тогда принимается в расчет. Приращение радиуса барабана, вызываемое рассмотренными силами, определяется из общего соотношения между напряжением и удлинением и будет

β=ψ> (4)

где Е—модуль упругости. Это приращение имеет между прочим значение при устройстве вставных цапф и составных многоступенчатых барабанов (фигура 4). Цапфа вставляется

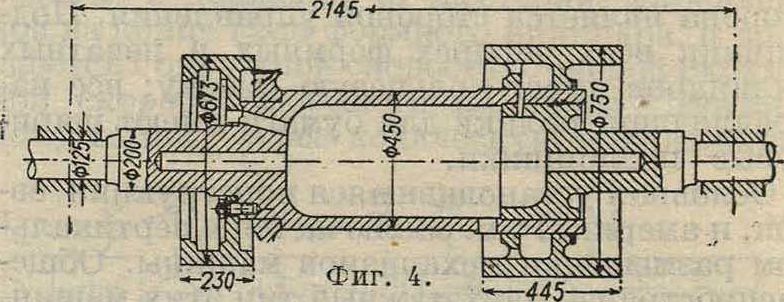
в нагретый барабан и при охлаждении его зажимается в нем. Соединение дополняется стопорами против проворачивания. Для того чтобы при вращении соединение не могло ослабнуть, необходимо, чтобы мера зажимания была больше приращения радиуса.

Барабаны с толстыми стенками, встречающиеся в якорях динамомашин, рассчитываются как диски постоянной толщины с центральным отверстием, что будет изложено далее.

Расчет быстровращающихся дисков. При значительных окружных скоростях от 100 м/ск и выше возможно применять только дисковые Р., выдерживающие скорости в 300 м/ск и даже более. Для постановки венца на периферии диска и для закрепления диска на валу внешняя и центральная части диска имеют уширенный профиль, т. ч. в диске различают три части: обод, собственно диск и ступицу. В последующих расчетах принято, что диск симметричен по отношению к средней его плоскости и что изменение ширины профиля диска происходит настолько постепенно, что можно пренебречь наклоном радиальных напряжений в плоскости профиля. При вращении возникают только радиаль ь*—

ные и касательные напряжения, которые с достаточной степенью точности можно принять равномерно распределенными по всей толщине диска.

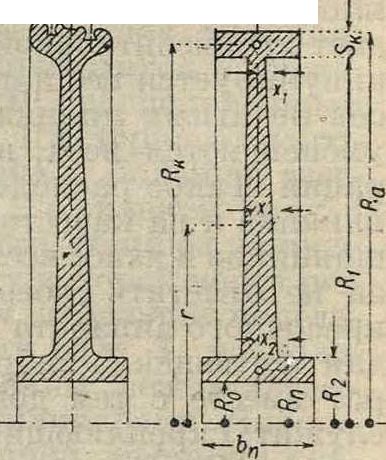
Основные обозначения, принятые при расчете, показаны на фигуре

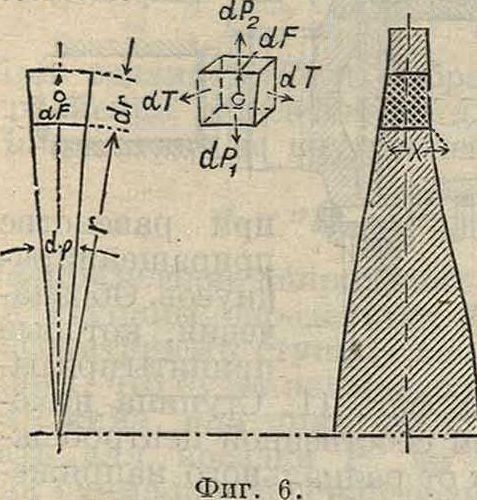
5. Выделив из диска элемент объёма dV=

=xrd<pdr (фигура 6), найдем, что он находится под действием центробежной силы dF, вызываемой его массой, касательных сил dT и радиальных сил dP_xи dP, действующих на его гранях. Для равновесия сумма проекций этих сил на направление радиуса, проходящего через ц. т. элемента, должен быть равна нулю:

dF + dP₂ — dP_x— dTdrp=0.

Фигура 5.

Но

clF=dm то²=⁷ dV ra>²=⁷ xrWdrdw, a g ^r

dT=xdr a_t,

dl=τχσ./Ιφ,

dPz=(r + dr) (ж + dx) (cr,. + da,.) clcp.

Вставляя полученные величины в ур-ие равновесия и отбрасывая бесконечно малые высших порядков, найдем первое основное уравнение:

^d (^ХГаГ) L?

dr

xa_t + - й)²г²ж=0.

(δ)

При радиальном напряжении σ_ν элемент получает относительное удлинение в радиальном направлении,

равное Это удлинение уменьшается тангенциальным напряжением на величину поперечного сжатия в том же направлении, рав-

^НУ^Ю тК ^{ГДе т}~ отношение удли- нения к поперечному сжатью .Тогда полное относительное удлинение в радиальном направлении ε_ν определится йз формулы:

(6)

(7)

Точно так же

Иь этих ур-ий

_ Em (me_r -f ε/)

^S> Е (^σ>· rn)

и a_t=*

_ Em (e_r -f me{)

Радиус r элементарного кольца получит при вращении диска приращение ρ, и окружность кольца увеличится на А=2 ло. Следовательно касательное удлинение

2 7JQ

2 лг

(8)

Приращение в радиальном направлении, соответствующее отрезку радиуса dr, будет do. Следовательно радиальное удлинение будет

Тогда

ar г )

dg dr’		(9)
Em
и at=—	dr r) m2-l	• (10)

r m2-i

Вставляя эти величины в первое основное ур-ие, разделив его на тхг и выполнив ди-ференцирование, получим второе основное уравнение:

d²g, de (d In х, 1 _дdr² ‘ dr V dr r) ^r , 1 din* 1 _Λ.

⁺ 4™~<r_r—_rir)-r⁴=o, (ii)

где

Em2 д

Диск равного сопротивления о_r=a_t=α= Const. Вводя это условие в ур-ие (5), получим:

σ г~ ^ν-ω4²χ=0,

откуда

I У СУ² ₇

-=— rd ί

α о и после интегрирования

_1пж=_А1^ _{+ С}.

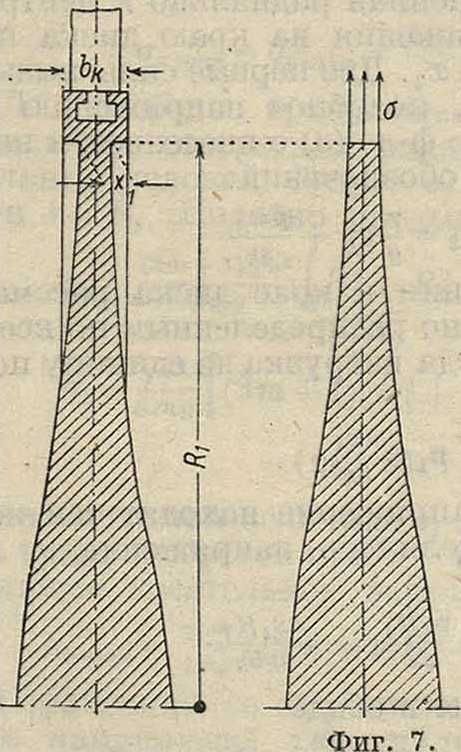
Постоянная С определяется из условия, что толщина диска у обода ж_х (фигура 7) не должен быть

JL

меньше определенной величины, как будет показано ниже. Т. о. ж=х₁ при г=R_x и след.

. .9 Т> 2

+ In ж_х.

Тогда

П — ^{у 0} 2fif"

1пж=1пж_х + £-^-(П²-

г²)

где х=x_xe^2ff<7

Jc -=— и ν-χ^ωΕχ. 111

(12)

Благодаря постоянству напряжения удлинение во всех точках диска имеет одну и ту же величину:

«Г=^е*= Μ^σ~™) ⁼

(m-l) σ mE

(13)

Следовательно приращение любого радиуса г будет

(m-l)ar ,_Λ ._ч

_ρ==ν·=—Т_. (14)

На следующей фигура 8 показаны четыре профиля диска, определенные на основании изложенного выше при ег=2 000 килограмм! см²,

Ry= 1 000лшиж_х =

= 20 миллиметров для окружных скоростей в 100,200,300 и 400 м/ск. Практически допустимый предел лежит около 400 лг/cjf, так как при дальнейшем увеличении скорости без увеличения при. этом допускаемого напряжения нарушится введенное ранее допущение постепенности изменения ширины профиля диска.

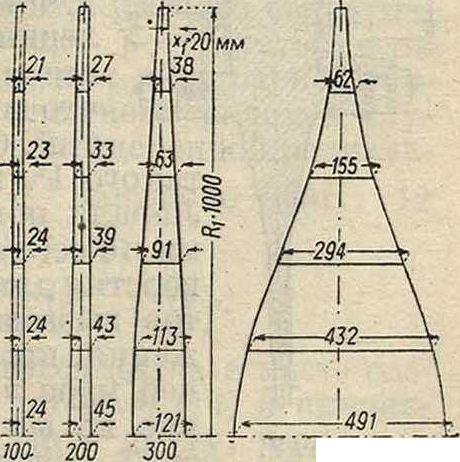
400 м/сек.

Фигура 8.

Для того чтобы в месте перехода от диска к ободу не возникало добавочных напряжений, необходимо, чтобы приращение внутреннего радиуса обода равнялось приращению радиуса края диска. Рассматривая обод как отдельное кольцо или часть барабана, находим, что на него действуют: 1) центробежные силы от его собственной массы и массы венца и 2) направленная радиально к центру нагрузка от напряжения на краю диска по всей толщине края х_г. Две первые силы вызывают напряжение, подобное напряжению в стенке барабана по формуле (3) с внесением в нее соответствующих обозначений:

_ffl + _ffl „}+£»«.

¹ Я ^{к 1} Sk

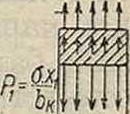
Влияние напряжения в крае диска рассматривают равномерно распределенным по всей ширине обода. Тогда нагрузка на единицу поверхности будет

ОХ i

Вызываемое ей напряжение находят тем же путем, как определялось напряжение σ» в стенке барабана:

_ _ Ρι Κι __ _ °XiRi _

³ sk skbk

Полное напряжение в ободе

^ак ^{= σ} 1 + ^σ·2 +

ох_г R i Skbk

(15)

Приращение радиуса обода при вращении находим по ур-ию (4):

o/tRk

~E~

Приравнивая его приращению радиуса края диска по ур-ию (14) при г=й_1; получим:

т-1 (7к= --

л, -т

tCl aw 5)	(16)
п_ _ m-1 ΚΛ i m Rk)	(17)

Нижний предел для х₁ определяется во всяком случае производственными возможностями и безопасностью в отношении разрыва диска. Stodola рекомендует не менее 7—12 миллиметров при циам. диска в 1 метров и 25—40 миллиметров при диам. в 3 ж. Исходя из выбранной величины х_г, определяют по уравнению (17) значение σ, которое кладут в основу дальнейшего рас-f· чета диска.

Ф-ла (12) для определения толщины диска выведена в предположении, что диск не имеет отверстий, Способ закрепления такого Р. на валу в турбинах Лавале показан на фигуре 9. Сами по себе очень небольшие отверстия для крепительных болтов вызывают местные напряжения, превышающие по крайней мере в два раза напряжение во всем диске. Поэтому в этой конструкции предусмотрена выточка в месте соединения диска с ободом, образующая слабое место на случай непредвиденного повышения напряжения, благодаря чему может оторваться только обод,

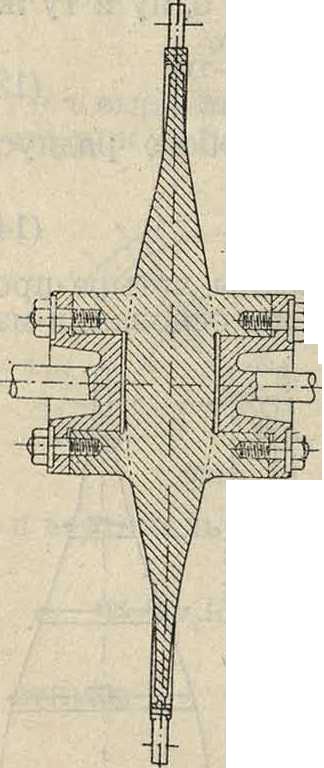
Фигура 9.

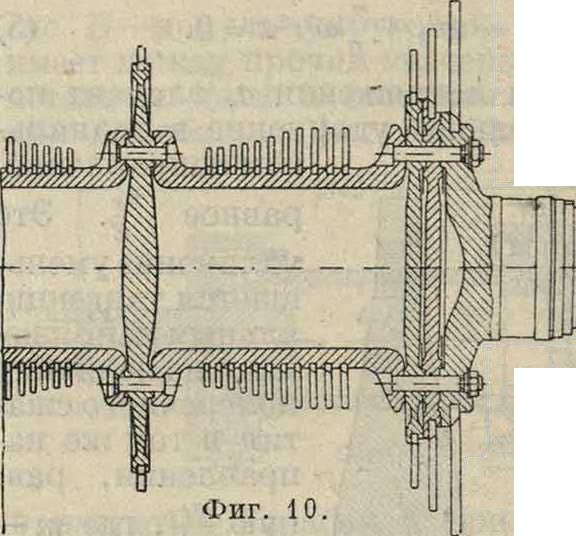
но не разрушится весь диск. В конструкции, показанной на фигуре 10, в местах, где имеются отверстия для соединения частей Р., сделано усиление дисков, служащее одновременно для взаимной центровки частей.

Если диск имеет центральное отверстие для посадки на вал, то толщина его в этом месте увеличивается, принимая форму ступицы. Подобно тому, как и для обода, необходимо в данном случае соблюдение условия,

чтобы ступица и диск в месте соединения испытывали назначенное радиальное напряжение

при равенстве приращенийра-диусов. Обозначения, которые приняты при расчете, показаны на фигуре 11. Ступица находится под действием собственной центробежной силы, нагрузки от радиального напряжения σ в диске толщиной ж₂ “ нагрузки на внутренней поверхности от давления р, которое создают при посадке Р. на вал во избежание ослабления соединения при вращении (фигура 12). Толщина стенки ступицы не является незначительной по отношению к радиусу; поэтому в данном случае нельзя принимать касательное напряжение равномерно распределенным по всей стенке, как это имело место для обода. Закон распределения напряжения можно приближенно принять по гиперболе

(фигура 13), и зави-

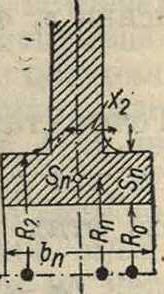
Фигура 11.

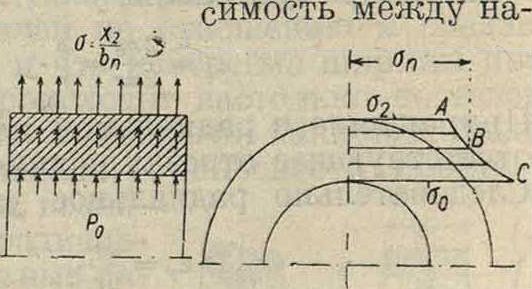
Фигура 12.

Фигура 13.

Шп

^σ<>=^σ» на пряжениями на поверхностях и средним напряжением выразится соотношениями:

Я».

Rs

Напряжение от центробежной силы σ₁₌ - ω²/?,²,.

1 д П

Принимая нагрузку от радиального напряжения в месте соединения диска со ступицей равномерно распределенной по длине ступицы, получим напряжение ах, К₂

Ь_п

Напряжение от давления на внутреннюю поверхность ступицы

О*=т- · — ·

„ Ро^о

Тогда полное среднее касательное напряжение в ступице будет

(18)

σ»-σ_ί+ϋ + σ^·-<*ΒΙ+-_ύΗβΛ _

Вторая зависимость получается из условия, что приращение радиуса диска в месте соединения со ступицей, определяемое по формуле

(14), должен быть равно приращению внешнего радиуса ступицы, которое равно

Е

так что или тЕ

ali, =

¹ о

Ни д ^n^sn

Ро^о

^sn

(19)

При заданном Я, и выбранном s„ из этого уравнения определяется длина ступицы Ь„. Напряжение на внутренней поверхности

(20)

?n-l R 2 m ^σ R_Q

Распределение напряжения по толщине стенки ступицы определится более точно, если рассматривать ступицу как диск равной толщины, что будет изложено в дальнейшем. Мера сжима, или припуск, который нужно давать для посадки Р. на вал, определится как сумма приращений радиуса ступицы о₀ от напряжения а₀ и давления р₀ и уменьшения радиуса вала e_w от давления Согласно формулам (8) и (7) имеем:

ρ₀=e_tR₀=-ψ (σ₀ + и п_ю=^ (ρ₀ -

Отсюда определяется припуск по диаметру для посадки Р. на вал:

2(о₀ -+ о_?£.)=—° (σ·₀ 4- 20_u) -

(21)

Диск равной толщин ы. ж=Const и dlnx=0. Вставляя эти условия во второе основное ур-ие (11), получим

d*Q. do 1

dr²

+

которое приводится к виду

П d(9T)-| dr [?* dr J

Произведя интегрирование, найдем:

-Аг. е=-

Лгз с !> С,

8 ^ 2 г

С-,

Тогда

‘"s — ° J,.·W ч , г

dr-~8^{A} И} г 8

Вставив эти величины в ур-ия (10), получим радиальное напряжение

С i 2

тЕ

(3m +1) + ~ (m + 1) —

-^f(m-l)]

(22)

и касательное напряжение тЕ Г Лг2, _Q4

о) -t

тЕ Г Аг2,

Щт + 1) +

О·

(23)

Постоянные С₁ и 6’₂ определяются из дополнительных условий для каждого случая.

Для сплошного диска без отверстия и с ненагруженным внешним краем, что имеет место например в гидравлич. тормозах, имеем а,. — 0 при г == II_х и σ,.=a_t при г - 0. Определив из этих условий постоянные С_± и С₂, найдем:

и а. =

(3.TI + l)ya>²(Rl — г“)

8 тд

yai2[(3m+l)K;-(m + 3)г2]

(24)

(25)

^t 8 тд

Наибольшее напряжение в центре диска

(3m + l)yo)2Hf ,_плч

max ~ max ~ g_тд (2u)

Для свободно вращающегося диска с центральным отверстием радиуса Д_а дополнительные условия будут: а,.= 0 при r=R_l и при r=R.,. Подобно предыдущему находим:

(3.-п + 1)у_Ш2 I _п„,

8 тд

(Ri+m-^-ιή (27)

II

-si·³

т + 1)(Щ+1П + (т + 3))² J.

1-2 )

(28)

По абсолютной величине a_t всегда больше а_г. На краю отверстия при г=возникает наибольшее касательное напряжение

О, шах - ™ [(Зж +1) Щ + (If — 1)RJ]. (29)

По сравнению со сплошным диском наибольшее напряжение увеличилось более чем в два раза. Оно возрастает по мере увеличения Л₂. II$! Stodola сверление небольших отверстий в любом месте диска изменяет напряжения на краю отверстия по сравнению с бывшими в этом месте до сверления напряжениями а, и a_t след, образом: в концах диаметра отверстия, который расположен по радиусу диска, a=3a_t—a_r и в перпендикулярном направлении σ"=3(Τ,. — a_t.

Если диск равной толщины имеет на внешнем или внутреннем крае радиальную нагрузку величиной соответственно а_г и а₃ кг/см², то возникают напряжения, определяемые из ф-л (22) и (23) при дополнительных условиях: со, а следовательно А=0, а,.=а₁ при г= /?, и а,.=σ₃ при г I!. Определив постоянные С_г и С₂, найдем:

Rj-Ri

1

Hi-jRjj

а₁Щ-а₂Щ-(а₁aji-l - σΒ -I- (ffj-

-^) ,.₂ |·

ν Ί r^rI

-ο ]-V·

(30)

(31)

Наибольшее напряжение на краю отверстия

°tmax=,[2σ₁β?-<τ₂(«ϊ + Щ)1 (32)

Расчет ступицы для диска равного сопротивления дает более точные результаты, если рассматривать ступицу как диск равной толщины. Приращение внешнего радиуса ступицы от равномерно распределенной радиаль ной согласно фигура 12

нагрузки а,.„=получается из ф-л (8) и (7):

Взяв приращение радиуса диска в месте соединения со ступипей по формуле (14) и приравняв оба приращения друг другу, имеем:

7П — 1

<JX2 ’ тb_п

Касательное напряжение а_ы слагается из напряжения от центробежной силы по ур-иш

(28) и напряжения от радиальной нагрузки по уравнению (31),вставляя в них й₀вместо R₂и R_r вместо и г и имея в виду, что σ_χ=~² и σ₂ =—Ро (фигура 12). Тогда

<*»=ШГ₉ [(«-!)«3 + (Зт +1) Я?] У

⁺ 5Ι^β<^Β>^+Β5)+^2ι,·^ΒΪ]

и выведенное выше условие равенства деформаций приведется к виду:

^ ^σ=Ш~_д ^[(W -^{1} Щ} + ^(3w +^{1} Щ]+}

⁺ ifblK(^Jii + ^i?o)+2p„R§]-^· (33)

Из ур-ия (33) м. б. найдена длина ступицы Ь_п.

Наибольшее касательное напряжение на внутренней поверхности ступицы равно сумме напряжений по ф-лам (29) и (32)

^_м*“[(Зт + 1)КЖт—1)До] +

+ - ^-Л2^Щ + рт + Щ)1

R₂-Ro^l °^{11 J}

Цилиндрич. ступицы больше деформируются к середине (фигура 14). Для избежания это-го ступицам придают I ^г Т Т форму, показанную на фигуре 15, или просто их усиливают против расчета.

В диске равной толщины со ступицей и ободом должен быть соблюдено условие равенства радиальных деформаций для обоих мест [стыка частей диска. Радиальные напряжения в этих местах обоз-

Шпачим через ог₁

tll i же/? ,ι ^{и а}н· Нагрузки, гйя:* Шл о_п действующие в отдельных частях, представлены на фигуре 16. Среднее касательное напряжение в ободе берем по ф-ле

(15) с соответ-

I

со

f Ро¹

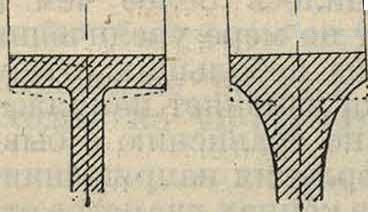
Фигура 14.

Фигура 15.

--

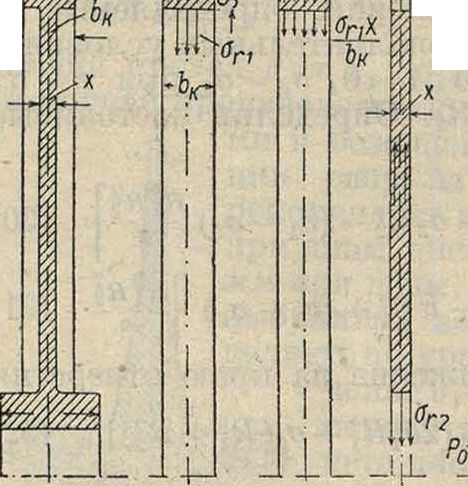
4·

Фигура 10.

ствующей заменой буквенных обозначений:

"*=3+^-^· С³⁴)

Приращение внутреннего радиуса обода должно равняться приращению внешнего радиуса диска в или

^a±^BJi ₌ 211 (о,

E ‘1 т

Касательное напряжение на внешнем крае диска σ“, слагается из напряжения от центробежной силы по формуле (28) и напряже ния от нагрузки на краях диска а_Гл и σ_Γο по формуле (31), заменяя г через Е_л. Тогда

pR_aR]₍

I v%R_k +

Skbk

= ^[(^т-1)^ + (з™ + 1)ад]

+

0r₁(R*+R_lIh)-20r₂R₁R2 °r

Ri-R 2

Г R 1· (35)

Подобным же образом находим зависимость, выражающую условие равенства приращений. внутреннего радиуса диска и внешнего радиуса ступицы

^[(3« + 1)ΛΪ+(«-¹)Κδ +

^ 2а_Гч Ri-Oy^Rl + R-i) ^σ?·₂

= ^[(m-l)Bl + (3m + l)Rg] +

_ЯХ

Rf-Rt

¹ 2

mb_n

(30)

⁺ ifbrg b·*^^{(Щ + R}ft+²p°^R{

Диск с гиперболическим профилем. Часто применяются для Р. диски с профилем, очерченным по гиперболе, отвечающей ур-шо х=cr-β. В этом случае второе основное ур-ие (11) принимает вид dze j_i-β<ΐο__β + ™· dr* ¹ г dr

ρ + Ar=О

и м. б. проинтегрировано. Общий интеграл этого уравнения

e=a)³ + Gy^v’¹ + C.₂r^v

^гда “ - Z ·^), ν-ι“ у *-^κ°ρ™ ур^ав-

нения у>² — βψ —=0, a C₁ и С₂—постоян ные интегрирования.

Введя значение ρ в ур-ия (10), найдем

У= ^ [(3 тонны + 1) «г² + <*w + 1) Су^-¹ +

+ (y>₂m+l) СУ *’^2-1], (37)

^σί= Ct- ι [(^то + 3)^α|2 + (^m + Vi) O-V^Vl-1 +

У (ш -|- y₂) С₂г^,“ ¹], (38)

Диск с произвольным с и м мет-p и ч н ы м профилем. Профиль диска разбивают на участки т. о., чтобы очертание каждого из них возможно близко подходило к гиперболе или прямой, параллельной оси симметрии. Возыцем например на участке b точки 4иВ (фигура 17) на расстоянии г_х и г₂ от

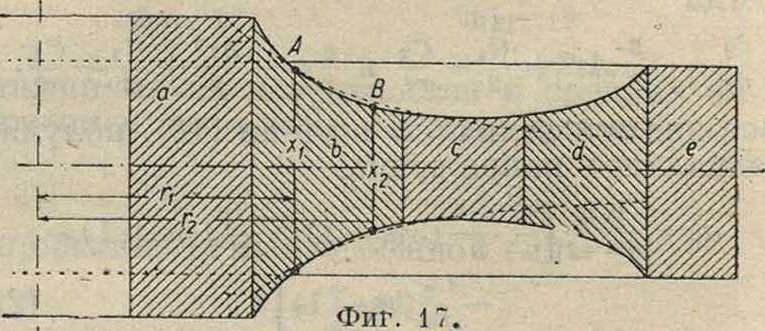
оси вращения, соответствующие толщинам профиля и ж₂. Для гиперболы должны иметь место соотношения х_х=сгϊ & и а?₂=сг„ " куда от-

(И) *1 rj

, "’i

"" ^β—^κ·

По точкам можно вычертить кривую, показанную пунктиром, и проверить точность при-

ближения. Действуя так же на других участках, получим ряд ур-ий очертания профиля

χ_α=Υ_ατ~^β>,

не исключая и участка, ограниченного прямой, параллельной оси симметрии, для которого β=0. В дальнейшем расчет ведется по ф-лам, изложенным для диска с гиперболическим профилем. Недостающие уравнения по числу неизвестных получаются из условия равенства радиальных деформаций на стыках всех участков.

Другой способ расчета основан на замене диференциалов малыми конечными разностями. Если выделить из диска элемент, ограниченный двумя цилиы-дрич. поверхностями 1 и 2 и двумя радиальными плоскостями! и II (фигура 18), и если известны напряжения сг,. и <т_гдля поверхности 1, то есть на расстоянии г, от оси вращения, и возможно определить изменения этих напряжений Аа_ги Δσ, соответствующие то на поверхности 2

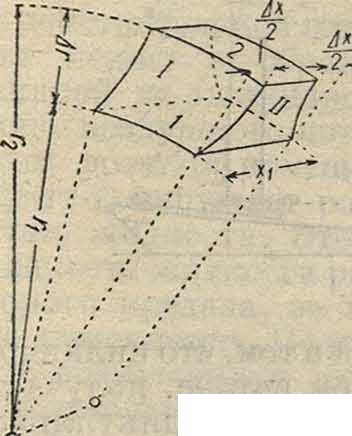
Фит. 18.

отрезку радиуса Δ?·, будут напряжения:

α= а,. 4- Ασ,. и α= о_г + Δσ₍. Конечные напряжения для этого элемента будут исходными для следующего элемента по направлению радиуса. Переходя так. обр. от элемента к элементу, можно определить напряжения во всем диске. Там, где толщина диска или напряжение претерпевает резкое изменение, величина Аг должен быть взята малой, около 0,5 см; в других случаях берут ее от 1 до 3 см. На внутреннем и внешнем краях диска должен быть соблюдены дополнительные условия, в частности радиальное напряжение на внутреннем крае должно равняться давлению от вала, к-рое остается еще при вращении, а на внешнем крае—напряжению от нагрузки, создаваемой венцом Р. Касательное напряжение на внутреннем крае диска устанавливается подбором. Если диск не имеет отверстия, то для его центра σγ=a_t.

Из первого основного ур-ия (5) находим

da,.=(a_t-σγ) -------rdr.

Заменяя диференциалы конечными разностями, получим:

Aa_r=(a_t - а,.) ~ - а,. ~ - со ²гЛг, (39)

откуда определяем Δ<τ,., посколько все величины в правой части ур-ия известны.

Радиальное удлинение в., м. б. выражено двумя зависимостями. По формуле (Р>)

«г=F К—2).

а из ф-л (9), (8) и (7) имеем, что Приравнивая обе величины, получим:

da г da_r

^: 07 — ---( i,.

¹ т ¹ dr т dr

откуда

7 гп. -f 1.

, dr. 1 - a_t)--h

r m

da,.

i Замена диференциалов конечными разностями дает:

А^=(п,-п₍)^ + 1Лп_г. (40)

Если величина касательного напряжения на внутреннем крае диска выбрана удачно, то для внешнего края диска определится напряжение, соответствующее заданной нагрузке от венца Р. В противном случае, что обычно и случается, расчет необходимо повторять вновь, изменяя выбранную величину a_t на внутреннем крае, до получения согласованных результатов.

Материалы и допускаемые напряжения. Высокие напряжения, возникающие в Р. благодаря быстрому вращению, требуют применения очень вязкого, хорошо прокованного и вполне однородного материала. Для устра-, нения внутренних напряжений перед последней обработкой производят тщательный отжиг при точно установленных t°. Пробные образцы для проверки качеств материала лучше всего брать из центральной части полуфабриката, т. к. в этом месте, во-первых, возникают наивысшие напряжения и, во-вторых, материал хуже всего прокован, так что проба даст наименьшие цифры. Для относительно мало напряженных роторов применяется в большинстве случаев обыкновенная мартеновская сталь с временным сопротивлением 5 000 килограмм /см², удлинением при разрыве в 30% и пределом пропорциональности от 2 300 до 2 70Окг/сж². При очень высоких напряжениях пользуются легированными сталями, особенно никелевой сталью с временным сопротивлением от 6 000 до 7 000 килограмм/см² и пределом пропорциональности 3 500—4 000 килограмм/см², а также хромоникелевой сталью с временным сопротивлением 7 000 килограмм/см², удлинением при разрыве в 15% и пределом пропорциональности 5 000 килограмм/см². Допускаемое напряжение выбирают в долях предела пропорциональности. Stodola рекомендует в расчетах дисков при нормальной скорости вращения принимать K_z=%5—40% предела пропорциональности. Относительно высокие по сравнению с обычными в машиностроении допускаемые напряжения объясняются тем, что в простых дисках и барабанах расчетные напряжения очень близки к действительности и тем, что при работе Р. находится под равномерной спокойной нагрузкой. Само собой разумеется, что материал должен быть безупречным, а обработка и сборка очень точной и тщательной. Stodola приводит пример, что ротор турбин Лаваля диаметром 760 миллиметров, вращающийся с окружной скоростью в 420 м/ск, при неуравновешенности в 0,1 килограмм на окружности вызывает неуравновешенную центробежную силу в 5 000 килограмм. Поэтому ро.ор подвергают очень тщательному уравновешиванию как статическому, так и динамическому.

Лит.: Д у б б е л ь Г., Паровые машины и паровые турбины, пер. с нем., Л., 1926; Stodola А., Dampf- und Gasturbinen, В., 1924; К a r r a s s R., Die Bauteile der Dampfturbinen, Einzelkonstruktionen aus dem Maschinenbau, hrsg. v. C. Volk, H. 10, B., 1927; Cammerer R., Vorlesungen liber Wasserkraftmaschi-nen. 2 Aufl., I.pz., 1921; Ostertag P., Kolben- und Turbokompressoren, 3 Aufl., Berlin, 1923; P f 1 e i d e-rer O., Die Kreisclpumpen, B., 1924; Lasehe O. u. Kieser W., Konstruktion und Material ira Bau топ Dampfturbinen und Turbodynamos, Berlin, 1925; S c h m о 1 z, Spannungsermittlung in Rotoren mit ausgepragten Polen, «Elektroteclinik und Maschinenbau», 1927; Keller, Berechnung von Radsoheiben, «Schwei-zerische Bauzeitung», Zurich, 1909, В. 51; G o u d i e W. J. Steam Turbines, 2 ed., L·., 1922. И. Орязиновский.