Рупор

Рупор, труба с жесткими стенками и переменным сечением, равномерно изменяющимся по некоторому закону от узкого к широкому концу. Р. применяется: 1) для усиления звуковой отдачи какого-либо источника (мембраны, голоса и др.), 2) для концентрации звукового излучения в области нек-рого б. или м. узкого телесного угла, 3) для усиления звука, приходящего от далекого источника путем его концентрации от широкого к узкому концу. Особенно важное значение имеют конический и экспоненциальный Р. Диференциаль-ное ур-ие распространения звука в Р. имеет в общем виде такую форму [¹]:

9(2 ° № ^т 9х

(1)

Здесь Ф представляет собой потенциал скоростей, производная от которого по координате дает скорость частиц (смотрите Гидродинамика), с—скорость звука, S—площадь поперечного сечения Р., ж—расстояние по оси Р. от его вершины. Для конического Р. S=i2ж², где Ω—телесный угол Р. Диференциальное ур-ие Р. принимает вид:

Э2ф _ ₂ 92ф 2С2 эф.

9(2 ~ ^С 9x2+ хдх’

его решение для случая распространения периодич. волн с круговой частотой ω будет:

Ф=^.cos(cot—kx), (2)

где к=j=-, λ—длина волны, А—амплитуда потока среды. Решение вида (2) выражает только прямую волну, идущую от узкого конца к широкому; такой процесс возможен лишь в бесконечном Р., где не будет отражения на конце. Если на расстоянии ж от вершины в Р. колеблется поршень сечения S, имеющий амплитуду скорости то величина

(амплитуда потока среды) и сила звука, порождаемого колебанием поршня на расстоянии ж от вершины, где сечение равно S, будет 7 - AH<L^c. ^h2 _ Игре fc²xf

2Sfi l + kixi 2SiS ‘ i + ft2jcf’

где ρ—плотность среды и fc ‘= —. Из формулы (3) можно заключить, что 1) при низких частотах (кх_х «1) сила звука в бесконечном коническом Р. будет пропорциональна квадрату частоты (фигура 1, кривые 2 и 3, нижний отрезок); 2) при высоких частотах сила звука асимптотически приближается к максимальной величине

А2дс· _ 1. 2SS, ~ 2

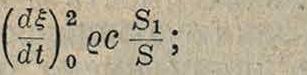
3) чем дальше от вершины отрезан конус, то есть чем больше х_1г тем равномернее будет частотная характеристика излучения, то есть тем при более низкой частоте будет достигнуто предельное значение излучения. На фигуре 1 кривая2

^w/cg

относится к Р. с углом при вершине в 4,6°, кривая 3—к Р. с углом 35,6°; если считать радиус узкого конца условно за 1, то первый Р. отрезан на расстоянии 24,9 от вершины, второй—на расстоянии 3,12. На фигуре 1 по ординатам нанесена не сила звука (звуковой поток), а отношение его сопротивления излучения w к сопротивлению излучения (смотрите Звук) для плоской волны (дс); если сопротивление излучения умножить на эффективноезначение скорости частиц (д - ?- (§|)_в> то получим

.общую излучаемую через Р. за 1 ск. энергию; если разделить эту энергию на площадь сечения S,то получится силазвукана расстоянии,?, которая дается ф-лой (3). Поведение Р. конечной длины будет отличаться от вышеописанного, т. к. здесь, будет иметь место отражение на конце., которое тем значительнее, чем больше длина волны по сравнению с размерами выходного отверстия [*]. При высоких частотах отражения на корце почти нет, и потому верхние части характеристик изменятся мало. Чем больше выходное отверстие Р., тем ближе его характеристика к кривым фигура 1.

Для экспоненциального Р., сечение которого изменяется по закону £=Sy^оа:, дифе-ренциальное ур-ие (1) для расходящихся периодических волн будет иметь решение:

Ар о

^ф=cos (^ω{ - Ρ^χ + ^θ)> (4)

где α—число, характеризующее расхождение Ρ., β=k ~ f 1 — jp, a θ—произвольная постоянная, определяемая из начальных условий. Скорость волны в экспоненциальном Р. будет:

V-.£ =. == ~-^-^е ·-*· (5)

У‘-ё~У‘

Если а² < 47с², то скорость волн в Р. будет больше скорости звука с в данной среде; при α= 2к екорость волн в Р. делается мнимой.

. о. если ω < —, то Р. перестает пропускать волны и действует аналогично конденсаторному фильтру. Сила звука в экспоненциальном Р. на расстоянии х от начала рупора т __ А^дс -I

¹ 2SSi V ¹ 1°)

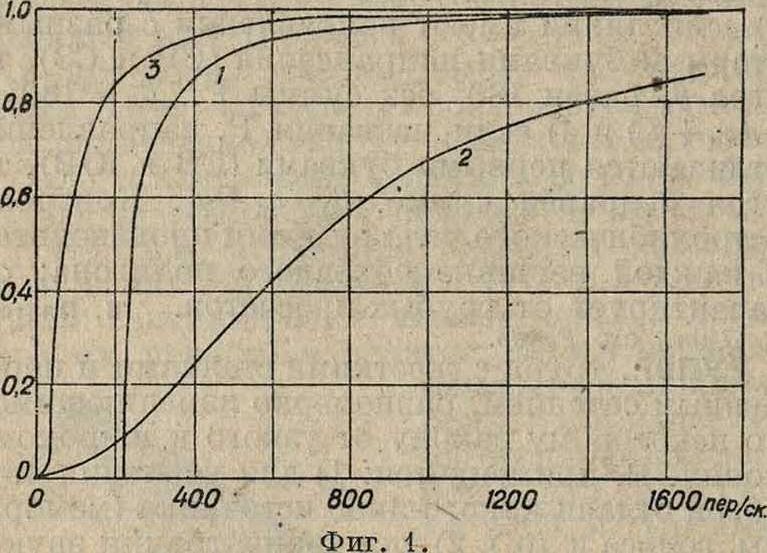
На фигуре 1 кривая 1 относится к бесконечному экспоненциальному Р.,имеющему одинаковые входное и выходное отверстия (ii,=2,5 сантиметров и R=18,5 см, а— 0,08) с коническим Р., к которому относится кривая 2, и одинаковую с ним длину 50 см. Из сравнения ясно, что экспоненциальный Р. отрезает низкую область частот, но зато в остальной части характеристика его имеет весьма равномерный ход и быстро достигает предельного значения. Поэтому практически экспоненциальный Р. имеет преимущество перед коническим,- тем более что его критич. частота со₀=^а| всегда м. б. опущена настолько низко, что отрезаемая область частот не будет играть роли Г³]. Так, для экспоненциального Р., к к-рому относится кривая 1 на фигуре 1, а>= 1 360, т. e. f₀= 217 пер/ск., что уже не вызывает серьезных искажений; ω₀ легко можно сделать еще гораздо меньше. Для Р. конечной длины на конце получается отражение и частотные характеристики принимают более сложный вид. На фигуре 2 даны сопротивления излучения для экспоненциального Р. (кривая 1), конического Р. (кривая 2) указанных выше размеров и для поршневой мембраны (радиуса 2,5 см), излучающей в открытое пространство (кривая 3). Из сравнения фигура 1 и 2 ясно: 1) что конечный экспоненциальный Р. уже не имеет резко выраженной критич. частоты; 2) что излучение обоих типов Р., проходя через ряд максимумов и. минимумов, приближается к общему пределу,.соответствующему сопротивлению излучения для плоской волны (ос); 3) что экспонен

циальный Р. раньше достигает предела и следовательно имеет преимущество перед коническим Р. в отношении равномерности характеристики; 4) что по сравнению с открытой поршневой мембраной излучение через Р. сильно повышается, особенно при низких частотах. Если длина волны больше диаметра выходного отверстия, возможно отраженно от конца и образование стоячих волн и соб-

, 2η+1.

или I=—j— λ,

ственных колебаний системы, а следовательно при передаче звука через Р. получится искажение тембра. Простейшая форма образования стоячей волны в коническом рупоре·— это стоячие волны по длине, подобно тому как это имеет место в органных трубах. Для Р., открытого с обоих концов, частоты собственных колебаний будут: ю_п=~ или 1=где

I—длина Е., Л*—длина волны η-ой гармоники, а п—целое число. Для Р., закрытого с одного конца (например мембраной), ω_η=-- ΐ- ”^с

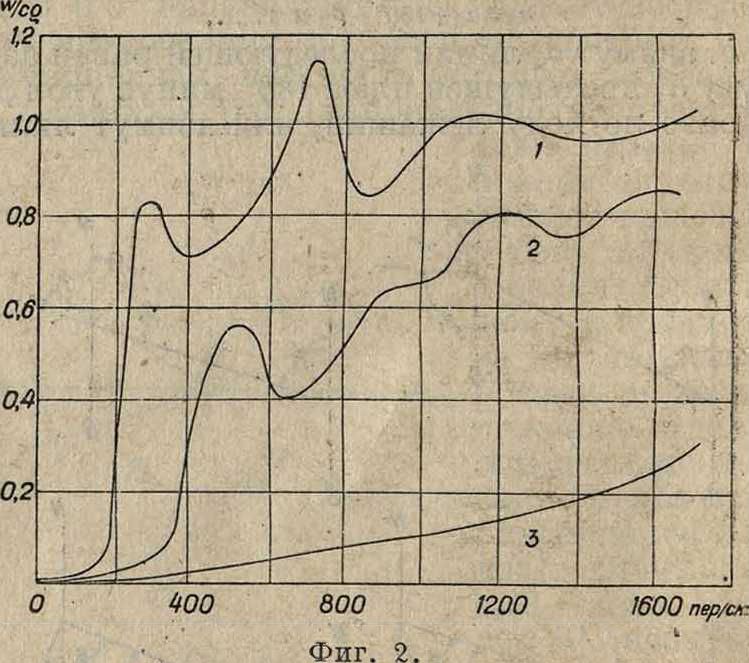
В экспоненциальном Р. образование стоячих волн происходит почти по тем же законам. Если Р. имеет тупой угол, то выходное отверстие велико и условия для образования, стоячих волн неблагоприятны, так как не будет сильного отражения; наоборот, для узких рупоров выходное отверстие мало и стоячие волны будут резко выражены, в виду чего узкие Р. дают сильные искажения тембра. Кроме образования стоячих волн в продольном направлении они могут возникнуть и в поперечном направлении, причем образуются узловые плоскости, проходящие через ось, и узловые конусы [·*], и ве.сь объём Р. делится на ряд ячеек (фигура 3).

Кроме резонансных частот, связанных с самим объёмом Р., могут резонировать и давать призвуки стенки Р., что то-жё отрицательно влияет на качество передачи; так наир., тонкий придает звуку. своеобразный резкий оттенок. Чтобы этого избежать, Р. лучше делать более массивным и из материалов со значительным внутренним трением (картон, папье-маше, дерево). При использовании Р. в электроакустич. приборах звук от мембраны площадью через переходную камеру проходит к входу в Р. (сечение /S,). Если принять, что Р. имеет предельное сопротивление излучения во всех частотах S-lQC, то, предполагая, что размеры камеры меньше длины волны, можно показать, что излучаемая энергия будет в SJS-i раз больше, чем если бы Р. с входным сечением S₂был приложен к мембране без переходной камеры. Уменьшая S·, можно сильно повысить излучение звлжа. Это соображение использовано Вейте и Турасом [⁶] для построения мощного громкоговорителя, который дал на опыте кпд до 50%; входное отверстие из переходной камеры представляло собой узкую кольцевую щель, постепенно расширяющуюся и переходящую в трубу Р. Стюарт и Линдсей дают следующий коэф. усиления излучения я через Р. по Сравнению с мембраной, излучающей в открытое пространство [*]: ^l

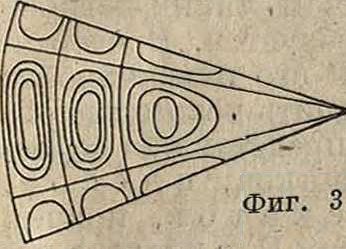
металлический

Р.

2л

Ssi

l + siiP lid

, « 7

Здесь d—длина переходной камеры и к=γ.

Если d мало, то усиление излучения α= —,

то есть при длинных волнах резко растет. Для коротких волн (высоких частот) формула уже неверна, ибо рупор не дает усиления излучения выше известного предела частот (фигура 1). Кроме способности усиливать излучение Р.

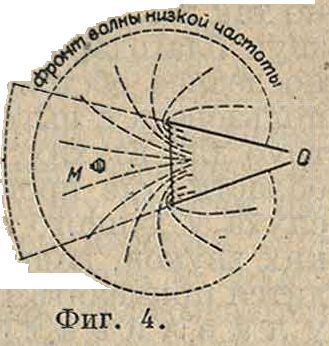
обладает еще свойством сосредоточивать звук в направлении своей оси, причем это свойство направленности звуковые волны сохраняют отчасти и по выходе из Р. Свойство это резко выражено лишь в области коротких волн (Λ<1ΐ), для длинных же звук расходится от конца Р. в форме сферич. волны (фигура 4, М— микрофон, О—источник звука), и никакого эффекта направленности при этом не получается. Т. о. ясно, что тембр звука суще-ственно меняется: по™ оси рупоравысокието-на передаются полностью, низкие же относительно ослаблены; в боковых направлениях высокие тона быстро ослабевают, остаются почти одни низкие, что ведет к неразборчивости при передаче речи. На фигуре 5 показаны характеристики излучения громкоговорителя

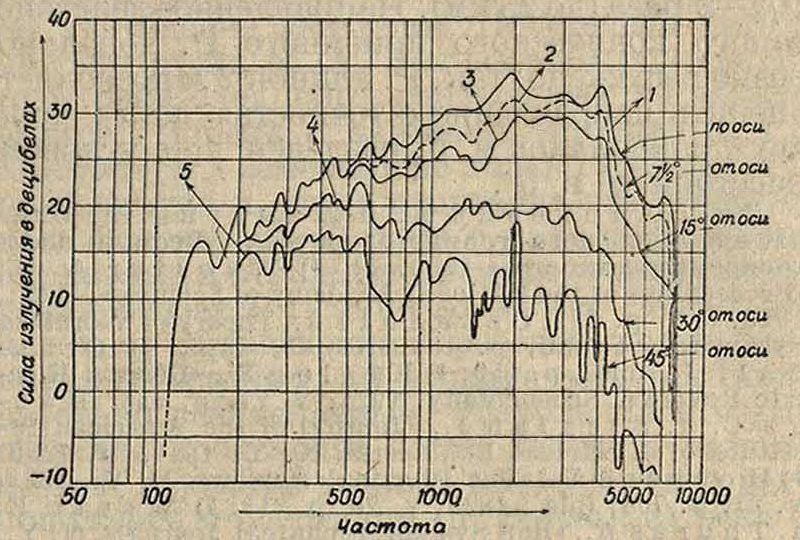
Фигура 5.

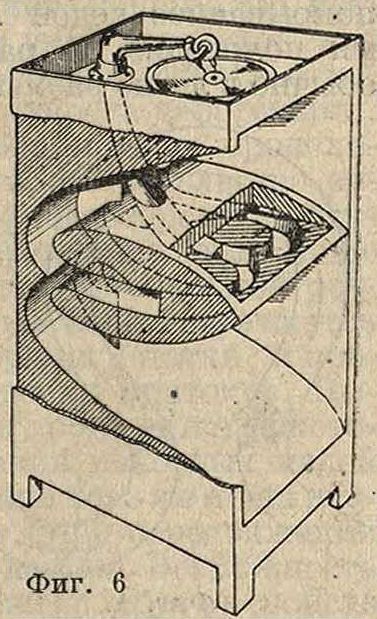
с экспоненциальным Р. (критическая частота 115 пер/ск.) на расстоянии в 3,6 метров при различных углах к.оси Р. (фигура 5: кривая 1—излучение по оеи Р., 2—7^х/₂° от оси, 3—15° от оси, 4— 30°от оси,5—45° от оси). При боковых направлениях сила звука высоких частот спадает и тем более резко, чем больше угол; при 5 000 пер/ск. излучение по оси примерно на 30 децибел, то есть в 1 000 раз, сильнее, чем под углом. в 45°. При использовании Р. в качестве м е-г а ф о и а (разговорной трубы) в направлении оси хорошо концентрируются обертоны выше 1000 пер/ск., которые имеют важнейшее значение для разборчивости речи благодаря чему разговор в мегафон возможен на расстояниях в сотни м. Для экономии места Р. может быть изогнут в несколько плавных оборотов, при этом его длина будет значительна, и выходное отверстие можно сделать достаточно большим. На фигуре 6 показан такой сложный изогнутый Р. для граммофона; канал Р. разбивается на две части, каждая из них снова на две части и наконец все четыре хода соединяются у выходного отверстия. Общее сечение рассчитывается по экспоненциальному закону.

Р. может применяться также для усиления при приеме звуковых сигналов или речи. Слуховая труба для глухих, амбушюр микрофона, медицинский стетоскоп служат примерами такого рода усиления по принципу концентрации звуковых волн. Воспринимающие Р. могут давать значительное усиление (в десятки раз), но так же, как и излучающие, они искажают звук благодаря резонансным, свойствам. Это последнее обстоятельство можно иногда использовать с выгодой при подборе слуховых труб для глухих, чтобы усилить звуки в той области, где произошла наибольшая потеря слуха у данного лица. Для восприятия низких звуков, например звуков аэроплана, приходится применять очень длинные Р. (з в у к о-улавливатели)с большим выходным отверстием. Так, Ветцман [⁷ ] применял конические Р. длиной в 2, 3 и 5 м; отношение длины боковой стенки к диаметру выходного отверстия выгодно брать ок. 2:1. Такие Р. позволили увеличить слышимость аэроплана в 1¹/₂—2 раза (до 25 км). Направленное действие такого конического приемного Р. довольно резко выражено; так, Р. длиной 2 метров позволяет оценить направление с точностью до 3°; звук двух аэропланов м. б. разделен при угловом расстоянии в 5°.

Лит.: ХаркевичА. и Ломагин К., Опыт расчета рупорного громкоговорителя, «Вестник электропромышленности», 1930, 11; г) Webster А. С., «Proceedings or the National Academy of Sciences», Wsh., 1919, У. 5, p. 279; Crandall J., Theory of Vibrating Systems a. Spund, p. 153, N. Y., 1926; Crandall J., ibiu., p. 150; ^г) К e ! 1 о g E., «General Electric Review», Schenectady, 1924, v. 27, p. 556; H anna C. a. Slepian J., «Journal, of the American Institute of Electrical Engineers», N. Y, 1924, p. 7250; a) Η о e r s c h V., «The Physical Review», N. Y., 1923, v. 21, p. 706; ibid., 1925, v. 25, p. 218; 5) W e n t e E. a. T h ur a s A., «Bell System Technical Journal», N. Y., 1928, v. 7, p. 140; «) Stewart a, Lindsay, Acoustics, p. 154, L., 1930; ’) W a e t z m a η n E., «Ztschr. f. techn. Physik», Lpz. 1921, B. 2, p. 166 и 191; Mu 1-

I er-P on i 1 lets, Lehrb. d. Physik, B. i, T. 3. p. 302,

II Aufl., Brschw., 1928. С. Ршевкин.