> Техника, страница 78 > Ряды

Ряды

Ряды. Числовые Р. Дана бесконечная последовательность чисел (положительных или отрицательных, действительных или комплексных): «₁, а_г, a_s, ., а,„ .; в математике под Р. понимают выражение:

fti + °2 + ^аз -f-. + я_в + — (1)

Сходимость Р. Пусть S„—сумма п первых членов Р. (1), то есть пусть

<Ь_В=и₁ + а₂ +. + а„.

Если S„ при неограниченном возрастании числа п стремится к нек-рому пределу S, то ряд (1) называется сходящимся, а величина S—его с у м мой. Таким образом

П

S=lim S„=lim ^ ^а

71—>СО ?1->0О ]_{=1

короче это записывают так:

оэ

S=«!+«„+. +Й,₍+. или S=2 а_к.

п=1

Простейший пример сходящегося Р.—геометрическая прогрессия со знаменателем, по абсолютной величине меньшим единицы. Сумма членов такой прогрессии дается ф-лой:

ft + о-й + ^аЧ^г + · · + ^п +···,= ’

где I <7 < 1. Из определения сходимости Р. следует, что изменение, прибавление или откидывание любого конечного числа членов Р. не отразится на его сходимости. Если S_nпри неограниченном возрастании п не стремится ни к какому конечному пределу, то Р. называют расходящимся. Примерами расходящихся Р. являются: геометрии, прогрессия со знаменателем, по абсолютной величине большим единицы, и Р. 1 Д(—1) + 1+.; для этого Р.

.1; я.-·· ·-$«·-i;

поэтому S,< при я->оо не стремится пи к какому

СО

пределу. Сходимость Р. 2% ^влечет за со-

1

со со оо бой сходимость Р. 2 № “ 2 ⁼ $ 2^··

111

со оо

Сходимость рядов 2 ^ак “ 2 ^^{>к влечет СХ0}Д^И“ 1 1

со мость Р. 2 (^α* + ^δ«·) и 1

00 оо со

2 (^αλ· + ь_к)=2 ^ак + 2

1 11

Признаки сходимости. Для сходимости Р. необходимо и достаточно, чтобы п+р

$п+р ⁼ 2 ^ 1

ft=n + l

при неограниченном возрастании числа п и при произвольном изменении положительного числа р стремилась к нулю (признак Коши). Необходимым условием сходимости Р. является условие lima„= 0; это условие получается

71—>00

из признака Коши, если р=1. Условие это не является достаточным условием сходимо-

со сти; так, Р. 2 расходится несмотря на то,

П=1^Уп

что это условие выполняется. Действительно

00

для Р. У] — сумма

1 Уп

^{Sn =} Ti ⁺ V2 ⁺ ··· ⁺

и следовательно limS_M=oo. Другим приме-

71->оо ром расходящегося Р., удовлетворяющего условию lim а_п=0, является гармонический ряд

П-+СО

1. 1. 1, 1,

Ϊ ⁺ 2 + 3 ⁺ · · · +П + · · ·

Абсолютная и условная сходимость. Сходящийся Р. (1) называется абсолютно сходящимся, если Р.

I «i I + I “а I + К I + ·. · + I «_м I + · · · (2)

сходится. Сходящийся Р. (1) называется сходящимся условно, если Р. (2) расходится. Пример абсолютно сходящегося Р.—геометрическая прогрессия с знаменателем q, если |gj < 1. Примеры Р., сходящихся условно, дает теорема Лейбница. Пусть p_lt р₂, ., р_п—положительные не возрастающие с увеличением п числа и такие, что Пт р_и=0; при этих

71-» ОО

предположениях Р.

Pl~Pi + P₃-Pi + ··. + (— l)^m+1 Рм + ···

сходится. Из приведенной теоремы следует, что Р.

—--4 + -4 —+.

Vi V2 V3 Vi

и

1-1+ ‘-1 +

сходятся. Сходимость этих Р. условна, ибо Р., составленные из абсолютных величин их членов, расходятся. Перестановка членов в абсолютно сходящемся Р. не нарушает сходимости Р. и не меняет его суммы. Перестановка членов в условно сходящемся Р. может нарушить его сходимость или, не нарушая сходимости, изменить его сумму. Пример Р.

СО

2 (- 1)^ί+11 условно сходится; Р. ‘ —1 +

й=1 132

+ - + ] — I + .) получившийся от закономерной перестановки членов в предыдущем Р., хотя и сходится, но будет иметь уже другую сумму. Но тот же условно сходящийся Р. можно сделать расходящимся путем соответствующей перестановки членов. Если по крайней ме-

СО ОО

ре один из двух сходящихся Р. 2 «я и 2 ^ъ«

п-1 71=1

сходится абсолютно, то справедлива следую· щая формула для произведения этих Р.:

ОО ОО ОО

2 ®я“ 2 ⁼2 (^а1^&и + ^asb„_₁ + а₃b„__г +

71=1 П=1 71=1

н----Μι)·

Сравнение Р. Признаки абсо-

ОО

лютной сходимости. Если Р. 2&*

71=1

(все b_к > 0) сходится и если I а_к I < b_ъ то Р.

ОО

2 ^ак абсолютно сходится. Доказательство это-1

го положения следует из признака Коши следующим образом:

п+р п+р п+р

2 «A· =S 2 I ^α* «Ξ 2 ^Ьк,

h=n+1 h=n+l n + 1

правая часть последнего неравенства при п -* со имеет пределом 0, следовательно то п+р же будет и с 2 I I·

71+1

Из сравнения данного Р. (1) с геометрической прогрессией получаются следующие достаточные признаки абсолютной сходимости: пусть lim ^αψ-=1. Если ϊ< 1, то со ^а«

Р. (1) сходится, и если I > 1, то Р. (1) расходится (признак Даламбера).

Пусть limy^,roJ=l; если I < 1, то Р. (1)

п—»оО

абсолютно сходится; если I > 1, то Р. (1) расходится (признак Коши). Пусть <р{х) положительная невозрастающая ф-ия, опре-

СО

деленная при 0 х со и такая, что J <p{x)dx

а существует (а > 0). Если члены ряда (1) удовлетворяют неравенствам | а_п | φ(ή), то Р. (1)

абсолютно сходится (интегральный признак сходимости).

Доказательство: по предположению Р.

СО k

2 ,f <p(x)dx

/i=l fe-1

сходится; члены Р. (1) не больше членов этого Р., так как к и

J <р(х) dx^ J φβ) dx=<p(k) ^ I а_к |.

^{h 4} fe-l

к-1

CAJ

Следовательно и Р. 2 I^а» сходится.

1

Примеры применения признаков сходимо-

СО

сти: Р. 2 йз“при I q | < 1 сходится, так как

lim! (ft+ila**¹

п-»ср

—_к— j=I q I меньше единицы. Р. 2~

П=1^П СО

при а > 1 сходится, т. к. J ~ существует а

(при а > 1). Приводим суммы указанных Р. при α= 2 и α= 4:

со со

2 1 _ π² _ Чуч 1 _ π*

71^{2 _} 6 ’ jLA η* ^— 90 *

71=1

71= 1

Р. функций. Дана последовательность функций

fi(x).1п(х), · ·

Ряд

/iO) 4- h(x) -

(3)

называется сходящимся в точке ж==а, если числовой Р.

Ш + f .0») + - · · т Ш + (4)

сходится. Суммой Р. (3) при ж=а называется сумма Р.(4). Р. (3) называется сходящимся в промежутке α=£ ж « 6, ес-ли он сходится в каждой точке этого промежутка. Р. (3) называется равномерно сходящимся в промежутке п^х^Ь, если каждому положительному числу ε можно поставить в соответствие такое число Ν, что при всяком η ^N, при произвольном положительном р и при любом х в промежутке « г= ж ί> удовлетворяется неравенство:

П-г V

V

f„(x)

h =п+1

Пример неравномерно сходящегося

СО

Р.: в промежутке -Нг$ + 1 Р. 2 ThSh·

к=о сходится к функции

S(x)=;

ί 0 при х=О

( 1 -f ж² при х φ 0.

Относительно равномерно сходящихся рядов справедливы следующие теоремы: равномерно сходящийся Р. непрерывных ф-ий сходится к непрерывной ф-ии. Равномерно сходящийся Р. интегрируемых ф-ий можно интегрировать по-членно, то есть в случае равномерной сходимости Р. (3) справедливо следующее равенство:

5 Г °° a L 1

Если Р., составленный из производных 1Дх) членов сходящегося Р. (3). сходится равномерно, то сумма S(x) Р. (3) диференцируе-

СО

ма п S(x)= 2 /*(£)

1

Степенным Р. называется Р. вида: а₀ а_гх + а₂ж² +. Если степенной Р. сходится при нек-ром значении ж= ж₀, то он сходится равномерно при х R < |ж₀|. Приме р: Р. fxy=l— х + х² — .· .равномерно сходится при I х I ^ R < 1. Интегрируя по-членно от 0 до х, получим:

]п(1 + х)=* —+ γ-. для I х |< 1.

Ряды Фурье. Система ортогональных функций (смотрите)

fi(x), f/x).f_n(x). (5)

называется полной, если кроме Fix)-0 не существует другой ф-пи F(x), удовлетворяющей равенствам: ь

J F(x)fi(x)dx= 0, где г=1, 2,. ., п,.

а

b

Числа a i=J F(x) f,(x) clx называются к о-

а зфпцпентами Фурье функции Е(ж).

^dx= ^ffa(^x)^dx·

Для любой F(x) с интегрируемым квадратом справедливо неравенство Бесселя:

г ⁰⁰

J [F(x)]*dx> 2^α«·

а 1

Если система (5) полна, то предыдущее неравенство обратится в равенство Парсе-в а л я:

Ь со

J[F(x)]² dx= ^ ^α«·

а 1

со

Ряд 2 ^аи /и (д) называется рядом Фурье, 1

порожденным функцией Fix). В случае полной системы (5) интеграл

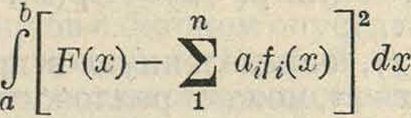
с неограниченным увеличением п стремится к нулю. Частным случаем системы ортогональных функций является система тригонометрических функций.

Тригонометрические Р. Система функций

1, sin ж, cos ж, 81п2ж, соз2ж,. .,

sinnx, соэиж,. (А>

ортогональна и полна в любом промежутке длины 2л. Эта система называется системой тригонометрических функций. Ряд

I а₀ + («j cos ж + b_х sin ж) 4- (а₂ cos 2ж +

+ &2^sin2a;)4- ··· 4- («„cosпх +

4- b_п sin ш) + ., (В)

где

4-71

а_п=* f f{x) cos пх clx

— Л

И

i ^+л

b_п=· J* f (ж) sin пх clx (п=1, 2, .),

— Л

называется тригонометрии. Р. Фурье функции fix). Тригонометрии. Р. Фурье применяются в целом ряде задач физики и техники (смотрите Диференциальпые уравнения). Про функцию fix) говорят, что она удовлетворяет условию Дирихле в промежутке от х=а до ж=b, если этот промежуток можно разбить на конечное число промежутков, внутри каждого· из которых ф-ия fix) непрерывна и имеет конечное число максимумов и минимумов. Примером ф-ии ^удовлетворяющей условию Дирихле, является любая непрерывная ф-ия, имеющая в рассматриваемом промежутке конечное число максимумов и минимумов (например· любой полином). Р. Фурье (В), построенный для ф-ии fix), периодической с периодом 2π и удовлетворяющей условию Дирихле, сходится. Сумма членов этого Р. равна ф-ии fix) во всех точках непрерывности fix); в точках разрыва /(ж) она равна среднеарифметическому /(^χ + ⁰> + ·4^χ-_°)_ правого [ (ж -Ь 0)] и левого [fix — 0)] предельных значений f(ж) в этой точке (теорема Дирихле).

Замечания: 1) если fix) имеет отличный от 2л период Т, то Р. (В) заменяется рядом

υυ

«о + 2 (^й«

2 71 ПХ ,7. 2 я пх

COS—ψ--τ О_п Sill -

где

α

^;я=J /(г) cos

_ ⁷

2

2л пл

+ ·>

&_М=У f f(x) sin clx (n=1,2,.);

_ T

2

2) если /(ж) четна, т. e. если f(—x)=fix), то все Ь_п(п=1,2,.) равны нулю. Если /"(ж) нечетна, то есть если ((—ж)=—/(ж), то а_п — О 0=0, 1, 2, .);

3) ф-ию ((ж), определенную в промежутке от ж=0до х=π, можно рйзлойсить в тригонометрии. Р. Фурье след, образом: пусть

<р(х)= >

у, (ж)=^еслн

So + S i -г ·. · -г -Sy)

n -i-1 ’

тде

Sn=γ- -1- 2 (^й*.·^{cos Ιχ} + ^bк sin Щ-

ft=l

Для любой непрерывной функции f(x) имеет место соотношение:

1 · Sn “f· Si -f* .·{“ S/i e, ·. lim -°-i-ry--- /(·);

n->oo

•ото соотношение и позволяет находить значе-ние функции f(x) поданным коэф-там Фурье. Примеры разложений в Р. Фурье:

со

1) х=2 (~I)™ ⁺¹1^{sinητ п}Р.и —я<х< -г π;

1

оо

i i π ХЛ 4 COS (2 ft-f 1) ГС

S) 1*1=2 — 2 —(Υί+Γ)» ^пр“

3)

~-Σ

sm г? гс η

при 0 < х < 2 :

Интеграл Фурье. Если J | f(x) {clx есть

— оо конечная величина и fix) удовлетворяет в любом конечном промежутке условиям Дирихле, то можно разложить f(x) в сходящийся Р. Фурье для любого промежутка (—/, + I). В пределе, при 1-* оо, р. Фурье обращается в интеграл Фурье:

(я + о) +/(X-

—=* J d/. j f (a) cos λ (х — a) da.

f (ж), если 0 < х < л — ((— ж), если — π<ж<0, φ (ж)—нечетна и следовательно для нее Р.

СО

(В) обращается в 2 sin ^пх> ¹¹⁰ при ^х З⁵ 0 1

ф-ии /(ж) и ?>(ж) совпадают, следовательно ф-ия f(x), определенная в промежутке от ж=0 до х=л, разлагается в Р. Фурье по одним синусам. Аналогично, полагая

0 < х < π fi— ж), если π < х < О,

убеждаемся в том, что f (ж) можно разложить в Р. по одним косинусам. Отсюда следует, что системы ортогональных в промежутке от 0 до π функций

1, cos“, cos2ж,. ., совтеж,. и,

siii ж, sin 2 ж,. ., sin паз,. полны в этом промежутке и периодическая функция fix) с периодом π разложима в тригонометрия. Р. Фурье по функциям каждой из этих систем.

Суммирование средними арифметическими Фейера—процесс, применяемый в случае расходимости Р. Фурье при отыскании непрерывнойфункнии по ее коэффициентам Фурье. Процесс этот состоит в нахождении предела выражения:

Представление функции в виде интеграла Фурье имеет большое значение для тех дифе-ренцнальных уравнений физики и техники, где ищется решение в бесконечном промежут-* ке (например теплопроводность неограниченной среды).

Лит.: С млг р н о в В., Курс высшей математики, т. 2, 2 изд., М.—Л.-, 1931; Курант Р., Курс дифе-ренциального и интегрального исчисления, ч. 1. М., 1931; Привалов И., Ряды Фурье, М.—Л., 1930; ftoursat Е., Cours d’analyse mathdmatique, t. 1—3, P., 1922—24; Knopp K., Theorie u. Anwendung d. unendlichen Reihen, 2 Aufl., B., 1924. M. Нргйнес.