 > Техника, страница 79 > Свободная поверхностная энергия
> Техника, страница 79 > Свободная поверхностная энергия
Свободная поверхностная энергия
Свободная поверхностная энергия,
избыток свободной энергии, заключенный в поверхностном слое на границе двух соприкасающихся фаз, отнесенный к 1 см2; называется иногда поверхностным натяжением (смотрите). Основными величинами, определяющими своеобразные свойства поверхностных слоев как на гладких поверхностях раздела, так и в дисперсных системах, являются: 1) поверхностное натяжение (или удельная свободная поверхностная энергия) а в эрг /смг=дин/см; 2) адсорбция, определяющая химия, состав поверхностного слоя Г в мол/сж2 или А=Г «Sj в мол/г (на г порошка-
адсорбента с удельной поверхностью St см2/г),
3)механич. прочность поверхностного слоя и 4) величины, определяющие электр и ч. свойства поверхности раздела — поверхностная плотность электрич. заряда (заряд двойного слоя) и скачок потенциала в пограничном слое.
Поверхностное натяжение определяется как работа сизотермич. побратим о г о образования 1 см2 данного поверхностного слоя, то есть как максимальная работа перевода в поверхностный слой необходимого для его образования числа молекул п1г из объёма граничащих фаз. Из самого определения следует, что а м. б. легко измеряемо только для жидких поверхностей раздела (жидкость—газ или жидкость 1—жидкость 2), то есть для поверхностей, образованных фазами, молекулы которых легкоподвижны и потому позволяют провести процесс образования нового поверхностного слоя практически вполне обратимо. Для твердых поверхностей раздела (твердое тело— жидкость или твердое тело—газ) обратимое проведение механич. диспергирования невозможно, и потому σ не м. б. измерено обычными прямыми методами, связанными с увеличением поверхности. Поверхностное натяжение твердых тел на границе с окружающей средой—жидкостью или газом, м. б. приближенно оценено однако работой диспергирования, то есть работой всегда определенным образом производимого, но необратимого измельчения тела (например со-шлифовывания, истирания или процарапывания). Такую работу или пропорциональное ей преодолеваемое усилие следует принять за меру твердости твердого тела. Твердость является т. о. мерой поверхностной энергии тела в данных условиях. Обычная шкала твердости дает расположение твердых тел (минералов) в порядке возрастания их поверхностной энергии (смотрите Склерометрия, Капиллярные явления и Поверхностное натяжение). Свободная энергия любого поверхностного слоя возрастает с увеличением различия в интенсивности молекулярных сил соприкасающихся фаз, то есть с увеличением разности их полярностей, и следовательно изменяется обратно взаимной растворимости обеих фаз, образующих поверхность, а убывает почти линейно для чистых жидкостей на границе с собственным паром при повышении г°, обращаясь в 0 незадолго до критич. точки, при которой полярности обеих фаз выравниваются. При низких t° с падает с ί°, причем для ассоциированных жидкостей кривая несколько выпукла, а для мало ассоциированных—почти линейна, что связано с практич. неизменяемостью полной поверхностной энергии E с Т:
Ε=σ-τ£=α + ς, §=°,
где q=——изотермич. тепло образования
1 ем2 слоя. Вблизи же t°Kpum. кривая, спадая до 0, загибает, касаясь оси абсцисс.
Адсорбция определяется как избыток массы данного компонента системы (растворенного вещества или одного из компонентов газовой смеси) в молях на 1 см2 поверхностного слоя. Адсорбция связана с понижением свободной поверхностной энергии того поверхностного слоя, в к-ром адсорбция происходит. Компонент системы, адсорбирующийся и тем понижающий поверхностное натяжение, называется поверхности о-a к т и в н ы м. За меру по-. верхностной активности удобно принять вели чину G, выражающуюся следующей формулой: G=-£=f(c,T)
в эрг см2/мол л1, зависящую от концентрации в одной из фаз, образующих поверхность, и от t°. Для определенности мерой поверхностной активности данного реагента удобно считать максимальное значение G=Gmax, обычно достигаемое при концентрации с=0 или при весьма малых концентрациях. Количественная связь между поверхностной активностью и адсорбцией дается ур-ием Гиббса дО γη Об я-=Г ИЛИ — 5— ди дс
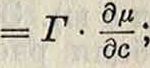
но химия, потенциал μ=RT In а + д0, где а— термодинамич. активность адсорбирующегося вещества в растворе а= /с; /—коэф. активности; для идеально разбавленных растворов=1; при с -> 0, — 1, а — с; итак в общем случае — ду=Г
или -Д=·=Г, где Δσ=σ0 — σ — пониже-
О 1П CL гС 1
ние о, вызванное адсорбцией. Вводя вместо Г А=рДу, площадь, занятую 1 молекулой в адсорбционном слое, имеем: кТ э=А, где к =
α= F иногда называется двухмерным давлением адсорбционного слоя. Для слабых растворов из условия а — с (при с — 0): — или ^ — jRf (с‘ G). Полагая в об ласти разреженных адсорбционных слоев G== ^ находим: Г — или F-A=кТ—уравнение состояния адсорбционного слоя, аналогичное ур-ию Клапейрона ρν=кТ (здесь ν =,
где V—объём 1 моля газа). В этом уравнении F играет роль двухмерного давления, а само ур-ие может рассматриваться как ур-ие состояния двухмерного газа.
Как это показано классич. исследованиями Гарди, Лангмюира и Гаркинса, адсорбция всегда связана с ориентацией адсорбирующихся молекул в пограничном слое. Поэтому типично поверхностно-активными являются вещества с полярными молекулами резко выраженной асимметрия. структуры типа @—Ь, где а — полярная группа (ОН, NHj, СООН, CSSH и др.), а b—неполярная часть молекулы (например углеводородная цепь)—СН2—СН2—СН2—.—СН3. Такие асимметричные молекулы ориентируются в пограничном слое, а следовательно и адсорбируются тем сильнее, чем больше разность полярностей обеих соприкасающихся фаз, причем адсорбция сопровождается уравниванием этой разности полярностей в пограничном слое, происходя поэтому обычно только тогда, когда полярность адсорбирующегося вещества лежит между полярностями обеих фаз системы. Этим правилом уравнивания полярностей объясняется то обстоятельство, что из водных растворов на поверхности «раствор— воздух» или «раствор—пар» адсорбируются поверхностно-активные растворенные вещества, полярность которых в чистом состоянии меньше полярности воды. Из газовых же сред на твердых адсорбентах адсорбируются, наоборот, наиболее полярные компоненты газовой смеси, т. к. твердые тела всегда полярнее окружающей их газовой среды.
Диференциальное ур-ие Гиббса связывает друг с другом две кривые: изотерму поверхностного
1Я
Т. Э. m. XX.
натяжения σ=f(c)T и изотерму адсорбции Г=F(c)T (смотрите фигура 1—2, на которых представлена форма этих кривых). Начальная, резко изменяющаяся часть кривой при малых с соответствует поверхностно-Фигура 1. му слою, еще далеко не насыщенному адсорбирующимися молекулами («газообразному» адсорбцион-п о м у слою). Эта часть кривых почти линейна—адсорбция растет пропорционально концентрации, и ориентация молекул (осями нормально к поверхности) начинает проявляться только к концу этого интервала. При больших с слой все больше насыщается с достижением предельной ориентации и принимает характер двухмерной кристаллической «твердой» пленки. При этом достигается предел адсорбции Гео, соответствующий минимальной площади *5*00, занимаемой каждой адсорбирующейся молекулой; при этом Soo=jr—pj (в СЛ*г на одну молекулу). Величина предела Гео и площади Soo зависит в основном ЛИШЬ ОТ природы f** см>
полярной труп-пы ориентирован- !·0
ной молекулы а, */>-
т. к. только эта зя-
группа занимает г,о место в поверхно- »,о стном слое. В качестве иллюстрации независимости Гоо от природы поверхности раздела приводятся результаты тщательных измерений (табл. 1), выполненных А. Б. Таубманом [*], над адсорбцией толуидина на разных жидких поверхностях раздела по методу измерения поверхностной активности.
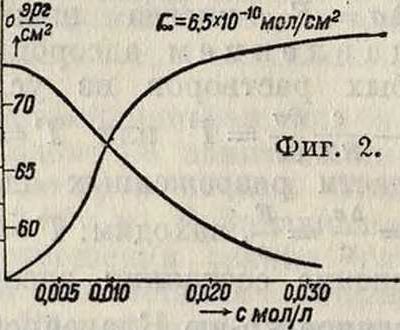
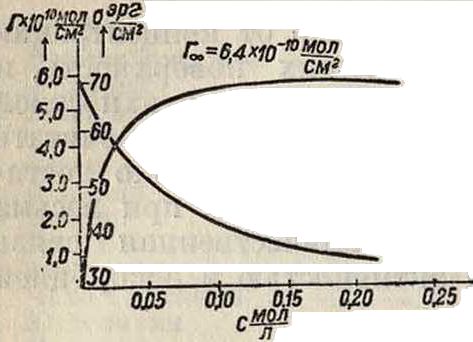
Таблица 1.—А дсорбционные константы р-толуидина на разных поверхностях _раздела._
| f
Символ величины |
Вода—бензол | Вода— гексан | Вода— воздух [пар] |
| Гос, М0MСЛ12.
Soo, еле“/мол. 6 (длина молекулы), см. |
6,4-1°·“
25,8-Ю"18 6,6-1°·8 |
6,3·10 ι°
26,2-Ю"18 6,5-10"8 |
6,5-10·?°
25,4-10’1в 6,7-ΙΟ-8 |
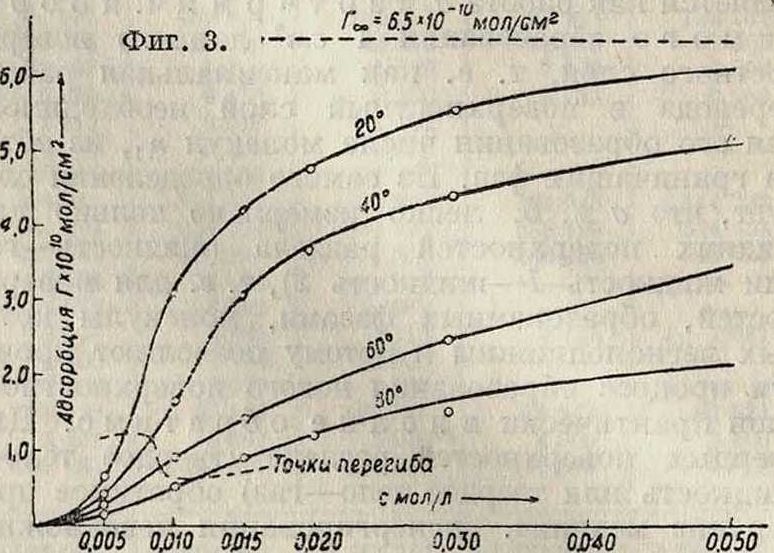
Понижающее влияние г° особенно сильно на «газообразные» ненасыщенные адсорбционные слои. С насыщением же слоя влияние t° становится все меньшим и адсорбционный предел не зависит от t° (Ребиндер), хотя он и достигается при тем больших равновесных концентрациях, чем выше t° опыта (фигура 3) f1]. В водных растворах поверхностно-инактивных веществ, повышающих поверхностное натяжение чистой воды
(для которых > О, G < О, Г < 0 — отрицательная адсорбция), поверхностно-активным веществом является сама вода, адсорбирующаяся в поверхностный слой. Поэтому такие достаточно разведенные растворы, то есть растворы с большим со-, держанием воды (слабые растворы минеральных солей, например КС1, AgN03 и др.), покрыты на поверхности мономолекулярной адсорбционной пленкой ориентированных молекул ни,,
воды I о; толщина такого слоя о=диаметру молекулы=3,5 · 10~8 см. При неполном насыщении адсорбционного слоя адсорбция Г убывает с Т (дезориентирующее действие теплового движения, фигура 3). С повышением Т адсорбционный предел Гео достигается поэтому при все более высоких концентрациях (а растет, см. далее), но величина Гоо (т. e. Sco) при этом не изменяется. Эти обстоятельства и объясняют ха
рактерные особенности изменения а растворов поверхностно-активных веществ по сравнению с чистыми жидкостями σ=σ0—Δσ, где Δσ обусловлено образованием адсорбционного слоя: Δσ= с
Jp
— dc σ0 приблизительно линейно падает о с г°, Δσ же вследствие падения Пег0 может и возрастать с г°. Поэтому кривые α= Ф (г)с несколько загибаются кверху и в случае поверхностно-активных веществ (особенно для ароматических фенолов, аминов) дают при средних концентрациях аномальное повышение а с f вместо нормального понижения f1] (фигура 4 и табл. 2). Для жидких поверхностей раздела поверхностное натяжение ом. б. измерено одним из извест-
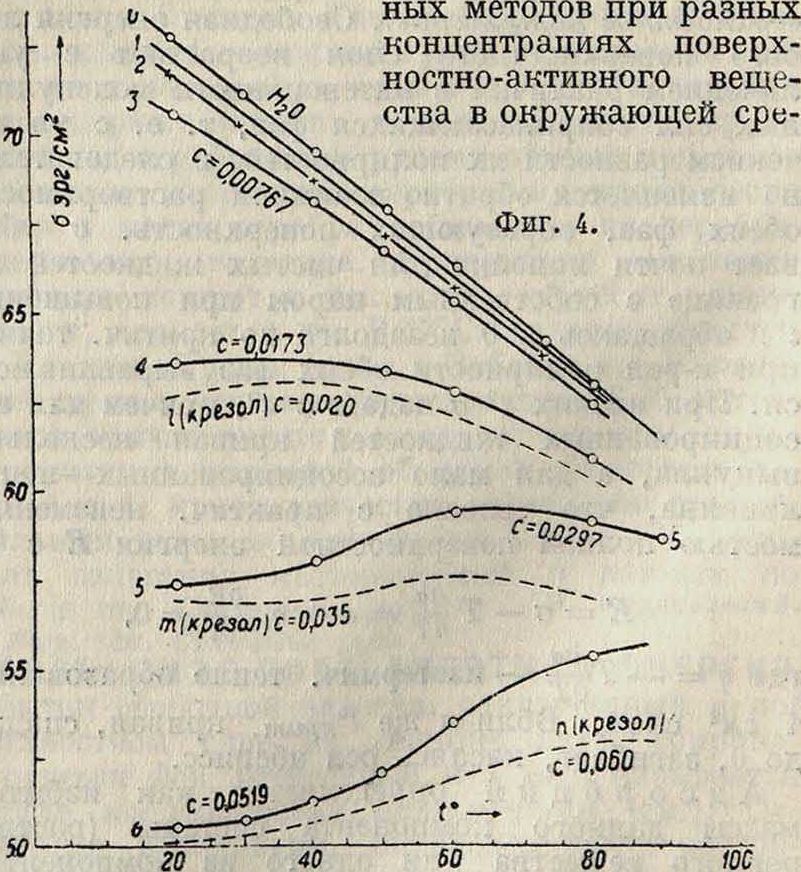
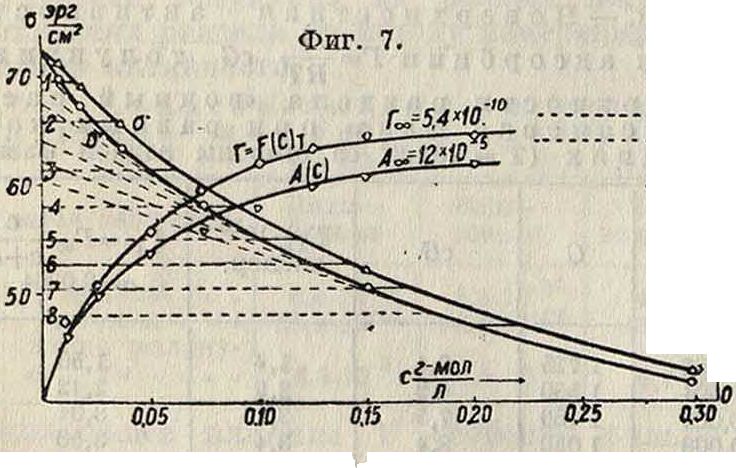
де, что позволяет по кривой σ=/(с) вычислить адсорбционную изотерму, то есть определить при разных концентрациях адсорбцию на 1 см2 жидкой, то есть «идеально гладкой», поверхности раздела (вода—воздух, пар, вода — органические жидкости, вода—ртуть). Такое вычисление удобнее всего производить одним И8 графических методов, например строя к заданным точкам изотермы σ (с) касательные и измеряя отрезки, отсекаемые ими на оси ординат от точки пересечения с той же осью горизонтали, проведенной через заданную точку (смотрите далее фигура 7). Длина такого отрезка ζ и дает величину cG,
пропорциональную адсорбции Г=fifcG;
ς. п дб f.
-=tg »=<?=-*-, ί =
cG.
Полученные значения Гс дают адсорбционную изотерму. В том простейшем случае, когда кривые а[с) и Г(с) имеют постоянный знак кривизны на всем интервале концентраций [кривая а(с)—выпукла, а кривая Г(с)—вогнута к оси абсцисс], обычно справедливо простейшее уравнение изотермы адсорбции Лангмюира— Райхинштейна:
Г=Г о с + а *
Г=г с
Здесь Гсо—адсорбционный предел, то есть значение Вт Г, а а — величина, являющаяся обрат-
С —► СО
ной адсорбционной активности о: α= i, из-
9^*10 * меряющей угловой коэфициент касательной к началу адсорбционной изотермы, то есть крутизну кривой Г(с) в начале. Уравнение Лангмюира позволяет, интегрируя с его помощью ур-ие Гиббса, найти зависимость σ=/(с)— ~Щ изотерму поверхностного натяже-фиг- 5· ния σ=σ0—Δσ, где
Δσ= RTFooln (-^ + l)—ур-иеШишковского. Для определения константы Гео удобно наносить значения Г в диаграмме, с j (фигура 5). В случае справедливости изотермы Лангмюира изотерма на такой диаграмме представится прямой линией
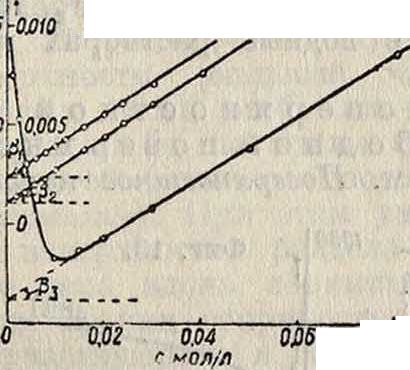
с,
по углу наклона которой легко определяется Гоо:
ψ—=tg β, Гоо=Ctg /?.
1 00
Вторая же константа ур-ия а определяется
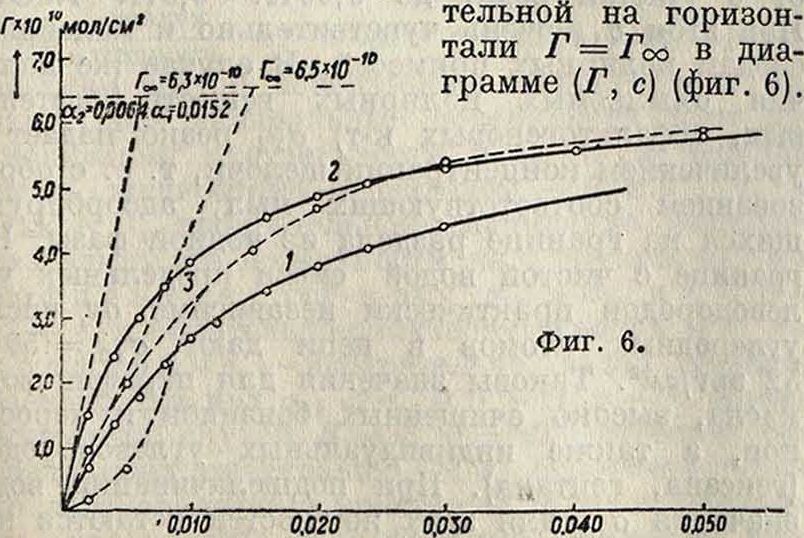
С, иол/л
Для твердых же поверхностей раздела а не м. б. определено непосредственным опытом, а потому в этих случаях адсорбция не вычисляется указанными методами, а измеряется обычно
Таблица 2. — С. п. э. pacTBODOB р-толуиди-н a CH3C6H4NH2 на разных поверхностях раздела.
|
а) Поверхность раздела «водный раствор — воздух» <42=(с) при разных ί° | |||||||
| С | 20° | 40° | 50° | 60° | 80° | ||
| 0
0,00096 0,00192 0,00382 0,00767 0,0173 0,0297 0,0519 0,0578 | 72,75
72,52 72,42 71,78 70.70 63.70 57,46 50,56 . 48,30 |
69,55
69,43 69,02 68,50 68,10 63,62 57,99 51,27 | 67.03 66,62 63,38 58,95
52.04 |
66,25
66,20 66,13 65,45 62,18 59,32 53,38 |
62,85
62,80 62,80 62,50 60,82 59,00 55,28 | ||
|
Ь) Поверхность раздела «водный раствор—бензольная фаза» | |||||||
| с молл в воде | С2 МОЛ /Л
в бензоле | “12 эрг/ам“ | |||||
| 0
0,0041 0,0096 0,0110 0,0134 0,0148 0,0187 0,0275 | 0
0,1400 0,3100 0,5570 0,7382 0,7202 0,9510 1,3510 | 35.0 31,8
27.5 26.5 24.6 23.6 22.1 20.6 | |||||
|
с) Поверхность раздела «водный раствор—гексановая фаза» | |||||||
| С МОЛ /Л
в воде | С2 МОЛ /Л
в гексане | “12 эрг 1см2 | |||||
| 0
0,0050 0,0121 0,0160 0,0207 0,0340 0,0392 | 0
0,0415 0,0723 0,1143 0,1400 0,2260 | 48.5
39.6 32.5 31,4 25.7 22.6 20.8 | |||||
Таблица 3. — Поверхностная активность G=— ~ и адсорбция Г— cG толуидина на поверхности раздела «водный раст-в о р—г ексановая фаза» при разных концентрациях (Т= 293,2° со стороны водной фазы).
| Cl | G | cG | Γΐ2·1010
экснер. |
Γΐ2=Γ« rk
α=0,0064 |
| 0,002 | 1 725 | 3,4 | 1,4 | 1,50 |
| 0,004 | 1 550 | 6,2 | 2,5 | 2,42 |
| 0,006 | 1 2.50 | 7,5 | 3,1 | 3,01 |
| 0,008 | 1 050 | 8,4 | 3,4 | 3,50 |
| 0,010 | 900 | 9,0 | 3,7 | 3,84 |
| 0,016 | 640 | 10,2 | 4,2 | 4,50 |
| 0,020 | 525 | 10,5 | 4,3 | 4,77 |
| 0,024 | 460 | 11,1 | 4,6 | 4,95 |
| 0,030 | 400 | 12,0 | 4,9 | 5,20 |
| 0,040 | 325 | 13,0 | 5,3 | 5,43 |
| 0,050 | 270 | 13,5 | 5,5 | 5,58 |
| (Γι2)οο =6 | ЗЛО10 | МОMОИ2. |
непосредственно по изменению концентрации адсорбирующегося компонента в окружающей среде в результате адсорбции (табл. 3—5). Для таких измерений требуется значительная поверхность раздела, достигаемая измельчением твердого тела в порошок; при этом остается неизвестной величина действующей поверхности S и потому на опыте определяется не Г, а адсорбция на 1 г адсорбента, образующего поверхность раздела с окружающей средой: А=Г · S i (фигура 7), на которой представлена
Таблица 4. — Адсорбция i-амилового а С5Н11ОН па границе «водный раствор— воздух».
| с мол/л | с G | „ 1
г_ ш Сb МОMСЛ2-101 |
экспер. | (#К |
| 0,005 | 5,4 | 2,2 | 2,3 | 2,3 |
| 0,010 | 8,2 | 3,4 | 3,0 | 3,0 |
| 0,020 | 10,6 | 4,4 | 4,5 | 5,5 |
| 0,030 | 11,8 | 4,8 | 6,2 | 6,7 |
| 0,040 | 12,0 | 4,9 | 8,1 | 8,1 |
| 0,100 | 12,2 | 5,0 | 20,0 | 19.0 |
| 0,150 | 12,8 | 5,2 | 28,0 | 28,0 |
| 0,200 | 13,2 | 5,4 | 36,0 | 36,2 |
| с» | ~ |
Г^—Ь,8-10—10 мол/<хи2.
Таблица 5. ·— Адсорбция р-т олуидина на границе «водный раство р—в о з д у х».
| 20° | 40° | 60° | СО
о о | |
| г· ш10 | г-ю10 | о н о
Ц |
г-ю10 | |
| 0,001 | 0,08 | 0,04 | 0,02 | 0,0 |
| 0,002 | 0,15 | 0,10 | 0,07 | 0,02 |
| 0,005 | 0,66 | 0,42 | 0,27 | 0,17 |
| 0,010 | 3,08 | 1,65 | 0,90 | 0,51 |
| 0,015 | 4,02 | 3,03 | 1,44 | 0,89 |
| 0,020 | 4,72 | 3,65 | 1,63 | 1,19 |
| 0,030 | 5,25 | 4,34 | 2,45 | 1,53 |
| 0,050 | 5,66 | 5,30 | 4,51 | 2,15 |
| 0,080 | 5,91 | |||
| Общий | предел адсорбции Г<*> | = 6,5·10"10· | S со = | |
| = 25,4-10 | 16 <хи2/мол | |||
адсорбция гс-бутилового а графитом из водного раствора: A=f(c), А(с) и а" для курейского графита (4 г); верхняя кривая Г=Т(с)т. При адсорбции поверхностью твердого тела
поверхностно-активные вещества вызывают также понижение свободной поверхностной энергии соответствующей поверхности, что выражается в данном случае понижением ее твердости (в смысле, указанном выше) [*].
Непосредствен-
__________η. Фиг 8 ные измерения по-
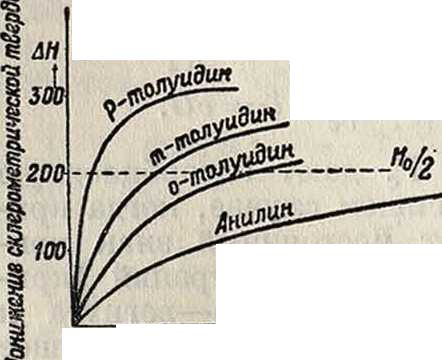
**ЙЙк»* называют [*], что твердость при адсорбции действительно убывает по кривой, идущей вполне параллельно адсорбционной изотерме, и достигает минимального значения при насыщении адсорбционного слоя. Для твердых тел понижение поверхностной твердости (поверхностной энергии)
Концентрация понизителя в ыол/л
1540
1040
Г
5*10ю
i-W*
Zm~*
w*
P#r*
означает понижение работы, затрачиваемой на механическое диспергирование и увеличение степени дисперсности получаемого при этом з продукта, что имеет большое значение для ускорения механич. обработки твердых тел в разных
областях техники,
например при металлообработке: шлифовании, сверлении, при шлифовании оптич. стекла, помоле в шаровых и коллоидных мельницах и бурении. Действие сущест-~ffi Ш ШЕ Ш IJS вующих в технике Концентра·* понизителя вмол/л обработки металлов Фигура 9 "
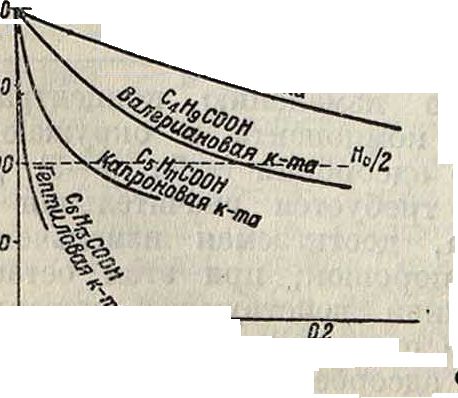
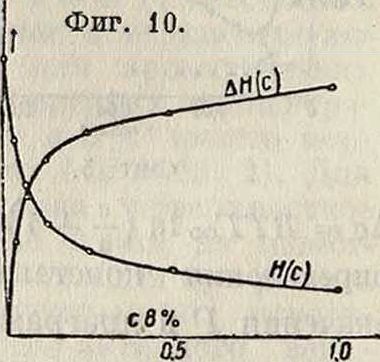
и стекла эмпирических рецептур, так называемых смазывающих или охлаждающих жидкостей, сводится к адсорбционному понижению твердости, и эти рецептуры представляют собой растворы поверхностно-активных веществ в неполярных минеральных маслах или в воде. В качестве иллюстрации адсорбционного понижения твердости можно привести фигура 8, 9 и 10: для мрамора в водных растворах жирных кислот и аминов (фигура 8 и 9) и для флуорита (CaF2, грань спайности, фигура 10) в водных растворах мыла (олеата Na).
Измерение поверхностной активности и свободной поверхностной энергии (смотрите Поверхностное натяжение) в особенности на границе двух анти- 1000 полярных жидкостей (вода — углеводород) может с успехом при- | меняться как чув-ствительный метод 2-физико - химического е анализа в различных областях техники.
В качестве примера можно привести метод определения содержания полярных примесей, то есть кислородных, сернистых и азотистых соединений, а также непредельных углеводородов в нефтепродуктах. Для этого следует измерять при 20° поверхностное натяжение данного нефтепродукта (или для вязких битумов и минеральных масел его раствора в очищенном неполярном керосине) на границе с водными растворами щелочи различных концентраций от 0 (чистая вода) до 0,001iV—0,012V NaOH. При этом σ12 очень чувствительно к малейшим следам полярных примесей. В случае же наличия омыляемых полярных веществ (нафтеновых, асфальтогеновых к-т) п12 резко падает с увеличением концентрации щелочи, то есть с образованием соответствующих мыл, адсорбирующихся на границе раздела из водной фазы. На границе с чистой водой смеси предельных углеводородов практически независимо от числа углеродных атомов в цепи дают σ12=50—52 эрг /см2. Таковы значения для парафинового масла, высоко очищенных бензинов и керосинов, а также индивидуальных углеводородов (гексана, гептана). При подщелачивании воды значения σι2 для этих жидкостей остаются неизмененными и получаются горизонтальные прямые в диаграмме (σ12, cNaOH). Бензол, и смеси непредельных углеводородов (наф-тенов, полиметиленов или олефинов) дают тоже горизонтальные прямые, но лежащие значи-
тельно ниже первых. Самое низкое значение получается для бензола: σ12=35 эрт/см2.
С чрезвычайно высоко развитой удельной поверхностью дисперсных систем и наличием избытка свободной энергии, адсорбционных и электрич. явлений [4] в поверхностных слоях у междуфазных поверхностей, связан целый ряд физико-химич. величин, специфичных именно для дисперсных систем и коллоидных растворов (смотрите Электроосмос и Электрофорез, Коллоиды). Из них здесь отмечаются лишь те величины, которые, будучи весьма тесно связаны со свободной поверхностной энергией, м. б. уже причислены к вполне строго определяемым физико-химич. величинам. 1) Работа сцепления или с обратным знаком—работа разрыва, дающая изотермич. работу разрыва тела с поперечным сечением в 1 см2·. Для жидкостей, где соответствующий процесс можно представить себе идущим обратимо, эта работа равна
W1=2σί (для жидкости 1) и
W2=2<т„ (для жидкости 2)
ит. о. прямо находится из значения поверхностного натяжения; 2) работа растекания W — а12 + а1—σ2 жидкости 1 по жидкости 2 и
3) работа прилипания W12=σ2 + σ2—σ12, при этом W12=W1—W; 4) смачиваемость данной поверхности (большей частью — поверхности твердого тела) либо на границе «жидкость— воздух» либо на границе двух антиполярных жидкостей (вода—углеводород) В=cos Θ (смотрите Смахивание). При этом угол, образуемый жидкой поверхностью раздела с поверхностью твердого тела вдоль периметра смачивания, то есть вдоль границ соприкосновения трех фаз (1, 2, 3, участвующих в процессе), называется краевым углом, или углом смачивания, Θ. Смачивание же, или смачиваемость, может быть удобно определено величиною В. Для границы твердое тело (3) | ((^ (причем жидкости
1 и 2 должны иметь возможно большую разность полярностей, как например в случае вода
1—углеводород 2) величина В может быть названа избирательным смачивани-е м. Смачиваемость связана с тремя поверхностными натяжениями на соприкасающихся по периметру смачивания поверхностях раздела простым соотношением (закон Юнга-Лапласа—Неймана):
β _ «23 — «13 «12
Тогда как смачиваемость на границе твердое I воздух тело I :кидкоеть не может служить для характеристики чистой поверхности твердого тела (так например, все минеральные поверхности дают при смачивании в отдельности и водой и неполярными жидкостями — бензолом — θ 3έ 0°, то есть £=+ 1), избирательное смачивание позволяет разделить все поверхности на 2 группы: а) гидрофильные, для которых σ22>σ15 и 0<β< ·< + 1, избирательно-смачиваемые водой, и б) гидрофобные,— избирательно водой несмачи-ваемые; для них σ23 < σ13 и 0 > В > — 1. Промежуточный случай В=0, Θ=90° отвечает безразличному смачиванию. К а) относятся типично гетерополярные кристаллы (окислы, сульфаты, карбонаты), гидрофильные коллоиды типа желатины, стекло и др. К б)—сульфиды, сера, графит, угли, гомеополярные органич. соединения, олеофильные коллоиды типа каучука. Металлы являются промежуточными телами;
обычно они покрыты тонкой пленкой поверхностного окисла (платина) и потому оказываются гидрофильными. Экспериментально было показано на обширном материале [5], что с введением в систему поверхностно-активного адсорбирующегося вещества абсолютная величина В всегда убывает, причем В меняет знак (инверсия смачивания); гидрофильные тела становятся при адсорбции полярных ориентирующихся молекул гидрофобными, так как в наружную среду обращены при этом углеводородные цепи адсорбированных молекул. Обратная ориентация при адсорбции на первоначально гидрофобной поверхности вызывает обратное изменение. Т. о. всегда
(дН
• дс
Измерения В можно производить, помещая каплю одной из двух жидкостей 1 или 2 на твердую поверхность 3, предварительно смоченную другой жидкостью 2 или 1. В зависимости от порядка смачивания получаются два значения В12 и В21, причем только в случае идеально гладких, чистых поверхностей
» _ Г> _ D __ «23 — «13
#12 — #21 — #i-—-
При образовании же адсорбционного слоя ориентированных молекул на твердой поверхности абсолютное значение разности В12—В21возрастает (знак ее определяется знаком В0) по адсорбционной изотерме. Разность В12—В21 (ста-тич. гистерезис смачивания) обусловлена наличием статич. трения вдоль периметра растекающейся капли; в обоих случаях В12 и В21 это трение различно. Гистерезис В сильно понижает точность и воспроизводимость измерений, особенно в случае не вполне гладких поверхностей. В случае смачивания на границе трех жидких фаз (или жидкости 1— жидкости 2—газа 3) гистерезис отсутствует вовсе вследствие идеальной молекулярной гладкости поверхности и полной подвижности периметра капли [8].
Лит.: 1) R eh bind er Р., «Ztschr. f. phys. Chemie», Lpz., 1924, В. Ill, р. 447; ibid., 1926, В. 121, р. 103; 3) Т a u b m a η n A., ibid., Lpz., 1932, В. А 161, 1—2, р. 129, 141; 3) R eh bin der Р., «Ztschr. f. Physik», В., 1931, В. 72, 3—4, p. 191; i) F rum k i η A., «Ztschr. f. phys. Chemie», Lpz., 1924, B. 109, p. 34; ibid., 1925, В. 116, p. 485; ibid., 1926, В. 123, p. 321; F r u m k i n А., «Ergebn. d. exakt. Naturwissensch.», B., 1928, B. 7, p. 235; s) Ребиндер II., «Журнал физич. химии», Μ., 1930, т. 1, вып. 4/5, стр. 533; Т а у б м а п А., там же, стр. 553; Липец М. Е.иРимскаяМ. М., «Цветные металлы», М.—Л., 1931, 5, S; Талмуд Д., «Журнал физ. химии», М., 1931, т. 2, стр. 744.—F г e u n d 1 i с h Н., Kapillarchemie, 4 Auli., В. 1—2, Lpz., 1930—32; R e h-b i n d e r P., «Biochem. Ztschr.», B., 1927, B. 181, p. 19 RehbinderP.u.TaubmannA., «Ztschr. f. phys Chemie», Lpz., 1930, B. 147, p. 120; F и c h s N. «Kolloid Ztschr.», Lpz., 1930, B. 52; Langmuir J., «Journ of the Amer. Chem. Soc.», Wsh., 1917, v. 39, p. 1048 Harkins W., ibid., 1917, v. 39, p. 354, 541; ibid. 1919, v. 41, p. 970; ibid., 1920, Y. 42, p. 700; Talmud D., «Ztschr. I. phys. Chemie», Lpz., 1931, В. A 156, p. 237 ibid., 1930, В. 151, p. 401. H. Ребиндеп