> Техника, страница 79 > Связанные системы

Связанные системы

Связанные системы, в электротехнике и радиотехнике—электрич. цепи (две или более), в которых при появлении меняющегося или переменного тока в одной из них в других появляются электрич. напряжения и токи. Обычно цепь, из которой получается энергия, называется первичной цепью; цепи, получающие энергию, называются вторичными. Однако вторичные цепи, получив энергию от первичной, сами начинают ее передавать в первичную цепь, благодаря чему явление сильно усложняется, т. к. на имеющийся уже переменный ток в первой системе накладываются токи, индуктированные из вторичных систем, имеющих каждая свой период и фазу. Математически сложный анализ явлений для нескольких С. с. в дальнейшем проводится лишь для наиболее характерного случая двух С. с., с которым часто встречаются в радиотехнике.

Характер явлений в С. с. зависит, во-первых, от параметров первичной и вторичной систем, то есть от их коэф-тов самоиндукции, емкостей и сопротивлений, которые в дальнейшем будут обозначаться соответственно /., С, В_г для первичной цепи и L₂, С₂, В ₂ для вторичной це пи; во-вторых, от коэф-та связи к между двумя системами, к-рый устанавливает величину взаимодействия между ними; в-третьих, явления, происходящие в С. с., зависят от параметров, характеризующих источник энергии, включенный в первичную цепь, или, если такового нет, от начальных условий, характеризующих первичный запас энергии системы, имеющийся в ней к начальному моменту времени, от которого ведется счет. Начальные условия позволяют определить постоянные интегрирования и дать ур-ия с числовыми коэф-тами. Т. о. для решения задачи надо знать напряжение Е источника энергии (например динамомашины) в V, период или угловую частоту его ω, фазу, соответствующую моменту включения, то есть величину мгновенного значения напряжения Е₀, какое имел источник тока в момент включения его в колебательные системы. Запас энергии, вложенный в систему, характеризуется энергией заряда конденсатора первичной сети

W_c=^-

и энергией, запасенной в магнитном поле самоиндукции первичной цепи, то есть

W_L =

Li Io

Т. о. токи и напряжения в С. с. являются ф-ияма времени и указанных выше постоянных, не зависящих от времени параметров цепей, т. e. L i, Сц Дц L₂, С₂, В₂, си, Е₀, 1₀ и к. Коэф. связи к, входящий в ф-лу, вычисляется на основании данных о взаимном расположении контуров. Для всех видов связи он определяется как отношение

к =

V XI Х₂

где х_т—величина реактивного сопротивления на общем связующем участке цепи, х_г—полное реактивное сопротивление первой системы, α·₂— полное реактивное сопротивление для второй из связанных систем.

Виды связи. Различают следующие виды связи. 1) Связь автотрансформаторная (частный случай индуктивной связи): контуры расположены согласно фигура 1 и имеют общий участок цепи— самоиндукцию L. В этом случае общее выражение для коэф-та связи приводит к ф-ле:

(oL L

Фигура 1.

к =

V ω (Li -(- L) о) (L₂ -i- L) Ϋ(Li- - L) (L₂-j-L)

В этой ф-ле, переписанной в виде к“ =

Lcoili

Lw₂I₂

(Li + L) will (L₂ + L) m₂I₂

первый множитель показывает отношение напряжения, индуктируемого во вторичной цепи, к полному напряжению, имеющемуся в этот момент на всей самоиндукции первичного контура, второй множитель показывает такое же отношение, характеризующее относительную величину напряжения, индуктируемого вторичной цепью в первичной. На этом основании коэф. связи часто дают в %, т. к. его максимальное значение по определению не м. б. больше 100% или единицы. Ф-ла в последней интерпретации служит базой для измерений к (смотрите Автотрансформаторная связь).

2) Связьиндуктивная, или трансформаторная, когда энергия из одной цепи в другую переходит через магнитное поле, создаваемое первичной самоиндукцией второго контура, и обратно; в этом случае самоиндукции расположены одна около другой, но непосредственной связи не имеют {фигура 2). Коэф. связи аналогично предыдущему вычисляется по ф-ле

^ _ ωΜ _ _ м

V ~L Lz

двух катушек определяет

Здесь

V in (Li + + Af)

Μ—коэф. взаимоиндукции самоиндукции L_xнапряжение, м и Lкаковой и индуктированное первичным кон-

Фигура 2.

Фигура з. туром во вторичном и обратно. О применениях индуктивной связи и измерении к см. Индуктивная связь и Катушки связи.

3) Третий случай имеет в виду емкостную связь, то есть такую, когда напряжение из одной цепи передается в другую за счет падения напряжения на емкостном участке цепи. В этом случае связанные контуры расположены согласно фигура 3. Коэф. связи в квадрате опять является произведением двух отношений напряжений в первом контуре и во втором контуре. Именно:, _h., _h >

I °к^шi) _ °к^ШЧ ( Cl <n) ( C₁y £02 j

ИЛИ г -К.—^-

. V Cl С„

А»=

определения

Та же формула получается из общего коэф-та связи i

* “Cl·

/с — ^т=- * ·

VxiXi -| (2--Ц lUi--U J—

У <oCi ‘ aiG^J юС0>С_к)

Здесь С и Сц—емкости (полные) контуров, состоящие каждая из двух последовательно включенных емкостей С_г и С_к, С₂ и С_к соответственно. Οι и Сц вычисляются по известной формуле последовательно включенных емкостей.

-2_=-L + -L,

Cl С С_к1

О,.

_L=J- +.

Сц С₂ ^т

Из ф-лы для к видно, что связь тем меньше, чем больше конденсатор связи. Об измерении к см. Емкостная связь.

4) Четвертый случай охватывает разнообразные возможности комбинированных связей, например индуктивной и гальванической (смотрите Гальваническая связь), за счет общих участков цепи, обладающих самоиндукцией, сопротивлением и емкостью. Этот случай в каждом отдельном виде должен быть разобран специально, ибо общей ф-лой он охвачен быть не может.

Колебания в С. с. Колебательное движение электричества в С. с. может быть результатом движения энергии, данной однажды первичному контуру в виде заряда емкости или магнитного поля самоиндукции. В этом случае энергия будет постепенно расходоваться в сопротивлениях системы, и колебания будут затухающими. Основным примером являются свя занные контуры искровых передатчиков (смотрите). Вторым источником колебательной энергии в связанных контурах является альтернатор или иной генератор незатухающих колебаний, включенный в первичную цепь. Этот случай мы имеем в современных” радиостанциях незатухающих колебаний. Физические соображения и матема-тич. расчет показывают, что в этом случае в первый момент после включения существуют собственные затухающие колебания контуров, одновременно с которыми устанавливаются через короткое время вынужденные колебания постоянной амплитуды, обязанные воздействию внешнего источника энергии. Через относительно длительный промежуток времени затухающие колебания исчезают и остаются одни вынужденные незатухающие колебания. Колебания первого рода называются свободными колебаниями С. с., колебания второго рода—в ыдужденными колебаниями С. с. Свободные колебания — всегда затухающие, вынужденные — обычно незатухающие.

Для математич. исследования свободных колебаний в С. с. можно воспользоваться схемою фигура 2, предположив, что энергия в эту систему внесена в момент 1= 0 в виде заряда конденсатора С_г до потенциала V_v После этого произошли электрич. колебания системы первичной и вторичной. При отсутствии постороннего источника энергии можно написать уравнения для первичного и вторичного контуров, изображающие закон равенства нулю суммы всех эдо замкнутого колебательного контура:

L-^ + M^+Rzh + Vz

_L.^h₊M^+R₂l.^v,=0.

Принимая во внимание, что

.Λ

dii

dVi

_ d»Vi

~ °¹ dt*

1 - r ^dY“. -*2 -4 Ш ’

dlz_ /i

dt - ° 2

d»V2 dt» ’

(1)

(2)

(3)

(4)

из (1) и (2) ур-ий получим

1-1 + ад ЧГ + ^МС* 47? +=°; (5)

адж + ад^+ад ^ + ^F*=°- (в)

Диференцируя (5) и (6) ур-ия два раза, мы получим еще четыре ур-ия, совместные с (5) и (6). Из последних пяти мы можем вычислить неизвестные нам величины:

djv г dii ’

d³T₂diз ’

d»Vz di2 ¹

в ф-ии параметров контуров и производных от Vi до четвертого порядка. В результате получим из ур-ия (5) после подстановки в него вычисленного значения

dzv₂

dt»

линейное диференциальное ур-ие четвертого порядка вида ад (ад - т + ад (ад + ад,) +

d³Vi

+ (ад + ад₂ + адад₂)+ + ад + ад) ££ + Vi=о.

(7)

Наиболее интересным в практике радио и достаточно освещающим метод расчета является частный случай: Д₁=й₂=0, то есть затухание контуров очень мало (им можно пренебречь). Положив затем, что

1 „ i

и учитывая, что

СП-г

C₂L₂

L1L2

(8)

(9)

получим после деления ур-ия (7) на С, С₂, L_lt Z₂ и подстановок из ур-ий (8) и (9) следующее упрощенное ур-ие:

(1 - Л²)

Такой же точно вид будет иметь и ур-ие для F₂, ибо отличие их было лишь в членах, содержащих сопротивление, а они исчезли после сделанного предположения, что=Д₂=0. Известно, что это ур-ие имеет решение вида

Fj=A₁ coscoi + Βχ cos a>t, (11)

F₂=А_г cos co"t + В» cos ω"ΐ, (12)

где ω и ω"— корни характеристич. ур-ия, получаемого путем подстановки:

F,=е^а

dl 2

= ω%^ωί и т. д.

(13)

Ур-ие (10) после подстановки из (13), сокращения на е^ш1 и деления на (1 — к²) получает вид

«>⁴ + r^«>² + T^t=o; (14)

ур-ие (14) биквадратное и дает четыре мнимых корня:

СО=±

после упрощения

! ± V <А - «ί о -.

ω :

- «ϊ (1 ± к)

1 — ’ или, не считаясь со знаками,

ωχ α>ι

ω =

ΥΓ-

ω =

Vi + k

(15)

(16)

(17)

Из ур-ия (16) следует, что характеристическое ур-ие имеет четыре мнимых попарно сопряженных корня, что нам указывает на синусоидальный вид Fj

У х — А + Βχ

,-V-l mi_+e+V-l

tat ^

-F— ΐω" i _e+V

leut ^ _

= A₁ cos ωί + B_t cos w"t. (18)

Из ур-ия (17) следует, что хотя до начала колебания оба контура и были настроены в резонанс на частоту Ш], во время колебаний появляются новые частоты связи, одна больше ω_χ _ е>1

VI - к а другая меньше ω_ιω"

Fi +к ’

Эти частоты связи можно получить и измерить с помощью волномера, и тогда мы, зная ω и си", можем вычислить к—коэф. связи по ф-ле:

cQ2 - (»ii

(α>)2 + (_ω)2 > (I®)

получаемой из ф-л (17) путем исключения из них ω_χ. Полагая /с=0,01, мы находим, что и частоты связи будут отличаться примерно на половину процента (у) от основной резонансной частоты. Эта точность достаточна для боль

шинства измерений по резонансному методу, почему такая связь считается весьма слабой и ее влиянием на результат измерений пренебрегают. При связях от к=0,01 до к=0,05 связь считается слабою, но она уже влияет на точность измерений и ее приходится учитывать. Свыше к=0,05 связь считается сильной.

Чтобы закончить исследование ур-ий (11) и (12), необходимо определить постоянные интегрирования Αχ, Βχ, А₂ и В₂. Их легко можно получить, зная начальные условия системы Е„ для заряда С_х и условия о том, что токи ίχ и г₂при г=0 равны нулю. В результате получим:

Vx=у (cos сог + cos ω"ι), (20)

= (cos ωί — cosea "г)· (21)

Из ф-лы (21) видно, что напряжение во вторичном контуре будет больше напряжения первичного контура в Y^-i. Последнее соотношение может быть использовано для повышения напряжения во вторичных контурах: в этом случае С₂ нужно взять значительно меньше Οχ. В радиотехнической практике, а равно и в области сильных токов могут встретиться случаи нежелательных и вредных повышений напряжений за счет резонанса системы, имеющей малую емкость, с системой, имеющей большую емкость, например когда катушка самоиндукции попадает в резонанс с колебательным контуром; в результате на концах ее возникнут опасные перенапряжения. Другой случай — короткое замыкание, вызвавшее колебательный разряд в одной линии, может в другой параллельной линии при резонансе обеих систем индуктировать повышенное напряжение в отношении Изучая ф-лы (20) и (21), видим,

что в первичной цепи сначала оба колебательных напряжения одинаковы по фазе, и следовательно их напряжения складываются, но затем разность их периодов приводит к тому, что одно колебание получает фазу, противоположную другому, в результате напряжения вычитаются. Явление это носит название биений (смотрите). Та же картина имеет место и во вторичной цепи, но здесь явление сдвинуто по фазе, именно максимум напряжения (сложение колебаний) произойдет тогда, когда в первичной цепи будет минимум. Это указывает, что в это время почти вся энергия перешла из первичной цепи во вторичную. Т. о. если в этот момент разомкнуть первичную цепь, то энергия уже в нее вернуться не может и останется во вторичной, создавши в ней свободные затухающие колебания с частотой вторичного контура и со свойственным ему затуханием. В радиотехнике искровой этот случай имел место при т. н. ударном возбуждении вторичной цепи. В этом случае первичная цепь, содержащая в себе искровой промежуток, разрывалась автоматически потуханием искры при ослаблении тока в первый же минимум, и вся энергия переходила во вторичную цепь, создавая в ней слабо затухающие колебания. Ускорению этого разрыва первичной цепи способствовали специально сконструированные разрядники: немецкий Вина и английский сист. Маркони.

В современной радиотехнике чаще встречается ударное возбуждение в виде вредного метания т. н. атмосферных разрядов и индустриальных помех от искр и вольтовых дуг трамвая, моторов, сварочных аппаратов, которые дают толчки вторичным системам—цепям радиоприемников, создавая в них затухающие колебания того же периода, на к-рый настроен приемник. Поэтому меры борьбы с этими помехами чрезвычайно затруднены, т. к. острота настройки приемника здесь уже не играет решающей роли. Общий характер явления изображен на следующих фигура 4 и 5. Фигура 4 показывает картину биений двух слабо затухающих

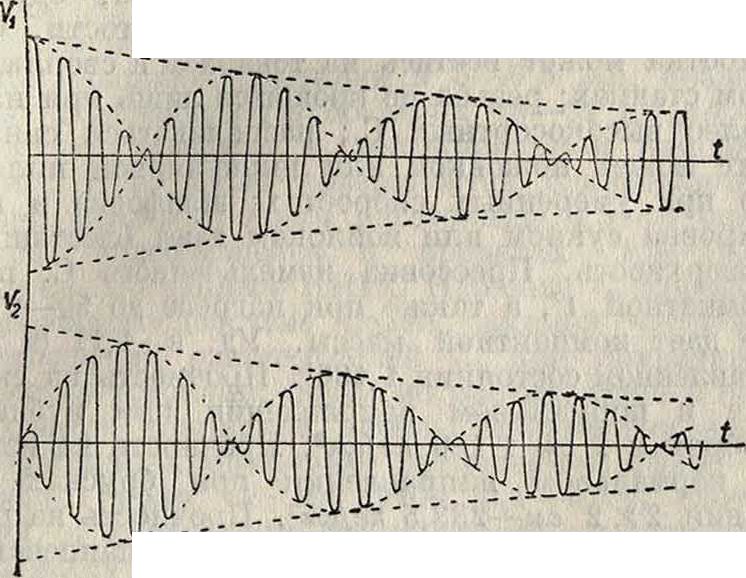
Фигура 4.

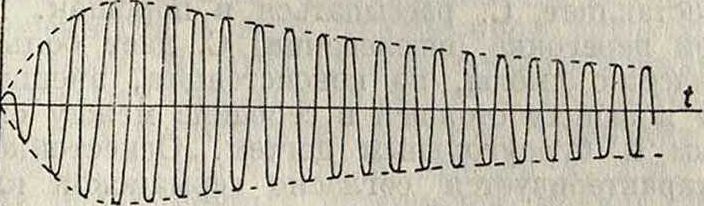
контуров; фигура 5 показывает характер явления при ударном возбуждении, когда первичная цепь разрывается путем погасания искры, а вторичная продолжает колебаться за счет запасенной энергии.

Если в первичный контур двух С. с. включен источник незатухающих колебаний с напряжением Е и частотою ω, то, как было указано,

У,

►

сначала в ооеих цепях устанавливаются незатухающие колебания. Вычисление токов их основано на

Фигура 5.

решении приведенных выше ур-ий (1) и (2), но в первом ур-ии необходимо сейчас во второй части написать вместо нуля E cos сοι, так как мы теперь имеем уже внешнюю эдс. Решение этого ур-ия складывается из решения ур-ий (1) и (2) без E cos <at, что дает первую часть решения (токи неустановившегося режима в виде затухающих колебаний). Добавление члена E cos со г вызывает прибавление новых членов для I! и /₂, зависящих от параметров контуров и параметров введенной эдс. Не проделывая расчета, который заключается в подстановке решения в основные диференциальные ур-ия и отыскании значений постоянных, удовлетворяющих ур-ию, мы выписываем значения установившихся сил токов 1_г и 1₂:

т E COS (coi — φ)

ⁱl------

(

Hi + R₂

ΜωΕ COS (ω£

2, Λί2<ο2 a

V ⁺ {^X1~~W^X2)

- Ή)

„ /’ ο, Μ2ο,2 2 Μ2β)2 2

² у (^Ηι+~ΊΓ^Β2)⁺(^χι—^-^χή

(22)

(23)

Здесь принято

:Ιω— --

¹ Qii<o

χ₉=Lo ω —

C₂o> * i

C%<o ⁹

(24)

В радиотехиич. практике чаще всего ставится задача, опираясь на эти ур-ия, получить путем настроек максимум тока во вторичной цепи. Рассматривая знаменатель ф-лы (23) для как ф-ию х₂, мы путем диференцирования находим, что знаменатель будет минимальным при

А(^г<о2

^х2 — ζϊ~ *ι > (2-э)

что нам после преобразований и подстановки в (23) даст максимум /₂ для этого случая. _г ΜωΕ

¹2 max Π

ΖιΗ₂ +

Μ 2 «|2 Ζΐ

Ηι

(26)

где

Cim)

Это следовательно достигается настройкой вторичной цепи, руководясь ф-лой (25

следует, что можно получить еще частный резонанс-максимум тока, обращая в нуль второе нам дает новое слагаемое знаменателя. Это условие настройки на этот контуре за счет изменения х,

М2гоЗ

*ι=—з-т *2

раз в первичном именно:

В этом случае вторичный ток будет равен

, ΜωΕ

2 max I

Ζ₂ Γ?ι +

jVf2 α>2 R2

Z_a

(27)

(28)

Ф-ла (26) для максимального тока 1_г показывает, что М входит и в числитель и в знаменатель; т. о., меняя связь контуров, возможно еще увеличить вторичный ток. Еще раз решая задачу на максимум для М, находим:

Подставляя возможный

^тах в формулу ток:

(26),

Hi получаем

(29)

наибольший

.г; (30)

условия для его получения из ур-ий (25) и (29) получаются в виде

(31)

! max-max II ’

*2 _ Щ

XI Hi ’

то есть должна быть пропорциональность между сопротивлениями активным и реактивным. Аналогично находим:

7=^Е

2 max-max I ., у

Лит.: Жеребцов И., Электрич. нолебания и резонанс, М.—Л., 1932,- Берг А., Основы радиотехиич. расчетов, Л., 1928; Р е и вер, Справочник по радиотехнике, пер. с англ., Москва, 1929; Ивановский В., Теоретик, исследование колебании в связанных системах, П., 1917; Электрич. колебании и волны, СО. основных работ под ред. В. Лебединского, вып. 4, Резонанс связанных цепей, СПБ, 1911, вып. 3, Резонанс несвязанных цепей, СПБ, 1911; Круг К., Основы электротехники, 3 нзд., т. 2, Колебания в связанных цепях, М.—Л., 1932; Pierce О. W., Electric Oscillations a. Electric Waves, Ν. Y., 1920; В e d e a u F., Cours dldmentaire de tdiegra-phie et tdliphonie sans fil, P., 1931; M о г с с г о 11 Y., Pinto A. a. Curry W., Principles of Radiocommunication, Ν. Y., 1927; F 1 e m i n g J. A., The Principles of Electric Wave Telegraphy a. Telephony, Damping a. Resonance, L., 1919; Turner L. B., Wireless a. Treatise on Theory a. Practice of High Frequency, Electric Signaling. Oscillatory Circuits, Cambridge, 1931. А. Углов.