> Техника, страница 79 > Семейство кривых и поверхностей

Семейство кривых и поверхностей

Семейство кривых и поверхностей.

Одно уравнение, связывающее текущие координаты, определяет на плоскости кривую, в пространстве — поверхность. Если уравнение кривой (поверхности) φ — 0 заключает кроме текущих координат еще независимый переменный, параметр с то при непрерывном изменении этого параметра кривая (поверхность) будет, вообще говоря, непрерывно изменяться по виду и положению. Полученная этим путем система кривых (поверхностей) и называется семейством кривых (поверхностей), зависящих от одного параметра. Каждому значению последнего соответствует определенная кривая (поверхность) семейства. Два бесконечно близких значения параметра с и с + Дс определяют две бесконечно близкие кривые (поверхности) семейства. Пересечение их может, при убывании с до нуля, стремиться к нек-рому предельному положению (характеристич. или предельная точка для кривой и характеристич. линия или характеристика — для поверхности). Для данного семейства совокупность этих предельных положений может образовать кривую (поверхность), называемую огибающей, или обверткой, этого семейства кривых (поверхностей), которые по отношению к ней называются огибаемыми. Огибающая касается каждой из огибаемых в общих с ней точках. В тех случаях, когда семейство имеет огибающую, ур-ие ее получается исключением параметра с из ур-ий: <р=0 и —=0. Примерами огибающих

(смотрите), парал-

кривых могут служить эволюта лельные кривые и др. Они , находят себе применение в различных областях естествознания и техники. Оптика например изучает т. н. каустики, или огибающие лучей плоского пучка, отраженных или преломленных на некоторой кривой, например на полуокружности (фигура 1); вдоль каустики имеет место сгущение световых лучей, вследствие чего их удается иногда наблюдать в виде светящихся линий. В военном деле важно уметь находить огибающую семейства траекторий снарядов.

Пример. Если снаряд выпускается из точки О с начальной скоростью ν„ под углом а к горизонту, то траекторией его (если пренебречь сопротивлением воздуха) будет, как известно, парабола (смотрите), уравнение которой дх²

у —×tg а 21)2 fios2 а ‘

(I	,4. ΛΛ
	/1
	Фигура 1.

Меняя угол а, но оставаясь в той ?ке вертикальной плоскости и сохраняя начальную скорость и,, получаем семейство парабол, зависящих от одного параметра, угла а. Найдем огибающую семейства; ур-ие последнего

. до²

* tg a 2t>2 cos² а

У=О,

-tga-ff (t "Ь tg²о) У

)0.

Введем новое обозначение параметра: тогда имеем:

же — !*! (t + c^s) У — 0.

tg а

Ищем частную производную этого выражения по параметру с:

откуда х-Ц-bе=0,

дх

Исключаем с из ур-ия семейства и получаем ур-ие огибающей:

_ О**

2(7 М ^-

У

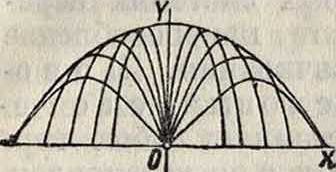
Фигура 2.

Итак здесь огибающая тоже парабола, называемая параболой безопасности, потому что точки, лежащие выше ее (фигура 2), недоступны для снарядов, вылетающих из точки О с начальной скоростью v_t).

Уравнение семейства кривых, зависящих от одного параметра, Ф(х, у,· с)=0 можно рассматривать как общий интеграл диференциального уравнения 1-го порядка F[x, у, 7/)=0(смотрите Диферен,-циалъные уравнения). Геометрически оба эти уравнения представляют одно и то же. семейство интегральных кривых. Уравнение в конечной форме определяет каждую отдельную кривую семейства как непрерывную последовательность ее точек; диференциальное уравнение — как непрерывную последовательность направлений, так как оно содержит угловой коэф-т у касательной и выражает то или иное свойство ее, общее для всех кривых семейства. Т. к. огибающая имеет те же касательные, что и огибаемые кривые в общих с ней точках, то координаты ее удовлетворяют ур-ию F (х, у, т/)=0, и ур-ие ее является одним из его решений. Вместе с тем ур-ие огибающей не содержит параметра, не получается из общего интеграла ни при каких значениях с; стало быть это не частный, а особый интеграл ур-ия F (х, у, у)=0. Т. о. особый интеграл представляет геометрически огибающую семейства интегральных кривых. Ур-ие огибающей или особый интеграл можно получить и непосредственно из диференциального ур-ия семейства, если рассматривать в нем у как параметр и исключить последний из системы ур-ий:

8F (х, у, у’)

F (*» У, У)

ду

= 0.

Ортогональные траектории данного семейства пересекают все кривые его под прямым углом. Если семейство кривых дано ур-ием F(x,y,y)=0, то ур-ие семейства его ортогональных траекторий будет F (х, ν>~ψ)=°-Технически важное значение ортогональных траекторий видно уже из того, что к ним принадлежат семейства силовых линий и линий уровня плоского силового поля, почему мы встречаемся с ними при изучении например плоского течения жидкости, плоского магнитного и электрич. полей и т. д. Семейство поверхностей Ф (х, у, ζ, с)=0, зависящих от одного параметра с имеет два типа огибающих: 1-й тип — поверхность, образованная характеристиками. Ур-ие ее является результатом исключения с из системы ур-ий:

^, ЗФ(ж, у, ζ, с)__п

Ф (X, у, ζ, с) =--_е--= О.

Она касается каждой из огибаемых вдоль всей соответствующей характеристики. Как на при мер такой огибающей можно указать на развертывающиеся поверхности (смотрите Линейчатые поверхности). 2-й тип — пространственная кривая (ребро возврата огибающей поверхности семейства), геометрическое место точек пересечения бесконечно близких характеристик; ее ур-ие получается исключением параметра с из системы трех ур-ий:

Ф (х, у, ζ, с)=W**0) ₌ о.

Ребро возврата есть огибающая семейства характеристик и касается каждой из них. Дважды бесконечное семейство поверхностей, зависящих от двух параметров а и Ь, ур-ие которого Ф(х, у, ζ, а, Ь)=0, имеет огибающую поверхность, ур-ие которой получается исключением обоих параметров из систем трех ур-ий:

Ф (х, 2у,г,а,Ь)=»»<*·%* ^Ь)== о.

В этом случае огибающая поверхность касается каждой из огибаемых уже не по целой линии (характеристике), а лишь в отдельных точках.

Пример. Каждую поверхность можно рассматривать как огибающую ее касательных плоскостей. Касательная плоскость к сфере или гиперболоиду зависит от двух параметров и касается огибающей поверхности только в одной точке. Касательная плоскость к конусу или цилиндру зависит от одного параметра, и касание происходит вдоль целой образующей.

Лит.: Г у р с а Э., Курс математич. анализа, пер. а Франц., т. 1, М., 1911; Чезаро Э., Элементарн. учебник алгебраич. анализа и исчисления бесконечно малых, пер. с нем., т. 2, Одесса, 1914. В. Коновалова,