 > Техника, страница 80 > Сила критическая
> Техника, страница 80 > Сила критическая
Сила критическая
Сила критическая. Устойчивость равновесия может зависеть как от геометрия, формы системы, так и от величины действующих сил; при малых силах равновесие м. б. устойчиво, при больших — неустойчиво. То значение силы, при к-ром равновесие из устойчивого переходит в неустойчивое, называется С. к.
Первые исследования в этой области принадлежат Эйлеру. Он показал, что прямолинейный стержень, сжимаемый двумя силами Р, прило-
Содершание металла в %
11.0— 12,0 РЬ
21.0— 23,0 РЬ
31.0- 34,0 РЬ
31.0- 32,0 РЬ
2.0- 2,5 Мп
6.0- 6,5 МП
7.0- 7,5 Мп
8.0- 8,5 Ми
2.2- 2,5 Со
6.2- 6,5 Со
2.2- 2,5 СО
9.2- 9,5 Со женными на концах и действующими вдоль оси его, сохраняет прямолинейную форму равновесия, пока силы Р невелики. При возрастании сил Р наступает такой момент, когда прямолинейная форма равновесия становятся неустойчивой и стержень искривляется. То значение сжимающей силы, при к-ром начинается искривление стержня, называется до настоящего времени Эйлеровой критической силой. Теория Эйлера была несколько далее развита Лагранжем, применявшим ее к расчету колонн., Идеи Эйлера долгое время не находили себе применения в технике, они были основательно забыты, и инженеры пользовались при расчете сжатых стержней различными эмпирич. ф-лами. Лишь во второй половине 19 в., когда развитие строительства мостов и других метал-лич. конструкций потребовало более точного расчета сжатых стержней и тонких пластин, выяснилась вся правильность и плодотворность идей Эйлера. Оказалось, что во всех тех случаях, когда один или два размера тела малы сравнительно с третьим (пластины, оболочки, тонкие стержни), всегда существует С. к. и она м, б. найдена по способу, указанному Эйлером. Появилось очень большое число работ в этой области, и в настоящее время при всех расчетах тонкостенных конструкций прежде всего считаются с этой С. к. Силы, действующие на сооружение, обязательно должен быть меньше критических.
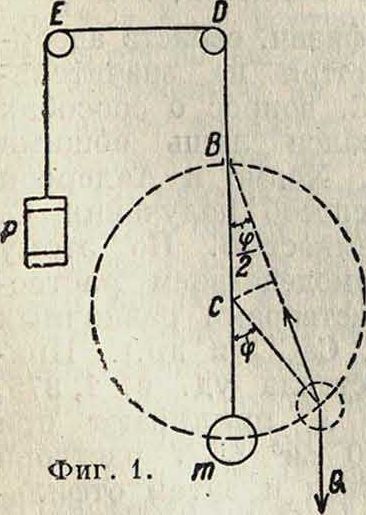
Если понятие о С. к. в теории упругости установилось уже давно, то в статике твердого тела первый довольно сложный пример бал дан Сутвеллом в 1913 году Несколько более простых примеров даны Динником. Наиболее просто находится С. к. в статике твердого тела следующим приемом: известно, что если работа А приложенных к телу сил при малом, но конечном отклонении его от положения равновесия отрицательна, то рассматриваемое положение равновесия устойчиво; если А положительна, то — неустойчиво. Если А меняет свой знак при возрастании силы Р, то С. к. существует; если же А сохраняет свой знак, то С. к. не существует. Для нахождения С. к. следует приравнять А нулю и решить соответствующее ур-ие относительно Р. Например маятник состоит из невесомого стержня Cm и шара весом Q (фигура 1). Нить mBDEP с грузом Р на конце проходит через кольцо В, лежащее на окружности радиуса I, как-раз над С и через блоки D и Е. Ясно, что положение равновесия (<р=0) является устойчивым, если Р мало сравнительно с Q, и неустойчивым, если Р велико, т. e. С. к. здесь существует; надо найти ее величину. Работа всех сил при отклонении маятника из положения равновесия на угол φ
А — —Ql (1 — cosy) + 2PI (l —cos -|) или при малом φ
A=-2Q + Ρ]-~·
Если Р < 2Q, то А < 0 и равновесие устойчиво; если же Р > 2Q, то Я > 0 и равновесие неустойчиво. С. к. находится из ур-ия А — 0, то есть Ркр.=2 Q. Для других систем для данного типа деформации существует вообще несколько значений С. к.; из них для технич. целей важно знать наименьшую. Высшие же С. к. в большинстве случаев не представляют никакого интереса. Для определения Ркр. существуют 3 основных способа. Не излагая их в общей форме, поясним суть дела на задаче о продольном изгибе.
1) Прямое интегрирование д п-ференциальных уравнений равновесия. Колонна (фигура 2) сжата силой Р, действующей вдоль оси ее. При малой Р колонна остается прямой. При увеличении Р может наступить такой момент, когда прямолинейная форма колонны делается неустойчивой и колонна искривляется. Для нахождения того значения Р, при к-ром начинается это искривление, предполагают, что колонна уже искривилась, и составляют диференциаль-ное ур-ие изгиба для малых отклонений от прямолинейной формы равновесия. При малых отклонениях это уравнение получается линейным. Интегрируют : его и определяют из граничных условий произвольные постоянные, вошедшие при интегрировании. Эта операция приводит к конечным уравнениям, в которые входят произвольные постоянные интегрирования, сила Р и размеры колонны. Критич. значение Р находится из того соотношения между силой и размерами колонны, при к-ром уравнение изгиба может иметь несколько решений, удовлетворяющих одним и тем же граничным условиям (изгиб продольный — см. Изгиб). Его иногда изменяют след, обр.: к силе Р, критич. значение которой надо определить, присоединяют еще какую-либо силу (например поперечную силу или момент^ и смотрят, при каком значении Р прогиб, вызываемый дополнительной силой, будет неопределенно возрастать. Это значение Р и будет С. к.
2) Метод потенциальной энер-г и и. Предполагают, что колонна уже искривилась, и составляют выражение для изменения потенциальной энергии AW системы при изгибе. В данном случае потенциальная энергия AW слагается из энергии изгиба ΔΕ и убыли энергии АТ при опускании груза Р:
I I
KW=f EIy"*dx—j f y*dx. о о
Критическая сила находится из уравнения AW=0.
Если известна форма той кривой, по которой искривляется наша колонна, то из ур-ия AW=О получают точное значение Ркр. Но в большинстве случаев форма этой кривой неизвестна. Тогда можно воспользоваться следующим приближенным приемом, подробно развитым ,С. Тимошенко: на основании опытных данных или рассмотрения аналогичных задач задаются подходящей формой кривой, причем ее ур-ие обязательно должно удовлетворять условиям на

Т. Э. m. XX.
границах и содержать один или несколько неопределенных параметров у— (ж, аг, а2, ., ап).
Далее составляют выражения для ΔΓ и ΔΤ, вносят их в ур-ие IPW=0 и находят Р. Наконец параметры аи а2,.,ап подбирают таким образом, чтобы РКр. имела наименьшую величину. Сравнение точных и приближенных решений показало, что этот простой прием при удачном подборе формы кривой дает очень хорошие результаты.
3) Динамический прием основан на рассмотрении колебаний системы около положения равновесия. Надо составить диференциаль-ное уравнение колебаний колонны, проинтегрировать его и вычислить период колебаний Т. Он зависит от величины сжимающей силы Р. То значение Р, при к-ром Т неопределенно возрастает, и является РКр. Физический смысл этого приема ясен: с увеличением Р колонна колеблется все медленнее и медленнее. При Р — РКр. колонна, отклонившись от прямолинейной формы, в нее уже не возвращается, а остается искривленной. С математич. точки зрения этот прием является наиболее сложным.
Самое интегрирование уравнений или вычисление энергии во всех трех случаях может быть выполнено или аналитически или графически. С этой точки зрения все приемы нахождения С. к. можно разделить на аналитические и графические. Результаты нахождения С. к. для стержней, пластин и оболочек — см. Устой-чивОСГПb. А® Дипняк.
Лит.: см. Устойчивость.