 > Техника, страница 80 > Система
> Техника, страница 80 > Система
Система
Система в те х н и к е, теоретич. оформление сооружения или механизма, отличающееся от действительного сооружения упрощениями, вводимыми для проведения расчета и вме-
сте с тем мало изменяющими условия работы сооружения. В С., теоретич. схемах сооружений, состоящих из отдельных брусьев, абстрагируются поперечные размеры отдельных элементов, образующих сооружения, влияние которых на величину расчетных усилий и деформаций невелико. По своему образованию С. разделяются на С. свободные, неизменяемость которых обеспечивается вне зависимости от опорных закреплений, и С. связанные, неизменяемости которых зависит от опорных закреплений, и составляют две основные группы:
1) С. плоскостные, составные элементы которых располагаются в одной плоскости, способные воспринимать на себя силы, действующие в той же плоскости, или передавать в ней движения;
2) С. пространственные, составные части которых не располагаются в одной плоскости, способные воспринимать на себя силы любых направлений или передавать движение в пространстве. Названные группы С. обнимают собой целый ряд других подразделений, объединяя С. с общими свойствами.
Плоскостные С. образуются из отдельных стержней или дисков, связанных между собой в общее целое. Входящие в состав С. диски могут сами составлять более простую С. Соединение стержней и дисков между собой может быть шарнирное (цилиндрич. шарнир) и жесткое. Шарнирное соединение исключает две степени свободы относительного смещения соединяемых частей и может рассматриваться как две стержневые связи между дисками с шарнирами на концах (фигура 1). Жесткое соединение исключает три степени возможных относительных смещений соединяемых частей на плоскости и может рассматриваться как три стержневые связи, не пересекающиеся в одной точке (фигура 2). Если образование С. таково, что перемещение Одного стержня или диска, образующего С., вызывает совершенно определенные конечные перемещения остальных стержней С. без изменения длин всех стержней, то такая С. является С. изменяемой и носит название плоской кинематич. цепи или механизма. Такие С. употребляются в машинах (смотрите Механизмы) для передачи движения. С., в которых взаимное перемещение .стержней или дисков м. б. только в том случае, если произойдет изменение длины или формы составляющих С. стержней или дисков, считаются С. неизменяемыми и применяются в сооружениях. По самой сути неизменяемая С. является той же кинематич. цепью с нулевой степенью свободы. В таких С. Фигура 2. взаимное перемещение отдельных составляющих С. частей и С. в целом является следствием только их деформаций от внешних сил и должен быть отно-
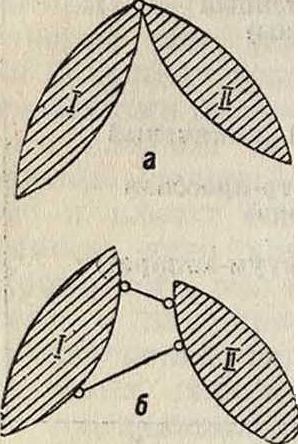
Фигура 1.
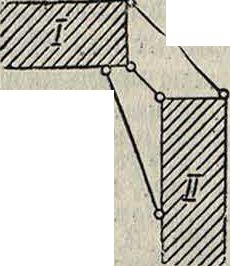
сительно мало по сравнению с основными размерами С., т. e. С. должна быть жесткой.
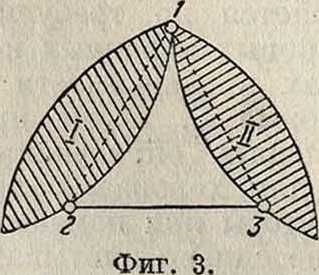
Неизменяемость плоскостной С. обеспечивают соответствующим ее образованием, соединяя стержни и диски между собой т. о., чтобы были исключены три возможные степени свободы относительных перемещений на плоскости. Это достигается введением между дисками трех связевых условий, которые м. б. в следующих ком бинациях: соединение двух дисков м. б. шарниром (два условия закрепления) и стержнем с шарнирами на концах (одно условие, фигура 3), заделкой или тремя стержнями, не пересекающимися в одной точке (три условия, фигура 2, см. Неизменяемость геометрическая). С., перед
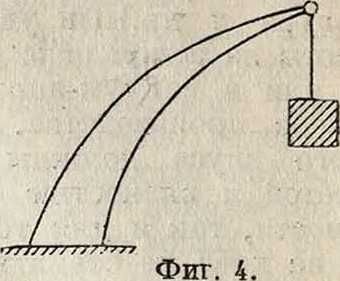
ставляющие, сооружения, кроме внутренней неизменяемости должен быть неизменяемо прикреплены к земле. Рассматривая С. как один общий диск, необходимо уничтожить его три степени свободы перемещений относительно земли, то есть ввести три условия закреплений (в общем случае три стержня, не пересекающиеся в одной точке, как между двумя дисками; фигура 2). Такими опорными закреплениями м. б.: а) заделка при наличии опоры (фигура 4), которая дает три связевых условия; неизвестными в ней являются величина, направление и точка приложения усилия или две составляющие его и момент; б) при наличии двух опор (фигура 5) одна
опора шарнирно - подвижная, исключающая одну степень свободы (один стержень), дающая неизвестное усилие по величине, и другая опора шарнирно-неподвижная (шарнир), исключающая две степени свободы, дающая усилие, неизвестное по, 2величине. и направ- : ’"Г"·— лению; в) при пали- : чии трех опор (фигура 6) -
каждая из них явля- 4* 8
ется шарнирно-под- |
вижной, исключаю- | Фигура 6.
щей одну степень свободы (один стержень); неизвестными являются величины трех усилий. При об-разовании плоскостной системы, состоящей из т дисков или стержней (опорные стержни исключаются), имеющей между ними п шарнирных и г жестких связей, условия неизменяемости требуют соблюдения неравенства
bт < 2п + 3/· + 3. (1)
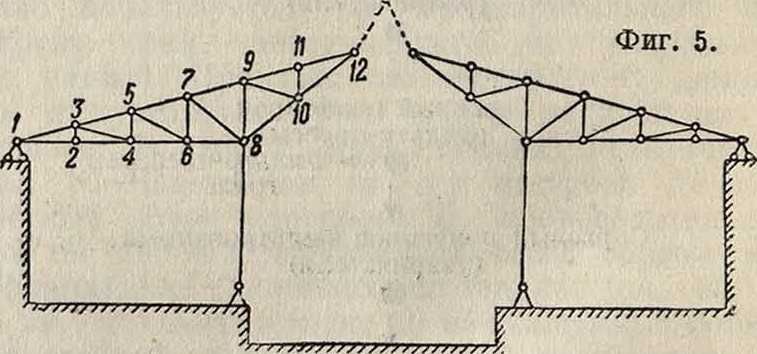
Количество шарнирных связей п подсчитывается по количеству стержней, образующих С., с которыми связан шарнир, без одного; точно так же количество жестких связей г — по количеству сходящихся, соединенных между собой жестко стержней без одного. Так, на "фигура 7а узел А имеет 4 сходящихся стержня, из которых 2 соединены между собой жестко (г=2 — 1), и шарнир принадлежит трем стержням — двум сходящимся и одному из жестких стержней, следовательно п=3—1=2. Обозначая количество связевых условий плоскостной С. с землей через к, условие внутренней неизменяемо-
сти С. и ее неизменяемого прикрепления к земле требует, чтобы
3т < 2л + Зг + к. (2)
На фигуре 7а и 76 для одной и той же С. сделан подсчет шарнирных и жестких связей в двух вариантах: а) считая верхнюю часть как составную (фигура 7а) и б) считая I как один общий
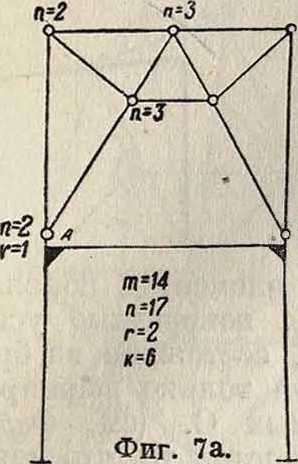
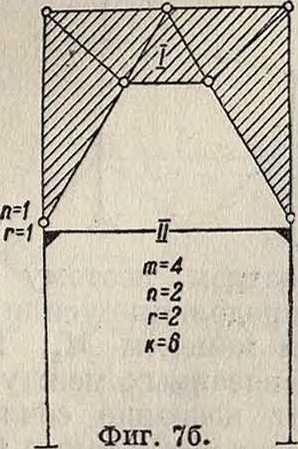
сплошной диск (фигура 76). Результаты в обоих случаях удовлетворяют условию (2). Условия (1) и (2) являются необходимыми для неизменяемости С., но недостаточными; последнее обстоятельство обусловливает необходимость особой проверки (смотрите Неизменяемость геометрическая).
С. называются простейшими, если легко проследить их образование на основании правила, вытекающего из условия соединений дисков: «присоединение каждого нового шарнира к неизменяемой С. должно быть сделано двумя дисками, не лежащими на одной прямой». На фигуре 5 и фигура 6 представлены простейшие системы. Из простейших систем можно получить целый ряд других всевозможных С. путем взаимозамены внутренних связевых условий, дисков и условий закрепления к земле, удовлетворяющих основному условию неизменяемости (2). Способ замены связевых условий состоит в j 4 том, что если из про-
стейшей С. убрать У один стержень или
Диск, входящий в ее
-----У образование, то усло-
Λ вие 3т=2л + Зг к не будет удовлетворено, и система превращается в кинематическую цепь—механизм. Введение новой связи в виде нового стержня или диска в самой С. или в виде дополнительного опорного закрепления, уничтожающих подвижность полученной кине-матич. цепи, дает новую С., удовлетворяющую условию (2) и геометрически неизменяемую.
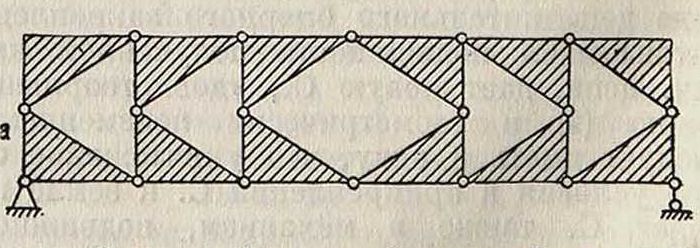
Следует иметь в виду, что уничтожение свя-зевого условия в прикреплении С. к земле превращает С. также в механизм, подвижность которого м. б. уничтожена только новой связью с землей же. Внутренняя связь м. б. заменена излишней связью с землей, превращая С. из свободной в связанную; обратная же замена связевых условий с землей из трех требуемых условиями прикреплений внутренней связью невозможна. Путем замены внутренних стержней получена сложная С., показанная на фигуре 8, б; она получается из простейшей С. (фигура 8, а) путем замены в последней стержней 2—6 и 2—3 стержнями 3—6 и 2—6. В этом случае т=9, л=12, к — 3 и г=0, что удовлетворяет равен-
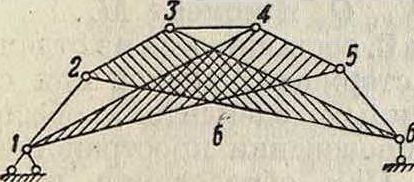
Фпг. 8.
ству (2): 3 · 9=2 -12 + 3. Полученную С. можно также рассматривать как два диска (2—4—3) и (2—3—6) (заштрихованы на чертеже), связанных между собой тремя стержнями (2—2), (3—4) и (5—6); тогда т=5, л=6, к=3 и г=О, и равенство (2) будет также удовлетворено. Количество шарниров уменьшилось потому, что теперь в каждом узле сходятся только два диска — стержня. При пользовании способом замены для образования системы необходимо следить за тем, чтобы заменяющий стержень или связь не были поставлены между узлами · или дисками С., не имеющими относительных смещений в кинематической цепи. Так, на фигуре 9 представлена простейшая С. При выбрасывании стержня 8—22 С. превращается в механизм, части которого могут поворачиваться вокруг шарнира 10. Заменяющий стержень очевидно м. б. поставлен в любом месте между двумя дисками 1—9—.21—10—7—4—3—1 и 10—.20—12—19— 18—15—14—10, например между узлами 4—13, и не м. б. помещен между узлами одного диска
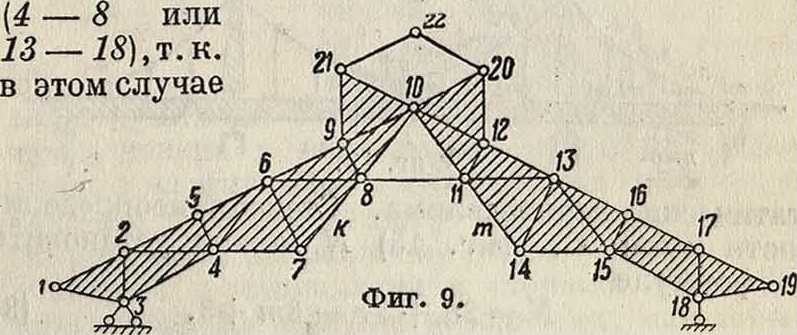
подвижность механизма не уничтожается; обычно заменяют стержнем 7—14, получая т. о. систему Полонсо. Также следует избегать ставить заменяющие стержни между точками двух дисков или между двумя узлами, относительное смешение которых имеет значение минимума или близкое к нему, так как в этом случае С. будет нежесткой, и в заменяющем стержне могут развиваться значительные усилия. На фигуре 9 малые значения относительных смещений имеют точки дисков, соприкасающиеся с шарниром 10; если заменяющий стержень поместить между точками кати постепенно приближать его к шарниру 10, тем самым точки кат приближаются к состоянию минимума относительных смещений, и усилие в заменяющем стержне к—т будет неограниченно расти.
По условиям внутреннего образования С., а также по условиям закрепления С. к земле различают следующие виды их: 1) Когда Зт=2л + + Зг + к и С. по образованию удовлетворяют условиям как внутренней неизменяемости, так и неизменяемого устойчивого прикрепления к земле, то такие С. являются в то же время С. статически определимыми, причем:
а) если 3т — 3=2л + Зг и к=3, то С. является свободной и м. б. как простейшей, так и сложной (фигура 8); условия закрепления к земле таких С. были указаны выше (фигура 4, 5, 6); б) если

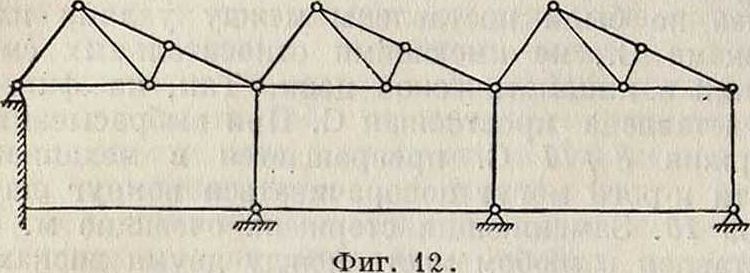
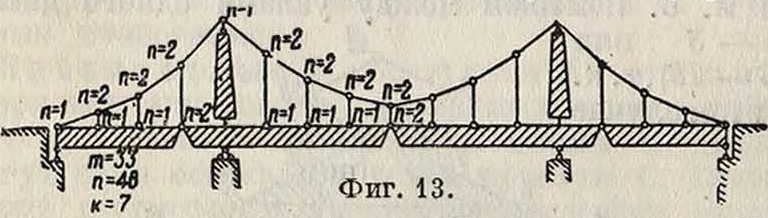
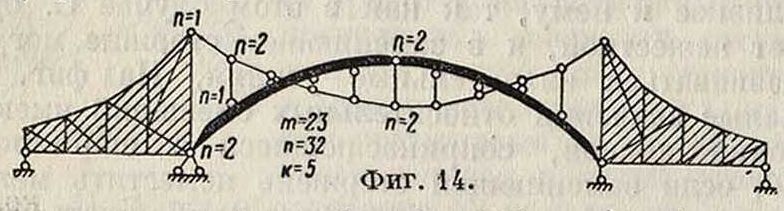
Зт — 3 > 2л + 3/·, но к > 3, то С. в целом не является свободной, т. к. в ее внутреннем образовании недостает необходимых связей, которые заменены опорными закреплениями числом более трех; примерами таких С. являются С. трехшарнирные (фигура 10), многоопорные (фигура 11, 12)
и комбинированные (фигура 13, 14). 2) Когда 3т < < 2ге + Зг + к и в процессе образования С. удовлетворено условие неизменяемости, то С. ста-
т=7 к-5 Y
n=S r»8 f| фигура И.
тически неопределима, причем: а) если 3 тонны — 3<2ге + 3ги&=3, то количество внут
ренних связей в С. больше, чем требуется геометрия. неизменяемостью, а потому С. внутренне
•статически неопределима. Степень неопределимости таких С. (фигура 15) N можно установить по формуле
7V=2re + 3r —Згег+З. (3)
Когда данная С. имеет замкнутые контуры, то неопределимость удобнее подсчитать по выражению
iV=3p-re, (4)
где р — количество замкнутых контуров при внутреннем образовании иге — шарниры в кон
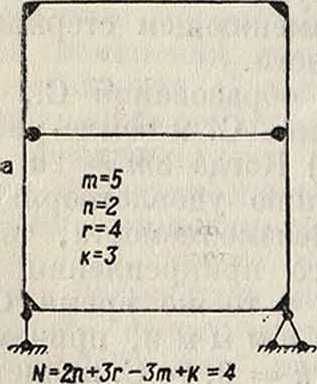
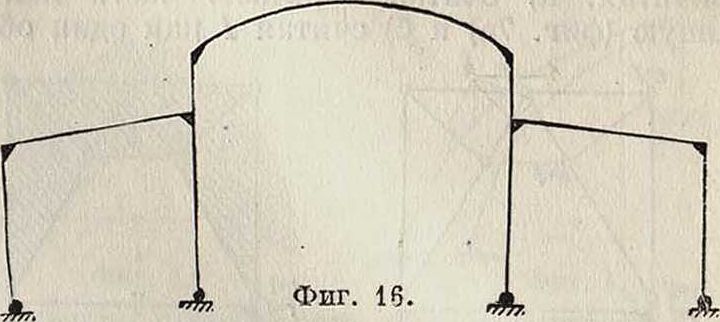
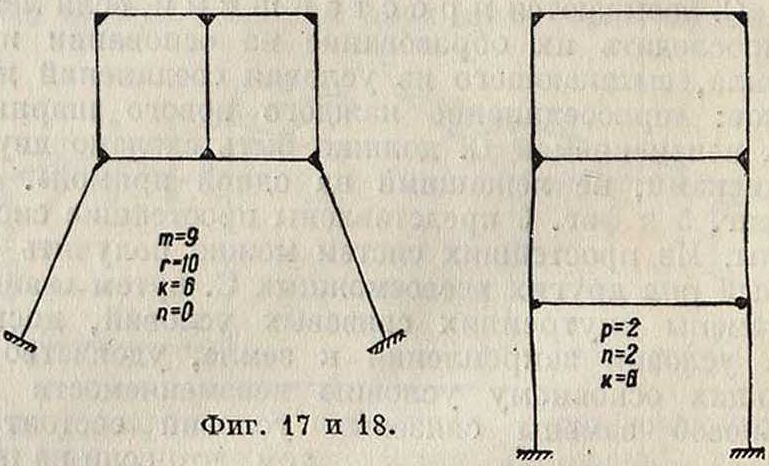
турах; б) если 3т — 3=2ге + Зг и к > 3, то си неопределимы относительно опорных реакций: степень неопределимости в этом случае равна количеству связей с землей без трех, то есть N=k— 3. Такая С. представлена на фигуре 16; в) если 3то—3 < 2ге + Зг и к> 3, то С. статически неопределима как относительно внутреннего образования, так и относительно опорных закреплений (фигура 17 и 18). Общая степень неопределимости получается из следующего равенства:
2V=2re-|-3r— 3 то + к (5)
или, считая по замкнутым контурам,
N=Зр—п- -к — 3. (6)
Так, на фигуре 18 замкнутых контуров внутреннего образования С. р= 2, п= 0, к— 6: 2V=3-2 + 6 —3=9.
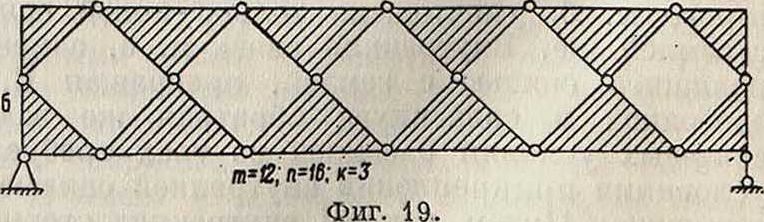
3) Когда Зго> 2ге + Зг + к, то С. представляет уже механизм, степень подвижности которого при указанных способах соединений будет равна Зто— 2ге — Зг—к. На фигуре 19 дана С. механизма с одной степенью свободы. стемы статически
Фигура 15.
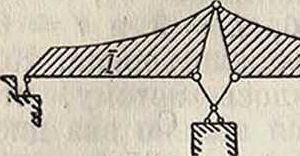
С., применяющиеся в сооружениях, можно также разделять на: 1) С., составленные из одного прямого бруса, — балки, статически оп- ределимые и статически неопределимые (нераз-резные), и из одного кривого бруса — арки (смотрите). Работа этих С. связана гл. образом с изгибом
и сжатием, поэтому в их элементах появляются продольные усилия Nx, поперечные усилия Qy и моменты Мг 2) С., состоящие из брусьев, связанных между собой только шарнирами, носят название сочлененных G. (смотрите Фермы). Особенностью таких С. является то, что нагрузки, приложенные в узлах (шарнирах), вызывают в каждом элементе только продольное усилие (фигура 5, 6); 3) С., состоящие из брусьев, связанных между собой жестко (заделкой), — р а μη ы е.системы (фигура 17; см. Жесткие рамы). Работа таких С. под действием нагрузки сводится в
общем случае к работе сил Nx, Qy и момента Mz;
4) С., представляющие сочетание указанных выше видов, называются С. комбинированными. По своей работе комбинированные С. могут иметь одновременно часть элементов, работающих только на продольную осевую силу, и часть — на усилия Nr, Qy и момент Мг.
Пространственны e С. составляются из отдельных плоскостных С., стержней, дисков или составных пространственных элементов, обеспечивающих в своем образовании пространственную неизменяемость. При образовании пространственных С. отдельные элементы, входящие
в состав С., соединяются между собой жестко или шарнирно, причем следует различать два вида шарнирных соединений пространственных С.: а) шарниры шаровые, обеспечивающие пространственное взаимное вращение частей;
б) шарниры цилиндрические, обеспечивающие вращение только в одной плоскости. Соединение двух элементов в одно пространственное целое требует уничтожения шести степеней свободы относительных смещений в пространстве соеди-
Фигура 20. Фигура 21.
няеыых между собой элементов, чему полностью удовлетворяет жесткое соединение, уничтожающее все шесть степеней свободы. Соединение шарнирно-шаровое исключает три степени свободы поступательных смещений, три же степени свободы вращательных движений остаются. Шарнирно-цилиндрическое соединение исключает пять степеней свободы, оставляя только вращение в одной плоскости. Рассматривая землю и пространственную С. как 2 части одного целого, необходимо для обеспечения относительной неподвижности (устойчивости) С. уничтожить также ее шесть степеней свободы по отношению к земле, для чего необходимо ввести шесть закрепительных связей, которые теоретически м. б. представлены как шесть соединительных стержней с шаровыми шарнирами по концам. Каждый такой стержень исключает одну степень свободы (поступательные движения по направлению стержня). Однако расположение закрепительных стержней должен быть таково, чтобы они при своем продолжении не пересекали одну и ту же прямую аb в пространстве, так как в этом случае сооружение имело бы возможность повернуться вокруг этой прямой (фигура 20 и 21). Как следствие закрепительные стержни не должны лежать в одной плоскости и пересекаться в одной точке и не должен быть параллельными. Если стержни при своем продолжении не пересекают матема-тич. прямую в пространстве, а располагаются на близком от нее расстоянии, то такое закрепление будет иметь значительные усилия в стержнях и может стать нереальным закреплением.
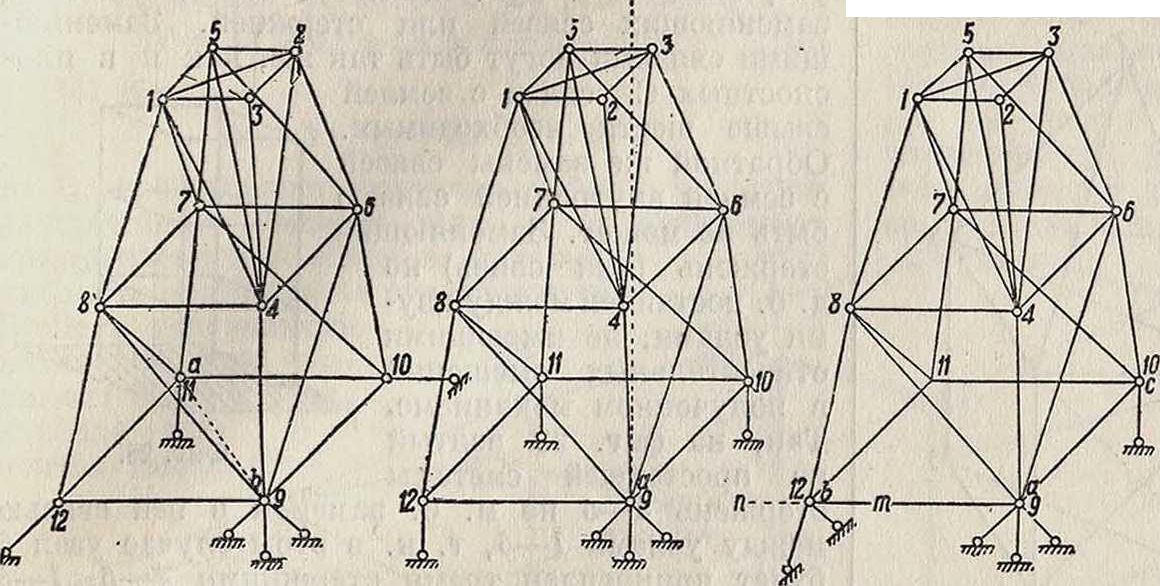
В практике прикрепление пространственных систем к земле осуществляется или в виде заделки или в виде специальных опорных частей, которые разделяются на три следующих вида. 1) Шаровая неподвижная опора, допускающая только вращательные движения, исключает три степени свободы, именно три поступательных движения, и выполняется в виде стального шара, заложенного между опорными плитами, имеющими сферич. углубления. Теоре-тич. оформление такой опоры м. б. представлено в виде трех стержней, пересекающихся в одной точке (узел а на фигуре 22). Такая опора дает три неизвестные величины опорной реакции (величину и направление ее в пространстве). 2) Цилиндрич. подвижная опора, допускающая вращательные движения и поступательные только по одной прямой (по линии передвижения цилиндрич. катков), осуществляется в виде цилиндрич. катков, зажатых между плоскими опорными подушками, из которых верхняя имеет шаровую неподвижную опору для сооружения.
Такая опора исключает две степени свободы С., теоретически м. б. представлена в виде двух опорных стержней (узел Ь, фигура 22), расположенных в плоскости, перпендикулярной к линии движения катков, и дает две неизвестные величины опорной реакции (величину силы и ее направление в плоскости расположения стержней). 3) Шаровая подвижная опора, допускающая вращательные движения и все поступательные движения в одной плоскости, практически осуществляется в виде стального шара, зажатого между плоскостными опорными подушками. Теоретически такая опора м. б. представлена в виде одного опорного стержня (узел с на фигуре 22), исключающего одну степень свободы и дающего одну неизвестную реакцию по величине; направление же ее известно — оно совпадает с направлением стержня. Для удобства опоры на чертеже обозначают, как показано на фигуре 26; число внизу значка указывает количество степеней свободы, которое исключает данная опора.
Три названные опоры дают необходимое количество связевых условий для присоединения пространственной С. к земле. Присоединение пространственной С. также м. б. выполнено и одним из указанных видов опор, но при достаточном их числе и надлежащем распределении. Если пространственная С. состоит из т стержней или дисков и имеет в своем образовании г жестких соединений, s шаровых шарнирных и п цилиндрич. шарниров, то необходимое количество связевых условий в образовании С. должно удовлетворять выражению
6(m—l)<3s-f-6r+5н, (7)
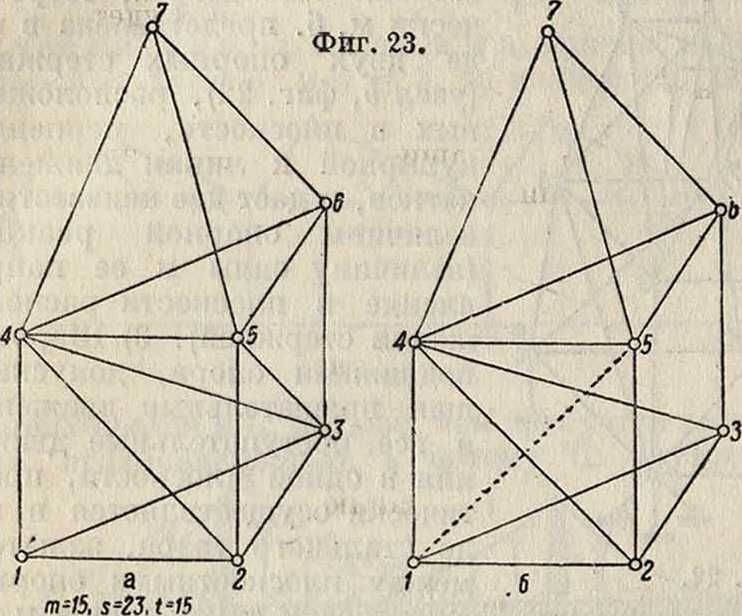
где s, г и п считаются по количеству стержней в узле, обладающих общей одинаковой связью, без одного. С., удовлетворяющие этому условию, способны воспринимать силы любых направлений и как угодно приложенные. Когда в образовании системы встречаются элементы, имеющие по концам шаровые шарниры, то такой элемент обладает одной степенью свободы — вращением вокруг собственной оси — и очевидно не может воспринимать на себя силы, не лежащие с ним в одной плоскости. Такая С. представлена на фигуре 23, б, где количество необходимых связей для воспринятая силы случайного направления, действующей на элементы с шаровыми шарнирами, не удовлетворяет условию (7), и в то же время С. геометрически неизменяема, то есть не меняет свою геометрич. форму без изменения этих составляющих С. частей. С. подобного образования, геометрически неизменяемые, м. б. применены в сооружениях только в случае, если силы, действующие на элементы с шарнирами по концам, будут лежать в одной плоскости с ними, то есть представлять собой плоскостную С. Для обеспечения геометрич. неизменяемости пространственной С.,
включающей в себя t стержней или дисков с шаровыми шарнирами по концам, должен быть удовлетворено условие
6 [т — l)<3s + 6r + 5rc + t. (8)
удовлетворяющая этому условию, показана на фигуре 23,а. Условие (8) является так же, как
и в плоскостных С., условием необходимым, но не достаточным в смысле установления неизменяемости (смотрите Неизменяемость геометрическая). Если количество опорных закреплений обозначить через к, то для обеспечения неизменяемости и достаточного (устойчивого) закрепления к земле необходимо, чтобы в G.
6т=3s + 6г + 5п + к -I- £. (9)
Системы, постепенное образование которых происходит или жесткой заделкой (фигура 25) или присоединением нового шарнирного узла тремя стержнями или дисками, не лежащими в одной плоскости, обеспечивающими неизменяемую пространственную форму тетраэдра, называются простейшими системами. Так, на фигуре 24
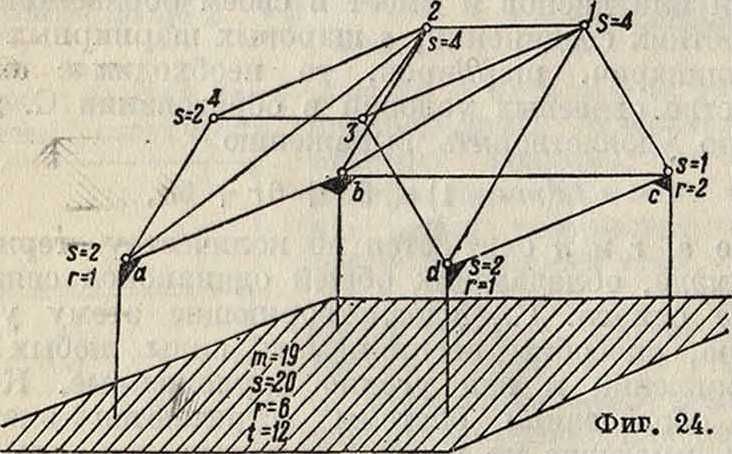
нижний этаж получен путем заделки стержней, а вверху узлы получены тремя стержнями; последовательный порядок образования их указан на чертеже. Полученная форма тетраэдра dbcl с вершиной 1 является геометрически неизменяемой, так как основание тетраэдра dbc расположено на стержнях db—be—cd, неизменяемое положение которых обеспечивается взаимной жесткой заделкой. С., не удовлетворяющие указанному образованию, называются с л о ж-н ы м и С. Из простейших С. можно получать другие простейшие С. и С. сложные путем замены связей или стержней. Прием заключается, как и в плоскостных С., в том, что из С. исключается связь или стержень; тогда очевидно равенство (9) будет нарушено, и С. будет превращена в изменяемую С. с недостающим количеством связей — в механизм. Если же связь или стержень ввести вновь в С. в другом месте в виде связи, способной исключить полученную при первом исключении подвижность С., то неизменяемость вновь восстановится и равенство (9) будет удовлетворено, но С. будет уже другая. Новые введенные в С. связи взамен устраненных в простейшей С. носят название заменяющих связей или стержней. Заменяющими связями могут быть так же, как и в плоскостных С., связи с землей свыше шести необходимых.
Обратной же замены связей с землей внутренней связью быть не может. Заменяющий стержень (или связь) не должен быть поставлен между двумя узлами, не имеющими относительных смещений в полученном механизме.
Так, на фигуре 23 взятый из простейшей системы стержень 3—5 не м. б. заменен в ней связью между узлами 1—5, т. к. в этом случае узел 5 будет прикреплен тремя стержнями 4—5, 1—5 и 2—5, лежащими в одной плоскости. Также заменяющий стержень не м. б. вставлен между узлами, которые при перемещениях механизма находятся в состоянии минимума, т. к. в этом случае малые упругие деформации заменяющего стержня вызовут большие перемещения С., которая становится не жесткой, а в заменяющем стержне могут возникать значительные усилия. С., неизменяемые и удовлетворяющие условию (9), являются в то же время статически определимыми, т. к. для каждой части, входящей в С., можно составить шесть ур-ий статики, определяющих шесть связевых условий в С.
По условиям внутреннего образования С., а также по условиям закрепления ее к земле можно различать следующие виды С.:
I. Когда
6т=3s + 6г + 5га + к +г и С. по образованию неизменяема, то она является С. статически определимой, причем а) если
6т — 6=3s + 6r + Ьп -j- t и к=6, то С. является свободной, м. б. простейшей и сложной (фигура 22);
б) если
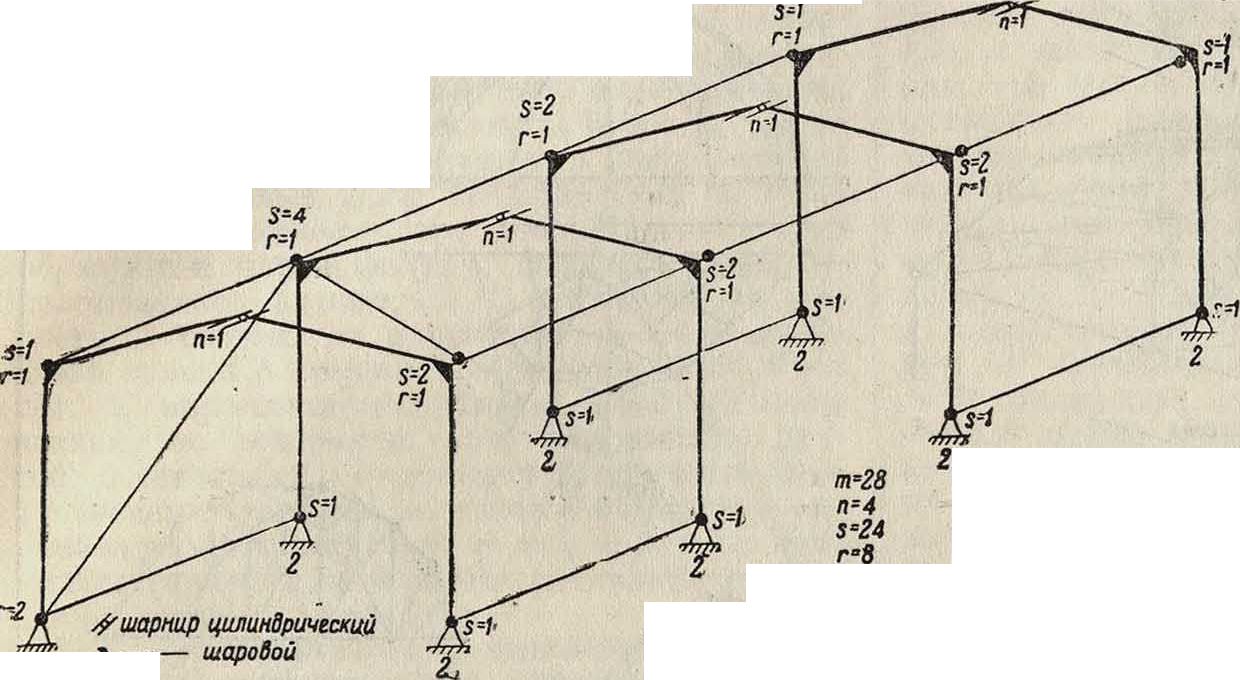
6т — 6 > 3s + 6/· + 5п -f- t и к > б, то С. является преобразованной — связанной С. (фигура 26).
II. Когда
6т < 3s + 6г + 5п + к -f t и С. по образованию неизменяема, то она статически неопределима, причем а) если
6т — 6 < 3s + 6r + 5ге -f t и к — 6,
то С. является свободной и статически неопределимой относительно внутреннего образования, так как число ее внутренних связей более требуемого по условию (8);
б) если
6т — 6=3s -f 6г+ Ьп -f- t и к >6,
то С. свободная и статически неопределимая относительно опорных закреплений (фигура 24);
в) если
6т—6 < 3s + 6г + 5η+ί и к>6,
то С. свободная и статически неопределимая как относительно внутреннего образования, так
и относительно опорных закреплений (фигура 25);
г) если
6 т— 6 >3s + 6r + 5re + £H к> 6, то С. является связанной и статически неопределимой относительно опорных закреплений.
Степень статич. неопределимости указанных выше С. можно установить из равенства:
N=Zs+ 6г+5п+к+Ч — вт. (10)
III. Когда
6m>3s+6r-(-5re+i· + £,
то С. представляет механизм с недостаточными внутренними связями или с недостаточным прикреплением к земле и не может находить применения в сооружениях.
Степень подвижности механизма при указанных способах соединения элементов также
t‘12
Фигура 26,
г можно определять равенством (10), получая отрицательные значения неопределимости.
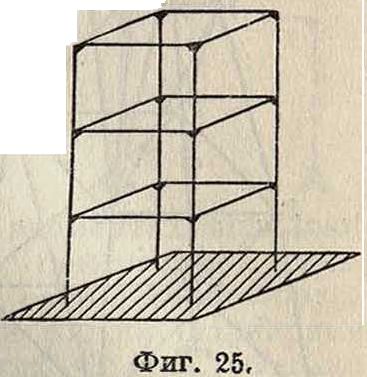
По своему образованию пространственные С. могут быть разделены на следующие С. 1) С., состоящие из отдельных брусьев и дисков, связанных между собой в одно жесткое монолитное целое, не допускающее взаимного поворота сходящихся в узлах брусьев (фигура 25); такие С. называются жесткими рамными С. и употребляются во всех видах инженерных сооружений. Особое развитие получили рамные С. с появлением и развитием железобетона как материала, обеспечивающего монолитность С. В таких С. в общем случае имеются изгибающие моменты, поперечные силы и моменты крутящие. Жесткие рамные С. по своему образованию всегда являются С. неизменяемыми вне зависимости от числа стержней и узлов, образующих систему, и в них возникают только вопросы о достаточном закреплении к земле и степени статической неопределимости, причем первый из них решается просто, второй же м. б. подсчитан по условию (10), к-рое в этом случае м. б. написано упрощенно:,
N=(61--т) + к.
Так, С., указанная на фигуре 25, имеющая т=24, /•=32, к= 24, имеет неопределимость
N=6(32—24) + 24=72.
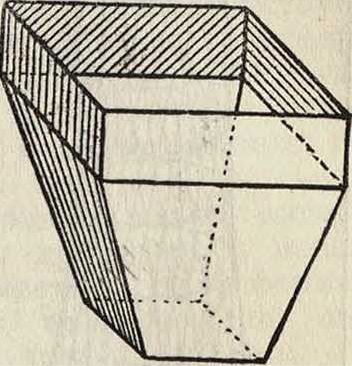
К таким же С. относятся С., состоящие из плоских плит (пластинок), связанных в одно пространственно-жесткое целое; они называются бункерами (фигура 27) и употребляются в силосах, углехранилищах и тому подобное. Сюда же надо отнести системы, состоящие из пластинок, имеющих одиночную или двоякую кривизну. К первым относятся цилиндрич. покрытия фигура 28), ко вторым относятся С., представляющие собой поверхности вращения с обра зующей, имеющей кривизну, например купола (фигура 29). 2) С. сочлененные (фермы), состоящие из отдельных стержней или фермочек и дисков, обеспечивающих свою пространственную неизменяемость, связанных между собой шаровыми шарнирами, допускающими взаимный поворот стержней (дисков) в любых направлениях. Благодаря этому усилие в стержне (диске) при нагрузках, приложенных в узлах, будет всегда осевое, направленное по линии центров шарниров на концах стержня. Пространственные сочлененные С. (фермы) могут воспринимать на себя силы, не лежащие в плоскости элементов, на которые они действуют. Геометрическая неизменяемость требует удовлетворения равенства (9), к-рое для сочлененных С. будет: т + к=Zq, где q— количество узлов в С. Основной формой, обеспечивающей пространственную неизменяемость по образованию, является тетраэдр 1—2—3—4 (фигура 23)—С., образованная из шести стержней. В простейших сочлененных С. присоединение нового узла производится тремя новыми стержнями, не лежащими в одной плоскости (фигура 23). Применяя способ замены стержней, можно получать из простейших самые разнообразные сложные сочлененные С., которые применяются для перекрытий общественных зданий крупных размеров, купольных и шатровых покрытий, в мостах, кранах, башнях, маяках и прочих инженерных сооружениях.
По своему внешнему виду и по назначению сочлененные пространственные С. могут быть разделены на мостовые, зубчатые, стропильные, балочно-сферические, купольные, пирамидальные, шатровые, крановые фермы и фермы мачт и пилонов. Особую разновидность свободных пространственных С. составляют фермы летательных аппаратов, аэропланов и дирижаблей (смотрите Аэроплан и Дирижабль). Мостовая ферма (фигура 30) состоит из шести отдельных плоскостных С., связанных неизменяемо в одно пространственное целое. Такая ферма при расчете на вертикальную нагрузку даст возможность разложить ее на отдельные плоскостные С., как обычно и поступают в практике (см.
Фермы). При езде пони- Фигура 27.
зу плоскостные сочлененные системы ABCD и EHFG "(фигура 30) заменяются жесткими рамами. Мостовая ферма м. б. составлена также из трех плоскостных G. (фигура 31) — т. н. трехпоясных С. Такие С. осуществлены за последние годы в практике мостостроения (Америка, Германия). Зубчатые стропильные фермы (или шедовые) применяются гл. обр. для перекрытия широких зданий мастерских, требующих большого освещения (фигура 32), для чего крутая часть перекрытия ABCD бывает застеклена, а пологая покрывается кровлей. Балочно- и арочно-сферич. покрытия применяются в зданиях, имеющих в плане форму правильных мн-ков, и состоят из отдельных радиально расположенных плоскостных ферм, имеющих очертание верхнего
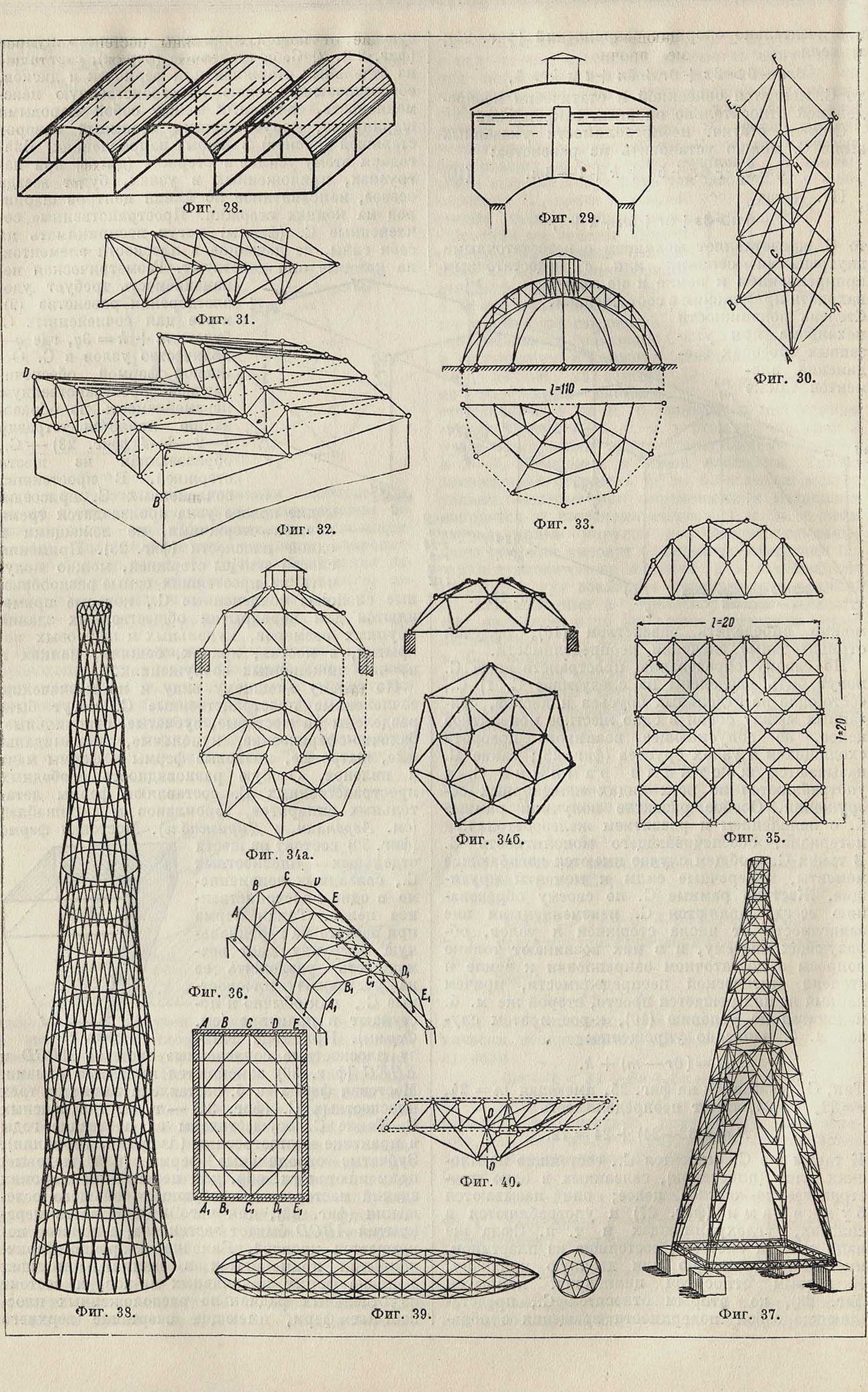
пояса по кривой и дающих внешнюю сферич. поверхность. Отличие арочно-сферич. покрытий от балочных то, что первые дают на опоры распор и требуют исключительно неподвижных опор или нижнего кольца, выполняющего роль затяжки. На фигуре 33 дана подобного рода система, составленная из серповидных арок, чем достигается использование внутреннего помещения. Взаимное пересечение плоскостных ферм обеспечивается особым барабаном, расположенным в центре. Купольные С. отличаются от сферических (балочных и арочных) тем, что в них внутренняя часть купола использована полностью. На фигуре 34 даны 2 купольные С.: а) С. Шведлера (фигура 34а) имеет внизу опорное кольцо, а сверху световой фонарь; поверхность ее состоит из плоскостей, имеющих более трех стержней, в ней лежащих; ребра С. располагаются по меридиональным и параллельным сечениям: первые дают представление об образующей поверхности вращения С., а вторые образуют в плане фигуру, подобную плану перекрываемого здания; б) С. сетчатая: поверхность ее состоит из плоскостей, в которых находятся только 3 стержня, меридиональных ребер нет, а параллельные фигуры подобны плану здания, но повернуты одна относительно другой; в сетчатых С. существует зависимость между чи стержней те, узлов q и граней f, выраженная ф-лой Эйлера: те=q + f — 2, чему удовлетворяет С. на фигуре 346, где т=49, q= 21 и /= 30, включая основание.
К С. купольным близко подходят С. шатровые (фигура 35)” служащие для перекрытия зданий с прямоугольным очертанием в плане. С. цилиндрические применяются для перекрытия длинных зданий, перронов и тому подобное. На фигуре 36 показана такого вида С., требующая дополнительных опор в точках А, В, С, D, Е и Аг, В1г С1;jDj, Ej. С. в виде башен и пилонов различного профиля (фигура 37) употребляются для опор виадуков, для причальных мачт дирижаблей, мачт электропередач, радиостанций и т. д. Среди этих С. особо следует отметить гиперболоид-ную С. (фигура 38), предложенную акад. Шуховым; поверхность ее образуется сеткой из прямых стержней, что обеспечивает простоту изготовления. На фигуре 39 и 40 показаны С. летательных аппаратов.
Лит.: Прокофьев И., Теория сооружений, ч. 1, М., 1926; Тимошенко С., Курс статики сооружений, ч. 1, Л., 1926; Подольский И., Пространственные фермы, М.—Л., 1932; Ривош О., Металлические стропильные фермы, 5 изд., М.—Л., 1931; Р a fill e e и ч П., Сборник задач по пространственным системам, 1911; S eh link W„ Statik d. Raumfachwerke, Lpz., 1907; Foppl A., Vorlesungen uber techn. Me-chanik, 7 Aufl., B. 2, Lpz.—B., 1926. If. Киселев.·