> Техника, страница 80 > Скважность

Скважность

Скважность, общее свойство твердых тел, выражающееся в существенном, не сводящемся к ошибкам измерения неравенстве значений занимаемого ими объёма, если последний измеряется разными способами. Под объёмом физического тела разумеют область непроницаемости, обусловленной присутствием этого тела; понятие об объёме без признака непроницаемости в отношении физич. тела не м. б. построено. Но признак непроницаемости соотносит понятие объёма с понятием о том конкретном физич. приеме, посредством которого устанавливаются границы области, непроницаемой для данного испытания. Прежде чем будет дано доказательство противного, в каждом частном случае нет оснований утверждать тождественность этих границ при разных приемах испытания, то есть производимых с помощью энергии в разных ее видах. Даже напротив, именно в силу различия видов энергий применяемых при зондировании непроницаемости, естественно ждать, что физическое тело будет реагировать на них различно; следовательно известные места пространства, непроницаемые для одного вида энергии, окажутся проницаемыми для другого, хотя при этом никогда не может оказаться проницаемости абсолютной для всех способов испытания, что означало бы простое отсутствие физич. тела. Т. о. в понятии объёма физич. тела необходимо диалектич. сопряжение проницаемости с непроницаемостью, каковое в целом и называется С. Геометрически С. схематизируется как отсутствие предела, к к-рому стремился бы убывающий ряд объёмов, остающихся за вычетом, согласно предыдущему приближению, из объёма тела тех областей пространства, которые в последующем приближении оказываются к объёму тела непринадлежащими—пор,

скважин, полостей, зазоров, трещин и других участков пространства, частично или|Полностыо окруженных веществом данного тела, но этого вещества в себе не содержащих. Однако подобный геометрический подход к понятью С., несмотря на свою заманчивую наглядность, на самом деле представляет не более как схему или модель, питающуюся физич. содержанием из вышеприведенного оперативного понятия, поскольку самый процесс подразделения объёма тела на участки пустые и на участки заполненные возможен лишь при проверке в физич. опыте их пустоты, то есть проницаемости, или заполненности, то есть непроницаемости. Т. о. общее понятие о С. подразумевает неопределенно широкий круг всяких возможных испытаний на проницаемость и непроницаемость, а конкретное понятие С. необходимо должно сопровождаться указанием тех приемов испытания, на основании которых и в виду которых это понятие построено. Принципиально м. б. утверждаема С. всякого твердого тела, даже вообще всякого тела; однако назвать скважным то или другое определенное тело без указания тех определенных приемов, которые имеются в виду в данном случае, было бы лишенным смысла, поскольку с равным правом за обсуждаемым телом С. в отношении других приемов испытания могла бы отвергаться. Так, сеть непроницаема для рыбы, но весьма проницаема для воды; галька непроницаема для булыжника, но проницаема для песка, как этот последний непроницаем для гравия, но проницаем для воздуха и для воды. Проницаемость гальки для булыжника и валунов окажется при всех испытаниях нулевою, и следовательно заполненный объём—одним и тем же; при подобных испытаниях мы должны были бы признать галь · ку материалом нескважным. Но та же самая галька при испытании ее проницаемости мелким гравием, песком различной величины зерна и наконец водою покажет различную степень заполненности объёма и потому не только должен быть причислена к телам скважным, но и получит в разных случаях разную оценку своей С. Однако указанными приемами испытаний ряд их не ограничивается. Проницаемость тела в отношении разных по степени дисперсности молекулярных сгустков, затем в отношении молекул, атомов, ионов, электронов и атомных ядер различна и потому следовательно будет оценена ими различная степень заполненности данного пространства; а потому весьма различною окажется и количественная характеристика С. Между значением С., равным нулю, и значением ее, весьма близким к единице и практически равным единице, как крайними пределами, полученными при разных приемах испытания одного и того же тела, лягут все прочие, то есть вне связи с определенными приемами испытания С. данного тела может быть приписано значение какое угодно во всем логически мыслимом диапазоне.

С. принадлежит к числу наиболее глубоких характеристик физич. тела, определяющих собою его свойства не только в количественном, но и в качественном отношении. При этом решающим здесь оказывается прежде всего топологии. строение скважин, а затем соотношение между собою геометрии, размеров как скважин, так и целого тела. Геометрией скважин объясняются в весьма большом числе случаев физико-химич. явления в физич. телах, причем качественный характер этих явлений обусловлен то-

пологией тех изъянов сплошности физич. тела, которые в совокупности составляют его С., а количественный—их метрикой. В соответствии с указанными обстоятельствами основания классификации С. должен быть проводимы по топология, характеру скважин, по их форме, по величине и числу. Далее идут важные, но отчасти производные классификации С.—по общему содержанию скважин, по удельной поверхности и удельной длине скважин,—и ряд специальных, разработанных применительно к той или другой области—геологии, почвоведению, дорожному строительству, анатомии растений и т. д. Прежде всего понятно, что С. получает весьма различное физич. значение в зависимости от того, доступно ли внутреннее пространство скважин проникновению туда деятелей из пространства внешнего для данного тела (деятелей данного рода)—газов, паров, жидкостей, в частности и в особенности влаги, тепла, электрич. тока и т. д. Тут следует различать следующие пять типов С.’: 1) скважины замкнутые (чаще называемые порами), вполне разобщенные как между собою, так и с внешним пространством (структура сырообразная); 2) скважины открытые, образующие карманы, т. н. слепые поры, б. или м. глубоко входящие в объём тела и в известных случаях даже проходящие через большую его часть, но тем не менее имеющие наружу лишь один выход, т. ч. непрерывный поток различных деятелей через подобные поры невозможен (структура порообразная); 3) скважины характеризуются наличием по крайней мере двух расположенных б. или м. далеко друг от друга выходов во внешнее пространство, т. ч. в подобных сквозных порах, или скважинах, в узком смысле слова, может возникать непрерывный проток различных агентов не только в определенных направлениях (структура древесинообразная, особенно часто встречающаяся в растительных тканях); 4) С., возникающая от соединения слепых и сквозных“ пор в одну связную систему, т. ч. от любого из входов в тело из наружного пространства идет свободный путь к любому из выходов (структура губкообразная)’; 5) С., возникающая из предыдущего типа через дальнейшее развитие скважин и слияние их между собою, с образованием в теле обособленных всесторонне окруженных скважинами участков; при этом не исключена возможность и такого случая, когда эти участки не связаны непосредственно с телом, но удерживаются на своих местах какими-либо уравновешенными силами; однако такая система, по строению подобная взвешенному в пространстве рою, не м. б. названа твердым телом в собственном смысле и практически обычно встречается в виде скопления непосредственно соприкасающихся друг с другом, хотя и не связанных в одно целое отдельностей; таковы пыль, песок, гравий и т. д. Вероятно таковы же многие геологич. образования, но при значительных размерах их отдельностей. Подобное строение в литературе было предложено называть пылеобразным. Классификация С. по величине скважин м. б. проведена лишь б. или м. условно, т. к. основанием деления здесь служит не естественное распределение скважин по величине, а наличные способы испытывать С. и отчасти явления, вызываемые скважинами того или другого размера; классификация по величине (табл. 1) может представлять особый интерес как с ха-

Таблица 1.—Размеры скважин различных фильтров.

Род фильтра	Размер скважин В μ
Фильтр Беркфельда..	8—12
» » ..	Б—4
Фильтровальная бумага Шлехера и Шюлля № 1450 (с тканевой подкладкой)	4,8
Фильтровальная бумага Шлехера и Шюллн № 5.8 (плотная).	3,3
Обыкновенная толстая фильтровальная бумага..	ОК. 3,3
Фильтровальная бумага Шлехера и Шюлля № 597 (средняя).	ОК. 2,9
Фильтровальная бумага Шлехера и Шюлля № 602 (жесткая).	2,2
Фильтровальная бумага Шлехера и Шюлля № 566 ..	1,7
Фильтровальная бумага Шлехера и Шюлля № 602 (очень жесткая).	1,5
Фильтровальная бумага Шлехера и Шюллн № 602 (наиболее тонкая).	1
Фильтр Чемберлена..	1,18—7,0 0,19—0,7
» » ..
Фильтр Гейхеля ..	0,16—0,18
Скважины в стекловидном геле крем-некислоты..	0,005

рактерных примеров тонкой С. В известных случаях может потребоваться классификация по плотности распределения скважин. В виду чрезвычайного разнообразия видов С. дать общую классификацию в этом направлении было бы затруднительно. В качестве же примера специальной классификации этого рода может быть дана (табл. 2) классификация горных по-

Таблица 2. — Классификация пород по зна-

чению трещиноватости.
Расстановка трещин	Границы числа ; трещиноватости j
Часто поставленные.	К > 5,0 i
Очень тесно поставленные.	5,0 >К> 2,5
Тесно, поставленные.	2,5 > К > 1,67 j 1.67 > К > 1,25
Средне поставленные.
Широко поставленные.	1,25 > К >0,833 0,833 > К
Очень широко поставленные.

род по значению т. н. трещиноватости К, то есть по числу (Kliiftigkeitsziffer), к-рое указывает, сколько раз встречается на п. м каменной породы отдельность, ограниченная трещинами; это число получают как среднее из большого количества измерений, например на длине, которая превосходит расстояния трещин между собою по крайней мере в 20 раз. Число трещиноватости в различных направлениях м. б. весьма различно, и потому при нем необходимо отмечать то пространственное направление, для которого дается степень трещиноватости. Классификация по значению С., то есть по количественному содержанию совокупного объёма полостей в объёме тела, тоже носит условный характер, поскольку границы между отдельными значениями пористости м. б. не произвольными лишь при обсуждении того или другого определенного класса тел. Как пример специального применения подобной классификации м. б. дана классификация горных пород по значению С. (табл. 3). С. L, или к о э ф. пористости, выражается в объёмных процентах. Наряду с коэф-том L вводится иногда сотая доля его (U), называемая степеньюнепло-т н о с т и породы, и другая величина—с т е-пень плотности, численно равная 1 — U.

Таблица 3 .—К лассификация пород по значению скважности.

Номер вида	Вид породы	Значение скважности	Характер скважин
I	Очень плотно		В первых двух
	сложенная.	0,5 >L	видах преоб
II	1 Плотно сложен- |		ладают сква
	ная.i	1,5>L>0,5	жины в виде
III	Умеренно плот		волосных тру
	но сложенная	2,5>L>1,5	бок и весьма
	Умеренно скваж-ί		малых зазо
	нан.,	5>L>2,5	ров между ми
IV	Скважная..	10>L> 5	неральными
V	Очень скважная	30>L>10	зернами
VI	Ноздреватая. 1	L> 30

Так например, известняковый песчаник из Аф-ленца, обладающий С. 34,70, характеризуется степенью неплотности 0,347 и степенью плотности 0,653. В сторону нижних значений С. ограничена пределом 0%, верхним же ее пределом служит 100%. К верхнему пределу можно подходить достаточно близко, создавая пенистые структуры с все более и более тонкими стенками; таковы наир, вспененные в расплавленном состоянии и затем застывшие смолы, которые могут дать тела с содержанием пор, весьма мало отличающимся от 100%, и тем не менее относиться к телам твердым. С. тел с пенистой структурой возрастает с утонением стенок отдельных ячеек и с уменьшением удельной поверхности тела. Тонкость стенок принципиально ограничена размерами молекул, образующих пленку, и для сохранения устойчивости и прочности пленка должна содержать в своей толще по крайней мере одну молекулу у углеводородов и две молекулы у жирных к-т. Так, по данным В. Г. Брэгга черное пятно на мыльном пузыре соответствует двойному слою молекул толщиною в 12 ш,и, а чернейшее пятно, появляющееся на черном,—единичному слою толщиною в 6 тц, причем этот единичный слой отличается наибольшей устойчивостью; по Перрену толщина единичного слоя 5,2 m/i, а по Уэльсу—4,2 τημ. При последовательном утолщении мыльной пленки кратными от единичного слоя она проходит через серый, затем чисто белый, соломенно-желтый, оранжево-красный, темнокрасный и наконец фиолетовый цвета; этот последний соответствует 37—38 элементарным слоям, то есть толщине 210 ηιμ. Единичные слои состоят из двух молекул олеиновой к-ты, получающейся вследствие гидролиза олеата натрия или калия. В твердых пленках длина двойной молекулы олеиновой кислоты равна приблизительно 3,6 τημ. Уменьшение удельной поверхности пленочных перегородок принципиально безгранично, т. к. для этого требуется лишь соответственное увеличение размеров отдельных ячеек. Понятно, что с возрастанием С. уд. в пористого тела (кажущийся уд. в.) при неизменности вещества, из которого построено тело, убывает и м. б. доведен до чрезвычайно малого значения; так например, нетрудно получить твердую пену уд. в до 0,0001 и ниже, если ячейки ее будут размерами порядка 2 см. Подобные тела однако пока не получены достаточно прочными и потому не нашли себе практич. применения как материалы. Из материалов же промышленного значения наименьшим уд. в., а именно 0,03, в сочетании с непроницаемостью для жидкостей, пока оказывается вспененная резина. Список нек-рых наиболее легких твердых материалов

Таблица 4.—Н аиболее легкие твердые материалы.

1 Материал	* Уд. в.
Пемза..1	1,0—2.2
Резиновая губка.! Бозенге (бокомбо, африканское	ОК. 0,4
флотовое дерево).!	0,295
Пробка (оиычных сортов).	0,24—0,25
Мраморная пробка.1 Бальза (вестиндское пробковое |	0,228
дерево)..i Заменитель бальзы из ртходов	0,070—0,117
кукурузы ..	ОК. 0,11
Пробковый кирпич «экспансит» Звукоизоляционные доски из	0,061
отходов кукурузы.	0,048—0,056
Сердцевина бузины.	—
Вспененная резина.	0,03

дан в таблице 4. Эти легкие материалы относятся преимущественно к пробке и композициям из нее (смотрите Пробка), а также к различным искусственным материалам из отходов кукурузы, выделываемым в последнее время в США на основании работ Винфрея и Свинея. На другом конце ряда С. стоят каменные породы и металлы, считающиеся особенно компактными. Однако ни у тех ни у других С. не равна нулю; у металлов, лишенных грубых или даже микроскопии, скважин, ультрамикроско-пич. С. тем не менее составляет несколько десятых процента; а у каменных пород от значений того же порядка она доходит до П/г—2% в случае кажущейся полной компактности (мрамор, гранит, плотный песчаник, сиенит) и до нескольких десятков процентов, наир, до 20— 35 при наличии более крупных пор. В табл. 5 и 6 даны в качестве примера сведения о С.

Таблица 5 .—С кважность некоторых горных пород Австрии (по Ганишу).

Порода	Пункт	Скважность (объёмный %)
Известняковый	Афленц, возле В иль до
песчаник	на (Штейермарк).	34,70
Порфир	Бранцолль (Тироль).	3,10—2,47
Серпентин	Эйнзидель, близ Ма-
	риенбада (Богемия).	0,85
Гранит	Грасштейн (Тироль).	1,53
Венский песча	Гюттельдорф (Нижняя
ник	Австрия).	4,57
Венский песча	Нейбург (Нижняя Авст
ник	рия) ..	0,33
Мрамор	Лаас (Тироль).	1,33
Гранит	Литберг (Нижняя Авст	1,61
	рия) ..
»	Маутаузен (Верхняя
	Австрия).	1,63
Плотный песча	Мори (Южный Тироль)	1,47
ник
Плотный песча	Нагс (Южный Тироль).	0,87
ник
Сиенит	План (Богемия).	1,54 !
Конгломерат	Перниц (Нижняя Авст-	7,40 !
	рия)..
Трахит	Шпицберг, возле Перна	12,39
	(Богемия).
Диорит	Вишковиц, возле Ма-	ί
	риенбада (Богемия).	0,59 i

некоторых горных пород. Все перечисленные группы материалов обладают строением одного из первых четырех типов, приведенных в классификации (ст. 75); четыре типа объединяются тем общим признаком, что С. соответственных тел не ограничена принципиально ни снизу ни сверху. Напротив, тела со строением согласно пятому типу, то есть состоящие из отдельных не связанных д!ежду собою зерен (пылевидные),

Т а 0 л. 6 .—С «важность некоторых пород (по Гари).

Порода		Пункт	Скважность (объёмный %)
Мрамор		Фюрстенберг, возле
		Шварценберга (Саксо-
		ния)..	6,3
Раковистый из-		Линия Мюльгаузен—
вестник		Треффурт (Тюрингия)	8,9
Роговообманко-		Таубенберг, возле Сец-
вобиотитовый		дорфа (Австрийская
гранит		Силезия).	0,7
Гранитит		Киндиш (Саксония).	1,4
»		Штерлен..	1,2—2,2
»		Депшиц (Силезия).	0,7—0,8
ΐ »		Гассероде—Вернигероде
		(Гарц) ..	0,8
»		Шварцвальд.	1,3
Кварцевый пор-		Моккрепна.	0,4
фир Кварцевый пор-		Оберреферсдорф.	3,3
i Фир
Кварцевый пор-		Шмальвассергрунд, воз
1 Фир		ле Дитгарца (Тюрин
		гия) ..	9,3
1 Кварцевый пор-		Лебейюн.,.	3,7
1 4“И i Габбро		Радаутале, возле Гарц-
1		бурга..	3,0
i Диабаз		Гогенберг (округ Шмаль-
1		кальден).	0,5
1 Лимбургит (ба-		Лихтенау.	0,4
! зальт)
i Полевошпатный		Локопф, возле Ремагена	0,6
! базальт
! Полевошпатный		Нидердрессельндорф.	0,4
1 базальт
! Известняковый		Габельшвердт.	2,2
песчаник
• Кварцевый пес-		Шмалькальден.	14,6
чаник
Вогезский пес-		Плэн, возле Шатпенэ.	9,7
! чаник
1 Глинистый ела-		Клейн-Блумберг в Нейе-
1 нец		тале..	1,9
; Грауваковый		Тальбекке, возле Гум-
, песчаник		мерсбаха (Рейн).	0,6

Фигура 1.

обладают С., значения которой! заключены в довольно узких пределах, которые могут расширяться только при существенно осложненном строении этих тел. В виду большого значения тел пылевидной структуры как для жизни природы, так и для промышленности необходимо остановиться на С. подобных систем особо. Простейшим примером подобных систем может служить та, в которой отдельности тождественны по форме и размерам и притом б. или м. шарообразны. Крайние случаи С., то есть наибольшего и наименьшего значения ее, соответствуют двум правильным или однородным распределениям шаров—ортогональному (фигура 1) и диагональному (фигура 2). В первом случае шары распределены по направлению каждой из трех взаимноперпендикулярных осей,т.ч. каждый из шаров находится в вершине куба с ребром, равным 2; при этом ортогональном расположении С. составляет 47,64%. Во втором случае каждый из шаров находится на вершине тетраэдра с ребрами, равными двум; при этом диагональном расположении скважность равняется 25,95%. При распределении неоднородном и в частности при статистически беспорядочном значение С. для системы из равных шаров лежит в промежутке между 25,95 и 47,64%. В нек-рых

Фигура 2.

случаях более удобно пользоваться соответственными значениями т. н. приведенной скважности, то есть отношением объёма пор к объёму твердой массы; предельные значения приведенной пористости будут соответственно 0,3503 и 0,9098. С. S. Slichter (1899) нашел, что С. Р однородного скопления шаров выражается следующим образом:

Р=1---₇—__, (I)

6 (1-COS φ) У 1 + 2 COS ψ

где ψ — угол между сторонами параллелепипеда при правильном распределении шаров. С. скопления неправильных тел приблизительно м. б. вычислена на основании предыдущих ф-л, поскольку форма их может более или менее приравниваться к шарообразной. Если кроме того элементы подобного скопления между собою не равны, то вычисление С. еще более затрудняется. Во всяком случае очевидна возможность понижения С. при сочетании в надлежащем соотношении частиц нескольких размеров, причем самые размеры тоже должен быть в определенных соотношениях между собою. Если число калибров подобных частиц м. б. сколь угодно увеличиваемо, то, принципиально (геометрически) говоря, С. м. б. приближаема к нулю, как угодно близко. О нек-рых подробностях в отношении С. зернистых смесей см. Наполнители.

Если частицы порошкообразного или зернистого тела не слишком малы и тяжесть каждой из них достаточно велика, чтобы при ссыпании или осаждении преодолеть трение и слипание с другими частицами, то они располагаются подобно рассмотренным шарам более (фигура 3) или менее (фигура 4) рыхло; поэтому скважность

с>иг. Фигура 4.

песка, гравия и подобных тел никогда не превосходит 50%, а приведенная С. 1,0, то есть наибольшего теоретически возможного значения. Наоборот, при малости ссыпаемых или осаждающихся частиц они могут удерживаться трением в тех местах, где впервые прикоснутся к частицам, осевшим раньше (фигура 5, где 1— жидкость, 2—падающие частицы, 3—поверхность осадка); тогда строение полученного тела будет губчатым (фигура 6) с наибольшей приведенной пористостью, как показывает опыт, ок. 4 (то есть 80 %).

Наконец частицы коллоидного размера вследствие броуновского движения вовсе не осаждаются, пока тем или другим способом не вызвана их коагуляция. Тогда в коллоидной среде образуются губчатые хлопья со строением, подобным описанному; приобретая бблыний вес, они теперь уже осаждаются подобно отдельным зернам и образуют собою губчатое скопление (фигура 7) с губчатым строением второго порядка.

Так как наибольшая приведенная скважность простой губчатой структуры равна 4, то приведенная *С. такой же структуры второго порядка должен быть 4², или 16, что соответствует С.

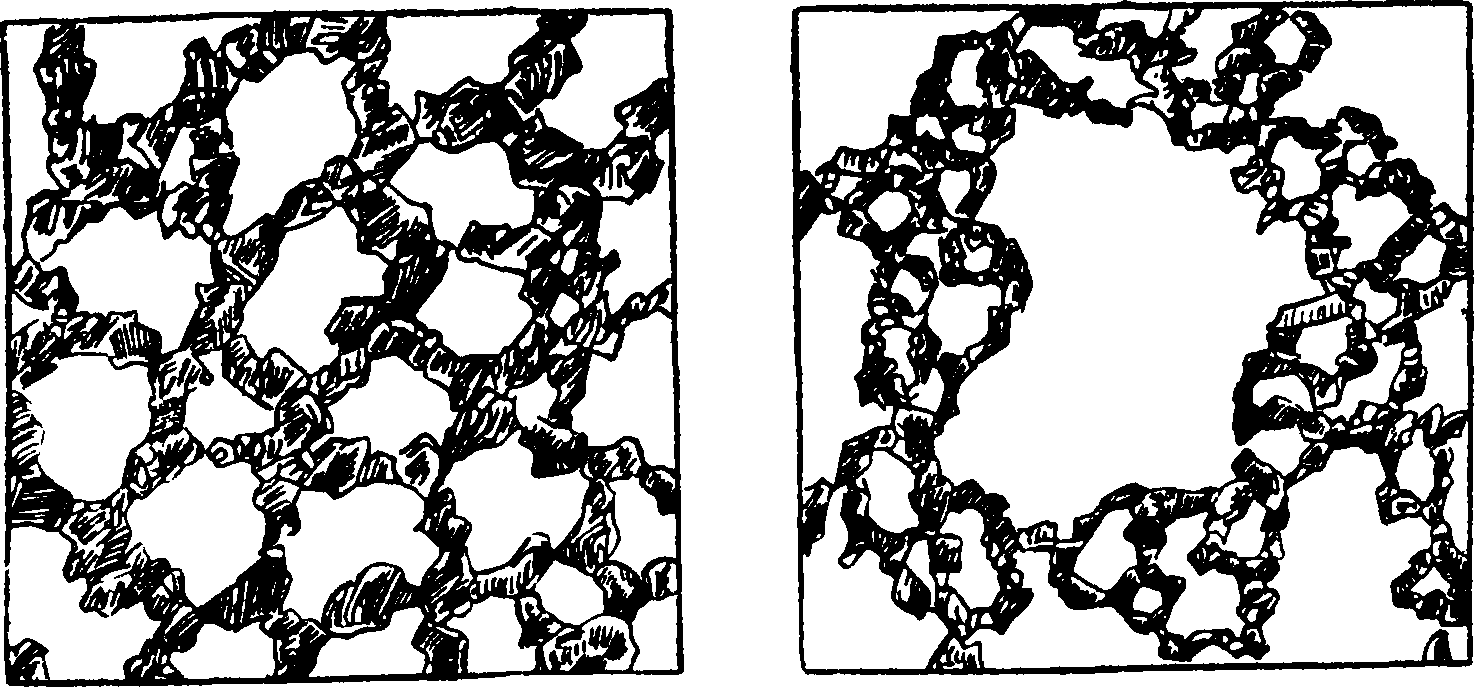
Фигура 6. Фигура 7.

в 94%. Опыт показывает, что мелкие порошки даже при усиленном встряхивании нельзя довести до плотности, свойственной более крупнозернистым скоплениям того же вещества.

Приводим несколько характерных данных об объёмной пористости (в %) нек-рьтх грунтов в естественном состоянии: смесь песка и гравия в равных количествах

23.1— 28,9; песок 35,6—40,8; гравий 38,4—40.1; суглинок

36.2— 42,5; суглинок, содержащий органич. вещество, 52,7; болотистая почва с 82% органич. вещества 84,0. Согласно данным Пифке гравий из ледниковых отложений обладал пористостью 24%, крупные пески *30 % и мелкие пески 33%. В табл. 7 представлена зависимость

Таблица 7. — Значение пористости для сыпучих пород разного диаметра.

Порода	Диам. зерна в миллиметров	Объемная пористость в %
		*1	*2
Мелкий песок.	<0,3	55,5	41,87
Средний ».	0,8—1,0	55,5	40,64
Крупный ».	1,0—2,0	37,9	37,38
Мелкий гравий.	2,0—4,0	37,9	35,47
Средний ».	4,0—7,0	37,9	35,93
Крупный ».	7,0—20,0	-	35,24

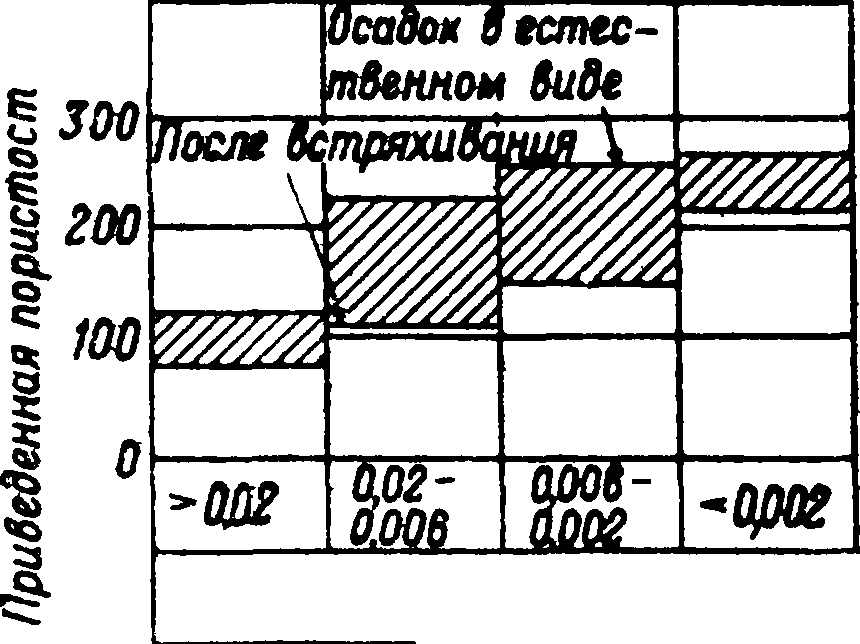
•i По Репку. *2 до Величковскому. пористости от 0 зерна. На фигуре 8 показано по К. Тер-цаги возрастание С. песка и глины с уменьшением зерна. На указанном явлении основано в частности определение величины зерна различных порошков, например красочных пигментов, серы и т. д., с помощью сульфури-метра. Сульфуриметр Шанселя (прибор, первоначально предназначавшийся для измерения зерен серы, применяемой для опыления ви- ?000г иоградпиков) состоит из цилиндрической стеклянной трубки 33 сантиметров длиною и 15 миллиметров диам., запаянной снизу и снабженной притертой пробкой сверху

1900

то

** 400

		Ш ж
	г— —	ГГ ^ is _о _ 8-1
	1Ш1
		II
		|!
0,02-Шй-	ЩЮ6- ш	-α002

Размер зерен в миллиметров.

Песон

Желтая осадочная глина

Фиг.

(фигура 9). Начиная от основания, трубка подразделена на 190 делений, каждое по ι/₄ см³, причем 100 делений (25 см³) занимают длину 100 миллиметров. Если порошкообразную серу встряхнуть с эфиром, то при оставлении взвеси в покое образуется слой, высота которого стоит в определенном отношении к тонкости помола. Для испытания серы она просеивается через сито с петлями в 1 миллиметров для освобождения от комьев. Затем 5 г взвеси помещают в сульфуриметр, наливают в него до половины эфир, безводный и по возможности при 17,5°, сильным встряхиванием разбивают комья, доливают эфиром на 1 сантиметров выше деления 100, снова встряхивают прибор и ставят отвесно. Число делений, до которого достигает верхний край осадившейся серы, дает тонкость в градусах Шанселя. Обычная размолотая сера показывает t° 50—55°, сера более тонкого помола, т. н. Zoifo maeinato, 70—75° и Zolfo ventilato 90—95°, причем в виноградном деле требуется не менее 60° и даже до 75°. У подобного же прибора системы Грейнера длина трубки до деления 100 равна 175 миллиметров, длина между делениями от 10 до 100° равна 154 миллиметров, внутренний диаметр равен ^βψφ 12,68 миллиметров. При испытании надлежит пользоваться эфиром, перегнанным над натрием, а прибор удер- i живать штативом и погружать его в воду при l 17,5°. Необходимо учитывать искажающее дей- ~ !

ствие всяких загрязнений. Так, 2%таннинаили j; _. -углекислого кальция повышают показания на 1ΓΛΙ 7—8°; 2% мыла снижают его на 40°; 0,4% биту- з мена снижают на 46°. _т

Водопроницаемость сы пуч и х тел. Большинство физико-химич. явлений в скважистых телах существенно связано с нахождением в их скважинах и

прохождением через таковые различных жидкостей и в особенности влаги. Вообще говоря, влага в подобных телах присутствует наряду с газами, в частности и в особенности—с воздухом, и это в связи с эффектом Жамена и эффектом Эвер-шеда делает возникающие здесь явления особенно сложными (смотрите Волокнистые изоляционные материалы). Проще всего обстоит дело, когда газы б. или м. отсутствуют; тут следует различать три типич

ных случая: 1) заполненность всех скважин неподвижной влагой, удерживаемой от полного или частичного ухода внешним препятствием;

2) поднятие влаги, засасываемой в сыпучие тела капиллярными силами; 3) протекание воды под напором через подобное тело. При пассивном пребывании в скважинах землистого тела неподвижной влаги количественное содержание ее определяется значением С. и легко может быть подсчитано. Физические свойства подобной системы—электрич., тепловые, акустич. и т. д.—существенно меняются. Подсчет их по соответственным свойствам твердой и жидкой фаз м. б. производим на основании ф-л смешения (смотрите Пластические массы и Наполнители). Капиллярное поднятие жидкостей м. б. вычислено в случае однородно расположенных шаров радиуса R по формуле Дж. Инабы (1928 год):

, SnR^a COS φ

¹ ~ dgtfv-inR³) ’ W

где h—высота поднятия, v—объём, приходящийся в теле на каждый из шаров, φ—угол соприкосновения между жидкостью и поверхностью шаров, о—поверхностное натяжение на границе жидкой и твердой фаз, <5—плотность жидкости и g—ускорение силы тяжести. Формула (2) м. б. представлена в виде

Atfcos? dgR~

(3)

где И=2,198 и 5,706 для ортогонального и диагонального расположения шаров соответственно. Эквивалентный радиус скважин г, то есть радиус капиллярной трубки из того же вещества, что и рассматриваемые шары, м. б. выражен соотношением

3v-4tnR³

“~4тгЁ2~

(4)

или

Г

3k — 4π 4π

(5>

где к определяется из соотношения v=kR³. Указанные величины получают значения в соответствии с табл. 8. Во избежание недоразумений должен быть особо отмечено, что эквивалентный радиус капиллярности не тождественен экви-

Таблица 8. — Частные значения некоторых величин в формулах.

ί Расположение	А	к	г
| Ортогональное.	2,198	8	0,910
1 Диагональное.	5,706	4Ϋ2	0,351

валентному радиусу С., а также другим видам эквивалентных радиусов — водопроницаемости, воздухопроницаемости, электропроводности и т. д. При наличии равномерно перемешанных шаров различных радиусов, расположенных однородно, но уже не в смысле упорядоченности, а, напротив, в смысле статистич. беспорядочности:

h

2Fa COS φ.

-G) ^!

.(6)

G =

3(50(1-

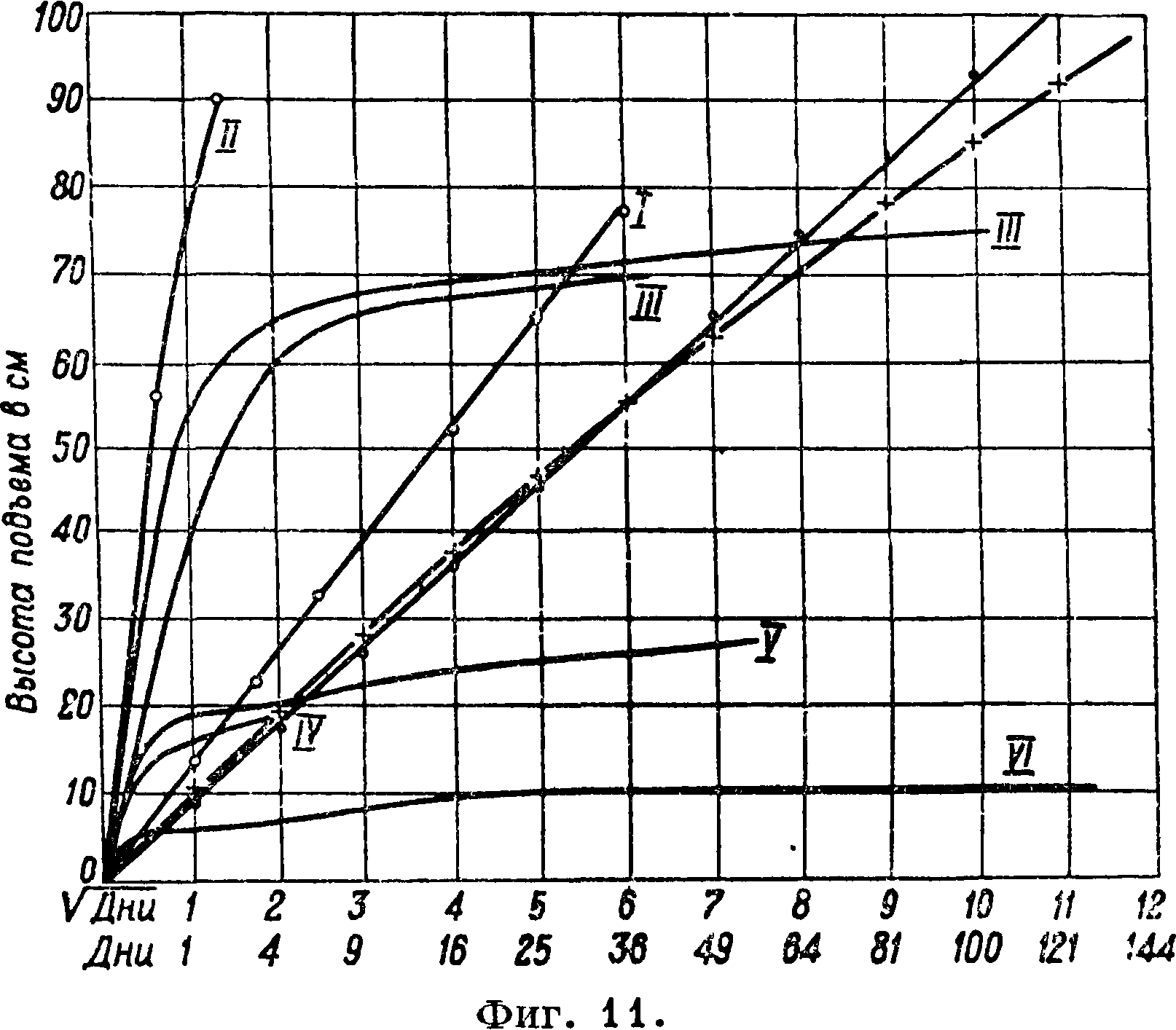
здесь F=4π (R₁N₁^Jr R₂N₂ + R_SN_Z .), a=⁴/₃ n(R*N% + R$N% + R%Nl ···), причем N_l9N₂, N_z и T. д. представляют собою числа содержащихся в единице объёма тела шаров радиуса Р_1? R₂, Р₃ и т. д. соответственно. Понятно, что значения величин F и G, а потому и значение h, зависят от расположения шаров. Как показали опыты Дж. Инабы, кварцевый песок, рассеянный на фракции различных размеров зерна, дал высоту капиллярного поднятия, среднюю между теоретически вычисленной для ортогональной и для диагональной систем, при отождествлении зерен песка с шариками соответственного диам. На фигуре 10 кривая 1 построена по вычисленным значениям капиллярного поднятия для ортогональной шаровой системы, кривая 2—то же для диагональной системы, а кривые А и В—экспериментальные кривые, полученные с различными фракциями корейских кварцевых песков, очищенных хромовой смесью и всыпанных в трубки единообразным механизированным приемом. Процессы капиллярного движения воды в грунте очень запутаны и до настоящего времени не выяснены еще даже приблизительно. Считают установленным лишь, что,чем мельче капиллярные скважины, тем выше поднимается вода и тем медленнее идет подъем (из-за ^внутреннего сопротивления). Особенно сильно удерживает и воспринимает воду лёсс. Наибольшая скорость в песке получается по Келлеру при величине зерен между 0,05 и 0,1 миллиметров. Напротив, при диам. зерен 2,2—2,5 капиллярное действие прекращается. В песке из зерен <0,3 миллиметров (46—50%) и 1,0—0,3 миллиметров (50—54%) высота капиллярного подъема по Гребе не превышает 33 см, а при мелком песке (зерен <0,33 миллиметров, 80%) не превышает 50 см. На фигуре 11 показана по данным Эдлера постепенность подъема воды для грунтов разной мелкости, причем абсциссою служат корни квадратные из времени подъема, а ординатою—высота подъема. Значения кривых таково: I—зерна диам.< 0,01 миллиметров, II—зерна 0,01—0,05, III—зерна 0,05—

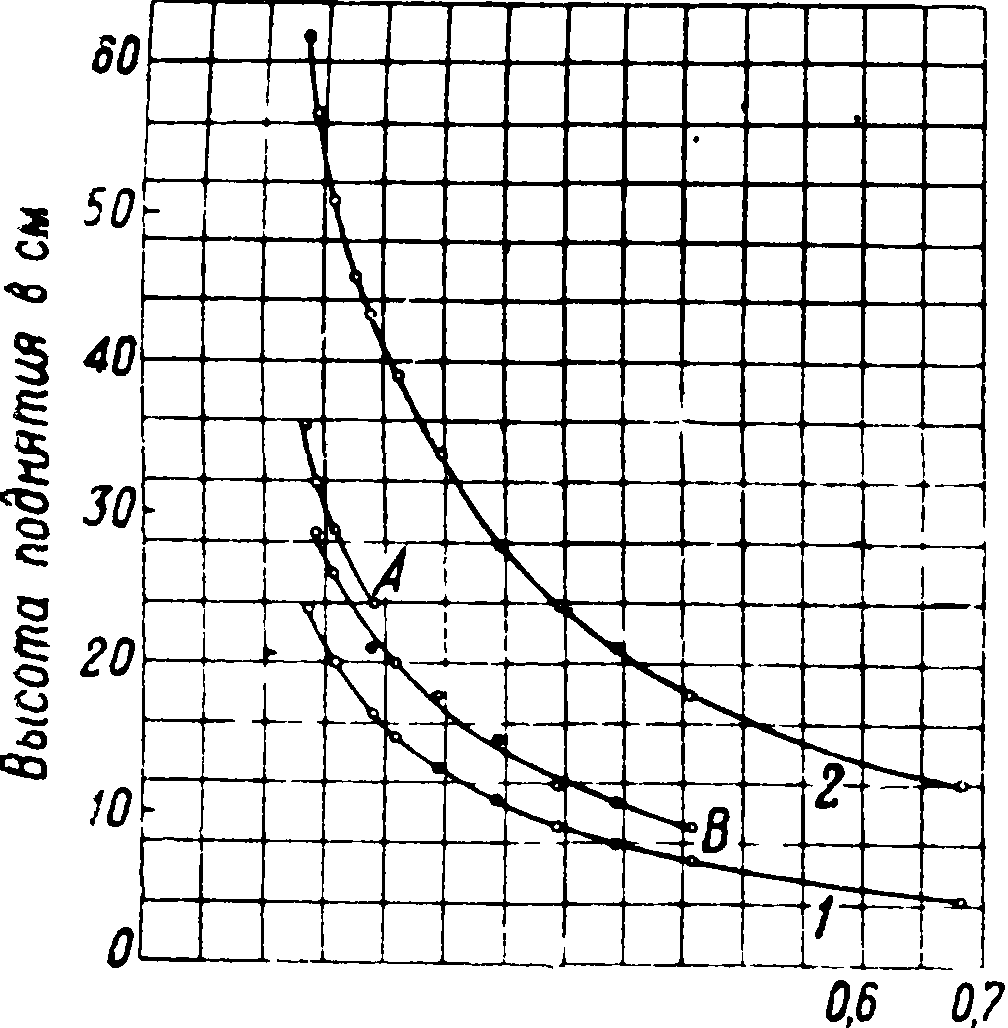
0,2 0.3 0,4 03

Размер зерен в миллиметров Фигура 10.

0,10, IV — зерна 0,10—0,25 миллиметров, V — зерна 0,25—0,50 миллиметров, VI—зерна 0,50—1,00 миллиметров. Высота подъема зависит от t° (уменьшается с повышением t°). Кроме того она зависит также от степени наличной почвенной влажности; так наир., по Бриггсу и Лафану высота капиллярного подъема в сухом песке оказалась 37 см, а в сыром—167 см.

Наряду с капиллярным движением по вертикали в почве наблюдается движение по гори

зонтальному направлению или наклонному. Существуют различные способы измерения скорости горизонтального движения: наблюдение над естественно возникающими или искусственно созданными волнами грунтовых вод, введение в воды поваренной соли (способ Тима), введение хлористого аммония (способ Сляйтера) с проверкою по проводимости воды, введение различных красящих веществ и в частности флуоресцеина, затем введение бактерий, пивных дрожжей и т. д. Числовые значения полученных; скоростей весьма различны и колеблются в пределах от 0,3 до 9,3 м/сутки и даже до 15,9 мIсутки; однако наиболее обычные значения этой скорости 1—3 м/сутки. Водопроницаемость зернистых тел численно характеризуется коэф-том к в формуле Дарси (Darcy):

Q=kSE, (7)

где Q — расход воды в ск., протекающей параллельными струями через водопроницаемое тело призматич. формы, S—площадь поперечного сечения тела и Е—гидравлич. градиент, равный отношению потери напора к расстоянию (h/l). Коэф. водопроницаемости к представляет скорость просачивания через единицу площади при гидравлич. градиенте, равном единице; размерность его равна см^-ск^-1. Закон Дарси действителен для движения воды в мелких и средних песках при средних значениях напора, ио неприменим к движению воды в крупном гравии и, как полагают нек-рые, также и в глинах. Значение к зависит от плотности распределения зерен и от их размера. Сляйтер теоретически вычислил к в предположении частиц шарообразных диам. R (в см} и дал ф-лу:

λ-= 3 084 —· (8)

С

Значение с зависит от расположения шаров и связано со С. и вязкостью жидкости Р и приведенной С., что видно из таблицы 9. Теоретическое соотношение между плотностью подобного тела и его водопроницаемостью доста-

Таблица 9. — Значение с в зависимости от расположенияшаров.

! Скважность Р { В % 1	Приведенная скважность	Значение с при t° 10°
1 1 ! 26	0,352	84,30
! 28	0,388	65,90
30	0,428	52,50
1 34	0,515	34,70
; 38	0,612	24,10
42	0,723	17,30
1 46	0,850	12,80

точно хорошо подтверждается опытной проверкой А. Газена на песке. Но значение ft для рыхлого песка оказывается 464/7^ и даже 600R²ef, если зерна приблизительно одного радиуса (тут R_ef—эффективный радиус по А. Газену, то есть радиус таких зерен, меньше которых в данном грунте по весу содержится 10%, тогда как теоретически наибольшее значение ft, то есть при 46% С., получается 241,2й^. Это расхождение объясняется неоднородностью скважин в песке. Границы, в пределах которых эффективный радиус песка может служить мерилом коэфициен-та водонепроницаемости, устанавливается при помощи особой характеристики песка, называемой коэф-том неоднородности. Этот последний определяется как дробь, знаменателем которой служит эффективный диаметр песка, а числителем—диам. таких зерен, что большие из них по размерам составляют 40% данного песка. Напр., если в песке 40% зерен крупнее 0,5 миллиметров поперечником и 10 %—мельче 0,25 миллиметров, то коэф. неоднородности будет 0,50:0,25=2,00. Чем больше этот коэф., тем неоднороднее песок, а при коэф-те неоднородности 1 величина зерен совершенно одинакова. По А. Газену коэф. проницаемости ft может выражаться через эффективный диам. при коэф-те неоднородности не выше 5. Необходимо также иметь в виду зависимость коэф-та проницаемости от характера распределения зерен и от формы их. Значение ft для нек-рых сыпучих пород показано в таблице 10.

Таблица 10.—Значение коэфициента проницаемости.

Наименование сыпучей породы	Диам. зерна в миллиметров	Коэф. проницаемости в м/сп
Дюнный песок из Голландии.	_	0,0002
1 о же со следами глины.	—	0,0008
Речной песок..	0,1—0,3	0,0025
» » ..	0,1—0,8	0,0088
Фильтровальный песок (Гам		0,0077
бург) ..	—
Мелкий гравий..	2,04—4,0	0,0330
Средний гравий.	4,0—7,0	0,0351
Искусственная смесь Дарси из зеоен 0,77 миллиметров 58%, i, 10 миллиметров
1 13%, 2,ои миллиметров 12%, гравия 17% !	~	0,0003

К. Терцаги дал для коэф-та водопроницаемости полуэмпирич. ф-лу:

к= - — /’-S—°’--J ²4β|_/-, (9)

^{40 чг} [у τ^ηΐ ^r

где % и r_tt—значения вязкости воды при 10° и при темп-ре t соответственно; п—приведенная пористость;с—эмпирич. коэф.,зависящий отчасти от степени однородности зерен песка и в особенности от их формы, значение которого изменяется в пределах от 800?;₀ (у песков с округлыми и гладкими зернами) и до 460//₀ (у песков с зернами неправильной формы и шероховатыми).

При помощи ф-лы Терцаги получается приведенный коэф. водопроницаемости, то есть отнесенный к пористости 50% (приведенная пористость 1) и к нормальной t° 10°, следовательно устанавливающий зависимость водопроницаемости грунта от формы зерен и их однородности. Ф-ла Терцаги в промежутке значений пористости от 26% до 47,6% (то есть 0,352 и 0,905 приведенной пористости) дает кривую водопроницаемости, весьма близко совпадающую с кривой Сляйтера. Но необходимо иметь в виду, что формула Терцаги остается действительной только для песка совершенно чистого и что даже ничтожная примесь глины делает эту формулу непригодной; равным образом результаты вычислений искажаются при наличии пузырьков воздуха. Искажающее действие глины объясняется формою ее частиц—весьма тонких и гибких минеральных чешуек, тогда как зерна песка жестки и б. или м. округлы (смотрите Пластичность); поэтому капиллярные каналы в песке обладают сечением, приближающимся к кругу, а капилляры в глине подобны щелям и притом непостоянного просвета. Терцаги дал для порошков из чешуеобразных зерен ф-лу, соответственную формуле (9), а именно:

Фигура 12.

* - ^ + в)4Л·, (10)

где е—приведенная пористость. Проверка ф-л (9) и (10) и установление их эмпирич. коэф-тов м. б. достигнуты путем установления зависимости между пористостью и коэфициентом водопроницаемости. При подобном испытании может применяться прибор Е. Принца (фигура 12) для почвы, добытой из буровой скважины, а также приборы Терцаги (фигура 13—для ¹ песка и фигура 14—для глины). В приборе Принца проба загружается возможно плотно в цилиндр 1, замкнутый ситом 2. Высота фильтрующего пласта должна равняться приблизительно 1 метров Вода наливается сверху и постоянство уровней поддерживается краном 3, сифоном и стоком 4. Фильтрующий пласт делится на 3—4 равные части, обладающие одинаковым сопротивлением. Давление в соответственных местах устанавливается по водомерным трубкам 5, снабженным миллиметровыми шкалами с нониусом.

Для удаления воздуха у тубусов, к которым присоединяются водомерные трубки, должен быть особое приспособление, трубки должен быть предохранены от засорения песком посредством пробок из ткани или ваты. Прибор Терцаги (фигура 13) для испытания песка представляет цилиндрич. фильтр, в к-ром песок 1 насыпается в латунную сетку. Вода может пропускаться как снизу вверх, так и наоборот; последнее особенно удобно. Потеря напора измеряется градуированной трубкой, находящейся под проволочной сеткой. При производстве опыта отмечается: площадь сечения и толщина слоя песка, способ его подготовки (рыхлый, встряхнутый, утрамбованный), пористость, средний уд. вес зерен, Г, механич. анализ песка, эффективный радиус зерен, их

.

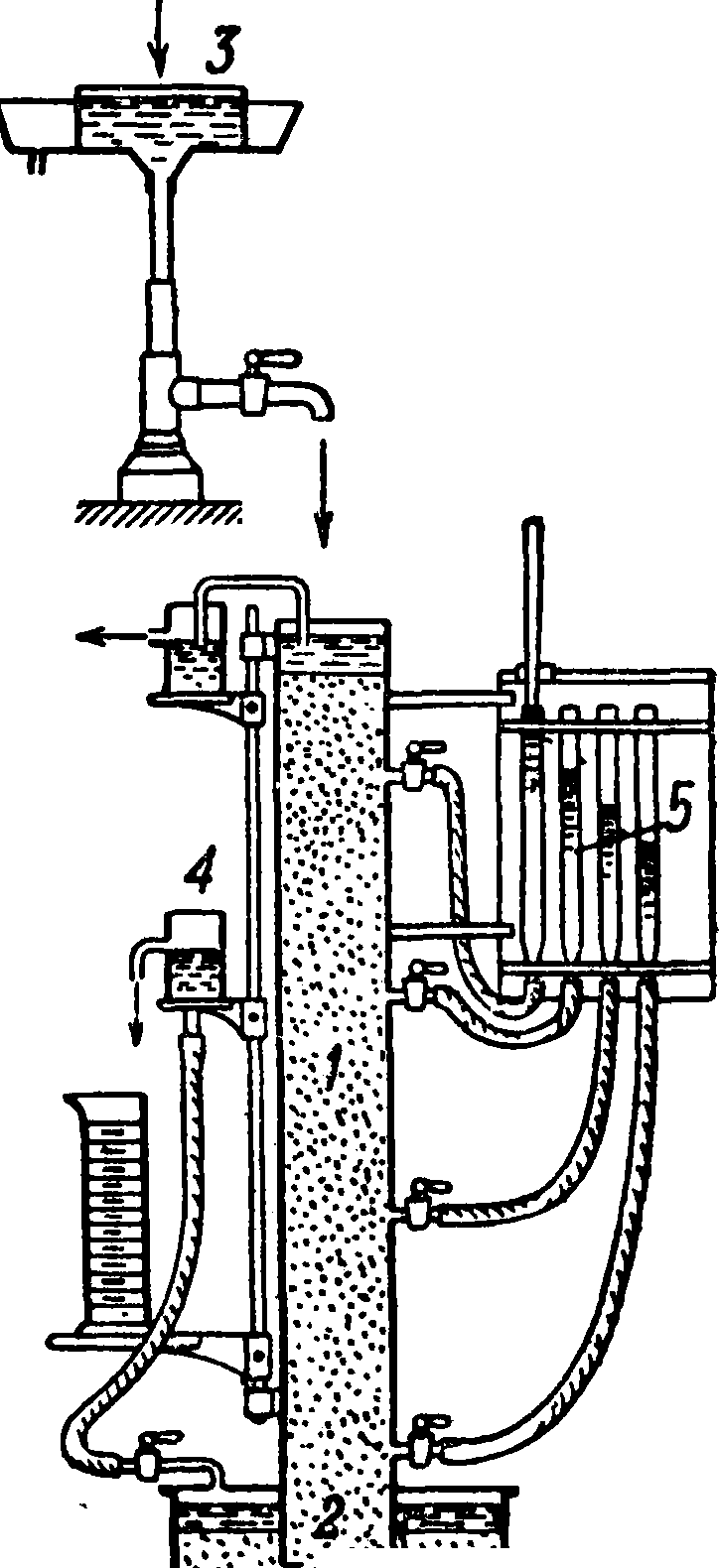
форма, количество профильтрованной воды и потеря напора. Прибор для испытания глины (фигура 14) состоит из сосуда, на внутренних Еысту-пах которого лежит дырчатая бронзовая пластиа-ка 1, прикрытая мелкой проволочной сеткой. На последнюю насыпается чистый кварцевый песок 2 (зерна 0,5 миллиметров) и затем кладется тонкий лист фильтровальной бумаги. На песок накладывается кольцо, заполненное на высоту 2,0 сантиметров пластичной жидкой глиной 5, и притягивается к сосуду с помощью другого кольца и болтов. На верхнюю поверхность глины накладывается фильтровальная бумага и затем песок 4. Заполненное водою пространство ниже дырчатой бронзовой пластинки сообщается с трубкой высотою 10 сантиметров и диам. 0,6 см. Вертикальная трубка заполнится водою, когда будет достигнуто равновесие глины и наложенного на нее груза. По скорости понижения уровня в трубке (наблюдения делаются трижды в день) вычисляется коэф. водопроницаемости. Опыты ведутся при нагрузках0,75, 1,6 и 24 килограмма/см², причем на опыт требуется 28—42 дня; требуется большое постоянство температуры, подливание воды в кольцевое пространство (в виду испарения и определения влажности в каждом из образцов глины

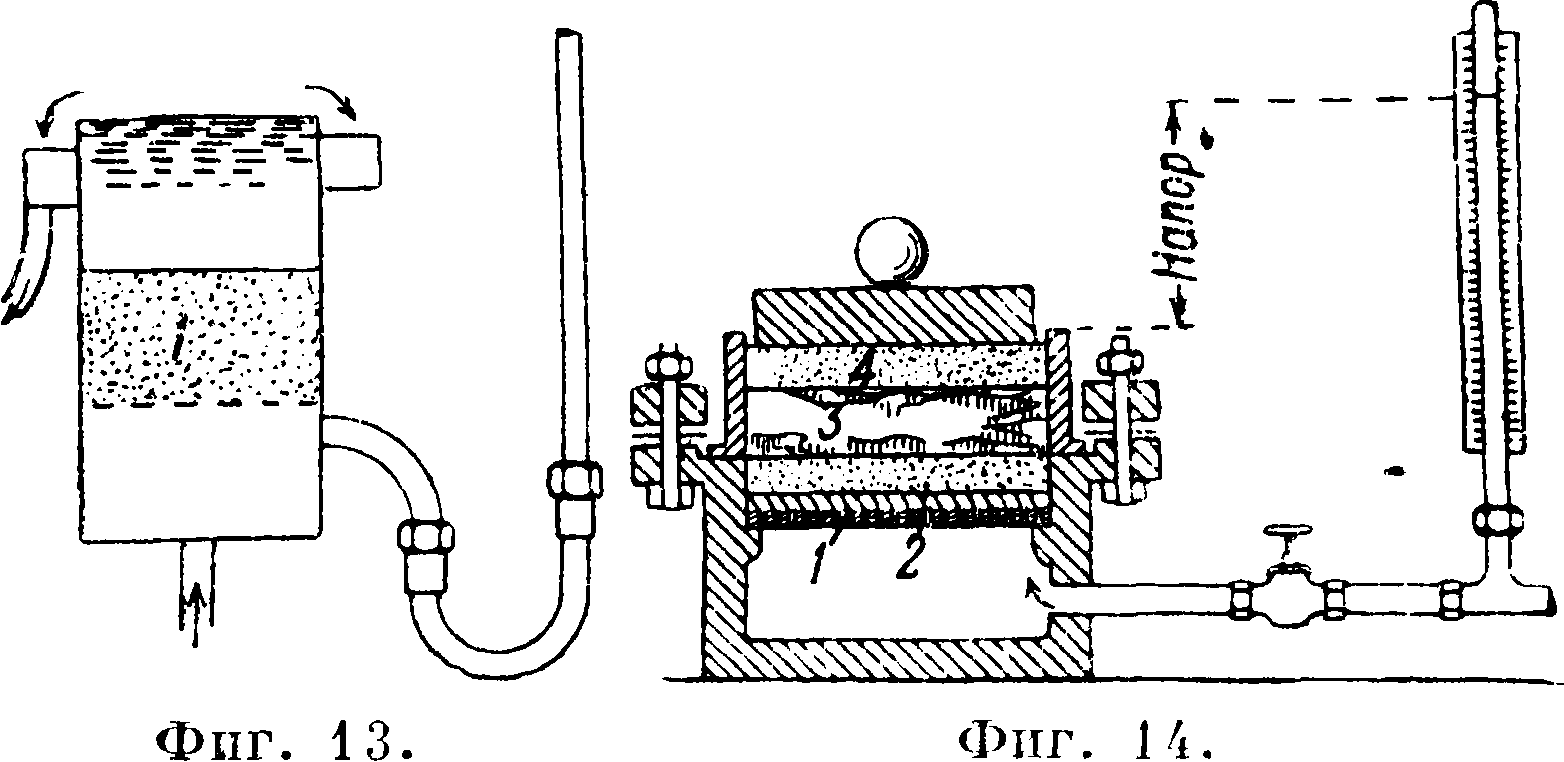
по окончании опыта). Как показали опыты, в пределах пластичности и в состоянии полутвердом глина подчиняется закону Дарси; напротив, полужидкие глины обнаруживают коэфи-циент водопроницаемости, уменьшающийся при уменьшении гидравлического градиента от 50 до 15—10 и принимающий постоянное значение лишь при малых напорах. Эта особенность стоит в связи с весьма большой рыхлостью полужидкой глины (приведенная пористость 2, тогда как для шаров она не более 0,91), то есть с с от о-о б р а з н Ым строением (фигура 6), т. ч. средний размер капилляров значительно превышает средний диам. частиц. Эти последние удерживаются на своих положениях начальным трением (по Терцаги не менее КГ⁶ дин на каждое соприкосновение между двумя частицами) и потому при значительном напоре воды подвергаются упругим и неупругим деформациям и перемещениям; в соответствии с этим изменяются размеры каналов и, значит, значение коэфици-ента водопроницаемости; лишь при весьма малом гидростатич. давлении исчезают упругие деформации, и коэфициент водопроницаемости устанавливается. Прохождение воды через полужидкую глину можно поэтому сравнить с потоком воды через систему тонких, очень упругих резиновых трубок. При чрезвычайной тонкости каналов у глины в состоянии пластичном (порядка 0,1 μ) необходимо учитывать изменение в них вязкости воды, из »;₀ в η₀, согласно формуле Терцаги:

^=%(ΐ + “₈). (11)

где г—радиус тонкого канала, а а—постоянная, содержащаяся в пределах 6- 1СГ⁴² и 2· 10~⁴³.

В виду сделанного указания Терцаги дает исправленную формулу для коэф-та водопроницаемости глины, а именно:

j,_ ^с Vo (в — 0,15)¹¹ (1 Ч~б) ^ ^2 (Т*Н

‘ ~ ^ « V— 0,15)·+4- ^tf

Rif

Зависимость строения глины от содержания в ней влажности (в противоположность песку, к-рый не набухает и геометрия которого от влажности следовательно не зависит) ведет к требованию характеризовать водопроницаемость глинистых грунтов не одним числом, а кривой, дающей водопроницаемость, как ф-ию влажности. Кроме того в отношении глин необходимо также учитывать адсорбционные явления, ведущие к сужению каналов и к постепенному снижению водопроницаемости.

Измерение С. Согласно общему определению, значение С., или пористости, как суммы всех полостей тела, отнесенной к объёму тела, меняется в соответствии со способом испытания и потому у одного и того же тела м. б. оценено весьма различно. Однако существует испытание, особенно распространенное и относящееся преимущественно к грубой С., доступной непосредственному наблюдению, то есть состоящей из макроскопич. и отчасти микроскопии, пор. Эта С. измеряется количеством жидкости, которую в состоянии воспринять в себя тело; так как в естественных условиях поглощаемою жидкостью бывает преимущественно вода, то этот вид С. называют также в л а г о- или в о д о-емкостью (Wasseraufnahmefaiiigkeit). При этом должен быть сделана оговорка, что порами, или скважинами, в материалах считают те полости, возникновение которых лежит в природе материала или его переработки, а также пороки, обусловленные длительно существующими способами производства или намеренно производимые, вообще те, которые составляют регулярно повторяющуюся нормальную характеристику данного материала; напротив, все случайные и нерегулярно повторяющиеся полости, как например в керамич. черепе—от обожженных кусков серного колчедана, марказита, обломков гипса, кусочков дерева, треснувших швов, трещин обжига и т. д., не должны входить в характеристику С. Количество поглощенной воды по массе и по объёму выражается одним и тем же числом, но отношение его к массе или к объёму поглощающего тела даст числа не тождественные, зависящие от уд. в самого черепа (табл. 11). Для практики важно как водопогло-

Т а б л. 11 .—П рим ер несовпадения объёмной пористости с весовою (по Г. Людвигу).

	Образец керамич.
Сопоставляемые величины	черепа
	I	II
Вес сухого образца в г.	100	200
» напит, водой образца в г.	120	240
Пористость по весу в %.	20	20
Объемный вес ..	2	3
Объем в слез ..	50	66,67 1
Пористость по объёму в %.	40	60

щение по массе (по весу) W_д, так и водопогло-щение по объёму W_v, причем первое особенно наглядно характеризует различные молекулярные процессы в теле, а второе—строение тела. Если объём насыщенного водою тела (так называемым кажущийся объём) обозначать через V_w, массу сухого тела—через G_t и наконец массу насыщенного водою тела через G_Wi то водопо-

глощение по массе, то есть число г воды в 100 г насыщенного водою тела,

TXT __ Gf) ¹⁰⁰ O” /104

”ΰ- GTr ^/0* ^(L;)

Водопоглощение по объёму, т. e. число см³ воды в 100 см³ тела (со включением пор),

w - (Sw-67)100 О,

^1У ~ V

У w

(14)

Нередко вместо воды берут другие жидкости, уд. в S₈, например: керосин, этиловый, четыреххлористый углерод, минеральное масло п другие. Пусть масса насыщенного ей тела G_s и кажущийся объём после насыщения F_e, тогда водопоглощение по массе

jj (G_s — G/) 100

bs-Gt

водопоглощение по объёму ш ___ (G_s-Gt)m S₈-V_s

о /о»	(15)
о /о“	(16)

При указанных способах испытания на учет берутся лишь открытые поры, тогда как замкнутые, во многих случаях тоже представляющие большую важность (например при выяснении усадки тела, его электрич. свойств и т. д.), оказываются не учтенными. Поэтому абсолютная пористость тела измеряется после обращения егр в порошок пикнометрически. Р^сли S— истинный уд. в испытуемого тела, то истинный объём тела V будет:

V=^G/

s

(1?)

Пусть далее кажущийся объём тела, то есть с включением пор, есть V_r, тогда абсолютная пористость тела по объёму будет:

· 100%=(1 - X) 1С0% (18)

ИЛИ

s^C"^: 100%=(l -_>fT^Gy) · 100%. (19)

П соответственно по массе:

v_rzv

G_r

G_t

100%

(£-0

Gt

100% -

ν,(ι-Χ)

= ~~gJ~ 1°°% >

Gt V_rS_ _t

— · 100%=· 100% =

_G±

SVy

Gt

100%_.

(20)

(21)

При испытании на пористость необходимо учитывать, что неполное насыщение водою открытых пор необходимо поведет к выводу о ложном избытке замкнутых. Поэтому на тщательность пропитки обращается постепенно все большее внимание. Так например, до постановления Берлинской конференции 20 сентября 1890 г. и даже после нее влагоемкость керамич. черепа определялась посредством сушки при 30°, последующего 24-часового частичного погружения в воду при комнатной t° и затем 24-часового полного погружения. По постановлению Берлинской конференции испытание должно вестись одновременно на десяти образцах. Пост (Chem. Techn. Analyse) рекомендует просушивать эти 10 образцов при 50° до постоянного веса -и затем следить за весом отчасти покрытых водою образцов, а затем вполне покрытых по прошествии 24, 72, 96 и 144 суток.

Такой способ пропитки не способен удалить из образца воздух. Поэтому было предложено пропитывать образец в течение J5—20 мин. под вакуумом. Согласно способу (применяемому на Герм, ф-ке камейного товара для канализации и химической пром-сти во Фридрихе-фельде в Бадене), введенному О. Гофманом, процесс пропитки ведется так: выбивают кусок 10x10 сантиметров (приставшие осколки должен быть тщательно удалены) и просушивают при 120° до постоянного веса. Тонкие соляные глазури, примерно до 5 миллиметров толщины черепа, не искажают результата, т. к. масса их слишком мала сравнительно с массою черепа. При более тонких черепах, особенно с толсто наложенными глазурями, шпатовыми, глиняными и другими искусственными глазурями, эти последние должны быть сбиты, сошлифованы и удалены песчаной струей (у всасывающих черепов—также травлением); у неглазуро-ванного товара с сравнительно коротким временем обжига (кирпич и т. и. материал) наружная корка обжига всегда более плотная, чем поверхностный плотный слой у товаров, изготовленных при сильном давлении (гидравлически отпрессованные пластины). Подготовленные, то есть просушенные, охлажденные в эксикаторе и взвешенные образцы погружаются примерно до половины в дистиллированную или хотя бы многократно вскипяченную бедную солями водопроводную воду и если они глазурованы, то в таком положении, чтобы глазурованная поверхность стояла вертикально (с целью устранить скопление воздуха под непроницаемым слоем глазури). Когда начавшееся сипение закончится, то практически достигнута граница свободно протекающего напитывания. Затем образец покрывается водою весь, чтобы избежать потери от испарения, вода нагревается до кипения, кипятится в течение часа и охлаждается; по прошествии 24 час. протертый полотенцем образец взвешивается, что при более точных работах делается в тарированном закрывающемся сосуде; получающаяся разность соответствует поглощению воды в г, при принятии во внимание уд. в насыщающей жидкости (измерять ί°!)—также в с.из, то есть объёму пор. Найденное значение выражается в весовых % и в объёмных %; для последнего случая должен быть определен кажущийся объём со включением объёма пор—у насыщенного одним из предписанных способов водою черепа, лучше всего в волюминометре. Особенными мерами предосторожности обставляется испытание плотных керамич. масс, применяемых в электротехнике высокого напряжения (смотрите Изоляторы электрические).

Влаговсасывающая способность и влагопроницаем ость. Под влаговсасывающей способностью (Wasseraufsaugever-rnogen) разумеется способность скважистых тел воспринимать при определенном напоре определенное количество влаги на единицу поверхности в единицу времени. Эта характеристика установлена в отношении керамич. материалов. Так например, согласно постановлению Берлинской конференции 20 сентября 1890 г. водовсасывание глиняных труб и кровельной черепицы при стандартных условиях должен быть порядка 20—25 см³. Значение этой характеристики зависит от толщины испытуемого образ ца, и потому сравнительные значения м. о. получены только при образцах равной толщины; однако приведение влаговсасывающей способности к 1 см³ не дает сравнимых результатов, поскольку пористость испытуемого тела (гл. обр. черепа) во внутренних слоях м. б. значительно больше, чем у поверхности—вследствие неравенства давлений при прессовке и образования корки обжига. Наряду с влаговсасы¹ вающей способностью у скважистых тел испытывается также влагопро-ницаемость, то есть способность пропускать через себя при определенном напоре определенное количество воды через еди-ницу поверхности за еди- ^w

ницу времени. Влаговсасывающая способность и влагопроницаемость измеряются при помощи прибора, изображенного на фигуре 15. Стеклянный цилиндр ок. 10 см² поперечного сечения (35 миллиметров диам.) герметически присоединяется

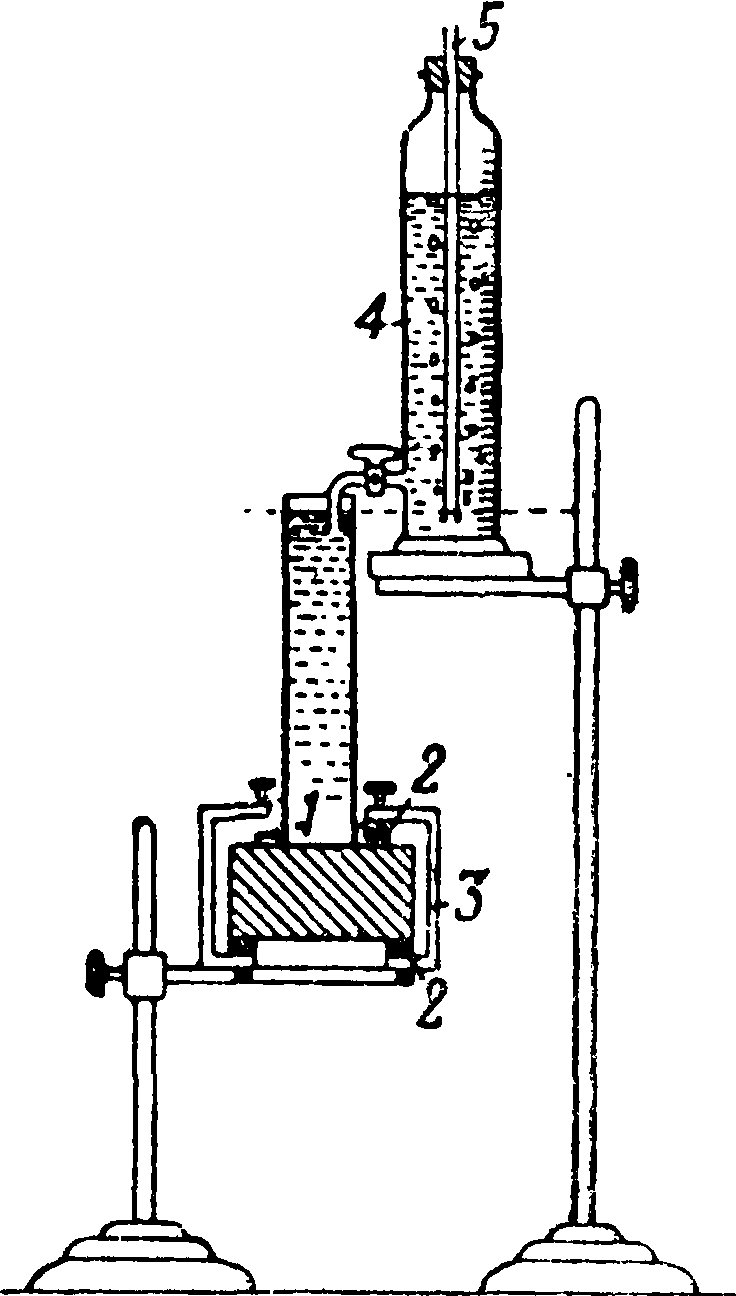
к испытуемому материалу (черепу размером 10 х×10 см), просушенному при 120° и свободному от глазури, причем вне цилиндра, за исключением поверхности такого же круга с противоположной стороны, все тело делается влагонепроницаемым и укрепляется так, чтобы нижняя поверхность его была доступна наблюдению. Герметичность присоединения достигается посредством примазки глицериновой мастикой и водонепроницаемого лака или же помощью резинового кольца 1, прижимаемого металлич. кольцами 2 и закрепляемого скобами 3. Затем в цилиндр вливается пипеткой 10 см³ воды, измеряется время всасывания ее, снова вливается 10—15 см^ъ, причем вода выступает на нижней поверхности, и наконец еще 10 cm^z, ведущие к образованию капель, для которых устанавливается время просачивания и соответственное количество воды. При другом способе испытания в цилиндр сразу вливается большое количество воды и по мере снижения ее уровня подливается вновь. Еще лучше вести испытание при постоянном давлении. Для этого высота вод. столба ок. 20 сантиметров (вливается 200 см^г) поддерживается на неизменной высоте при помощи мариоттова сосуда 4 (фигура 15, 16, 17, 18),

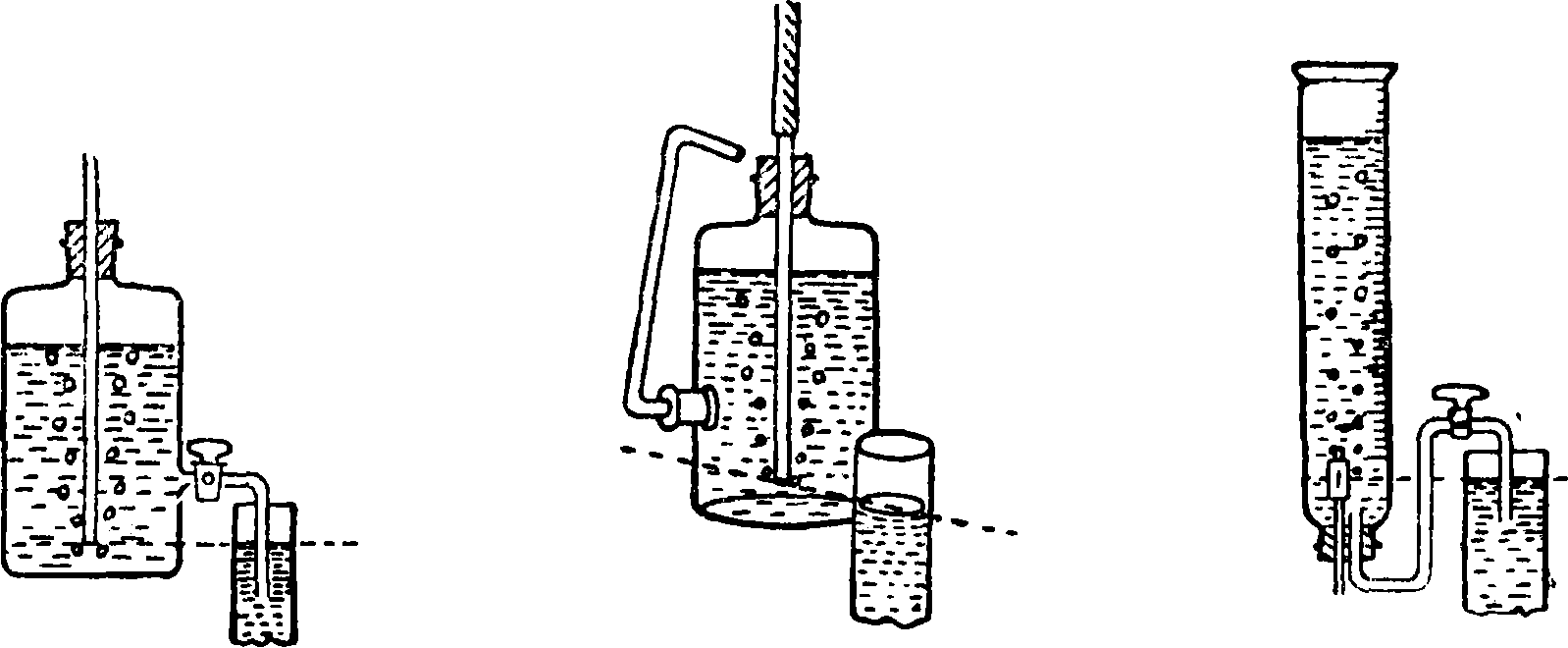
Фигура 16. Фигура 17. Фигура 18.

нижнее отверстие воздухоприводной трубки 5 которого должен быть на одном уровне с вод. столбом в цилиндре. Определяется время до появления выпота и росы на поверхности испытуемого тела и до образования капель, а также количество воды, просочившейся за определенное время; количество просочившейся воды м. б. определено в частности отсчетом потребленного количества ее (фигура 18). Если материал в условиях службы может находиться временами под внутренним давлением, то указанные испытания нужно вести в обоих направлениях,каждый раз на свежем или заново просушенном образце.

В отношении материала керамиковых труб представляет практический интерес преимущественно влагонепроницаемость водонасыщенного черепа и притом по обоим направлениям, а в отношении кровельной черепицы—водопроницаемость как сухого, так и влажного материала, но только в направлении просачивания. От нек-рых материалов проницаемость, напротив, требуется. Так наир., керамиковые диафрагмы, применяемые при электролитич. и электросинтетич. процессах, должен быть достаточно тонко пористы, чтобы обладать необходимой механич. прочностью (и притом не убывающей от электрохимич. воздействия тока) pi не допускать значительного перехода электролитов или ионов из катодного пространства в анодное, и наоборот; но вместе с тем сумма поперечных сечений всех капиллярных скважин должен быть достаточно велика, чтобы электролитич. сопротивление диафрагмы было возможно малым. На практике диафрагмам приходится работать в электролитических ваннах при t° почти до 100°. Что же касается концентраций, то увеличение их ограничено отсутствием достаточно стойких материалов (концентрация серной кислоты может доходить до 90%, а щелочи до 10%). Обычные плотности тока 1—2 А/дм²· при 3,5—4,5 V, но в отдельных случаях 6—8 А/дм² при 6 V. Испытание диафрагм на электропроводность ведется путем измерения разности потенциалов в ванне с диафрагмой и затем без диафрагмы; при 5 миллиметров толщины диафрагмы и плотности тока 0,15—0,20 А /см² наличие диафрагмы в ванне с 20% H₂S0₄ при 20° должно вызвать потребность в добавочных 0,15—0,20 Y. После длительной службы диафрагмы стареют—в кислых электролитах весьма увеличивают свое сопротивление, а в щелочных утрачивают механич. прочность; поэтому испытанию должны подвергаться образцы как свежие, так и предварительно обработанные пропиткою и проваркою в соответственных средах, при изменении концентрации, темп-ры и времени. Испытание ведется в ванне 12x12x20 см, снабженной вертикальной бороздою (фигура 19). Испытываемая диафрагма может быть быстро укреплена в этой борозде посредством резиновой трубки, из которой выкачан воздух, достаточно плотно закрывающей зазор по вхождении воздуха. На деревянной раме, накладываемой на ванну, укрепляют два параллельных электрода 8 х×19x0,2 сантиметров во взаимном расстоянии 7,5 см; в случае тонкости пластинок они примазываются к стеклянным. Материал электродов: железо— в щелочных ваннах, медь—в меднокупоросных, свинец—в сернокислых. Схема установки для испытания по Кольраугау показана на фигуре 20, где 1—аккумуляторная батарея, 2—амперметр, 3—мостик Кольрауша, 4—диафрагма, 5—электроды, 6—стеклянная ванна, 7—скользящий контакт, 8—индукторий (катушка Румкорфа), 9—реостат, 10—рубильник, 11—магазин сопро

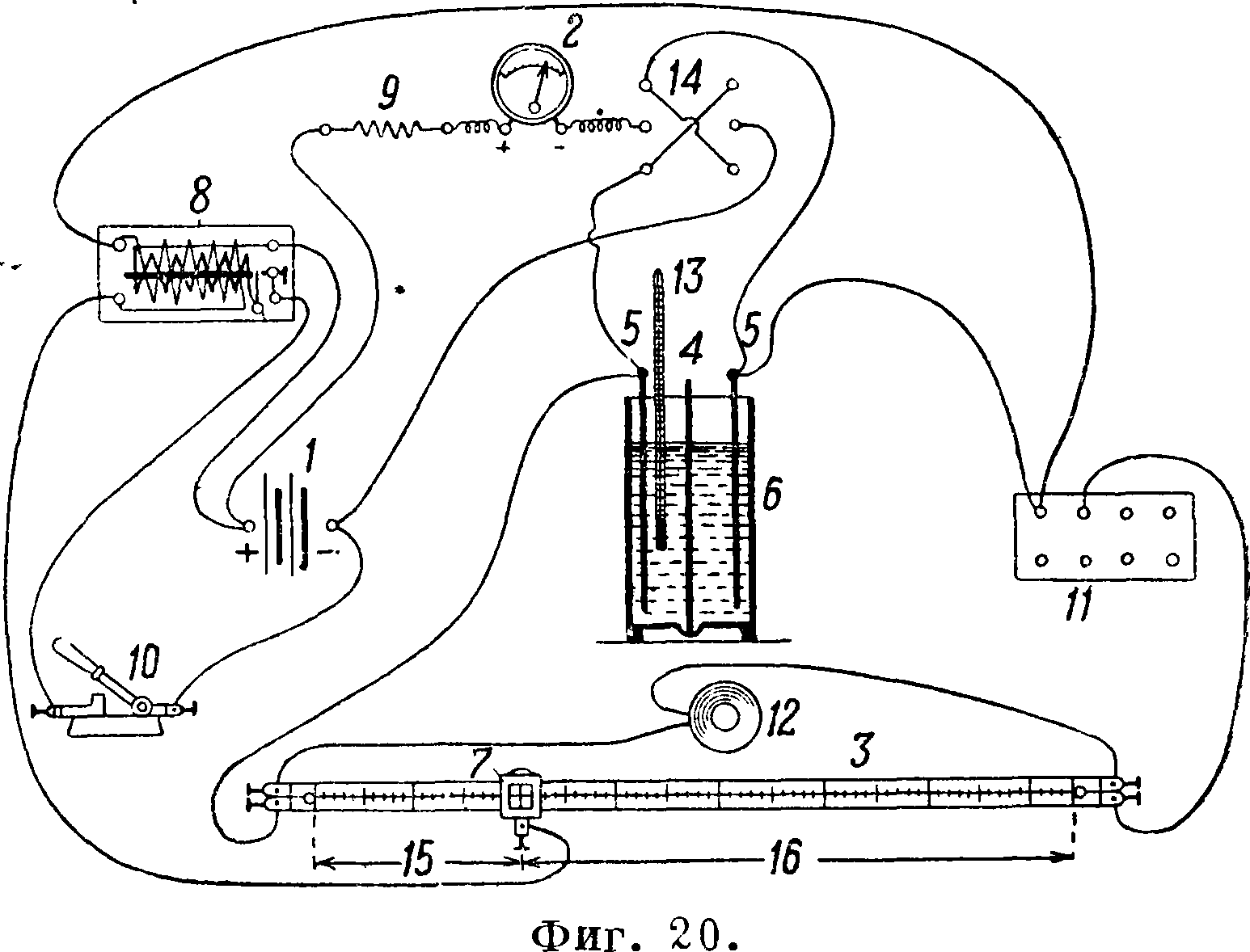
тивления, 12—телефон, 13—термометр, 14—переключатель, 15 и 16—отрезки струны, дающие минимум звука в телефоне. Перед каждым измерением первичный ток индуктория прерывается рубильником 10, а переключателем 14 пропускается через электролит, примерно в течение 3 ск., поляризующий постоянный ток в 2—3 А при 8—10 V. После этого дается на 3 мин. переменный ток, затем контакт реохорда устанавливается на минимум звука в телефоне и вычисляется сопротивление ванны как с диафрагмой (w_d), так и без нее (гс₀). Константа cl, характеризующая способность диа-

фрагмы пропускать ток, выражается по Меллеру соотношением:

d =

h

wo

L-(L-l)

(22)

где J,—межэлектродное расстояние, a h—средняя толщина стенки диафрагмы. Соотношение это основано на указанной Лебланом пропорциональности между электропроводностью канала и его сечением (хотя жидкостепроводность пропорциональна квадрату сечения), и кроме того Меллером вводятся две предпосылки лишь приблизительной точности, а именно: приравнивается длина скважин в диафрагме к ее толщине и пористость поверхностной корки диафрагмы—к пористости внутренних слоев. На самом деле однако длина скважин превосходит толщину стенки, а поверхностная корка—плотнее внутренних слоев. Поэтому сравнимые данные м. б. получены лишь при испытании образцов одной и той же толщины. Влагопроницае-мость диафрагмы измеряется помощью прибора (фигура 21) Керди и Гюи. Испытуемый образец в виде круглой пластинки диам. в 11,5 сантиметров и толщиною 0,5—0,8 сантиметров зажимается с прокладкою уплотнительных резиновых колец между двумя большими воронками с фланцами, затем извне примазывается и заливается сплавом из 2— 3 ч. канифоли и 1 ч. пчелиного воска. Затем нижняя воронка наполняется подкисленной водой, свободной от пузырьков воздуха, и после осторожного укрепления присоединяется к нижней системе труб. После этого наполняется подкисленной водой из ма-риоттова сосуда 1 верхняя воронка. Трубка 2 показывает верхний уровень давящего столба жидкости, а трубка 3—нижний, т. ч. напор р м. б. отсчитан непосредственно по шкале. Если за время τ через диафрагму толщиною h и поверхностью q протекает ш см³ жидкости, то константа С материала, характеризующая его вла-гопроницаемость, выражается соотношением:

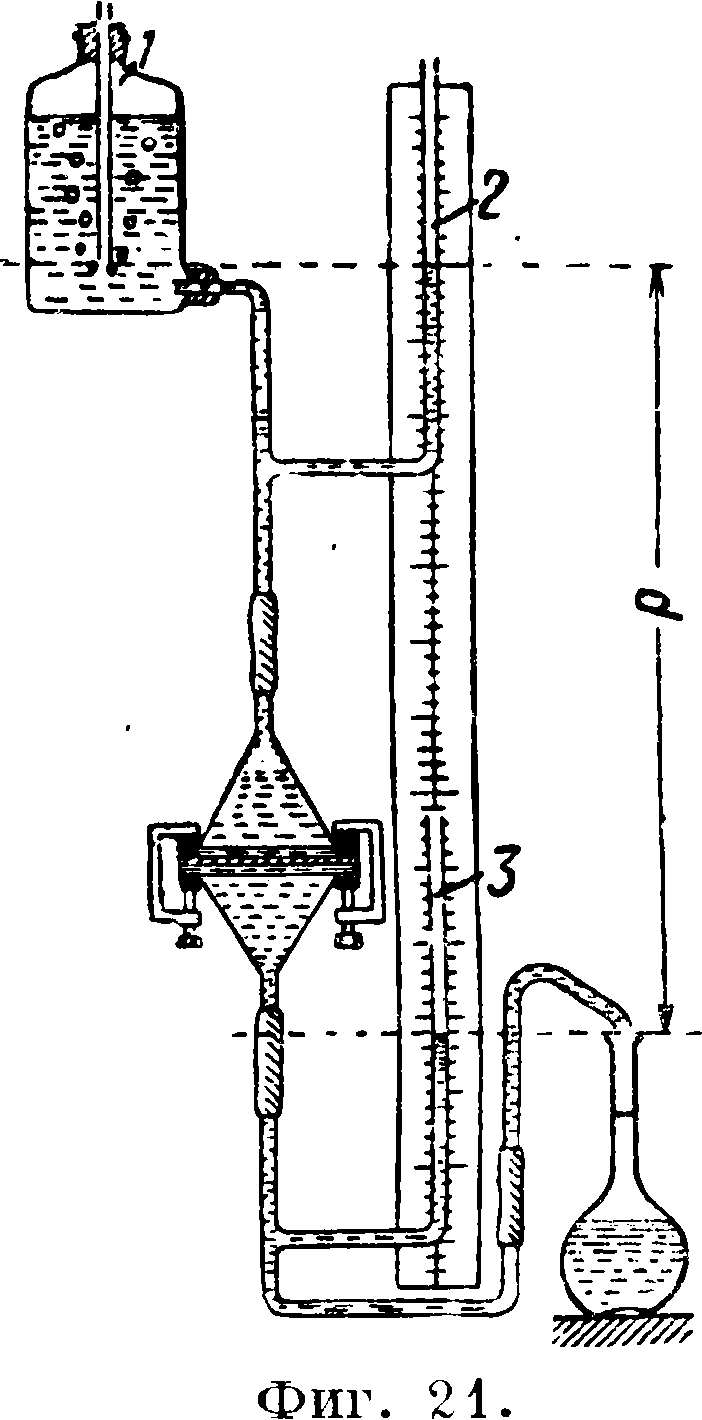
hm

qpr

(23)

По соображениям, указанным выше, сравнимые результаты м. б. получены лишь при испытании пластинок равной толщины.

Влагоподнимающая способность. Под влагоподнимающей способностью (Wassersteigfahigkeit) разумеется способность скважистых тел к капиллярному подъему воды, к-рый служит мерою несопротивляемости соответственных материалов проникновению влаги, например из земли в стены фундамента. В отношении кирпича испытание ведется по Краце (Кга- _

ze) в плоской ван-не, в которой неп-рерывно течет вода **’ _{фиг 22}

с такою скоростью,

чтобы глубина слоя была все время 1 сантиметров (фигура 22). В этой ванне устанавливаются наголову целые кирпичи и затем определяется время, проходящее до появления влажности на верхней голов-

Фиг. ной стороне. Водоподнимающая способность выражается в ск. этого времени., отнесенного к объёму кирпича в см³ (кажущемуся объёму со включением пор). Индикатором влажности, прошедшей через кирпич, может служить насыпанная на верхнюю головную сторону кирпича кучка какого-либо порошка, при наличии влажности пристающего к пальцам при легком сжатии, вполне просушенной размолотой глины, крахмала, кремнекис-лоты. Пользуются и кристаллами железистосинеродистого калия или роданистокалиевой бумагой, при- _Lчем в последнем слу- ~ чае к всасываемой воде добавляется хлорное железо.

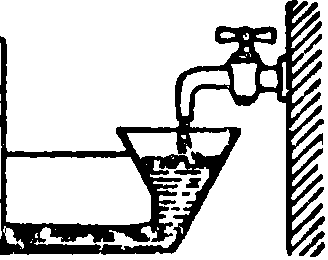
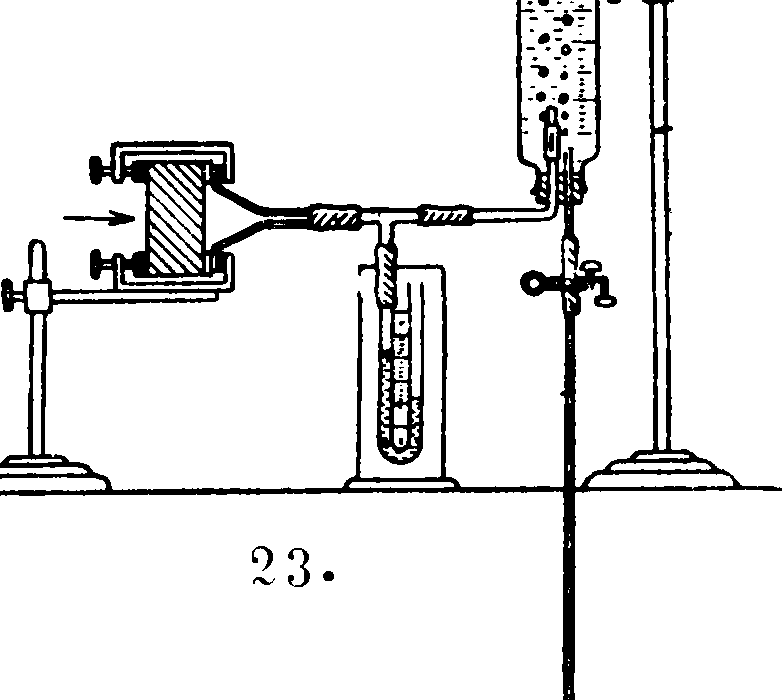
Измерение газопроницаемости. Газопроницаемость, то есть свойство материала данной толщины пропускать в единицу времени определенное количество газа при определенном давлении и t° через единицу поверхности, измеряется при помощи установки (фигура 23), принятой Герм, ф-кой каменных товаров для канализации и химич. пром-сти во Фридрихс-фельде в Бадене. Пластинка испытуемого материала, примерно 10x10 см, покрывается несколько раз со всех сторон газонепроницаемым лаком, причем оставляют непокрытыми две точно лежащие друг против друга круглые поверхности (например 20 см² площадью, то есть 5 сантиметров диам.); вместо покрытия лаком можно примазывать к пластине шаблон, для воздуха—к одной стороне, а для других газов—к обеим; еще целесообразнее пользоваться резиновыми уплотняющими кольцами. Затем к пластине герметически присоединяется воронка с фланцем, сообщающаяся с манометром и градуированным цилиндром, содержащим воду или другую непоглощающую газ жидкость; это сообщение делается посредством бунзеновского клапана—закупоренной на конце резиновой трубки, надрезанной на 1 сантиметров длины. Спуская воду из цилиндра при помощи трубки, введенной в него через пробку, устанавливают по мано

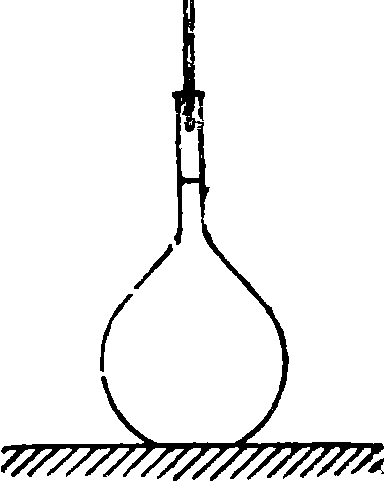
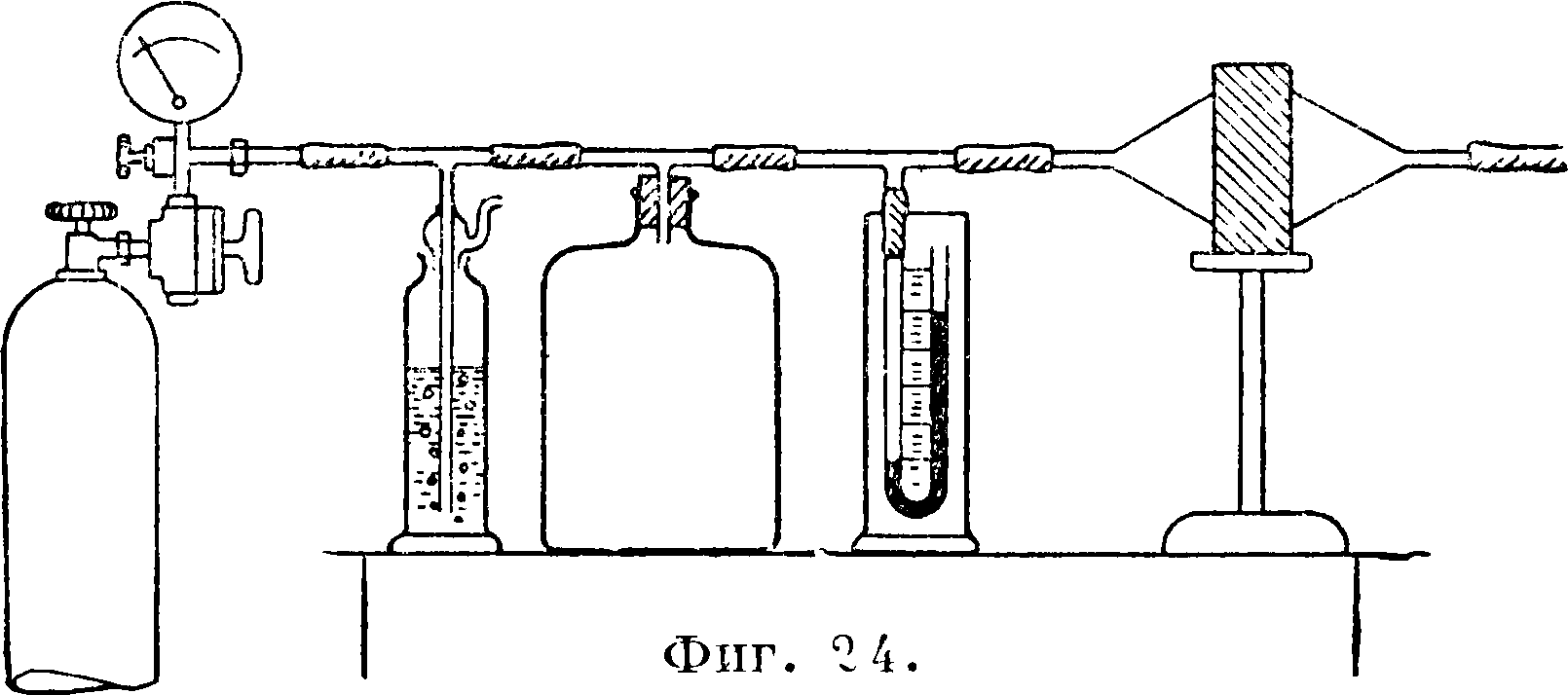
метру желаемое давление и затем замечают время, в к-рое объём разреженного газа возрастает на 1 000 или на 2 000 см³. По данной t° и давлению объём газа пересчитывается к нормальным условиям. Объем разреженного газа м. б. измерен также по количеству вылившейся воды, и тогда вместо цилиндра можно пользоваться большой бутылью. Если испытание ведется с газом, отличным от воздуха, то на противоположной стороне испытуемой пластины укрепляется другая воронка, которая присоединяется к газометру или к бомбе с сжатым газом, причем необходимо включить pi второй манометр (фигура 24). В вышеописанных установках измеряется количество воды и соответственное разрежение со стороны, куда направлен ток газа. Вологдиным предложено измерять количество вытесненной воды и соответственное избыточное давление со стороны пря

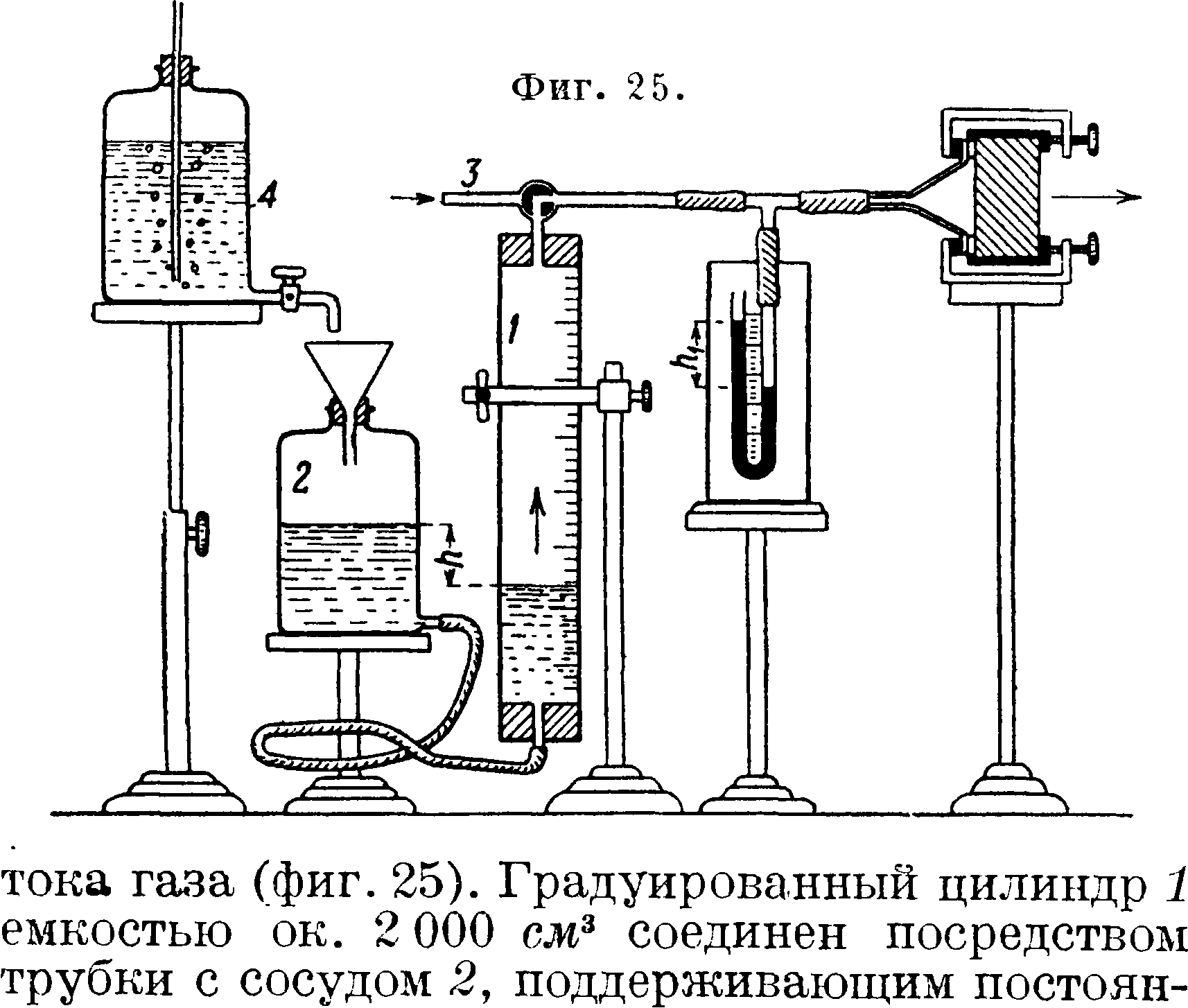
ный уровень жидкости. Тройник 3 в верхней части цилиндра присоединяется к манометру и заправленному ранее описанным способом образцу скважистого тела. Для заполнения цилиндра газом кран 3 открывается наружу, из сосуда 2 цилиндр 1 наполняется водою, затем сосуд 2 опускается, газ отсасывается в цилиндр 1 и кран 3 запирается. Посредством подъема сосуда 2 устанавливается в цилиндре 1 желаемое манометрич. давление Л_1? для чего в сосуде 2 и цилиндре 1 должен быть разность уровней h, к-рую поддерживают неизменною мариоттовым сосудом 4. При испытании определяется время, необходимое для подъема уровня в цилиндре 1 на определенное число делений. Как и в ряде ранее упомянутых случаев, необходимо учитывать, что пересчет к единичной толщине испытуемого материала может повести к существенной ошибке, и потому испытания должны непосредственно вестись на пластинах одной толщины. Газопроницаемость керамич. масс имеет значение как отрицательное, так и положительное,—первое в отношении керамич. материалов, служащих непроницаемыми оболочками, а второе в отношении носителей катализаторов, то есть пористых керамич. тел, пропитанных контактным веществом. Однако и в том и в другом случае особый интерес представляет газопроницаемость при высоких t°. Соответственные испытания ведутся при помощи аппаратов, описанных выше; но части их, подвергающиеся нагреву, делают из газонепроницаемого глазурованного фарфора или из пифагорейского фарфора, а также из специальной массы Саксонской фарфоровой фабрики в Мейссене. Нагрев ведется в электрической печи. В систему газопроводов включается газонепроницаемый холодильник.

Измерение величины скважин. При наличии б. или м. крупных скважин, макро- или микроскопических, но приблизительно одной величины и притом б. или м. правильной формы—цилиндрич., сферич. и т. д., измерение их величины не представляет особых трудностей. Промер макроскопич. скважин м. б. произведен с желаемой степенью точности одним из приборов для измерения, причем особенно большая точность требуется сравнительно ред ко в виду редко наблюдаемого точного равенства отдельных скважин между собою. Микроскопии. поры измеряются на поверхности излома, среза или шлифа в отраженном свете или на прозрачном срезе или шлифе в проходящем свете; видимость пор м. б. повышена в одних случаях применением поляризованного светз, в других—посредством пропитки шлифа или разреза окрашенным парафином, в третьих— посредством втирания в исследуемую поверхность вазелина с сажей, китайской туши и т. д. (смотрите Изоляторы электрические, испытание фарфора). Самое измерение проводится либо непосредственно над микрокартиной помощью окулярного микрометра либо измерениями помощью линейки над спроектированным на экран изображением, зарисовкою или микрофотографии, снимком. Однако прямое измерение величины скважин даже в тех случаях, когда они не слишком малы, оказывается мало целесообразным, если скважины не равны между собою, и средние известного числа измерений оказываются нисколько не характеризующими действительную С. тела. Найти же функцию распределения скважин по величине бывает слишком затруднительно. Указанные средние значения величины скважин вовсе теряют свой смысл, если скважины не обладают на своем протяжении постоянной толщиной, как например это бывает в вате (смотрите), в телах войлокообразных (смотрите Волокнисты изоляционные материалы), в гравии (смотрите), в песке (смотрите) и т. д., то есть в материалах, представляющих особенно практическое значение. Но если бы точное знание размеров подобных скважин по всему их ходу и было достигнуто, все-таки это знание принесло бы мало пользы, потому что подсчет соответственного эффекта этих скважин в отношении различных деятелей оказывается весьма затруднительным, а в большинстве случаев—и просто недоступным. Поэтому независимо от легкости или трудности непосредственного измерения подобных скважин бывает выгодно знать не их подлинные размеры, а размеры нек-рых фиктивных, равных между собою средних скважин, которые своей совокупностью могли бы в отношении обсуждаемого деятеля произвести эффект, равновеликий эффекту действительной системы скважин. Величина этих эффективных, или действующих, скважин может иметь мало общего со скважинами действительными; это видно хотя бы из того, что в отношении различных деятелей величина эффективных скважин оказывается далеко не тождественной, т. ч. при сообщении размеров эффективной скважины необходимо должен быть указан и тот деятель, эффект которого в данном случае имеется в виду.

Измерение скважин в ультрафильтрах.В ультрафильтрационном аппарате Бехольда ультрафильтры делаются из пропускной бумаги, пропитанной раствором коллодия или желатины. Плотность ультрафильтра и соответственно размах скважин обусловлены концентрацией пропитывающего раствора; С. понижается с увеличением плотности раствора. В табл. 12 приведены два крайних случая ультрафильтров. Размер скважин может измеряться одним из трех предложенных Бехольдом способов. 1) Испытание помощью стандартных коллоидов. Список коллоидов, расположенных по возрастающей дисперсности (табл. 13), позволяет в случае прохождения через него соответствен-

Таблица 12.—П рим еры ультрафильтров (по Ж. Дюкло).

Наименование данных	Скважистый I фильтр 1	Плотный фильтр
гоотян ( а 96°. Эфира 65° · ·	500 см“	250 смз
	500 см	700 см“
) Нитроцеллю-питки 1 лозы.	20 г	50 г
Толщина пленки.	1/з миллиметров	0,02 миллиметров и бо
Содержание сухого ве		лее
щества ..	8%	40%
Вес пленки на 1 м“. Фильтрационная спо	30 г	10 г
собность в отношении воды через 1 дм“ за 1 час..	500 см“ *1	5 СЛ*3 *2
Скважистый фильтр полностью задерживает желези-
стосинеродистую медь и сернистый ; плотный фильтр—почти все коллоиды.— *1 При давлении
50 сантиметров воды. ** При давлении 100 сантиметров воды.

Таблица 13 .—С тандартные коллоиды возрастающей дисперсности (по Г. Бехольду).

Коллоид	-Размер частицы, ΎΥΐμ	Мол. в.
Суспензии..I	_	_
Берлинская лазурь.	—	—
Золь платины Бредига.j	— I	—
Гидрозоль окиси железа.	—	; —
Казеин .. Сернистый (Жигмонди	- 1	1 “
№ 4).. Бисмон (коллоидн. окись вис	ОК. 44 1
мута по Паалю). Лизаргин (коллоидн. серебро по	—
Паалю) .. Коларгол (коллоидн. серебро по	“
Гейдену) ..	ОК. 20	—
Золь золота (Жигмонди № о).	ОК. 1—4	—
1%-ный раствор желатина.	—	—
1%-ный раствор гемоглобина.	—	ок. 16000
Сывороточный альбумин. Дифтери тный токсин (проталь-	—	5 000—150С0
бумоза)..	—	—
Коллоидная кремневая к-та.	—	—
Лизальбиновая к-та.	—	—
Дейтер альбумозы А.	—	ОК. 2 400
Дрйтер альбумозы В.	—
Лакмус ..	—	—
Декстрин..	—	ОК. 965
Кристаллоиды .*.

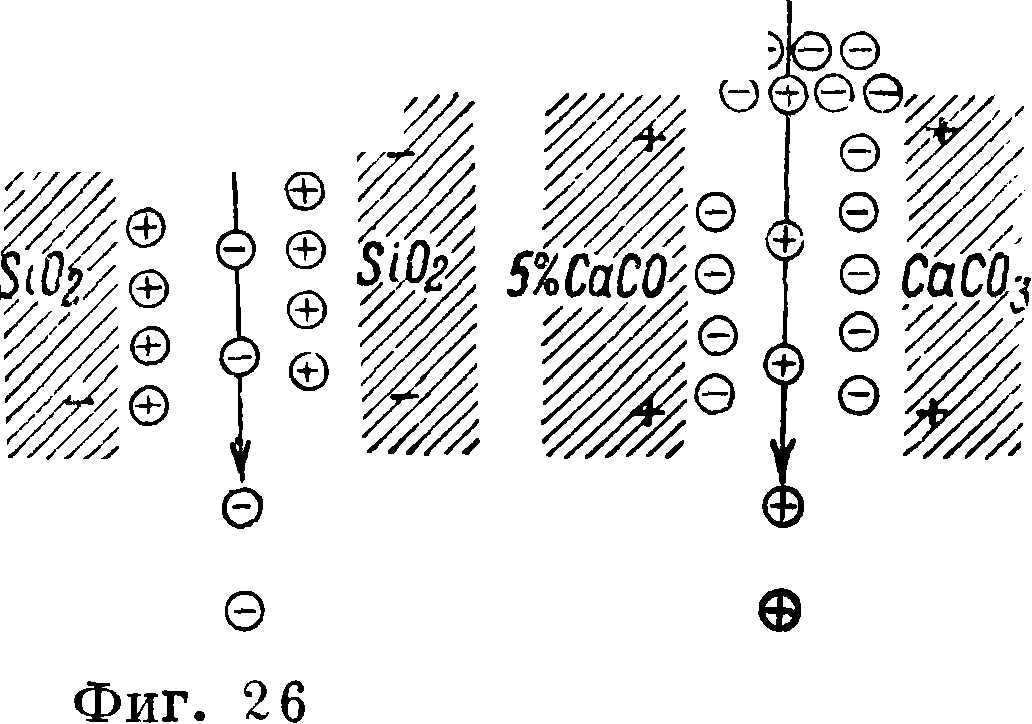
ных частиц путем фильтрации через данный ультрафильтр установить верхний предел размера его скважин. В. Оствальдом предложено испытывать ультрафильтры помощью свежеприготовленных растворов ночной голубой (или гидрозоля мастики), красной конго и коларго-ла (размер частиц ок. 20 τημ). Четырехпроцентный коллоидный фильтр должен давать фильтраты всех трех растворов бесцветные; 3%-ный фильтр не пропускает лишь ночную голубую, а иногда и красную конго; 2%-ный фильтр задерживает одну ночную голубую, если только стандартные растворы изготовлены не слишком слабые. Вариантом указываемых способов следует считать гемоглобинный способ Бехольда, состоящий в фильтрации 1 %-ного раствора гемоглобина. Однако при этом способе испытания необходимо иметь в виду, что задержка частиц на стенках скважин не во всех случаях бывает механич., но иногда обусловлена взаимодействием электрич. зарядов частиц и стенок фильтра. Поэтому мелкопористый фильтр пропускает иногда частицы, задерживаемые фильтром с более крупными порами. Так например, силикатные фильтры Беркефельда (фигура 26), изготовляемые из инфузорной земли или тре-

Фигура 27.

пела, получают отрицательный заряд, тогда как гипсовые фильтры электрически нейтральны, а углекислокальциевые заряжены положительно (фигура 27). Смесь Si0₂ и СаС0₃ дает фильтр нейтральный, тогда как двухслойный фильтр из указанных материалов— θθΙθθ ®©|θθ

фильтр двоякоза- ^

ряженный, задерживающий как от-, рицательный, так и положительный заряды. 2) И с-дытание помощью фильтрации воды.

В этом способе размер скважин ультрафильтра устанавливается по скорости q просачивания воды через фильтр под определенным давлением Р. На основании ф-лы Пуазейля

«-ТГ· <²⁴

где h—длина капиллярной трубки, приравниваемая толщине стенки фильтра, s—площадь поперечного сечения трубки, а η—вязкость воды при t° опыта. Отсюда м. б. определено значение диам. D эффективной скважины. Бехольд пользуется видоизмененным законом Пуазейля и на основании его дает соотношение:

(l + a)qhy _/<Жч

PSa ’ V^⁰

где S—площадь фильтра, а—отношение пространств, содержащих воздух, к пространствам, заполненным твердым веществом; значение остальных букв то же, что и в предыдущей формуле (24). Относительно величины а естественно предположение, что она весьма мала; однако предположение это ошибочно: даже для столь плотного фильтра, как 5%-ный, Бехольд установил значение а в 0,95, то есть весьма близкое к единице. 3) Испытание помощью продавливания воздуха. Чтобы продавить воздух через капилляр диам. D в пленке, заполненной водою и погруженной в жидкость, необходимо довести давление до нек-рого значения Р. Согласно Кантору давление Р должно удовлетворять соотношению

ΌΡ=2ог, (26)

где о—поверхностное натяжение на границе воды и воздуха, при 18°=7,7-10 дин /см. Если Р выражено в atm, то (по Кантору)

^ ~ Р -1,033 -105 * (^)

Значения Р, соответствующие различным Z), характеризуются данными табл. 14. Этот спо-

Т а б л. 14.—Д а в л е н и е, необходимое для продавливания воздуха через скважину ультрафильтра (по Г. Бехольду).

D

Давление,	Диам. сква	Давление,	Диам. сква
atm	жины, mμ	atm	жины, mμ
1	300	100	3
10	30	1 000	0,3

соб был более подробно разработан А. и А. Думанскими и Е. Струковой. Сконструированные ими приборы изображены на фигуре 28 и 29. Достаточно большой стеклянный сосуд 1 (фигура 28), в к-ром находится воронка 2, дно которой представляет испытуемое скважистое тело; воронка присоединяется к толстостенной кол-

т. Э. m. XXI.

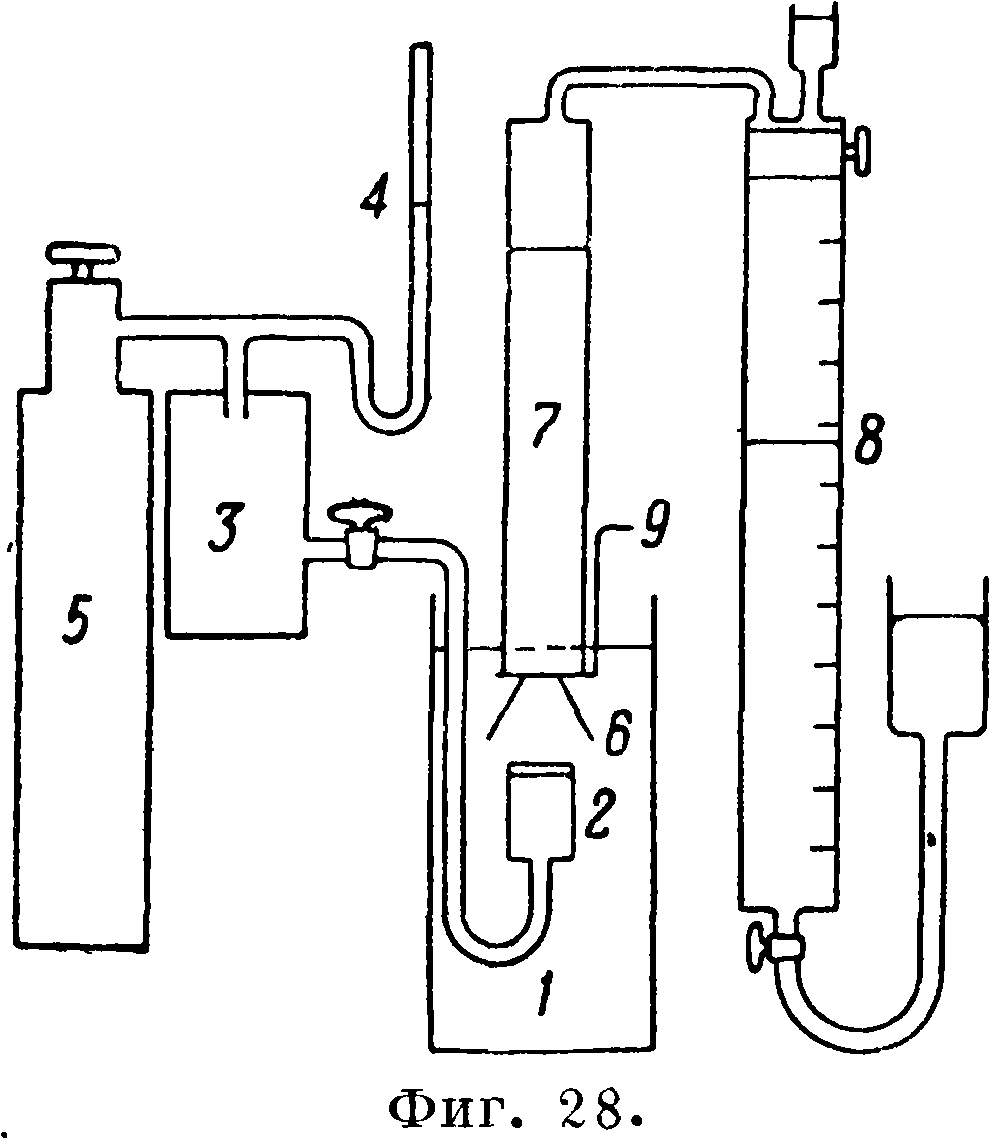
6e 3, сообщающейся с манометром 4 и и 5 со сжатым воздухом. Над воронкой 2 помещается опрокинутая воронка 6 с обрезанным концом, направляющая пузырьки воздуха, продавливаемые через скважистое тело, в эвдиометр 7, присоединенный к газовой бюретке 8.

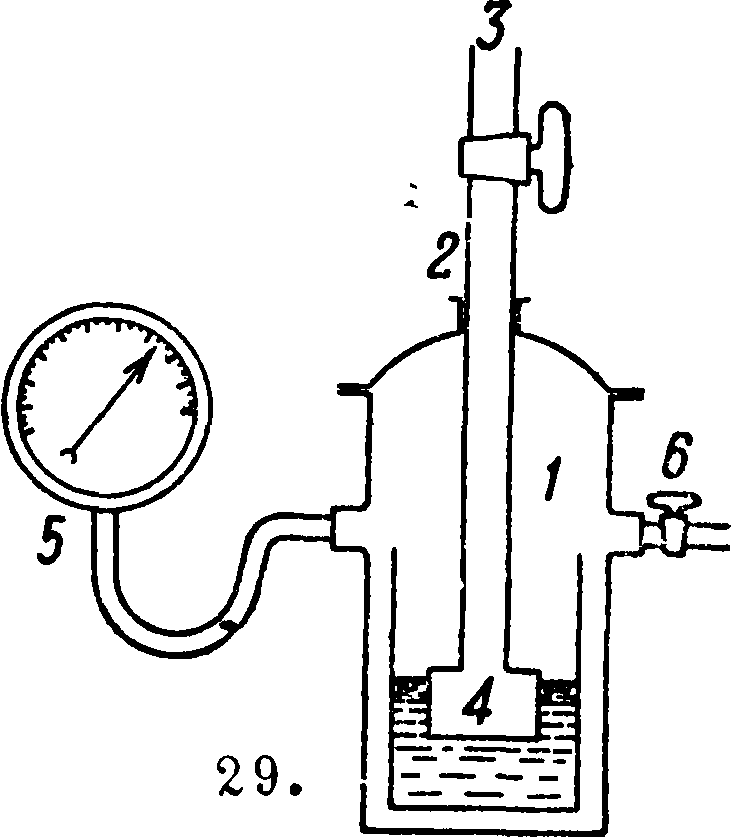
Задвижка с рукояткою 9 позволяет впускать в 7 лишь нужные порции воздуха. Прибор на фигуре 29 состоит из герметически закрытого сосуда 7, через верхний тубус которого 2 проходит трубка с краном 3, расширенный конец которого заделан скважистым телом 4, погруженным в жидкость (например в воду). К сосуду 1 присоединены манометр 5 и трубка б, идущая к разрежающему насосу. Означенные приборы позволяют на основании соотношения Кантора измерять размеры скважин как в телах с одинаковыми скважинами (и з о п о р о з н ы х), так и в телах со скважинами различной величины (г е т е р о πο-ρ о з н ы х). В обоих случаях вычисление ведется по скорости и истечения газа, определяемой ур-ием Торичелли

, (28) где к—коэфициент пропорциональности, Р— давление, продавливающее воздух через данный капилляр, a P—давление, вызывающее ток воздуха. При равенстве скважин все поры пропускают газ при одном давлении Р; диаметр их Ώ находится по формуле (27).

Точно так же истечение газа происходит из всех пор при одном и том же давлении Р. Измерив объёмную скорость этого истечения ν, можно установить и число N этих пор по следующей формуле:

Таблица 15Д явление, необходимое для продавливания воздуха через скважину, заполненную водою (по А. Думанскому и Е. Струковой).

Фиг.

Ν=-

_· (29)

kn dYP-P ^}

При наличии в теле скважин разного размера Ζ)₁>Π₂>-^3 ^{и т}· Д· ^в количествах N_lt N₂, и т. д. соответственно нек-рое давление Р_х будет способно продавить газ лишь через скважины диам. Pi, но не меньшие, и давление Р[ лишь через скважины Р_х будет давать ток газа. При возрастании давления будет наконец достигнуто значение Р₂, выдавливающее газ из скважин диам. D_x и Р₂, но не меньшим, и давление Р_х, выделяющее газ через скважины диам. D_x и Р₂. На основании этой постепенности участия различных скважин в процессе м. б. подсчитана кривая распределения скважин разного диам. Для удобства вычислений можно пользоваться табл. 15. Указанным способом В. Фердинандов измерил С. скорлупы и пленки куриных яиц. Скважины скорлупы обладают поперечником 6—16 μ, тогда как скважины пленки не крупнее 20—30 ηιμ. Для примера в таблицах охарактеризованы С.: а) в таблице 16 двух образцов яичной скорлупы и

	Давление, сантиметров Hg	Диаметр, μ	Давление, сантиметров Hg	Диаметр, I μ
	76	3,0	40	5,8
	74	зд	38	6,1
	72	3,2	36	6,4
	70	3,3	34	6,8
	68	3,4	32	7,2
	66	3,5	30	7,7
	64	3,6	28	8,2
	62	3,7	26	8,9
	60	3,8	24	9,6 ί
	58	4,0	22	Ю 1
	56	4,1	20	И ί
	54	4,3	18	13 !
	52	4,4	16	Η 1
	50	4,6	14	16
	48	4,8	13	18
	46	5,0	12	19
	44	5,2	11	21
	42	5,5	10	23

Таблица 16.—Распределение скважин в яичной скорлупе по их поперечнику (по В. В. Фердинандову).

	Образец I		Образец 11
	Диаметр	Численное	Диаметр	Численное
	скважины,	содержание,	скважины,	содержание,
	μ	%	μ	%
	11	4,2	12	2,3
	10	2,6	10	4,7
	8,6 7,5	10,0	6,6	27,0
		11,5	4,9	66,0
	6,6	0,0	3,9	0,0
	6,0	18,3
	5,2	50,0
	4,5	3,4

б) в таблице 17—С. древесины ольхи, срезанной перпендикулярно сосудистым пучкам, и в той же табл. 17 стеклянного фильтра Шотта.

Таблица 17.—Р аспределение скважин в стеклянном фильтре Шотта и в древесине ольхи (по А. и А. Думанским).

Стеклянный фильтр Шотта		Древесина ольхи * !
Диаметр, μ	Численное содержание, %	Диаметр, μ	Численное содержание, о /о
19	0,3	55	67,8 30,6
16	0,7	61
14	1,5	74	1,6
11	6,4
7,7	21,0
5,8	70,1
* Пластинка толщиною 0,5 миллиметров, вырезанная пер-
пендикулярно сосудистым пучкам.

4) Испытание помощью фильтрации эмульсии, способ, предложенный в 1910 году Гатчеком.

С. газовых фильтров. В первом приближении естественно принимать С. газового фильтра тем бблыней, чем грубее частицы тумана, проходящие через данный фильтр. Однако такое положение оправдывается лишь на частицах сравнительно крупных и может весьма нарушаться для частиц, не достигающих определенного поперечника. В табл. 18 показано в качестве примера соотношение между проницаемостью газового фильтра (то есть величиною, обратной его активности) и радиусом частиц аэрозоля, проходящих через данный фильтр; как видно из приведенных данных, частицы

Таблица 18.—С оотношение между проницаемостью бумажного фильтра и размерами частиц аэрозоля, образованного дифенилхлорарсином (по В. Гиббсу).

Диаметр, μ	Часть аэрозоля, проходящая через фильтр, о /о
j i <o,i j	52,4
1 0,1—0,2 !	87,6
1 0,2—0,4 ;	93,9 !
j 0,4—0.8 j	30,4 !
0,8—1,6	4,2 j
1 >1,6

поперечником менее 0,2 μ проходят через фильтр со значительно большей задержкою, чем частицы 0,2—0,4 μ. В еще большей степени это относится к молекулярно-дисперсным (газовым) смесям. Такая задержка более крупных частиц и газовых молекул объясняется завихрениями газового потока в скважистом теле. Более грубые частицы отбрасываются тогда центробежною силою к стенкам скважин и механически задерживаются ими, тогда как более тонкие частицы увлекаются далее возникшим завихрением. Так например, слой древесного угля из зерен поперечником ок. 1 миллиметров нацело извлекает из смеси с воздухом хлор, поглощая его вследствие весьма развитой внутренней поверх-ности, тогда как табач- _{т а б л}. ^.-Данные ный дым,пары серной кислоты, а также туманы и дымы, получаемые при е разных органич. жидкостей, проходят через указанный фильтр без изменения своего состава. По той же причине фильтры из войлока и бумаги оказываются более действительной защитой от дымов и тумана, чем угольный фильтр, служащий тем не менее хорошим противогазом. Точно так же бумажный фильтр из неплотной массы длинных волокон более действителен, чем плотный из волокон коротких, т. к. строение первого благоприятствует появлению длинных извивающихся каналов.

С. поглотителей. Сильно развитая система весьма мелких скважин в поглотителях (активные угли, силикагель, поглотительные глины и т. д.) ведет к большим значениям их удельной поверхности и потому к резко выраженным сорбтивным свойствам. Во всех подобных телах имеется развитая система микроскважин (пример дан на фигуре 30—сечение активного угля, видимое под микроскопом). Однако подобные микроскопические поры в животном и др. углях, табашире (смотрите), силикагеле (смотрите) и прочих поглотительных веществах могут объяснить лишь капиллярную поглотительную способность, а не специфическую, согласно терминологии Ченея (Chaney). В силу этой способности активные вещества поглощают газы в большом количестве, но столь же легко отдают их обратно; напротив, специфич. поглощение газов менее значительно, но необратимо или труднообратимо. Это последнее связано согласно Гербсту с ультрапористостью поглотителей, существующей наряду с обык новенной пористостью. Существование весьма малых каналов, по крайней мере в 100 раз меньших чем объекты, доступные микроскопу, подтверждается различным поглощением газов с молекулами различной величины. Если поглощение мелких молекул (например СО_а) выражается числом А_у а поглощение больших (например S0₂) числом Б, то величина

(30)

17=^100,

называемая падением ультраактивности (Гербст),-характеризует относительное содержание более крупных пор. Величина уль-трапор вычисляется по формуле Андерсона:

2(7 (5р. 0,4343 _П1ч

d-Po-lgCPo/Pi) ’ ^{К 4}

где г—средний радиус ультрапор, а—поверхностное натяжение жидкости, пар которой поглощается (при 25° для воды 72,1 дин/см); <5₀— плотность поглощаемого пара (для воды при 25° 22,75 -10⁶); d—плотность жидкости (для воды при 25° 0,99707); р_{)—упругость поглощаемых паров (для воды при 25° 31,20-10 дин/см); Р_х—упругость пара в капилляре. Вычисленные так. обр. Лаури (E. Н. Lowry) и Гелетом (G. A. Hullet) данные об ультрамикроскопич. С. активных углей сопоставлены в таблице 19;

Лаури и Гелета об ультра к апи л лярной С. активных углей.

Наименование угля	Диам. капиллярных ходов, ταμ			Полная уд. поверхность		Уд. объём капилляров, смз/г
	наименьший	наибольший	средний	м2/г	М^/СМЗ
А 909.	0,67	4,1	2,8	230	130	0,2728
Nela.	0,67	5,5	3,7	440	200	0,4406
Английский.	0,16	1,9	8,3	300	40	0,7828
Германский.	0,20	1,3	2,5	160	40	0,3543

Фигура 30.

впрочем значение активной поверхности угля (160—436 м²/г) Лемп, Вильсон и Ченей оценивают выше, до 1 000 м²/г. Активная кремне-кислота (силикагель, табашир, гидрофан, по-луопал) при микроскопии, исследовании обнаруживает ячеистую структуру и скважины диаметром (по вычислению Андерсона) 1—1,5 μ. Но вместе с тем там имеются скважины диам. от 2,4 до 5,98 ηιμ.

С. растительных тканей. Растительные ткани обладают С. различных видов, биологически служащей для обмена веществ (растительных соков, влаги и выдыхаемых газов, различных секретов), а при использовании-растительных тканей в качестве технич. материала обусловливающей у этих материалов^ особенности, с которыми необходимо считаться. Так, покровная кожица растений содержит’ межклеточные щели — газовые устьица, число“ которых варьирует в весьма широких пределах и в некоторых случаях достигает 600 на 1 миллиметров% поверхности кожицы и даже более. Эти устьица могут раскрываться и закрываться. Размеры газовых устьиц не очень разнообразны и могут быть охарактеризованы на удачу примерами: 31x7 μ у листа гиацинта и 62x42 μ у папоротника Aneimia. В тех случаях, когда поверхность покрыта налетом воска (до 5 миллиметров толщиною), к устьицам через восковой слой идут каналы, например у Klopstockia cerifera—поперечником около 10 μ. Наряду с газовыми существуют водные устьица (г и д а т о д ы), служащие для выделения капельно-жидкой воды и обладающие весьма различными размерами;

водные устьица у Tropaeolum majus обладают размерами ок. 120 х 125 μ. Значение С. в строении древесины настолько велико, что морфо-логич. классификация элементов древесины, предложенная Санио, основана на форме пор (табл. 20). С. древесины обусловлена преиму-

просов весьма отстало от потребностей промышленности, и в отношении С. древесины можно сообщить очень немногое. Л. Крибсом (1928 год) изучена длина трахеид у Pinus bank-siana в зависимости от положения по высоте ствола для деревьев разного возраста, от 1

Таблица 20.—Классификация элементов, возникающих из камбия (по Санио).

Группа	I Составляющие элементы	Поры	Физиологии, функция
Паренхимная	Типичная древесная паренхима и прозенхимные тонкостенные, заменяющие волокна	Простые круглые	Место скопления органич. запасных веществ
Лубовидная	Простой и перегородчатый ли-бриформ Сосуды (трахеи) и сосудовидные клетки (трахеиды)	Щеле видные	Механич. опора
Сосудистая		Окаймленные или со спиральным утолщением	Влагоносная система

щественно сосудистой группой элементов, состоящей из сосудов (трахей) и сосудовидных клеток (т р а х е и д). Сосуды образуются слиянием продольных рядов клеток, причем поперечные перегородки, разделяющие отдельные клетки, растворяются или продырявливаются; получающиеся сплошные трубки в некоторых случаях могут равняться длине всего растения. Обычно длина сосудов не превосходит 10 см, но у дуба встречаются сосуды до 2 метров длиною. Диаметр сосудов весьма различен даже у одного и того же растения; в некоторых случаях он доходит до 0,5 миллиметров (у лиан). Сосуды в различных случаях (физиологически и патологически—на зимний сезон, при поранениях древесины и т. д.) могут закупориваться особыми выростами паренхимных клеток (т и л л а-м и) или выполняющими клетками. Сосудовидные клетки не обладают сквозным сообщением, но зато снабжены окаймленными порами. У хвойных деревьев древесина почти целиком состоит из трахеид, а у лиственных эти послед- ⁴ ние часто группи-^ руются вокруг сосудов. При технич. |j использовании дре- ⁴⁰ весины, особенно для пропитки (смотрите), S консервации (см.

Дерево, к о н с е р- 5 в а ц и я Д.)иуясне- 1 ния физич. свойств древесины, кж анизотропного материала, весьма важно знать характер со- о ю го зо 40 so во 70 судистой системы Возраст дерева в годах древесины в зави- Фигура 316.

симости от породы дерева, возраста, географич. условий произрастания и положения данного участка по высоте ствола. Систематическое изучение этих во-

до 61 года. Результаты непосредственного промера 12 500 трахеид даны на фигуре 31а и 316 (цифры при кривых — высота в фт. над уровнем почвы) и 32 (цифры при кривых—возраст

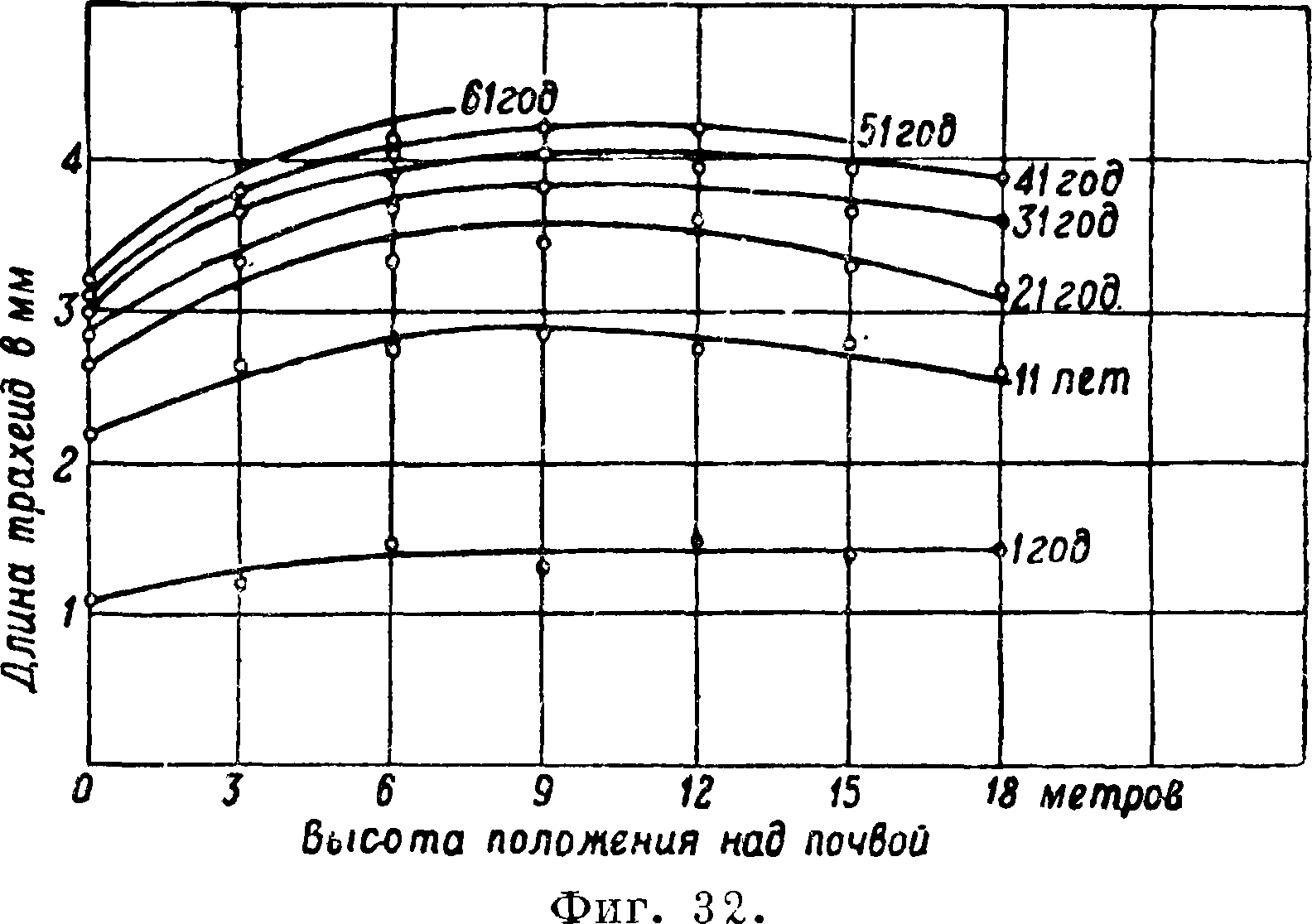
дерева). Максимальная длина трахеид оказалась

5,05 миллиметров; средняя—3,20; минимальная—0,75. Коэф, линейной корреляции между возрастом дерева и длиною трахеид оказался высоким, порядка 0,95; длина трахеид увеличивается как с возрастом, так и с высотою над уровнем почвы. Другие сведения в рассматриваемой древесине сопоставлены в таблице 21. А. Дж. Стеммом (1929 г.) изучена С. различных видов

Таблица 21.—Н екоторые данные, касающиеся С. древесины (по Л. Крибсу).

1 ! Древесина	Поперечник трахеид, μ		Толщина клеточных
i	** 1	1 *2	стенок, μ
Весенняя.	34	52	2,4
Летняя.	21 ί	36	6

*¹ В тангентальном направлении. *2 в радиальном направлении. мягкой древесины в том же продольном направлении при помощи разработанных им нескольких способов. Первый способ основан на электроосмосе и приводится на аппарате Брикса, Стриклера и Мэтьюса, схематически изображенном на фигуре 33^ перегородка 1 вырезывалась из испытуемой древесины толщиною от 0,04 до 1,45 сантиметров и площадью 7,76 см²;2и2—~ электроды из платиновой спирали в расстоянии ок. 6,5 сантиметров между собою и при разности потенциалов от 1,08 V и выше до 45 V. Прибор заполнялся дистиллированной водою уд. сопротивления 1,85-10* Q-см (рН=5,4). Соедини-

					01	~~5
		А				41
	%
j	w	п
1	Г—
Г
L

0 10 20 30 40 50 60

Возраст дерева в годах Фигура 31а.

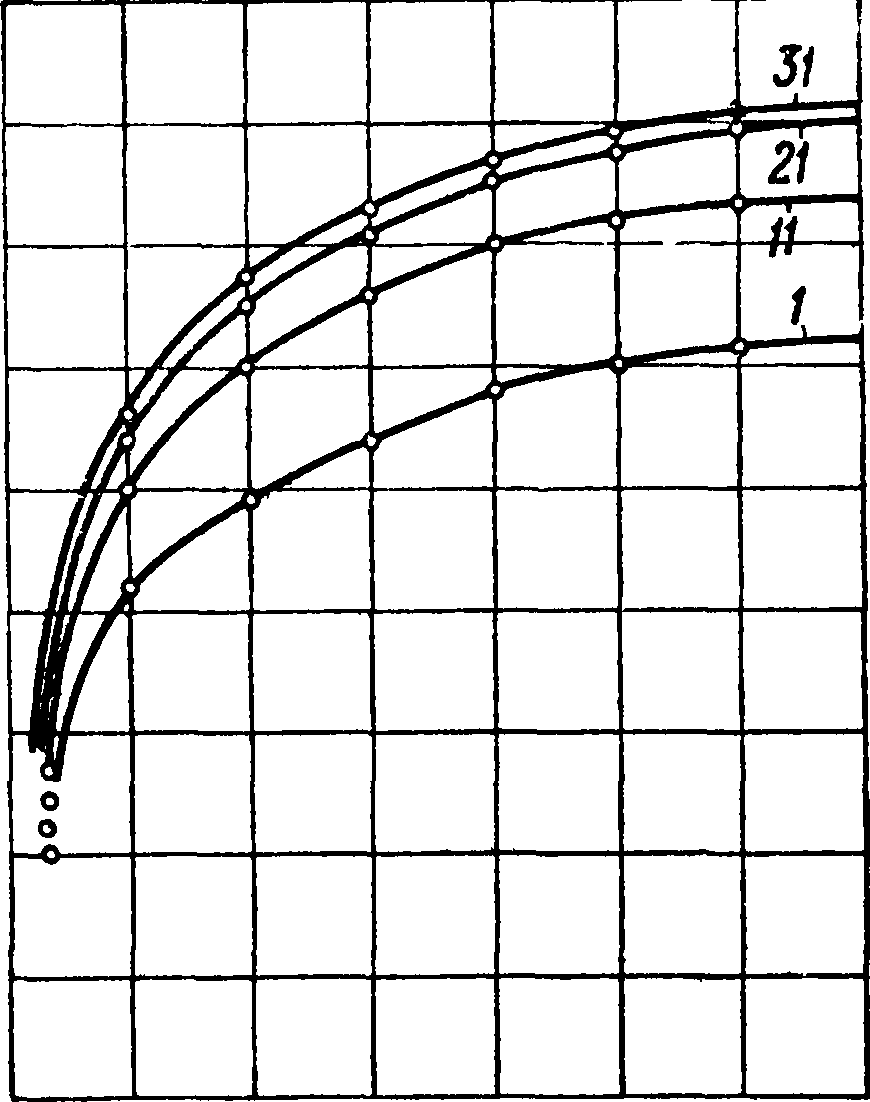
тельная трубка (сечением 0,0251, 0,0550 или 0,0909 см²) содержала пузырек воздуха^З, слу

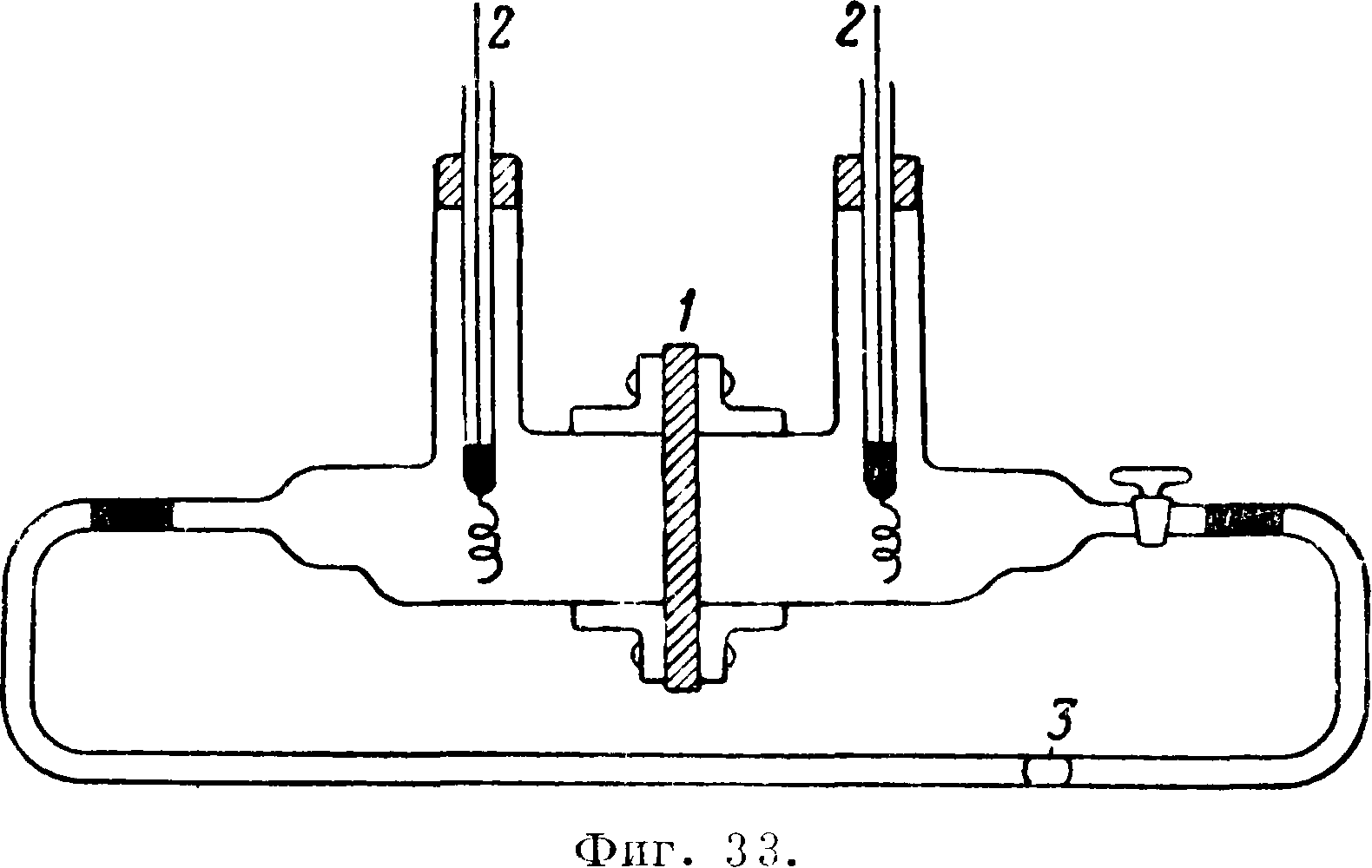
живший указателем. Вычисление производилось по формуле

£=(300)²^-, (32)

где ζ—контактный потенциал на границе древесина—вода, η—вязкость жидкости, V—объёмная скорость жидкости, проходящей через перегородку, ρ—уд. сопротивление жидкости в перегородке, I—сила тока, а ε—диэлектрич. коэфициент жидкости. При соприкосновении а Е—градиент наложенного поля. Линейная зависимость ν от q достаточно хорошо подтверждается для каждого среза, но лишь в определенном интервале толщины испытуемой пластины; для толщин, превосходящих верхнюю границу этого интервала, скорость ν быстро убывает и затем становится близкой к нулю. Такой ход этой зависимости объясняется конечной длиной трахеид и дает возможность вычислить эту длину. В табл. 23 сопоставлены результаты подобного вычисления и данные непосредственного промера. Второй способ, использованный Стеммом, основан на применении формулы Пуазейля:

яг“Р _ аг³Р 8ηΙ 8 ηί

(34)

где Р—приложенное давление, г—радиус капиллярной трубки, I—ее длина, а—ее поперечное сечение, a ν—скорость протекания жидкости; формула эта применима для скоростей, не дающих завихрения, то есть примерно до

— <1,200. При наличии N капилляров эффективного совокупного сечения

Nnr^P _ qr²P 8η I 8ηί

(35)

В случае нормального распределения поперечных сечений по кривой Гаусса радиус эффек-

Таблица 22.—И змерение эффективной С. древесин электроосмотическим способом

(по А. Дж. Стемму).

Вид древесины	Плотность	Поперечное сечение эффективных скважин, отнесенное к полной площади древесины, %
		*1	* 2	*3
Ель ситковая (Picea sitchaensis)..	0,304—0,408	60,5—76,5	1,59—1,97 0,67—0,73	0,15—0,16
Кедр аляскинский (Chamaecypans nootkatensis).	0,442—0,508	61,7—63,6		0,12
Туйя, кедр западный красный (Thuja plicata).	0,200	73,6	0,41—0,46 0,68—0,75 1	j 0,11—0,12 1 0,15—0,17
Цуга, гемлок западный (Tsjga heerophylla).	0,343	75,2
! Пихта дугласова (тип скалистогорный, Pseudotsu-1 ga taxyfolia)	0,526	54.8 62.8	0,22—0,30	0,09
j Оосна западная желтая (Pinus ponderosa).	0,410		0,46—0,58	0,15

*¹ В продольном срезе. В тангентальном срезе. *³ В радиальном срезе. с чистой водой древесина получает потенциал отрицательный, т. ч. вода в приборе движется от анода к катоду, численное значение контактной разности потенциалов варьирует с видом древесины и направлением сечения, наир, в пределах 13,1—14,4mV. Результаты измерений эффективной С. сопоставлены в таблице 22. Из ф-лы (32) следует, что

ν=к, (33)

где к—коэф. постоянный для данной древесины и для данной среды, q—эффективная С.,

тивного капилляра близок к среднему. По найденному экспериментально значению ν и найденному ранее (электроосмотически или иначе) значению ν м. б. вычислен эффективный радиус г. Вместо непосредственного измерения ν Стемм предложил диференциальный способ, при котором протеканию жидкости через деревянную перегородку противостоит таковое же через калиброванную стандартна ю капиллярную трубку. В приборе, придуманном для этой цели (фигура 34), эти встречные сечения продолжаются до тех пор, пока не станут равны в силу

Таблица 23. — Данные о длине трахеид различных древесин (по А. Дж. Стемму).

1 1 Вид древесины	Длина трахеид, см
	по непосредственному промеру			по вычислению из элек-троосмотических данных
	наимень шая	средняя	наиболь шая	наимень шая	средняя	наиболь шая
J Ель ситковая (Picea sitchaensis).. ] Кедр аляскинский (Chamaecyparis nootkatensis). Туйя, кедр западный красный (Thuja plicata). Цуга, гемлок западный (Tsuga heterophylla). Пихта дугласова (тип скалистогорный, Pseudotsuga taxyfolia).. Сосна западная желтая (Pinus ponderosa).	0,18—0,24 0,31 0,18 !	0,28—0,42 0,38 0,31 0,32 1	0,37—0,54 0,45 0,37	0,32 0,31 0,33 0,31 0,32 0,30 1	1 0,38 0,35 0,38 0,38 0,38 0,35	0,52 0,46 0,53 0,55 0,50 0,57

изменившихся давлений Р_г и Р₂, измеряемых ртутными манометрами. Тогда

^ri —

nrji it 2 Я.ih^pi ’

(36)

где индекс 1 относится к испытуемой пластинке дерева, а индекс 2—к капиллярной трубке. В табл. 24 сопоставлены результаты получен-

Т а б л. 24.—Д анные по значению поперечника скважин в древесине, измеренных непосредственно с помощью продавли-вания жидкостей (по А. Дж. Стемму).

Вид древесины	Поперечник	скважины, μ
	*1	*2
Ель ситковая (Picea sit-chaensis).	22,1—22,8	26,3
Кедр аляскинский (Cha-maecyparis nootkaten-sis)..	18,2—18,4	23,1
Туйя, кедр западный красный (Thuja plicata)	18,8—21,2	27,6
Пихта дугласова (тип скалистогорный, Pseu-dotsuga taxyfolia).	18,5—20,2	20,6
Сосна западная желтая (Pinus ponderosa).	18,3—19,9	23,0
** Вычисленный по продавливанию воды. *2 Не-
посредственно измеренный.

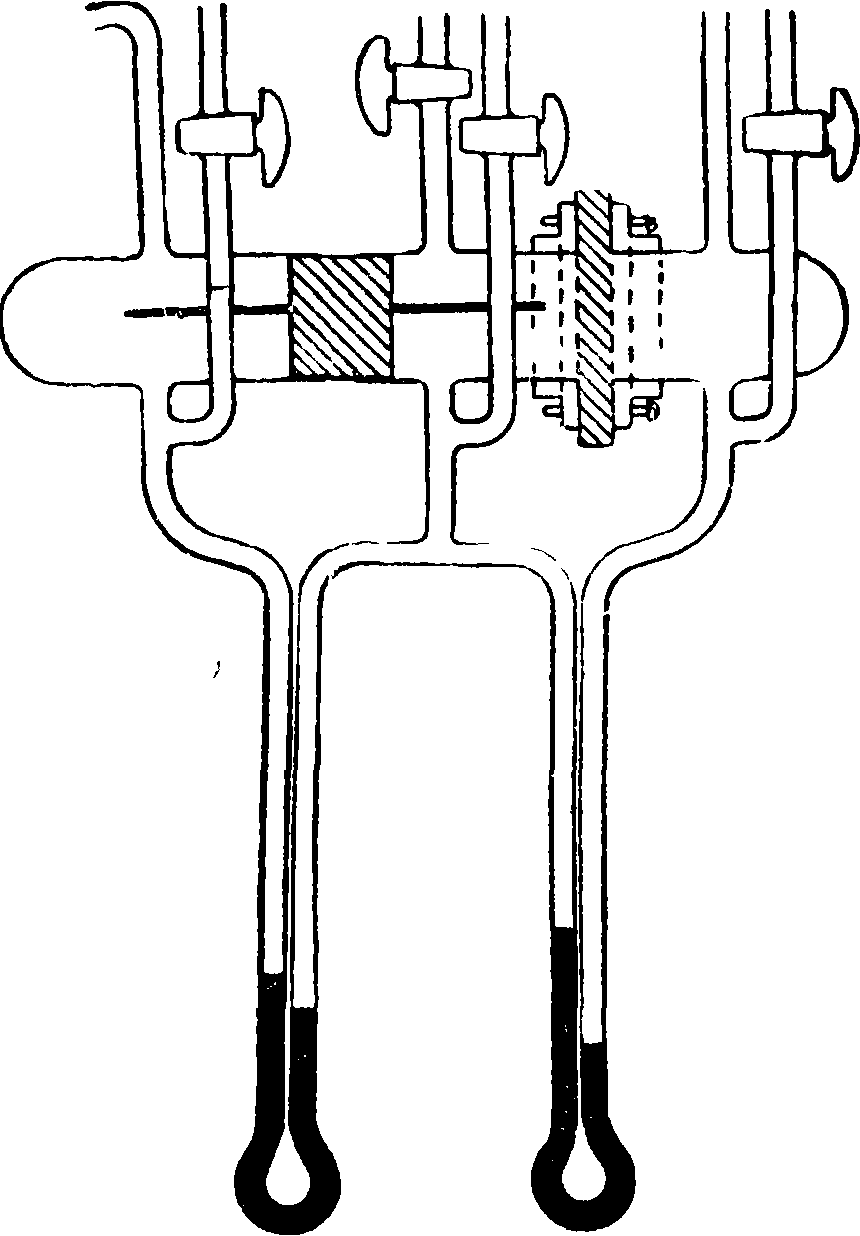
Фигура 3 4.

ных измерений. Наряду со сравнительно грубого С. растительных тканей, обусловленною наличием сосудов, устьиц и других специальных органов, растительные ткани обладают ультраскважностью, которая обусловлена междумиц ел л ирными проходами в веществе самих волокон. Этою С. обусловлены многие свойства материалов из растительных тканей и в частности древесины—свойства, неустранимые самой тщательной пропиткой (смотрите Пропитка, Наполнители).

С. пол икри стал-л и ч. тел. Все тела, состоящие из кристал-лич. многогранников, обладают скважинами, проходящими между некоторыми из соприкасающихся граней. Возникновение этих скважин объясняется темп-рными изменениями размеров, причем прилаженность граней друг к другу неизбежно нарушается. Причин этого нарушения несколько: во-первых, неоднородность химич. состава поликристалли-ческой системы с вытекающим отсюда неравенством усадки при затвердевании и коэфици-ента теплового расширения; во-вторых, неравенство усадки по разным направлениям для однородного кристалла и, в-третьих, неравенство коэф-та теплового расширения по разным кристаллографическим направлениям одного и того же коисталла. Микроскважины поликри-сталлических систем наблюдаются в частности на каменных породах. Несколько более они изучены в мет. Попытка доказать С. металлов была сделана в 1661 г. членами Флорентийской академии, подвергнувшими полый золотой шар с водою ударам молота до выступления на поверхности шара росы. В протрав ленном металлическом шлифе скважины м. б. непосредственно наблюдаемы под микроскопом. Фарадей указал на существование микроскважин в тонком листовом золоте (смотрите Золото сусальное), а Физо (1862 г.) и затем Амбронн (1893 г.) наблюдали трещины и щели в тонком слое серебра, нанесенном на стекле; ширина их по Амбронну 0,4—0,1 μ и меньше. Возникновение микроскважин в металле по Г. Там-манну составляет необходимое следствие поликристалл ическо го строения металлов, причем у граней полиэдров нет определенного кристаллографии. направления, и следовательно при затвердевании и охлаждении металла, которое сопровождается и соответственным сокращением объёма, между гранями (в силу различия ко-эфициента расширения по различным направлениям) образуются зазоры. При слабой механической обработке металлы обычно несколько уплотняются в связи с заполнением указанных зазоров между кристаллитами; но затем, при более сильной механич. обработке, между кристаллитами и в самих кристаллитах вследствие сдвигов возникают новые пустоты, и плотность металлов начинает убывать. Подвергнутые отжигу после указанной обработки металлы вновь уплотняются, так как капиллярное натяжение сваривает пластинки, образовавшиеся на плоскостях скольжения, и закрывает соответственные пустоты. В табл. 25 показаны последова-

Т а б л. 25. —Данные по уменьшению плотности металла при переходе егоиз отожженного в холоднотянутое состояние (по Г. Кальбауму и Штурму).

Металл	Уменьшение плотности при обработке, %
Сталь (фортепианная струна).	0,25
Никель ..	0,19
Чистая платина..	0,13
Алюминий (проволока).	0,13
Иридистая платина ..	0,08
Алюминий (жесть).	0,07
Кадмий..	0,06
Серебро ..	0,06
Золото ..	0,05
Медь..	0,00
Цинк..	0,00

тельные изменения плотности платины при различных обработках, а в таблице 26—разница плотности одного и того же металла в состоянии твердом и в состоянии отожженном. В связи с подобными же процессами стоит и усталость металла. Как показали исследования Юинга и Гемфри, при напряжении, меняющем знак, па зернах металла появляются линии сдвигов, постепенно увеличивающиеся в числе и затем расширяющиеся; дальнейшее накопление подобных линий ведет к появлению трещинок, к-рые, разрастаясь, перебрасываются на соседние кристаллиты и ведут к разрушению металла.

С.кристаллов. Наряду со сравнительно крупными (микроскопическими) скважинами поликристаллич. тел, проходящими как между гранями, так и внутри самих кристаллич. многогранников, в указанных телах существует система более тонких, но и более многочисленных скважин, систематически нарушающих целость кристаллической решетки отдельных кристаллич. многогранников, и свойственная кристаллич. телам как таковым, хотя бы они находились в виде одиночных кристаллов, вне связи с другими. Существование подобных ультрамикроскопич. трещинок в крист

Таблица 26. — Данные по изменению плотности пЛатипы при механич. и термин. обработке (по Г. Кальбауму и Штурму).

Способ обработки	Изменение плотности	Значение плотности
		I	II	III
Исходный материал —три платиновых цилиндра	-	21,2137	21,3060	21,4144
Проковка в стержне и прокатка	Значительное увеличение	21,4314	21,4194	21,4144
Протяжка на холоду в проволоку 1 миллиметров	Уменьшение в случае I и увеличение в случаях II и III	21,4136	21,4226	21,4233
Отжиг в течение 3 мин.	Заметное увеличение	i 21,4314	21,4323 21,4157	21,4324
Протяжка на холоду в проволоку 0,7 миллиметров	Уменьшение	21,4181		—
Отжиг в течение 3 мин.	Увеличение	21,4314	21,4315	21,4332
Протяжка на холоду в проволоку 0,4мм Отшиг в течение 3 мин. при ί° белого каления	Уменьшение	21,4142	21,4147 21,4310	21,4134
	Увеличение	21,4308		21,4317

утверждается одними исследователями на основании несоответствия между электрич. и механич. прочностью обособленных кристаллов, фактически наблюдаемой и вычисленной по данным ионной решетки, а другими—как наиболее удобный способ объяснить поведение тел, в частности кристаллических, в электрич. поле. Прочность кристаллов на растяжение примерно в 500 раз меньше теоретически вычисленного значения ее. Подобным образом электрич. крепость оказывается примерно в 100 раз меньше теоретически вычисленной (для каменной соли 1 MV/см вместо 100 MV/см). Ряд исследователей сводит наблюдаемую недостаточную электрич. крепость к внутренним трещинкам, которые облегчают электрич. пробой. Размер трещинок Грифите и Вольф, а также В. Фойгт, Селла и Г. Мюллер устанавливают в 0,01—0,1 μ, а другие исследователи в 0,5—0,02μ по длине и 0,001 μ по ширине. В. Гевеши и многие другие полагают, что электропроводность кристалла происходит именно за счет указанных трещин, из стенок которых легче вырываются ионы и в зазорах которых могут циркулировать ионы конденсирующегося водяного пара. На основании указанных и других соображений одиночный кристалл уже не м. б. рассматриваем как состоящий из единой, нигде не нарушаемой, кристаллич. решетки, но должен считаться совокупностью б. или м. хорошо связанных обломков кристаллич. решетки, причем соответственные кристаллографии. оси во всех участках тела сохраняют свое направление, но периодичность узлов от участка к участку нарушается. Т. о. по своему строению одиночный кристалл в известном смысле м. б. сравниваем с поликристаллич. телом, но с соответственным увеличением масштаба и, если идти далее в сторону увеличения масштаба, то возможно сопоставление с горными образованиями, распадающимися на разделенные трещинами отдельности.

Скважность и влажность. Наличие тонких скважин во всех телах, особенно природных, ведет к особой форме равновесия между водяным паром окружающей атмосферы и заключенной или скопляющейся в этих скважинах капиллярной воды, причем эта вода содержит в себе растворенные газы и различные электролиты. При научном изучении естественных тел и при техническом использовании их нередко недостаточно учитывают эту влагу, вследствие чего возникают теоретич. и практич. ошибки,—в частности наир, при химич. анализах и при таком использовании материалов, для которого присутствие влаги, хотя бы и в небольшом количестве, м. б. существенно важно (например электрич. изоляция). Как указывает В. И. Вернадский, «мы не знаем в природе ни одного твердого тела, которое не имело бы в своем составе воды». До t° ниже 100° вода удаляется из всевозможных природных тел от сотых долей % до^ нескольких % влаги; минералы и горные породы, представляющиеся нам сухими, содержат влаги от 0,05 до 3,5% по весу. Эта вода частью уходит при 100°, частью при более высокой t° до 300° и более. При этом полное удаление воды из многих тел происходит не раньше как при t° разложения самого тела. Капиллярную воду повидимому следует представлять в виде пленочной воды, проницающей сплошь весь минерал или горную породу, как губку. Так например’ согласно опытам А. Уайтмана диффузия йодистого калия в мраморе, помещенном во влажную атмосферу, идет количественно так, как будто весь кусок мрамора представляет сплошную массу воды равных ему объёма и формы. Капиллярная вода не есть вода чистая и содержит газа не меньше η-КГ³ %, а твердых компонентов не меньше η· 10"⁵ и до 40% и более, то есть может быть пресной (3-10“⁸—МО"¹⁰ % примеси), соленой (МО¹— 5,0% примеси) и рассолом (5—40% примеси).

2п-т

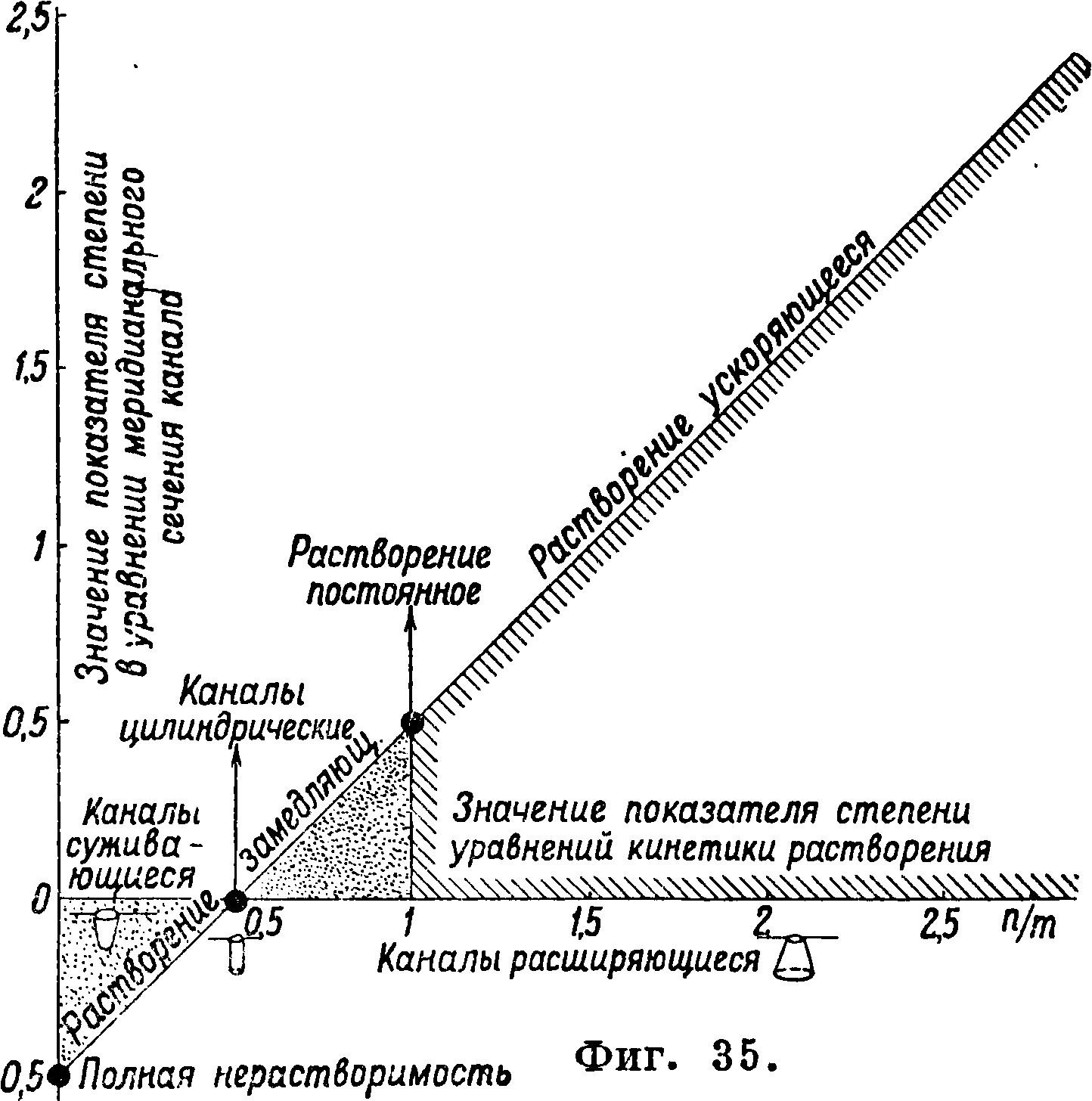
Значение этой конденсации влаги в скважинах еще не учтено в его полном объёме и лишь в последнее время начинает проникать в разные области познания твердого вещества (теория изоляционных материалов П. Бенингра, теория почвенных вод А. Ф.Лебедева и т. д.); однако в ближайшем будущем можно предвидеть углубление в эти всеобще распространенные процессы.

Установление формы скважин. В рассуждениях о С., проницаемой для газов

Тела с зернистой нерастворимой фазой

Тела со скорое гью растворения быстро возрастающей и стремящейся к бесконечности; тело разрушается

Тела, представляющие двухфазные дисперсные системы.

Тела с зернистой растворимой фазой

I I

Тела со скоростью Тела со растворения бы- скоростью стро убывающей и растворе-в определены, мо- ния возра-мент становящей- стающей ся нулем; тело по- η > т лучает изъязвленную поверхность

Тела с каналами расширяющимися:

2 п > т

I

I

Тела со скоростью растворения постоянной п=т

Тела со скоростью растворения убывающей п < т

Тела с каналообразной растворимой фазой

Ϊ

Тела с каналами цилиндрическими 2 η=m

i

Тела со скоростью растворения убывающей 2 п=т

Тела с каналами суживающимися 2 η < m

i

Тела со скоростью растворения убывающей 2 η < m

Тела со склубле-ниями каналообразной растворимой фазой

Тела со скоростью растворения сперва либо возрастающей, либо постоянной, либо убывающей, но потом в определенный момент становя-щейся нулем и жидкостей, скважины обычно считаются цилиндрическими или по крайней мере в своей совокупности такими, что м. б. заменены эквивалентной системой скважин цилиндрических. Однако такое сужение вопроса о С. может стоять в противоречии с действительным строением тела, и далеко не всегда система цилин-дрич. эффективных скважин м. б. подобрана. Тогда кроме вопроса об эффективных размерах и числе скважин должен быть поставлен вопрос и о форме их—не каждой скважины порознь, а об эффективной форме, или о такой средней форме всех скважин, предполагаемых одинаковыми,

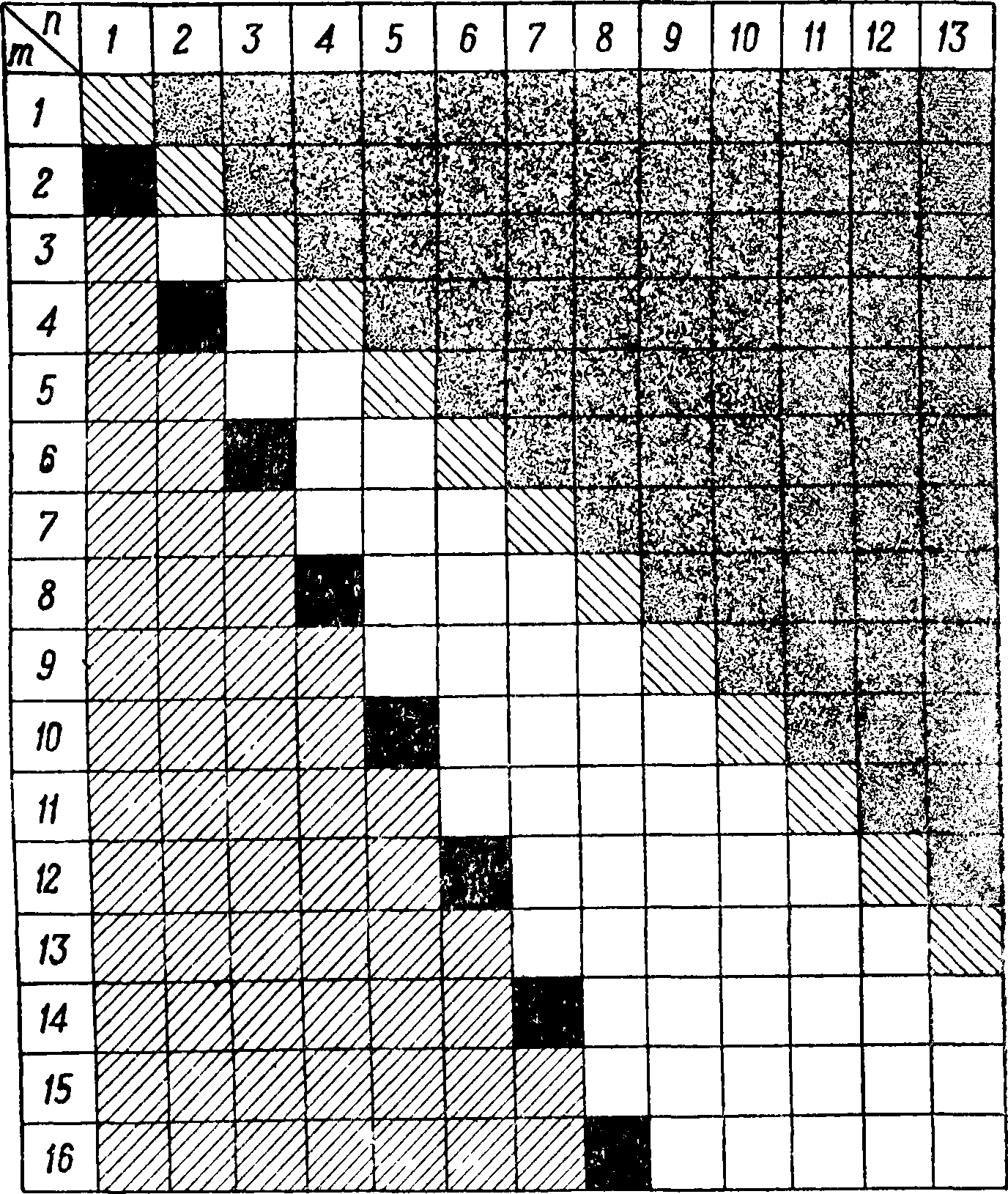
а 3

1 §

с§ ε

Растворение постоянное

Ускоряющееся растворение

Область веществ В С цилиндрическими каналами □ С расширяющимися каналами щ С суживающимися каналами

^ IС расширяющимися каналами

^ J

Виды каналов Q

&

υ

а

Фигура 36.

к-рая могла бы дать тот же эффект, что и совокупность скзажин наличных. Такой вопрос м. б. решен для того сличая, когда скважины заполнены веществом, отличным от вещества исследуемого тела и способным подвергаться растворению в некоторой жидкой среде. Изучая ки нетику этого растворения, можно составить известное представление и об эффективной форме. Если опытно дана зависимость между количеством растворенного вещества Q и временем τ в виде

(37)

то форма канала, как тела вращения около оси, может быть выражена функцией (h), равной

, (3S)

где Н_г и Н₂ — ф-ии, зависящие от одного только h и получаемые простым способом. В частности, если зависимость Q от τ, как это часто оказывается в опыте, выражается функцией

(С 9)

(где М—любое отрицательное, а к—любое положительное число), то

f2k ~]fe -1

c+m^i, (40)

где С и Ό—постоянные. Если к—рациональное число вида ~, то меридианное сечение эффективной скважины выражается уравнением

τ-, ₇ 2 Ύΐ-m ,

У=(⁴¹>

где Е—коэф., к-рый можно вычислить простым способом. Это уравнение позволяет соответственно классифицировать все скважистые тела—двухфазные дисперсные системы (табл. 27). Графически соотношение между собою различных классов представлено на фигуре 35 и 36.

Лит.: Лебедев А. Ф., Почвенные и грунтовые воды, 3 изд., М.—Л., 1931; ПринцЕ., Гидрогеология, пер. с нем., М.—Л., 1932; Терцаги К., Основания механипи грунтов, пер. с англ., М., 1926; Наумов В. А., Химия коллоидов, 3 изд., Л.,1932; Таммани Г., Металлография, пер. с нем., М.—Л., 1931; Одинг И. А., Прочность металлов, М.—Л., 1932; Кухарей-к о И. А., К а г а и о в И. Н. и Красильщиков Б. Е., Активные угли и их применение в сахарной промышленности, Киев, 1927; Флоренский П. А. и О л а в а т и и с к и и А. С., Элементные угли, «ВЭТЭ», М., 1929, 6, стр. 225—258; Флоренский II. А., Пористость изоляторного фарфора, «Труды госуд. экспер. электротехн. ин-та», М., 1927, вып. 19; Дума некий А. В. и Струкова Е. П., Определение пористости гетеро-порозных стенок, как пример пористости яичной скорлупы, «Ж», часть хим., 1929, т. 61, вып. 3, стр. 380—391, вып. 8, стр. 124—125; ФлоренскийП. А. и Андрианов К. А., Кислотостойкость органич. диэлектриков, «Вестник электротехники», М.—Л., 1931* 5—6, стр. 83—118; Субботин М., Естественные строительные камни, Одесса, 1926; Горовиц Г. Е., Принцип Гриффитса и диэлектрич. прочность, «Ж», часть физич., 1927, т. 59, 3—4, стр. Я69, 5—6, стр. 533; Тег-z agli i К., Erdhaumechanik auf fcodenphysikal scher Grundlage, Lpz. u. W., 1925; Lung e-B eri, Chemiseh-tecbnische Untersucbungsmethoden, 7 Aufl., B., 1924; «American Society for Testing Materials», Tentative Standards, N. Y., 1928; К r i b s D. A., Length of Tracheids in Jack Pine in Relation to Their Position in the Vertical and Horizontal Axes of the Tree, «University of Minnesota Agricultural Experiment Statiori»; «Techn. Bull.»,

1928, 54, August; Bechhold H., Kolloidstudien mit der Filtrationsmethode (Ultrafiltration). «Ztschr. f. Phy-sikal. Chemie», Lpz., 1907, B. 00, 3; Bechhold H., Ultrafiltration, «Biochemisches Ztschr.», 1906, В. 6, H. 5

u. 6; B e r t a r e 1 1 i E., Ultrafiltration u. Ultrafilter, «Zentralblatt f. Bakteriologie», Jena, 1914, B. 42, 22 u. 23; Hatschek E., Die Trennung von Emulsionen durch Filtration u. Ultrafiltration, «Ztschr. f. Chemie u. Industrie der Colloide», 1888, B. 6, H. 5; Washburn E. W., «Proceed, of the National Academy of Sciences», Wsh., 1921, v. 7, p. 115 и «The Physical Review», N.Y., 1921, v. 17, p. 280; Griffith A. A., «Proceed, of the Royal Society of London», L., 1921; Wolff K., «Ztschr. f. technische Physik», Lpz., 1921, p. 209; Wolff K., «Ztschr. f. angew. Mathem. u. Mechanik», B., 1924, p. 107; Griffith u. Joffe, «Ztschr. f. Physik», B., 1924, 22, p. 286; W e i с k e r, «FTZ», 1 926, p. 1 7; Garner W. E. a. Kingmann E. E., «Trans, of the Faradey Soc.»,

1929, v. 25, p. 24 (внутренняя поверхность угпя); R u f O., Active Kohle u. ihr Adsorbtionsvermogen, «Ztschr. f. anorg. Chem.», Lpz., 1925, Jg. 38, 51, p. 1164—69; J i r о z a e-mon Inaba, Analitical Considerations Concerning the Capillary Phenomens in Sand Strata, «Memoirs of the College of Engineering», Kyushu Imperial University, 1928,

v. 5, 2, p. 93—119; S li chter C. S., Theoretical Inves

tigation cf the Motion of Ground Water, «19 Ann. Rep. of the U. S. Geological Survey», 1897—98, Part. 2, p. 295; Darapsky L., Filtergeometrie, «Ztschr. f. Mathemat. Physik», 1912, p. 7«; S 1 i c h t e r C. S., «Ann. Rep. of the U S. Geological Survey», 1899, 19, p. 311; Me С о у, Alex W., Some Effects of Capillarity on Oil Accumulation, «J. of Geol.», 1916, 24, p. 798;В echhold, Be-stinunung d. Porenarosse aus d. Durchflussigeschwindig-keit von Wasser, «Ztschr. f. physikalische Chem.», Lpz., 1909, p. 339; Bigelow S. L. a. Bartell E. E., Size of Pores on Porcelain a. Osmotic Effects, «Journ. of th- American Chemical Society», Easton, Pa, 1909, v. 31, p. 1194. П. Флоренский.