Скин-эффект

Скин-эффект, вытеснение т о к а (дословно: кожное явление), неравномерное распределение плотности переменного тока по сечению проводника, причем плотность тока убывает от поверхности проводника к его середине. Ток как бы вытесняется к поверхности проводникаблагодаря пульсации магнитного потока. Влияние С.-э. возрастает вместе с частотой тока, проводимостью, магнитной проницаемостью и поперечными размерами проводника. Кроме того С.-э. зависит от распределения соседних токов и связанных с ними магнитных полей. Вследствие С.-э. активное сопротивление провода переменному току R„ всегда больше сопротивления постоянному току R₌.

Мерой С.-э. можно считать отношение Jc =

С энергетич. точки зрения можно сл. образjm уяснить себе возникновение С.-э. При передаче электрич. энергии эта энергия распространяется вдольпроводов. Часть электромагнитной энергии проникает в провод перпендикулярно к поверхности. Скорость распространения электромагнитной волны в меди равна ~ 6 м/ск. Энергия электромагнитной волны поглощается металлом., При проникновении на половину длины волны в толщу металла амплитуды плотности тока и напряженности магнитного поля снижаются приблизительно до 4,3% их первоначальных значений на поверхности металла. При частоте в 50 Hz длина электромагнитной волны в меди равна - 6 см, а при частоте 5 000 Hz эта длина волны равна 6 миллиметров. Необходимость неравномерного распределения плотности переменного тока следует из элементарного применения закона индукции. Падение напряжения в токовых нитях, расположенных на различном расстоянии от оси провода, должен быть различным, т. к. между этими нитями пульси рует магнитный поток. Разность этих падений напряжения равна магнитному спаду, то есть скорости уменьшения магнитного потока, охваченного этими токовыми линиями.

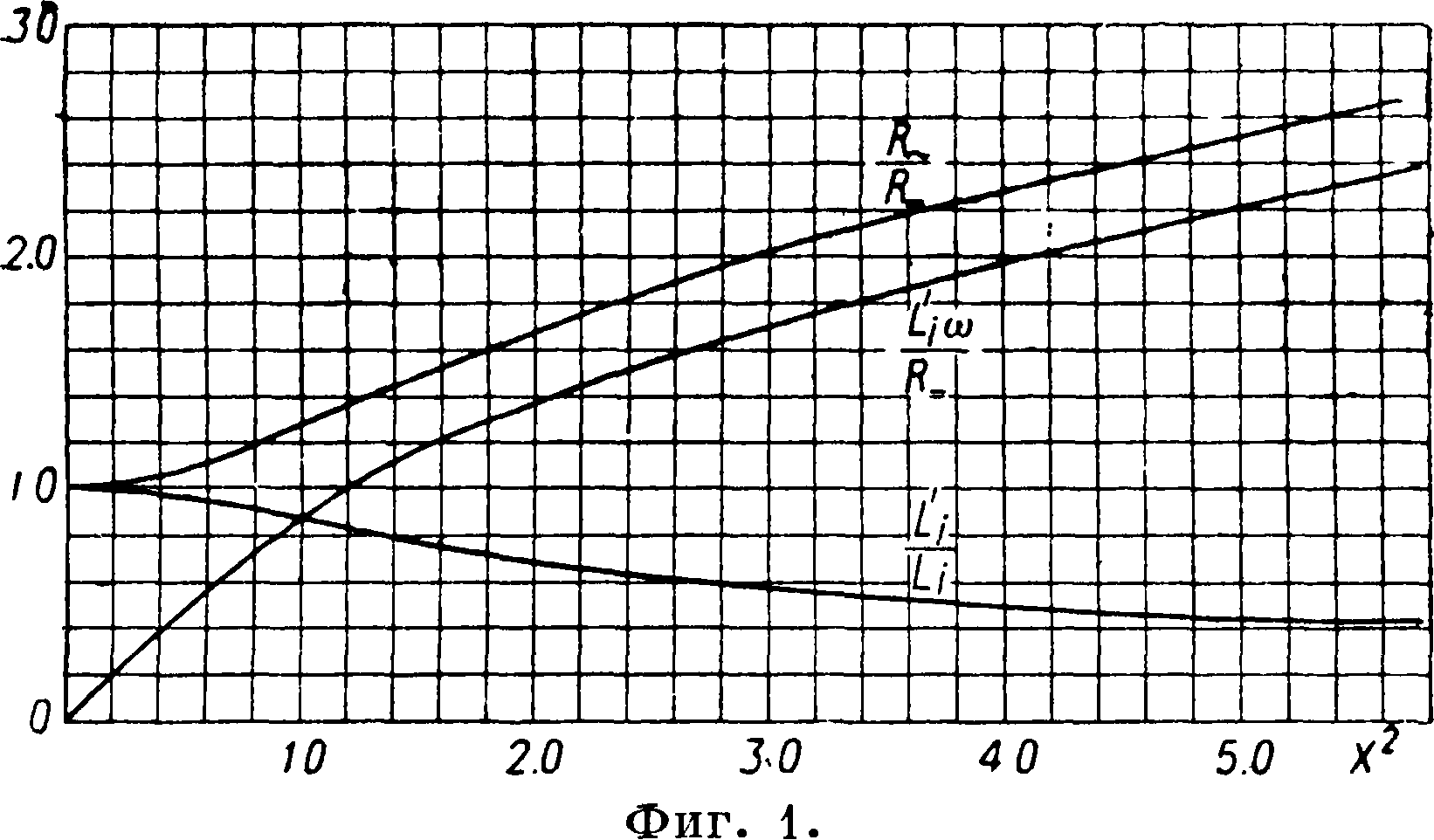
Прямолинейный круглый провод. С.-э. в уединенном цилиндрич. проводе зависит от отношения внутреннего реактивного сопротивления провода Li=~ μω к его омич, сопротивлению при постоянном токе —. Это отношение

_κ? _/^лла2(° Li(о ^κ 2ρ ⁼ ’

где μ—магнитная проницаемость, ω—круговая частота тока, а—радиус провода, ρ—удельное сопротивление провода, —сопротивление постоянному току единицы длины данного провода. Одновременно с увеличением активного сопротивления уменьшается при С.-э. внутреннее реактивное сопротивление провода L· · ω. На фигура 1 и в таблице даны значения, — и ^ в ф-ии κ².

*2	R ~ R =	Li ω R==	Li Li
0,5	1,078	0,4806	0,9612
0,55	1,094	0,52i6	0,8538
0,60	1,111	0,5674	0,9457
0,65	1,127	0,6092	0,9372
0,70	1,144	0,6500	0,92o6
0,75	1,164	0,6897	0,9196
0,80	1,183	0,7279	0,9099
0,85	1,203	0,7653	0,9003
0,90	1,223	0,8015	0,8906
0,95	1,244	0,8365	0,8805
1,00	1,264	0,8/05	0,8705
1,10	1,308	0,9351	0,8501
1,20	1,351	0,9960	0,8300
1,30	1,393	1,052	0,8092
1,40	1,437	, 1,106	0,7900
1,50	1,479	1,157	0,7713
1,60	1,520	1,205	0,7531
1,70	1,561	1,250	0,7353
1,80	1,601	1,293	0,7183 j
1,90	1,641	1,334	0,7017 !
2,00	1,678	1,373	0,6835
2,20	1,750	1,446	0,6573
2,40	1,820	1,516	0,6317
2,60	1,885	1,580	0,6077

Для значений κ² < 0,5 с погрешностью, меньшей 0,5%, можно написать приближенно:

= 1

κ4

LjQ> R_

Для значений κ² ^ 2,5 С.-э. выражается приближенными ф-лами (Зоммерфельд) с погрешностью < 0,5%:

+ 2 + 11 R₌ 4 ^ 61 κ

Ыа ₌ „а__IL.

64*

128 *2

Приведем еще таблицу значений (Потье):

*2.	0,5	1	1,5	2,0	2,5		3,0-
R~	. 1,078	1,265	1,479	1,678	1,853		2,007
R ₌ * ‘	. 1,078	1,265	1,479
*2.	3,5	4,0	4,5	5	8	10	26
R„	. 2,146	2,274	2,394	2,507	3,095	3,415	3,798·
R₌ * ‘	. 2,146	2,274	2,394

Следует отметить, что для одного и того же материала отношение не меняется, если остается постоянным от², например для телефонного провода α= 1 миллиметров, ω=2π · 5 000 или для провода сильного тока а — 10 миллиметров, ω=314. Для выво-

да ф-л распределения плотности тока Δ и напряженности магнитного поля Н пишут закон полного тока и закон индукции, связывающий

этивеличины при установившемся синусообразном токе, и получают после преобразований диференциальные ур-ия цилиндрич. ф-ий:

dx^{2 1} х dx

о,

dsff

dx²

1 d_H x dx

+ (^г-Й

Л=О,

где х²=~τ²μωλ 10~⁸j=κ²Γ²; j=— 1; г—расстояние от оси; μ—магнитная проницаемость в F/см (для воздуха μ₀=1,256 · 10“⁸F/c.m), Я=^

удельная проводимость в мо-см. Интеграл этих ур-ий с учетом граничных условий дает для С.-э. выражение:

Z _ R^+jLio) __kal₀(xa)

R₌ β_ ~ 2 Ι_χ{κα) ⁵

где 1₀(х)—Бесселева ф-ия нулевого порядка первого рода, 1_г(х)—Бесселева ф-ия первого

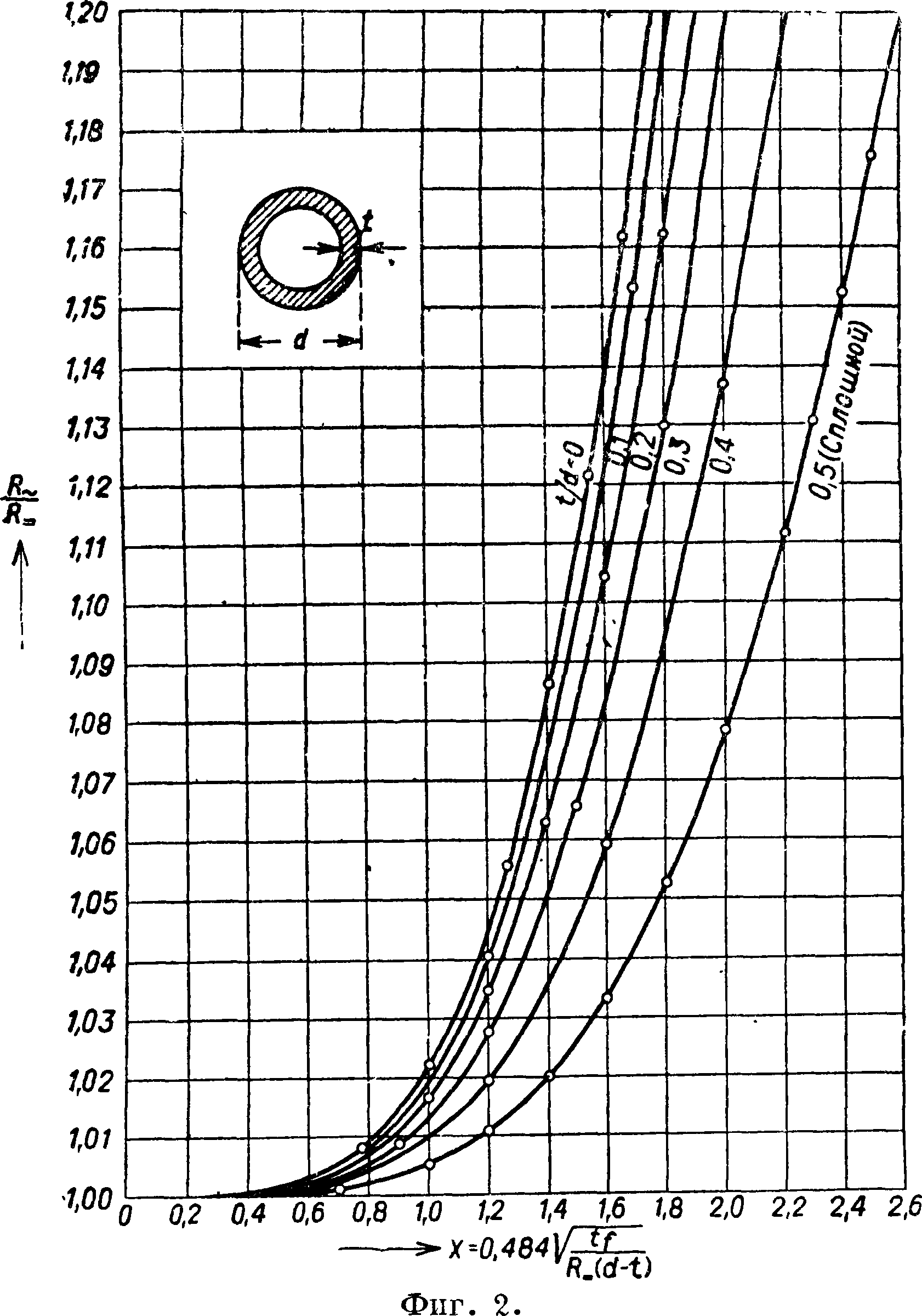
порядка первого рода. В случае полых проводов интегрирование диференциальных ур-ий оказывается сложнее, т. к. кроме ф-ий первого рода появляются еще ф-ии второго рода. A. W. Ewan [^г] произвел подобный расчет для трубчатых проводов. На фигуре 2 дано отношение в ф-ии от

*=0,484/" idktj’

где t—толщина трубы, d—диам. трубы, /— частота тока в герцах, R—сопротивление трубы в Ω /т. На фигуре 2 даны кривые для различных значений

Биметаллические провода. В этом случае надо интегрировать диференциальные ур-ия отдельно для внутренней жилы и отдельно для внешнего цилиндра, а затем использовать условия непрерывности на границах. Для расчета применяют также формулу для отношения тока в биметаллич. проводе к току в эквивалентном сплошном проводе:

1бим. ^_ 2 1 1

¹ сплоти. п хb I_х (xb)

где

УС /i

/₀(*а)— Ι_χ(χ_χα)~Ι_χ(κα) — /„(* _xa)

Λ1 Λι

ч>=——-1--¹--;

— Π (KiVA + j- Ι₀(κ_χα)Β *ι ^λι

A=Ι₀(κα)Ν₀(κϋ) — Ι₀(κ&)Α₀(κα);

В=Ι₀(κδ)^₁(κα) — Ι_χ{κα)Ν^{κΙ)

Ν₀₎ Ν_χ—цилиндрич. ф-ии нулевого и первого порядка второго рода, 2b—внешний диам. провода, 2а—диам. внутренней жилы, λ и λ_χ— проводимость внешнего и внутреннего металла;

κ²=— ]μωλ · 10“⁸,

«i=— ]μ₁ωλ₁ · ΙΟ"⁸.

Расчет для биметаллич. проводов медь-железо приведен А. А. Снарским [²].

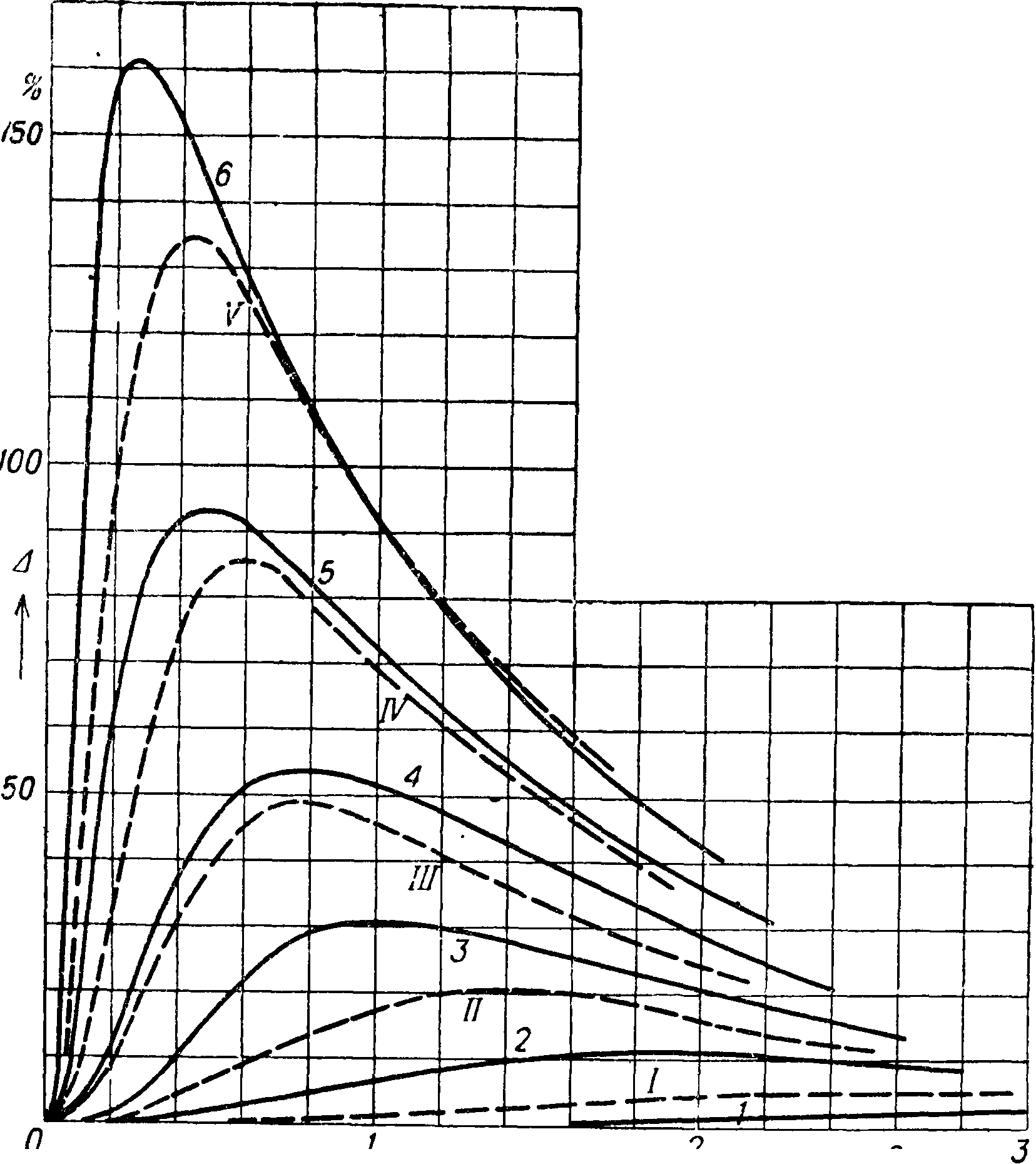
Железные провода. С.-э. железных проводов весьма значителен благодаря большой проницаемости,но приведенные ф-лы в этом случае неприменимы, так как μ зависит от плотности тока. На фигуреЗ приведено приращение эффективного сопротивления в %, определенное экспериментально при 50 Hz в ф-ии от

А/мм“

Фигура 3.

плотности тока для железа, обладающего удельной проводимостью 7,3 и временным сопротивлением на разрыв 70 килограмм /мм². Кривые 1—6 относятся соответственно к проводам диаметром

1—6 миллиметров. Кривые I—V относятся к кабелям, свитым из 7 жил, имеющих соответственно диам. 1—5 миллиметров. Для плоских пластин С.-э. определяется по ф-ле

_ R„ _ sh 2xcf4-sin 2nd ~ K ₌ ^ Ch *2κοί — COS 2κά *

где d—толщина пластины, κ²=^.

При малых значениях κά эта формула принимает вид

1 +

(2*d)4

130

Так, для меди при со=314, μ₀=1,256 · 1<Г⁸, ~=1,8 · Ю^вй-сж;

κ_γ=1 + 0,11 d⁴.

Сопротивление пластины толщиной в 1 гл? увеличивается на 11% из-за С.-э. При больших значениях κά приближенная формула принимает вид

κ_τ=κά=2π i//Я10"⁹ · d.

С.-э. в пазах электричес ких маши н. Если в пазу электрич. машины расположено друг над другом т соединенных последовательно стержней прямоугольного сечения, то отношение потерь на нагревание в этих проводах при переменном токе к потерям при постоянном токе определяется по ф-ле:

1 +

где α= —отношение неактивной длины к ак-

тивной длине провода;

h—высота стержня, b—ширина стержня, а— ширина паза, λ—удельная проводимость меди (при60° λ^50), /—частота;

ψ(ί)

- sh 2f + sin 2ξ _t

* ch~2$- COS 2ξ ’

Ψ(ξ)=2ξ

sh ξ- sin ξ ch £-f cos ξ

Эти значения м. б. взяты из следующих данных:

ξ.	0	0,2	0,4	0,6	0,8	1,0
4(ξ).	1,0	1,0	1,002	1,011	1,035	1,086
ν(£).	0	0,0005	0,0085	0,0129	0,1343	0,32
ξ.	1,5	2,0	3	4	5
<Ρ(£) - - -	1,38	1,9	3,0	⁴,ο	5,0
Ψ(ξ) - - -	1,41	3,25	6,52	8,1	10,0

Более сложные случаи исследованы в специальных работах. Я. Шпильрайн.

При токах высоких частот (радиочас-^L

тот) можно для нахождения прямолинейных проводов пользоваться приближенной ф-лой [³]

Й=р=²’³⁵йг где d—диам. провода (имеющего μ=1) в миллиметров, а λ—длина волны в км (λ=с — скорость света в км/ск, f —частота в Hz). В случае получения величины по расчету <1, следует считать=1.

Когда проводсветаут в катушку, распределение тока в части одного витка видоизменяется от действия соседних витков. Абрагам и Блохи [⁴] для расчета нового увеличения сопротивления, вызываемого распределением соседних токов и связанных с ними магнитных полей, дали ф-лу

R ~кат-> R~

3=1+00-1)1^

где q₀—параметр, зависящий от отношения шага намотки к диам. провода (в миллиметров), определяемый графически^] или из следующих данных:

Шаг катушки 1 2 3456789 10

Диам. провода 3,4 1,95 1,53 1,3 1,2 1,15 1,1 1,05 1,03 1

Значения]/"Е—^определяются графически [⁵] или м. б. взяты из следующих данных:

прир 1 1,2 1,4 1,6 1,8 2 3 4 5 7 9 10

]/"-Eui о О, 41 0,51 0,62 0,66 0,71 0,82 0,86 0,89 0,92 0,93 0,94

По тем же источникам [⁴,⁵] для учета увеличения сопротивления от неквазлстационарности тока по всей длине провода в катушке (когда частота f близка к собственной частоте катушки /₀) следует найденное по предыдущему значение R умножать еще на коэфициент т, определяемый в ф-ии от графически [⁵] или из данных:

/о

Е о ОД 0,2 0,3 0,4

/о т 1 0,95 0,83 0,65 0,5

Т. о. для токов радиочастотных общее увеличение сопротивления провода вследствие С.-э. определяется в самом общем случае как

= pqm.

В. Баженов.

Лит ; ⁴) E w а η A. W., «General Electric Review», Ν. Y., 1930, ν. 33, ρ. 249; ²) Снарский А., Биме-таллич. провода для воздушных линий связи, М.—Л., 193 2; ³) М e s η у R., Usage des cadres et radiogoniomOt-rie, P., 1925; 0 Abraham H., Bloch L. et В 1 о c h E., Notice № 4269 de l’^tablissement Central du matOr.el radiotOlOgraphique, P., 1919; ⁵) Баженов В., Основы теории радиоприема, М-Л., 1930; Жане П., Общий курс электротехники, перевод с франц., т. 2, М., 1929; Френкель Я., Теория переменных токов, М.—Л., 1928· Field А. В., «Ann. Inst, of Electr. Eng.», 1905, p. 659; E m d e F., «EuM», 1908, p. 703; Rogow-ski W., «Arch. f. Elektrotechnik», B., 1913, H. 3; R i c h-ter R “, Elektrische Maschinen, В. 1—2, B., 1924—30; Richter, «Arch. f. El.», B., 1914, H. 12, 1915, H. 1, 1916 H. 1,2,1917, Η 11; S p i e 1 r e i n, Lumi6re dlec-trique, P., 1914; Miller J. M., «Bull, of the Bureau of Standards», Wsh., 1915, p. 259; E r m о 1 a e v A., «Arch f El.», B., 1930, B. 23, p. 101; J a h n k e E. u. EmdeF., Funktionentafeln mit Formeln u. Kurven, 2 Aufl B.—Mch., 1923; Stutt M., «Arch. f. Elektrotechnik», B., 1 927, B. 17, p. 533—35, B. 18, p. 282, 1 919, B. 8 p. 190—194; Cockcroft J., Skin Effect m Rectangular Conductors at High Frequencies, «Proceedings of the Royal Society of London», L., 1929, p. 533_542 Я. Шпильрзин.