> Техника, страница 80 > Скорость критическая

Скорость критическая

Скорость критическая поршневых двигателей, или критич. число оборотов рабочего вала таких двигателей. Под критич. скоростью следует понимать такое количество оборотов рабочего вала, при к-ром периодически изменяющиеся силы и моменты двигателя вызывают во всем двигателе, в одной или нескольких его основных частях или в связанном с ним фундаменте и тому подобное. более или менее резкие вибрации, вредно влияющие на правильную работу двигателя. хранения п л о- Зная периоды изменения этих сил и моментов. мы можем разложить их на составляющие гармоники (смотрите Гармонический анализ) и исследовать влияние каждой из этих гармоник на упомянутые вибрации. Каждая из этих составляющих гармоник способна вызывать соответствующие вибрации, если собственный период упругого колебания вибрирующего двигателя или его частей совпадает с периодом данной гармоники или сравняется с тройным, пятерным и т. д. периодом этой гармоники (смотрите Колебательное движение). Скорость двигателя (количества оборотов его вала), достигнутая при этом, носит название критической по отношению к данной гармонике. Т. о., если период какой-либо из составляющих гармоник равняется например 0,1 ск. то эта гармоника и вместе с ней соответствующая скорость двигателя будет критической по отношению к тем частям двигателя, собственный период колебания которых равняется 0,1 ск., 0,3 ск. 0,5 ск., 0,7 ск. и т. д. Доказать это положение можно следующим образом.

Представим себе например, что тангенциальные силы на кривошипе какого-либо двигателя изменяются по изображенной на фигуре 1 гармония.

	Г----АА УК.
iy {	W7 Ху

Фигура 1.

кривой с периодом аb=t ск. Если упругий вал этого двигателя или какая-либо связанная с ним часть, например пропеллер, обладает собственным периодом вибраций, также равным t ск., то синхронизация этих периодов неминуемо должна вызвать чрезвычайное усиление колебательных движений вибрирующего тела. Для упрощения рассмотрения вопроса можно представить себе вал двигателя подверженным скручиванию двумя силами: одной—постоянной Р, которая равняется расстоянию средней линии нашей кривой от нулевой линии и не может вызвать вибраций, и другой—переменной Q, изменяющейся от наибольшей положительной до наибольшей отрицательной величины, причем изменение этой силы происходит по показанной на фиг, 1 гармония, кривой. Т. о. мы в нашем примере можем рассматривать только силу Q. Эти силы при синхронизации их периодов с естественным (собственным) периодом вибраций рассматриваемой части двигателя увеличивают эти вибрации до тех пор, пока импульсы молекулярных и других сил, сопровождающих эти вибрации, не начнут поглощать при каждом новом колебании импульс сил А + В=2А, величина которого равна сумме заштрихованных площадей. Когда достигается это равенство между импульсами крутильных моментов, действующих на наш вал двигателя, и импульсами внутренних молекулярных сил, являющихся следствием упругого гистерезиса, а также импульсами и другихсил, например сил трения, сопровождающих крутильные вибрации вала, последние приобретают устойчивый характер, при к-ром амплитуда колебаний становится величиной постоянной. Энергия этих импульсов превращается при этом в теплоту молекулярного движения материала вала и внешнего трения при его вибрационном движении.

При постепенном увеличении скорости двигателя выше критической постепенно уменьшаются вибрации соответственных частей, пока наконец совсем не прекратятся в тот момент, когда естественный период вибрации этих частей не станет равным 2аЬ=2t. В этом случае вибрации развиваться не могут, т. к. сумма импульсов сил Q в течение каждой половины периода вибраций и следовательно в течение всего периода равна 0. При дальнейшем увеличении скорости двигателя, когда естественный период вибрации соответствующих частей двигателя становится равным ас= Заb=3t, скорость двигателя становится снова критической, причем сумма импульсов сил Q в течение каждого периода вибрации снова становится равной импульсу 2А=А + С—В+ _D + F—Е. Как нетрудно видеть, амплитуда возникающих при этом под влиянием сил Q вибраций будет в три раза меньше амплитуды Q_x (смотрите ниже). Следовательно критич. скоростями двигателя по отношению ко всему двигателю или к какой-либо из его частей являются такие скорости его, при которых естественный период вибраций этих частей равняется £,3ί,5ί, 7 £,., где t—период изменения сил двигателя. Отсутствием вибраций этих частей отличаются такие скорости двигателя, при которых этот естественный период равняется 2t_f4t,6t,. При постепенном уменьшении скорости двигателя ниже первой критич. скорости рассматриваемые вибрации постепенно уменьшаются и становятся равными 0 при скорости двигателя, при которой естественный период вибраций равняется ¹/₂t. При дальнейшем уменьшении скоростей двигателя вибрации развиваться не могут.

Высказанное нами положение, касающееся критических скоростей двигателя, можно формулировать также и сл. обр.: данная скорость двигателя будет критическою по отношению к тем частям двигателя, собственный период вибраций которых равен нечетному числу периодов ί, то есть равен t, 3t, 5ί, 7ί,. Наоборот, эта же скорость будет наиболее благоприятной, не вызывающей никаких вибраций по отношению к тем частям двигателя, естественный период вибраций которых равен четному числу периодов ί, то есть равен 2ί, 4i, Gt и т. д.

Как уже было показано, при всех этих критич. скоростях двигателя импульс сил, поглощаемый упругим гистерезисом соответствующих вибрирующих частей, равен 2 А (фигура 1), причем

^=<3x1= ©а³; =05^=·.·

Отсюда

Ql ⁼ 3 ζ?3=5 ζ?5 ⁼

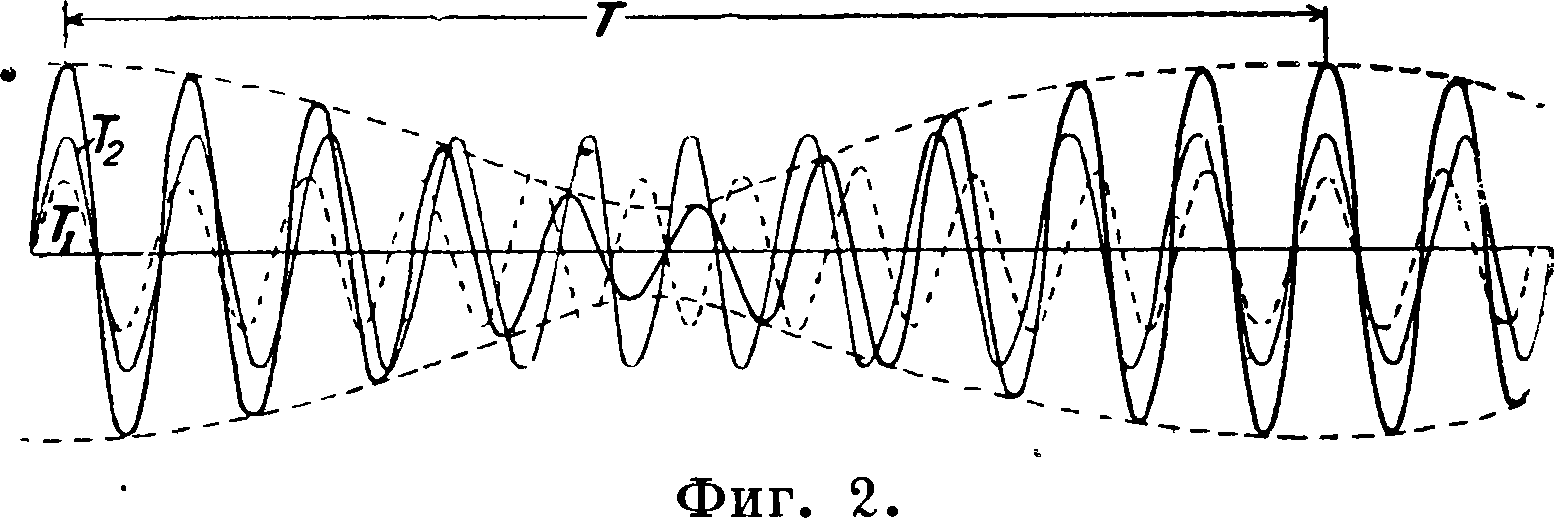
После всего сказанного остается решить вопрос о том, каковы будут колебания упругого тела, когда его собственный период колебания не совпадает ни с четным ни с нечетным числом периодов внешних сил, действующих на данное тело и изменяющихся гармонически. В этом случае мы имеем дело с т. н. комбинированным колебанием с постоянно изменяющейся амплитудой, то увеличивающейся то уменьшающейся. Как его амплитуда Р, так и сдвиг фазы 0 являются величинами переменными, зависящими от времени t. Подобные колебательные движения известны в физике под названием биений. Амплитуда Р определится из уравнения Р² sin² Θ + Р² cos² Θ=Р²=С sin² Ay +

+ [С + С_г cos Ayl² - С² + С + 2СС_г cos Ay, где Ay есть разность периодов. Из этой формулы видно, что амплитуда Р изменяется в пределах от ±(С + С_г) до ±(С— С_г), причем это изменение происходит в течение нек-рого периода времени Так, если бы собст венный период колебания упругого тела отличался от периода гармоники внешних сил на Vio долю последнего, то есть если бы Ау=0,1, то период Т был бы в 10 раз больше периода Т_ггармоники внешних сил. Период Т называется периодом биения и формула его пишется в виде

rji Т ιΤ 2

~ т₂-т₁⁹

где Т₂—собственный период колебания упругого тела. На фигуре 2 показан случай такого биения, когда Т₂=1,1 Т_г.

Обычно при разложении сложных периодич. сил двигателя на простые гармония, составляющие довольствуются четырьмя и во всяком случае не более как пятью порядками этих составляющих. Более высокие порядки гармоник отличаются очень малыми амплитудами и поэтому не принимаются во внимание. Т. о., если период сложной кривой сил, действующих в данном

2 · 60

четырехтактном двигателе, равен ск., где п—количество оборотов рабочего вала в минуту и к—число цилиндров двигателя, то при разложении этой кривой на четыре составляющие гармоники мы будем иметь следующие периоды гармоник, которые могут вызвать вибрации:

1-го порядка 2-го порядка 3-го порядка 4-го порядка

2 -60

- СК.

2 · 60 2 · п · к

СК.

2 -60 3 - п к

СК.

2 · 60 4 ·η· к

СК.

Каждая из этих гармоник может вызвать, как уже было показано, вибрации с периодом, равным периоду этой гармоники, а также с периодом в 3, 5, 7,. раз большим. Т. о. данные силы могут вызвать вибрации со след, периодами:

1- го порядка:

120 В60 600 840

пк ⁹ пк ⁹ пк ⁹ пк ⁹

2- го порядка:

60 180 300 420

пк ⁹ пк ⁹ пк ⁹ пк⁹

3- го порядка:

40

nk ⁹

4- го порядка:

зо

nk ⁹

120	200	280
nk 9	nk 9	nk
90	150	210
nk 9	nk 9	nk

ск. ск.

Обозначим такой собственный период колебания двигателя или одной из его частей через S. Тогда критич. скоростями двигателя будут следующие:

для составляющих гармоник 1-го порядка:

120 360

Sk

Sk

для составляющих гармоник

_ 60 180 300

ⁿ~Sk’ Ж⁹ Ж⁹ * * для гармоник 3-го порядка:

_ 40 120 200

ⁿ~sk’ Ж⁹ Sk ⁹ *·

2-го порядка: об/м.,

, об/м.,

для гармоник 4-го порядка:

30 90 150 -.

ⁿ~Sk⁹ Sk⁹

Проиллюстрируем высказанные положения практич. примером. Допустим, мы имеем 6-цилиндровый четырехтактный двигатель, собственный период крутильных колебаний вала которого S=0,05 ск. Тогда критич. оборотами двигателя по отношению к этим крутильным колебаниям будут следующие. Для составляю-

щих гармоник: 1-го порядка.	400,	1 200,	2 000,	2 800,.	об/м.
2-го порядка.	200,	600,	1 000,	1 400,.	об/м.
3-го порядка.	138,	400,	667,	983,.	об/м.
4-го порядка.	100,	300,	500,	700,.	об/м.

Не все перечисленные критич. обороты двигателя будут сопровождаться одинаково резкими вибрационными явлениями и будут в одинаковой степени вредно отражаться на работе двигателя. Энергия каждого вибрационного колебания пропорциональна квадрату амплитуды и равна

Е=а · Q²,

где а—нек-рая постоянная. Т. о. величина энергии, затрачиваемой при каждом периоде вибрации, зависит только от амплитуды и не зависит от длины периода. Количество энергии, затраченное в единицу времени, равно

Если обозначить амплитуды наших составляющих гармоник через Q_l4 Q_2f ζ?₃ “ Q4> ^{то мы} найдем, что амплитуды колебаний, вызванных этими гармониками, будут пропорциональны следующим величинам. Для колебаний, вызванных составляющей гармоникой 1-го порядка, будут соответственно пропорциональны Q_l9Vs Яг, ^г!ь Qi,.

Для колебаний, вызванных гармоникой

2- го порядка. Q₂, V3Q2, V5Q2, ···

3- го порядка. Q₃, V3Q3, V5Q3, ···

4- го порядка. Qi, V3Q4, ¹/sQi, ···

Величина энергии, затраченной на эти колебания в единицу времени, напишется в виде: для 1-й гармоники:

Qi-bQl -- Q, £_oQI,

313

для 2-й гармоники:

bQl, т®>-

Как видно из этого, величина энергии вибраций будет максимальной при п=400, 200 и 133 об/м. Для всех других критич. оборотов она рез ко уменьшается. В конечном итоге из всех перечисленных критич. оборотов можно рассматривать как опасные лишь п=400, 200 и 133. При всех остальных скоростях вызываются лишь незначительные вибрации.

Остановимся теперь на тех силах (смотрите Динамика поршневых двигателей), которые могут вызывать вибрации в двигателях, и на характере этих вибраций.

А. Инерционные усилия J. Эти силы в вертикальном двигателе, показанном на фигуре 3, передаваясь через фундамент в почву, могут вызвать в последней (при синхронизации одного, трех, пяти и т. д. периодов первого порядка изменения сил J с периодом волновых движений почвы) весьма значительное усиление этих движений почвы, которые наподобие водяных волн, возникающих при падении камня на поверхность воды, могут распространяться концентрич. кругами на значительные расстояния (иногда до 1 км) от двигателя. Эти волнообразные движения почвы очень часто приво- ; дят близлежащие зда- ¹ ния в опасные ритмич. колебания. Такая синхронизация произойдет следовательно в том случае, если период колебательного движения почвы будет равен времени одного или трех, пяти,. оборотов вала двигателя. Часть второго порядка сил J может в свою очередь вызвать колебательные движения почвы (одновременно или независимо от первых колебаний), если произойдет синхронизация периода колебательных движений почвы с перио-

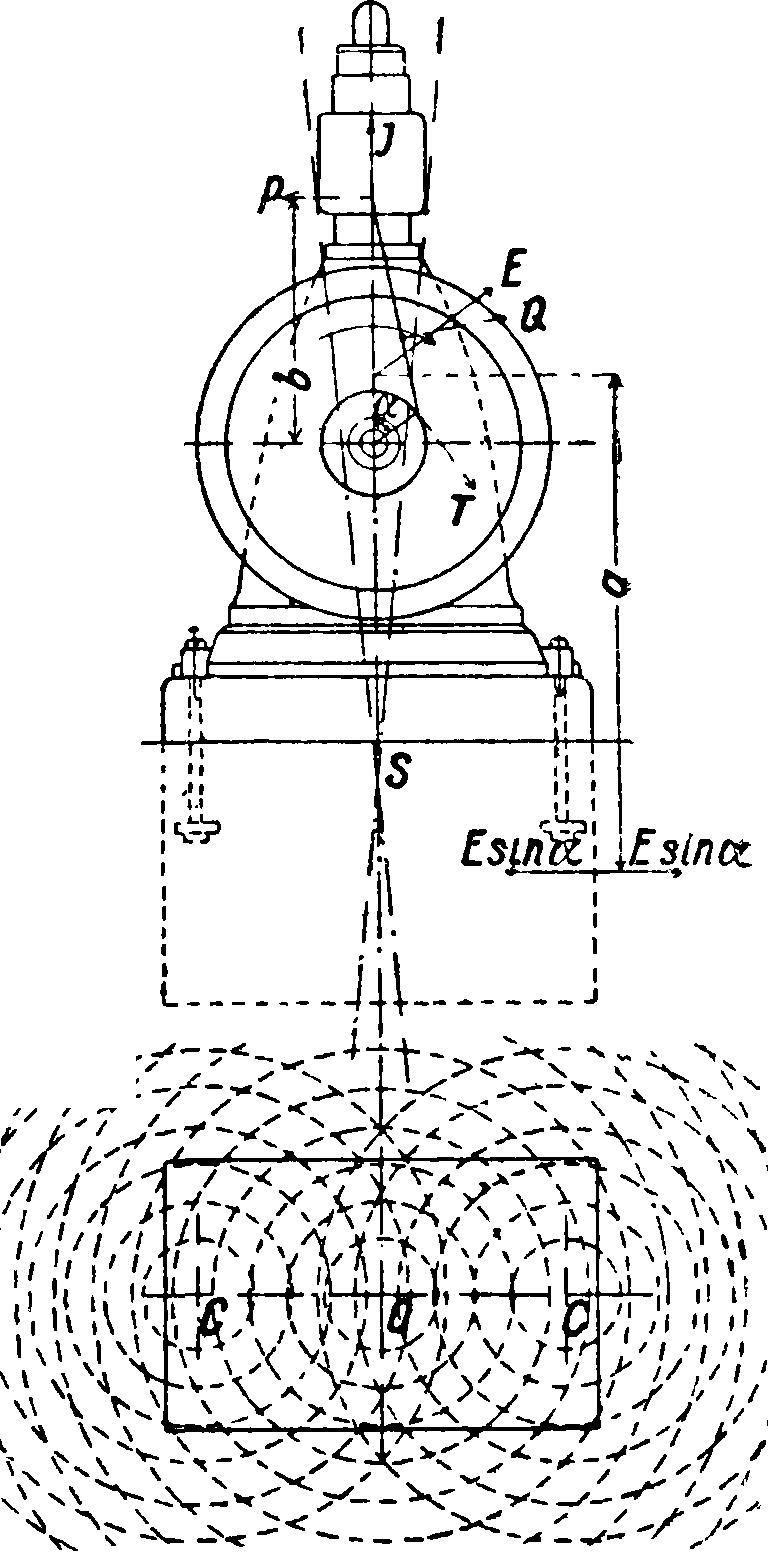
Фигура з. дом времени 7₂

³/₂, или ^б/₂, или ⁷/₂

оборота вала двигателя. Т. о., если почва обладает собственным периодом колебаний, равным к ск., критич. скоростями двигателя будут такие скорости, при которых количество оборотов вала двигателя в секунду будет т

h⁹ k

а также

_А _5_

Jk⁹ Tk⁹ 2k ’ *··

В горизонтальных двигателях инерционные силы J могут вызвать аналогичные явления колебательных движений почвы, распространяющихся также на большие расстояния от двигателя в направлении преимущественно по оси его. Эти колебательные движения почвы называются продольными в отличие от первых, уже описанных нами, называемых поперечными. Продольные колебательные движения называются часто также волнами уплотнения, и в них движение колеблющихся частиц почвы происходит в направлении распространениявсшны. Поперечные колебательные движения называются также волнами сдвига, и в них движение колеблющихся частиц почвы происходит в направлении, перпендикулярном к направлению распространения волны. Собственный период таких колебаний почвы зависит прежде всего от состава, плотности, а также и других физич. свойств ее и обыкновенно равен от 0,02 до 1 ск. и меньше. Амплитуда колебаний почвы при работе двигателей доходит до 1 миллиметров; обыкновенно—

значительно меньше. Работа, расходуемая на колебания фундаментов двигателей, достигает иногда значительных размеров—до 5% и более полезной работы двигателя.

Борьба с этим явлением возможна прежде всего путем уравновешивания (смотрите) двигателей. Если же такое уравновешивание почему-либо невозможно, необходимо рассчитать фундамент машины т. о., чтобы собственный период колебаний почвы с фундаментом был по возможности близок или равен 2£,4£, 6£,. Это требование сводится к тому, чтобы собственный период колебаний почвы с фундаментом равнялся чет

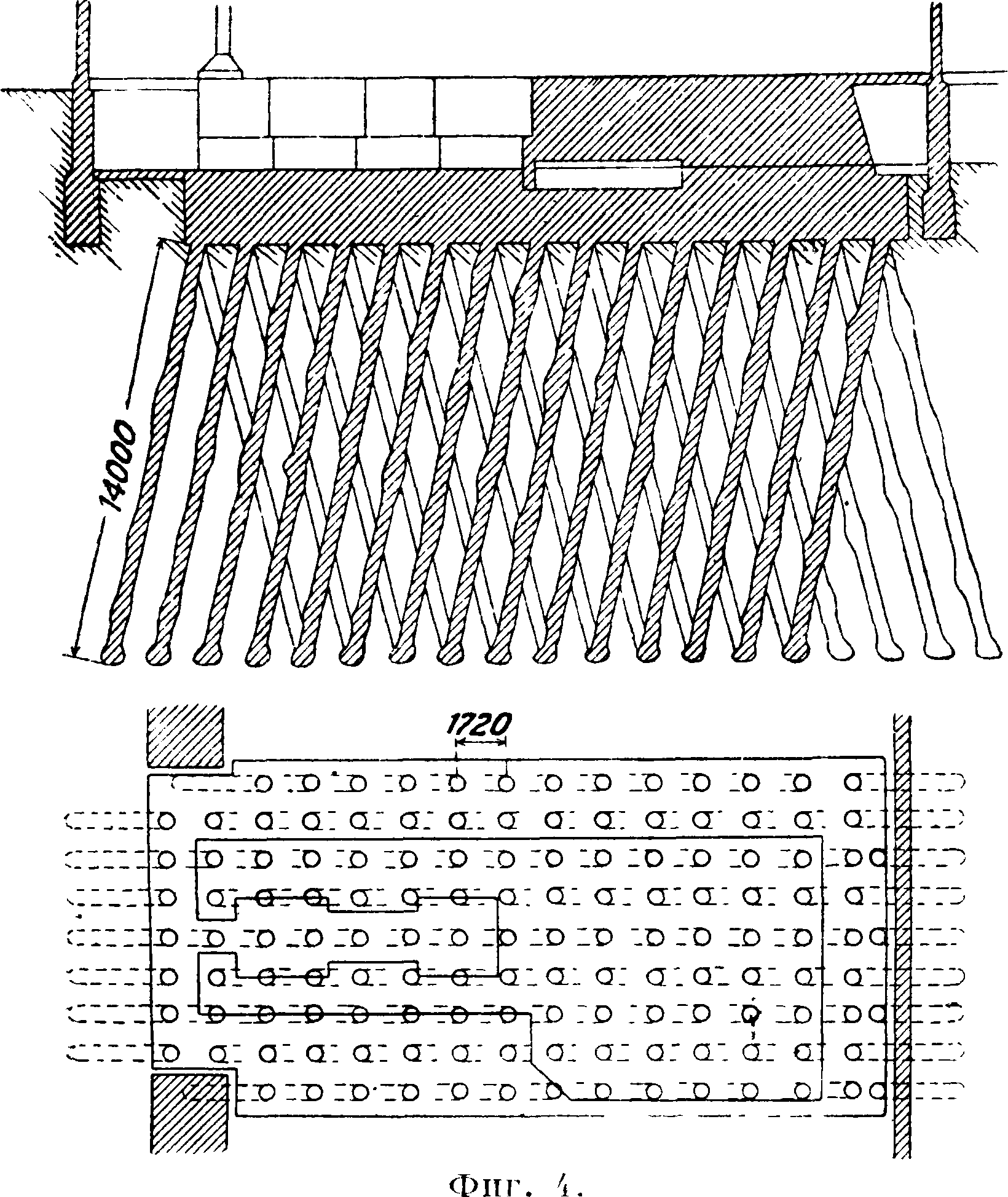
ному числу периодов одного оборота вала двигателя. При этих периодах в почве под влиянием рассматриваемых сил колебания возникнуть не могут как в отношении сил инерции лервого порядка, так и в отношении этих сил второго порядка. В виду невозможности заранее точно определить собственный период колебания почвы с фундаментом массу последнего и колеблющейся вместе с ним почвы делают возможно большей для получения большого собственного периода их колебаний (смотрите например фундамент на фигуре 4). При этом, если нечетное число периодов одной из действующих гармоник сил и совпадает с периодом колебания фундамента и почвы, амплитуды этих коле-

230обор

220

280

240" 230”

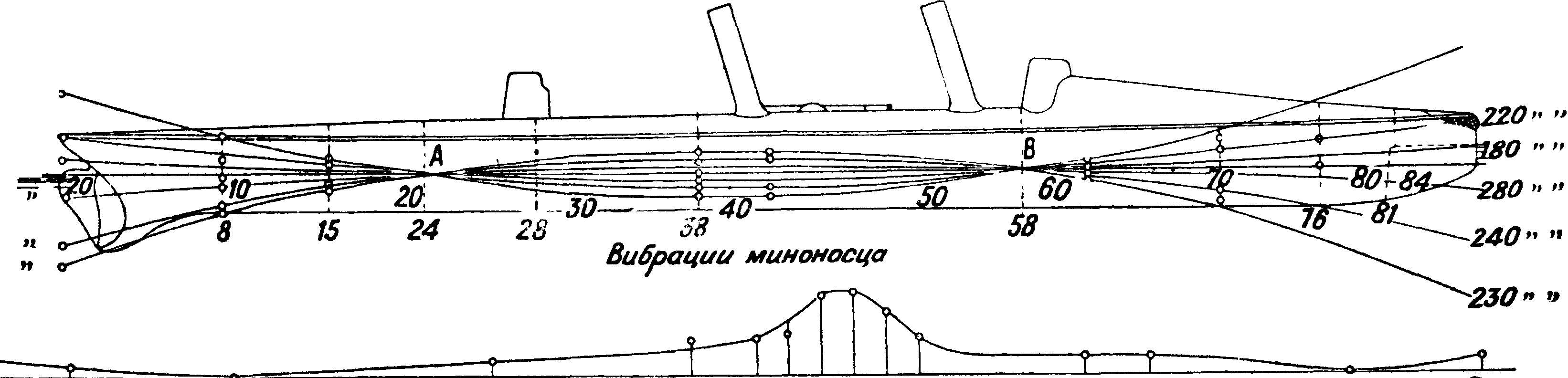
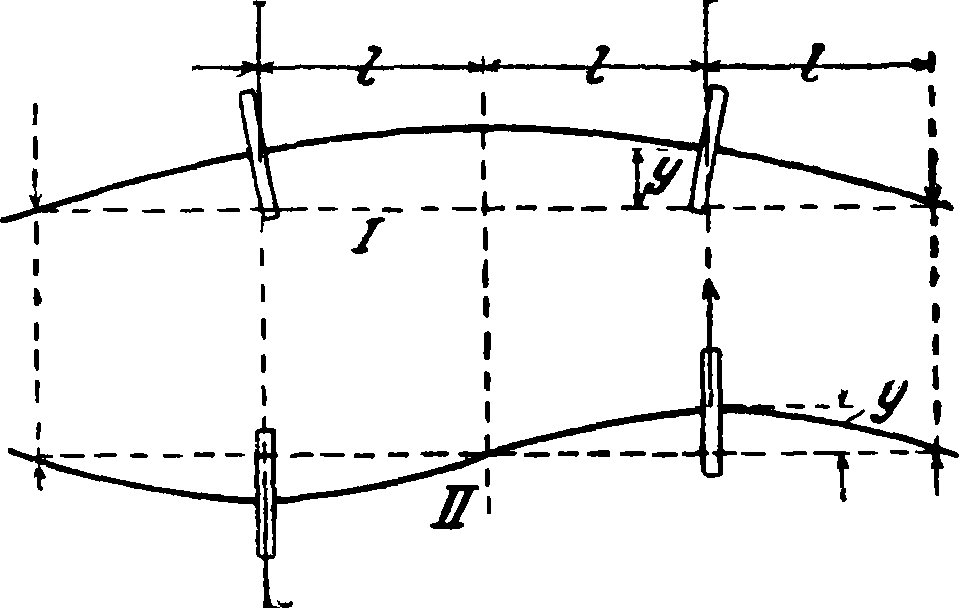
телях, покоящихся на упругих стальных балках. Весь корабль можно рассматривать как упругую балку очень сложного строения, в различных частях которой под влиянием периодич. сил двигателя могут возникнуть вибрации. Вследствие сложности строения корабля в нем может возникнуть и обыкновенно возникает большое количество вибраций (всего корабля в целом и его частей) с различными собственными периодами или, как иногда говорят, с различными «тонами», возникающими при «синхронизации» или «резонансе» этих периодов с периодами соответствующих гармоник сил двигателя. Фигура 5 показывает колебания миноносца, у которого экспериментальным путем были определены колебания при различных скоростях двигателя. Как видно из этой фигуры, колебания корпуса этого миноносца происходили около двух узловых точек А и. В. При количестве оборотов двигателя, равном 230—235 в мин., колебания корпуса судна были наиболее резкими. Увеличение и уменьшение количества оборотов двигателя сопровождалось уменьшением вибраций, достигавших минимума при 154 и 308 об/м. двигателя. Вибрации судна происходили под влиянием основной гармоники сил инерции двигателя. Как нетрудно видеть, собственный период колебания судна был около ¹/₁₇₇ ск. (77 колебаний в ск.). При синхронизации количества оборотов двигателя с количеством собственных колебаний судна или с тройным или с пятерным количеством этих колебаний вибрации судна должен быть максимальными. При совпадении количества оборотов двигателя с четным числом собственных колебаний судна вибрации последнего должны быть минимальными и хо_гд его наиболее спокойным. На фигуре 5 показаны амплитуды колебаний судна в зависимости от количества оборотов двигателя в пределах от 115 до 330 об/мин. Измерения производились по длине миноносца в точках, отмеченных на фигуре кружками.

Мерой для устранения этих вибраций судна может служить прежде всего выбор соответствующих скоростей двигателя, при которых вибраций судна не происходит. Если по каким-либо причинам скорость двигателя не м. б. изменена, необходимо прибегнуть к уравновешиванию его сил инерции и в известных случаях к выравниванию его вращательных моментов.Часто может помочь делу перемена места установки судового двигателя. Так, если вибрации судна происходят под влиянием одной лишь равнодействующей сил инерции двигателя, причем моментов эти силы не образуют, достаточно

-230обор

	Ql	&		? S5 ^ ^ ^	£
			M	<N N sj <SI <SI c, ^	N N	$ N	**

- «м ^ N

Амплитуды колебаний при различных скоростях дВигателя

Лчт.т. С

Фигура 5.

баний будут все же соответственно очень малы.

Вибрации, подобные только-что описанным, возникают очень часто в корабельных двига поместить двигатель в одной из узловых точек А или В судна. Если однако при уравновешенных силах инерции остаются неуравнове-

шенными моменты этих сил, стремящиеся опрокидывать двигатель в продольном направлении, помещение двигателя в узловых топках судна может вызвать указанные вибрации судна при синхронизации периода колебания судна с периодом моментов сил инерции двигателя. В этом случае выгоднее поместить последний между узловыми точками А и В.

Б. Центробежные силы Έ и пары сил Р b. Вертикальные составляющие этих сил слагаются с силами J, и их влияние на вибрационные явления те же, что и влияния сил J. Горизонтальные составляющие сил вызывают в почве, окружающей фундамент, продольные колебания под влиянием сил Е · sin а. Кроме этого под влиянием этих же сил на двигатель действуют пары сил а-Е sina (фигура 3), которые вместе с другими парами Р* b сил бокового давления поршней раскачивают двигатель в вертикальной плоскости поперечного сечения около некоторой неподвижной точки S, производя в окружающей фундамент почве нек-рые поперечные волнообразные движения с двумя центрами С. Колебательные движения двигателя при этом раскачивании достигают иногда весьма значительной величины. Пары сил Ε·α sin a являются при этом периодическими парами первого порядка. Пары сил Р-b состоят из пар сил, моменты которых равны и направлены в сторону, противоположную направлению вращательных моментов сил инерции, и из пар сил, моменты которых противоположно направлены и равны вращательным моментам давления газов двигателя. Как те, так и другие вращательные моменты изменяются по сложным периодич. кривым, которые м. б. разложены на простые гармоники нескольких порядков (обыкновенно ок. 4 или 5). По отношению к каждой из этих гармоник может возникнуть ряд критич. скоростей двигателя. Таких скоростей у двигателя часто может оказаться несколько. Чтобы поставить двигатель в условия наименьшей возможности колебаний под влиянием этих гармоник, необходимо сделать собственный период его вибра-щий возможно большим, соответственно увеличивая вес фундамента.

В. Тангенциальные силы на кривошипе двигателя (в результате действия сил инерции и давления газов в цилиндре). Являясь периодическими, изменяющимися по закону сложных периодич. кривых, эти силы производят неравномерное, периодически изменяющееся скручивание рабочего вала двигателя. В результате такого скручивания, при синхронизации естественного периода крутильных колебаний вала с одной из составляющих гармоник тангенциальных усилий, на валу двигателя могут возникнуть крутильные вибрации, особенно опасные в виду малого упругого гистерезиса материала вала и часто поэтому ведущие к поломкам этого вала. После всего сказанного о критич. скоростях двигателя мы можем не касаться этого вопроса для данного случая. Задачи предохранения вала двигателя от влияния этих крутильных гармоник заключаются в постройке такого вала, собственный период колебания которого не мог бы синхронизировать с нечетным числом периодов гармоник, составляющих сложную периодическую кривую тангенциальных усилий. В последующем изложении мы коснемся способа определения собственных периодов крутильных колебаний коленчатых валов. Здесь же отметим, что крутильные колебания этих валов могут служить причиною весьма значительных потерь мощности двигателей. Экспериментальные исследования показали, что эти потери при критич. скоростях двигателя составляют обычно 1—3% его мощности и нередко доходят до 10% и более.

Не останавливаясь на других возможных вибрациях в двигателях, имеющих меньшее значение, иапр. вибрациях под влиянием сил, изгибающих шатуны, вибрациях изгиба различных валов ит. д., коснемся способов определения собственных периодов вибраций коленчатых валов. Собственный период t крутильных колебаний простого цилиндрич. вала с одинаковым диаметром по всей его длине:

t=СК.,

где ·=т ~—полярный момент инерции мае-сы т вала, С—крутильная жесткость последнего, то есть момент, к-рый необходимо приложить к данному валу для того, чтобы скрутить его на угол, равный единице.

Определение собственного периода колебаний вала с массою М (фигура 6) производится по ф-ле

CZ

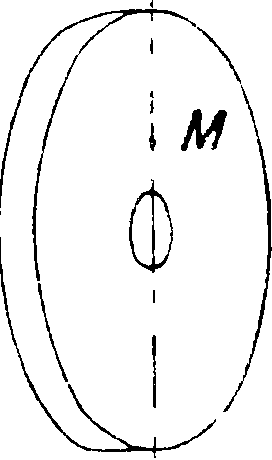
Фигура 6.

= 2π Ύ~

СК.,

j 1 + j 2

Г С*2 ^С

где J_x= ж -Q—момент инерции массы ж вала,

J₂—момент инерции массы М. Для определения собственных периодов валов сложных сечений (коленчатых и др.) необходимо привести (редуцировать) их к такому воображаемому цилиндрич. валу с одинаковым диаметром по всей длине, к-рый при одинаковых крутильных моментах скручивается н а тот же угол, на который скручивается данный вал сложного сечения. Собственный период крутильных колебаний такого воображаемого вала можно принять равным периоду колебаний данного вала. Для такого редуцирования коленчатого вала последний делится на цилиндрич. части, конические и на колена. Нахождение вала, равнозначного каждой из этих частей данного вала, производится сл. обр.

1) Цилиндрич. части вала с диам. d и длиною I будут равнозначны в отношении скручивания валу длиною 1_г и диам. d_lf тогда как угол скручивания при крутящем моменте M_d в обоих случаях будет равен у, то есть м₍1 _{1 =} м_{(1 1}.

JpG JpiG ^Lli ndf

Фиг. у=-

nd4.

здесь J_p=—; J_pl= G (модуль скольжения) равен 820 000 килограмм/см².

Отсюда получим:

h d f м

^L di ’ d*

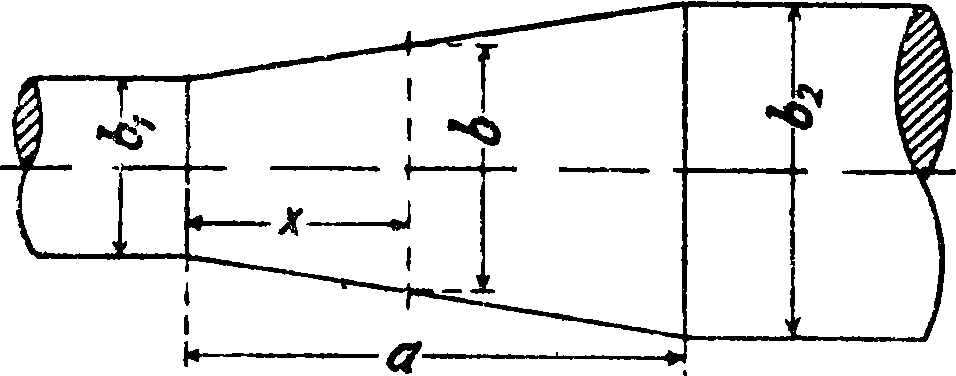
2) При редуцировании конич. частей (фигура 7) валов, если таковые имеются, а

dx

коленчатых получим:

Г. э. т. XXI.

dx =

ba- bi

^{2 2}Jkbi 3 ’

или редуцированная длина l₂ будет равна: ^ia ~ ^aa2 зТз^Г

3) Редуцирование колена кривошипного вала представляет собой чрезвычайно сложную математическую задачу, которая м. б. решена только приблизительно. Существует несколько таких приближенных решений задачи. Наиболее простой является формула Гейгера (Geiger). Согласно этой формуле редуцированная длина 1₃ кривошип-

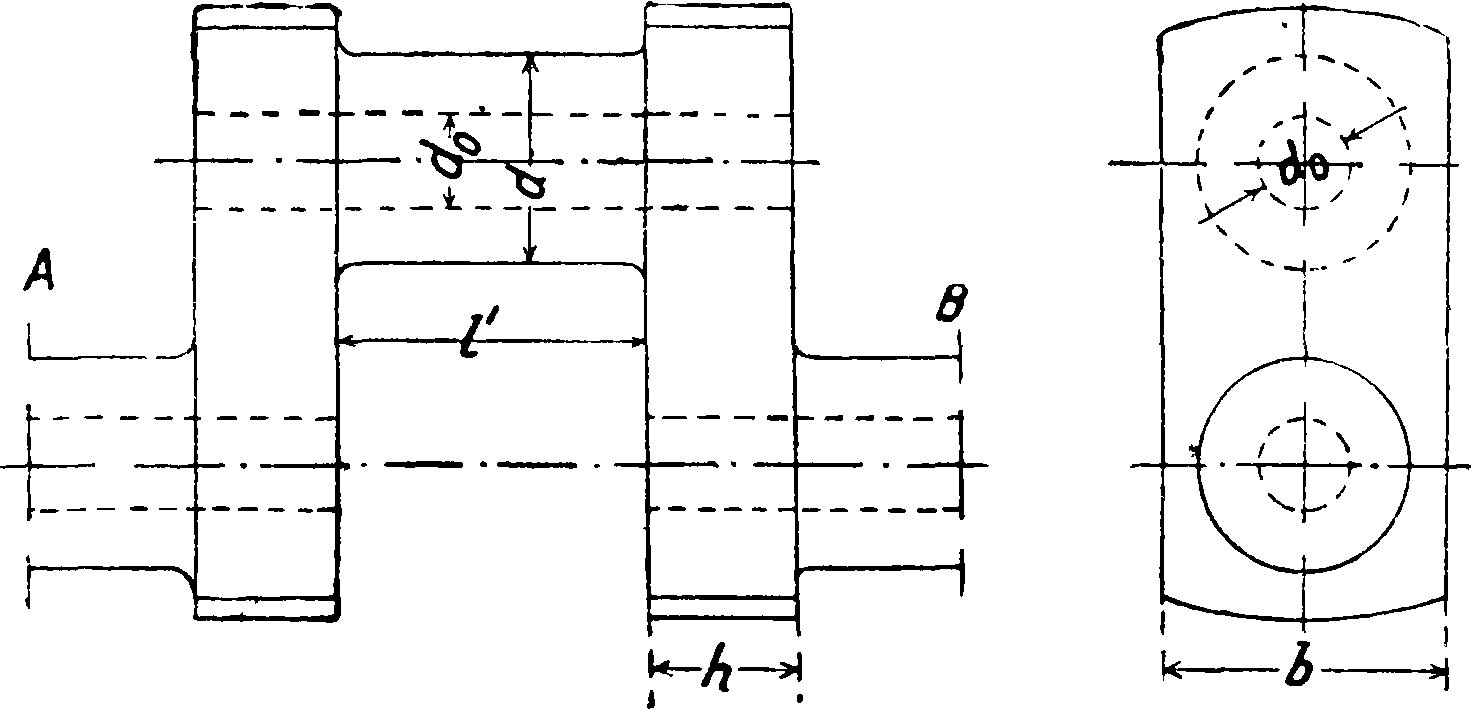
Фигура 8.

ного колена (фигура 8), если диаметр редуцированного вала d,

h ⁼ h dr h dr ^e>

где 1₄=длине коренного подшипника +0,4h_f

Л=0,92(Д-й<Г)+^.

В последнем выражении к=0 + 0,4 в зависимо-

b R

сти от отношений ^ и. В среднем к=0,25. Отбрасывая d$, получим

?₅=0,92 (R — 0,25 d),

h= длине пальца кривошипа + 0,4ft=Г + 0,4/г. Под коленом кривошипа понимается в данном случае часть вала между двумя сечениями А и Б, проходящими через средины двух смежных коренных подшипников. Как показывают многочисленные вычисления, редуцированная длина одного колена кривошипного вала мало отличается от действительной длины этого колена, если .диаметры коренных цапф и цапф кривошипов одинаковы. Тогда можно принять i₃=0,96 I, где I — действительная длина колена и 1₃—его длина, редуцированная по отношению к действительному диаметру цапф вала.

Показанный нами способ редуцирования коленчатых валов дает возможность определить размеры воображаемого цилиндрического вала, равнозначного в отношении крутильных колебаний данному коленчатому валу. Степень точности такого определения показывает след, пример, данный проф. Р. Дуббель. Коленчатый вал шестицилиндрового двигателя был испытан в отношении крутильных колебаний. На основании полученного т. о. количества собственных колебаний определялась редуцированная длина вала, которая затем проверялась вычислением по вышеуказанным ф-лам. Результаты получились следующие. Редуцированная длина каждого колена вала, полученная путем 1) измерения крутильных колебаний вала, определенных без верхних крышек коренных подшипников, равнялась 723,2 миллиметров; 2) измерения этих колебаний, определенных с верхними крышками коренных подшипников—693 миллиметров; 3) путем вычисления—634 миллиметров. Это показывает, что получаемые путем вычислений результаты м. б. только приблизительными. Также приблизительны будут и вычисленные при помощи редуцированной длины вала собственные периоды крутильных колебаний последнего. Этим не исчерпывается ненадежность полученных путем вычислений результатов. Даже при точном определении редуцированной длины вала мы сможем определить собственный период колебаний вала только для немногих простейших случаев. Для многоцилиндровых двигателей определение редуцированной длины вала и собственного периода не дает возможности с удовлетворительной степенью точности определить те составляющие гармоники тангенциальных сил, которые смогут вызвать крутильные колебания вала. Дело в том, что в многоцилиндровых двигателях точка приложения импульсов тангенциальных сил не остается постоянной на валу двигателя. Она все время меняет свое положение, переходя от одного конца вала к другому. Для четырехтактных двигателей порядок, в к-ром происходит перемещение точки приложения этих импульсов: для четырехцилиндровых двигателей—I, II, IV, III или I, III, IV, II; для шестицилиндровых двигателей—I, II, III, VI, V, IV или I, V, III, VI, II, IV. При этом перемещении точки приложения крутильных импульсов возникают чрезвычайно сложные крутильные колебания между отдельными коленами вала, не поддающиеся точному определению. Для определения колебательных движений коленчатого вала необходимо знать массы, вращающиеся вместе с валом, и редуцировать эти массы по отношению к произвольно выбранному радиусу (чаще всего радиусу R кривошипа). Редуцированная масса dM бесконечно малой частицы dm массы, находящейся на расстоянии ρ от центра вращения,

dM=dm ~

Интегрируя это выражение, получим у—удельный вес массы; д—ускорение силы тяжести; Ь—ширина вращающейся массы вдоль оси вращения; J_p—полярный момент инерции. По этой формуле легко вычислить редуцированную массу колена кривошипа и его пальца.

Что касается возвратно движущихся частей двигателя, то, поскольку эти части принимают участие в колебательном движении вала, их необходимо принимать во внимание. Редуцируя эти массы по отношению к радиусу кривошипа, мы можем принимать во внимание для наших расчетов только ту часть массы шатуна, которая м. б. принятой вращающейся вместе с цапфой кривошипа, то есть М₂~, где?—расстояние ц. т.

шатуна от малой головки его. Кроме этого по предложению Фрама часто к этой массе прибавляется еще половина массы поршня и четверть массы шатуна. Таким образом согласно предложению Фрама необходимо учитывать следующую массу:

м^+ м, + I м₂- I Μι + м₂.

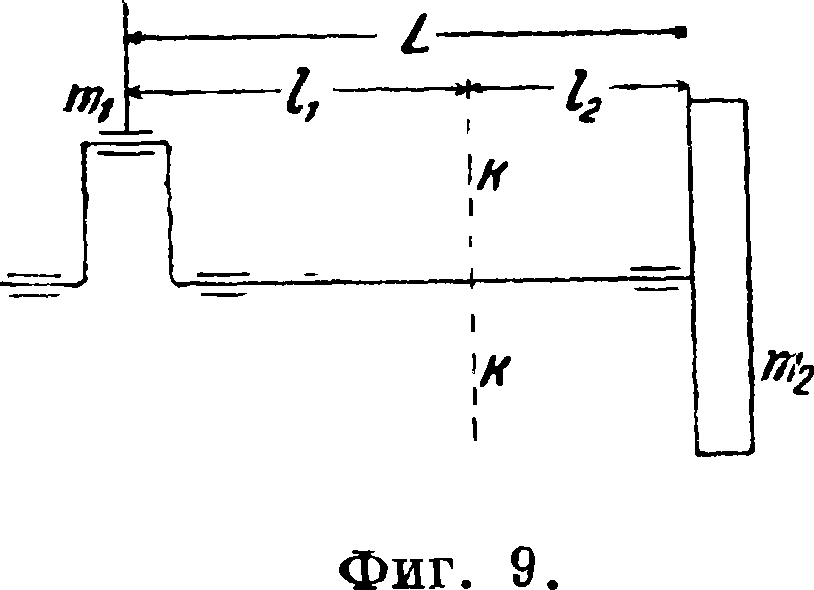
После редуцирования данного коленчатого вала можно вычислить его собственный период колебаний по следующим ф-лам. 1) Для вала с двумя массами т_х и т₂ (фигура 9) (маховиком т₂

и массой т_х на кривошипе), пренебрегая массою самого вала, имеем следующее выражение: — /2зт ² m₁+m₂__Q

V t ) ^{+ С 12} m_xm₂R2 ^υ·

Здесь массы ж₄ и т₂ приведены к радиусу кривошипа R, и с₁₂ является крутильною жесткостью редуцированного вала между массами

• "b

[т,

и ш

Фигура 10.

т_г и ж₂. Собственный период крутильных колебаний вала определится т. о. из

t =

2π

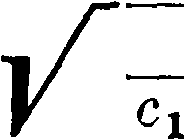
m_xm₂R^

2 (mi +m₂)

Массы ж_х и m₃ колеблются при этом в разные стороны и между ними находится нек-рое узловое сечение кк, остающееся неподвижным.

2) Для вала с тремя мае сами ж_х ,ж₂ и ж₃ (например массы на кривошипе ж₁₅ маховик ж₂ и якорь динамомашины ж₃, изображенные на фигуре 10). пренебрегая массою самого вала, имеем следующее уравнение:

Чг)‘у(?Г-^в(?)+^с=⁰·

Положив=х — ~А, получим кубич. ур-ие вида ж³+рж+ q=0, откуда и определим три корня этого ур-ия, которые дадут нам три собственных периода вибраций данного коленчатого вала с четырьмя массами. Узлы колебаний могут при этом возникнуть либо возле правой тяжелой массы ж₄ (обыкновенно маховик или пропеллер) при одном узле и наиболее продолжительном собственном периоде колебания вала, либо между первой и второй, второй и третьей массами при двух узлах колебания, либо наконец между каждой парой соседних масс при трех узлах колебаний. Вообще, если на валу закреплены п масс, то возможны η — 1 собственных периодов колебаний при количестве узлов этих колебаний от 1 до η — 1.

Описанный метод разработан Гольцером (Holzer) и основывается на следующем его ур-ии для валов с п массами:

/2я *(И"1>, /2я 2(П-2)

^ап~1 + ^an-zyj-J +

, /2 π 2^Ж. /2 π 2

+ · * · + ^ах j-) +. + «1 y-γ) +α_Ο=0·

Этот метод вычисления собственных периодов валов является вполне надежным и легко при-

(¥)‘

-(¥№

т₁ + т₂т₁ т_г R 2

Отсюда определим два значения для t: t =

+ ^C2i

rn-2 -r m₃m_t m₃ jR2

)+

Cio

mi + m₂ + m₃* m_x m₂ m₃ К⁴

= 0.

2π

у и»

mi 4- m₂

^ϋχ2 m₁m₂R ^{2 Сзз}т₂т₃ R

где e₁₂ и c₂₃—скручивающие моменты,^необходимые для скручивания на угол, равный единице, сечения вала I относительно сечения II и соответственно сечения II относительно сечения III. Такой коленчатый вал имеет 2 собственных периода колебаний, один более длинный, когда правая тяжелая масса колеблется в одном направлении и 2 другие массы в противоположном, и другой более короткий период, когда средняя масса колеблется в одном направлении и две крайние массы в противоположном направлении. Узлы колебаний будут при этом наq ходиться соответ-^ ственно или в б л и-з и правой массы ж₃ (один узел колебания) " или в промежутках между массами т_хи ж₂ и массами ж₂и ж₃ (два узла колебаний).

3) Значительно более сложный случай, чем предыдущий, представляет вал с четырьмя массами (фигура 11). Употребляя тот же метод, как и в предыдущем случае, мы при тех же обозначениях получим следующее ур-ие:

⁶. /2π ⁴ [ т 4- m_{2 о t}

т₂т₃К 2

т₂ 4- т₃

) ±-2 V i*

т₁ 4- т₂¹² т_хт₂ К 2

— G,

т₂ 4- т₃²³ т₂т₃ К2

YjL 4^С-12 ^С23

~ т| к⁴;

О

Фигура И.

(?) +(ТУ

, ^т2 4- т₃

12 (Г Р2 °23

+

I ^m3 + т₄

"И т₃т₄К² тх 4-т₂ т₃ 4-т₄‘ тцп₂К⁴ * т₃т₄

m_t 4- т₂ 4-т₃m_lm₂m₃R*

°12^G23 +

^С12^34

. т₂ 4- т₃ 4- т₄‘ т₂т₃т₄й⁴ 2з°з4

) ⁺

, т1 + т₂ + т₃ + пг₄ „ „ _п + - т_1т,т,т;йТ- <*1^2^34 - “·

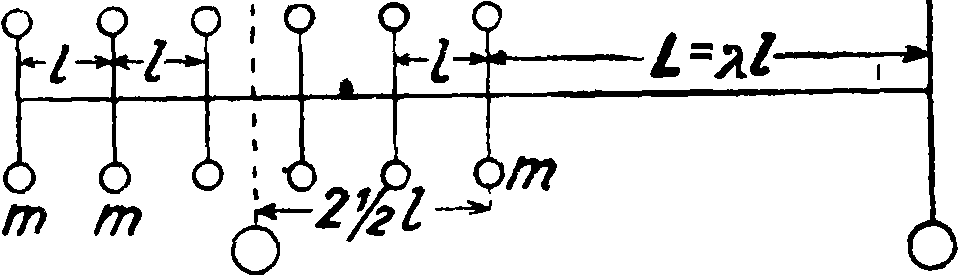
Фигура 12.

Зная массы ж и моменты с мы легко приведем это ур-ие к следующему виду:

меним на практике для количества масс на валу, не превышающего четырех. При большем количестве масс применение этого метода представляет очень ~ большое затруд-нение и для количества масс от 8 и больше становится практически невозможным, так как составление коэф-тов а в ур-ии Гольцера становится крайне затруднительным. Это обстоятельство вынуждает прибегать к методу приближенных вычислений при определении периодов собственных колебаний валов с многими массами. Сущность этого метода состоит в том, что колеблющиеся с валом массы заменяются меньшим количеством масс, статически равнозначных данным массам. Последние можно свести таким обр. к двум, трем или четырем массам и производить вычисления с соответствующей степенью приближения с одним из этих количеств масс. Так, коленчатый вал с семью массами можно в целях приближенного вычисления заменить валом с двумя (фигура 12), тремя (фигура 13) или четырьмя (фигура 14) массами и соответственно упростить вычисления.

Для того чтобы можно было судить о точности вычислений с различными степенями приближения для таких систем, приведем пример

О ( *7-	) с -Z-	р с	? (	) с	> 1~λ 1 - г
О ( т		Ь с -л-	!> с	> 1	п

Зт дт

Фигура 13.

вала с восемью массами, приведенными к 2, 3, 4, 5 и 8 массам (табл. 1).

Таблица 1.—П р и μ е р вала с в о с е м ь ю массами

Число

Данные восемь масс заменены массами

колебании вала в минуту	двумя	тремя	че тырьмя	ПЯТЬЮ	во семью
Ай.	1 213	1 304	1 350	1 361	1 367
А"2.	—	2 195	2 210	2 214	2 219
А3.	—	—	1 050	4 584	4 935
А4.	—	— i	—	6 253	7 739
Νδ.	—	—	—	—	10 140
А6.	—	—	—	—	11 970
ν7.					13 120

Существуют еще и другие методы вычислений собственных периодов крутильных колебаний валов. Из этих методов отметим метод Толле, примененный им во время империалистич. войны для расчетов 9 9 Υ V коленчатых валов

О ! о о 1 О О ! о

i ; i γψ-

о ο„,ό, ό_Λ.ο : о

-ί-λΐ-

-.-21-^21 ό ό

2т 2т

~

2т

Фигура 14.

ό

qm

двигателей подводных лодок, дирижаблей и самолетов.

Для определения собственного периода колебаний коленчатых валов можно употреблять также и графич. методы. Из последних наибольшим распространением пользуется метод Гюм-беля (Giimbel), усовершенствованный Гейгером. Этот метод заключается в следующем. Скручивание двух поперечных сечений вал а, отстоящих друг от друга на 1 см, определяется следующим выражением:

М<]

Gc-Jp

<Р ^:

Здесь M_d —момент скручивания, J_р—полярный момент инерции площади поперечного сечения вала, G—модуль скольжения. Угол скручивания двух сечений, отстоящих друг от друга на расстоянии ?, будет

ν=ν·^ι=£τ_ρ¹·

Если радиус вала обозначим через г, то дуга скручивания на поверхности вала будет м_д

α= уг= φ Ir =

-lr.

G · Jp

Вместо M_d можно подставить величину Pr. Тогда имеем

Р№

G ’ Jp

α=

Дуга скручивания на единицу длины вала равна таким образом а _ Р

г ~т *

г²

G · Jj)

Представим себе на цилиндрич. поверхности нашего вала прямую, начерченную по образующей цилиндра. При скручивании вала несколькими моментами, расположенными в разных его сечениях, эта прямая превратится в некоторую пространственную кривую, изломанную в местах приложения скручивающих вал моментов. При развертке цилиндрич. поверхности вала на плоскость эта кривая превратится в нек-рую ломаную линию, состоящую из нескольких прямых участков, расположенных между каждой парой смежных скручивающих мо ментов. Допустим теперь, что в какой-либо точке г (фигура 15) вала дуга скручивания равна а_{.

В другой точке г+1 действует некоторая скручивающая сила

М-А 9Jo

Фигура 15.

Р_{г + 1} на плечо г. Относительное скручивание а получится тогда из выражения ^а_ Р/₊₁

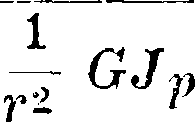
Начертим рядом с тр-ком АВС другой тр-к, одна из сторон которого равна P_i+1 ι другая равна полюсному расстоянию Н=—GJ_P. Этот тр-к будет подобен первому. Возьмем еще одно сечение г+2 (фигура 16) вала и, поступив так же, как и в первом случае, получим, с одной стороны, веревочную кривую г, г+2 и, с другой стороны,— силовой многоугольник с полюсным расстоянием, равным Н. Таким образом возможно ©пределить для всего вала кривую скручивания в виде веревочной кривой.

Этот метод возможно применить и для случая, когда вместо статических скручивающих момен

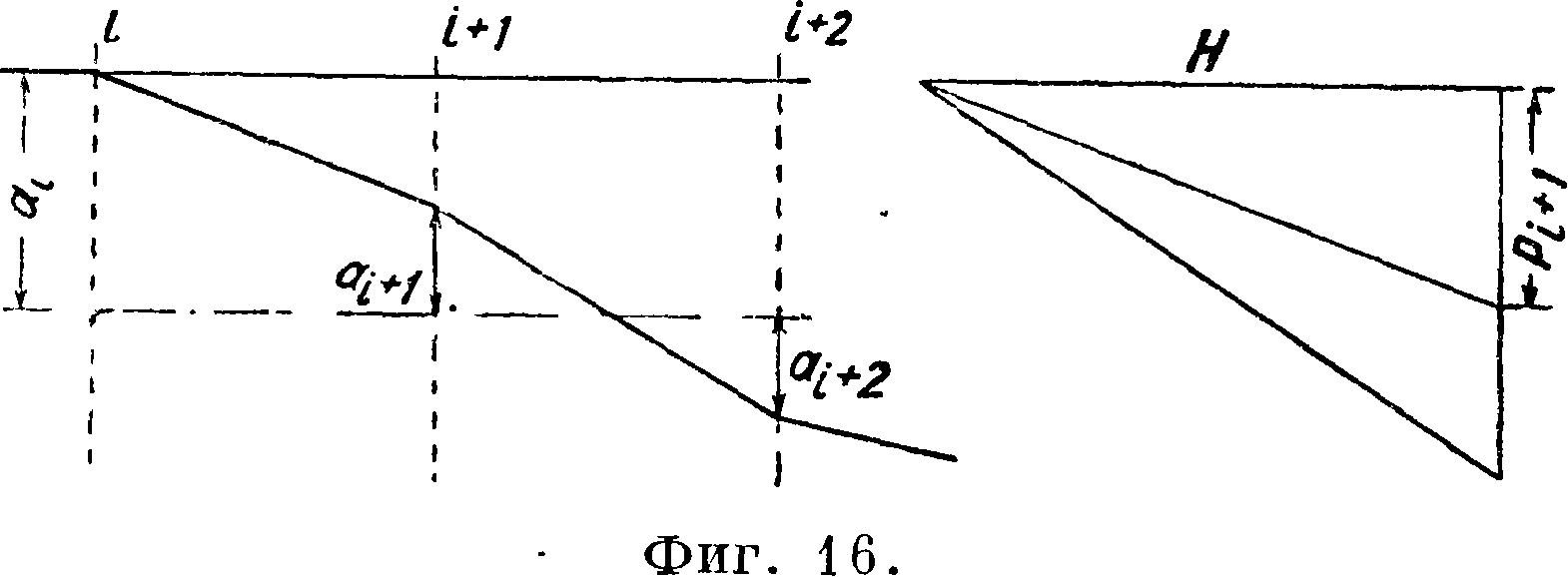
тов мы имеем гармонические, производящие колебания вала. При этом необходимо принимать во внимание кроме гармония, сил также и силы инерции вибрирующих масс. Последние равны

Р=т=тш²а,

2 л где со=—-нек-рая угловая скорость, соответ ствующая периоду t. Для определения этих сил необходимо т. о. значение величины а. Допустим, что в крайнем левомсечении! (фигура 17) действует гармония, сила Р. Левее сечения 1 вал свободен от действия сил, что выражается на фигуре параллельностью участка веревоч-

н

Фигура 17.

ной кривой левее первого сечения оси вала. На силовом мн-ке наносим силу Р и принимаем произвольное скручивание α_λ для первой массы.

J G

Имея полюсное расстояние Н=-²~-, мы определим величину скручивания а₂. Отсюда полу-

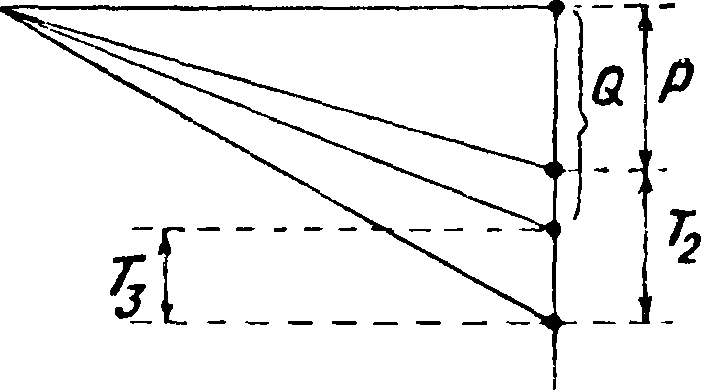
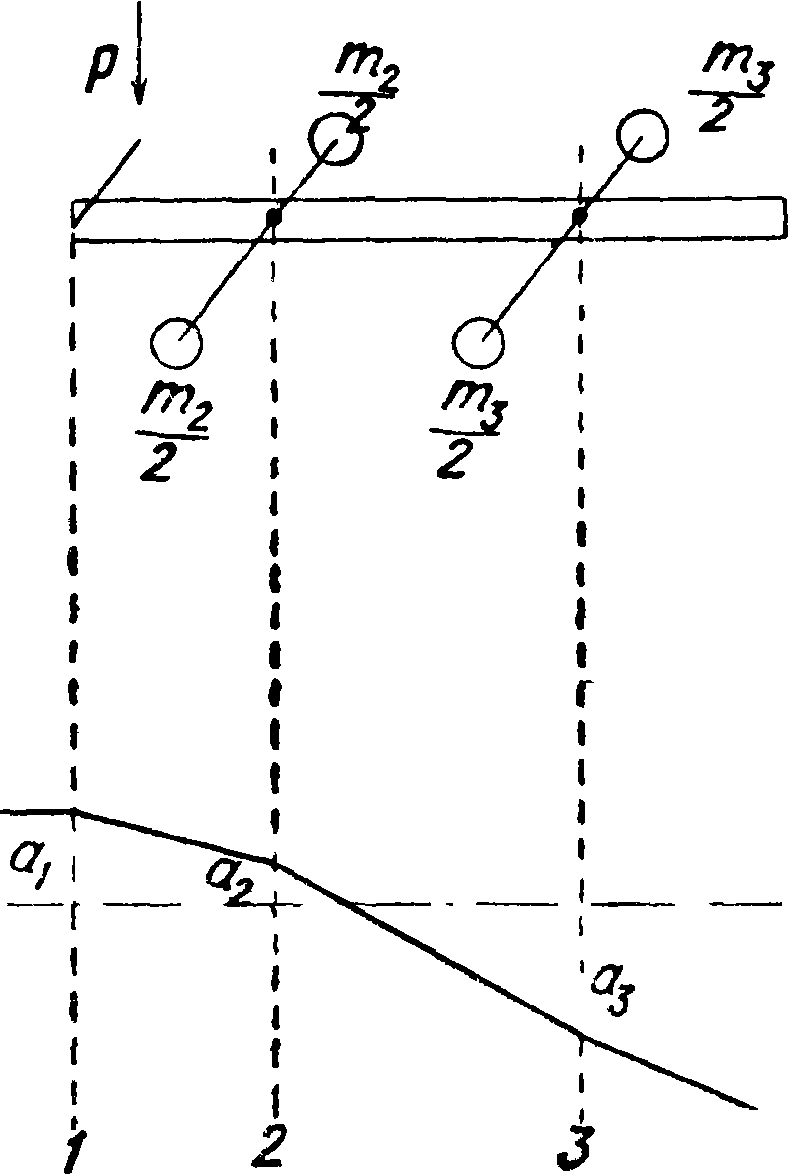
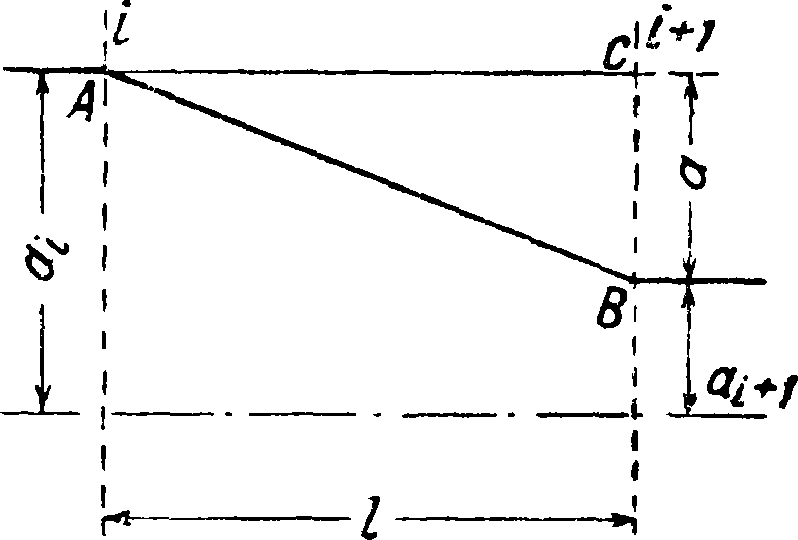
чим величину силы инерции Т₂=т₃ео²а₂, к-рую мы также наносим на силовой мн-к и определяем скручивание а₃. После этого находим величину Т₃, которая определяет направление последнего луча силового мн-ка. Как показывает этот мн-к, при принятом скручивании а_г и данной ω вала, состояние равновесия не достигнуто. Для достижения этого равновесия необходимо приложить в сечении 3 еще нек-рую дополнительную силу Q. Т. к. такой силы в действительности не существует, то для достижения равновесия необходимо изменять взятое значение ω так, чтобы мн-к сил замкнулся и сила Q стала равной нулю. Кроме этого, поскольку мы имеем дело со свободными колебаниями вала, внешние силы не принимаются в расчет. Принятая сила Р становится т. о. также равной нулю. Полученные после этого силы инерции Т дадут возможность определить собственный период колебания из выражения

t ) πια

Лит.: Львов Е., Тракторы, их конструкция и расчеты, 2 изд., М.—Л., 1931; Мартенс Л., Динамика поршневых двигателей, М.—Л., 1932; G- ϋ m b e 1, Ver-drehungschwingungen eines Stabes mit fester Drehachse u. beliebiger zur Drehachse symmetrischer Massenvertei-lung, «Z. d. VDI», 1912, p. 1025; G- e i g e r J., Mecha-nische Schwingungen u. ihre Messungen, B., 1927; H о 1-z e r H., Die Berechnung d. Drehschwingungen, B., 1921; L e h r K., Schwingungstechnik, В. 1, 1930; T о 1 1 e M., Regelung d. Kraftmaschinen, 3 Aufl., B., 1921. Л. Мартенс.

С. к. роторных машин. При самом тщательном уравновешивании насаженного на вал ротора все же его центр тяжести не совпадает с осью вала, благодаря чему при вращении остается неуравновешенная центробежная сила, вызывающая прогиб вала. Вследствие этого расстояние от ц. т. до оси вращения увеличи-,s

к ¹ а -

вается еще более и растущая центробежная сила может повести в конце-концов к поломке вала. В дальнейшем изложении использованы подробные исследования, сделанные в области критич. скорости проф. Стодола.

Возьмем простейший случай вертикального вала с насаженным на него одним диском (фигура 18). При этом вес вала не оказывает влияния на его прогиб. Неуравновешенная центробежная сила

F=ш(у + е) ω², (1)

где т—масса диска, ω—угловая скорость вращения, е—расстояние от ц. т. диска S до точки W на оси вала (эксцентриситет) и у—стрела прогиба вала. Эта сила должна равняться противодействующей силе упругости вала, которая пропорциональна величине деформации

Р=°У, (2)

где а—коэф. пропорциональности, зависящий от размеров вала и условий его закрепления. Т. о.

ш(у ф е) о)²=ау, (3)

откуда

y=7rs^i- О)

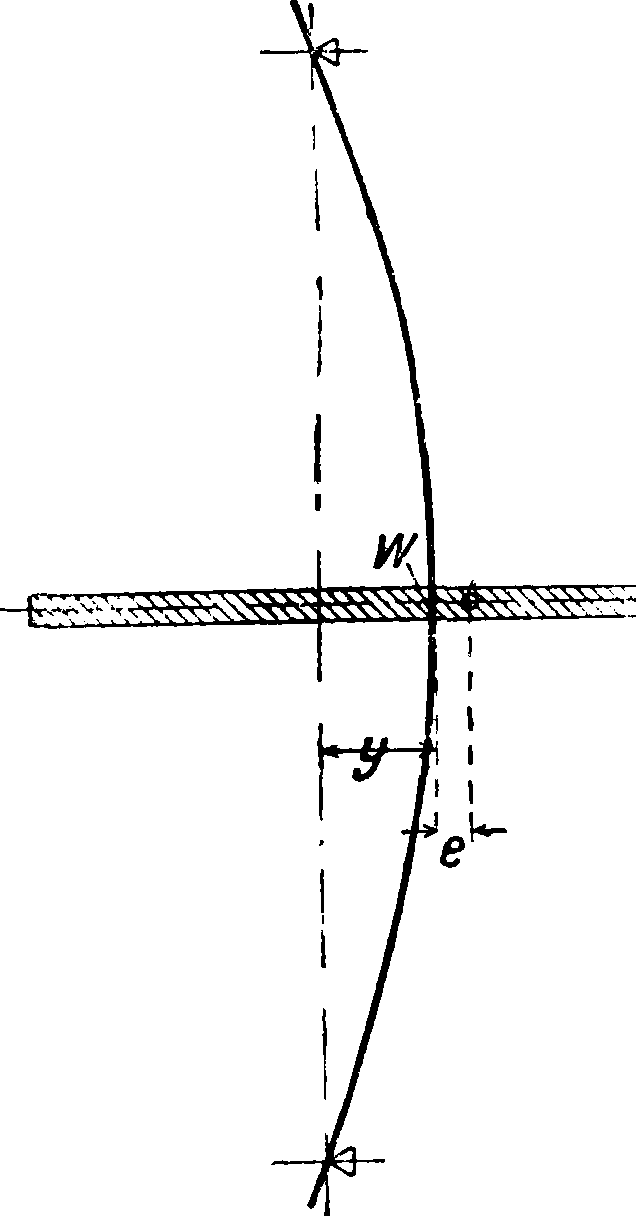
Фигура 18.

Прогиб вала увеличивается вместе с ω и у=оо при а — πιω²=0. Соответствующее этому условию значение угловой скорости

(δ)

.-V;

Фигура 19.

есть С. к. Число об/ск. при этой скорости

Это выражение совпадает с ф-лой частоты собственных поперечных колебаний системы.

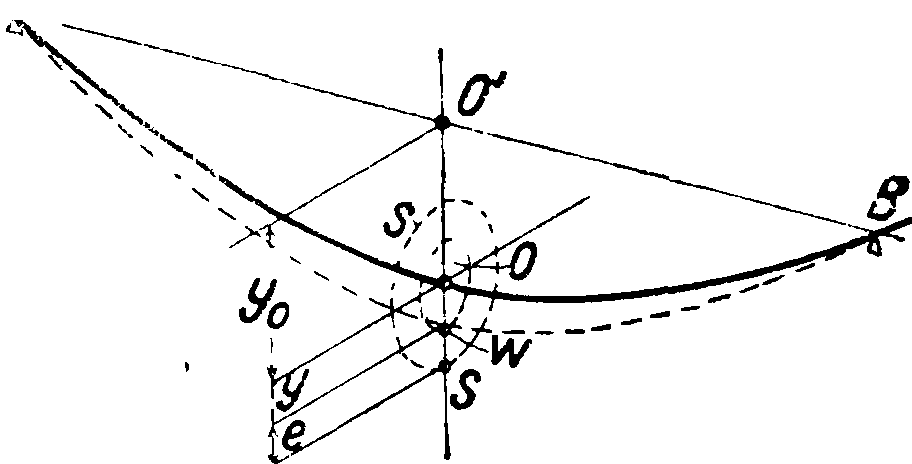
Если вал лежит горизонтально, то -¹ от его веса возникает прогиб ?/₀ (фигура

19), направленный вниз и не зависящий от числа оборотов. Ц. т. диска S будет также описывать окружность радиусом (у + ё), но не около точки О, а около точки О. Ф-лы для определения прогиба и С. к. остаются те же самые. В действительности пе-риодич. повышения и понижения ц. т. вызы- вают колебания угловой скорости и нарушение кругового пути перемещения ц. т., что может создать особое критич. состояние. Но практически, в частности в условиях турбиностроения, это явление не оказывает заметного влияния на С. к. и можно принять, что при любом положении вала—вертикальном, горизонтальном или наклонном—С. к. остается одна и та же.

Можно достигать критич. числа оборотов и переходить через него без опасности поломки вала, если диск имеет достаточно длинную втулку, препятствующую изгибу вала. Как Фигура 20. показали опыты в согласии с теорией, при увеличении скорости выше критической возникает вновь состояние устойчивого равновесия, при котором ц. т. переместится и будет расположен между линией, соединяющей опоры, и изогнутой осью вала (фигура 20). При этом ур-ие для определения прогиба представится в следующем виде:

т(у — е) о)²=ау, (7)

откуда

У =

7к 0)2

(8)

Т. о. за С. к. величина прогиба вала уменьшается и стремится в пределе к величине эксцентриситета е, &огда изогнутый вал будет вращаться около ц. т. диска.

Для совершенно уравновешенного диска, то есть при е=0, ур-ие (3) примет вид ту о)²=ау. (9)

Согласно ур-ию (5) и если у не равен нулю, ур-ие (9) возможно только при ω=o)_k. Следовательно совершенно уравновешенный вал находится в критич. состоянии при любом прогибе в равновесии.

Величина прогиба вала от собственного веса G

У 0=V

Но по ур-ию (5) α=> тт и кроме того G=тд, откуда

mg _ иг (Ю)

У 0 =

₌ G

mcOft mj.

Выбором С. к. определяется следовательно деформация от собственного веса независимо от того, какие размеры будет иметь вал.

Если средняя плоскость диска перпендикулярна к оси вращения, как предполагалось выше, то появляются лишь центробежные силы. Но она может оказаться наклонной к оси вращения как вследствие прогиба вала, так и от неправильной посадки диска на валу. При этом центробежные силы, вызываемые отдельными элементами массы диска, образуют пары сил, влияющие на прогиб вала. Рассмотрим

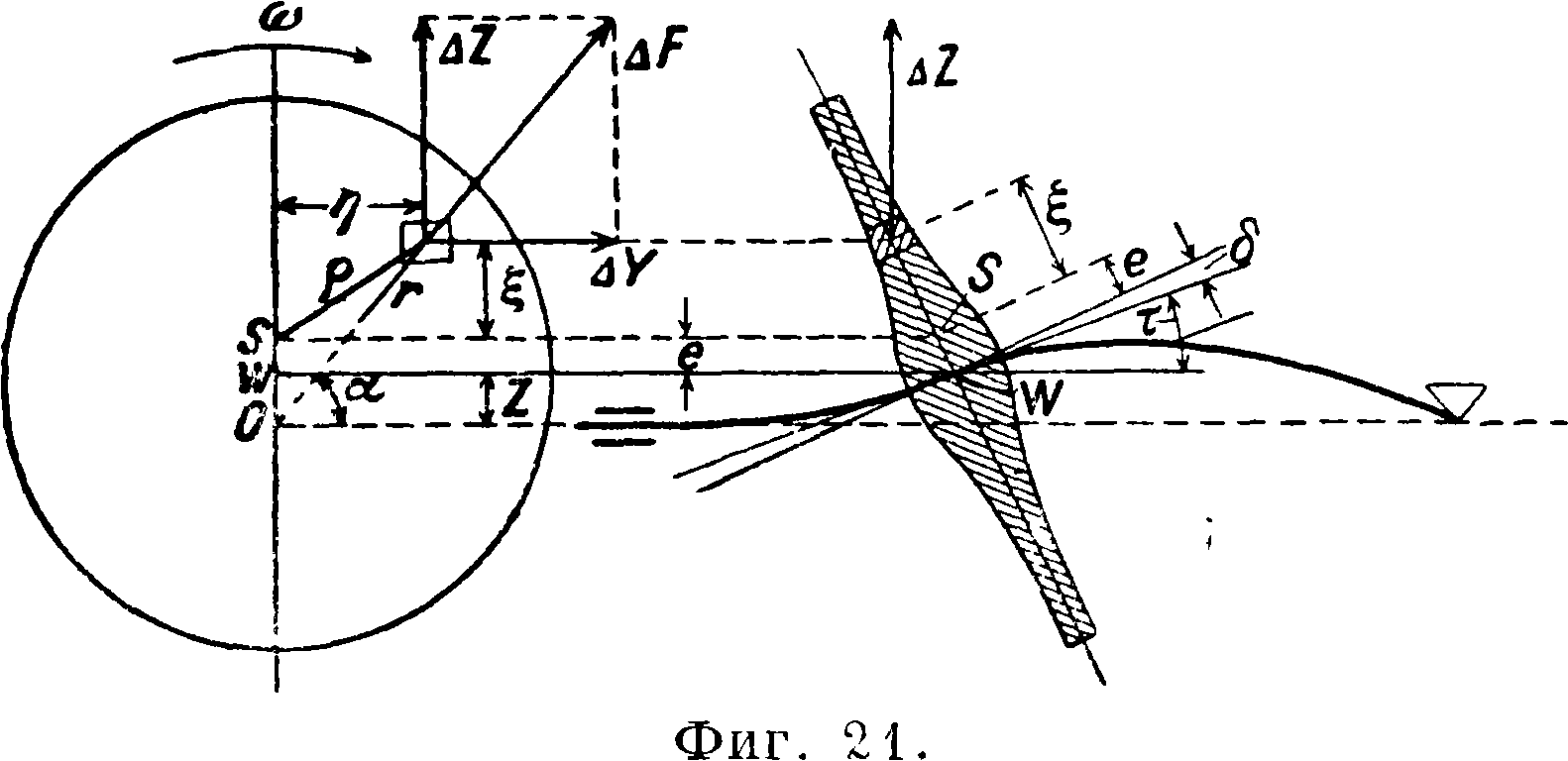
случай одного диска, показанный на фигуре 21, где т — угол наклона упругой линии и <5 — угол между осью диска и осью вала от неточности выполнения конструкции. Центробежная сила ΔF от элемента массы диска dm разлагается на две составляющие: ΔΖ, параллельную плоскости изгиба вала, и ΔΥ, перпендикулярную к ней:

AZ=Ат- τω² sin α= Δm · ω²(ζ + е + £),

ΔΥ=Ат · ω²η.

Результирующая составляющих ΔΥ, как видно, равна нулю. Величина жироскопич. момента будет

Μ_/=ΣΔΖ·£(τ + ό),

принимая sin (τ + δ)=(τ -f- δ) по малости угла. Следовательно

М_г=ΣΔm · ω² (ζ + e + i) ξ (τ -{- δ) =>

= ω² (τ + <5) Σ dm · ξ(ζ + e + |). (12)

В виду того что (e + ξ) мало по сравнению с ξ,

можно принять

M_f=co²( τ + δ)θ_ά, (13)

где θ_α—момент инерции массы диска, отнесенный к диаметру. Влияние момента как видно, выражается в уменьшении угла г, то есть он препятствует прогибу вала и увеличивает критич. число оборотов.

В предыдущем предполагалось, что угловая скорость вращения плоскости изгиба вала такая же, как угловая скорость вращения самого вала и диска. Но возможны случаи, когда угловая скорость вращения плоскости изгиба Я

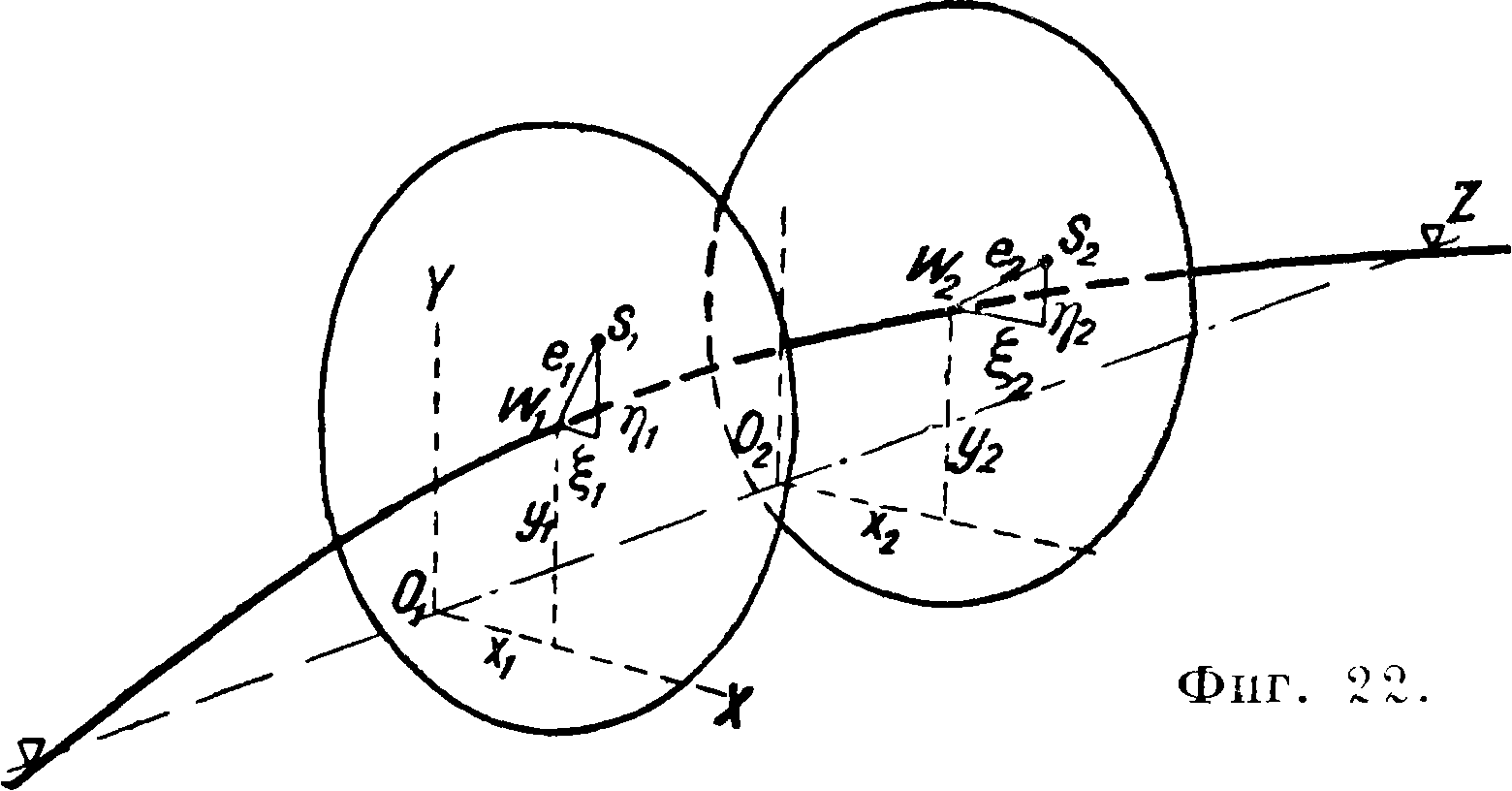
направлена в обратную сторону и отлична по величине от ω. Это происходит при недостаточно плотной посадке диска на валу. Тогда действующий момент

М_с=( 2λω + λ²)(τ + δ)θ_ά (14)

содействует увеличению угла г, то есть прогибу вала. При Я=ω

Μ_]£=3ω²(τ + δ)Θ_ά=3Μ_ί. (15)

В случае невесомого вала с двумя насаженными на него дисками, схематически изображен

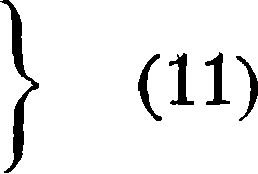
ного на фигуре 22, центробежные силы от масс дисков т_х и ж₂ м. б. разложены наследующие составляющие:

= Он + fi) т_гм²9 Y_x=(у_х + 7_h) т_х(о², )

^2=(ж₂ + ξ₂) Щм², Υ₂=(уа + η₂) т₂о)², f ^К

где x_lf у₁₉ и ж₂, у₂—координаты центров дисков W_x и Wo относительно точек О и 0_1; лежащих на оси, соединяющей центры подшипников, £i, Vi и ξ₂, η₂—координаты ц. т. дисков ^и^ относительно центров дисков W₁ и TY₂ и е₁₉ е₂— эксцентриситеты масс дисков. Скручивание вала по отношению к изгибу всегда так ничтожно, что изменением угла между направлениями эксцентриситетов можно пренебречь. Величина прогиба вала под действием этих сил будет:

^Xl^{= a}il^l 0₁₂Х₂, Vl^{= a}ilYl 0₁₂Y₂, I χ₂= α₂₁Χ_χа₂₂-Х₂, У2⁼ o_2XY _х -f- n₂₂Y₂, i

где значения а исключительно зависят от размеров и способа закрепления вала, причем о₁₂=а_2г. Вставив выражения для соответствующих центробежных сил, получим четыре ур-ия:

(а_пт_±м² — 1) х_г + а₁₂т₂м²х₂ + α_ηξ^_χω² + ^

+ а₁₂£₂т₂(о²=О,

а₂₁т_хт²х_х + (а₂₂т₂о)² — 1) + а₂₁|₁т₁а)² +

+ а₂₂£₂т₂со²=О,

(α^Μχω² — 1) Ух + а₂т₂(о²у₂ + α_χιη^_χω² + + а₁₂г}₂т₂(о²=О,

а₂₁т₁м²у₁ + (а₂₂т₂а)² — 1)у₂ + α₂₁η^_χω² γ Υ а₂₂у₂т₂т²=0.

(18)

Величины х₁₉ у_х и x_2i у₂ возрастают до бесконечности, если

{а_х1т_хм1 - 1) (а₂₂т₂а)1 - 1) - а ₂т_хт₂т%=0. (19) Следовательно существуют два значения для С. к., квадраты которых определяют- ·— ся из этого последнего ур-ия. Как видно, значения эти не зависят ни от величины ни от положения эксцентриситетов. В случае равных масс и симметричного расположения дисков на валу имеем т_х=т₂&_хх ⁼⁼ й₂2 ⁼⁼⁼ & и йjo⁼⁼ Тогда

amcol — 1=± b т,

I откуда

Ь ^{и Ш(}°^{к2 =}

Фигура 23

mo)_ki

(20)

1

При двух равных дисках, расположенных на гладком валу на расстояниях I от опор и 21 между дисками, возможна упругая линия двух показанных на фигуре 23 видов. В первом случае

4PJ3

У~~ 3 ЕЛ и во втором

Р13

у ~ 6Ё ’

«1 =

3 EI

4 i³

6£7 гз

V·.

VI

(21)

(22)

откуда

”*1

^ω*2

VbVi-

(23)

В данном случае значения С. к. относятся друг к другу, как 1 :2,83. Подобным же образом можно убедиться, что число различных значений С. к. будет равно числу дисков на валу.

Принимая во внимание массу вала, можно рассматривать последний как бесконечный ряд бесконечно тонких дисков, которому теоретически соответствует бесконечный ряд С. к.; однако лишь некоторые из этих значений необходимо принимать во внимание. Как и для центры тяжести масс стремятся приблизиться к оси, и вал автоматически центрируется.

Для валов, переменного сечения, нагруженных несколькими различными, произвольно расположенными дисками, аналитич. способ определения критич. скоростей является столь

— 940

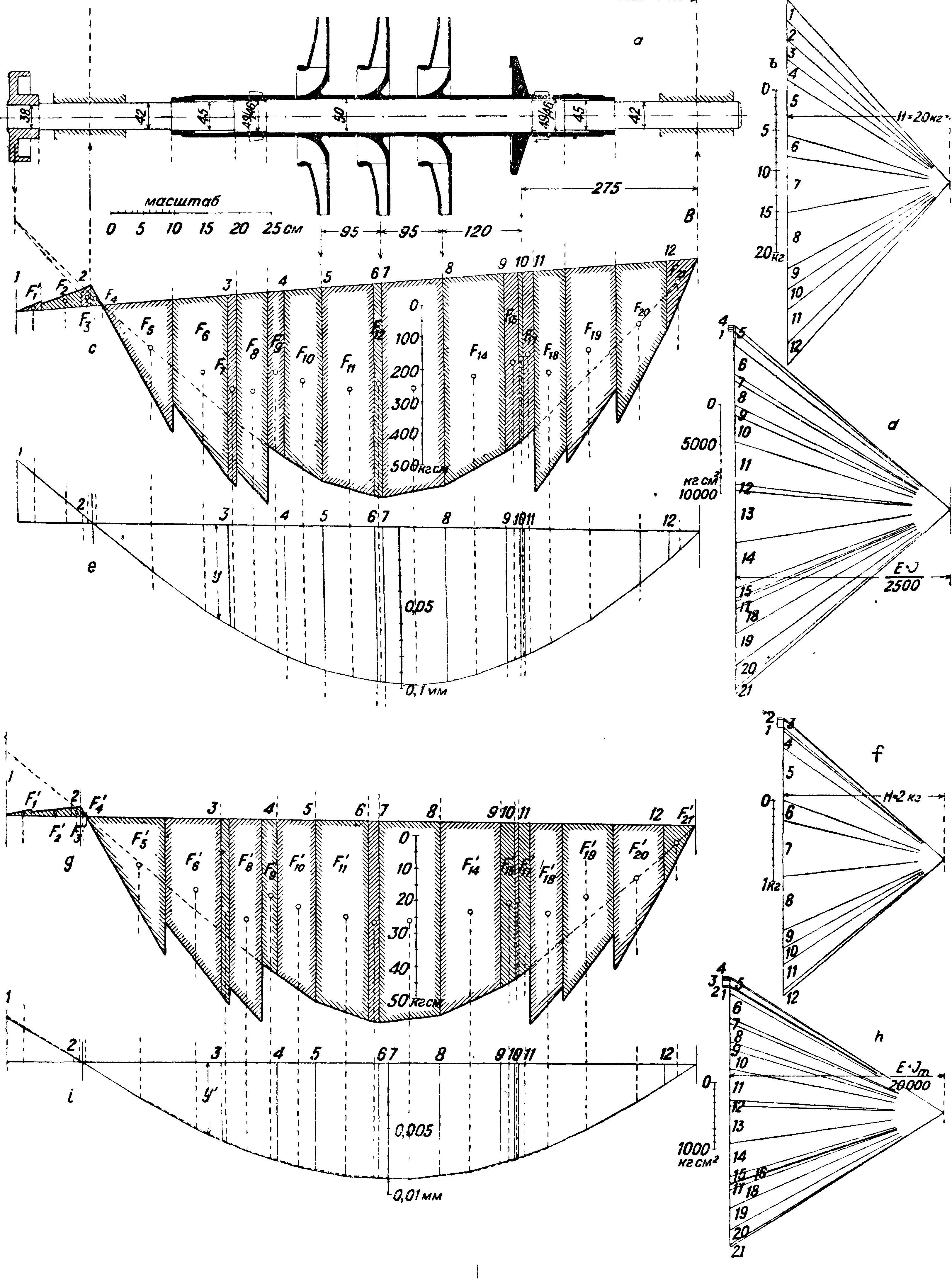
Фигура 24.

случая с одним диском, в этих общих случаях сохраняют свою силу выводы относительно влияния собственного веса и относительно зависимости между числом собственных колебаний вала и критическим числом оборотов. При бесконечно растущей скорости вращения сложным, что прибегают к графическому методу. Исходя из определения линии прогиба вала под действием весовых нагрузок, определяют центробежные силы шут^, соответствующие отдельным массам, на которые разбит вал, и относящимся к ним прогибам, при угловой

Таблица 2. — Центробежные силы отдельных масс вала.

Точки		2	з	4	5	6	7	8 1	9 1	10	И 1	12, !
Сосредоточенные ве-сбвые нагрузки G, кг..	2,5	2,5	2,5	2,5	7	1 1 1 2, о	1 7	7	2,5	2,5	4,2	2,5
Прогибы от весовых i нагрузок у, ! QM ИГЗ.	-3,8	-5,0	+ 6,4	8,1	9,0	1 9,6	9,6	9,4	8,3	8,0	7,9	1,8 1
! Центробежная сила i бг 2 1 —νωο, кг.	-0,097	-0,013	+0,163	0,206	0,643	0,245	0,686	0,672	0,212	0,204	0,338	0,016 j

скорости ω₀, выбирая последнюю в виде круглого числа 10 или 100. Рассматривая эти силы статически приложенными к валу, строят упругую линию. Полученные вновь прогибы у не будут совпадать с принятыми первоначально, потому что ω₀ не есть С. к. Но т. к. взятые в качестве нагрузки центробежные силы пропорциональны как квадрату угловой скорости, так и прогибам, то получаем соотношение:

Посредством мн-ка сил (фигура 24, /) строят диаграмму моментов (фигура 24, д) и по ней посредством мн-ка сил (фигура 24, h)—упругую линию от действия центробежных сил (фигура 24, г). По принятому масштабу определяют прогибы,

например в точке 7 прогиб у=8,8 · 1(Г³ см, а по скольку в таблице для этой точки у=9,6-10 ³, то по лф-ию (24)

, ю фУ^11,3

У-У

VC

(24)

На фигуре 24, а—г показано для примера определение С. к. для вала трехступенчатого водяного насоса. На фигуре 24, а представлен вал. На фигуре 24, b—е сделано определение упругой линии вала от собственного веса. Весовые нагрузки проложены в 12 точках. Строят мн-к сил (фигура 24, b) с полюсным расстоянием Н==20 килограмм и соответствующий ему веревочный мн-к (фигура 24, с), дающий диаграмму изгибающих моментов. Для получения численной величины момента в любом сечении вала нужно ординату диаграммы-моментов, относящуюся к этому сечению, умножить на полюсное расстояние Я, измеренное в масштабе сил многоугольника сил (в нашем случае 20 килограмм), и на обратную величину масштаба длины чертежа 1 : т, то есть на Нт. Для построения упругой линии нужно построить новый веревочный мн-к, для которого полученная диаграмма моментов должна служить диаграммой воображаемых нагрузок. Чтобы учесть изменения диаметров вала, приводят все моменты к одному общему диаметру (в данном случае к среднему), умножая их на отношение ¹-~, где 1_т и I—моменты инерции в средней части и в любом сечении вала. Полученные трапецеидальные площадки от Е до F₂₁ на фигуре 24, с представляющие собой новые нагрузки, умножают на Нт² для выражения в килограммах-см² и строят мн-к сил (фигура 24, d) с полюсным расстоянием 1_тЕ, где Е— модуль упругости материала вала. По условиям места полюсное расстояние на фигуре 24, ^

взято равным, причем 1_т=^7Т^=3 068 см⁴

и Я=21,5 · 10⁵. Построенный на фигуре 24, е веревочный мн-к представляет упругую линию в масштабе, определяемом след. обр. Если на фигуре 24,d 1 сантиметров=К кгсм² и полюсное расстояние равно а см, то полученные прогибы нужно ум-

mha

ножить на ф-~ для получения истинных вели-

J _mL·

чин. Полученный масштаб нанесен на чертеже.

Исходя- из найденной упругой линии, подсчитывают центробежные силы отдельных масс, соответствующие полученным прогибам, при ω₀= 100. Результаты показаны в таблице 2.

<*>1с

,=330 ск. ¹

8,8 10“3

и соответствующее критич. число оборотов в мин щ=^=3150. у

Отношение ~ должен быть одинаковым для всех точек вала, но поскольку первая упругая линия только приблизительно верна, то возможны отклонения. Если они не слишком велики, то, исходя из второй упругой линии, строят новую линию прогибов. Если необходимо учесть моменты, вызываемые жироскопическим действием, то на диаграмму изгибающих моментов, вызываемых центробежными силами, накладывают диаграмму моментов, вызванных парами центробежных сил, и ведут построение по суммарным моментам.

Лит.: Тимошенко С., Теория колебаний в инж. деле, пер. с англ., 2 изд., М.—Л., 1931; S t о d о 1 а А., Dampf- u. Gasturbinen, 6 Aufl., В., 1924; Р f 1 e i d е-rer C., Die Kreiselpumpen, B., 1924. И. Фрязиновский.