> Техника, страница 81 > Сопротивление материалов

Сопротивление материалов

Сопротивление материалов, наука, которая охватывает теорию деформаций, общие сведения о материалах, гл. обр. о мет, и указывает также общие методы расчета машин и сооружений. С. м. служит вводной наукой во всех областях инженерного образования: в строительной технике С. м. вводит в статику сооружений, в машиностроении С. м. предваряет все расчетные курсы—двигателей,станков, грузоподъемных устройств, котлов и прочие; в других отраслях техники, в архитектуре и художественной деятельности С. м. формирует и рационализирует внешние выражения творческих идей н композиций. В настоящее время теория С. м. разделяется на три основные части: а) С. м. (в элементарном изложении), б) прикладная теория упругости и в) теория упругости. Предмет ведения, объём вопросов и глубина их изложения распределены между С. м., теорией упругости и прикладной теорией упругости недостаточно определенно. Наблюдается постоянное перемещение материала из одной части в другую и взаимное влияние их методологии. Все же следует принять, что С. м. представляет первый концентр познаний шгженера относительно общих свойств материалов и наиболее простых методов изучения их работы в конструкциях. Прикладная теория упругости включает в свой объём уже более сложные проблемы и, отказываясь во многих случаях от строгой формы их изложения, стремится дать практич. применение решений в различных отраслях техники. Теория упругости развивается как отдел физико-математических наук и содержит решение наиболее сложных задач относительно упругого и пластического состоя ния материалов и работы конструкций в строгой математической форме.

В С. м. исходят из опытных или экспериментальных данных и пользуются простейшими приемами математич. анализа при изложении теории с намерением (в иных случаях) скорее“ получить заранее оправданный результат. В курсах С. м. содержатся теории простых деформаций—растяжения (сжатия), сдвига, кручения и изгиба (поперечного и продольного) б. ч. прямолинейных стержней, иногда и криволинейных,—сложного сопротивления и описание свойств материалов в их главнейших характеристиках, которые определяют прочность материалов для каждой деформации. В качестве дополнения в С. м. излагают теорию расчета статически неопределимых систем, теорию упругих колебаний, теорию упругого удара и, в зависимости от склонностей и намерений автора, отдельные задачи из той пли другой технической области.

Основные п о л о ж е н и я С. м. С. м. рассматривает всякий материал как упругое тело с одинаковыми свойствами по всем направлениям независимо от его размеров (изотропное тело). Предполагается, что материал в своих упругих изменениях следует закону Гука кроме тех случаев, которые явно противоречат опыту (например чугун). Основной метод С. м. для выяснения зависимости между внутренними и внешними силами—это метод сечения и отвердевания (принцип, открытый еще Стевином): выделенная часть упругой системы находитея в равновесии, если к действующим на эту часть внешним силам присоединить внутренние и рассматривать ее как твердое тело. Также принимается, что в единице объёма упругого тела действует вектор внутренних сил и отсутствует момент внутренних сил, то есть йЛИЖ*)⁰·

где Г сила, М —момент, F—площадь и V— объём; а выражается напряжение и измеряется в килограммах/мм² пли кг/см², причем напряжение м. б. нормально к плоскости действия или лежат!» в плоскости (нормальные и касательные напряжения). Деформации предполагаются малыми и обратимыми. Для каждой деформации, рассматриваемой прежде всего изолированно, выдвигается рабочая гипотеза, приложение которой оправдывается опытом, и вышеуказанным приемом сечения выясняется механизм внутренних напряжений. Из условий равновесия статики или динамики выводят ур-ия прочности и деформации, которые служат для определения размеров конструкции и деформаций ее частей и в целом. Сравнение действительных напряжений и деформаций с теми, которые признаны Допускаемыми, дает окончательное суждение о пригодности принятых размеров. Допускаемые напряжения и деформации назначаются на основании данных инженерного опыта, особые для каждой конструкции и детали, или устанавливаются для данного случая по соображению с т. н. коэф-тами Вёлера. Опыты Вёлера дали основание разделить все виды действующих сил на три группы: 1) группа сил, действие которых не меняется (спокойная нагрузка), 2) группа сил, которые при своих изменениях не переходят через значение нуль (переменная нагрузка), 3) группа сил, переменных по величине п знаку (колебательная нагрузка). Соотношение между допускаемыми напряжениями для этих групп берется 3:2:1, причем для спокойной нагрузки допускаемое напряжение назначается (для углеродистых сталей) не более четверти временного сопротивления (смотрите) или же не более половины предела текучести £для сталей, термически обработанных и специальных). Промежуточные виды сил учитываются дробными чи интервала 3—1. Допускаемые напряжения для тех сил, действие которых сопровождается ударами (динамическая нагрузка), выбираются на одну ступень ниже: при динамическом действии первой группы сил принимаются напряжения, годные для второй; при динамич. действии второй — годные для третьей; в случае третьей группы сил берут 7₂—²/₃ обычного для этого случая напряжения. В различных отделах машиностроения и строительной техники указаны основания для выбора допускаемых напряжений и величины последних в зависимости от обстоятельств работы конструкции и материала. В соответствующих таблицах (смотрите Прочности нормы) указаны средние значения допустимых напряжений для трех групп сил; необходимо заметить, что вопрос о прочности при колебательной нагрузке связывается со способностью металла к затуханию и с гистерезисом (смотрите Усталость металлов).

Простые деформации. Теория деформации растяжения развивается на

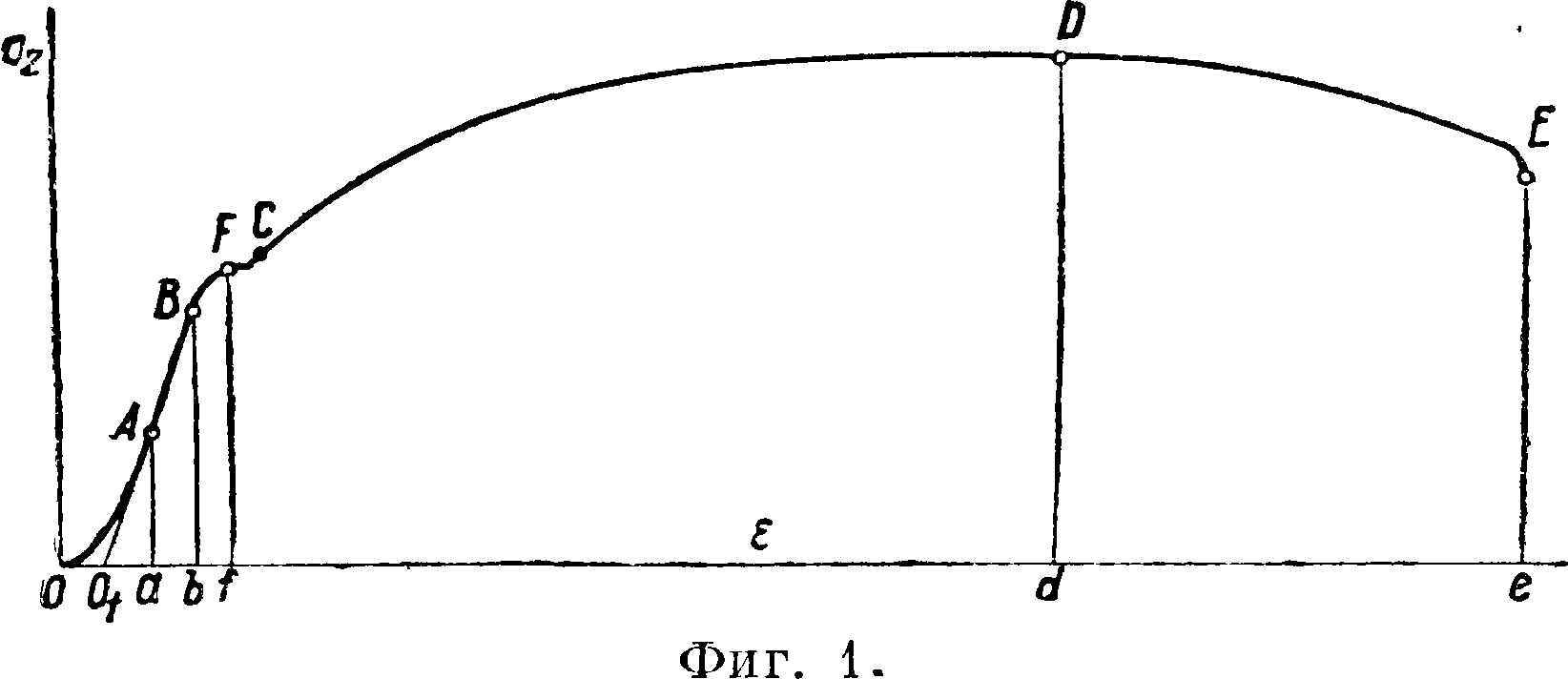
основании опытного закона Гука. Диаграмма состояния упругого тела, типичная для железа и мягкой стали, представлена на фигуре 1 (в координатах «напряжение и относительная деформация»). Часть ОБ соответствует области упругих деформаций, в которой напряжение и деформация следуют закону Гука; часть BCDE— область пластич. деформаций (остающихся). Ордината ВЬ изображает последнее напряжение по закону Гука (предел пропорциональности), Ff—напряжение в период текучести, Dd—временное сопротивление, Ее—напряжение при разрыве. Этим напряжениям соответствуют относительные удлинения (аналитич. выражение которых ^{е =} у) ^в разных стадиях деформации. Во всех конструкциях материал работает под напряжениями в пределах АО_гАа, где Аа^~,

но пригодность материала для известной конструкции или для изготовления изделия определяется по величинам, характеризующим его свойства в пластической области: временному сопротивлению, относительному удлинению и поперечному сужению при разрыве, а также площадью всей диаграммы. Временное сопротивление характеризует прочность материала; удлинение и поперечное сужение—вязкость и ковкость; площадь диаграммы,площадь которой о^£ ™_Μ7·, характеризует работоспособность материала. Работоспособность рассматривается как качественный показатель стойкости материала против ударов и как сравнительный критерий безопасности во время службы при наличии ударов. На фигуре 2 изображен нормальный образец из железа на растяжение в различных фазах деформации: в начальном состоянии—в состоянии, соответствующем точке D диаграммы; в момент после разрыва, поперечное сужение измеряется отношением

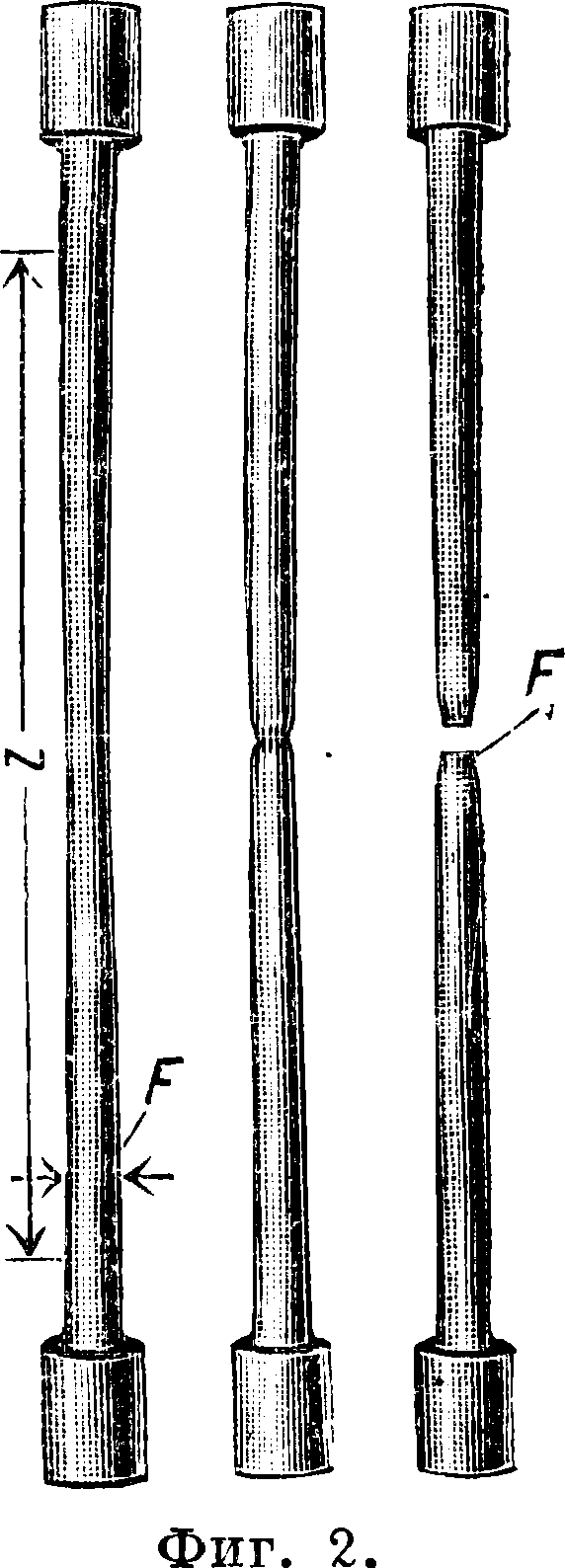
Напряжение в точке Е диаграммы, отнесенное к площади Г¹! (шейки образца), называется истинным. Некоторые авторы расценивают это напряжение как наиболее характерное для каждого металла и наиболее постоянное свойство его в различных стадиях холодной обработки. На фигуре 3 представлена диаграмма в координатах «истинное напряжение и поперечное сужение», полученная из опытов над холоднотянутым металлом; из очертаний кривой легко усмотреть, что линия напряжений действительно только слегка наклоняется к оси абсцисс. На фигуре 1 tg угла наклона прямой O_tB к оси абсцисс дает значение коэф-та пропорциональности между напряжением и деформацией—модуль Юнга Е, который является постоянным числом с размерностью кг/см² для металлов в различных изотермич. состояниях после холодной и термич. обработок. Модуль Е в адиабатич. процессах должен быть больше Е в процессах изотермических, но различие между ними мало и приборами не может быть установлено с достаточной точностью. Значения модуля даны в таблице 1.

12000

тоо | юооо 9000 %8000 %7000 * 6000

5000

				т	2		1			„ -я	0			--	--	га	тс	ль
		4с		i--			-о-											ез1	i
													2
			iuS						з			4									0
												г—
/I	1	3	0	5	)	7	0	S	0	л	0	/3	0	11	0	/;	0	1S	0	2	0%

28& 42 & b 97109,5 121 134 J% &

12000 тоо юооо			—	-с	та	ль						1	2		7
				J	Kej	ез(	г								Л	га
п, оооо							1,		2		j
8000																/5
N э 7000										Г
•о 6000
чппп		1	1	2	1				0			6	0	I i.		8	0		I	100
32 4									ί54		Щ15578		64	5 726 78 (1-ψ)					%

Фигура 3.

Качество металла для работы в условиях динамич. нагрузки определяется пробой на удар (смотрите Испытание материалов). Для частей конструкций, где требуется точный монтаж, для частей трущихся (цапфы) испытание на твердость (смотрите Твердость) служит непременной дополнительной характеристикой, а для обрабатывающего инструмента это испытание наряду с химич. анализом составляет исключительный источник для суждения о качестве его. Металло-графич. исследование металла (смотрите Металлография) доставляет сведения о структуре металла и об ее изменениях при термич. обработке,

Таблица 1.— Модули упругости для железа, чугуна и сталей.

, Сорта металла	Модуль Юнга Е, кг (см2	Модуль сдвига G, %г}см2
Сварочное железо в на
правлении, параллельном прокатке.	! 2 000 000	770 000
Литая сталь St 37.. Строительная сталь по-	2 100 000	810 000
выптенного качества St 48..	2 100 000	850 000
Кованая литая сталь. Рессорная сталь, без за	2 100 000	850 000
калки ..	) Г	850 000
Рессорная сталь, зака	>2 100 000
ленная ..	J 1	880 000
Никелевая сталь для
мостов (2—3,5% Ni).	2 090 000	—
Литая сталь.	2 150 000	830 000
Чугун ..	1 750 000 850 000	290 000 400 000
1 * Е почти совершенно	не зависит от	степени за-
калки, однако опыты с хромовой сталыо обнаружили увеличение 1 : Е с увеличением степени закалки.

Ш

сведения о распределении компонентов металла, которые дополняют механич. испытания. Сочетание металлографических (включая и рентгенографические) и механич. испытаний приводит совместно с химическим анализом к пол-ному познанию свойств металла. ^{1 1} Технические испытания обнаруживают, что большинство металлов подчиняется закону Г^ка, что дает все основания построить на нем теорию С. м. Напряжения в любой точке сечения шп растягиваемого бруска не зависят от ее координат и всюду равны (фигура 4). Это положение является гипотезой теории растяжения. Условие равновесия отрезанной части будет

Р=R,

-4

Фигура 4.

(1)

где Р—действующая сила, R—равнодействующая внутренних сил. Согласно гипотезе равномерного распределения напряжений

R=Fa_z, (2)

где F—площадь сечения, σ_ζ—напряжение. Сравнение (1) и (2) дает

P=Fg_z, (3)

откуда можно наити напряжение при известных размерах сечения или площадь Сечения при известной величине напряжения. Чаще всего пользуются ур-ием для последней цели, и с_а при этом будет допустимым напряжением для данной конструкции, а ур-ие (3)—ур-ием прочности при растяжении. При помощи закона Гука (σ_ζ=Εε) и ур-ия (3) выводится ур-ие деформации:

Р ¹ Р

^s=ef> ^или (⁴)

и

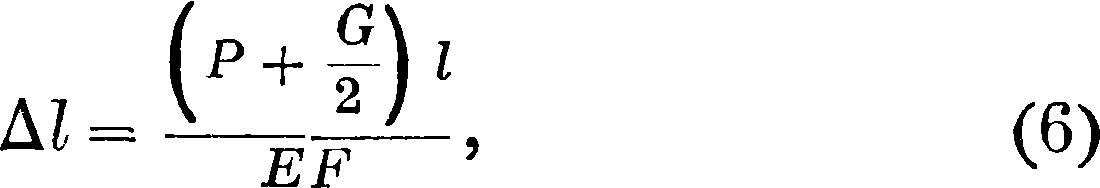
где у—уд. в килограммах/см³, G—полный вес бруска. Эпюра напряжений изображена на фигуре 5, откуда следует, что сечения бруска, различно удаленные от точки приложения силы, подвержены разным напряжениям, и т. о. материал всюду, за исключением наиболее удаленного сечения, недостаточно использован. Стремление получить эпюру напряжений в виде прямой АВ, то есть получить одинаковую нагрузку, и притом наибольшую для всех сечений, привело к особой форме бруска, которая известна под названием тела равного сопротивления. Тело равного сопротивления имеет наименьший вес по сравнению с призматич. или цилиндрич. телом и наибольшую деформацию при одинаковых условиях нагружения. Ступенчатый брусок *по своим свойствам занимает среднее положение между телами равного сопротивления и ци

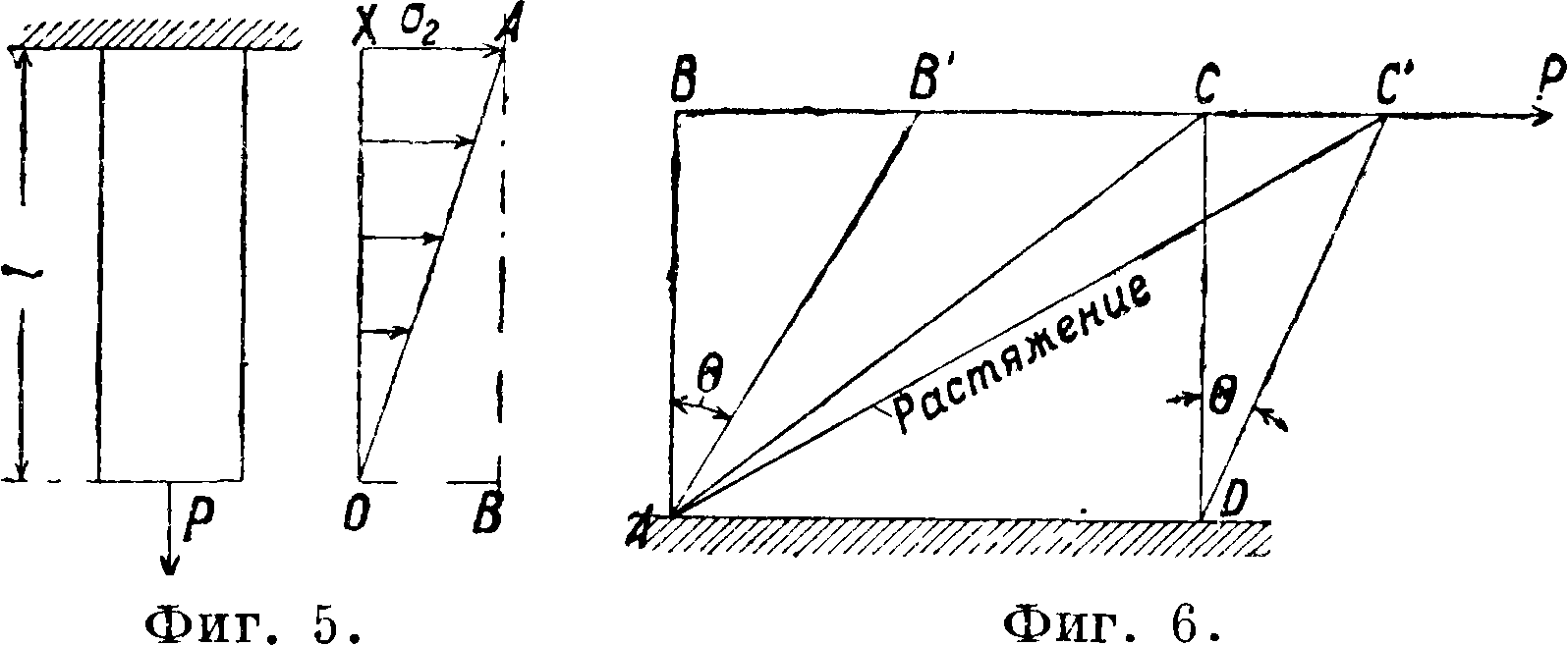
линдрическими (тоже призматическими), изготовляется без особых трудностей и поэтому находит применение при большой длине брусков (шахтные канаты).

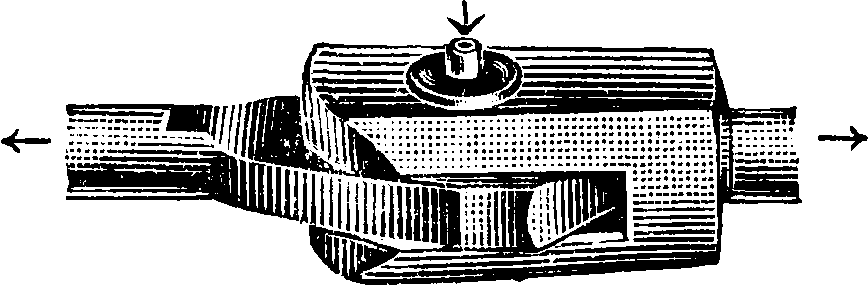
Деформация сдвига представлена на фигуре 6 и 7. Фигура 6 изображает сдвиг, к-рому сопутствует растяжение и ^в сжатие; фигура 7—чистый сдвиг, в котором нет по-

ОБРАЗЁЦ

о

Фигура 7. Фигура 8.

сторонних явлений. На фигуре 8 дана фотогра фия тех условий, в которых производят обычно опыт на сдвиг, откуда видно, что явление сдвига осложняется изгибом. Поэтому для сдвига принимают закон Гука не как результат опыта, а в качестве первого приближения к действительному закону

r=G-y, (7)

где G—модуль поперечной упругости, у—угол сдвига. Ур-ие прочности при том же допущении, что и при растяжении, получает вид

Р=F · R_s, (8)

по к-рому в случае, если размеры даны, находят величину абсолютного удлинения ΔΪ бруска. Эта величина имеет свои границы, которые определяются по особым соображениям для каждой конструкции. Если брусок имеет большую длину (1>10м), собственный вес должен быть принят в расчет. Ур-ия прочности и деформации получают вид по к-рому определяется площадь сечения прц заданной нагрузке и выбранном допустимом напряжении R_s. Последнее принимают в соответствии с чи Вёлера, причем наибольшее касательное напряжение (то есть для первого случая нагрузки) равно 0,75—0,8 от нормального для того же случая. Ур-ие деформации будет

(3)

Модуль G отыскивается или по зависимости между Е и G

С ^

2(1 + μ)

(10)

где μ—коэф. Пуассона (равный * * для ста ли и железа), или из опыта на кручение.

Кручение имеет в своем основании гипотезу о равенстве угла кручения на единицу длины стержня:

т=£ (П)

(смотрите Кручение, фигура 1). Это предположение оправдывается опытом. Закон распределения касательных напряжений при этих условиях устанавливается в виде линейной зависимости и графически выражается в виде прямой линии; уравнения прочности и деформации для круглых сечений получают простой вид: уравнение прочности

w — Мл ^{0 _} «8

и уравнение деформации для цилиндра М₈1

^{φ =} 7&’

(12)

(13)

где М_ё—крутящий момент, 1₀ и W₀—момент инерции и момент сопротивления, I—длина, G—модуль сдвига, R_s—допускаемое напряжение, ψ—угол кручения двух сечений на расстоянии I. Другие сечения—см. Кручение.

Теория изгиба (смотрите) прямолинейных стержней построена на гипотезе плоских сечений Бернулли и указывает закон распределения нормальных напряжений в виде прямой линии (Навье). Отказываясь во многих случаях от учета касательных напряжений (для стержней достаточной длины и стержней поперечного сечения достаточных размеров), производят расчет на прочность по ур-ию

ψ_=Μρ!2Ζ (J1)

Нь н определяют деформацию по ур-ию

EL

(1²У

= М_г

(15)

Здесь 1₃ и W₃—момент инерции и момент сопротивления поперечного сечения, М_х и М_тах— изгибающие моменты соответственно в сечении х и наибольший, R_b—допускаемое напряжение на изгиб, —кривизна в данной точке изо гнутой оси балки. Ур-ие (15) имеет различные решения в зависимости от законов изменения для изгибающего момента М_х и момента инерции I_z. Общий вид всех решений следующий:

У шах ^α * El ·, ’ (1^)

где Р—нагрузка стержня, ί—длина, а—коэф., величина которого зависит от закона изменения нагрузки ц способа закрепления концов. В

табл. 2 даны схемы нек-рых нагрузок и значения а и М_шпх. Касательные напряжения при изгибе учитываются дополнительно. Из условий равновесия обнаруживается их существование и устанавливается закон распределения по поперечному сечению. Закон распределения в случае отсутствия сил, действующих по касательным к поверхности стержня плоскостям, будет парабо-

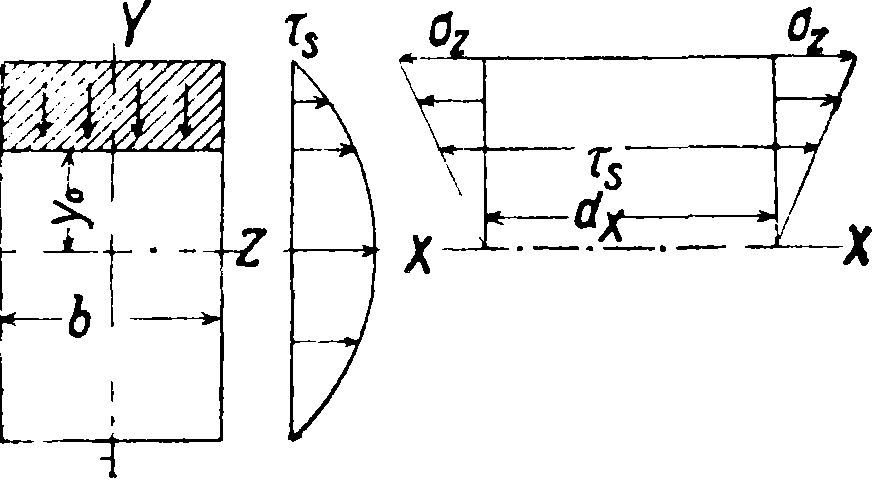
Фигура 9.

Таблица 2. — 3 н а ч е и и я а и М_тах для самых употребительных случаев изгиба.

Л?

Схемы нагрузки и балки а для Р или в середине

- -

1

48

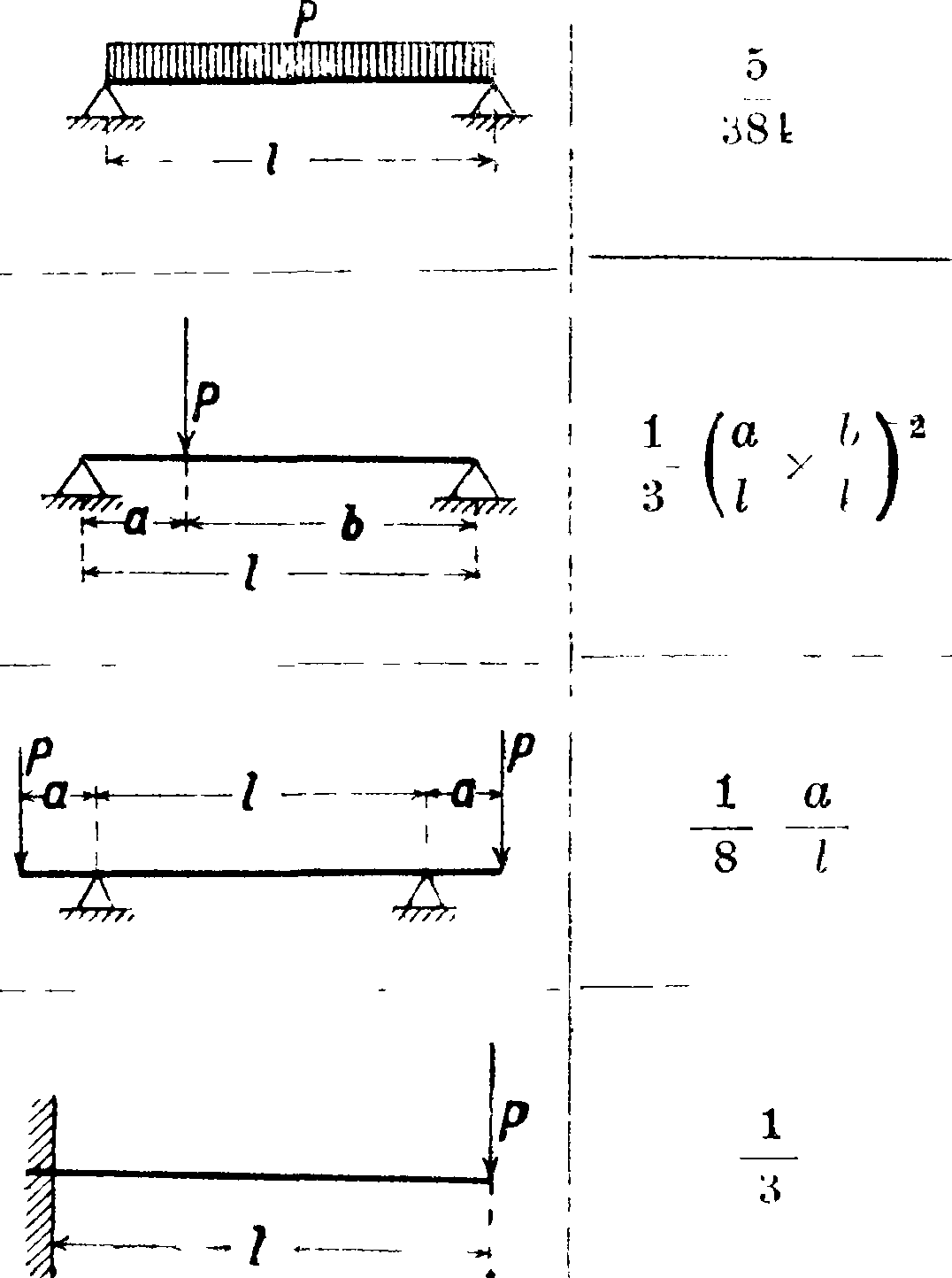
у

(9 (Н

%

1

192

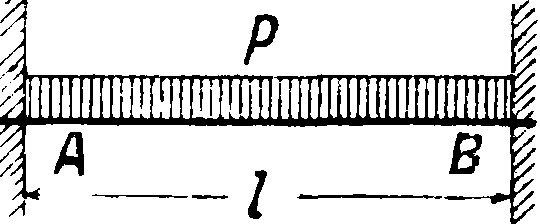
1

381

Р1

4

Р1

Ра

Р1

8 ‘

М_С

Р1

ΡΙ * 12

л ой (фигура 9). Величина напряжений определяется по vp-ию г _ Q.r ^Sz

причем. (λρ—перерезывающая сила, равная сумме сил, лежащих левее того сечения, в котором отыскивается напряжение, S_s—статич. момент площади поперечного сечения относительно оси изгиба (заштрихованной на фигуре 9), I_z — момент инерции сечения. Ь — ширина сечения в том месте, где будет искомое τ. Закон распределения касательных напряжений для различных сечений изображен в таблице 3. В той же таблице указано наибольшее значение этих напряжений. Подробности—смотри Сдвиг. При расчете длинных стержней обычно ограничиваются одной проверкой высоты наибольших касательных напряжений, которая должна быть в известных пределах для каждой конструкции (в клепаных железных балках R_s=800 килограмм/см²). В случае коротких стержней ведут расчет на сложное сопротивление.

Таблица 3-Касательные напряжения при изгибе.

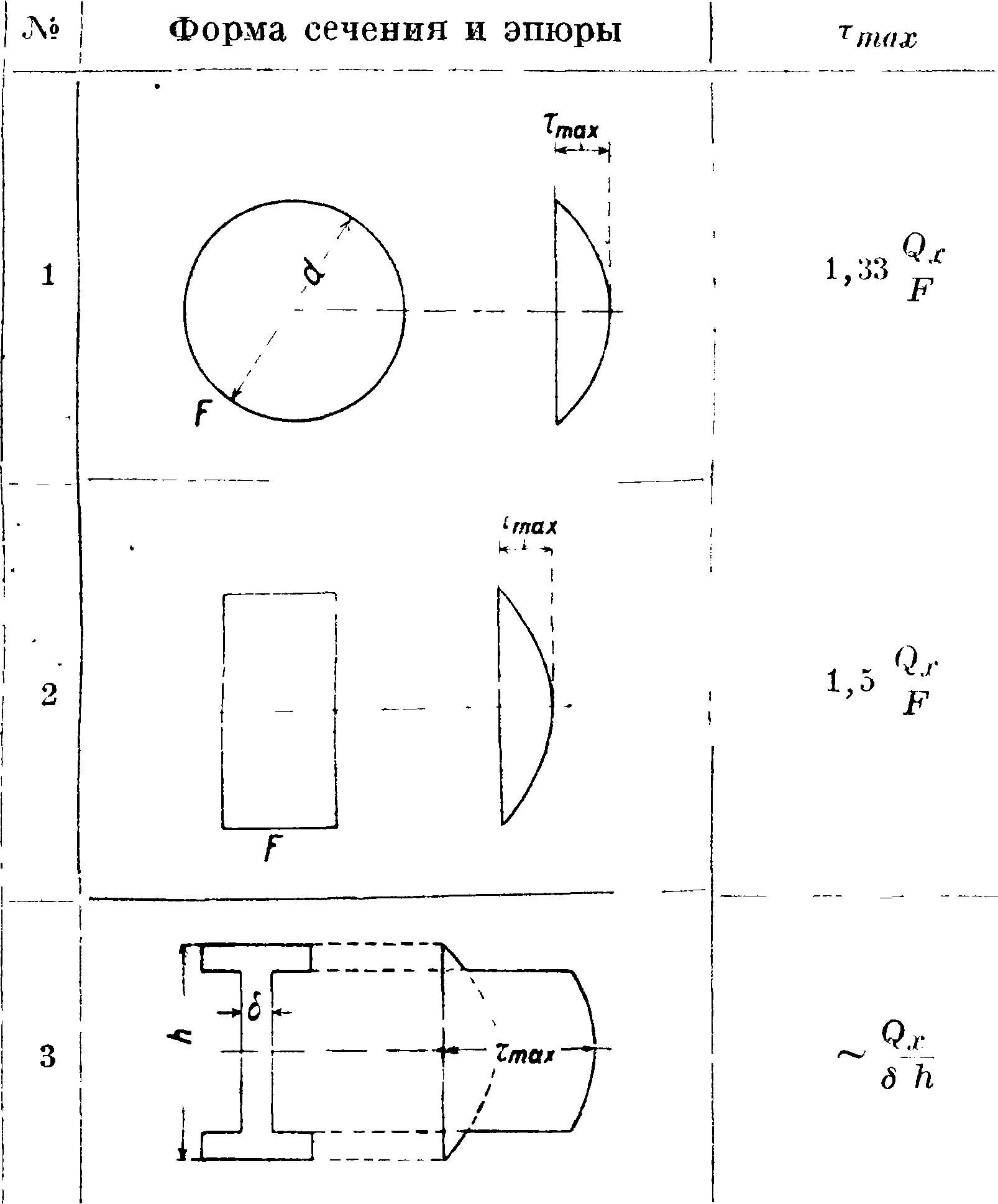
Сложное сопротивление составляется из двух или более деформаций. Число видов сложного сопротивления возможно следующее: а) сочетаний из двух деформаций—6, Ь) сочетаний из трех деформаций—4, с) сочетаний из четырех деформаций—1, всего 11. Способ изучения сложных деформаций — принцип наложения (суперпозиции), согласно которому последовательное и совместное появление деформаций равнозначно, создается тождественное напряженное состояние, то есть равные напряжения и равные результирующие деформации. Этот принцип широко применяется, хотя хо-Фигура ίο. рошо известны случаи,

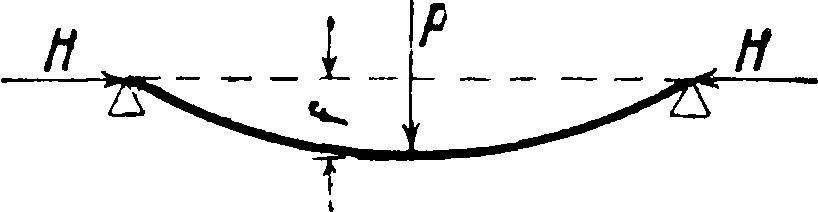
в которых пользоваться им совершенно недопустимо. Подобный случай изображен на фигуре 10, в к-ром при принятых обозначениях в действительности

V + H/,

между тем по принципу наложения М =^Pl-

•^iVA max

Все виды сложного сопротивления разделяются на три типа: 1) сложение нормальных напряжений, 2) сложение касательных напряжений, 3) сложение нормальных и касательных напряжений. В случаях первого типа сложение напряжений алгебраическое, в случаях второго типа—геометрическое. В случаях третьего типа из условий равновесия бесконечно малого параллелепипеда, вырезанного около известной точки напряженного тела, определяют главные силыупругост и—наибольшее нормальное напряжение и наибольшее касательное напряжение или главные деформации — наибольшее удлинение и наибольший угол сдвига. Расчет в случаях третьего типа производится по различным основаниям в зависимости от того, что принимают за причину разрушения конструкции. Обычно приписывают разрушение второй

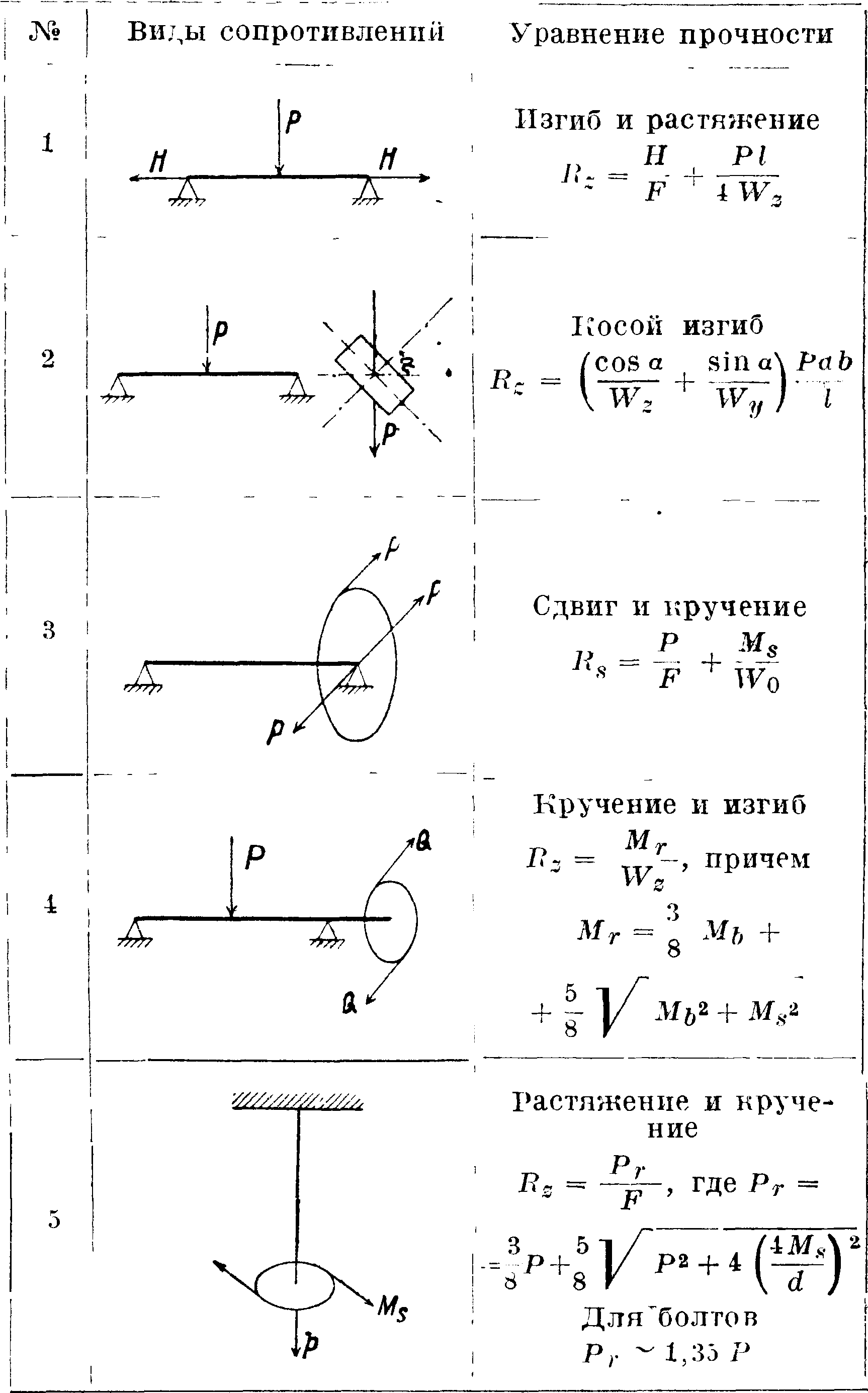
, главной силе упругости (касательному напряжению) или первой главной деформации (наибольшему удлинению). Ур-ия прочности для наиболее употребительных комбинаций сложного сопротивления сведенгл в таблице 4 (смотрите Прочность).

Таблица 4.—С ложные сопротивления.

Продольный изгиб (смотрите Изгиб) представляет собою элементарный вид неустойчивого равновесия, когда простая деформация сжатия при определенной нагрузке переходит в другую форму—деформацию изгиба. Расчет производят или по формуле Эйлера (теория изгиба) в случаях, если развивающиеся при этом явлении напряжения при критич. значении силы остаются в пределах упругости, или по эмпирическим формулам Тетмайера, Кармана и таблице Ясинского (сжатие), если эти напряжения оказываются вне этих пределов.

Из обширйейшей теории расчета статически неопределимых систем в С. м. включаются основания для расчета неразрезных балок—способ Релея и Клапейрона.

Теория упругоети разделяется на три части, которые содержат: а) изучение напряжений и деформаций изотропного упругого тела в статич. условиях и в состоянии движения (Elastostatik und Elastokinetik), б) теорию анизотропного тела, гл. обр. теорию кристалла (Elastokristall),

в) теорию пластич. деформаций изотропного тела (Plastizitat) и г) теорию упругого удара (Stoss). Теория изотропного упругого тела построена на законе Гука и имеет в виду деформации настолько малого размера, что квадрата-

ми относительных перемещений точек при деформации можно пренебречь. Остальные гипотезы, к-рыми пользуется С. м., здесь устранены первоначально; в развитии теории упругости они или подтверждаются вполне, или частью, с известным приближением, или отвергаются в связи с анализом отдельных деформаций. Элементарные теории растяжения, кручения круглых брусков, чистого изгиба вполне согласуются с теорией упругости. Изгиб в присутствии срезывающих сил, как оказывается, подчиняется закону прямой линии (гипотеза Навье), но не закону плоскости (гипотеза Бернулли). Касательные напряжения при изгибе распределяются по закону параболы, но только в тех сечениях, которые имеют незначительную толщину при большой высоте (узкие прямоугольники). В других сечениях закон распределения касательных напряжений совершенно иной. Для балок переменного сечения, к которым в элементарной теории прилагают закон прямой линии и параболы, теория упругости дает другие решения; в этих решениях значения напряжений и деформаций гораздо выше, чем по элементарной теории следует. Общепринятый способ расчета пластин по Баху как обыкновенных балок не оправдывается теорией упругости. Ф-лы С. м. для кручения некруглых стержней не соответствуют таковым в теории упругости. Теория изгиба кривых стержней решительно не совпадает с элементарной теорией Баха-Баумана, но результаты расчета по строгой теории и на основании гипотезы плоских сечений достаточно близки. Поставлена и разрешена для ряда случаев- задача о распределении местных напряжений (в местах приложения нагрузки или изменения сечения), которая совершенно недоступна теории С. м. Вопрос об устойчивости деформированного состояния, элементарную форму которого представляет в С. м. продольный изгиб, получил в теории упругости общее решение Бриана (Bryan), Тимошенко и Динника. Помимо многочисленных форм устойчивости стержня, сжатого сосредоточенной силой, изучены также явления устойчивости стержней переменного сечения под действием равномерно распределенных сил и другие явления устойчивости балок при изгибе, равномерно сжатой трубы, кольца, оболочек, длинного стержня при скручивании и прочие Теория упругого удара— долевого, поперечного—занимает большое место в теории упругости и включает все большее и большее число технически важных случаев. Теория колебаний получила настолько прочное положение в теории упругости и в практике, что методы расчета на колебания проникают в область С. м., конечно в элементарном виде. Изучены распространение волны в неограниченной упругой среде (решение Пуассона и Кирхгофа), движение волны по поверхности изотропной среды (решение Релея), волны в всесторонне ограниченных упругих системах с одной, конечно многими и бесконечно многими степенями свободы. В связи с этим находятся решения, относящиеся к колебаниям струн, мембран и оболочек, различной формы стержней, пружин и пластин.

Основные методы теории упругости. Методы теории упругости—весь аппарат математич. анализа и механики. В статике упругого изотропного тела основными представляются ур-ия равновесия бесконечно малого параллелепипеда, дополненные ур-иями поверхностных условий. На фигуре 11 изображен параллелепипед, выделенный из упругого деформированного тела, под действием возможных в самом сложном случае сил. Независимо

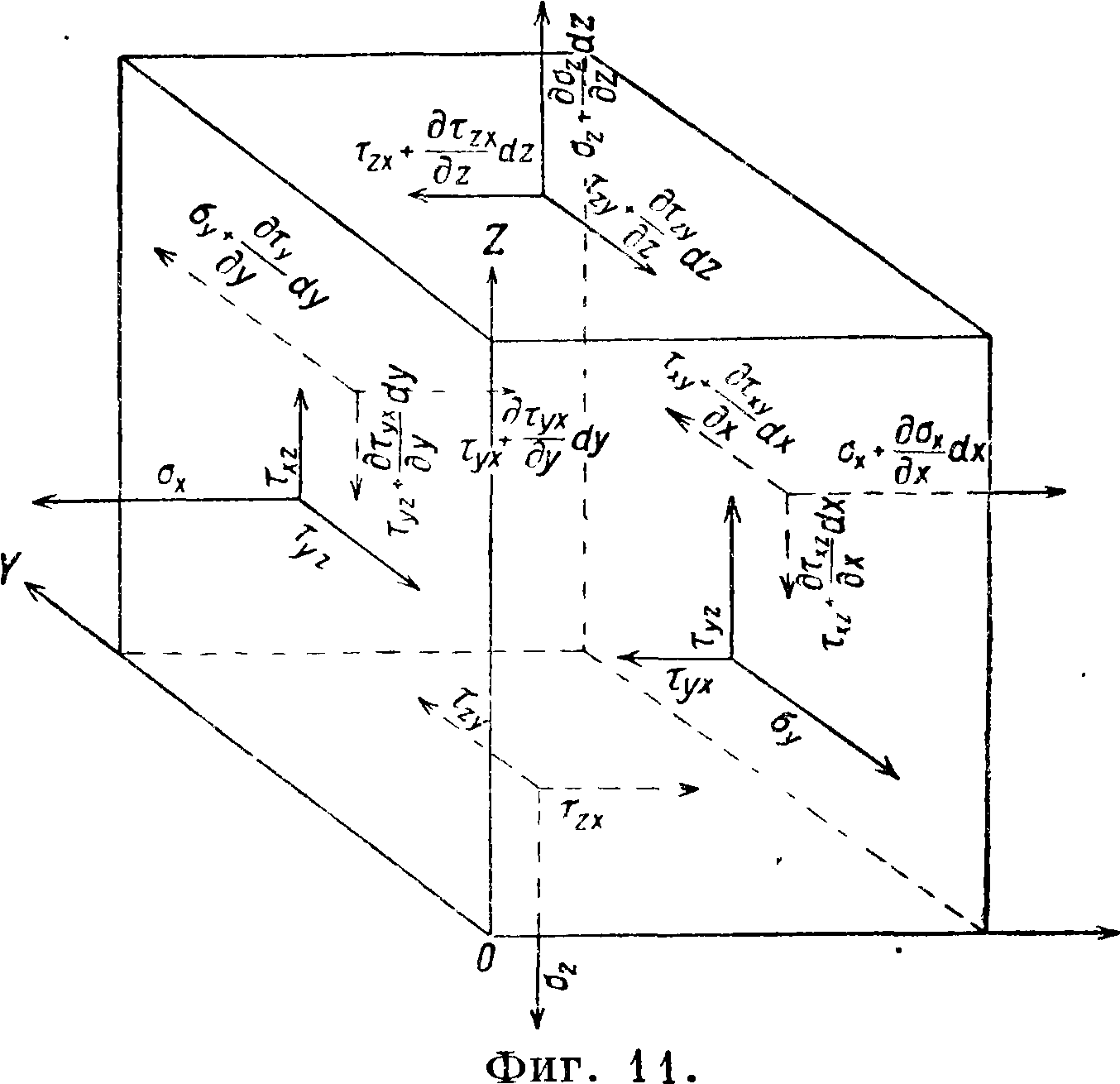
от того закона, которым связаны напряжения и деформации, при одном лишь условии, что эти величины являются непрерывными функциями координат, получаем из условий равновесия шесть ур-ий Коши:

дх дОу ду

δσ_ζ

dz

дТху	JL	®τχζ
оу	1	dz
дТху	+	fayz
дх		dz
dTzx		дтуг
дх		ду

+ X-Q= О, + Υ·ρ=0, Т· Ζ · Q=О,

^bХу

Τ ту »

^lyZi

причем X, Υ, Ζ—компоненты объёмной (веса идр.), ρ—уд. масса. Последние три возможны лишь при допущении, что

Пт —=О,

(18)

(19)

(20)

(21)

(22)

(23)

СИЛЫ

ур-ия и выражают закон двойственности касательных напряжений. На поверхности упругого тела должен быть соблюдены еще пограничные условия равновесия, т. .е.

<Гпх=Οχ cos (X, η) + τ cos (Υ, η) +

+ t„cos(Z,·»), (24)

и другие два им аналогичные ур-ия, причем σ_ηχ, а_пу и σ_ηζ означают компоненты силы, действующей на площадку с нормалью п. Из последних трех ур-ий (24) с помощью геометрии, соотношения

cos²(X, n) + cos²(Y, n) + cos²(Z, ή)= 1, если направление силы совпадает с нормалью, получаем:

σχ -	R,	Тху>	τχζ
τχψ>	°ν~	-R,	τνζ
τχζ>		<*ζ-	-R

где R—главный вектор внутренних сил. Отсюда находим три значения R, которые названы главными напряжениями, а соответствующие взаимно пер пендикулярные нормали—главными направлениями напряжений. Три значения R не зависят от положения системы координат и при ее вращении остаются неизмененными: они — инварианты упругого состояния. Наибольшее касательное напряжение оказывается равным полуразности между главными (наибольшим и наименьшим) и лежит в плоскости под углом 45° к плоскости главных. При малых деформациях и малых значениях производных относительное удлинение в любой точке - упругого тела выражается ур-ием:

в=cos² ge, η) + Ц COS² (У, η) + ψ- cos²(Ζ,η)+

+ cos (X, η) cos (Υ, η) ) +

+ cos (Υ, η) cos (Ζ, η) + ·|^) +

+ CCS (X, η) cos (Ζ, η) (If + ff) · (26)

Здесь U, F, IF—перемещения точки по осям координат, cos (X, ?г) и прочие указывают направление рассматриваемого элемента длины. Вы-air dV dW

ражения ^=в_Х9 - е_у,=ε_ζ —удлинения вдоль осей,=У_Ху и т. д. (смотрите Дефор-

мация)—углы сдвига между осями и называются компонентами деформации в данной точке. В случае однородной деформации ~,

dW _ ^V

-fo являются постоянными. Поворотом осей члены уравнения (26), которые содержат произведения cos-ов, можно устранить, и тогда оси новой системы координат совпадают с главнымР1 направлениями деформации, а удлинения будут также главными и представляют инварианты деформации. Сумма их е=ε_λ + ε₂ + ε₃называется относительным объёмным расширением. Диференцированием выражений отдельных деформаций (26) получаем зависимости Сен-Венана д^2еж i д^2еу __ д²Уху ^у

ду2 дх² дх ду д²*У, ₌ d²Vvz I.

άζ2 д/ζ ду dz f »

(27)

их“ dz² ax dz

также ду д

:=А(_

z дх V

dx

dz

(23)

Т. о. шесть компонент деформаций должны удовлетворять шести зависимостям. В случае, когда эти компоненты зависят от первой степени координат, условные ур-ия (27) и (28) всегда удовлетворены. Копш сделал допущение, что направления главных напряжений и главных удлинений совпадают. Тогда на основании закона Гука напряжение в любой точке м. б. выражено через три компоненты ур-иями:

^ах — ^αει + се₃ 1

а_у=αε, + Ье₃ + ce₁ I. (29)

а_л=αε₃ + bе₁ + се₂ )

А так как упругое тело считается изотропным, то нет никакого основания для различия между коэф-тами b и с поэтому b=с=к, α=λ- -2ν и получим

^ах=-Ь %^ν)^ει + Α(ε₂ + ε₃)> (30)

где λ и г—коэф-ты Лямэ, которые связаны с модулями упругости Е и G соотношениями:

«5 __ &Е, , fi Е

(ϊ+ϊόίΓ⁷^) ’ ^V ~ ^Ь - 2(1+^) ’ где μ—коэф. Пуассона. Для напряжений неглавных (поворотом осей) получим: от.;=Ае + 2νε_χи 2 подобных; также

^гух=Пх_У (31)

и 2 подобных. Подстановкой из ур-ия (31) в (27) и (28) имеем:

(1 + М) ?²<^ + |~=0

(ΐ + /*)ν 4 + 0=0

•. (1 + /Ov*^ + S-0

(1 + /*)ν4» + ^=0

(ΐ+Αθν**» + ^=ο _

Здесь у²—оператор Лапласа;

^θ=о’х + Су + μ =.

(32)

Объемные силы отброшены. Ур-ия,(32) вместе с (18)—(24) содержат решение статических задач теории упругости. Вопрос о существовании интегралов—решений основных ур-ий—самый трудный в теории упругости. Имеются доказательства существования решений Корна н Лихтенштейна. Оба доказательства относятся к случаю отсутствия объёмных сил и связаны с теорией потенциала. Однозначность решения ур-ий была доказана Кирхгофом для тел с односвязным контуром при том допущении, что до появления объёмных сил и внешних в упругом теле нет напряжений (естественное состояние). Простой случай продольного изгиба однако приводит к заключению, что ур-ия упругости могут иметь несколько решений. Обычный прием решения ур-ий—принять подходящую форму части напряжений и перемещений, затем определить по ур-иям остальные неизвестные и доказать их совместимость. Этот по-луобратный метод указан Сен-Венаном. Решение основных ур-ий в пространственной системе координат сделано Буссинеском для случая действия силы на поверхность неограниченных размеров, но сверху ограниченную плоскостью, и Герцем .для случая малой поверхности давления по сравнению с радиусом кривизны основной поверхности. Обе задачи имеют чрезвычайно важное значение для теорий шариковых и роликовых подшипников, мостовйх опор и прочие и повлияли очень сильно на учение о твердости. Разрешены основные уравнения для ряда задач о тепловых напряжениях, которые возникают вследствие неравномерного нагрева упругого тела (пустотелый цилиндр и др.). Особенно широко и с большим успехом пользуются основными ур-ями для плоских задач. В случае последних остаются только три компоненты напряжений σ_χ, σ_ν, т_ху; остальные тождественно равны нулю. Следуя предложению Эйри, принимают напряжения за производные, некоторой произвольной ф-ии ψ (х, у):

дН. ду2 ’

agy>.

ОХ² ’

^тху

<Э²1/>

судх

~gqx.

(33)

Подстановкой в ур-ия (18) и (19) и исключением объёмной силы получим ур-ие:

, 9. ^д*У> ₌ о дхь ^ дх“ду² <Эг/4

(34)

Это ур-ие представляет в случае плоской деформации решение любой задачи независимо от величины и направления действующих сил к упругих свойств тела (однако не всегда удобное); должен быть выполнены только в каждом случае особые пограничные условия (24). Объемной силой обычно пренебрегают. Весь вопрос разрешения частной задачи сводится к выбору под-

ii

Т. а. т. XXI.

ходящей ф-ии Эйри (Airy). Для нек-рых задач она выбрана в виде алгебраич. полиномов, для других в виде тригонометрии, строк (конечных и бесконечных) или в виде произведений алгебраич. и тригонометрии. ф-ий. Последний прием чаще всего употребляется в том случае, когда ур-ие составлено в полярных координатах и упругое тело ограничено криволинейными поверхностями. Таким путем разрешен ряд задач

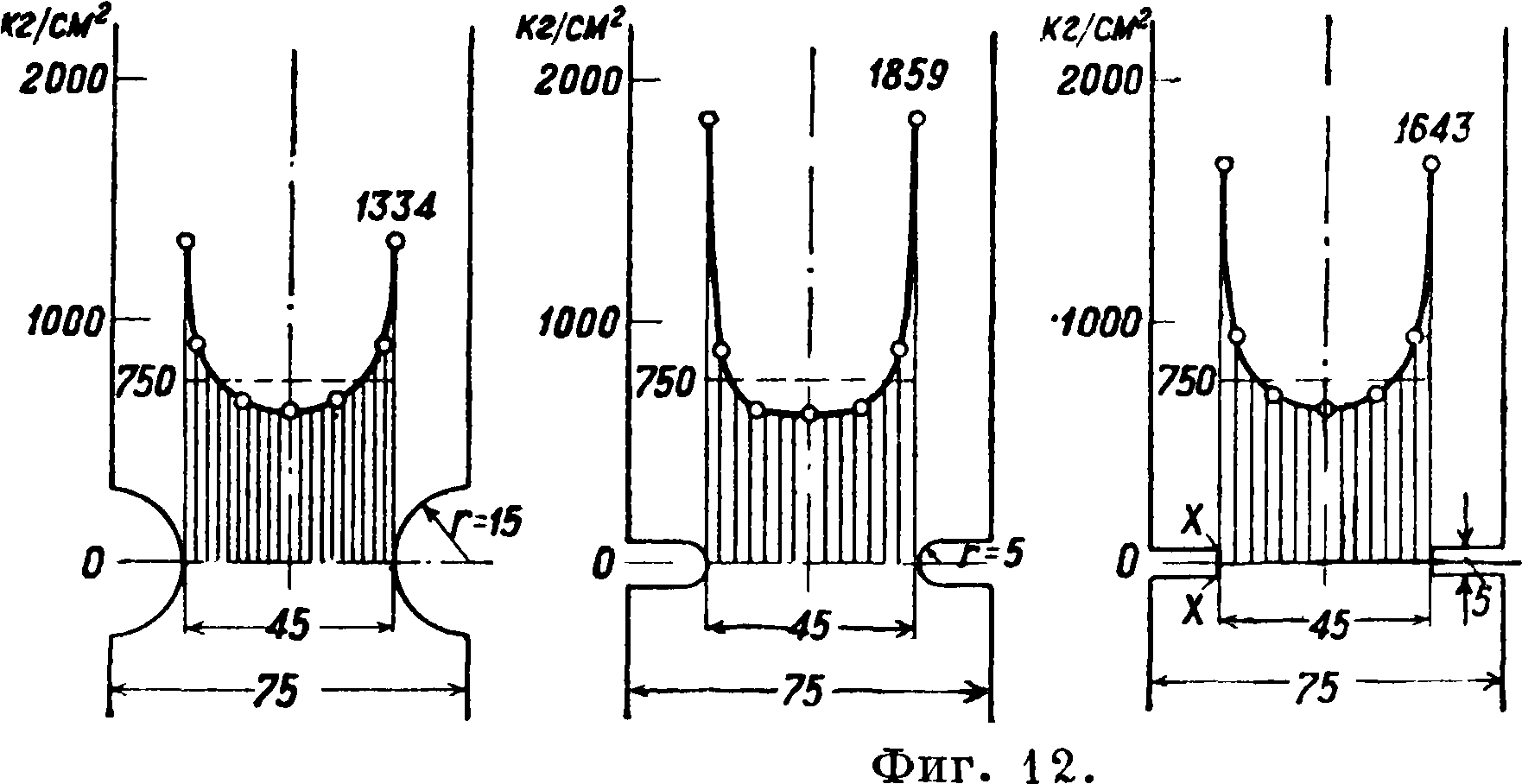
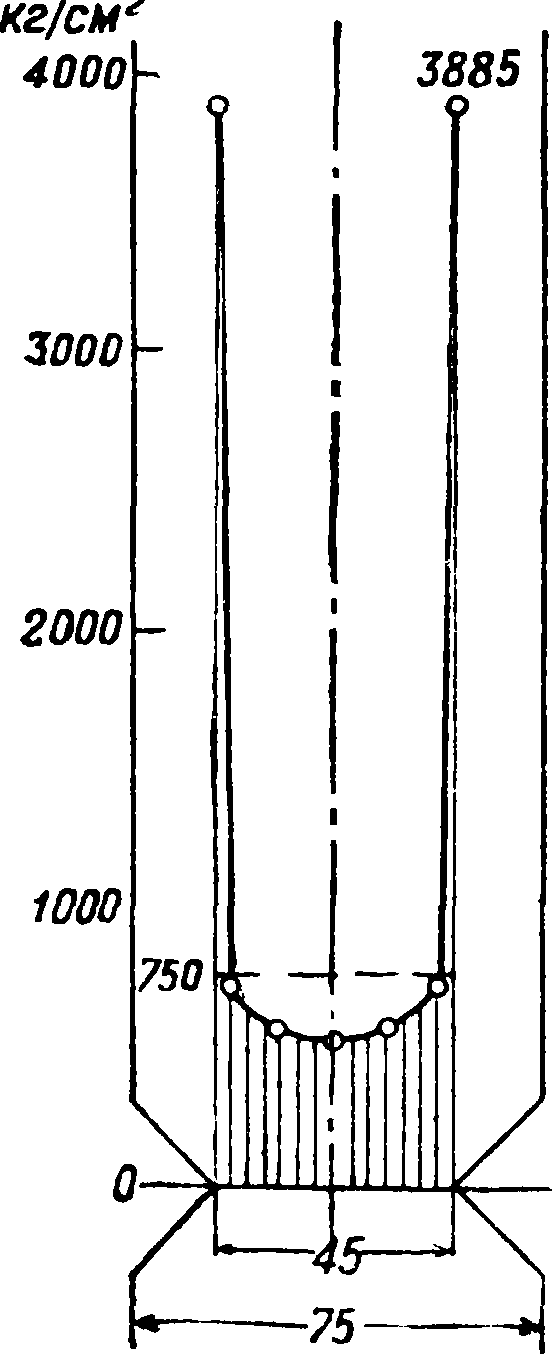
о местных напряжениях; результаты решений изображены на фигуре 12. Существует способ ре-

Недавно предложен метод, к-дэый сочетает достоинства того и другого приема (Фёппль).

Преимущество ур-ия Эйри (34) заключается в том, что решение его относится в случае односвязного дсонтура к любому упругому телу с любыми свойствами, вследствие чего результаты м. б. проверены опытом. Разработан и применяется оптич. метод изучения напряженного состояния различных плоских форм на слюдяных пластинках и т. о. получают подтверждение уже решенные проблемы (например Буссинеска и Герца) и дается ключ к» отысканию решений в других более сложных случаях. К сожалению показания опыта—скорее ка-чесгвенные, так как эксперимент в современной постановке не может дать соизмеримых с точностью теории результатов. На вкладном ли

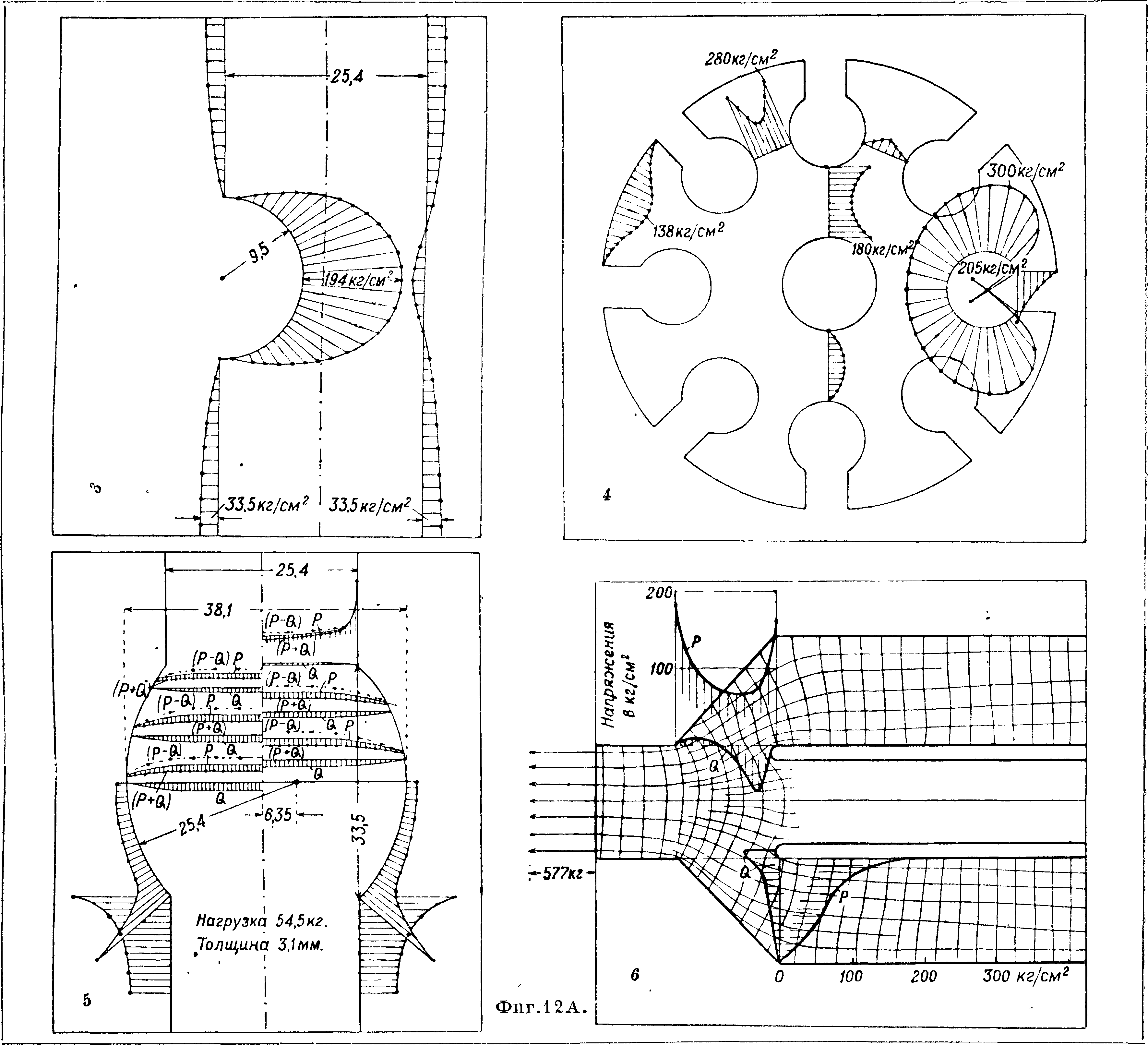
шения основных ур-ий с помощью ф-ий Грина I сте представлены фотографии исследования оп-(Green) и теории конформного изображения. | тическим методом задач Буссинеска и Герца,

^члУ fJ;^Y

о о -Л

.г#. .?>ν,

л

где ясно видны круги напряжений Буссинеска (вкл. л., 1, £)· Распределение напряжений—на фигура 12А и цветные снимки вкл. л., 3, 4, 5 и 6 взяты из опытов проф. Кокера (Coker): 3 дает распределение напряжений вблизи выточки в растянутой полоске; сбоку показана полоска без выточек при том же освещении при нагрузке, вызывающей в целой полосе напряжение в 476 фн./дм.². На вкл. л., 4 представлено распределение напряжений при нагрузке 8 радиальными силами, каждая величиною 4,8 англ, фн.; вкл. л., 5 и 6 относятся к сварным швам и показывают просвечивание моделей шва с двумя приваренными накладками; йа вкл. л., 5 изображено распределение напряжений для шва с двумя приваренными накладками в плоскости, перпендикулярной к линии действия силы величиною в 120 англ. фк. при среднем напряжении 988 англ, фн./дм.²; на вкл. л., 6 распределение напряжений для долевого шва на длине с постоянным сечением (напряжение здесь равно 1 270 англ, фн./дм.²), также в переходных сечениях, где напряжение достигает 3 000 англ, фн./дм.², и в местах сварки.

Удобным и достаточно точным для практических целей является также метод, разработанный фирмой Майбах в Германии. Объект, напряженное состояние которого подлежит изучению, покрывается лаком особого состава с известными упругими качествами. Покрытие лаком может быгь распространено на любую часть изучаемой поверхности. Затем объект подвергается нагрузке обычно того наивысшего значения, которое зле дует ожидать в действительной работе. При определенной величине нагрузки в лаковом покрытии объекта, когда нагрузка превышает вязкость лака, появляются трещины. Направление трещин перпендикулярно к направлению наибольшего удлинения в данной точке напряжен-юго объекта. С помощью специально конструи-юванного прибора, к-рый клеем присоединен к гаучаемому месту, измеряют расстояние между трещинами и т. о. определяют непосредственно шпряжение при растяжении, сжатии и изгибе; ;ля кручения и сложных деформаций необходим юдсчет по основным ур-иям главных удлине-шй. Измеряемая длина колеблется от 2 до 15 миллиметров. Точность измерения—0,48 миллиметров на 10мм. Вкл. л.,

показывает линии удлинения сжатого цилинд->а (пустотелого). Вкл. л., 5 относится к тому ке цилиндру, только лаковое покрытие было шнесено на нагруженном цилиндре и трещины юявились после разгрузки. Вкл. л., 3 изобра-кает состояние цилиндра, подвергавшегося кру-юнию, вкл. л., 11 и 12 также указывают рс-ультаты кручения плоских стержней, вкл. л.,

1—чистого кручения, вкл. л., 12—растяжения кручения. Вкл. л., 7 показывает влияние от-ерстия при кручении пустотелой трубы (сталь-ой) на распределение линий удлинения. Вкл. ., 10 и 9 изображают результаты изгибов плос-ого стержня, вкл. л., 10 на двух опорах, вкл. ., 9 в виде консольной балки с заточкой. Вкл. ., 8 представляет линии удлинения для растя-утого шатуна авиамотора. Вкл. л., 6 изображает линии удлинения для алюминиевого порш-я, к-рый находится в сжатом напряженном со-гоянии. Вкл. л., 2 относится также к сжатому апряженному состоянию колена вала при дей-гвии наивысшей рабочей нагрузки. Вкл. л., 1 редставляет течение линий удлинения на верх-зй лобовой стороне картера авиамотора (левая 1сть) и на наружной стороне картера, обра-енной к пропеллеру (правая часть). На фо тографии указаны вычисленные величины напряжений в нек-рых точках картера.

Устойчивость упругих форм деформации. Вопрос об устойчивости упругих форм был поставлен и разрешен для частного случая Эйлером (известная задача на продольный изгиб), в самой общей форме сформулирован Брианом и Саутвеллом (Southwell) и широко использован для ряда задач С. П. Тимошенко. Признаком устойчивого состояния по Бриану является минимум потенциальной энергии в данном состоянии по сравнению с другими, ему близкими, то есть _т

<5²(F + А) > 0, (35}

где обозначает вариацию 2-го порядка, А—. потенциал внешних сил, V—энергия внутренних сил. Обычный метод Тимошенко—сравнение вариаций энергии деформации и работы внешних сил при бесконечно малом изменении деформации тела:

δ А + SV=0. (36)

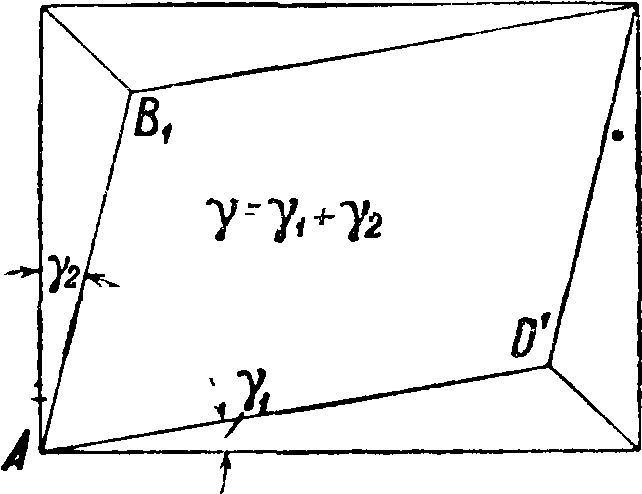
Из этого ур-кя определяется критич. значение силы, при к-ром данный вид деформации неустойчив. Для случая фигура 13 ур-ие должен быть со

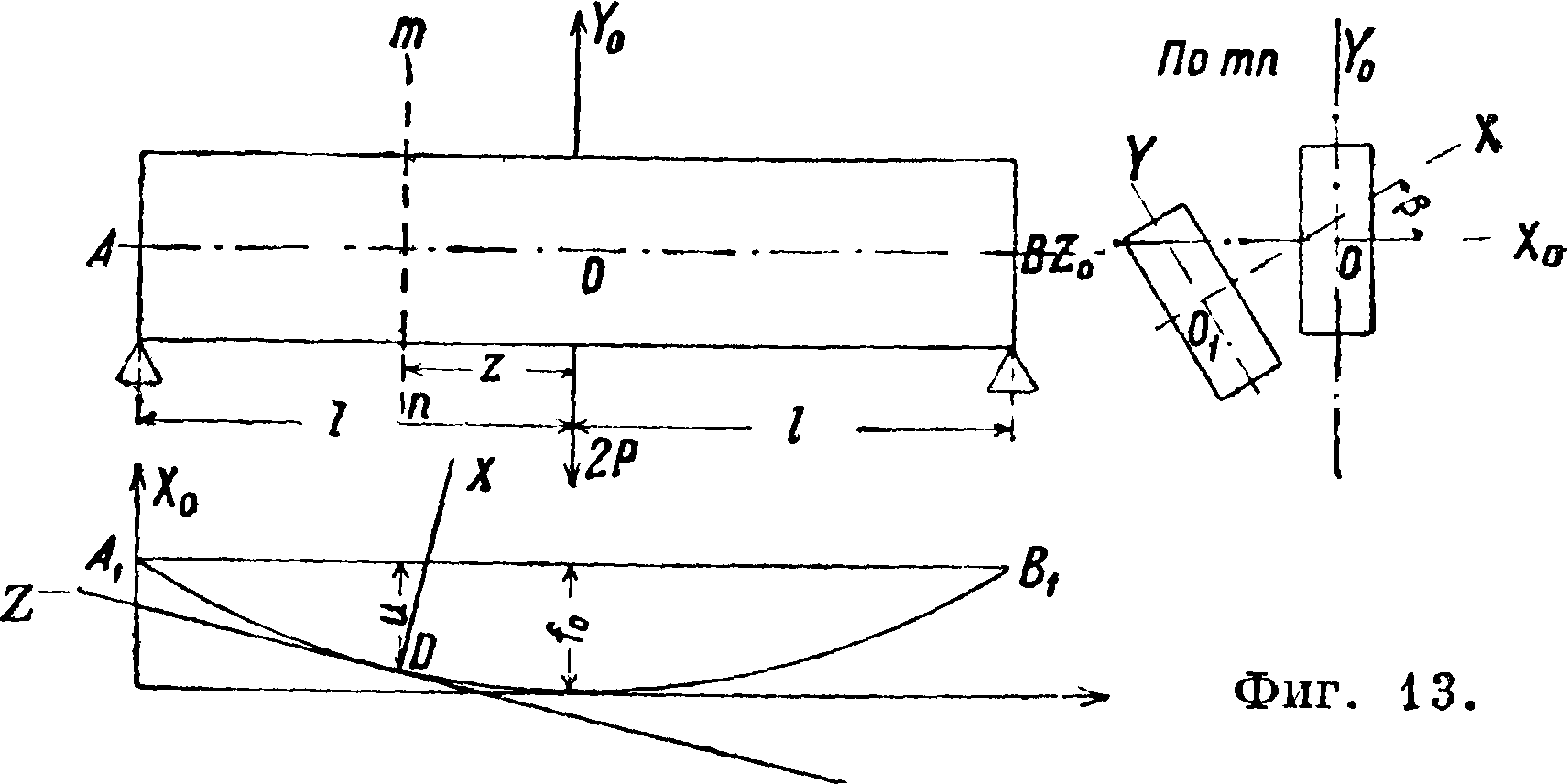
ставлено след. обр. Момент в сечении т-п в случае выпучивания равен а) относительно оси X:

М_х=— Р(1 — я),

б) относительно оси У:

Μ„=Ρ(1-£)β,

в) относительно оси Ζ:

М_г=-Р(1-г)%-Ри,

где и—перемещение центра сечения по оси X. Первые два—изгибающие моменты, последний—крутящий. Энергия от изгиба в плоскости наименьшей жесткости равна

SV^ElJ {£?)·“; (37)

о энергия от кручения равна

«F,= C (38)

О

Работа внешней силы на пути, связанном с изгибом в плоскости наименьшей жесткости и кручением, равна

f2P^dzdp(l.-zrf, (39)

о

d²u -J

где ^ · az представляет угол поворота сечения ζ, а все выражение—путь силы 2Р при выпучивании. Т. о. имеем по ур-ию (36):

о о

I

= f 2Р(1-г№0. (40)

о

Для изгиба дополнительно имеем, ур-ие:

^Е1у^=т-г)Р· (41)

Путем исключения получим:

irj^^l-^^d^^chw^ds· ⁽⁴²⁾

^ О О

В случае, если концы полосы не вращаются около оси Z, зависимость между β и -г м. б. представлена тригонометрии, рядом:

β=α₁ cos 2] + α₂ cos ^+ % cos +. (43)

Ограничиваясь первым членом, придем к ур-ию:

щ! сов“ ^

^J О

I

= С f «1 S ^sin2 if ^dg (44)

О

и затем к выражению ___

17,2 j/e7„c 9 р _ “

(₂[)2

(45)

из которого определяется критич. значение внешней силы для начала выпучивания. На фигуре 14, 14а и 146 изображены соответственно дву-

У₀

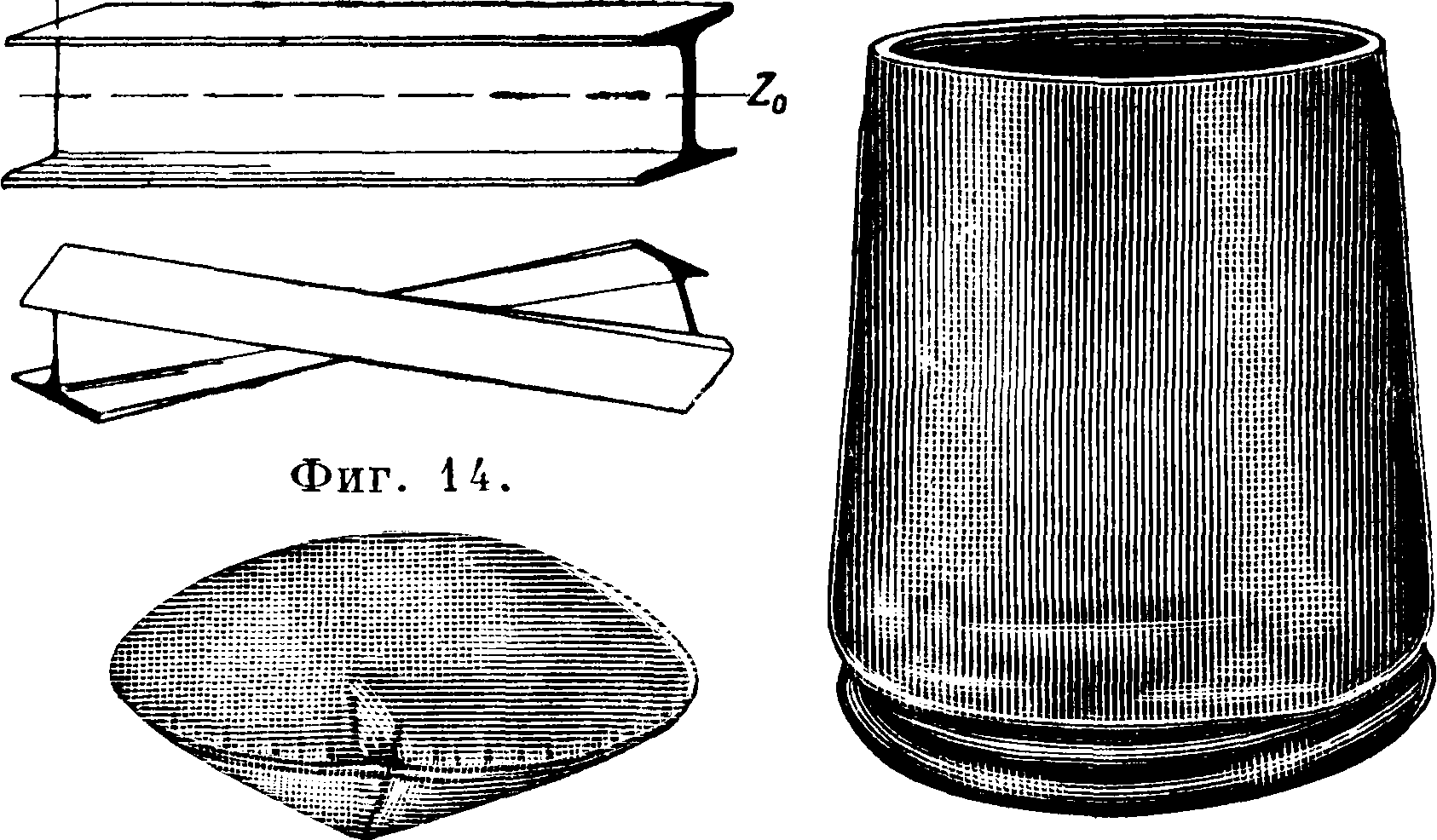
Фигура 14а. Фигура 146.

тавровая балка в неустойчивом состоянии (покоробленная), эллипсоид под внутренним давлением и сжатая труба. Второй метод решения вопросов устойчивости—составление ур-ия равновесия для бесконечно малого отклонения от устойчивого состояния. Задача Эйлера в эде-ментарном изложении разрешается этим методом. Первый метод ведет в значительном числе случаев к удобному и быстрому решению, особенно при удачном выборе функциональных зависимостей, подобных (43), причем точность решения м. б. увеличена в соответствии с требованиями практики. Второй метод иногда приводит к решениям в замкнутой форме, но чаще в виде бесконечных рядов. В табл, δ приведены окончательные ф-лы для вычисления критич. нагрузки в различных случаях.

Теория колебаний и удара. Теория упругих колебаний и удара м. б. построена на общих ур-иях динамики. В условия равновесия бесконечно малого параллелепипеда необходимо ввести силу инерции (Д’Аламбер), которая для бесконечно малого параллелепипеда имеет вид:

д“и asy d²w ^ ai* ’ ^ρ dt* ^{9 ρ} at a ’

и ур-ия (18)—(20) должен быть заменены следующими:

ЁХи г Ё1Ш _i_ Хр=р — (46)

дх ^ ду ^ дг ^ ^ * dt* ^к

и двумя ему подобными, где U—проекция пе ремещения данной точки на ось X; V и W— проекции соответственно на оси Y и Z. Ур-ия

(46) выражают закон, которым определяется распространение упругой деформации в упругом изотропном теле. Обычно напряжения в уравнениях (46) заменяют через перемещения по ф-лам для относительных удлинений и сдвигов (26) и при помощи ур-ий (31) получают особые ур-ия для непосредственного определения деформаций:

ае, _ д“и

V ^V*U + (λ + V) £ + ρΧ=О

dt*

(47)

к два других посредством круговой замены, Условия на поверхности примут вид ур-ий х»=te COS (X, η) + V [Ц + Ц cos (X, те) +

+ II cos (у, те) +~ cos

дх

(г, те)]

(48)

и двух ему подобных. Решения этих ур-ий для специальных случаев м. б. получены по способу Римана или Пуассона и Кирхгофа, также по принципу наложения колебаний Ре-лея. а) Ур-ия (47) проинтегрированы для колебаний в бесконечной упругой среде, для упругих поверхностных колебаний, для колебаний неограниченных пластин, бесконечно длинных цилиндров и струн. Рассмотрены случаи свободных колебаний (без участия внешних возбуждающих сил) и вынужденных (с участием внешних возбуждающих сил). Для плоских колебаний, в которых нет объёмных сил (упругое тело не имеет веса), ур-ие (47) получает вид:

. о ч 02и 02и е + ²”) 5ΪΤ=е

0*2

(49)

и носит название ур-ия продольной плоской волны (звуковые волны). Для плоских колебаний, в которых нет вихря и объёмных сил (е₀=Const, х=0), имеем ур-ия:

νψϋ=о ~ (50)

и два других. Это—ур-ие поперечной плоской волны. Газы и жидкости не могут распространять поперечных волн (только продольные), поэтому колебания упругих тел доступны нашему исследованию лишь посредством оптических или электромагнитных волн, б) В технически важных колебаниях большим распространением пользуется способ Релея и Ритца. По Релей выбирают основной тип колебаний, хотя бы грубо подходящий к характеру колебаний изучаемого случая, и таким путем по ур-ию

(47) находят частоту колебаний основного типа, причем частота колебаний будет всегда преувеличенной, но очень близкой к действительной (разница -3%). Способ Ритца (удачно модифицированный Б. Галеркиным) связан с вариационным исчислением и сводится к отысканию максимума или минимума нек-рого интеграла, к-рый представляет сумму работ сил инерции и приращения потенциальной энергии системы на бесконечно малом возможном перемещении, то есть

δ А + SV=0. (51)

в) Вместо ур-ий (47) в технич. вопросах пользуются ур-иями динамики в форме Лагранжа. Вид этого ур-ия для изучаемых вопросов:

А (ЁА _ ЁА 4- ЁУЁ ₌ ф

di WJ д<р д(р ^Ψ’ (р^г)

где φ—обобщенная координата перемещений, Ф—то же внешних сил, остальные обозначения даются в соответствии со всеми предыдущими.

Т. Э,

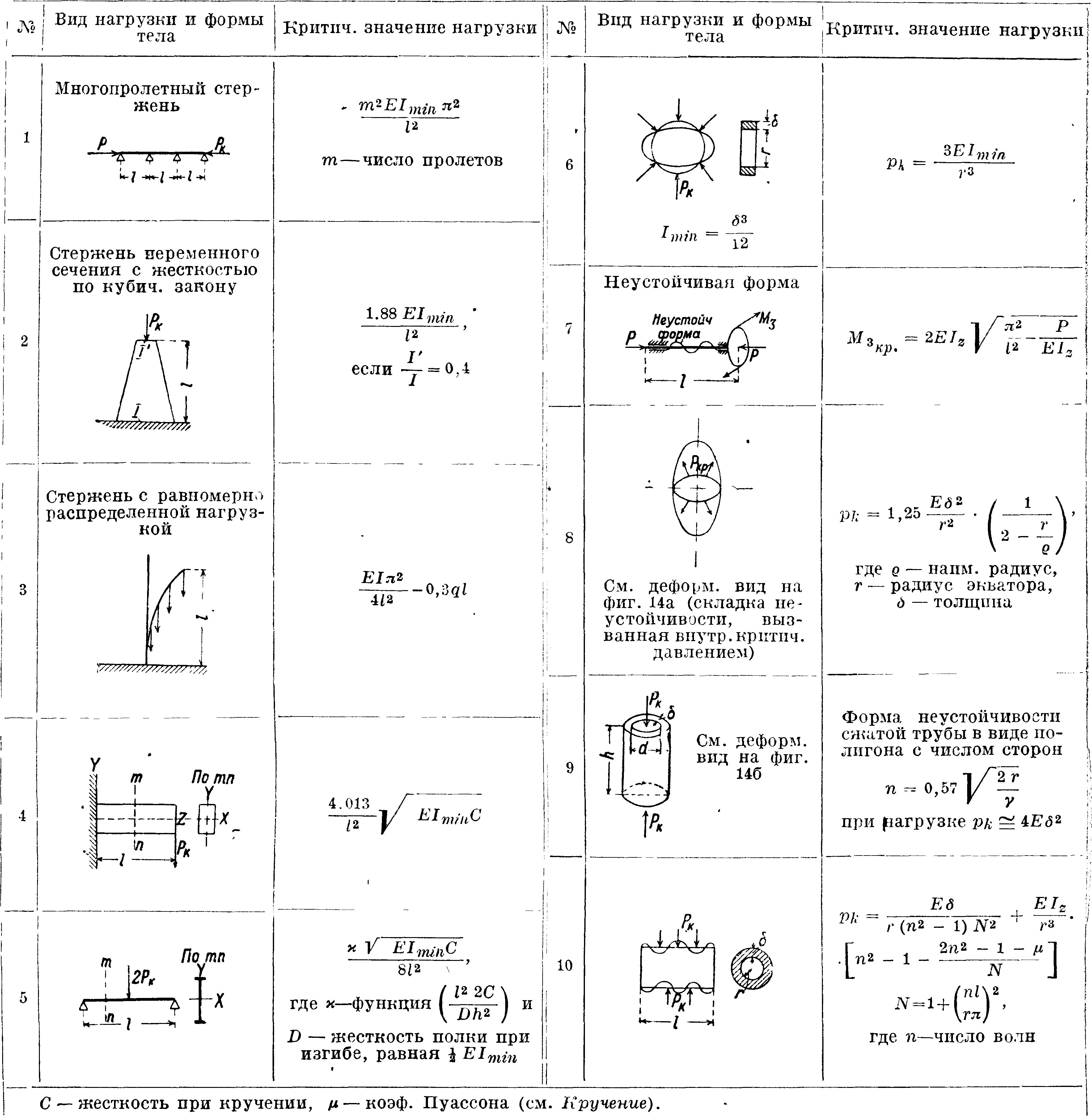
Для V в случае малых деформаций принимают выражение Клапейрона-Томсона

V=₂ а>ц<Р² + 2 ^22^² + 2 ^а33^² +

+ а>12ΨΨ + αιζψθ + · · · (53)

(называемое выражением упругого потенциала); также для А:

А ⁼ 2 ^ЬП<Р² 2 ^22^^/2 + 2 ^33^+

+ Ь₁ ζψψ + b_1з<рв +. ., (54)

гдеа_п, а₂₂,. ., Ь_1и b₂₂,. обозначают упругие константы материала. По ур-ию (52) можно составить систему линейных ур-ий с постоянными коэф-тами. Надлежащим выбором координат обычно устраняют члены, зависящие от их произведения (53) и (54), и получают линейные уравнения в нормальных или главных координатах в следующем виде:

bг<р +0^1=Φχ 1

^2^1 + ^а2<Р2 — ( * (55)

Каждое ур-ие представляет простое гармонии, колебание в зависимости от одной из главных координат; наложение их друг на друга характеризует колебания системы с числом п степеней свободы. Колебание с самым длинным периодом называется основным (также низким). Решение задачи сводится почти всегда к нахождению периода или частоты основного колебания. Выражения для нормальных координа-по Релей выбирают в виде тригонометрии. строк с таким расчетом, чтобы были удовлетворены пограничные условия, чаще в виде суммы или произведения sin-ов и cos-ob. При Ф_г== Ф₂ =.=0 колебания свободные, при Ф_гф О, Ф₂Ф 0,. —вынужденные. Общее решение ур-ий

?)₁=c₁ccs(p₁f + a_t) Ί

ψ₂=e₂ cos (ρ₂ί + a₂) >. (⁵⁶)

где ρχ, р₂, .—частоты колебаний, a—фазовый угол. Для мембраны (табл. 6, N° 10) например

№

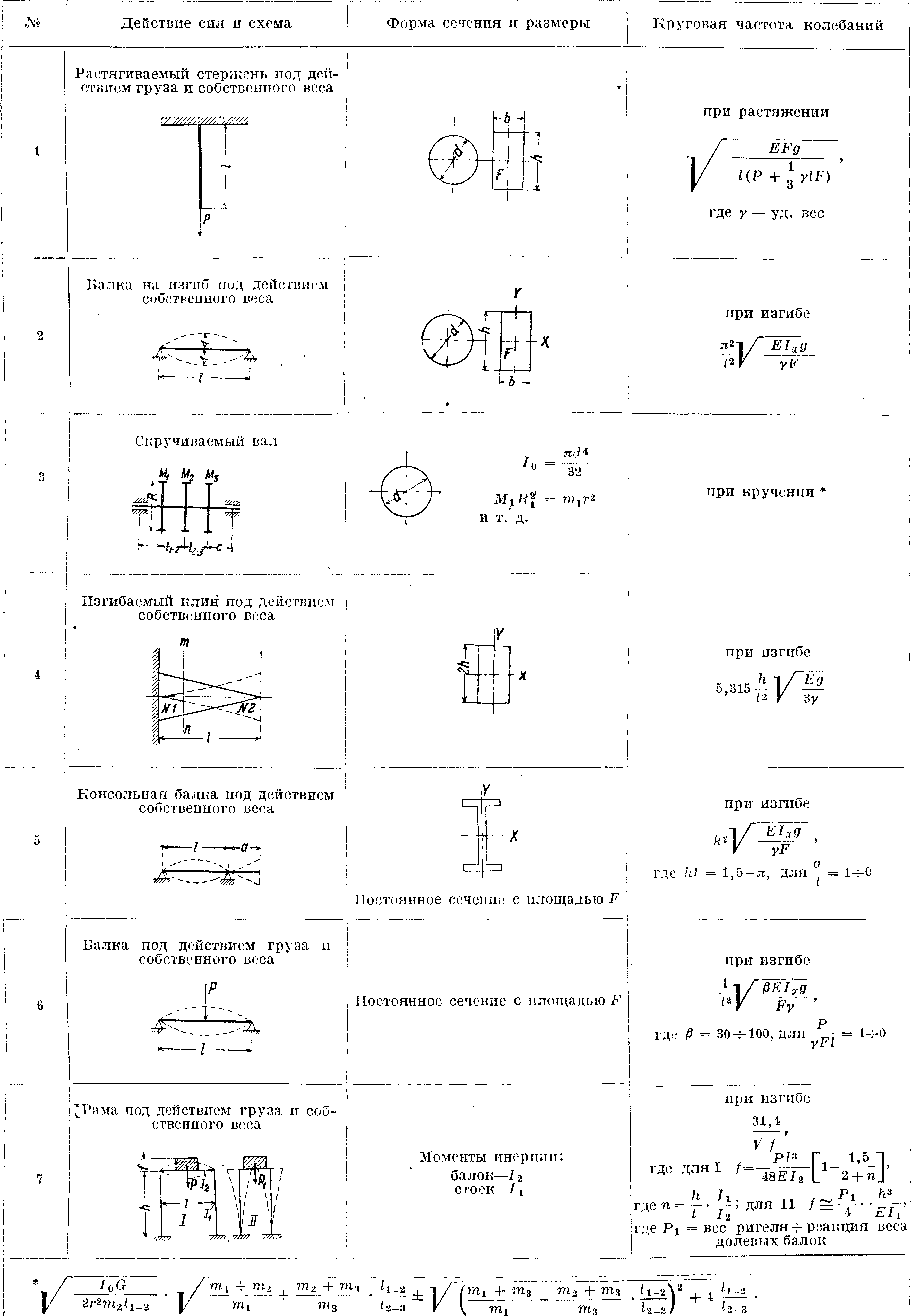
10

Действие сил и схема

Форма сечения и размеры

Тонкостенная труба под действием собств. веса

Радиальные колебания

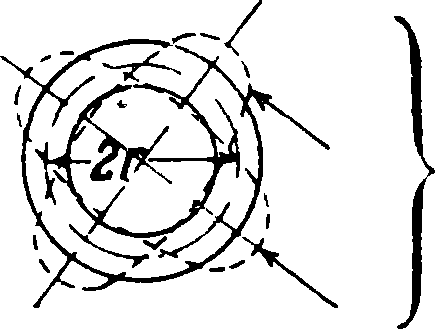
Кольцо под действием собствен- ι ного веса I

-Ψ ->

I— Г-

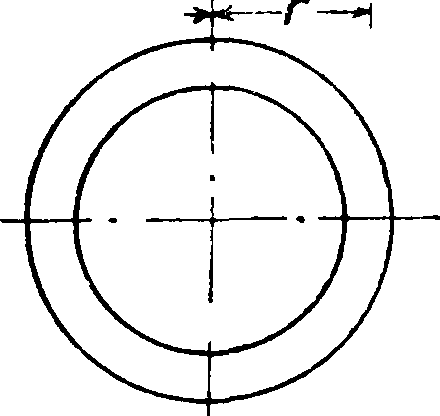
Круговая мембрана под действием собственного веса

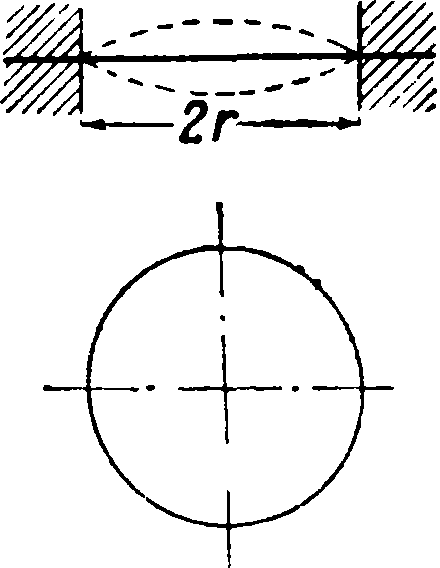
Пластина под действием собствен- j ного веса I

Постоянное сечение

То же

То же

Круговая частота колебаний при растяжении

Eg

уг2

где γ — уд. вес при кручении

Ед!_х уг“1₀

где 1_Х—момент инерции сечения относительно оси X; Т₀ —полярный момент инерции того же сечения

2,404

а, b — размеры свободной пластины

У

gs Q ’

где S — натяжение мембраны; q -вес единицы площади при изгибе

, где h—толщина

9Л

γΗ Ehз

12(1—μ²) пластины, μ— коэф. Пуассона потенциальная энергия при малых деформациях φ по направлению оси Ζ

⁷=ЩШ£)^,+Н£)^,}^Ав*»’ ⁽⁵⁷>

о о где S—натяжение, одинаковое во всех точках при начале колебаний. Кинетич. энергия мембраны

^A-£fh*Y^dxd*· ⁽⁵⁸>

о о причем q—вес единицы площади мембраны. Принимаем зависимость между φ и t, х, у в следующем виде:

ш=со α= со

?>= Σ ftosin^ (59)

m — 1

η=1

где а и b—размеры прямоугольной мембраны. Диференцируя (59) и подставляя в (57) и (58), разрешая интегралы подстановкой в (52)

при Ф=0 (свободные колебания), получим какое угодно число ур-ий типа:

I ? + 8«£ (£ + £)=0. (60)

Для ш=п=1 имеем:

Г(0 + ^^г/(0“ °, (61)

откуда круговая частота р₀ основных колебаний:_

Ро=*К?(*г + й· (⁶²)

Подстановкой других значений тип будем иметь частоты 2, 3,. порядка. Разрешены таким путем задачи о продольных колебаниях стержней постоянного и переменного сечений, также о поперечных колебаниях при различных способах закрепления; рассмотрены колебания колец, мембран, дисков и различных оболочек. Сделаны попытки определить величину напряжений при колебаниях Лером (Lehr). Все же в технических расчетах делают проверку только на частоту колебаний. В табл. 6 приведены частоты колебаний для различных случаев. С теорией колебаний тесно связано явление упругого удара. Кроме элементарных решений об ударе твердых и вполне упругих тел (смотрите У дар) существует теория долевого удара цилиндров Ф. Неймана. Последняя построена на общих уравнениях теории упругости и сводится к решению известного ур-ия волны (в цилиндрич. координатах):

ata ^с ох“ ^

Здесь W—ф-ия хи t (не радиусами означает перемещение по оси цилиндра, с—скорость звука,

— для данного материала (Е—мо--удельная масса). Напряжения равная дуль Юнга, ρ в цилиндре определяются по ур-иям:

сг_х т_Х!/=0 (касательное напряжение). (64)

Интеграл ур-ия дан Кирхгофом в виде:

W=(х + ct) + ψ (х — ct), (65)

где и ψ—произвольные ф-ии. Д. б. приняты во внимание пограничные условия. Для двух цилиндров, длины которых 1_г и 1₂, при начале удара имеют место следующие соотношения: ί=0:

~йГ=if (ж) - ψ (ж)] с=ν_λ (для 0 <×< I х),

aw (⁶⁶)

=U (ж) - ψ (ж)] c=v₂ (для г₁<ж<г₁+г₂=21),

причем г?! > v₂. Удлинения в начале еще нет, поэтому должен быть соблюдены соотношения:

= Г (*) + «»(*)= о (67)

для 0 < ж < + 1₂=21.

Если концы свободны от напряжений, то

-Εψ-= 0

дх

(68)

дляж= 0 и ж — 21 и всех значений t. Вследствие непрерывности для обоих цилиндров в момент соприкасания

^w*=^w» ΘγΘ, (^б9>

также для всех значений t. Таким образом заключаем из (66) и (67):

^а>

для 0 < ж < I;

v₂

для ?! < ж < 21;

a) ГС)=_2с

b) ?(®)=-|£,

и из (68):

a) f(ct) + v>(-ct)=0,

b) f(2l + ct) + v>(2l-ct)=0.

На фигуре 15 представлено протекание удара по этой теории. Подобным образом разрешена задача об ударе массы

-2flrQ		f!^ на свободный конец стержня, другой конец которого закреплен. Те- (г) «
				« ΓΤΐ *>
□-Р	—	h W	AUSQ 2(1,%) ι, ι2 2с Фигура 15.

ория удара Герца основана на учении того же автора о деформациях при йажатии упругих тел и допущении, что в месте соприкасания тел деформации имеют только упругий характер,

хотя время взаимного касания достаточно для развития заметной деформации. ΊΙο теории Неймана и Сен-Венана, наоборот, время взаимного касания очень коротко по сравнению с периодом упругой волны. Опыт точно не соответствует ни той ни другой теории. Были сделаны попытки добиться согласования путем введения в расчет свойств промежуточного слоя между ударяемыми телами, но они не дали положительных результатов.

Теория деформаций анизотропного тела. Теория деформаций изотропного тела потребовала только двух констант (коэфициента Лямэ). Анизотропное тело, упругие свойства которого по всем направлениям различны, не м. б. охарактеризовано только двумя постоянными. Пуассон и Коши одновременно указали для анизотропного тела 36 постоянных, из которых каждое указывает на то или другое качество тела. Вследствие существования упругого потенциала (53), доказанного В. Томсоном, количество постоянных сокращено до 21. Для нек-рых кристаллич. систем это число м. б. еще уменьшено, но не ниже 3. Закон Гука для анизотропного тела или постулируется или м. б. выведен из теории кристаллич. решетки (Борн). Рассмотрено состояние анизотропных тел под всесторонним давлением, при простых растяжении и сжатии, также изгибе и кручении. В тех-нич. вопросах теория анизотропных тел занимает еще малое место, несмотря на то что металлы, железобетон и другие материалы большей частью анизотропны. Губер вывел уравнение состояния ортогонально-анизотропной пластины, Штейерман распространил теорию изгиба симметрично расположенных и нагруженных оболочек (Лове-Мейснер) на случай анизотропных стенок.

Теория пластических деформаций заключает математическое описание напряжений и сопутствующих явлений в случае остаточных деформаций и прилагается к металлам с кристаллической структурой и материалам пористым, подобным песку и земле. До предела текучести металл подчиняется закону Гука, при наступлении предела текучести деформации особый характер—они в некоторой части остаются после снятия нагрузки. Эти пластич. деформации настолько значительны, что упругой частью их можно пренебречь (теории Прандтля,Надаиидр.).

Рейс (Reuss) дал решение и для того случая, когда в пластич. состоянии упругая и пластич: части деформации—величины одного порядка. Основная задача теории пластич. деформаций—выяснить механизм и причину разрушения упругих тел и законы протекания пластич. деформации, которая тесно связана с технологии, операциями (пробивание, волочение, резание и другие механич. операции). Пластич. деформация зависит от скорости, с которой происходит это явление. Однако в теории пластич. деформаций влияние скорости не учитывают. Для изучения пластич. деформации применяют общие ур-ия упругости и дополнительное условие пластичности. Последнее было предложено Треска (Tresca) и Сен-Венаном и обобщено Мором в форме:

(^ах — ^σ!/)² + 4тΙ_ν=4τ²0.

приобретают

(70)

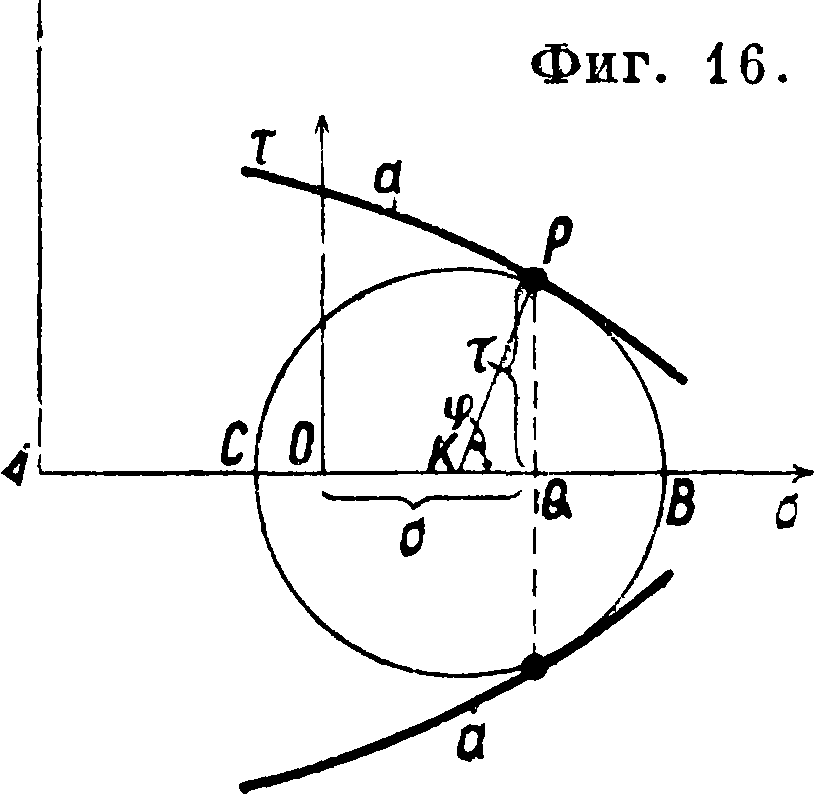
Графич. изображение условия пластичности представлено на фигуре 16. Если АВ равно σ_χ,

АС=PQ=·&ιη2φ, то есть указывает ве личину касательного напряжения в площади под углом φ к оси X. Наибольшее касательное

напряжение для данных нормальных оказывается под углом 2φ=90° и равно

Решение его в случае, когда х_ху=f(y)₉ дает:

°*=С + ¥ >· (75)

^ТдУ ⁼ “ ~сГ )

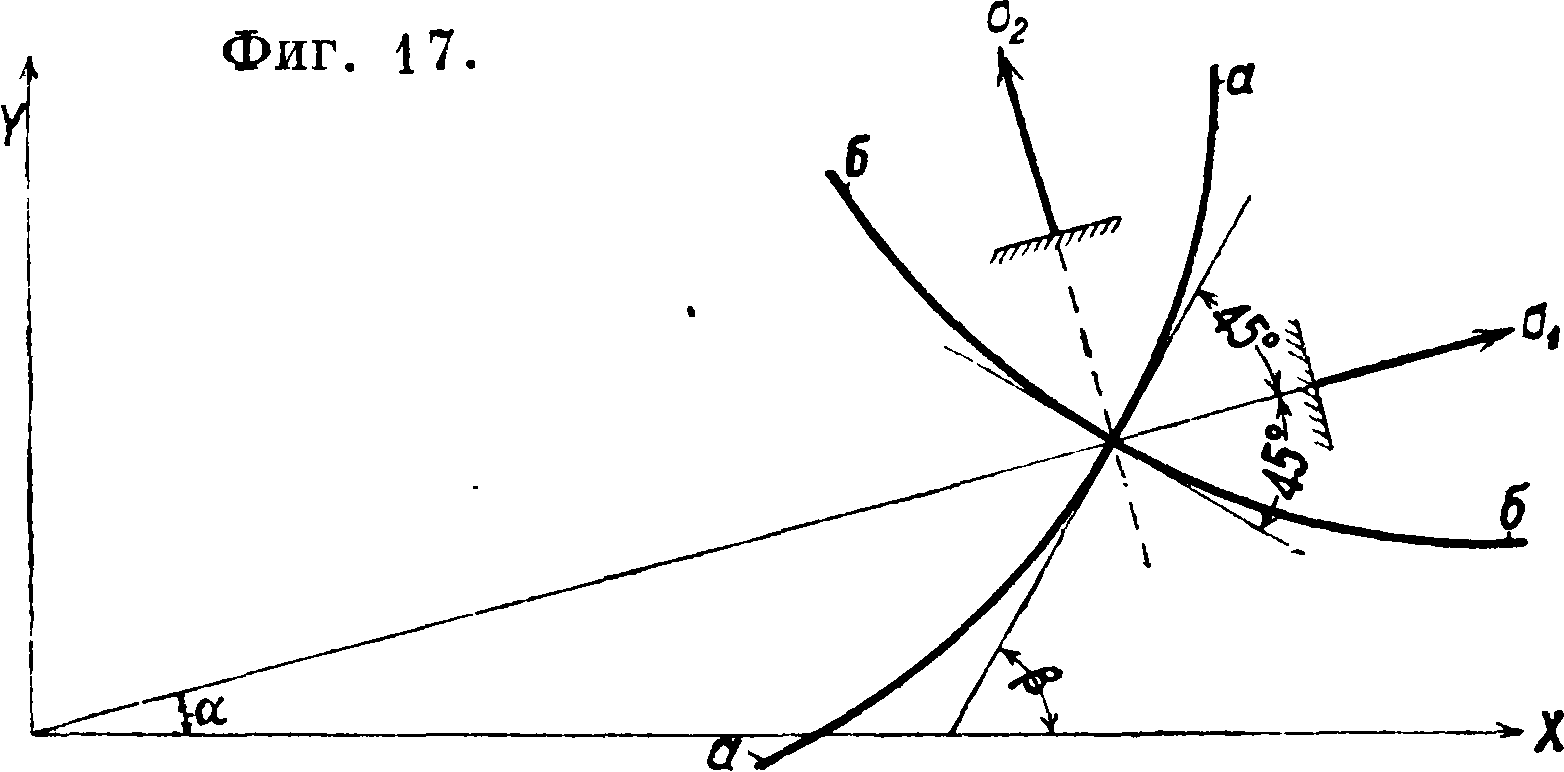
Здесь С и а—постоянные интегрирования. Дп-ференииальные ур-ия линий скольжения будут (4 иг. 17)

^=<*/»· S=~^ct^· (76)

Заменяя ф-ии угла β через напряжения, получим ур-ия линий скольжения:

Семейство I Г=-«(2/J +sin2/J)+Const]

у=а cos2β I

Семейство II !*=а<?Р~*ЬЮ + Const

y= acos 2β )

^v xy max ·

-Oy

т. е‘. радиусу круга Мора. Изменяя σ_χ и а_у между их· наименьшим и наибольшим значениями для данного металла, получим ряд кругов, огибающие которых а являются граничными кривыми Мора. Точка касания с окружностью Мора характеризует состояние тела: длина ординаты измеряет касательное напряжение при пределе текучести, угол нормали, проведенной в точке касания с осью абсцисс, является половиной угла между плоскостями скольжения. Если деформация сложная и существуют одновременно в данной точке нормальные напряжения о_х pi а_у и касательное т_, наибольшее напряжение в такой точке равно

Фигура 17а. т-| Via_x-a_yY + 4:xi_y. (71)

По теории Мора нек-рая величина этого напряжения определяет начало пластич. деформаций и разрушения от сдвига, отсюда и условие пластичности в виде ур-ия (70). Условия равновесия вполне пластичной массы на границе течения согласно (18)—(20) будут:

да_х, дт_худх ‘ ду

-=о

4- ϋΐ2!ϊ=0 ί

ду οχ )

к которым добавляется условие ^по Надаи):

а_х=то COS 2а + σ₀а_у=σ₀ — т₀ · cos 2а т_ху=т₀ sin 2а

(72)

(71). Полагаем

(73)

где

»+^а<

У о причем а₀—среднее значение нормального напряжения, т₀—наибольшее касательное. На фигуре 17 изображены направления напряжений (σι—главное направление удлинения, а и б— первое и второе главные направления сдвига). Исключая из ур-ий (72) д (73) σ_χ и а_у, приходим к ур-ию:

д²т

, ^²^^то ^тху дх ду

^тху дх2 "

д^2тху ду“

(74)

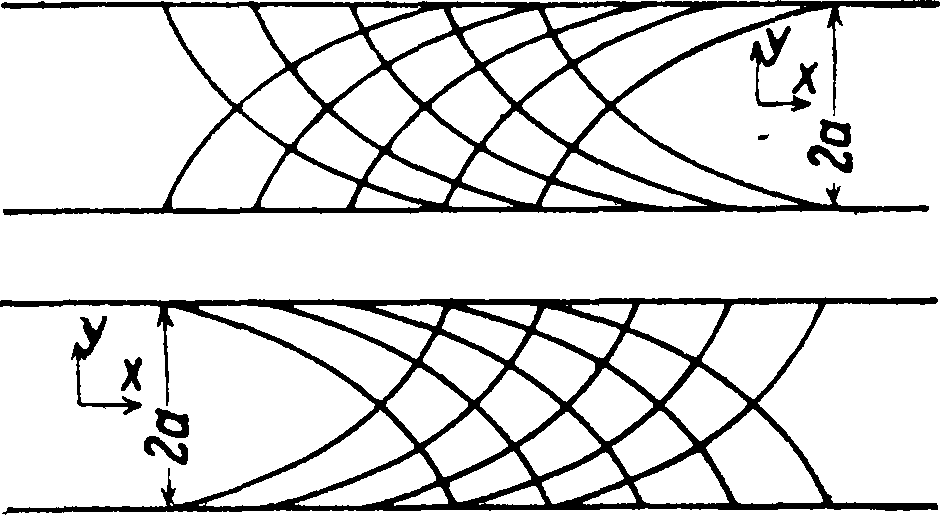
Т. о. линии скольжения между двумя параллельными плоскостями, подвергнутыми сжатью (фигура 17а, холодная ковка), представляют по-луциклоиды. Решение того же ур-ия (72) для случая толстостенной трубы представляется в следующем виде:

нормальное радиальное напряжение:

о_г=± 2т„ In, (78)

нормальное тангенциальное напряжение:

<τ_τ=±2τ₀(ΐ-1η“), (78")

касательное напряжение:

г=0. (78^///)

Здесь г—радиус прока, а—постоянная,

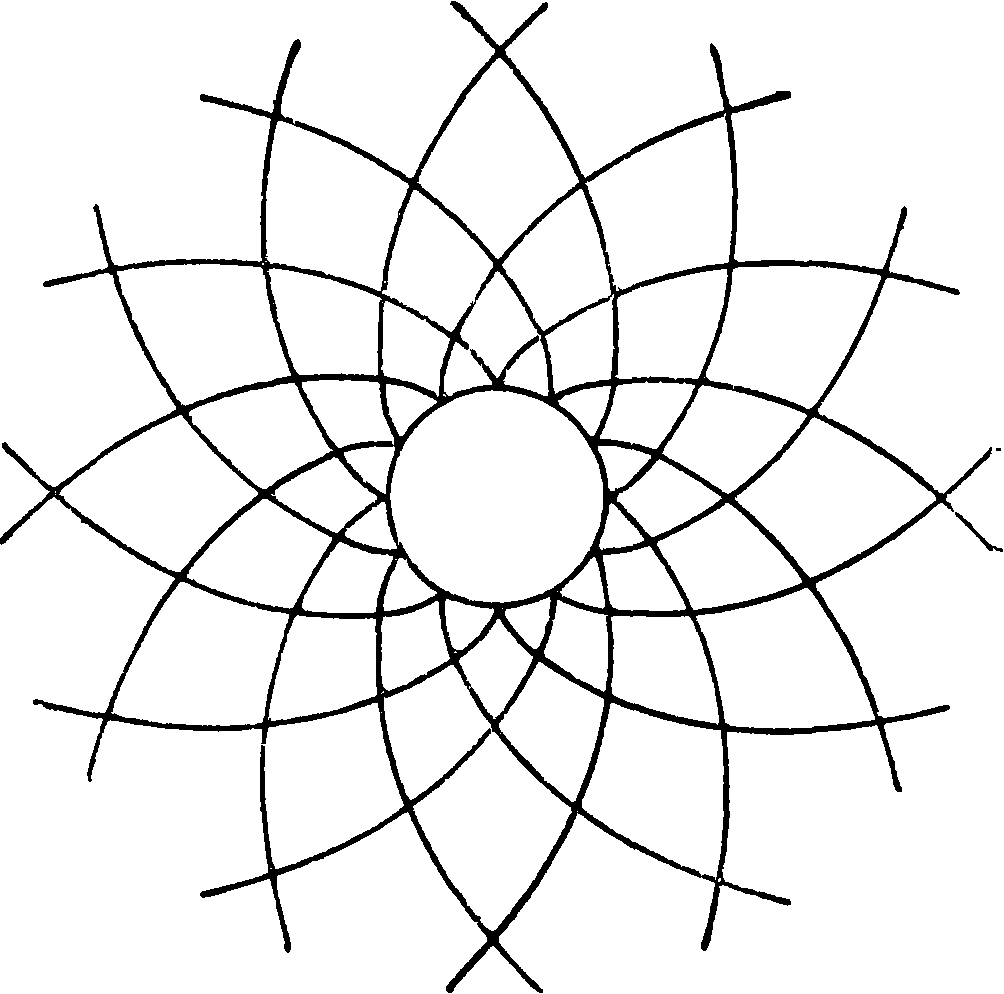
(+) для наружного давления, (—) для внутреннего. Линии скольжения—две" системы лога-рифмич. спиралей, направления которых взаимно перпендикулярны. На фигуре 18 изображены действительные кривые, которые получены травлением железного листа после вдавливания цилиндрического прока.

Прандтль получил ур-ия линий скольжения для ряда плоских задач, выбирая в качестве обертки линий скольжения простые, но применяемые В ΤβΧ- Фигура 18.

нологии кривые

(две параллельные линии—тупое лезвие, две пересекающиеся—острое лезвие). Теорию больших пластич. деформаций дал Генки (Hencky). Последний для своей теории принял металл за несжимаемую вязкую жидкость, вполне однородную, которая под большим давлением медленно течет и изменяется при постоянной t°. Ур-ия Генки по структуре подобны основным ур-иям теории упругости, но содержат вдвое большее число неизвестных. Вторая половина этого числа неизвестных характеризует металл в пластич. состоянии как вязкую жидкость. Напряжения для пластич. части металла построены по закону пропорциональности в форме:

г_х=2fc · е_х "I (79)

Ί×у ~ ^ * Уху )

где к—коэф. внутреннего трения металла и величина постоянная при изотермич. процессе, ^£х> Уху—деформации растяжения и сдвига, г_х, г —нормальное и касательное пластич. напряжения. A priori принято, что вектор деформаций коаксиален с вектором напряжений упругих и пластических. Отсюда 1

(^ах - О у)

(80)

Уху ~ λ

ху

Здесь, а_у, ^—напряжения упругие; коэф. пропорциональности λ определяется из ур-ия пластичности. Условие пластичности по Мизесу (Mises) принято в таком виде:

[(^ах ~ °^)²_+ (^ау —&z)² + (^σχ — ?_s)²] +

^J у) 1 У С I ^χ

+ 6[т|у + τ² у + ту=:

(81).

причем 2τ₀—предельное касательное напряжение при одноосной деформации. Генки применил, свою теорию к определению напряжений при прокатке и волочении и расхода энергии при этих процессах, а также указал закон изменения поперечного сечения в пластич. области растягиваемого бруска в зависимости от свойств материала. Вид последней зависимости:

<⁸²>

где F и F₀—переменная и начальная площади сечения, σ₀, т, β—постоянные, значения которых должен быть особо найдены для каждого металла, t— время. Эта зависимость м. б. проверена опытом.

Лит.: Бобарыков И., Сопротивление мате риалов, М., 1925; Проскуряков Л., Строительная механика, ч. 1, 7 изд., М.—Л., 1928; Т и м о ш е н-к о С., Курс статики сооружений, ч. 1, Л., 1926; Про-к о ф ь е в И., Теория инженерных сооружений, ч. 1—2, М., 1928; Штейерман, Теория анизотропных оболочек, «Изв. Киевского политехнич. ин-та», Киев, 1924; Timoshenko S., Tbration Problems in Engineering, New York, 1928; Navie r L., Resume des legons don-nees a 1’jScole des Fonts et Chauss6es sur 1’application de la m6canique к P6tablissement des constructions et des machines, Paris, 1833; С 1 e b s c h A., Theorie de l’ela-sticit6 de corps solides, P., 1883; Castigliano A., Th6orie de l’^quilibre des systemes 61astiques et ses applications, Turin, 1879; Love A. E., A Treatise on the Mathematical Theory of Elasticity, v. 1—2, Cambridge, 1928; Mises R. u. Frank P., Die Differential- u. Integralgleiehungen d. Mechanik u. Physik, 7 Aufl., Brschw., 1925—27; Southwell R. V., On the General Theory of Elastic Stability, «Philosophical Transactions», 1914; Rayleigh, The Theory of Sound, L·., 2 ed., y. 1—2, 1926; H ort W., Technische Schwingungs-lehre, 2 Aufl., B., 1922; Neumann F., Yorlesungen fiber die Theory d. Elastizitat, p. 179, Lpz., 1885; S.-Y e-nant, M6m. des savants strangers, P., 1886; Nadai

A., Der bildsame Zustand d. Werkstoffe, B., 1927; R e j-t 6, Einige Prinzipien d. theoretischen mechanischen Technologie d. Metalle, 1924; BachC.u. Baumann R., Elastizitat u. Festigkeit, 9 Aufl., B., 1924; F 6 p p 1 A., Yorlesungen liber technische Mechanik, B. 3, 10 Aufl.,

B. —Mch., 1927, B. 5, 4 Aufl., 1922; TodhunterL.,

A History of the Theory of Elasticity, v. 1—2, Cambridge, 1886—93; «Ztschr. f. angew. Mathematik u. Mechanik», B., 1920—30. С. Лебедев.