> Техника, страница 81 > Сосуды

Сосуды

Сосуды. В сопротивлении материалов сосудами называют резервуары для жидкостей, газов и сыпучих тел в виде напорных баков для воды, бункеров для сыпучих тел или котлов для различного назначения (для производства пара, горячей воды, окраски и прочие), а также цилиндры двигателей и трубопроводы. Различают тонкостенные и толстостенные С. Расчет тех и других, в принципе совершенно одинаковый для известного содержимого, в практич. приложениях разнится очень значительно.

Тонкостенные С. рассчитывают, полагая что: а) их поверхность является поверхностью с осями симметрии, б) толщина стенки незначительна по сравнению с внешними размерами, в) внутренние напряжения распределены равномерно по толщине стенки, г) длина С. велика по сравнению с его поперечными размерами, и т. о. влияние опорных реакций исключается, д) нагрузка симметрична относительно осей С. В этих условиях в материале С. с жидкостью или газом возникают преимущественно одни растягивающие напряжения под действием внутреннего давления. Из условий равновесия бесконечно малого элемента, вырезанного из С.двумя меридиональными и двумя параллельными плоскостями, следует фигура 1)

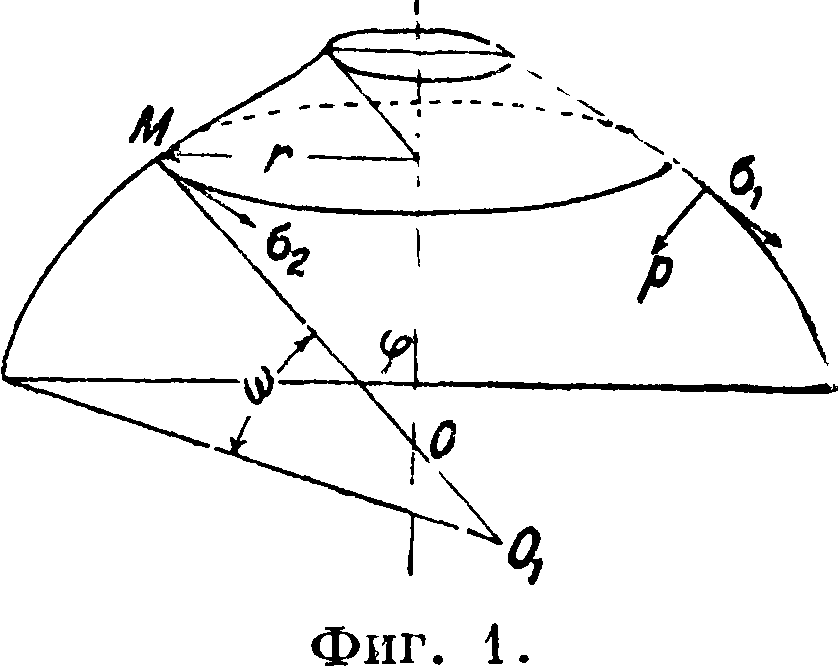
^σ I _:

61 02

(1)

где ОМ=и OjM=ь₂—главные радиусы кривизны, а од и а а—растягивающие напряжения меридионального и параллельного сечений, р—внутреннее давление и δ—толщина стенки, которая предполагается постоянной. Ур-ие содержит две неизвестные величины. Второе ур-ие м. б. получен» из условия равновесия против смещения элемента в направлении касательной к меридиану:

d (га_г)

d<p

= cos φ.

(2)

Здесь г—радиус параллели, φ—угол между нормалями к параллели и поверхности С. Обозначая о_хд и σ₂δ через N и N_l9 получим те же ур-ия, но вместо с_г и <г_я будем иметь N и Ν₁. Решение ур-ий дает:

d (rN sin φ)=pr dr.. (3)

Если давление постоянно (р= Const), как бывает в газгольдерах и паровых котлах, то

rN sin φ — (rN sin <p)₀=p ·

(4)

Для шарового С. имеем всюду ρ.=ρ₂ ^{и по} ур-ию (1)

Ν- -Ν₁=ρρ₁. (5)

По ур-ию (4) для вершины С. г₀=0, поэтому для шара дт. рг-2

г Λ · sin φ=~-

и в вершине следовательно Ν_χ

N =

Р0у

2

(6)

VQ i 2

/i=-g—, то есть напряжения во всех то“чках шарового С. одинаковы. Расчетное ур-ие имеет вид

d=-^PQl

2 it

ay

где R—допускаемое напряжение.

Для конич. С., к-рый также имеет вершину_г

г₀=0 и N sin <р=-£-

или

PQ 2 2

л^т=-

Поэтому из ур-ия (1) имеем:

Я,-«(2-й),

(8)

но ρι=οο, т. к. меридиональное сечение имеет форму тр-ка; отсюда для всех сечений конусα= (10) то есть напряжение кольцевое вдвое больше напряжения по образующей. Для конуса с углом при вершине 2а и радиусом основания ρ₀ напряжение в кольце основания

₌ VQ о ² δ COS а

(11)

там же по меридиану

₌ _РОп__β

¹ 2(5 COS а

Ур-ие (11) будет расчетным в виде

(12)

VQo

R COS α ’

(13)

где R—допускаемое напряжение.

Для цилиндрич. С. г=г₀, φ=90°, поэтому из ур-ия (4) имеем N=Const =. Ур-ие (1) дает

-№ι=Ρ?2=Ρ*ο, (И)

то есть напряжения распределены т. о., что они всюду постоянны и кольцевые вдвое больше меридиональных. Расчетное ур-ие получает вид

(15)

где R—допускаемое напряжение.

Для эллипсоида вращения (днищам котлов очень часто придают эту форму)

_а²Ь²

(а² sin² φ-f- b² cos² у)·!² а²

(a²sm²<p+b²cos²90

(16)

где а и Ь—полуоси эллипса меридионального течения. Обозначая

1

(причем V --имеем а также

⁵¹=V^s=----тг—г,-

о“ а²- b¹.,

l+-_T2--sm^

1 на полюсе и г;=^ на экваторе),

а²

а²

Ь

2f=^p®;2f₁=^.p(2i-i)· (17)

В вершине эллипсоида (г/·=1), N=JVj.=~ р, то есть напряжения одинаковы и оба растягивающие. В экваториальном сечении

^=(18)

является усилием растяжения, а

^=(18)

имеет знак в зависимости от значений ^Ь. Если а то Νι является также растягивающим усилием; если Ь <, то становится сжи мающим усилием; т. о. днище при этих размерах эллипсоида представляет неустойчивую форму равновесия, не Применяемую без особых мер предосторожности. По уравнению (17) зона сжатия по обеим сторонам от экватора ограничена параллелями с радиусом, соответствующим определенному значению v, а именно

V² < 2 или —sin² φ >1 при условии, что

Если давление в С. изменяется в зависимости от высоты (гидростатич. давление), то ур-ие (1) остается без перемены, но ур-ие (3) изменяется. Для р=yh (где h — расстояние параллели, для которой р=0 и у—уд. в.) ур-ие (3) получает вид:

d (rN sin φ)=yhr dr. (20)

Для шарового С., открытого по большому кругу, h=— ρ₂ cos φ и r=0₂sin<p. Поэтому у о t

N sin² φ=-γ COS³ φ + JV₀, (21)

где N₀—усилие по меридиану, нормальное к плоскости экватора, представляет величину распределенных реакций со стороны подвески:

о“ II 1 ^ 03	(22)
Следовательно
N sin2 φ=(1 -f cos3 φ).	(23)

Если φ=π₉ то Ν=^~· *

Здесь давление равно р_п=γρ₂ и следовательно N =. По ур-ию (1)

N + Νχ= — γρί cos ψ и

AT ^V62 ( ¹, COS*φ

^Nl---T in^ ⁺ im^+^{3cos φ})

Когда φ=90°, то

(24)

(25)

то есть в экваториальной плоскости происходит сжатие. Если=π, то Ν₁=~-=·р_п·= Ν, то есть в вершине оба напряжения равны и являются растягивающими. Зона сжатия определяется из условия:

1 + COS³9>

sin²?>

+ 3 cos φ > О

и лежит между плоскостью экватора и плоскостью, отклоненной от экватора приблизительно на 20° в сторону возрастающего давления.

Для цилиндрич. С. при переменном давлении по ур-ию (1) кольцевое напряжение в стенке при толщине δ равно

—

yhr

~Т⁹

(26)

а меридиональное по ур-ию (4)

yhr

Ίίδ

(27)

Каждому звену цилиндрич. или конич. С. соответствует определенное давление yh, по к-рому отыскивают толщину стенки в этом звене. В практич. исполнении часто С. представляет собою сочетание из двух или трех поверхностей, выше рассмотренных (смотрите Резервуары). Паровой котел образуется из стенок цилиндрич. формы и днищ эллиптической, плоской или шаровой формы. Расчет их в основном сводится к определению толщины стенки по заданным объёму к давлению и производится с помощью приведенных выше ф-л с нек-рым увеличением размеров в виду ржавления и ослабления швами. Переходящее сечение от одной поверхности к другой подвергается особому действию сил, т. н. местным напряжениям, и требует дополнительного изучения. Опорные части С. и прилегающая к ним поверхность должен быть изучены точно так же особо. Решение задачи здесь сводится к рассмотрению равновесия оболочки под действием растягивающих и срезывающих сил и изгибающих моментов. Для этого случая ур-ия равновесия м. б. составлены след. обр. Деформации по направлению касательных к меридиану и параллели будут и — о _ и Ctg ςτ - о

— --, - — ·

01 “ Q 2

Изменения кривизны 1-й и 2-й равны

d& _ ₇ & Ctg φ

кг и 1с о-------

Qldqr ρ._ζ

(28)

(29)

Здесь и и w — перемещения по направлению касательных к меридиану и параллели, #— угол между двумя касательными к меридиану. Усилия на единицу длины дуги и изгибающие моменты на ту же длину равны (фигура 2):

У=Ό(ε_χ + /bs₂), ЛД - D (ε₂ -f /ιε_±),

Μ_χ - — В (к_х + μΐΊ), М₂=- В(7с₂ -f д/д), (30)

ГД«‘

Ί)

2 Εδ 1 - μ

η

В -=

2 Е δ ·"

з7Г:г_Я2)·

Условия равновесия для случаев полной симметрии оболочки относительно оси и следовательно при отсутствии срезывающих сил п крутящих моментов в плоскости 2-й кривизны имеют вид:

а) относительно касательной к меридиану

d (Λ^τρ₂ sin 9?) άφ

— Ν₁ρ₁ COS φ -f Sill φ

+ Χθ_±ρ₂ Sin φ=0,

(31)

]>) относительно касательной к параллели

d(Qo₂ sin<p), лт ·

- —-- + JS₁Q₁ Sill Ψ -f- No₂ Sin φ -f

-r^SLll^=9, (31)

с) против вращения

d (Μ ι£>2 sln^) _1Г Г, · r /οι/л

—~ ^² -i ^C0S ^ 2i ^{s 111} 9³ 0, (31 )

гр×и Z—компоненты внешней нагрузки.

Если заменить деформации через,соответствующие выражения сил и моментов на единицу длины дуги кривой и принять во внимание, что

d w

то получим ур-ие:

+ ^αψ [ЩЯ1 + №->) - Νμρ, + /<_ρι)] } =‘2Е₃₁Л.

Стодола, Рейсснер, Мейсснер и другие дали решение этих уравнений для частных случаев, причем последний показал, что вся задача всегда м. б. сведена к одному ди-ференциальному ур-ию 2-го порядка. Точное решение для иек-рых случаев показывает, что влияние изгибающего момента распространяется на узкую зону вдоль границ оболочки. Если принять эту идей при составлении ур-ий равновесия, то придам к следующему ур-шо 4-го порядка:

ΔΔ0+ ³⁽¹

(33)

Решение его будет:

9=Се~^1и“ sin (1с ω -f- ψ)· (34)

где 7.: Л^//:,<У-^/-;^)е » ° ¹¹ V—ф-ии от φ. а С—

*(5²02

произвольная постоянная, зависящая от граничных условий, где значения сил или деформаций известны: .С=(<т₂)₀ · — —^——. Для сво-

dk sin (ψ + Μ

бодного края стенки (возможен поворот стенки) ψ=0, для заделанного края стенки у =

Т а П гг. 1 .—3 н а ч е н п и н апря ж о π и it*¹ и д рформяц и Л д л яразличн ы х сече н и ii о б о л о ч к и“².

	0 1	15-	90°	135°	180°	1 225°	Род
С		‘T	~k	РГ-	~k~	к	опор
s (см)	0 ί	0,83 1 c.Oi	1,731 ρ 2 (5	[ 2,59 Ερ^	3,46 YQz6	; 4,32 Ϋρλδ
	t ! QX cte φ, (σ*)ο 5, MГ		Наибольшее	Перегиб		1 ί
σι		0	- 0,208 (σι)0	-Ο,ΙΗίσΟο	1	ί 0	чи
			-	______________	1-----_---		3 И
	Пе]>егио			Наибольшее	Перегиб		I О
ai	(σ2)θ	0,322 (σ2)0	о	i - 0,706 (σ2)о	i
Деформация	Наибольшее ·	Перегиб			Наименьшее	Перегиб	О
г>	(>)·* !	о;645 0O j			0,043 #о
1		Наибольшее	Перегиб	1		Наиболь-
ah j	0	0,553 (cr2)0 1	0,378 (σ2)0		0	j шее
	Перегиб			I			1
1 σι	, s. 0 i ct gq> j (σ2)0 · -, 1 Ol « j	о о	0	Наибольшее 1 1	Перегиб
	Наибольшее I	Перегиб · I		1	Наименьшее i Перегиб		3 as
σ, 1	Юо	0,645 (ч2)о		о !	- Ο,043(σ2)ο		<3 п
Деформация	I	Наибольшее 1	Перегиб i			Наиболь	S
		0,С45 к (ε3)β (Д I V <? i о 1			I	шее	t3
0 !	0 i			0			а со
!			Наименьшее,	Перегиб
°b 1	1,Ыо (cr_ ) 0	0	- 0,36(σ2)0 (	- 0,244 (σ2)0		%

*i σ_ΐ4 σ₂—напряжения от растяжения, а ,—от изгиба. *² В незаполненных клетках должен быть промежуточные значения указанных величин; они не вычислены, как совершенно безразличные для расчета .С.

Т. Э.т. XXI.

15

(<r₂)o—кольцевое напряжение в краевом чении. Силы и моменты равны:

N= — ~ · tg ω · Ce~^ka> · cos (Ίζω + ψ);

· &ι/2 · Ce~^k(0· sin (ΐϊω + Ψ -r д); Q=~ · Ce~^kco · cos (/cco + yO;

M₂ =

<5³

• cos (ko> + ψ +

Ch · e

-ы

™ <**1.9 + _μΜχ.

(Χ-μ*) 02 ^

ce-

(35)

Значение M₂ очень мало, если изменение поверхности происходит достаточно медленно (Пастернак). Расчет должен быть сделан только для одного момента М_г и действующих сил N, N_L и Q, и ур-ие (33) м. б. получено непосредственно из условий равновесия между моментом М_г и силами N и N_t. В табл. 1 приведены значения напряжений для различных ω или s (ω—угол широты для меридионального сечения, a s—расстояние от края в см) и различных условий за

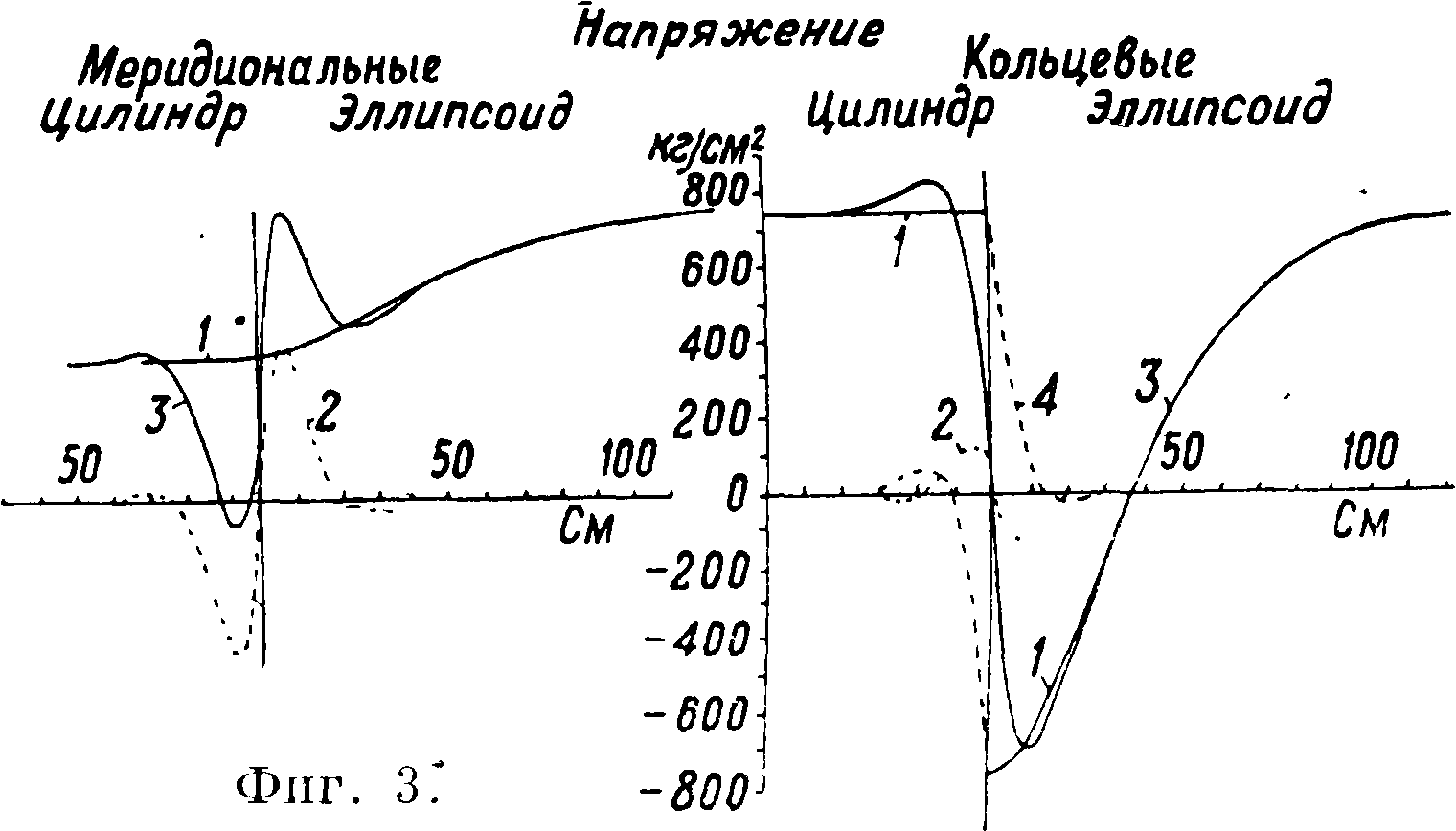
крепления. На фигуре 3 показано распределение напряжений в цилиндрич. котле с эллиптич. днищем при рабочем давлении 7,5 atm; диаметр котла 2 метров и δ=10 миллиметров; эллипс с отношением полуосей 1:2. Кривые здесь выражают: 1— напряжения по обычной формуле для котлов, 2— напряжения от изгиба, 3—суммарные напряжения, 4—напряжения растяжения в переход-

Напряжение

дено условие. Очевидно при проектировании на форму днища следует обращать наибольшее внимание. При расчете толщины стен-

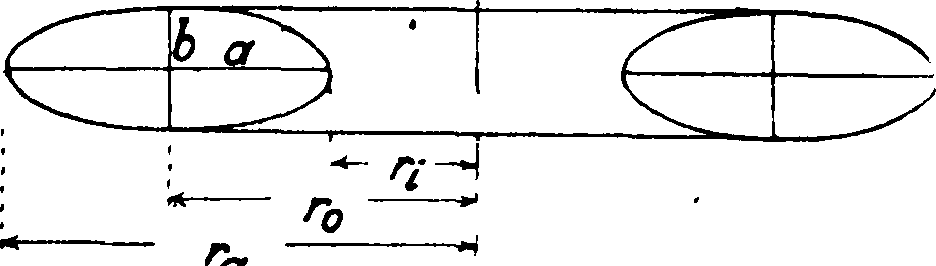
путем будут учтены повышенные напряжения в переходных сечениях. Для котлов с жаровой трубой поверхность днища м. б. образована вращением эллипса с полуосями а и b около оси котла (фигура 6). Напряжение по меридиану равно: во внешнем кольце:

во внутреннем кольце:

кольце: }

Кольцевые напряжения: во внешнем кольце:

во внутреннем кольце:

(36)

(37)

Здесь ρ_χ—радиус кривизны поверхности в меридиональном сечении. При условии, что радиусы кривизны поверхности всюду удоЕлет-•воряют требованию а

2г„

)·

кольцевые напряжения не превышают нигде значения ^ (напряжений в цилиндрическом котле) больше, чем на 12%. Для эксцентрического расположения трубы (фигура 7) напряжения будут иметь

Фиг.

Фигура 7.

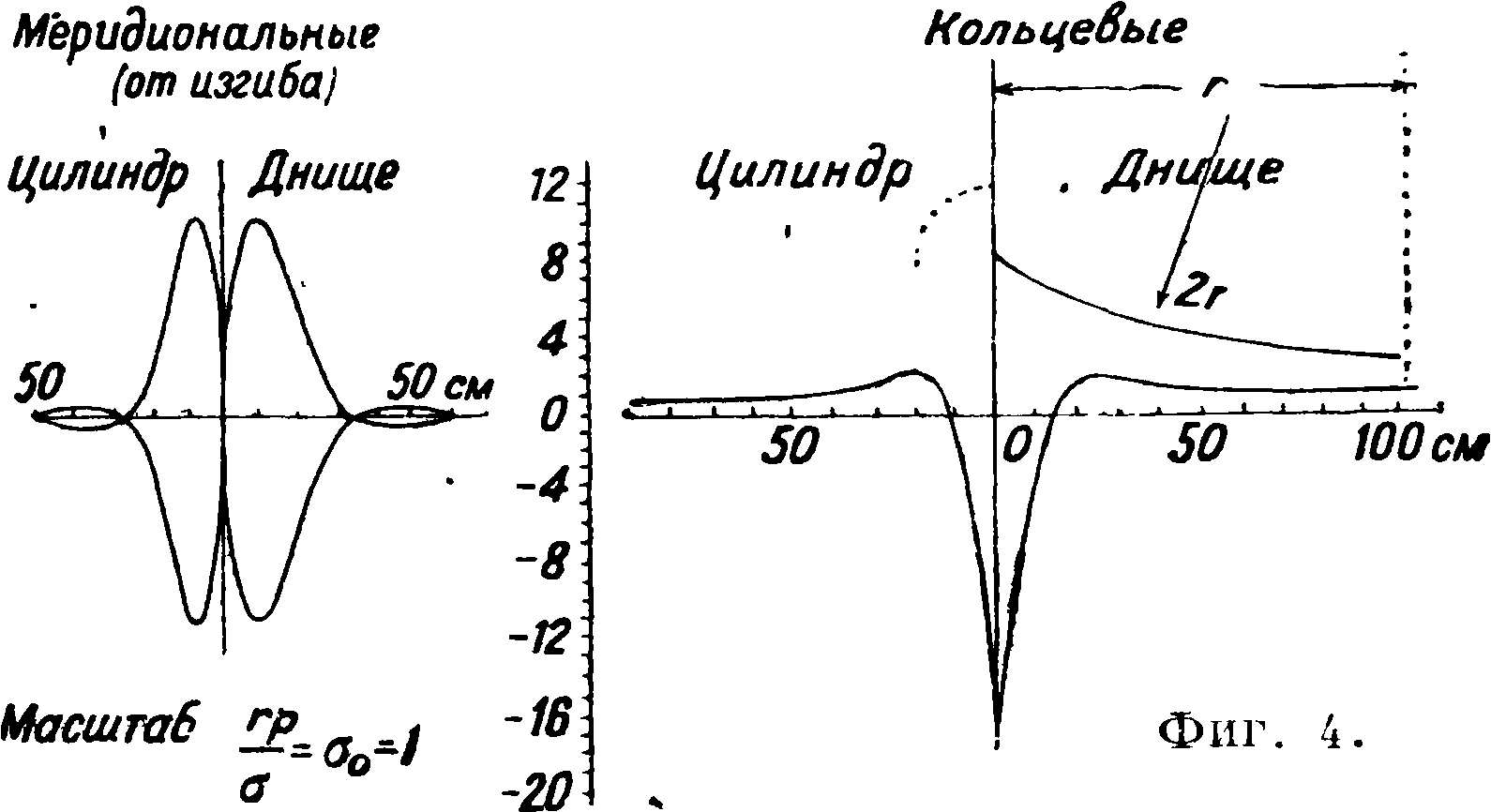
ном месте. На фигуре 4 изображено распределение напряжений в случае цилиндрич. котла и сферич. днища с острыми переходами при отношении радиусов цилиндра и шара 1:2. На фигуре 5 показана обстановка опыта для подтверждения расчета Гекелера—совпадение результатов с теорией совершенно достато^шое. Подробные исследования переходных напряжений в С. приводят к заключению, что наивыгодней-щей формой днища является эллипсоид вращения с отношением полуосей 1:2, причем наименьший радиус закругления должен быть не менее четверти радиуса цилиндра, то есть должен быть соблю-

ту же указанную величину, если радиусы поверхности связаны зависимостью

(^3S>

Опорное кольцо, которым висячее днище опирается на кладку или ферму, должен быть проверено на критич. сжатие р_к со стороны меридиональных напряжений по условию

I где р_к=причем G—вес наполненного

С., а—угол касательной к меридиональной кри-I вой с горизонтом, г—радиус опорного кольца.

Высокие баки защищают против действия ветра, опасного при незаполненном С., кольцами из углового железа. Расстояние между кольцами определяется по ур-ию (в м)

1=15,2(40)

где δ—толщина стенки в миллиметров, D (диаметр бака) и I в м. Соединение отдельных барабанов производится заклепками, причем употребляются также швы с накладками. В табл. 2 приведены нормальные размеры листового материала для стенок, заклепок и уголков для колец.

Таблица 2.—Л и с т ы, з а к л е п к и и уголки для колец (по DIN).

Толщина ЛИСТОВ (5, миллиметров	Диам. заклепок d, мм	Шаг t“, мм	Расстояние от края а, миллиметров	Угловое железо, №
2	8	29	16	40/5
3	9	32	17	40/5
4	10	35	17	40/5
5—6	11	38	18	45/7
6—8	14	1 47	21	50/9
8—12	17	56	25	75/12
11—15	20	65 !	30	80/12
* Вообще f=3d+5.

Получает широкое распространение также соединение при помощи «варки. Заклепочные сое-

Фигура 8.

Фигура 9.

динения для котлов—см. Заклепочные соединения и Котлостроение.

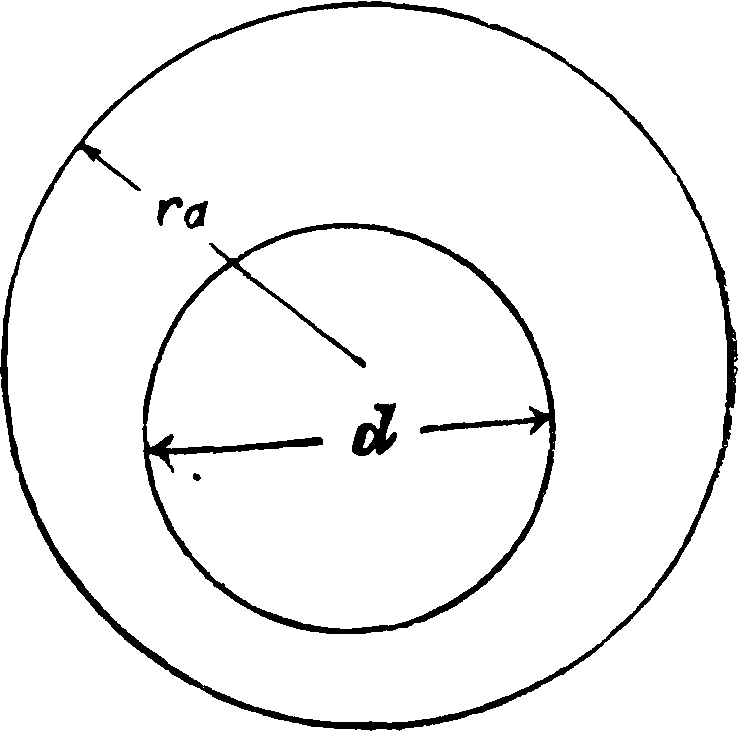
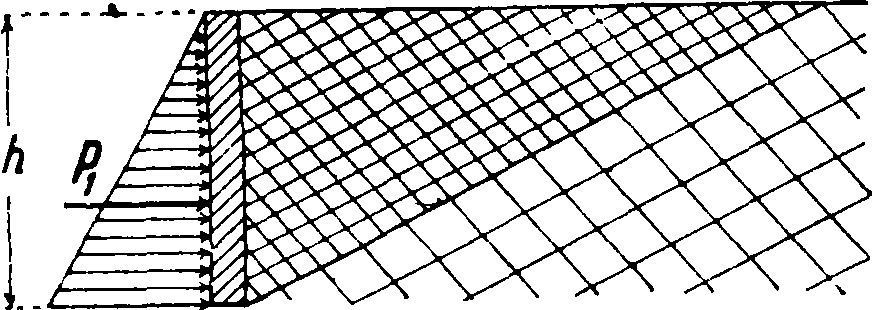
Расчет бункера связан с теорией давления сыпучих тел. Несмотря на существование новейших теорий давления сыпучих тел [Рейсснера, Мора, Падай (Nadai) и др.] в основание расчета полагают старую теорию Ранкина. По этой теории поверхности скольжения сыпучего тела—наклонные плоскости (фигура 8 и 9), причем величина нормального (здесь горизонтального) давления в случае перемещения сыпучего тела под действием внешней силы (пассивное давление) определяется по ф-ле

2

Фигура 10.

Рг

(41)

эта же величина в случае перемещения стенки под действием скользящего сыпучего тела (активное давление) вычисляется по ф-ле

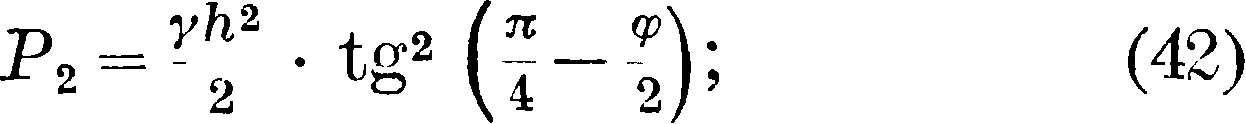
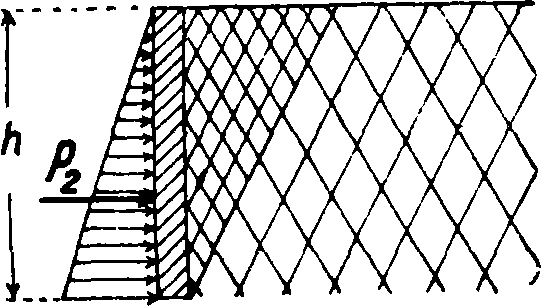
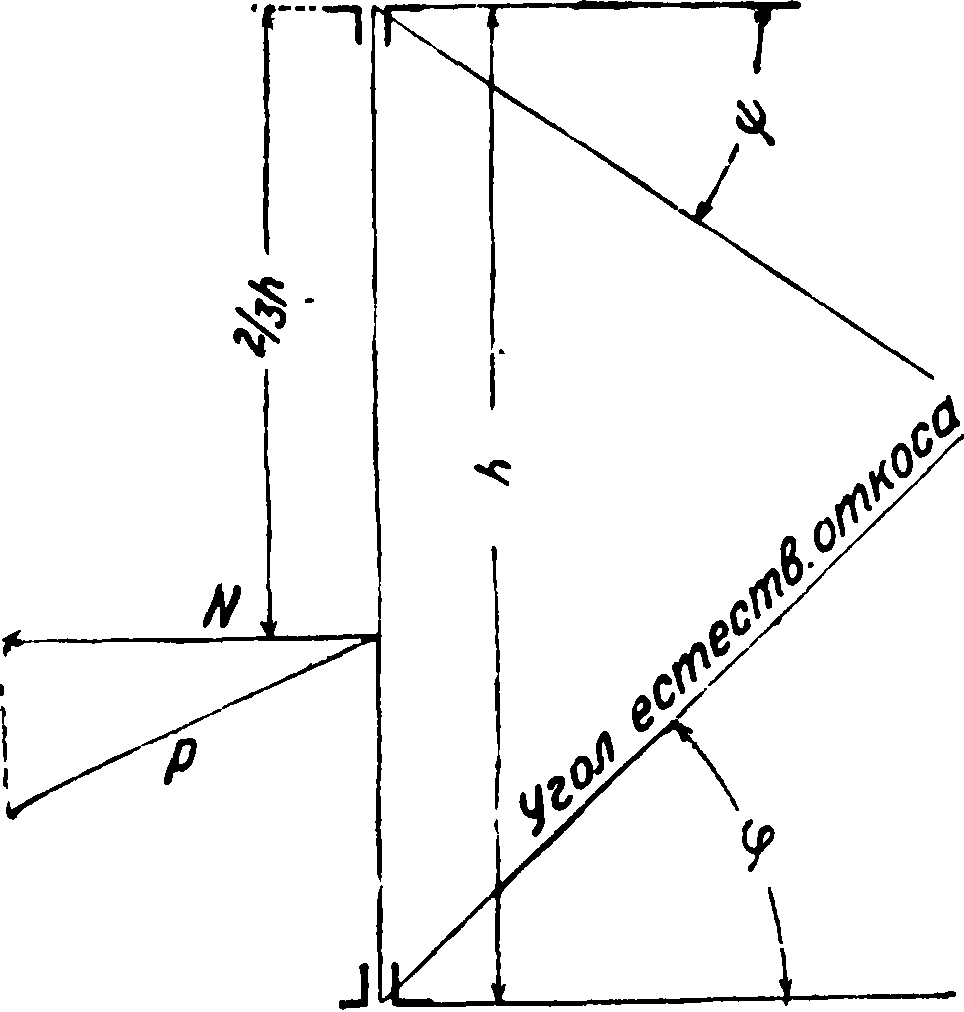
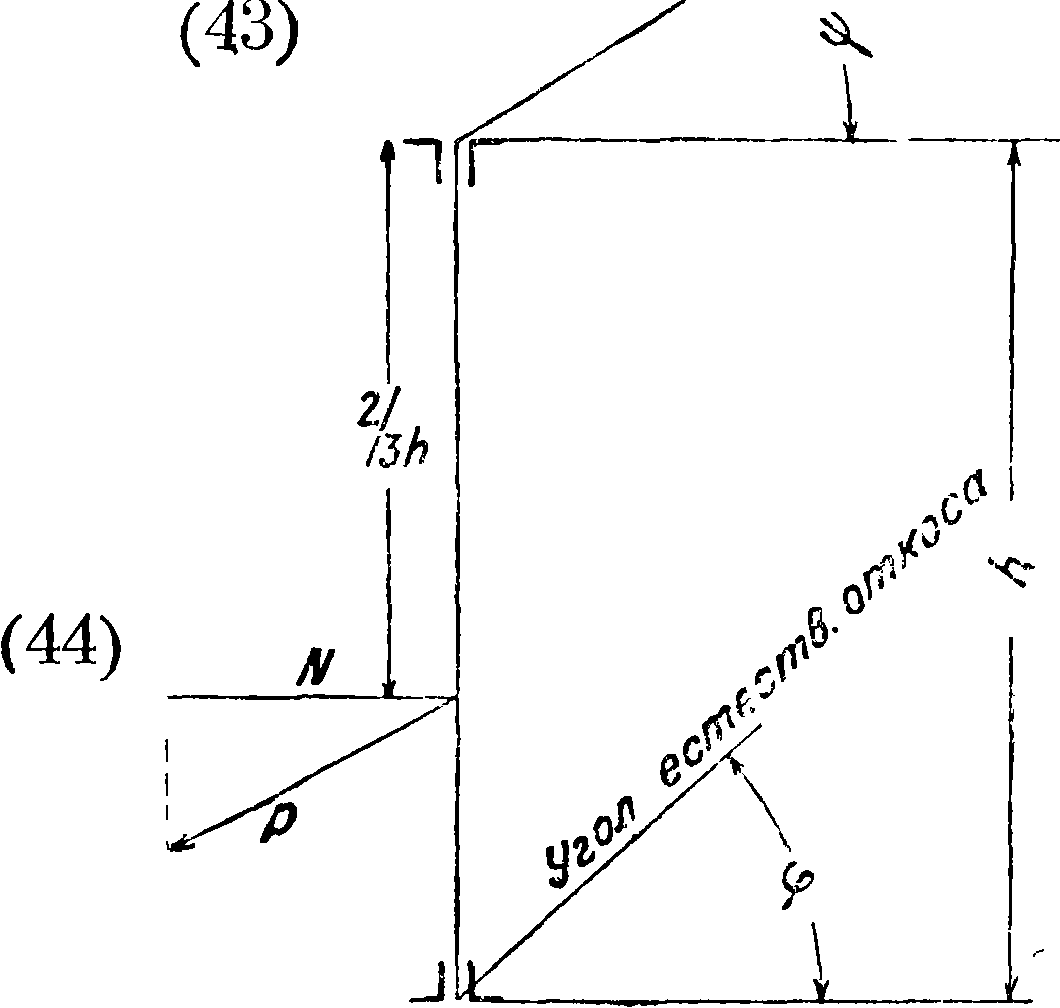
здесь у—уд. в и φ—arc tg f (f—коэф. внутреннего трения сыпучего тела). При составлении ф-л не принято во внимание внешнее трение сыпучего тела о стенки, и предполагается, что стенка—вертикальная, а поверхность сыпучего тела—горизонтальная. Для вертикальной стенки с недогрузкой на угол ψ (фигура 10) или с перегрузкой на тот же угол ψ=φ (фигура 11), причем φ— угол естественного откоса, активное давление· будет

COS² φ.

Для наклонной стенки и горизонтального уровня сыпучего тела (или с перегрузкой на угол естественного откоса) давление будет

, γ№ ² 2

COS<p

sin θ ⁵

Фигура И.

причем Θ < ₉ + arc tg/,

где /—коэф. трения сыпучего тела о стенку. При 0>~+arctg

для наклонной стенки и горизонтального уров ня сыпучего тела давление равно р =

² 2

Углы естественного откоса тел приведены в таблице 3.

Таблица 3.—У глы естественного откоса удельные веса сыпучих тел.

·«(?-!)

COS φ. (45)

и уд. в сыпучих

Материал	Уд. вес в К ’/.из	Угол естественного откоса в градусах
Каменный уголь.	1 500	35
Антрацит ..	1 700	27
Шлакующийся уголь.	1 400	40
Кокс..	1 400	32
Зола..	1 200	40
Железная руда.	5 200	35

Фигура 12.

Различают бункер мелкий, когда плоскость скольжения (обрушения) пересекает свободную поверхность сыпучего тела, и глубокий, когда плоскость обрушения проходит внутри насыпи. Приведенные выше формулы относятся к мелкому бункеру. Если бункер поддерживается вертикальной рамой, расположенной в углах бункера, то он называется просто бункером. Бункер, поддерживаемый только за пояс (фигура

12), называют висячим. Расчет того и другого существенно различен. Расчет насыпного бункера производят по указанным формулам. Определяют давление на стенку, принимая, что оно изменяется по законутреуголь-ника. Величина давления распределяется на узлы тем же способом, как отыскиваются реакций простой балки. Стержневой полигон бункера рассматривается как ферма, для которой по одному из известных способов находят усилия в стержнях и реакции колонн. На фигуре 13 и 14 показано графин. решение задачи для угольного бункере с углом естественного откоса в 30°. Построение

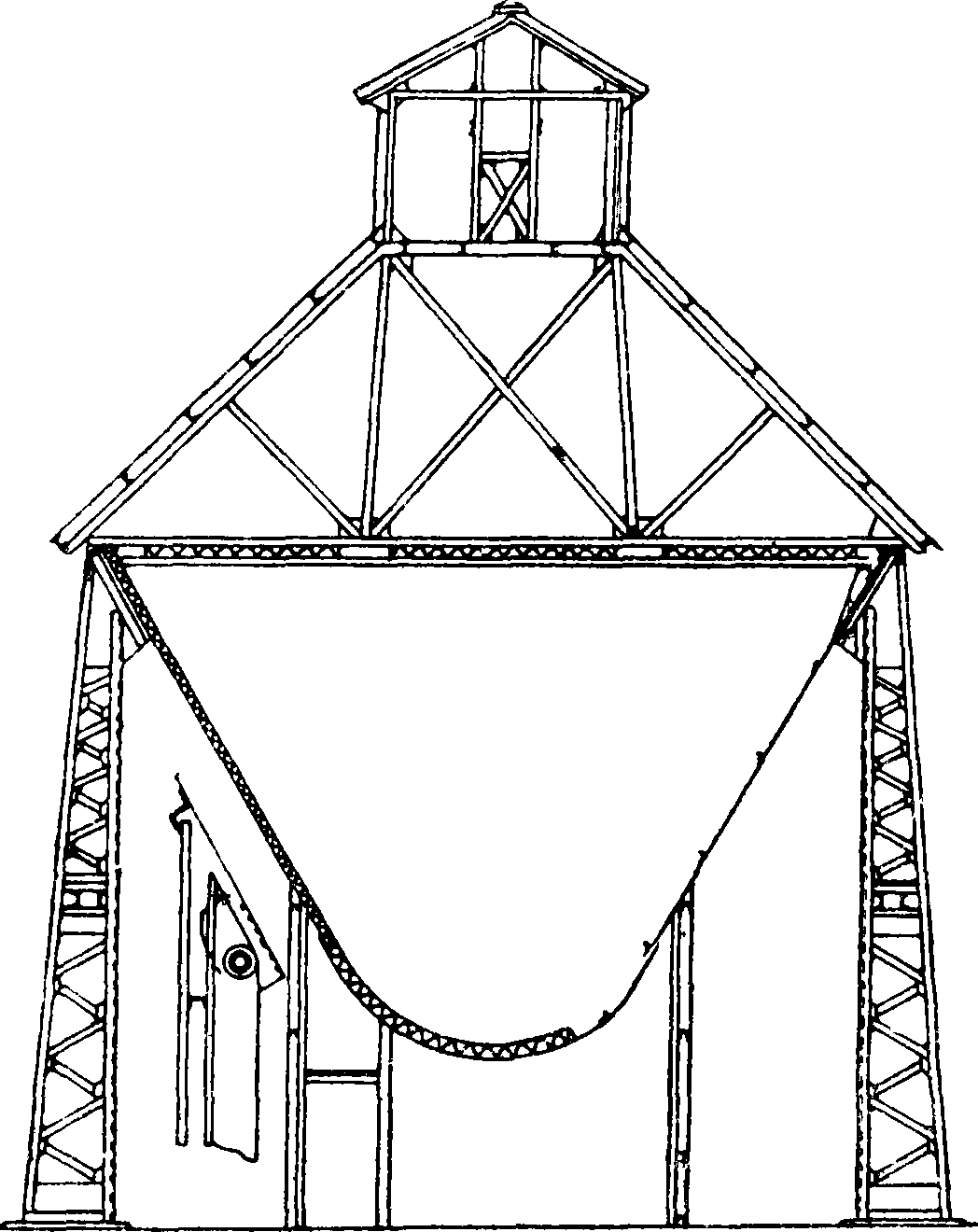
сделано для бункера, фермы которого находятся на расстоянии 5 метров одна от другой. Величина нагрузок в узлах показана на фигуре 13. По спосо-

---Юм -—

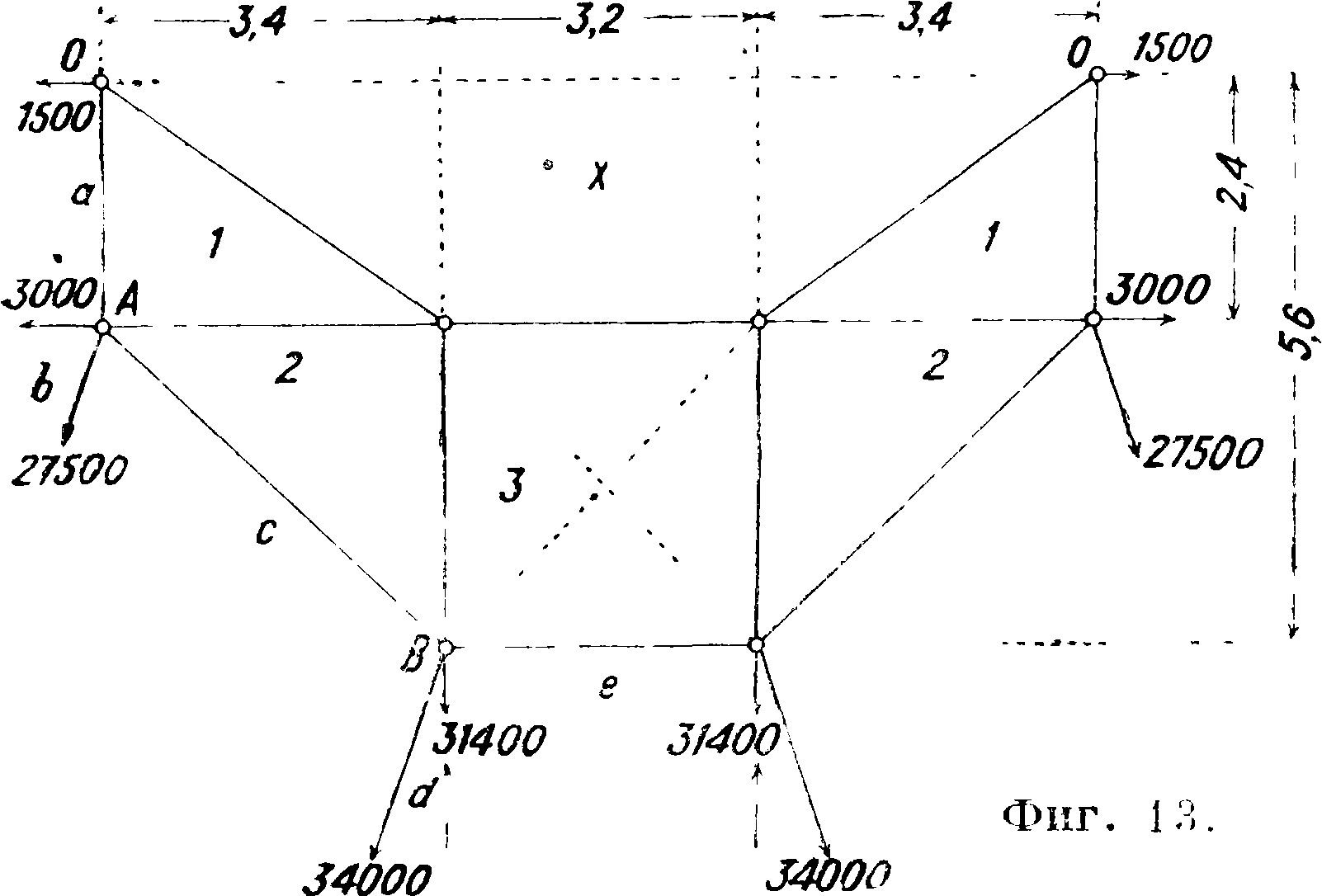
бу Кремона (фигура 14) определяются усилия во всех стержнях и реакции колонн. Площади сечений стержней отыскиваются по ур-иям прочности на растяжение, сжатие и продольный изгиб в зависимости от направления усилия, причем напряжения в виду возможных ударов и вибраций принимают не свыше ²/₃ допускаемых для гражданских сооружений. Толщина котельного железа, которым покрывается стержневая система бункера, м. б. найдена по ф-ле_ Баха-Грасгофа р. > ¹ w. ^а2*⁾². ^v

где^р—давление в данном слое бункера в килограммах;см², а иД>—размеры пластины в см, δ—толщина, железа в см, φ =0,75 -у для закрепленной пластины (прикрепленные Левая сторона К СТеряшям ЛИСТЫ) И

9?=-1,125 для свободной, R_b—допускаемое напряжение на изгиб в килограммах/см². Очертание бункера представляется здесь ограниченным плоскостями, как чаще всего Фигура 14. бывает.

19000 200L0 ЗОООО 4CD0Q

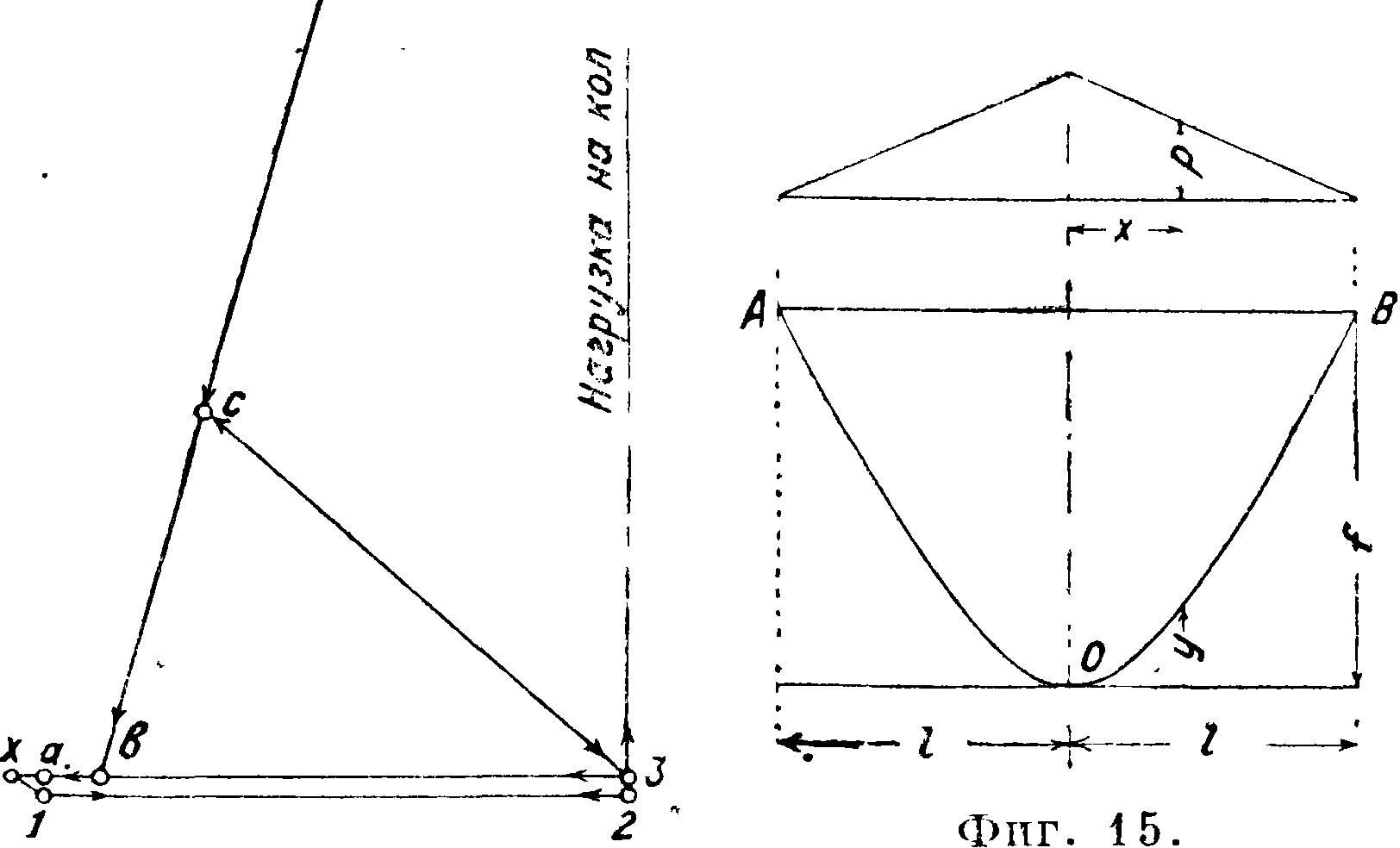
Висячий бункер (фигура 15) также принимается нагруженным по закону треугольника и дает в сечении вертикальной плоскостью па-раболич. кривую вида.

<⁴⁷)

где /—глубина бункера, 21—расстояние между опорами, начало координат в точке О. Тогда емкость бункера с горизонтальной поверхностью на 1 п. м длины бункера у-

(48)

Наибольшее давление в бункере в килограммах на 1 п. л? длины его:

I V ι·ϊ· Μ·"

Горизонтальное усилие (фигура 16) в нижней точке бункера в килограммах на 1 п. м:

11 =

Су

3Г ^:

(50)

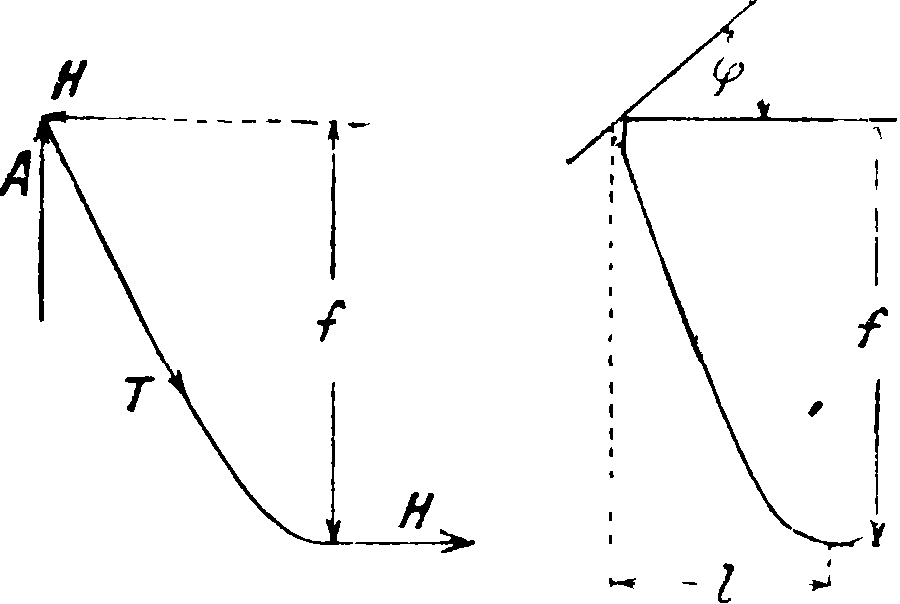
вертикальная реакция А=₂Су меридиональное усилие в той же точке:

т · го·:;:· (51)

Если бункер перегружается до угла естественного откоса (фигура 17), построение кривой очертания должен быть доведено до точки пересечения с ней линии естественного откоса.

По найденным усилиям ЯиТ (50) и (51) определяют толщину листов тела бункера из условий прочности на растяжение по ф_пг. 16. Фигура it.

уравнению (26). Заклепочные швы выполняются при помощи заклепок с утопленными головками. Бункеры с круглым сечением часто делают железобетонными.

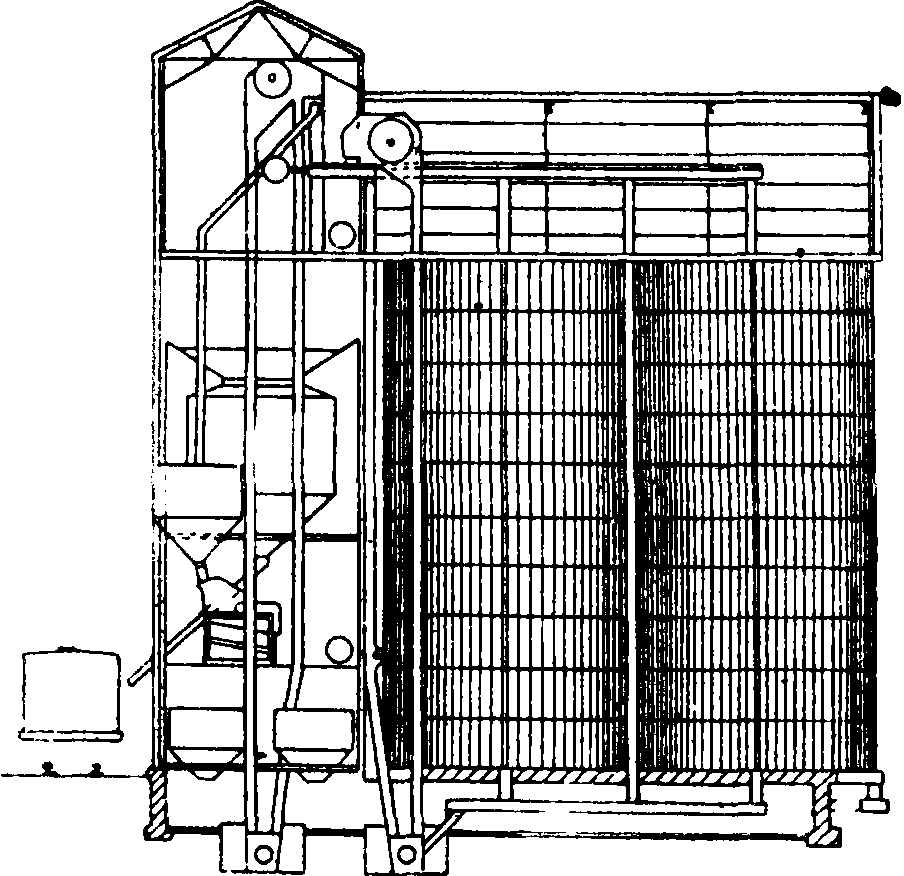
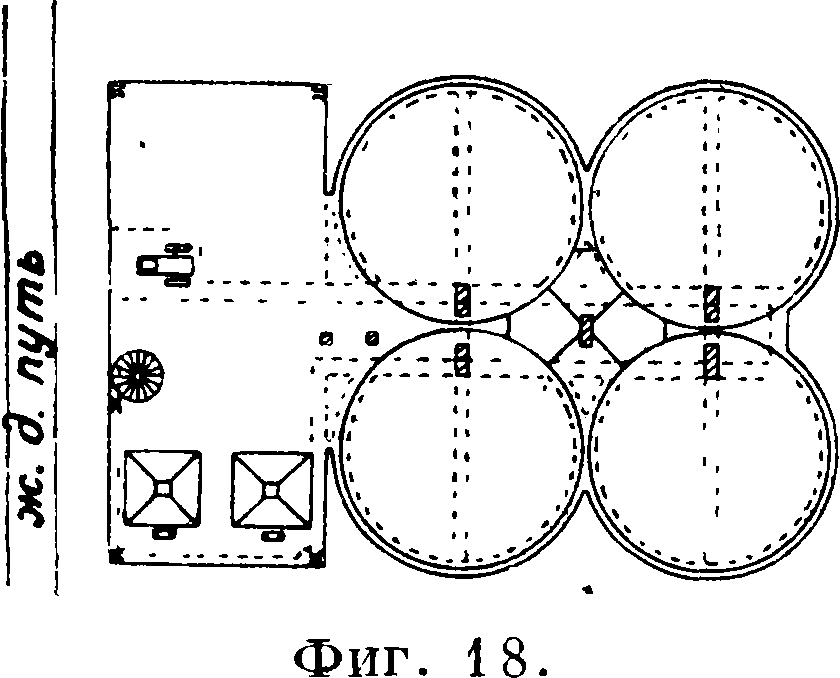
Глубокие бункеры употребляются в качестве силосов (фигура 18) и рассчитываются по теории Джансена (Jansen) и Джемесо-на (Jamieson). Согласно этой теории, давление зерна на стенку и вертикальное давление его пропорциональны. Нагрузка в каком-нибудь слое зерна для бункера с круглым сечением представлена на фигуре 19. Обозначения даны на чертеже; кроме того назовем: F — площадь горизонтального сечения бункера, /—коэф. трения зерна о стенку бункера. Условие равновесия Ψ a_zF — (a_z + da_z) F + γ F dy — α_μ dy ·2л=0. (52)

-<*г

2 лт

При а_у=1х радиус ρ=

da

Интеграл равен а_г -=

Отсюда получим, вводя гидравлический

ka_zf

Q

hf

1 -e

) <!У-	(53)
kfv
·)	(54)
]ify
^ ) • Г	(55)

Если глубина бункера больше его диаметра в 2¹/₂—3 раза, последний член опускают и при нимают просто сг₂ =

kf

Для круга и окончательный вид формул:

_Л _ У?

³ 2 kf I

vr

(56)

2 j

Коэф-ты и к определяются из опыта. В табл. 4 приведены эти коэф-ты по Плейсснеру.

Т а б л. 4.—3 начение поэфиц центов ния и пропорциональности. т р е-

Конструкция силоса

Продукты закры-

закры-, тый обшитый тый i круглого досками сечения железо-бетон- i ный ¹

Пшеница-J ^

Рожь. j i I k

Свекла < _i

К

0,4—0,5 I 0,4—0,5 0,34—0,46 0,3—0,35 • 0,43 ¹ 0,58 I 0,25 i 0,71

0,23—0,32 0,3—0,31 ;0,3 —0,45; 0,3

0,51 I 0,78 jo,37—0.55 0,85

— — I 0,5—0,6 —

— — 0,5—0,6 ¹ —

* I

Толщина листового железа для круглых бункеров определяется по тем же ф-лам, как для котлов, то есть

(5 =

^aU^r V · Rz ⁹

или

<5 --

yr-i

(57)

2) · η · R_z

где R_s <: 1 000 килограмм/cjn², η—коэф. прочности шва. равный 0,57 для однорядного шва внахлестку, 0,73—для двойного и 0,8—для швов с накладками. Допускаемые напряжения в заклепках—общие с гражданскими сооружениями. При расчете должен быть принято во внимание давление ветра, к-рое определяется согласно нормам для данной местности и считается при л о-

*у,	с=> <=о О CZD cz>
	ZP vJ c=> СЭ c=> c=> c=> O <=><=)<=> «=> c=>

Фигура 19.

женным на уровне ²/₃ высоты силоса. Напряжение от ветра в горизонтальных швах силоса _ 8 Md Ш /коч

^ 2πδά3 πδά* ’

где Μ—изгибающий момент от действия ветра,

d — диаметр силоса. Для жесткости стенки силоса укрепляются стержнями Z-образного или швеллерного сечения. При высоте силоса не более 2^г/₂диаметров его стержней для жесткости обычно не ставят.

Толстостенные С. в условиях практики находятся под действием внутреннего давления или преимущественно внешнего. При обозна-

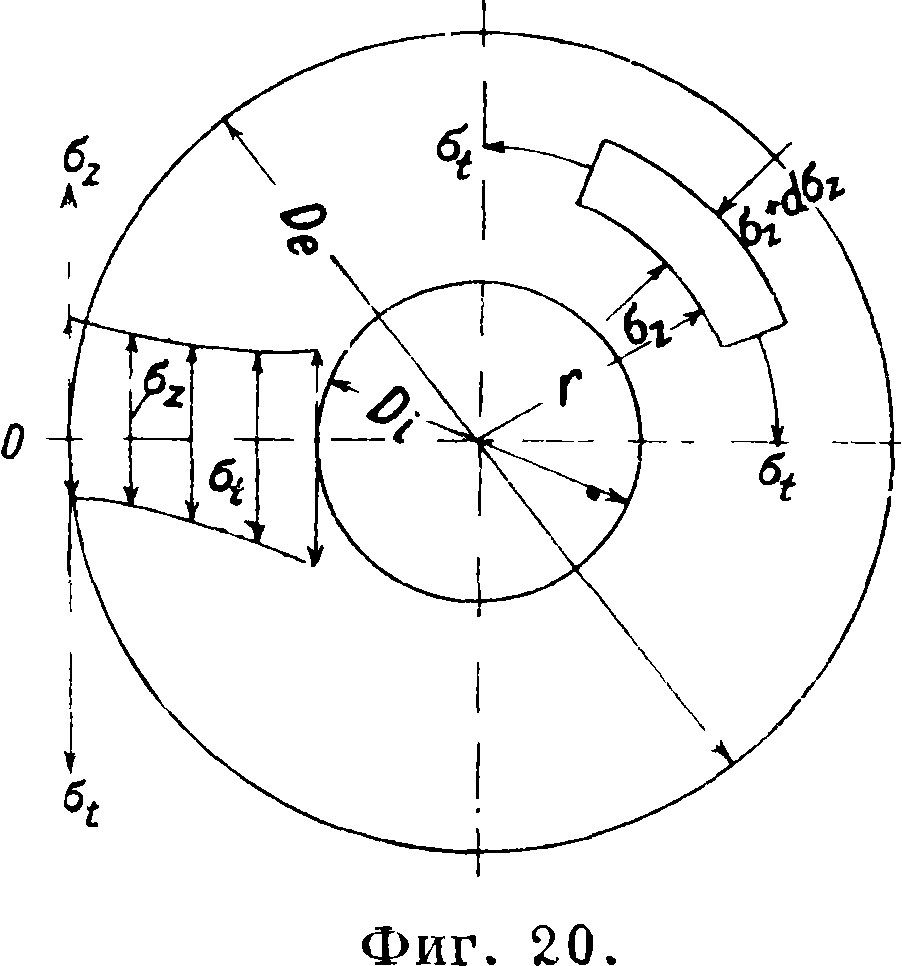
или преимущественно чениях согласно фигура 20 для цилиндрич. С. с полной симметрией ур-ия равновесия получают вид:

г

day

dr

“ ^at -°ν·

(59)

»У ^л~* IlVliXiJi

o_t=A-

G_r-

a_r

A —

в

_Г2 ’

где А и В—произвольные постоянные, которые определяются из граничных условий, именно для г “ о,. - — р; для г=^ а_г=-р_е.

На фигуре 20 представлено также распределение напряжений.

Если в основание расчета положить теорию Сен-Венана, то имеют место следующие расчетные ф-лы для внешнего давления:

J]e _ _Л Г Д Di У R-i,7p_e

(60)

При отсутствии внешнего давления {р_е=0) и при внутреннем давлении ρ_έ ф-лы принимают вид:

D_f R-_г ОДр, П; У R — 1,3 р,

(61)

для закрытой трубы и

1>Г ₌₁ Д-0,7 Pi D У R -1,3 Pi

для открытой. При расчете по теории ф-лы имеют вид:

о,^н Di У R-^:fpi

Для шаровых С. расчетные ф-лы таковы:

Dg ^/~ Д “Г 6,4 Pi D i~ У R - 0,65 Pi при внутреннем давлении и

1ч у К-1,05р_е

№

Мора

(63)

(61)

(65)

при внешнем давлении. Очень часто для определения толщины стенок толстостенных С. используют расчетную формулу тонкостенных сосудов с нёк-рым изменением именно в следующем виде:

ό

Pjd

2 R

С,

(66)

причем для чугунных труб до <5=55 миллиметров при допускаемом напряжении R=250 т/см²

С-О.б^-з^)

(67)

и поэтому в этих пределах

О 1.78 Pjd + (100 ^Й=1 000—

Для δ > 55 миллиметров

V Pfd PiO.

” 2 к ~ 5С0 *

(68)

(09)

При малых внутренних давлениях толщина стенки выбирается по технологии, соображениям и соображениям безопасного транспорта изделий. Для рабочего давления р_г·^ 10 atm

при вертикальной отливке δ=^ + 0,7^<ш,при горизонтальной ^=(^ + 0,9^ см. Трубы железные рассчитываются по той же ф-ле:

⁵=(!π + °’¹) ^см> С»)

где ψ^Ι для цельнотянутых, φ=0,8 для сварных. <р=0,57 -f- 0,63 для клепаных труб. Запас прочности (по отношению к временному сопротивлению) принимают для водяных труб в 4,5, для газовых и паропроводов—5,6, для кипятильных—7,1. Все указанные ф-лы служат для расчета труб, цилиндров двигателей, прессов и насосов. Допускаемые напряжения приведены в таблице 5.

Таблица 5.—Д опускаемые напряжения для сосудов (в ksJcm*).

1			Материалы
Сосуды	Чугун	Железо	Сталь	Медь	Фосф. бронза	Сплав алюми ния
Трубы. Цилиндры	210	350—400	! 600	200	-	200—250
двигат. Цилиндры	200—300	—	600	—
прессов. Цилиндры	750	1 800	1 500	—	1 000	1
насосов.	150		250

Трубы, подверженные внешнему давлению, проверяют по способу устойчивости их формы на то критич. давление, при к-ромiначинается изменение конструкции. Для трубы, соединенной с днищем или укрепленной ребрами (жаровая труба паровых котлов), критич. давление равно (по Мизесу)

2Е<5, 2Еб“ Г _{2 1} 2п² ->1 — μ~|

Рк-

d(n²-l)JV² 3dHl-μ^)

N

“], (71)

где N=1 +, I и d—соответственно рас-

стояние между ребрами трубы (или днищами, если нет ребер) и внутренний диаметр трубы, δ—толщина стенки, μ—коэф. Пуассона, п— число волн, при к-^эом р_к достигает минимума, п определяется по табл. 6:

Таблица 6.—3 начения п для железа и стали.

Ж :..1 500		200	[ 100	50
21 —.	2	2	2	2
21 -^—=10. Р	4	3	2	3
^..	5	4	3	3
.	1 8	6	5	4
Под жирной чертой значения относятся к области вне границ упругости.

Если принять ~ оо, то есть пренебречь влиянием длины, формула Мизеса переходит в более простую формулу Пресса:

₌ 2Εδ³ ™ d 3(1 - μ%)

(72)

Часто принимают критич. давление равным четырехкратному рабочему, т. e. p_k=4p_et и по ур-ию (72) определяют устойчивую толщину стенки. Для волнистой трубы (жаровые трубы Фокса, Мориссона) вместо S³ в формулу (72) следует поставить δ³ + I <57ι², причем h обозначает высоту волны.

Лит.: Тимошенко С., Курс теории упругости, ^ч* 1 ГГ., 1914—16; Ш т ай е ри ан И., Упругая устойчивость трубы, Киев, 1929; Б о б а р ы к о в *И., Сопротивление материалов, ч. 2, М.—Л., 1929; Лебедеве., Влияние эксцентриситета трубы на ее прочность, «Изв. Ив.-Возн. политехи, ин-та», Ив.-Вознесенск, 1928, т. 11; Худяков П., Сопротивление материалов, 5 издание,

М., 1928; Подольский И., Строительная механика, ч. 1, вып. 1—2, М., 1924; Euler L., De sono Campanarum“, «Novi commentarii Academiae scientiarum imperialis Petropolitanae», Pctropolis, 1776, v. 10; Cauchy A., Exerc. de Math., t. 3, p. 285, 1828; Love, «Philosophical Transactions of the Royal Society of London», L., 1888, v. 179 A, p. 491; Lame et Clape γ-το n, «Mbmoires prbsentbs par divers savants h l’Acadbmie des sciences de l’lnstitut de France», P., 1833, t. 4, p. 465; Meissner, «Physicalische Ztschr.», Lpz., 1913, B. 14; F 6 p p 1 A., Vorlesungen iiber technische Meehanik, B. 5, 4 Aufl., B.—Lpz., 1922; Geckeler J., Ueber die Festigkeit aehsensymmetrischer Schalen, Forschungsar-beiten auf d. Gebiete d. Ingenieurwesens, B., 1926, H. 276; Pasternak P., Schweizerische Bauzeitung, Zurich, 1925, B. 86, p. 129; R e i s s n e r, Muller-Breslau, Festschrift, Lpz., 1912; S t о d о 1 a A., Die Dampf- u. Gasturbinen, 6 Aufl., B., 1924; Forchhei-m e r Ph., Die Berechnung ebener u. gekriimmter Behal-terboden, 3 Aufl., Leipzig, 1909; К etchum M., The Design of Walls, Bins a. Grain Elewators, 3 ed., N. Y., 1926; Steuerman E., Die Theorie rotationssymme-trischer Schalen mit d anisotropen Wandung, «Zeitschrift fiir angewandte Mathematik u. Meehanik», Berlin, 1925, B. 5, p. 449. С. Лебедев.