> Техника, страница 81 > Спад

Спад

Спад, понижение уровня воды в открытых каналах или руслах, которое наблюдается при увеличении кинетич. энергии жидкости вдоль русла и представляет собою частный случаи неравномерного движения жидкости в открытых каналах или руслах. Кривая линия свободной поверхности воды на продольном профиле реки или канала, получающаяся при спаде, носит название кривой С. Определение кривой спада и нахождение отметок точек свободной поверхности при С. имеет большое технич. значение. Ур-ие кривой С. в каждом данном случае м. б. получено из общего ур-ия неравномерного движения жидкости в открытых руслах. В дифе-ренциальной форме это ур-ие имеет вид:

г

dy _ d ν“, u2

ds ds 2g j cZR

где i—уклон свободной поверхности жидкости; У—ордината точки свободной поверхности от некоторой плоскости сравнения; s—длина канала или русла от некоторой начальной точки; ν— средняя скорость движения жидкости в рассматриваемом сечении канала; R—гидравлический радиус рассматриваемого сечения канала; с— коэф. ф-лы Шези; а—коэф., вводимый в формулу за счет вычисления количества движения по средней скорости; д—ускорение силы тяжести. Если в этом ур-ии исключить переменные у и ν и вместо них ввести новые: h—глубину воды в канале и ω—живое сечение потока жидкости, то ур-ие получит вид:

i Q²

dh ⁰ с²а>² R

ds ⁼ _t aQ2 В ’

9 ω3

здесь Q—расход воды; В—ширина канала поверху в рассматриваемом сечении; г₀ —уклон свободной поверхности воды в канале, к-рый имеет место при равномерном движении того же количества жидкости в том же канале; остальные величины имеют прежние значения. Последнее ур-ие м. б. представлено в более удобной форме путем введения условий равномерного движения и критич. условий. Гидравлич. элементы канала (гидравлич. радиус К₀, живое сечение ω₀, уклон г₀, коэф. ф-лы Шези с₀), которые получились бы в канале, если бы то же количество воды, что и при данном неравномерном режиме, протекло по каналу равномерно, и составляют условия равномерного движения. Критич. условия получаются в канале тогда, когда протекающая по каналу жидкость имеет наименьшую удельную энергию. Удельная энергия жидкости относительно дна канала м. б. выражена так:

E=h

aQ²

Го ,^² _ ^, Ро,

7" ^{+ а} 2^~^ll + T + 2ga>2·· минимум величины Е соответствует критич. глубине h_Kpкритич. живому сечению ω_κρкритич. ширине поверху В_кр. Т. о. гидравлич.элементы канала называются критическими, если протекающая по каналу жидкость несет в себе минимум удельной энергии. Условие минимума величины Е дает соотношение:

aQ² _ ω*_κρ.

9 Вкр.^?

.из которого при данном расходе Q можно определить критич. глубину воды в канале. Вводя указанные условия, получаем ур-ие неравномерного движения в следующем виде:

, ФрДр

dh _. с²о)2К²

ds ~ ^b° _t ^ωκρ. ³ В ω ) В_Кр.

Ур-ие можно еще упростить, если ввести модуль расхода при данном неравномерном движении К= cwV R и модуль расхода при равномерном движении Кр=с₀со₀ ГК₀; тогда уравнение получит вид:

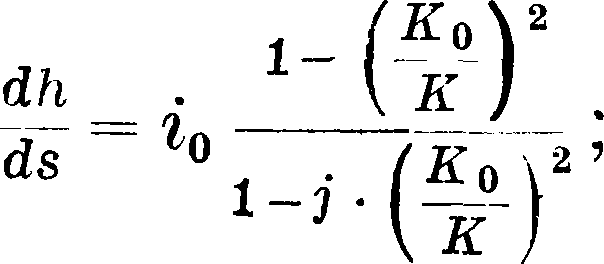
• ac²io В

здесь 1=—у · —, где χ—смоченный периметр в сечении канала. Интеграл этого уравнения дает уравнение кривой свободной поверхности при различных случаях неравномерного движения жидкости.

Если принять, что поперечное сечение канала представляет собою прямоугольник, ширина которого не меняется по длине канала, что гидравлич. радиус R равен глубине h воды в сечении и с=с₀, то диференциальное ур-ие неравномерного движения представится в виде:

dh

ds

h*-h%

№—Ькт).

Интеграл этого ур-ия, данный Брессом в виде т£=%->?1- (l—^-) [?>(%)-<Р(/?!>],

может служить для построения кривой С. В этом ур-ии L—расстояние между двумя рассматриваемыми сечениями канала, глубины воды в которых соответственно равны h_± и h«.

Величины i7i=^- и г_г-=~ представляют со-

бою отношения глубин воды в рассматриваемых сечениях к глубине равномерного движения; ψ (η) представляет собою ф-ию Бресса, получающуюся при интегрировании. Значения φ(η) определяются по данному η по специальным таблицам, и обратно η—по φ (η). Ф-ия Бресса выражается так:

<р(п)=^1п

б?-1)² п² + п + 1

+

1

Ев

arc tg

2r? + 1 Гз

Если принять, что поперечное сечение канала представляет собою параболу с вертикаль ной осью к с постоянным параметром по длине канала, смоченный периметр равен В, а еле-

довательно R=-=^ ft, ^{и с=с}о>—⁷⁰ Д^и_

ференциальное уравнение неравномерного движения представится в виде:

dh. h* - ho

^ds ° hi-hiep.

Интеграл этого ур-ия, данный Толкмиттом для кривых С., имеет вид:

[Ψι(ηύ-Ψι(4ι)]·

Ф-ия ψ_λ(ή) представляет собою ф-ию Толкмитта для кривых С.:

ψι(<ί)=ϊ in ₊1 _{arc t}g ,_h

Для пользования уравнением Толкмитта составлены особые таблицы, как и для уравнения Бресса. Уравнения Бресса и Толкмитта получены для кривых С. в предположении русла правильной формы с поперечным сечением в виде прямоугольника или параболы.

Пользуясь методом Бахметева и введенным Павловским понятием гидравлич. показателя русла, можно проинтегрировать диференциальное ур-ие неравномерного движения для русла с поперечным сечением любой формы. Кроме того метод Бахметева учитывает и разницу в коэф-тах с и с₀. Полагая, что отношение квадратов двух модулей расхода при двух различных движениях одного и того же количества воды в канале равняется отношению глубин воды при этих же движениях в канале в некоторой степени х, получаем следующее соотношение:

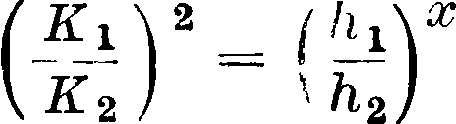
здесь х называется гидравлич. показателем русла. Гидравлич. показатель русла м. б. определен, если знать какие-нибудь два условия течения воды в канале, например равномерное и критическое. Тогда

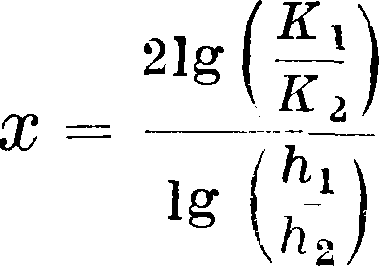
В случае, если известны размеры нескольких сечений, то гидравлич. показатель русла м. б. найден по графику, на оси абсцисс которого откладывают lgQ^, а на оси ординат lg

Удвоенный тангенс угла наклона прямой, построенной по точкам, даст гидравлич. показатель х данного русла. Имея указанное соот-

io <*s= rc-:

~dh,

ношение, мы можем представить диференциаль-ное vp-ие неравномерного движения в виде:

(S

sr

или же

iods ₌ ηΧ-j,

К ηΧ-Ι ^а‘

Ур-ие неравномерного движения приведено к этому виду и затем представлено в интегральной форме Бахметевым. Интеграл имеет вид:

^ - ч. - *?! - (1 - ?)[ВД - -БЫ];

обозначения те же. Ф-ия Бахметева должен быть определена для каждого показателя русла х:

Б(п)= JVV

Для практич. вычислений имеются таблицы, составленные для следующих показателей:×= 2,00; 2,50; 3,00; 3,25; 3,50; 3,75; 4,00; 4,50; 5,00 и 5,50. Для других гидравлич. показателей русла значения ф-ии Β(η) можно получать путем интерполяции. Величину j=вхо дящую в уравнение Бахметева, вычисляют по средним значениям с В и χ на данном участке:

^С1 + ^с2.

в =

и % =

XI + *2

Т. о. кривая С. всегда м. б. построена по точкам с желаемой степенью точности.

Т. к. при спаде кинетич. энергия по длине канала увеличивается, то глубина воды уменьшается, а следовательно величина ^ должен быть отрицательной. Из ур-ия

dh. w-hp

ds - ^г» Λ»_

видно, что ^ будет отрицательным в двух случаях. когда hjcp. h ^ hp и когда lip <с h <с, т. e. С. имеет место, когда глубина воды в сечениях канала при неравномерном движении находится в промежутке между глубиной равномерного движения и критич. глубиной. В первом случае, когда h_Kp. < h < h₀, кривая С. выпуклая. Вверх по течению кривая С. асимптотически приближается к прямой равномерного движемм, а вниз по течению, когда глубина h, уменьшаясь, доходит до величины h_KP9кривая С. имеет вертикальную касательную“.’

Прямая равномерного движения

4----_L - -L _ _ΊΤΠ ^^Прнмаякритичесн

А ·< < _. глубины

4гТ7 ^, h, ^Ли"“*^д"°

Фигура 1.

Здесь имеет место водопад. На фигуре 1 показан этот случай неравномерного движения; ясно, что такой вид движения получается тогда, когда внизу по течению имеется перепад. При вычислении отметок свободной поверхности можно исходить из следующих положений. Над перепадом или на пороге водослива должна получиться критич. глубина, которую можно вычислить, зная расход воды в канале. Также можно вычислить и глубину равномерного движения. Зная глубину на пороге водослива в начале водопада, можно найти сколько угодно точек кривой С. вверх по течению, пользуясь одним из трех указанных ур-ий (Бресса,

Толкмитта или Бахметева). Практически считают, что кривая кончилась там, где разность h₀—h весьма мала, например равна 1 см, или где η—весьма близка к единице, например >7=0,98. Во втором случае, когда h₀ < h < h_Kp>, кривая С.—вогнутая. Здесь, наоборот, кривая, опускаясь вниз по _

Фигура 2.

3___прямая критич с >ьсй глубины

-Лйямоя рабномррнрго движмив

У

Линия дна течению, асимптотически приближается к прямой равномерно- —_v„.

го движения, на ⁷.

чинаясь вверху по течению от какой-нибудь глубины, определяемой отверстием сооружения, из которого вода вытекает, или же начинаясь от критич. глубины. Такой случай неравномерного движения получается при вытекании из-под щита в лоток с крутым уклоном, ббльшим критич. уклона для данного канала. На фигуре 2 показан пример такого движения. Случай вогнутой кривой С. имеет место также на лотке быстротока, как это видно из фигура 3. Быстроток нрибоя имеет уклон больше критического, вследствие чего глубина равномерного движения в нем получается меньше критической глу-

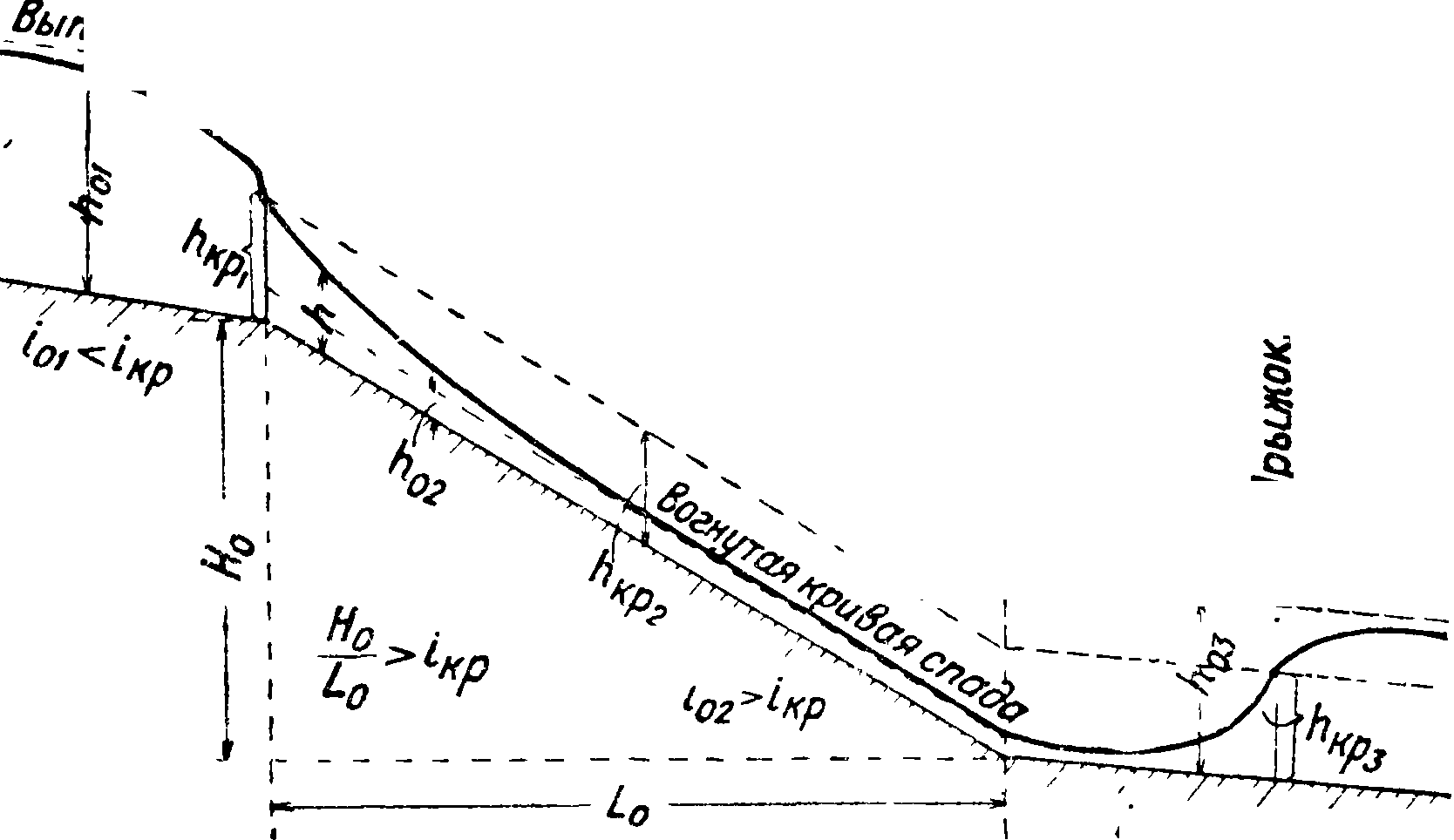
Фигура з.

^В°^гпрпо7Г^вай

¹°з^<1нр бины. Так как при устройстве быстротока два канала с уклонами, меньшими критического, в которых глубины равномерных движений более критической глубины, сопрягаются лотком с крутым уклоном, ббльшим критического, то в начале лотка быстротока получается критическая глубина, являющаяся концом выпуклой кривой С. в первом канале и дающая начало вогнутой кривой С. на лотке быстротока. В конце лотка вследствие перехода в канал с малым уклоном вогнутая кривая С. (если она не успела еще закончиться) переходит в вогнутую кривую подпора, заканчивающуюся прыжком воды (смотрите). Прыжок воды м. б. при желании уничтожен путем надвижения воды третьего канала на лоток быстротока. Можно отметить, что во всех тех случаях, когда уклон канала менее критического, а значит и глубина равномерного движения более критич. глубины, при т. н. спокойном течении, получается выпуклая кривая С., и наоборот, когда уклон канала более критического, а значит и глубина равномерного движения менее критич. глубины, при т. н. бурном течении, получается вогнутая кривая С.

Лит.: Бахметев Б., О неравномерном движении жидкости в открытом русле, Л., 1932; Ахутин А., Рабочая книга по специальному курсу гидравлики, М.—Л., 1931; ПавловскийН., Учебный гидравлич. справочник, Л., 1931; Справочник для инженеров строительной специальности, Москва, 1928; Banki D., Energie-Umwandlungen in Fliissigkeiten, Berlin, 1921; Forchheim er Ph., Hydraulik, 3 Auflage, Leipzig— Berlin, 1930; Schoklitsch S., Der Wasserbau, T. 1, Wien, 1930. В. Брилинг.