 > Техника, страница 82 > Статистика
> Техника, страница 82 > Статистика
Статистика
Статистика имеет предметом своего изучения совокупность индивидов, внешне обособленных и независимых и в то же время внутренне между собой связанных. Внутренняя связь, то есть та качественная основаf на которой индивиды объединяются в целое, выявляется лишь в массовом совокупном действии индивидов сквозь порождаемый внешней их независимостью стихийно случайный процесс. Характерной чертой статистической совокупности является качественная однородность индивидов, объединяющихся в ней на основе определенной кинкретной связи. И в этой связи индивиды совокупности различаются лишь количественно. Количественные отношения, существующие для совокупности как целого, не могут выступить в отдельных индивидах именно в силу их внешней независимости, а выступают как общий средний итог массового совокупного действия индивидов. И этот общий средний итог выражает общую меру индивидов совокупности, то есть количественное отношение, существующее для всей совокупности и проявляющееся во всей массе входящих в ее состав индивидов. Общая мера индивидов совокупности выявляется при наличии большого их числа. Именно тогда и осуществляется бесконечное разнообразие усто-вий, создающих уклонения в каждом индивиде от их общей меры. И при таком бесконечном разнообразии уклонения в одну сторону возникают столь же часто, как и уклонения в другую сторону. Все эти уклонения в конечном результате взаимно погашаются, и мера обнаруживается как исходная и общая всей совокупности величина.
Ярким примером разбираемого нами массового явления может служить количественное соотношение между ценой и стоимостью, анализируемое Марксом в его «Капитале» сл. обр.: «Величина стоимости товара выражает. необходимое имманентное самому процессу созидания товара отношение его к общественному рабочему времени. С превращением величины стоимости в цену это необходимое отношение проявляется как меновое отношение данного товара к находящемуся вне его денежному товару. Но в этом меновом отношении может выразиться как величина стоимости товара, так и тот плюс или минус по сравнению с ней, которым сопровождается отчуждение товара при данных условиях. Следовательно, возможность количественного несовпадения между ценой и величиной стоимости, или возможность отклонения цены от величины стоимости, заключена уже в самой форме цены. И здесь нельзя видеть недостатка этой формы, наоборот, именно эта отличительная черта делает ее наилучше приспособленной к такому способу производства, при котором правило может прокладывать себе путь сквозь беспорядочный хаос только как слепо действующий закон средних чисел».
В статистич. совокупности находит свое чрезвычайно четкое выражение диалектика случайного и необходимого, диалектическое единство возможности и действительности; осуществляющееся в форме случайного. Количественные различия индивидов относятся к их общей мере, как внешнее случайное выражение необходимого к необходимому внутреннему. Случайное, как определенное количественное значение
индивида, уклоняется в ту или другую сторону от общей меры. Но в потоке индивидов каждый из них несет в себе необходимое, проявляющееся через взаимное уничтожение в общей массе отклонений от него в ту или иную сторону отдельных индивидов. В каждом единичном необходимое превращается в случайное, внутреннее—во внешнее, и в количественном значении индивида выражается как необходимое, так и уклонение от него, созданное теми особенными условиями, в которых осуществляется единичное. Вне этих особенных условий случайное не существует как действительное, но только лишь как возможное.
При данной величине стоимости товара возможна, говоря совершенно абстрактно, продажа его по любой сколь угодно от этой стоимости уклоняющейся цене. Но чтобы возможность превратилась в действительность, необходим целый ряд условий—конкретных обстоятельств данной товарной сделки, которые ближайшим образом определяют то случайное внешнее количественное выражение цены, к-рое принимает стоимость в данном конкретном случае. При наличии этих условий возможность возвышается до действительности, становится действительностью. Именно так и возникает единство возможности и действительности, осуществляющееся в форме случайности.
Теория С. тесно связана с теорией вероятностей. Связь эта состоит в том, что теория вероятностей исследует теоретически предмет С. в его существенных моментах в наиболее общей форме. Глубокая связь между этими науками коренится в том историч. факте, что обе они ротдились в одно и то же время и в одном и том же месте—именно в передовых странах торгового капитала и мануфактуры 17 в.: Англии, Голландии, Франции. Возникли и развились эти науки на почве развития мирового рынка и капитализма, на почве развития массовых общественных процессов. Основой таких массовых процессов явилось автоматич. строение товарного общества, масса самостоятельных разрозненных товаропроизводителей. При такой структуре общественного производства обмен оказывается единственной формой связи между товаропроизводителями. Обмен осуществляется как бесконечная череда единичных, внешне независимых актов. Но сквозь внешнюю независимость прорывается их внутренняя связь, их единство как формы проявления определенных количественных соотношений в распределении общественного труда. Только в силу внешней их независимости меновые отношения приобретают черты стихийно случайного процесса.
Абстрактная теория стихийно случайного (стохастического) процесса. Разумеется, почерпнутых из стихии обмена понятий совершенно недостаточно для вскрытия статистич. закономерностей экономии. процессов, как недостаточно их и для выявления статистич. закономерностей в биологии, в физике и т. д. Этого не могут понять буржуазные теоретики С., культивирующие совершенно неправильные, порой извращенные, представления, в особенности о природе экономических процессов. Однако в то же время этих понятий оказывается вполне достаточно для построения теории статистич. совокупности в ее всеобщей абстрактной форме, иными словами—для построения теории вероятностей * как теории количественных законов стихийно случайных процессов в их наиболее общем !
Т. Э. т. ХМ.
виде. Закономерности таких процессов теория вероятностей изучает при посредстве своеобразных моделей. Классическими моделями издавна служили различного рода азартные игры: в кости, в орлянку и тому подобное. На игре в орлянку с?лед. обр. выявляются значения основных понятий теории вероятностей: вероятность и равновоз-можность. При этой игре, как известно, подбрасывается много раз подряд монета, сделанная из однородного материала и симметричная. В случае однократного бросания возможны два результата: герб и решетка. Оба эти результата не только возможны, но и равновозможны, поскольку монета симметрична и однородна. При ответе на вопрос, как велика вероятность выпадения герба, приходится принять в расчет, что имеется один из двух возможных и притом равновозможных шансов. И таким образом число 1/2, как отношение 1:2, оказывается искомой числовой, оценкой вероятности выпадения герба. В каждом бросании возможность выпадения герба и решетки превращается в действительность. Самый процесс бросания составляет совокупность условий этого превращения. Результат каждого бросания осуществляет единство возможности и действительности в форме случайного.И именно в этой форме случайного проявляется общая мера, равная половине. Каждое отдельное бросание несет в себе эту меру, но выражает ее в форме случайности. Результат каждого бросания дает отклонение от меры: появляется либо герб либо решетка. Значит каждый результат не дает указания на меру. Мера же прорывается наружу лишь при большом числе опытов. Только тогда выявляется равночисленность выпадений герба и решетки. Наиболее совершенную модель статистической совокупности выдвинула статистическая практика в виде случайной (или эквивалентной ей механической) выборки. Выборка представляет собой такого рода операцию, когда вместо исчерпывающей регистрации всех единиц каждой данной совокупности используют только частичную регистрацию. Случайная выборка организуется так, чтобы каждая отбираемая единица имела такую же вероятность попасть в выборку, как и любая другая единица той же совокупности. В результате отбора достаточно большого числа единиц образуется такая выборочная совокупность, числовая характеристика которой близко воспроизводит соответственную характеристику всей совокупности. Наир, при определении пороков хлопкового волокна каждой данной партии поступают след, обр.: из всей партии «отбирают случайные пробы; из их совокупности образуют“ средний образец. По этому среднему образцу судят о качестве всей партии, например если в полученном образце уд. в такого порока, как угар, определен в 0,"б%, то именно эта цифра и служит характеристикой уд. веса угара во всей партии в целом. Другой пример из практики статистич. изучения леса. При обследовании лесных массивов б. Нижегородского края (работа т. Здорика 1926 г.) проверялась степень близости между результатами сплошного учета и учета выборочного. Между прочим определен был средний диаметр ели на высоте груди человека. Т. обр. выборочный метод дал цифру 20,3 см, тогда как сплошной дал 20,4 см.
В какой же именно мере результаты применения случайной выборки способны воспроизводить количественные характеристики целого? Ответ на этот вопрос дает математич. исследо-
30
вание стихийно массового процесса, или, как в дальнейшем будем говорить, стохастич. процесса. Пусть в составе S индивидов какой-либо определенной статистической совокупности (будем называть ее генеральной) имеются М индивидов, обладающих каким-либо определенным признаком, и остальные S — М индивидов этим признаком не обладают. Тогда М :S представит собой долю признака в генеральной совокупности. Отношение М : S=р будем в дальнейшем называть коротко долей. Пусть, далее, из состава такой генеральной совокупности вслепую отбираются s индивидов. Среди них может оказаться любое количество ш обладателей данного признака. Крайние возможные значения этого щ суть Ohs. Число т называется частотой данного признака, а отношение т : s=w называется его частостью. Крайние возможные значения w суть нуль и единица:
О w ^ 1.
Можно доказать, что Цри достаточно большой выборке частость w должна довольно близко воспроизвести долю р. Схема доказательства такова. Сначала определяют значение Рт вероятности того, что среди s ^случайно отобранных индивидов окажется т обладателей данного признака. Величина Рт оказывается равной:
s!
m (s - m)!
рт(1 — p)s
Эта точная формула неудобна для вычисления. Несравненно более удобно для вычислений приближённое выражение Рт, предложенное Лапласом:
(т - sp)2
Pm~Pspe 2βρ(ΐ-ρ),
где Psp — вероятность частоты, равной sp, а е— неперово число. Из ф-лы Лапласа непосредственно видно, что частота sp имеет за собой наибольшую вероятность,частоты же, отличающиеся от sp, возникают с тем меньшей вероятностью, чем больше разность m — sp, например при объёме выборки s в 100 000 индивидов из совокупности с долей признака, равной 0,1, наиболее вероятная частота есть 10 000; частоты, отличающиеся от 10 000 на 100, то есть частоты 9 900 и 10 100, возникают с вероятностью меньшей. Именно:
1002
Рщ»± хоо=ΡχοοοΑ^=0,574 Р10000.
Иными словами, частоты, отличающиеся от наивероятнейшей на 1% (100:10 000=0,01), обладают по сравнению с ней почти в половину меньшей вероятностью. Вероятности же частот, сильней отличающихся от 10 000, например 300 (3%), гораздо меньше. Именно:
3002
Р юооо ± зоо = -^юооо б=0,00674 .Рюооо·
Т. о. эти частоты почти в полтораста раз менее вероятны, чем частота 10 000. И уже совсем ничтожной вероятностью обладают такие частоты, которые отклоняются от наивероятнейшей, положим, на 600 (6%). Имеем для этого случая: 6002
-Рюооо ± eoo ~ Рюооое — 0,000000002 · Рюооо·
Т. е. оказывается, что из всех возможных частот заметной вероятностью обладают лишь те, которые не слишком сильно (на 1—2%) отличаются от наивероятнейшей частоты.
При определении границ, внутри которых частоты обладают б. или м. заметными вероятностями и вне к-рых, наоборот, вероятностями ничтожными, играет роль, как видно из пре дыдущего положения,
(m - sp)2
сомножитель при Р<
spy
т. e. е
2sp(l - р)
Этот сомножитель становится малым, когда отклонение m — sp достигает разме ра, в несколько раз превосходящего |/sp(l — р). Действительно, если
ш-
где *-
•sp=± t Vsp (1 — р),
-число порядка нескольких единиц,тогда:
(m - sp)2 t2gp (i - р) _ 12
2sp(l-p) 2sp(l-p) 2
В таком случае получаем для рассматриваемого
_t_2
сомножителя следующее значение: е 2, которое оказывается малым уже при f, равном 2 или 3. Т. о. при определении искомых границ расчетной мерой служит выражение
Ksp(l-p).
Именно эта мера служит для оценки отклонений m — sp. Если теперь от абсолютных отклонений m — sp перейти к относительным по отношению ко всему объёму выборки, тогда эти относительные отклонения представят собой разности между частостями и долей признакар. Действительно:
т - sp m
-p=w — p.
И мерой для оценки отклонения w—p посл>-жит величина:
Esp(l — р)
V
р(1 -Р)
Величина
V
р(1-р)
при достаточно большом s
становится очень малой. Отсюда вытекает следующая теорема: при достаточно большом объёме выборки весьма мало вероятно, чтобы частость w сколько-нибудь заметно отличалась от доли р. Эта теорема была впервые доказана более 200 лет тому назад Яковом Бернулли. Теорема Бернулли есть первая наметка той теории стохастического процесса, которая носит название «закона больших чисел» и которую, следуя Марксу, мы будем называть «законом средних чисел».
Покажем на примере применение теоремы Бернулли. Обследуется коллектив студентов, половину которого составляют рабочие от станка, следовательно доля признака р равна 0,5. Производим случайную выборку 100 студентов. Определим степень близости частости w к доле 0,5. Мерой оценки отклонения w—0,5 служит,
ΙΑ - -
как мы видели выше, величина р(1-р)
которая в данном случае оказывается равной 0,05. Отсюда вывод: при данном объёме выборки частость w может отличаться от 0,5 на величину порядка 0,05. Если объём выборки довести до 2 500, то степень точности выборки усилится. Будем иметь:
V
Р( 1
__= о 01
2500
В этом последнем случае можно заранее сказать, что случайная выборка даст частость примерно 0,49—0,51.Надо здесь отметить следую-
щее обстоятельство. Перед впервые знакомящимися с теорией выборки всегда возникает вопрос: как можно пользоваться для предва-
лГ р(1 — р)
рительных расчетов выражением у ——,
которое нельзя вычислить без предварительного знания доли р? На этот вопрос теория отвечает: произведение р (1 — р) никогда не может превзойти величины 0,25 и поэтому, если нель-
1 р(1 — р)
зя вычислить заранее размер у ——, то во всяком случае отпадает опасность его преувеличения и значит отпадает риск недооценки возможных расхождений между w и р.
Дальнейшее развитие теории стохастического процесса привело к установлению более общего выражения закона средних чисел как закона средних величин. Этот новый шаг вперед был сделан русским математиком Чебышевым (1821—94 гг.). Для выяснения сути теоремы Чебышева необходимо предварительно^устано-вить нек-рые понятия. Когда какой-либо признак индивидов данной статистич. совокупности варьирует количественно, то такой признак называется варьирующим признаком, а отдельные значения такого признака называются вариантами. Пусть например, имеется генеральная совокупность 200 тыс. деревьев, состоящая из: 40 тыс. деревьев 0 10 см, 100 тыс. 0 20 см, 60 тыс. 0 30 см. Здесь 10, 20 и 30 суть варианты; их численности 40, 100 и 60 тыс. определяют собой удельный вес каждого из вариантов во всей генеральной совокупности. Варьирующий в пределах данной совокупности признак м. б. охарактеризован средней величиной этого признака для^ всей совокупности в целом. Такая средняя обычно определяется как средняя арифметическая, взвешенная в соответствии с уд. весом каждого варианта (общая теория средней изложена ниже). В применении к данному примеру получаем для среднего диам. ж величину 21 см, которая определяется из следующего выражения:
— 10-40 000 + 20 · 100 000 4-30-60 000 _
Х = 40 000+ 100 000 + 60 000 “
Эту величину в дальнейшем будем называть генеральной средней. Такая средняя характеристика оставляет без освещения степень рассеяния признака. Эта степень рассеяния требует своей особой характеристики. Насколько это необходимо, можно судить по следующему примеру. Пусть наряду с вышеупомянутой совокупностью деревьев имеетсй еще другая, состоящая из 7 тыс. деревьев 0 10 см, 166 тысяч 0 20 см, 27 тысяч 0 30 см. Эта новая совокупность характеризуется таким же средним диаметром, как прежняя:
10-7000 + 20.166000+30.27000 _ 01Х ~~ 7 000 + 166000 + 27 000 ^
Но в то же время вторая совокупность отличается от первой тем, что крайние ее варианты обладают меньшим уд. весом. Значит варианты ближе прижимаются к среднему диаметру, их рассеяние здесь меньше. Для выявления отмеченного различия пользуются <г. н. средним квадратическим отклонением (обозначим его символом v0). Определяется оно как квадратный корень из среднего взвешенного квадрата отклонений вариантов от их среднего арифметического. В применении к нашим двум совокупностям получаем:
vq =
V
(10 - 21)2.40000 + (20 - 21)2 .100000 + (i0 - 21)2.60000 40000 + Ϊ00000 + 60 000 :
= У 49 « 7;
"I /~ (10 - 21)2. 7 000 + (20 - 2Ϊ)2 -166 000 4+30 - 21)2 .27 000 V0^ V 7000 + 166000+27000
= Vl6=4.
Полученные две характеристики отражают на себе различие в степени рассеяния признака: в первой совокупности он обладает почти вдвое большим рассеянием, чем во второй. Положим теперь, что для определения среднего диаметра деревьев упомянутых выше совокупностей прибегают к случайной выборке. Средний диаметр случайно отобранных деревьев— будем называть такую среднюю выбороч ной и обозначать символом х—может охарактеризоваться любым числом в пределах между двумя крайними вариантами 10 сантиметров и 30 см. Чебышев доказал, что при достаточно большом объёме выборки s весьма маловероятно, чтобы выборочная средняя х сколько-нибудь заметно отличалась от генеральной средней х. Мерой для оценки отклонений х от х служит величина
~, где v0—квадратич. отклонение, a s—число У s
отобранных индивидов. Т. о., если например из указанных выше совокупностей деревьев отобрать вслепую по 10 000 деревьев из каждой, то обе выборки должны дать для средних диаметров величины, равные -21. Однако первая выборка по сравнению со второй должна дать несколько менее точные результаты, поскольку мера расхождения между жиж оказывается в первой выборке равной » а в0 второй —
, следовательно для первой выборки /10000 ^
ж=21 ± 0,07, для второй ж= 21 ±0,04. Предложенный прием оценки результатов применения выборочного метода имеет тот недостаток, что размеры среднего квадратич. отклонения vQ заранее не бывают известны. Обычно вместо величины v0 используют значение среднего квадратического отклонения в выборочной совокупности (обозначают его символом σ0). Величина σ0 обыкновенно мало разнится от ν0, и потому оценка результатов выборки не встречает тех препятствий, которые на первый взгляд кажутся непреодолимыми.
Вариация при стохастическом процессе. Если вариация признака является порождением стохастич. процесса, то в таком случае распределение вариантов принимает характерные для этого процесса черты! Пусть имеется совокупность, в которой доля признака равна р. Из этой совокупности наудачу выбирают s индивидов. Среди s отобранных индивидов может оказаться любое число ш обладателей данного признака. При таких условиях ж представляет собой варьирующую величину, могущую принять любое значение в пределах от 0 до s. Каждый из этих вариантов возникает с определенной ве оятностью Рт. Графическое изображение Рш как функции от аргумента ш обладает характерными очертаниями. Получающаяся кривая имеет максимум при ш — sp; при продвижении переменной ж вправо или влево от значения sp кривая вероятностей приближается к оси абсцисс; при этом в средней своейчасти кривая обращена к оси абсцисс вогнутостью, а вправо и влево от средней части обращена выпуклостью. Такие же характерные очертания приобретает кривая, служащая отображением стохастич. вариации, возникающей в таком процессе, специфич. особенность которого состоит в игре слепого случая при взаимном столкновении, взаимном комбинировании отдельных, независимых друг от друга единичных процессов. Биологич. С. дает^многочислен-ные примеры такой вариации, графич. изображение которой подсказывает идей о стохастич. ее происхождении. С таким подсказом вполне гармонируют установленные современной биологией законы. Установлено существование особых-носителей различных свойств организмов, передаваемых по наследству. Эти особые носители, выступающие в качестве отдельных самостоятельных единиц, называются генами. Относительно генов установлены два закона (известные под именем законов Менделя): 1) гены не влияют друг на друга; 2) они наследуются друг от друга независимо. Законами Менделя и объясняется то, что количественная вариация различных свойств организмов, например мышечной силы или крепости хлопкового волокна, возникает в условиях стохастического процесса. Так, измерение мышечной силы левой кисти руки у 366 ленинградских вагоновожатых дало следующее распределение этой силы:
Си ла, кг
Числен ность
12.5— 17,5
17.5— 22,5
22.5— 27,5
27.5— 32,5
32.5— 37,5
6
13
38
74
106
Сила, кг
37.5— 42,5
42.5— 47,5
47.5— 52,5
52.5— 57,5
Числен ность
85
30
10
4
Измерение крепости одиночной хлопковой нити при прядении через три банкаброша дало следующие результаты:
В случае измерения крепости нити при упрощенном плане прядения (без перегонного банкаброша в одно сложение на тонком банкаброше) получилось следующее распределение крепости нити:
| Крепость, Г | Уд. в дан. 1 крепости, % | 1 Крепость, Г | 1 Уд. В. дан. крепости, % |
| 110—130 | I! | 210—230 | 1 20 |
| 130—150 i | 2 ; | ! 230—250 | ! 15 |
| ! 150—170 1 | 8 | 250—270 | 1 13 |
| ! 170—190 | 12 | 270—290 | 1 6 |
| ! 190—210 1 | 18 i | 310—330 | 2 |
Распределения вариантов по их численности во всех случаях, подобных приведенным, м. б. оформлены при помощи ф-лы Гаусса:
(Х-Х)2 2ν0
е где х — х —отклонения варианта х от среднего арифметического х, a v0—среднее квадратич. отклонение; что же касается величины Р%, то она определяется из выражения:
| Крепость, Г J | 1 Уд. в дан. крепости, % | Крепость, Г | Уд. в дан. крепости, % | |
| 150—170 | 1 | 250—270 | 22 | |
| 170—190 | 4 | 270—290 | 14 | |
| 190—210 | И | 290—310 | 8 | |
| 200—230 | 16 | 310—330 | 2 | |
| 230—250 | 21 | 330—350 | 1 | |
где. s—общая численность вариантов (в первом примере 8=366, а втором 8=1, поскольку сумма уд. весов вариантов была приведена к 100%, то есть к единице), а—размер интервала группировки (в первом примере 5, а во втором 20). Для первого примера, в к-ром 8=366, а=5, ж=34,7, г0= 7,38, получаем:
(Х-Х)2 (Х-Х)2
Рх.£=— Д=· е 2(7,38)2 =99е
7,38/2π
Для второго примера, в к-ром 8=1, α= 20, х=246,6 и ν0=35,2, получаем:
(Х-Х)2 (Х-Х)2
”2 478“
р Ь20
35,21/27*
е 2 (35,2)2=0,227е
Для третьего примера, в к-ром 8=1, α=20, х=220,4, ν0=40,6, получаем:
(х- X)2
Ρχ-χ=0,197
Сопоставление распределений, указанных во втором и третьем примерах, так же как и сопоставление их средних характеристик х и ν0, дают ясное указание на заметное различие двух способов пряде- 25
I ю
£
| Т | ||||||
| й/ч | ||||||
| 1 | ||||||
| j | ||||||
Крепость нити 6 г Фигура 1.
ния: через три банкаброша и без пере- *>2о тонного банкаброша | в одно сложение на | « тонком банкаброше.
Второй способ дает явно худшую продукцию: с одной стороны, средняя кре- » пость ослабляется (220,4 г против 246,6 г), с другой стороны, усиливается неров-
нота нити, поскольку среднее квадратич. отклонение увеличивается (40,6 против 35,2). Сопоставление этих распределений представлено на диаграмме (фигура 1).
Сравнение различных распределений м. б. осуществлено двояким образом: а) либо путем непосредственного сопоставления конкретных распределений б) либо путем сопоставления средних их характеристик х и ν0. Статистич. практика обычно предпочитает второй путь, поскольку им достигается более легкая обозримость всего материала. Однако названные средние могут действительно служить полной характеристикой распределения лцшь при наличии однородной совокупности индивидов. В качестве примера явно неоднородной совокупности приведем следующие данные геологии. С. Вся земная поверхность, подразделенная на км2, представляет собой совокупность единиц, различающихся между собой по высоте, суши над уровнем моря и по глубине океанов. Получается след, распределение:
Варианты глубин океанов, км
Относит. числен ности
Варианты высот суши, км
До 6 5—6 4—5 3—4 2—3 1—2 0—1
0,010
0,165
0,233
0,139
0,047
0,029
0,085
0—1
1—2
2—3
>3
Относит. числен ности
0,213
0,047
0,020
0,012
Итого
1,000
Данное распределение ясно указывает на существование двух совершенно различных групп высот земной поверхности: одной, отвечающей материковым плато, и другой, отвечающей дну океанич. впадин; общая средняя в данном слу+-чае не имеет никакого смысла.
Закон ошибок Гаусса, выраженный в упоминавшейся выше формуле Гаусса, дает теорию стохастич. процесса, возникающего при многократных измерениях. Среди каких именно индивидов происходит этот стохастич. процесс? Теория закона погрешностей утверждает существование элементарных ошибок, различных по величине и направлению и возникающих с одинаковой вероятностью. Каждая фактически возникшая ошибка есть суммарный результат множества скомбинированных друг с другом таких элементарных ошибок. В действительности дело обстоит гораздо сложнее и запутаннее. Бесчисленное множество элементарных, незначительных влияний среды, переплетаясь многоразличным образом не только в форме суммы, но и в форме других более сложных функций, в конечном результате может рассматриваться как сумма элементарных исчезающе малых величин. Т. о. элементарные ошибки и их сумма представляют собой лишь упрощенное математическое отображение процесса измерения в его бесконечных опосредст-вованиях—связях, зависимостях от различных влияний среды. В качестве примера использования закона ошибок Гаусса возьмем результаты изменения заряда электрона, произведенные известным экспериментатором Милликеном. По условиям эксперимента определялся не самый заряд е, а связанная с ним величина е2/з · 108. Результаты проделанных 58 измерений изображены в следующей таблице в порядке возрастания численных значений.
| 60,79 | 61,03 | 61,09 | 61,14 | 61,21 | 61,28 |
| 60,86 | 61,04 | 61,10 | 61,15 | 61,22 | 61,30 |
| 60,87 | 61,01 | 61,11 | 6Г,16 | 61,22 | 61,31 |
| 60,95 | 61,06 | 61,11 | 61,16 | 61,22 | 61,35 |
| 60,97 | 61,06 | 61,12 | 61,18 | 61,23 | 61,36 |
| 61,00 | 61,06 | 61,13 | 61,18 | 61,23 | 61,37 |
| 61,00 | 61,07 | 61,13 | 61,18 | 61,23 | 61,38 |
| 61,00 | 61,07 | 61,13 | 61,20 | 61,24 | 61,39 |
| 61,01 | 61,07 | 61,13 | 61,20 | 61,24 | |
| 61,02 | 61,09 | 61,14 | 61,21 | 61,26 |
Средняя ж =61,139; среднее квадратич. отклонение v0= 0,1280. Распределение результатов измерений в сопоставлении с распределением, исчисленным по закону Гаусса, представлено в следую цет таблице:
Численность измерений
| Варианты | фактическая | исчисленная |
| ДО 60,819 I | 1 | 0 |
| 60,819—60,947 j | 4 · I | |
| 60,947—81,075 | 1 16 | и |
| 61,075—61,203 | 20 | 22 |
| 61,203—61,331 | 14 | 14 |
| 61,331—61,459 | 5 | 4 |
| 61,459 и выше | 0 | о !
1 |
Из сопоставления численности фактической и исчисленной видно, насколько хорошо закон Гаусса отображает действительность.
Средние. При наличии стохастич. вариации средние х и v0 играют вполне определенную роль характеристик такой вариации. Использование средних широко распространено в практике не только для характеристики стохастич. вариации, но и всякой вариации, возникающей в любом массовом процессе. Бур жуазные теоретики и практики игнорируют то обстоятельство, что вне рамок стохастич. процесса средние теряют свой специфич. смысл и приобретают иное содержание. Всякая совокупность, с которой имеет дело С., состоит из многих различающихся между собой индивидов, например рабочие какого-либо завода различаются между собой и своей квалификацией и заработной платой и т. и. При сопоставлении нескольких совокупностей возникает надобность в числовых характеристиках каждой из них. На вопросы, обладают ли рабочие данного предприятия большей квалификацией по сравнению с рабочими другого предприятия и получают ли они большую заработную плату, ответить можно лишь после того, как квалификация и заработная плата на каждом предприятии охарактеризованы одним числом. Такую именно цель и ставит перед собой средняя: она должна при посредстве одного числа дать характеристику относящейся к ней реальной совокупности; она должна запечатлеть количественное отличие качественного определения данной совокупности от любой другой. Так, средняя заработная плата данной совокупности рабочих отличает ее по заработной плате от любой другой совокупности. Средняя является в результате абстрагирования от количественной вариации данного признака в пределах совокупности. Но абстрагируясь от количества, мы не абстрагируемся от качества, а наоборот, стремимся количественное выражение этого качества запечатлеть в средней. Вместе с тем средняя не может отобразить характера вариации признака внутри данной совокупности. И ^ем более средняя не может охарактеризовать известные признаки таких совокупностей, которые по этим признакам разбиваются на ряд отдельных совокупностей. В качестве разительного примера глубоко, ошибочного использования средних можно привести отмеченную в свое цремя Лениным ошибку народников. Они строили свои выводы на основании средних, определяемых для всей совокупности крестьянства. Ленин показал, что народническое понимание крестьянства как единой совокупности представляетсобой мешанину из отдельных совокупностей сельских капиталистов, мелких самостоятельных товаропроизводителей и пролетариев. «Получаемые от такого сложения средние затушевывают разложение крестьянства и являются поэтому чисто фиктивными».
Средняя должен быть заранее рассчитана на отображение какого-либо одного свойства, к-рое называется определяющим, т. к. оно определяет, как именно следует вычислить среднюю, например средняя заработная плата должен быть рассчитана так, чтобы общая сумма реальной заработной платы всей совокупности рабочих не потерпела изменений. Т. о. средняя есть величина признака ж, характеризующая каждый индивид в абстрактной уравненной совокупности, заменяющей реальную совокупность и сохраняющей нетронутым количественное выражение определяющего свойства реального коллектива. Пусть определяющее свойство выражается ф-ией Си, ж2, xs), где хг, х2, ., х$— варианты данного признака. После уравнивания его вариации на место жг- станет средняя х. Тогда величина, измеряющая определяющее свойство, окажется равной (ж, ж,. ж). Здесь все операции, обозначаемые символом /, следует произвести уже не над значениями
Χι, а над значениями того же признака в уравненной совокупности. Т. о. получается ур-ие, называемое ур-ием средней:
f (Xi, х2> ···» xs)=f(x’ х> ···» х)-Пример 1. Определить среднюю заработную плату рабочих данного предприятия, исходя из того, что общая сумма заработной платы должна остаться неизменной. Ответ:
%1 + + · · · 4- xs=χ 4- х 4- · ·· 4- х=sx,
откуда получаем для искомой средней форму средней арифметической
~ _ ^2 + · · · XS
~~ s
Пример 2. Определить среднюю скорость молекул газа, исходя из того, что общая сумма живых сил молекул должна остаться неизменной. Полагая массу каждой молекулы одинаково равной т, получаем следующее ур-ие:
I mvi + mvl + · · · +~ mvj =
= 1 mv2 + ~ mv2 + ··· + * mv2
1
или после сокращения на 2 т:
8
2 vi=sb2’
г=1
откуда“ находим:
-] iSi·
то есть^средняя скорость молекулы должен быть определена как средняя квадратическая.
Пример 3. Каждая единица продукции требует со стороны различных рабочих неодинаковых затрат рабочего времени. Требуется определить среднее на единицу продукции количество рабочего времени, ориентируясь на неизменность общей суммы продукции. Имеем:
— + — +··· + —= —. а?! X; xs х х х откуда:
X] X2 « Xg
то есть средняя определилась как средняя гармоническая.
Пример 4. Средний диаметр деревьев при ориентировке на средние линейные размеры этого признака исчисляется как средняя арифметическая по ф-ле:
где s—количество деревьев данного ^диаметра или, как принято говорить, данной ступени толщины. При иной ориентировке форма средней соответственно видоизменяется, например средний диаметр деревьев, ориентированный на определение средней площади сече^ ния стволов, определится в форме средней· квадратической:
т. к. площадь сечения пропорциональна квадрату диаметра.
Проиллюстрируем сказанное на конкретном примере. Имеются 46 деревьев лиственницы, распределенные по ступеням толщины сл. обр.;
| Ступени толщины | Число деревьев | Ступени толщины | Чис о деревьев |
| 8 | 4 | 24 | 5 |
| 12 | 12 | 28 | 3 |
| 16 | 12 | 32 | 1 |
| 20 | 9 | Итого | i 46 1 |
Средняя арифметическая исчисляется так:
Тч 8.44-12·124-16·12 + 20·9 + 24·54-28-34-32*1 ^ 44-Ι24-Ι24-94-54-34-Ι ~Ί| li,U
Средний же диаметр, исчисленный по форме средней квадратической, равен:
44-ШЛ24Г5И124-4JQ·94-576»54-78Ь Н-й)2Ь1 ^ 44-124" 12—I— —I— Ь —I— 3 —I— 1=18,00.
Средняя квадратическая, как и всегда это бывает, оказалась больше, чем средняя арифметическая.
Пример 5. Для шарикоподшипников некоторой машины требуется комплект шариков различных радиусов.
| Радиус, | Численность, |
| см | % |
| 1 | 20 |
| 2 | 30 |
| 3 | 40 |
| 4 | 10 |
| Итого | 100% |
Как велик средний радиус шариков * ориентированный на средний их вес? Т. к. вес шари- ков пропорционален их объёму, а объём пропорционален кубу радиуса, то искомая средняя определится как средняя кубическая:
R=3/13 · 0,2 + 22 · 0,3 + 3» · θ,4 + 4* · ОД=2,7.
Для сравнения определим среднюю арифметическую по формуле:
R == 1 · 0,2 2 · 0,3 -f- 3 · 0,4 -f- 4 · 0,1=2,3.
В приведенных выше примерах ф-ия f выступала каждый раз как сумма одинаковых ф-ий φ от соответствующих xf. в первом примере ψ—первая степень от xif во втором— квадрат Х{, в третьем—обратная величина ж“·. Такое суммальное строение ф-ий f есть общая форма определяющей ф-ии, т. к. .форма эта вытекает из самой сущности статистич. совокупности. Эта совокупность с чисто количественной стороны есть нек-рое множество различных количеств. А наиболее общей, Hj3 то лее время первоначальной и простейшей, формой такого множества является именно сумма: произведение есть частный случай сум-мё1, ибо возникает при наличии одинаковых слагаемых, степень—частный случай произведения (при одинаковых сомножителях). Т. о. общая форма определяющей ф-ии имеет следующий вид:
f (®ι, х2, Xs)=Ψ (Χι) 4- Ψ (®2) 4- -·- 4- Ψ Соизмерение связи. Каждый количественно определяемый признак какого-либо явления зависит от ряда условий. И т. к. эта зависимость имеет количественный характер, то она находит свое отображение в виде функциональней связи как всеобщей формы связи в области количественных: отношений. Влияющие на данный признак условия выступают как аргументы, а величина
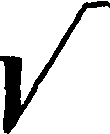
признака—как их функция. Измерение параметров этих ф-ий, а также измерение тесноты связи составляет одну из главных задач С. Как было указано выше, при определении средней величины признака абстрагируются от всех влияющих на его величину аргументов, и в таком случае средняя выступает как величина достоянная. Если от такой полной абстракции обратиться к учету влияния одного или нескольких аргументов, тогда средняя становится уже величиной переменной, зависящей"от вводимых в расчет аргументов, в той или иной форме и с той или инойтеснотой связи, то есть средняя оказывается ф-ией одного или нескольких агрументив. Какой именно ф-ии—линейной, квадратической, показательной или еще какой-либо,—этот вопрос решается рассмотрением -природы зависимости. Ур-ие, запечатлевающее описанную выше зависимость, называется уравнением прогрессии. (В статистич. литературе оно называлось до сих пор и уровнем, и теоретич. уровнем, и ур-ием регрессии.)
Уравнение прогрессии. Как возникает и составляется ур-ие прогрессии, выясним на конкретных примерах.
Пример 1. Каждый рабочий какого-либо предприятия вырабатывает в течение месяца известное количество продукции. Месячная продукция каждого рабочего представляется варьирующим признаком. Абстрагируясь от учета аргументов, обусловливающих эту вариацию, получаем в качестве характеристики месячной продукции каждого участника совокупности рабочих данного предприятия средний месячный размер продукции. Обращаясь теперь от полной абстракции к учету времени (в часах), отработанного рабочим в течение месяца, получим, что прежняя постоянная средняя должна стать переменной, функционально связанной с указанным выше количеством времени. Т. к. связь между этими величинами есть связь пропорциональная, то она должна запечатлеться в форме линейной ф-ии. Обозначим через у продукцию отдельных рабочих, через у—среднюю постоянную, то есть без учета времени, через ух среднюю переменную, зависящую от аргумента х—количества часов работы; тогда у=а, где а—норма месячной выработки; ур-ие прогрессии:
~ух=кх,
где к—норма часовой выработки. Параметр к этой ф-ии представляет собой величину постоянную в той мере, поскольку она, характеризуя среднюю часовую выработку, является результатом абстрагирования от всех условий, ее определяющих, то есть и от типа оборудования, и от степени его изношенности, и от квалификации рабочего и т. д. И еще особо следует отметить, что влияние аргумента х будет учтено в чистом виде лишь при непременном условии независимости к от х. Нельзя конечно в данном случае считать такую независимость полной, однако можно определенно утверждать, что связь между к и х—весьма отдаленная по сравнению со связью между временем х и количеством продукции у. Величина ух при каждом фиксированном х отклоняется более или менее сильно от соответствующих ух, поскольку месячная выработка отдельных рабочих при одинаково затраченном времени х не становится еще одинаковой. Но отклонения ухот соответственных ухв среднем окажутся ниже, чем среднее отклонение общей средней у от индивидуальных у.
Пример 2 (из материалов, собранных в 1926 году Здориком в б. Нижегородских лесхозах). О связи между высотой дерева и его диаметром на уровне груди человека (1,3 м) для деревьев различной породы и различного качества— бонитета. Исследование велось на специально отобранных модельных деревьях. Имеются следующие сведения о высотах 634 деревьев“ели II бонитета. Вся эта совокупность деревьев распределилась по высоте следующим образом:
| Высота в м | Коттич. дерев. | Высота в м | KOFH4.
дерев. |
Высота в м | Колич. дерев. |
| 8 | 29 | 15 | 30 | 21 | 28 |
| 10 | 36 | 16 | 38 | 22 | 72 |
| 11 | 1 | 17 | 21 | 23 | 52 |
| 12 | 35 | 18 | 40 | 21 | 55 |
| 18 | 38 | 19 | 29 | 25 | 57 |
| 1 11 | 0 | 20 | 42 | 26 | 31 |
Средняя высота Я определилась как средняя арифметическая из ф-лы:
Я=-^=18,91
(в этой формуле s—количество деревьев каждой высотной группы и=634). Но высота дерева связана с его диаметром“. Рост дерева определяется в первую очередь количеством питательного вещества, проникающего от корней до самой верхушки. Т. к. количество протекающего вещества должен быть приблизительно пропор-
| 4 | 20т | Т | ||||||||||||||||||
| 4 | Г | 1б | 1 | 2 | 2 | |||||||||||||||
| <з1 | 18 | 2 | 1 | 2 | ||||||||||||||||
| 4у | & | 1 | 12 | |||||||||||||||||
| 16 | 39 | 3 | 14 | |||||||||||||||||
| ,ю | 18 | |||||||||||||||||||
| * | & | |||||||||||||||||||
| 24 | ||||||||||||||||||||
| 6 | & | |||||||||||||||||||
| у | 16 | |||||||||||||||||||
| 3? | г | |||||||||||||||||||
| «у | <24 | |||||||||||||||||||
| 7 | ||||||||||||||||||||
| 3 | ||||||||||||||||||||
| ь | 6l | |||||||||||||||||||
| А | ||||||||||||||||||||
| 25 | 11 | |||||||||||||||||||
| 29 |
8 12 16 20 24 28 32 36 40 44 48
Ступени толщины 8 см
Фигура 2.
ционально площади поперечного сечения дерева, то есть приблизительно пропорционально квадрату диаметра, то высота Я в конечном подсчете должна выразиться как квадратич. ф-ия от диам. D (одного из частных значений диаметра дерева, к-рое определяется на уровне груди человека). Таким образом получается следующее уравнение прогрессии:
Hj)=Мд -J- a1D -f- Q/2-D^·
Посмотрим теперь, что дает группировка материала не только по высоте Я, но и по диаметру D. На фигуре 2 дана зависимость между высотой дерева и его диаметром (ступенями толщины): кривая линия характеризует уравнение прогрессии. Данные диаграммы, весьма явственно указывающие на наличие достаточно тесной зависимости между и и Б, позволяют определить численные величины параметров а0, аги а2. Параметры эти исчислены были при помощи наиболее удобного в техническом отношении способа наименьших квадратов. В применении к нашему примеру способ наименьших квадратов приводит к следующей системе ур-ий:
α0Σ$ 4- a{ZsD 4- a^sD2=SsH; a0ZsD + a^sD2 + a2lsD3=Σε HD; a^sD2 + a{ZsD3 4- a2lsD4=2$ЯЯ2;
здесь s—численности группы, отвечающие каждой данной паре значений Я и Я; отсюда а0=2,158; аг= 0,9964; а2=-0,0105.
Таким образом ур-ие Нв=а0 4- oxD + a2D2 приобретает вид:
Нв=2,158 4- 0,9964D - 0,0105Я2.
Давая D ряд значений от 8 до 48, получаем соответственные значения Нв. Они приведены в нижеследующей таблице. В этой же таблице представлены в целях сопоставления средние значения Нв для каждой изолированной, ограниченной пределами каждого данного диаметра, группы деревьев:
| D | 11 п | D | нп | 1 | |
| 8 | 9,5 | 9,5 i
12,6 ; |
32 | 23,3 | 23,2 |
| ! 12 | 12,6 | 36- | 24,4 | 24,3 | |
| ! 16 | 15,4 | 15,6 1 | 40 | 25,2 | 25,5 ί |
| 20 | 17,8 | 17,7 ! | 44 | 25,6 | 25,3 I |
| 21 | 20,0 | 19,6 : | 48 | 25,8 | 25,3 * |
| 28 | 21,8 | 21,7 ! |
Коэфициент корреляции. Выше уже отмечалось, что зависимость между переменной средней и ее аргументами может проявляться с той или иной теснотой связи. Задача измерения тесноты связи разрешается при помощи определения коэф-та корреляции. Как он вычисляется, покажем на разобранном выше примере зависимости высоты Я дерева от его диам. D. Как было указано, вне учета размеров диам. D высота деревьев в среднем определилась в 18,91 метров Эта средняя отклонялась от реальных высот, варьирующих в пределах 9—26 метров Средний размер отклонений, будучи определен как средний квадрат отклонений νξ значений от общей средней Я, оказывается равным 26,00:
2 Σδ(Η-Η) 2
Is
= 26,00.
Примем далее в расчет связь Я и Я в форме определенного выше ур-ия прогрессии. Исчисленные Нв при каждом D отклоняются от соответственных Нв гораздо слабее, например при Я=12 имеем:
Яд =12,6; Яд=12 и 13
и отклонения оказываются равными 4-0,6 и — 0,4. Средний размер этих новых отклонений, оцененный точно так же^_как средний квадрат отклонений ν значений Яд от соответственных Яд, получается равным:
=0,43,
Коэф. корреляции г определяется при помощи выражения:
г^л/^±Л.
* Ра
Для нашего случая имеем: г=
26 υο-υ,43
26,00
0,992.
Чтобы ясней представить себе значение полученной цифры, определим коэф. корреляции для предельного случая, когда все значения Яд совпадают в точности со значениями Яд, то есть средний квадрат отклонений ν=0. В таком предельном случае коэф. корреляции оказался бы равным 1:
В другом предельном случае, когда учет аргумента Я никак не отражается на значениях Яд, то есть значения эти всюду совпадают с Я (общим средним), нет никакой разницы между vl и ν и коэф. корреляции
/Ψ
-0.
Т. о. г выражается всегда правильной дробью. Полученное выше значение г=0,992 свидетельствует о чрезвычайно тесной связи между высотой ели и ее диаметром, по крайней мере в пределах данного бонитета.
Разберем пример измерения связи из практики нефтяной пром-сти. Для определения ожидаемого годового дебита скважин учитывается зависимость между годовыми дебитами двух смежных годов. Ур-ие прогрессии дает возможность на основании данных текущего года перед вычислить дебит следующего года, а коэф. корреляции укажет размер возможных расхождений между предвычисленной цифрой и действительностью. При этих расчетах обычно исходят не из абсолютных размеров дебита, а из их логарифмов. И так делают по следующей причине. Дебит скважин падает, как это установлено проф. Лейбензоном, в среднем по закону геометрической прогрессии у=Акх, или по следующему выражению
lgy=lgA + xlgk.
Обычно пользуются вторым выражением в виду его большей вычислительной простоты. Обозначив логарифм дебита каждой скважины текущего года через г, а логарифм дебита следующего года через uVf получаем для ур-ия прогрессии следующую линейную форму:
Hv^CLt + ajV.
По данным IV пласта Раманинского района Бакинского месторождения имеются следующие сведения (смотрите таблицу на стр. 945—946). На основании этих данных получилось конкретное ур-ие прогрессии:
uv=0,3154 4- 0,7848г.
Коэфициент корреляции оказался равным 0,855, то есть он оказался достаточно высоким по своей величине.
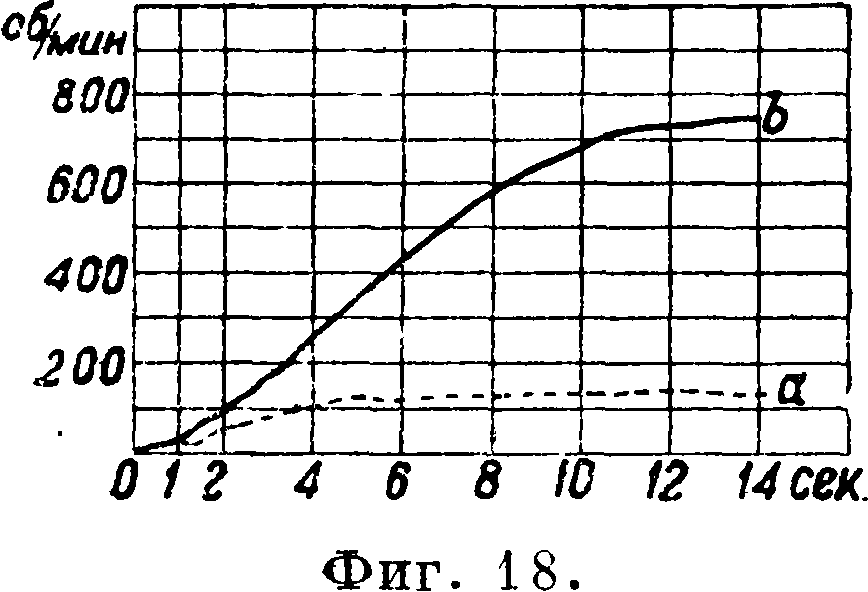
Наконец рассмотрим пример из практики исследования продолжительности горения
| *
/. £ |
0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 | 2,1 | 2,3 | 2,5 | 2,7 | 2,9 | 3,1 | 3,3 | Итого |
| 3,5 | 1 | 0 | 1 | 0 | 2 | 1 1 | 5 | |||||||
| 3,3 | о | 2 | 2 | 1 | 6 | 3 | 14 | |||||||
| зд | 1 | 1 | 1 | 12 | 10 | 6 | 37 | |||||||
| 2,9 | 3 | 2 | 4 | 10 | 13 | 15 | 1 | 48 | ||||||
| 2,7 | 3 | 2 | 14 | 18 | 39 | 13 | 2 | 91 | ||||||
| 2,5 | 2 | 2 | 6 | 22 | 54 | 28 | 2 | 116 | ||||||
| 2,3 | i | о | 5 | 15 | 64 | 54 | 5 | 1 | 145 | |||||
| 2,1 | 1 | 2 | 11 | 17 | 58 | 72 | 14 | 2 | 177 | |||||
| 1,9 | 1 | 5 | 14 | 36 | 51 | 13 | 4 | 124 | ||||||
| 1,7 | I | 0 | 6 | 27 | 27 | 14 | 2 | 77 | ||||||
| 1,5 | О | 5 | 12 | 36 | 10 | 3 | 66 | |||||||
| 1,3 | 3 | 5 | е | 7 | 1 | 1 | 23 | |||||||
| 1,1 < | 1 | 7 | о | 0 | 1 | 2 | 11 | |||||||
| Итого | 5 | 19 | 32 | 97 | 102 | 155 | 190 | 153 | 90 | 44 | 28 | 15 | 4 | 934 |
| _. | - | _ | _ | __ | __ | _____ |
электрич. ламп при разной нагрузке. Подвергается сравнению средняя продолжительность горения ламп различных серий, характеризуемых материалом нити. В пределах каждой серии лампы распределяют на две равночисленные группы: в первую группу относят лампы с сильной нагрузкой, а во вторую—со слабой. Затем для каждой пары групп определяют соответственную пару средних, которые в дальнейшем подвергаются сопоставлению в ряду различных серий, как это можно видеть из следующего конкретного примера:
| Серии | Средняя продолжительность горения | Серии 1 | Средняя продолжительность горения | ||
| Слабый нагрев | Сильный нагрев | Слабый 1 нагрев | | Сильный нагрев | ||
| t
1 |
1
3181 |
1907 | 12 | I
1963 |
1 722 |
| I 2 | 4784 | 1465 | 13 | 1101 | 483 |
| 1 3 | 2924 | 1638, | 14 | 2864 ! | 1 892 |
| 4 | 2004 | 878 | 15 | 1712 | 824- |
| 5 | 2293 | 1604 | 16 | 2415 | 1143 |
| 6 | 3799 | 866 | 17 | 2046 | 929 |
| , 7 | 2808 | 1501 | 18 | 2831 | 1431 ! |
| 8 | 1781 | 833 | 19 | 1996 | 1153 i |
| 9 | 2590 | 1307 | 20 | 2327 | 1150 |
| 10 | 2755 | 1274 | 21 | 2237 | -935 ! |
| 11 | 2300 | 912 | |||
Данные вышеприведенной таблицы представлены также на фигуре 3. Ставится задача: опреде
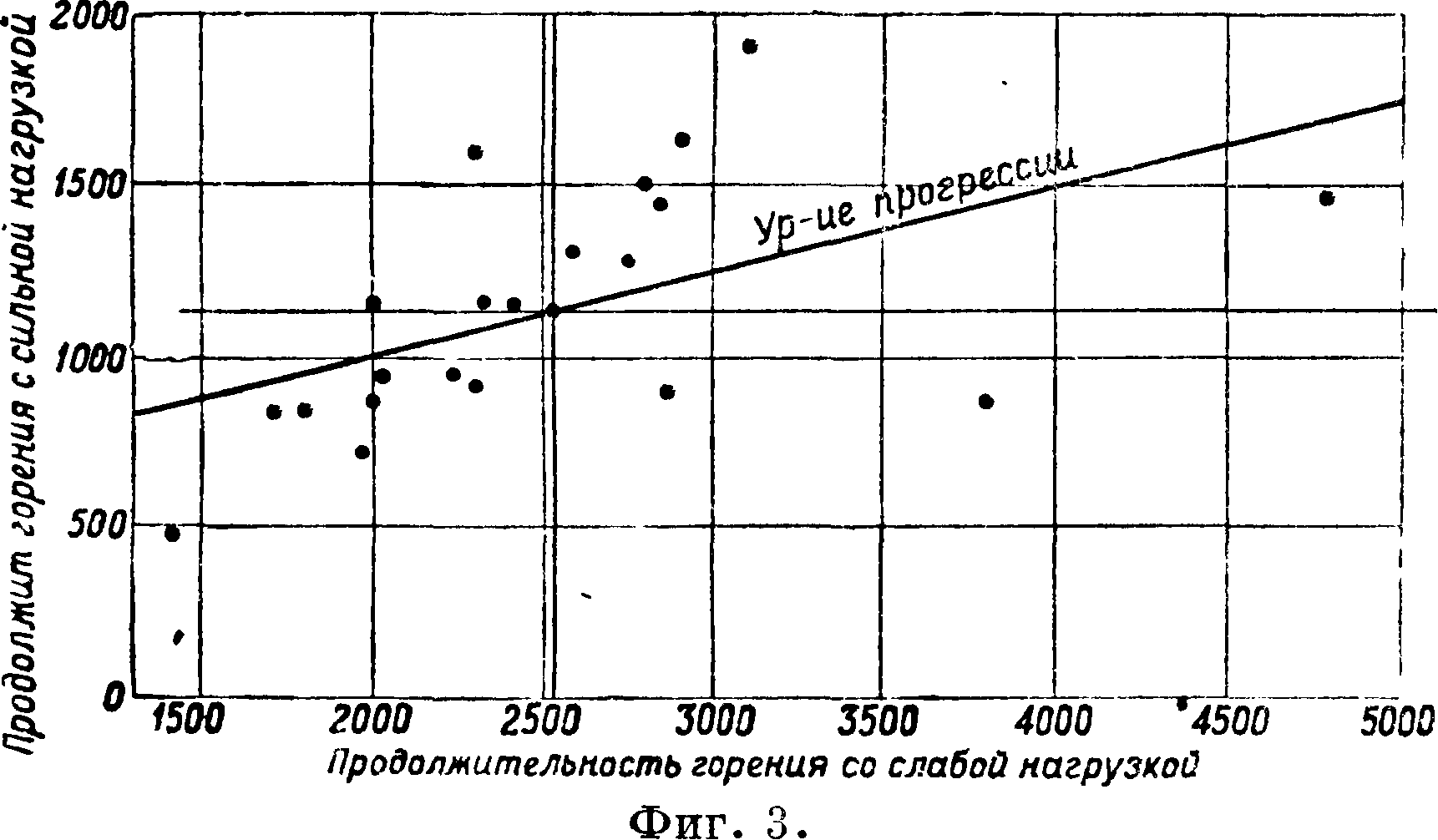
лить форму и тесноту связи между продолжительностями горения слабой и сильной нагрузок. Форма связи, то есть ур-ие прогрессии, мТ б. сочтена в порядке первого приближения линейной. Поэтому имеем:
Ух~ У=а(х-х),
где х—продолжительность горения сильной нагрузки; х—общая для всех серий средняя продолжительность горения сильной нагрузки; Ух—средняя продолжительность горения слабой нагрузки, поставленная в зависимость от продолжительности х горения сильной нагрузки; у—общая для всех серий средняя продолжительность горения слабой нагрузки. Коэ-фициент а определится по способу наименьших квадратов:
„ 2 (у-у) (х-х)
(i=—-·
Σ(Χ-Χ)Ζ
Средние х и у оказываются равными: х=2 524 и у= 1 136; α= 0,243. Т. о. искомое ур-ие прогрессий принимает вид:
ух- 1 136=0,243 (х - 2 524)
или ух=523 -f 0,243 х.
Мера тесноты связи между исследуемыми переменными, то есть коэф. корреляции, определится из ф-лы (вывода ее здесь не даем):
(У~У)2-(У~Ух)2 ^
Чу~у)·
Σ (У ~у) (Х — Х) Q 02Ί*
VΣ (у-у)2 ·Σ(χ-χ)2
Теснота связи, как видно, не особенно велика“ что и усматривается из фигура 3. Рассеяние отдельных измерений в данной диаграмме несравненно выше рассеяния, запечатленного в диаграмме фигура 2, где коэф. корреляции был равен 0,992.
Лит.: Статистика, учебник для вузов, составленный бригадой КоМакадемии под руководством В. И. Хотимского, М.—Л., 1932; Боярский А. и другие, Теори® математич. статистики, под ред. Б. С. Ястремского и В. И. Хотимского, 2 изд., М.—Л., 1931. Б. Ястрзмский.