> Техника, страница 84 > Съемка

Съемка

Съемка в геодезии, изображение участка местности на бумаге в виде плана. На план наносятся контуры, очертание и взаимное расположение различных предметов местности: дороги; населенные места, угодья, реки, озера и т. д и рельеф поверхности земли. Полевая работа при этом сводится к измерению линий и углов не только в горизонтальной, но и в вертикальной плоскости; камеральная обработка полученных материалов состоит в составлении (накладке) и вычерчивании плана. Некоторые виды съемочных работ дают возможность составления плана непосредственно в поле; в этом случае на долю камеральной обработки остается Вычерчивание и отделка плана. В соответствии с инструментами и методами работы С. подраз-. деляются на угломерные и углоначертательные, имеющие в свою очередь различные градации в зависимости от той точности, которая им ставится и ими достигается. Особо стоит С. тахеометрическая (смотрите Тахеометрия), как бы промежуточная между С. угломерной и углоначертательной, по своим методам весьма сходная с современными С., производимыми углоначертательными инструментами—мензулами (смотрите), но сопровождаемая измерением горизонтальных и вертикальных углов и линий. В последние годы в съемочных работах получила широкое применение фотография как наземная, так и воздушная, с самолетов. С. с применением фотографий составляет особый вид—фотосъемку (смотрите).

По своему назначению все виды С. могут носить специальный характер: лесные, землеустроительные, магнитные, геологические, гидрометрические, маркшейдерские, городские и прочие В каждой из этих С. выделяются элементы местности, относящиеся к данной специальности, и кроме того вводятся нек-рые технич. особенности в производство самих С., удовлетворяющие запросам данной специальности.

А. Угломерная С., как и всякая другая, требует создания на снимаемом участке опорного каркаса, то есть геодезич. основы, в виде отдельных точек или в виде ломаных линий. В первом случае геодезич. основу составляет тригонометрия. сеть (смотрите Триангуляция) или геометрия. сеть: точки сети располагаются так, чтобы образовалась сеть треугольников, близких к равносторонним; во втором—речь идет о поли-гонометрич. сети, проложенной между пунктами тригонометрия, сети (смотрите Полигонометрия).

1. Точные угломерные С. производят преимущественно в целях земле- или лесоустроительных. В этих случаях каждый участок,

подлежащий С., обходят по его границам, причем измеряют все внутренние углы и стороны, и таким путем получают основной сомкнутый полигон окружной межи. Кроме того прокладываются дополнительные диагональные ходы, примыкающие в начале и в конце к вершинам или сторонам этой межи; они необходимы как для С. внутренней ситуации (магистрали), так и для более точного определения положения всех точек снимаемого участка. Углы измеряются обычно одноминутным теодолитом (смотрите), одним или двумя приемами, при двух положениях трубы (вертикальный круг, или кремальера,—«право» и «лево» от трубы); применяют и менее совершенные инструменты, как астролябия, гониометр и пантометр. Стороны окружной межи и диагональных ходов измеряются стальною лентою; при наклонах к горизонту больше 3° исправляются введением поправки приведения к горизонту, вычисляемой по формуле поправки на единицу длины линии где I—длина измеренной линии, г—угол наклона ее к горизонту. Для поправок на наклон пользуются готовыми таблицами (смотрите табл. 1).

Таблица 1,—Поправки на наклон линий.

1 г	А1 1	г	А1 1	г	А1 Г	i	AI l
1°	0,0002	6°	0,0055	11°	0,0181	16°	0,0387
2°	6	7°	75	12°	219	17°	437
3°	14	8°	97	13°	256	18°	489
4°	24	9°	123	14°	297	19°	515
5°	0,0038	10°	0,0152	15°	0,0311	20°	0,0603

Все данные по измерениям сторон и углов записываются в геодезич. журнал. Одновременно с обходом окружной межи и проложе-нием диагональных ходов и магистралей производится С. внутренней ситуации, то есть производятся измерения, необходимые для нанесения на план очертаний и расположения угодий и других предметов местности. Для этого измеряют длины перпендикуляров от главнейших поворотов контуров на стороны полигонов. Эти промеры в зависимости от требуемой точности производят или рулеткой или шагами. Углы в 90° к линиям хода строятся или эккером (смотрите) или перпендикуляры намечаются глазомерно.

Все данные такой С. заносятся в абрис (фигура 1), к-рый ведется производителем работ в произвольном масштабе, с возможною тщательностью, в пдле карандашом и является дополнением к геодезич. журналу. Помимо описанного способа С. контуров перпендикулярами при угломерной С. можно также применить способ засечек (смотрите). Однако в виду кропотливости, дальнейших построений этот способ не является основным в угломерной С.; к нему прибегают лишь в отдельных случаях для определения

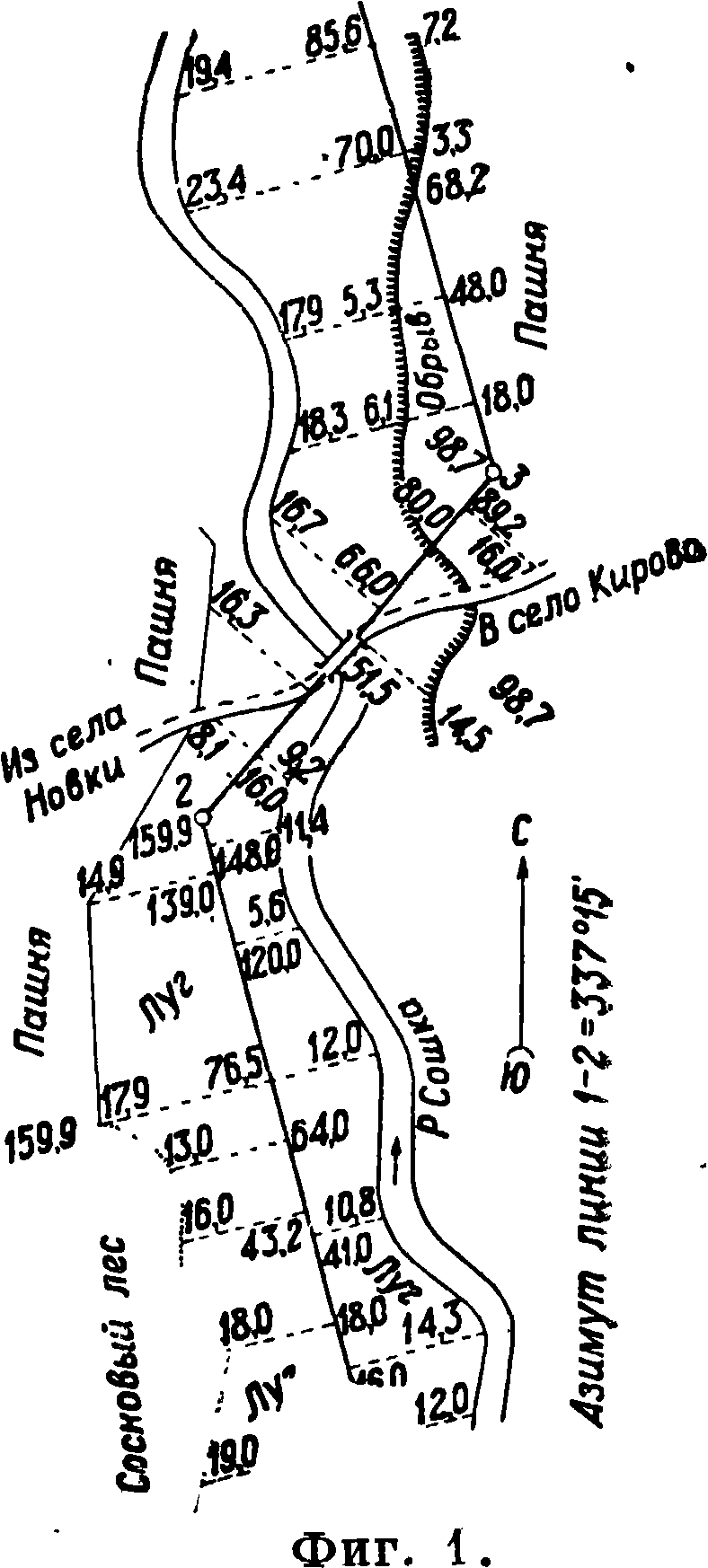
положения уединенных или недоступных точек и расстояний. То же можно сказать и о полярном способе, к-рый, наоборот, имеет исключительное применение в мензульной и тахеометрии. С. Измерение углов полигонов (многоугольников, диагональных ходов, магистралей) в случае наличия буссоли при инструменте сопровождается контролем их с помощью румбов (смотрите), которые записываются для каждой стороны полигона. Теодолитом измеряются углы, лежащие по одну сторону хода—правую или левую, почему величина их колеблется в пределах от О

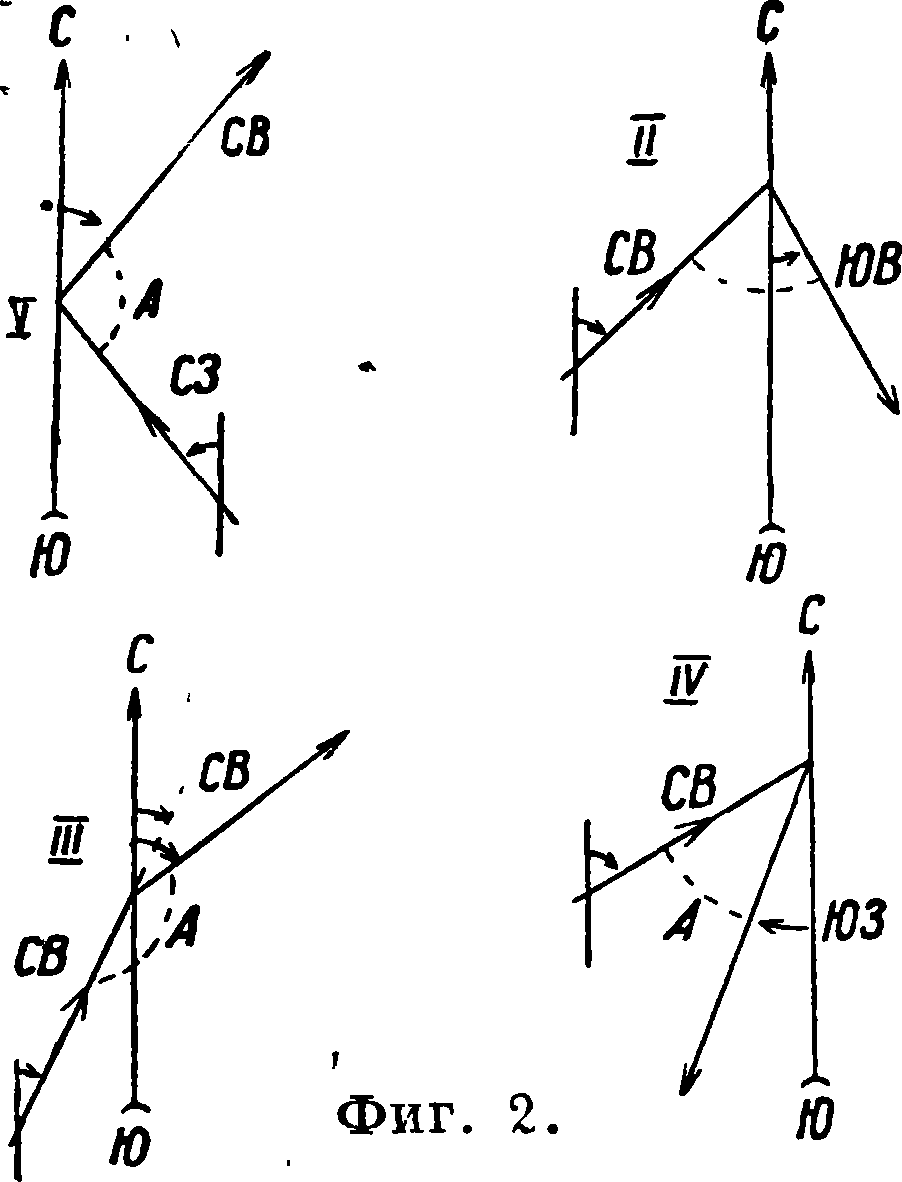
до 360°. Если ход сомкнутый, то такие углы называются внутренними. В отличие от них астроляби-ческими называются такие углы, которые всегда меньше 180°, а потому могут лежать по правую и по левую стороны хода; они легко получаются из измеренных углов полигона. Если в каждой точке поворота записаны румбы каждой последующей линии, то в сочетании с румбом предыдущей линии получаются четыре случая соотношений этих румбов с астролябия, углами, а отсюда и четыре правила проверки их (фигура 2): 1) если первые буквы названий румбов предыдущей и последующей линий хода одинаковы (например СЗ и СВ), то астролябия, угол равен 180° минус .сумма румбических; 2) если вторые буквы названий румбов одинаковы (например СВ и ЮВ), то астролябия, угол равен сумме румбических; 3) если все четыре буквы одинаковы (например СВ и СВ), то он равен 180° минус разность румбических; 4) когда все буквы разные (например СВ и ЮЗ), то астролябия, угол равен разности румбических. Необходимо однако напомнить, что румбы по буссоли отсчитываются с точностью до ¹U—7г градуса, в то время как угломерный инструмент дает точность измерения угла 1—5; т. о. контроль по румбам ограждает только от грубых просчетов. Во всяком случае измеряется азимут или румб первой линии хода для того, чтобы затем весь план ориентировать по магнитному меридиану. По данным геодезия, журнала и абриса строитсй план снятой местности. Работа начинается с подсчета и увязки суммы внутренних углов; затем вычисляют азимуты и румбы сторон окружной межи и накладывают окружную межу по азимутам или румбам, что можно выполнить построением их с помощью транспортира и отложением длин сторон полигонов (окружной межи) по масштабу; если получена допускаемая невязка, ее увязывают раскладкой пропорционально длинам» сторон. Накладку окружной межи можно произвести по вычисленным координатам вершин, при этом достигается большая точность построения и независимость положения каждой точки полигона от положения предыдущей точки. Сумма внутренних измеренных углов полигона сравнивается с суммой теоретической, равной 180°(w — 2), где п—число углов полигона. Допускаемая невязка в углах зависит от точности цзмерения углов и определяется πό формуле 1,5 · Vn; ее распределяют поровну на все углы с обратным знаком. Если в полиго

не имеются более короткие линии, то на образуемые ими углы поправки несколько увеличивают. После увязки сумма углов должен быть в точности равна“ теоретической. Далее, исходя из азимута первой стороны .полигона и пользуясь исправленными внутренними углами, вычисляют“ азимуты всех последующих сторон хода по ф-ле

^аг + 1 ^{== а}г "Ь 180 — А_г·,

если измерялись правые по ходу углы, или

^аг+1 “ ^аг + 180 + А^,

если измерялись левые по ходу углы, где а_г· и а_г+1—азимуты предыдущей и последующей сторон полигона, А_г—угол между ними. Если, при подсчете азимутов получается величина“, большая окружности, из суммы отбрасывается 360°. Азимут первой линии, вычисленный до последней, должен в точности получиться равным измеренному для этой стороны, что и послужит контролем правильности вычислений. Накладку плана транспортиром, треугольником и линейкою удобнее вести по румбам от меридиана, проведенного на плане в виде прямой от верхнего края плана к нижнему; север на плане всегда помещается вверху, юг—внизу. Если полигон растянут по долготе“ то проводят’ через некоторые промежутки несколько параллельных меридианов. Вычисляемые румбы строят по транспортиру на меридиане с таким расчетом, чтобы полученное направление каждой последующей стороны можно было перенести движением треугольника по линейке к соответствующей вершине в виде параллельной линии, где и проводят ее острым карандашом. Наложенный полигон-многоугольник обычно не сомкнется и в нем обнаружится невязка. Она является следствием как погрешностей измерений в поле, так и неизбежных погрешностей построения полигона на плане. Если, те и другие· носят лишь случайный, неизбежный характер, то невязка А А не будет более 1 : 200 длины периметра фигуры. При хороших чертежных. инструментах и достаточном опыте производителя работ не-. вязка уменьшится даже до 1 : 400 длины периметра. Грубые промахи отыскивают либо в углах, расположенных в стороне полигона, противоположной невязке (например в угле С фигура 3), либо в отложении сторон, параллельных невязке; если промахов не обнаружено, то“ просматривают и повторяют все вычисления в, журналах и наконец в случае необходимости повторяют нек-рые измерения в поле. Когда т. о. полигон будет построен и исправлен и невязка фигуры не будет превосходить 1 : 200 длины периметра, полигон увязывают Но способу параллельных линий. Через все вершины построенной фигуры проводят прямые, параллельные направлению невязки АА, и притом в сторону от A к А. На этих прямых откладывают отрезки, составляющие части невязки АА, пропорциональные расстояниям от начальной точки А до соответствующих вершин. Длина отрезков Ff, Ее, Dd, Сс, Вb получается из дополнительного построения в виде прямоугольного тр-ка АаА (фигура 3), в к-ром основанием AA служит периметр всей фигуры, взя-

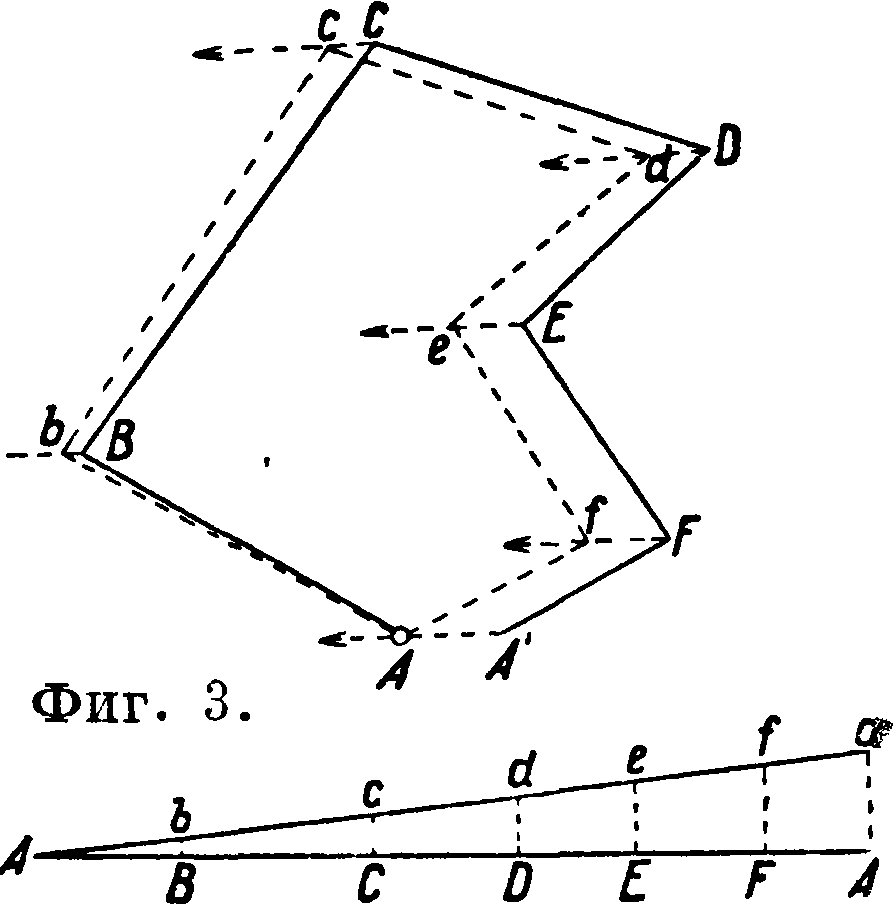
тый.в уменьшенном масштабе, а высотою Аа— величина невязки АА, но в масштабе самого плана. Длину этих отрезков можно конечно вычислить также из пропорций:

Ff=(AB + BC+ CD + DE + EF),

Ее=^£-(АВ + ВС + СВ + DE)

И,

Ш=ή(ΑΒ + ВС + CD) и т. д.,

где Р—периметр фигуры. На плане все отрезки по параллельным линиям откладываются в одну сторону, в направлении к начальной точке полигона, к-рый таким путем и замыкается, если затем все полученные точки (Ь, с d, е, /), начиная от начальной А и кончая ею, соединить прямыми. Если внутри основного полигона проложен, как было указано, диагональный ход, то угловая невязка (разница против теоретических сумм углов) смежных сомкнутых фигур распределяется преимущественно на углы основного полигона, если эти невязки имеют один знак; если знаки невязок различные, то выгоднее большую часть их разложить на углы диагонального хода; при увязке углов поправка более одной минуты в один угол не вводится. Составление плана после накладки и увязки окружной межи и диагональных ходов исполняется по абрису, откуда берутся все данные для построения контуров. Эта мешкотная работа повторяет на бумаге проделанные в поле измерения, причем расстояния по сторонам ходов откладываются по масштабу всегда от начальной вершины. Перпендикуляры, опущенные из точек контуров на стороны полигонов, строятся треугольником и линейкой; расстояния по ним откладываются циркулем и берутся с поперечного масштаба. В виду того что, во-первых, транспортир, применяемый для построения румбов, является весьма несовершенным прибором, во-вторых, потому что положение каждой последующей точки и линии полигона при построении его описанным способом зависит от предыдущей, погрешности в построении одной вершины полигона передаются другой—последующей; величина невязки фигуры т. о. получает зависимость от самого способа построения фигуры. Для избежания этого применяется способ построения вершин полигонов и диагональных ходов по их прямоугольным“ координатам. Этот способ дает возможность наносить вершины полигонов и ходов независимо одна от другой; применение транспортира при этом совершенно исключается. За начало коор-

X динат принимают одну из вершин поли

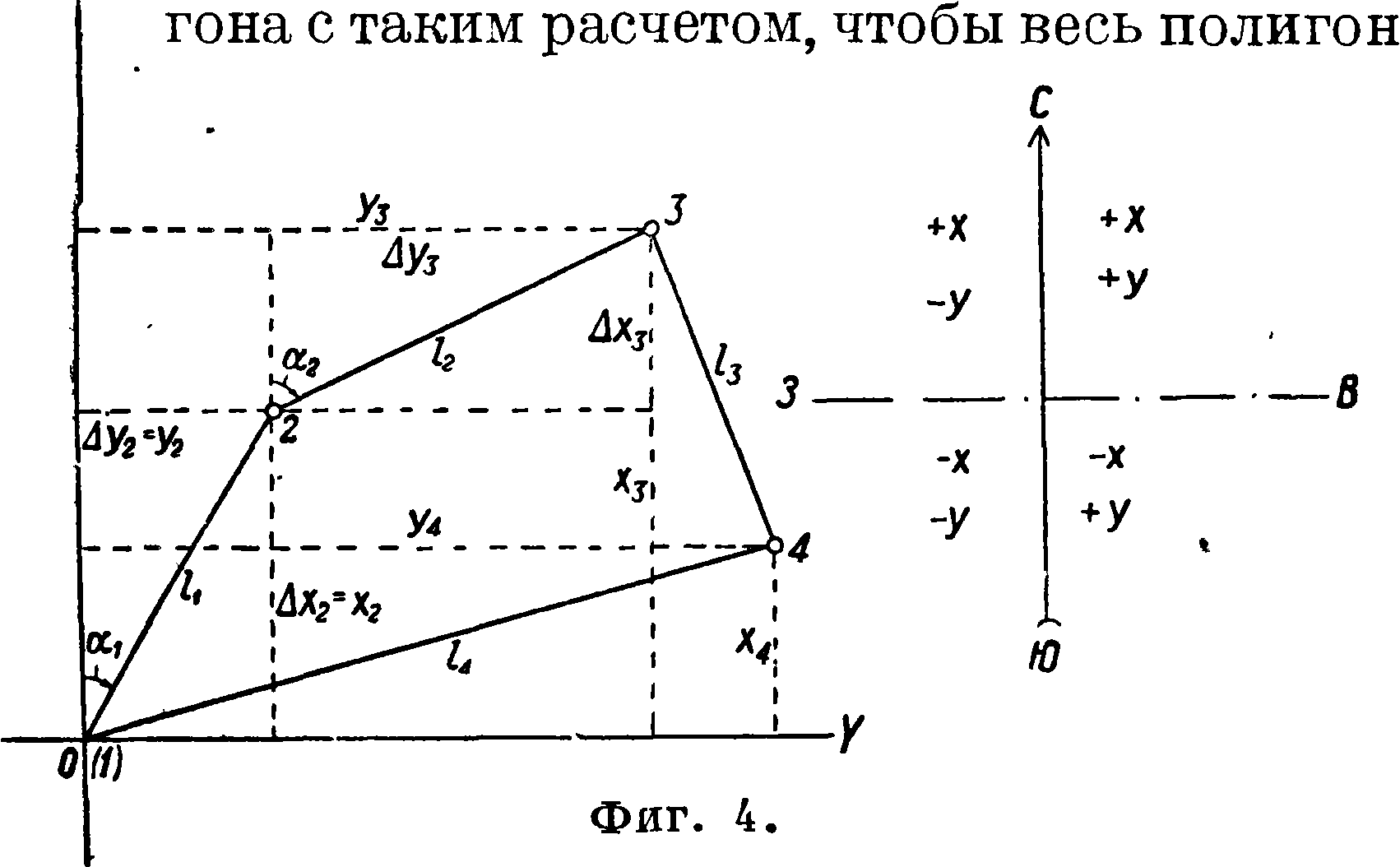
удобно разместился на бумаге. Ось Х-ов направляется по магнитному или истинному мери диану, если определено склонение магнитной стрелки. Ось Г-ов направляется по линии восток—запад. Знаки абсцисс и ординат показаны на чертеже (фигура 4), где первая точка полигона принята за начало координат. Точка, выбранная за начало координат, привязывается к пунктам тригонометрия, или полигонометрич. сети; это дает возможность получить координаты всех точек относительно того начала координат, к к-рому отнесены координаты точек тригонометрия. и полигонометрич. сети. Кроме этой точки для контроля привязываются и другие точки окружного полигона. Если длины сторон обозначить через 1_1з 1₂, £₃,. и азимуты их через а₁₉ ^а2> а₃,.и если 1-й точке дать координаты ж_х=0 и у 1=0, то приращения абсцисс и ординат выразятся следующими равенствами: Ах_г=0 Аух=0

Аж₂ ~ ’i cos α_χ Ay2=?i sin α_χ

Аж₃=2г^C°S ^α2 Ay₃=l₂sina₂

* Аж_и= l„_iCOSa_w_₁

Αχχ=l_n cos a_n__

ΣΑχ= 0

Сами координаты точек следующим образом:

a?i=0 ж₂=Аж₂

Х₃=Х₂ + Аж₃Х₃=Х₃ + ^ДЖ₄

Ьуп=Ϊ«-1 Sin

Aj/i=l_n 8Ш a_n _

SAj/= 0

полигона получатся

2/ι=0

У =^2/2 2/з=2/2 + Ау₃2/4=2/з + Ayi

Х_п — %п — 1 “Ь ^Х_п у_п Уп — 1 “Ь &Уп

%1 ~ %n "Ή Ажп+ i 2/l=2/га + ^Уп+1

Т. к. азимуты а₁₉ а₂,. м. б. более и менее 180°, то величины Аж₂, Аж₃, ., Аг/₂,Аг/₃,. получатся со знаками ( + ) или (—), что укажет на необходимость придачи или вычитания величин Ах_1зАж₂, ., Ау₁₉ Ау₂,. из координат ж и у предыдущей точки. Если полигон имеет вид сомкнутого многоугольника, то теоретически сумма приращений координат по каждой оси, то есть ΣΑχ и ΣAy должна равняться нулю, т.е. координаты точки (1) (фигура 4), вычисленные по приращениям всех точек полигона, должны получиться ж=0 и у=0. На самом же деле вследствие неизбежных ошибок измерений в поле вместо нулей, вычисленные координаты точки (1) получатся некоторой величины Аж и А у, которые являются координатами конца отрезка, изображающего невязку фигуры. Самая невязка вычисляется по ф-ле

/= V(Аж)² + (А^)²,

т. к. Аж и А у—катеты нек-рого прямоугольного тр-ка, у которого гипотенуза—невязка /. Величина невязки признается допустимой, если она не превзойдет 1 : 1 000 периметра L полигона. Если невязка оказалась допустимой, то подсчитываются поправки к приращениям координат, которые берутся пропорциональными длинам сторон по ф-лам:

бХо

Ах

Ау т

δχ₃=ψΐ₂

δ x_n=^l_n-

S ^AX Ί

6% i —

Σδχ=Αχ

δ Уп=Т¹п-

8Уг=%1„

Σδν=А у

Σδχ и Σδy подсчитываются как контроль правильности подсчета поправок.

После нахождения поправок δχ%, δχ_Ά, ., <5г/₂, <5г/₃,. к приращениям координат Аж и Δ? приращения исправляются и затем вычисляют уже самые координаты×и Υ для всех точек полигона. Т. о. невязка в периметре графически здесь не выявляется, и после описанных -вычислений полигон строится по найденным координатам; конечно он сомкнется без всякой невязки. Для вычисления координат полигона применяются пятизначные таблицы логарифмов; имеются готовые таблицы приращений координат, вычисленных для всех углов от 0 до 90° через минуту и для расстояний от 10 до 1 000 метров (таблицы Гаусса); могут быть составлены графики для грубого контроля вычислений ит. д. По вычисленным координатам сомкнутой фигуры вычисляется площадь ее по следующим двум ф-лам (для контроля)

Ρ=|Σ[Χ„(Υ_η.₁-Γ_η_₁)]

ИЛИ

Ρ=|Σ[Υ_η(Ζ_η__1Γ-Χ„₊₁)].

из которых первая читается так: площадь многоугольника равна полусумме произведений каждой абсциссы×на разность ординат последующей и предыдущей вершин мн-ка.

По окончании накладки полигонов, диагональных ходов и контуров план угломерной С. вычерчивается тушью и отделывается установленными условными знаками в тушй, что удобно для размножения к с плана с помощью фотографии, или план иллюминуется красками. План сопровождается соответствующими надписями и подписывается как документ производителем работ и инспектирующими лицами. Площадь угодий внутри всего полигона, очерченных контурами, вычисляется механич. путем—с помощью планиметра (смотрите); результаты суммируются и сравниваются с общей площадью построенной фигуры (полигона), вычисленной по координатам; разногласие не должно превышать 0,5% всей площади.

Для нанесения на план угломерной сьемчи рельефа местности можно поступить двояко: а) разбив план на квадраты по размеру мензульной доски, нанести горизонтали в поде, как это делается в мензульной инстру-менгадьной С., или б) произвести нивелирование (смотрите) поверхности участка и затем по полученным отметкам провестигоризонтали, произведя их сводку обязательно на местности.

2. Упрощенная угломерная С. производится буссолью (смотрите), но в настоящее время, при развитии мензульных С. различных градаций по точности, С. буссолью выполняются цесьма редко и лишь с целью дать подсобный материал рекогносцировочного характера к работам другого вида. При буссольной С. три-гонометрич. сети не требуется; опорная система создается замкнутыми ходами, примыкающими последовательно один к другому; в дополнение к ним выдающиеся и отовсюду хорошо опознаваемые точки местности (ориентировочные точки) определяются прямыми или обратными засечками, длд чего на них или с них берутся азимуты направлений на соответственно расположенные вершины ходов. Вместо углов поворотов измеряются буссолью азимуты сторон этих ходов и длина их—шагами. Очертания и расположения местных предметов и контуров относительно сторон полигонов намечаются глазомерно и заносятся в абрис. В абрисе ведутся глазомерные наброски рельефа местности с помощью основных линий рельефа и горизонталей. Геодезический журнал не ведется: всё данные съемки заносятся в подробный абрис, который затем и претворяется в план простейшими приемами, подобно уже описанным выше. Невязки ходов допускаются до 1 : 100 их периметра. План отделывается карандашом применительно к условным знакам, установленным для точных съемок.

Самостоятельное значение буссольные С. получают чаще всего в работах экспедиционного характера в малонаселенных "и необследованных странах, причем самая С. чаще всего выливается в форму маршрута, т. e. С. пути следования экспедиции и ближайшей к нему полосы местности с необходимыми ответвлениями в стороны. В этом случае следовательно работа лишается опорных ходов сомкнутого характера и потому требует для своего обоснования определений астрономических пунктов (смотрите Триангуляция) по пути маршрута. В противном случае маршруты остаются «навесу».

Б. Углоначертательная С., производимая уг-лоначертательными инструментами, отличается от углохмерной тем, что все данные полевых измерений обрабатываются тут же в поле и сейчас же наносятся на план, причем как правило снимаются не только контуры, но и рельеф поверхности земли, выражаемый обычно горизонталями и иногда затем вычерчиваемый штрихами. Эта съемка, называемая мензульной, имеет весьма широкое распространение в СССР. Геодезич. основой (обоснованием) служат: тригонометрич. и полигоно-метрич. сети или астрономич. пункты; охватывая обширные пространства, мензульная С. служит в СССР главным материалом для картографии страны. Масштаб государственной мензульной С. от 1 : 25 000 до 1 : 100 000; для целей землеустройства в населенных местах, а также для инженерных работ масштаб— 1 : 10 000, 1 : 5 000 и крупнее.

1. Мензульная инструментальная С. выполняется мензулою (смотрите) и кипрегелем-высотомером-дальномером (смотрите Кипрегель), причем для крупных масштабов, как 1 : 10 000 и 1 : 5 000, берут типы больших тяжелых инструментов, а для мелких, как 1 : 100 000, пригодны более легкие, т. н. жальте мензулы, очень компактно укладываемые вместе с кипрегелем в один нзбольшой ящик, где помещается и ориентир-буссоль (смотрите); планшет и штатив этих мензул упаковываются в особые кожаные или брезентовые чехлы, так что получается возможность весь комплект инструментов перевозить на вьюке. Опытные производители работ обычно пользуются одновременно тремя дальномер-ными рейками (смотрите), которые также изготовляются возможно более легкими. В мензульной С. широко практикуется определение положения точек прямыми и обратными засечками (смотрите). Определение точек прямою засечкою дает хорошие результаты при условии, если расстояние между данными точками равно или несколько больше или немного меньше расстояния до искомой точки. Если же она удалена или приближена настолько, что угол при засечке образуется слишком острым или тупым (меньше 40° илц больше 140°), то определение оказывается мало надежным. Условия надежной обратной мензульной засечки такие же, как и прямой. Практич. значение имеет также способ определения четвертой точки по трем данным, причем с мензулою становятся один раз только в искомую точку.

Этот способ известен в геодезии под названием з а-дачи Потенот а—французского академика (1660— 1732), к-рый дал простейшее ее геометрич. решение. Для определения четвертой точки по трем данным становятся с инструментом в искомую точку D (фигура 5) на местности и измеряют углы а и β, которые затем строят при точках а и b на бумаге; если полученную вспомогательную точку е соединить с третьей данной точкой С и провести затем окружность через точки а, Ь и е, то пересечение ее с прямою Се даст искомую точку d. Это вытекает из равенства углов: Zcda — /пbа и Zcdb—/_mab. Однако геометрическое решение задачи Потенота на мензуле с построением углов и проведением окружности не применяется. Геодезисты: Бонненбергер и Бессель, Грунерт, Леман и др. дали приемы, с помощью которых 4-я точка по трем данным определяется непосредственно на мензуле. Особенно просто это определение достигается способом Лемана.

В этом способе задача упрощается и сводится к простои обратной засечке, если только удастся правильно ориентировать мензулу, став в искомую точ-Ч_Г1 ку D на местности. Легко доказать,

что если

	A,h*
	^ /Il-J ~ - ,1
т ,Ί	/’ j
jiff (а11 ч	1 ·’ J 1

е

Фигура 5.

стороны подобных треугольников АВС и аbс (фигура 6) соответственно параллельны, то направления, проведенные через одноименные вер

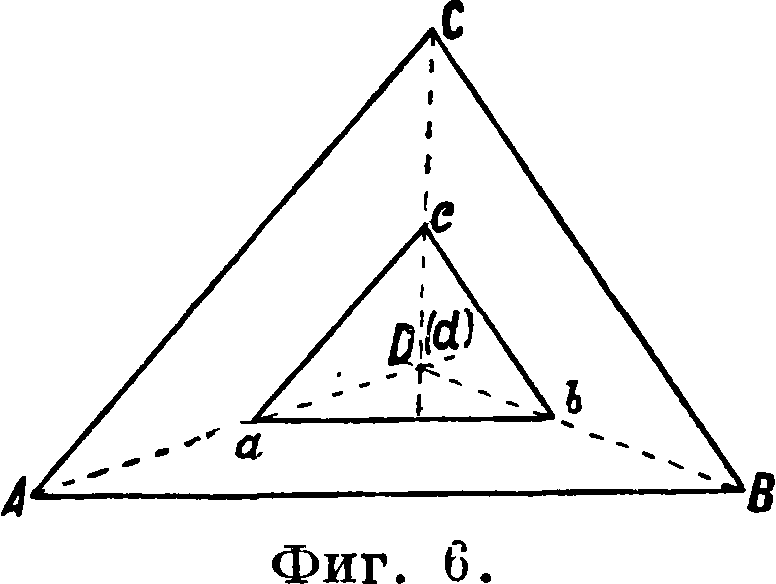
шины их, пересекутся в одной точке. Отсюда и вытекает простейшее решение задачи Потенота, к-рое на практике широко применяется: если на планшете уже имеются три определенные точки а, Ь, си требуется найти четвертую, то мензула устанавливается на этой искомой точке D местности и ориентируется по буссоли, то есть стороны на планшете устанавливаются параллельно соответствующим сторонам на местности. Затем через все три данные точки на планшете проводят направления (визируют) на соответствующие точки на местности. В пересечении этих трех обратных засечек и получается искомая точка. Однако неточность ориентирования по буссоли может обусловить неточное пересечение направлений, в результате чего получается т. н. тр-к погрешности (фигура 7); если он не велик, то окончательное положение

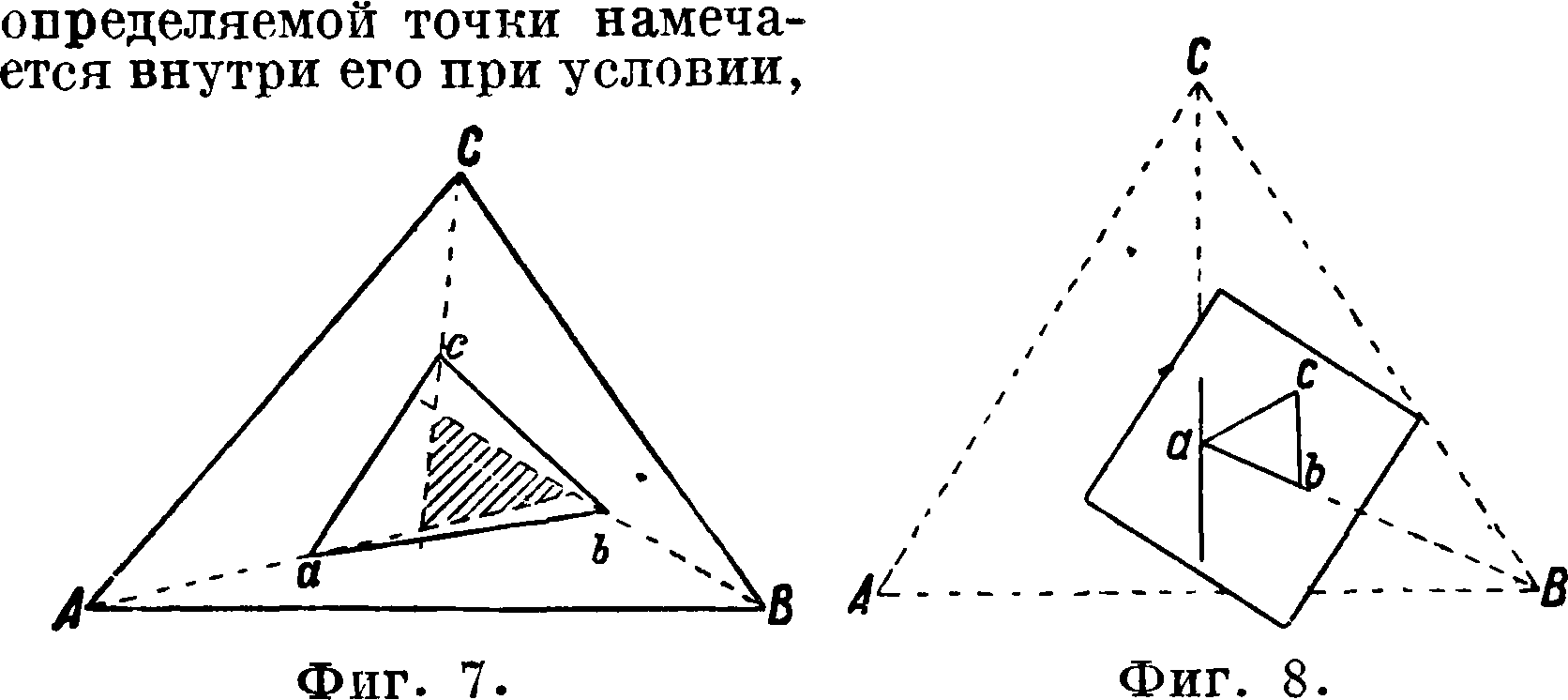
что сама определяемая точка на местности находится внутри тр-ка, образуемого тремя данными точками. Леман дал теорему по отысканию положения искомой точки относительно тр-ка погрешности; В. В. Витков-ский развил теорему Лемана теоретически. На практике в случае значительного тр-ка погрешности определяемая точка отыскивается просто несколькими попытками (последовательным приближением). В редких случаяхневозможности воспользоваться буссолью при мензульной С. в силу больших и резких изменений склонения магнитной стрелки в пределах данного участка можно применить для решения задачи Потенота способ Бонненбер-гера и Бесселя, к-рый дает возможность непосредственного определения искомой точки. Для этого мензулу

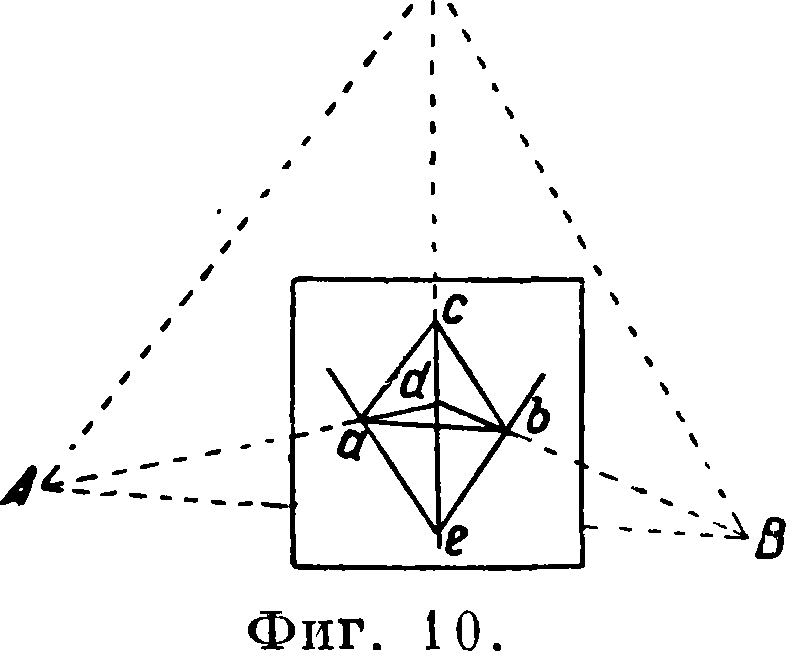
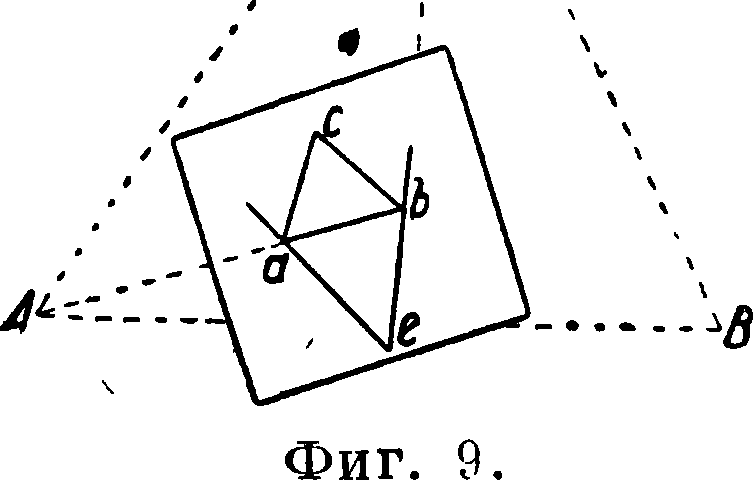
устанавливают на искомой точке на местности (фигура 8, 9, 10) и вращением мензульной доски, ориентируя ее по линии аb в направлении на точку В, через а визируют на С; затем вращением мензульной доски ориентируют по линии Ьч в направлении на точку А, через b Еизируют на С; т. о. прочерчивают дважды направления·на точку С; это значит, что при точках а и b строят графически и непосредственно, не измеряя их, углы а и β (фигура 5). Пересечение двух линий визирования на С дает вспомогательную точку е на мензуле. Мензулу поворотом доски окончательно ориентируют по линии ес в направлении на точку С местности, после чего искомая точка d определяется на планшете тремя обратными засечками через точки а, Ь, с; таким путем получается даже и контроль определения. Описанный метод называют еще способом определения четвертой точки по трем данным поворотам мензулы. Необходимо отметить, что точность определения искомой точки зависит от ее расположений относительно данных, т. к. соответственно этому расположению получается различная длина ориентировочной линии; между тем ориентирование тем точнее, чем эта линия длиннее. На основании этого практически д целесообразно осуществлять такое опреде- ~

ление только в случаях расположения искомой точки внутри тр-ка, образуемого. данными точками (фигура 11). Допу-.

скается становиться с мензулою в искомой точке вне тр-ка против одной из вершин его VI. Решение практически невозможно, если ис- ⁷ комая точка располагается вбли- зи или на самой окружности, про- | ходящей через три данные точки

IV; в этом случае вспомогатель- ная ориентировочная линия об- /i ращается“в точку и решение становится неопределенным. При работах по рекогносцировке старых карт или дополнению их различного рода специальными данными, например геологич.характера, нежелательно пестрить такую карту, наколотую на планшете, излишними карандашными линиями. В этом случае рекомендуется для решения задачи Потенота пользоваться калькой“ к-рую накладывают на планшет, установленный над искомою точкою местности. Затем через произвольную точку на кальке проводят три направления на данные точки А, В и С. Далее кальку сдвигают и подыскивают такое положение для нее, когда три прочерченных направления пройдут через три данные точки на планшете. Искомую точку накалывают сквозь кальку. Этот способ был предложен Болотовым; он применяется чаще всего моряками при промерах глубин: там углы а и β измеряются в море секстантом (смотрите), строятся затем протрактором (см Прокладочные инструменты), и искомая точка разыскивается на плане перемещением протрактора, пока три его линейки не пройдут через три данные точки на плане; искомая точка лежит в центре транспортира-протрактора. Применяется хорошо разработанный способ определения двух точек по двум данным без установки в них мензулы. Однако в этом случае приходится все же выбирать и становиться с мензулою на вспомогательную точку, почему этот способ мензульной С. не привился.

Фигура 11.

Работы по мензульной С. участка местности, помещающегося на одном планшете, проводятся следующим порядком. После объезда и общего беглого осмотра участка на всей открытой площади его разбивается геометрии, сеть в виде системы тр-ков, одна из сторон которых (базис) предназначается для непосредственного измерения. Размеры сторон тр-ка при крупных масштабах составляют не более 0,5 а в масштабе 1 : 25 000 и мельче доходят до 1—3 км. В таких же пределах меняется и длина базиса. Имея в виду площади планшетов в масштабах 1 : 10 000 до 18 км², 1 : 25 000 до 100 км² и 1 : 50 000 до 300 км², число точек геометрии, сети на одном планшете доводят до 30—90, отмечая их на местности вехами из жердей с пучками соломы вверху. В число точек геометрии. сети включают имеющиеся на местности обозначенные сигналами или знаками точки тригонометрии, и полигонометрич. сети, а также астрономические пункты. Базис измеряется стальною лентою в прямом и обратном направлениях; длина базиса поверяется дальномером во избежание пропуска ленты или другой грубой ошибки. Определение точек геометрии, сети начинается с нанесения на планшет линии базиса. Для этого мензула устанавливается над одним из концов его, ориентируется по буссоли, после чего по скошенному краю линейки кипрегеля, наведенного на корень вехи другого конца базиса, прочерчивается его направление; длина базиса тщательно -берется по масштабу и откладывается на прочерченном направлении; место базиса на планшете избирается с таким расчетом, чтобы весь участок разместился на планшете. Если подготовлена тригонометрии. сеть, то базисом мензульной С. могут служить стороны ее тр-ков, поместившихся в рамках данного планшета, или стороны полигономе-трич. сети. Пункты триангуляции наносятся на мензульный планшет по их координатам. В этом случае планшет, ориентированный по пунктам триангуляции, тем самым ориенти-. руется и по истинному меридиану. Далее прямыми засечками определяется положение на планшете всех точек геометрич. сети последовательно, начиная от близлежащих к базису или к пунктам триангуляции и кончая находящимися около рамок планшета. Точка считается определенною лишь в том случае, если она получена пересечением трех направлений с вех, ранее засеченных, при этом два соседних направления не должны составлять угла менее 30° или более 150°; только для точек сети, находящихся на отлете, допускаются пересечения двух направлений, но под углом не менее 40°, причем в этом случае обязательна поверка определения обратною засечкою хотя и по тем же направлениям. Определение точек геометрич. сети производится поверенным кипрегелем при каком-либо одном положении вертикального круга, например «лево». Благодаря этому исключается влияние остаточных погрешностей инструмента: коллимационной ошибки трубы и наклонности ее оси вращения.

Мензульная доска (планшет) подготовляется: на нее натягивается коленкор, прибиваемый гвоздиками к боковым ребрам доски; на коленкор наклеивается лучший сорт ватманской бумаги. Когда она хорошо просохнет, се покрывают чехлом из александрийской бумаги, приклеиваемой только к ребрам мензульной доски; эта бумага служит для прочерчивания на ней направлений геометрич. сети, чтобы не чертить на ватманской бумаге. По окончании разбивки сети направления вычерчиваются тушью; точки сети накалываются сквозь покрышку иглою на ватманскую бумагу, на которой собственно наносится и вычерчивается все снятое с местности: гидрография, контуры, отдельные местные предметы, рельеф; покрышка для этого подрезается снимается постепенно по мере движения работы. Благодаря этому остающаяся часть верхней александрийской бумаги вследствие своей толщины предохраняет ватман от непосредственного трения по нему нижней плоскости линейки кипрегеля и позволяет сохранить планшет чистым; для той же цели по мере движения работы снятые пространства вновь заклеиваются кусочками бумаги в виде заплаток к надрезанной покрышке. Для уменьшения деформации плана ватманскую бумагу вместо коленкора иногда наклеивают на алюминиевые листы 1—2 миллиметров толщиною или на фанеру— переклейку.

Одновременно с засечками точек геометрич. сети определяют их высоты, приняй какой-либо

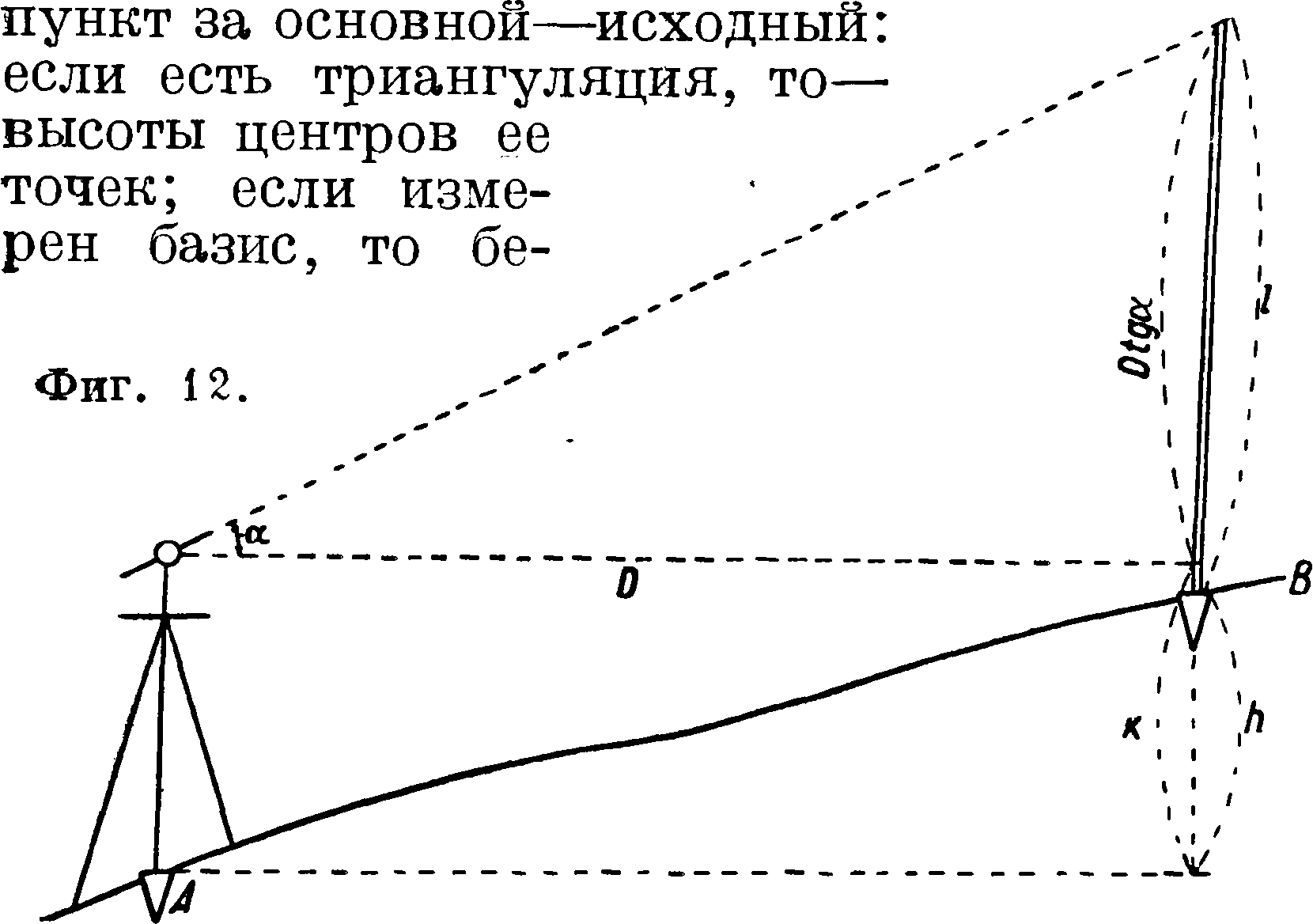
рут высоту одного из концов его, определенную геометрической нивелировкой от ближайшей марки или репера (смотрите). Иногда выводят высоту исходной точки над уровнем океана из наблюдений анероида или наконец берут условную отметку. Высоты остальных точек геометрич. сети получаются затем последовательно, начиная от исходной, для чего опре деляются разности высот h (превышение) между двумя соседними точками по ф-ле

fo=Z>tga + fc-? + 0,16|s

расстояние D (фигура 12) получается засечками и берется с планшета по масштабу, к—высота инструмента—измеряется непосредственно рейкою, I—длина вехи на той точке, высота которой определяется; она измеряется также рейкой или рулеткой; 0,16 --небольшая поправка на кривизну земли и рефракцию—берется из особой таблицы при расстояниях, больших 350—800 метров в зависимости от требуемой точности работы; a—вертикальный угол—получается непосредственно измерением по вертикальному кругу кипрегеля при двух его положениях— «круг право» и «круг лево»—и вычисляется по формулам:

при круге право. a=Л — М₀при круге лево .α= М₀ — Л

откуда где П—отсчет по вертикальному кругу при положении его справа от наблюдателя и Л—такой же отсчет при круге слева; М₀—место нуля кипрегеля, то есть тот отсчет по вертикальному ^КРУ^ГУ» к-рый соответствует горизонтальному положению оптич. оси трубы кипрегеля при том условии, что пузырек уровня, прикрепленного к алидаде, находится на середине. Самый прием измерения вертикального угла выполняется наблюдателем сл. обр.: при круге «право» горизонтальная нить сетки наводится на верхний конец вехи I; одновременно с этим приученный к тому рабочий подводит пузырек уровня на середину; записывается отсчет Л по кругу; далее те же действия при круге «лево». Помимо того для исключения влияния всякого рода погрешностей систематич. характера, напр: влияния рефракции, а также для контроля определение разности высот h повторяется, для чего те же измерения производят в обратную сторону, перейдя на определяемую точку и визируя на исходную. Т. о. получают все данные для определения той же разности высот h, но с обратным знаком. За окончательный результат берут среднее из двух абсолютных значений h туда и обратно. Самое вычисление члена D tg a производится различными способами в зависимости от привычки производителя работ: по специальным полевым четырехзначным таблицам логарифмов, отпечатанным на шести страничках и наклеенным на картон; по таблицам высот Савицкого, в которых помещены готовые вычисленные разности высот ддя расстояний до 900 метров и для углов до 6° через каждую минуту; такие же таблицы для гористых местностей вычислены другими авторами для углов до 30° (Серебренникова) и до 45° (Кипияни) с помощью ло-гарифмич. линеек.

Вычисления даны по следующей схеме:

П=2°	Я -	lg D =2,9125	hnp.	= + 28,66
Л=357	461 “. 45	+ lg tg a=8,5878	ho6p.	= - 28,52
	44]
М о=359	- 58	lg h=1,5303	hop.	= ± 28,59
CL +2°	13	h =,+ 33,88
D=875,6	м	k=+ 1,28	HucXf	= 191,50
k=1,28		l=- 6,50
1=6,50		h=+ 28,66	Ннабл.	= 223,09

взято из таких же вычислений обратного измерения вертикального угла; Н_исх:—высота (отметка) исходной точки геометрической сети; Н_набл.—высота наблюдаемой.точки. Разница «между прямым и обратным h не должна превышать 0,04 метров на 100 метров горизонтального расстояния, в общей же сложности не более 1 метров на 3 км. Таким путем определяются окончательные средние разности высот между соседними точками геометрич. сети, но не между всеми, а по схеме, составленной заблаговременно при расстановке вех геометрич. сети. Эта схема определений разностей высот должен быть соображена так, чтобы получились замкнутые ходы определений или, как говорят, полигоны, для того, чтобы достигнуть контроля в работе вычислением повторной отметки исходной точки. Невязка в сумме разностей высот в каждом отдельном полигоне не должна превышать 0,3— 0,5 метров при полигонах, следующих один за другим и примыкающих один к другому. Увязка высот в каждом полигоне производится по следующей простой схеме:

Увязан-

Высоты Поправки ные вы

			СОТЫ
Исходная веха№ 1= Разность высот	194,5 метров + 2,4 М	0,00	194,50
№ 6=	196,9 метров — 6,5 м	+0,05	196,95,
№ 13=	190,4 метров + 9,6 м	+0,11	190,51
№ 9 =	200,0 метров - 11,4 М	+0,16	200,16
№ 7 =	18о,6 метров - 1,6 м	+0,22	183,82
№ 5=	187,0 метров + 2,1 м	+ 0,28	187,28
№ 10=	189,1 метров + 5,0 м	+ 0,34	189,44
Исходная веха № 1=№ 1=	194,1 метров 194,5 м	+0,40	194,50
Невязка	0,4 м
Следующие полигоны примыкают к			первому

и подсчитываются точно так же от одной увязанной высоты к другой и т. д. При желании получить наилучшим образом согласованные высоты точек в местах стыков различных полигонов рекомендуется применить уравнивание высот методом узловых точек (смотрите Полигопо-метрия); однако в широкой практике производится обычно простейшая описанная увязка на планшете. Таким путем после увязки высот получаются окончательные высоты всех то“Гек геометрич. сети и составляется список их, называемый каталогом. Если основою сети служит триангуляция и следовательно на каждой вехе мензула имеет точную ориентировку по истинному меридиану, то этим случаем пользуются и на каждой вехе записывают склонение магнитной стрелки, устанавливая для этого ориентир-буссоль. Описанный способ разбивки геометрич. сети возможен лишь на открытых участках снимаемого планшета. В местах, покрытых- лесом или густым кустарником, и в случаях лесистой местности распространение геометрич. сети засечками становится невозможным, почему прибегают к проложению мензульных инструментальных ходов. Они начинаются от какого-либо пункта триангуляции или точки геометрич. сети и примыкают неподобной же точке. Работа выполняется так же, как в ходах угломерной С., но мензула ориентируется или по прочерченному направлению на заднюю веху или по буссоли, если нет магнитных аномалий; углы не измеряются, а про черчиваются непосредственно. Длина линий хода определяется дальномером кипрегеля; разности высот между соседними вершинами хода измеряются туда и обратно. Проложенный ход (в плане) увязывается способом параллельных линий, причем невязка в плане не должна превышать. 1 :150 периметра хода. Невязка по высоте не допускается более высоты сечения, принятого для выражения рельефа горизонталями. Чтобы избежать излишних вычислений по определению разностей высот, прибегают к некоторые упрощениям в измерении вертикальных углов, а именно: наводят горизонтальную среднюю нить сетки трубы на метку на рейке, высота которой над землей равна тут же измеренной высоте инструмента; другими словами, I делают равным к, и формула для вычислений h упрощается: h=D tg а. Кроме того, убедившись при работе на точках геометрич. сети в устойчивости М₀, измеряют углы при одном положении круга, например «право», тогда угол вычисляют по формуле α= Л— М₀.

Если С. не ограничивается одним планшетом, а район работ охватывается несколькими“ планшетами, то для общей связи в плане и- по высоте засекаются и определяются также и за рамками планшетов общие с соседними производителями работ точки геометрической сети и инструментальных ходов.

После составления геометрич. сети и всех вычислений начинают С. подробностей одновременно как контуров, так и рельефа. Местом для начала работ м. б. избрана любая из определенных вех, которая вынимается, и мензула устанавливается над отверстием в земле;планшет нивелируется (приводится в горизонтальное положение) по уровню на линейке кипрегеля; затем мензула ориентируется по одному из прочерченных направлений. Для С. контуров применяется т. н. «полярный способ»: рейка ставится на изгибах и поворотах очертаний ближайших угодий и местных предметов; труба наводится на рейку, отсчитывается расстояние до нее по дальномеру, к-рое сейчас же откладывается циркулем по масштабу вдоль скошенного края линейки. Полученные наколы цирку-^ ля затем соединяются ломаной линией (карандашом), глядя на местность, и т. о. получается на планшете фигура, подоб- ная натуральному контуру на мест- ности (фигура 13). Для тех же целей при- ^<^^иг* ¹³; меняется и способ засечек, однако только для одиночных предметов или С. недоступных островков, небольших групп леса, кустарника на болоте и тому подобное. При С. контуров производитель работ определяет высоты нек-рых реечных точек, а затем рейки ставятся последовательно вокруг каждой точки стояния на всех главнейших вершинах и их подошвах, на седловинах и других перегибах и характерных линиях рельефа местности, необходимых для нанесения рельефа. Высоты этих точек определяются измерением вертикального ytvia при одном положении круга кипрегеля, приняв во внимание уже известное М₀—место нуля кипрегеля; расстояния при этом отсчитываются по дальномеру, откладываются по масштабу, и точка сейчас же накалывается циркулем. Разность высот получается графически по чертежу, назы-

ваемому масштабом высот (фигура 14). Для этого построения берут клетчатую бумагу, намечают слева внизу начало координат и откладывают по оси Y расстояния; параллельно оси X, направо строят тангенсы углов через каждые 5—10, полученные точки соединяют прямыми

4° 30 3°5040Ш0· Ю 2° s 50 5 тонн s 230? s 2 го‘8 в 4 ί

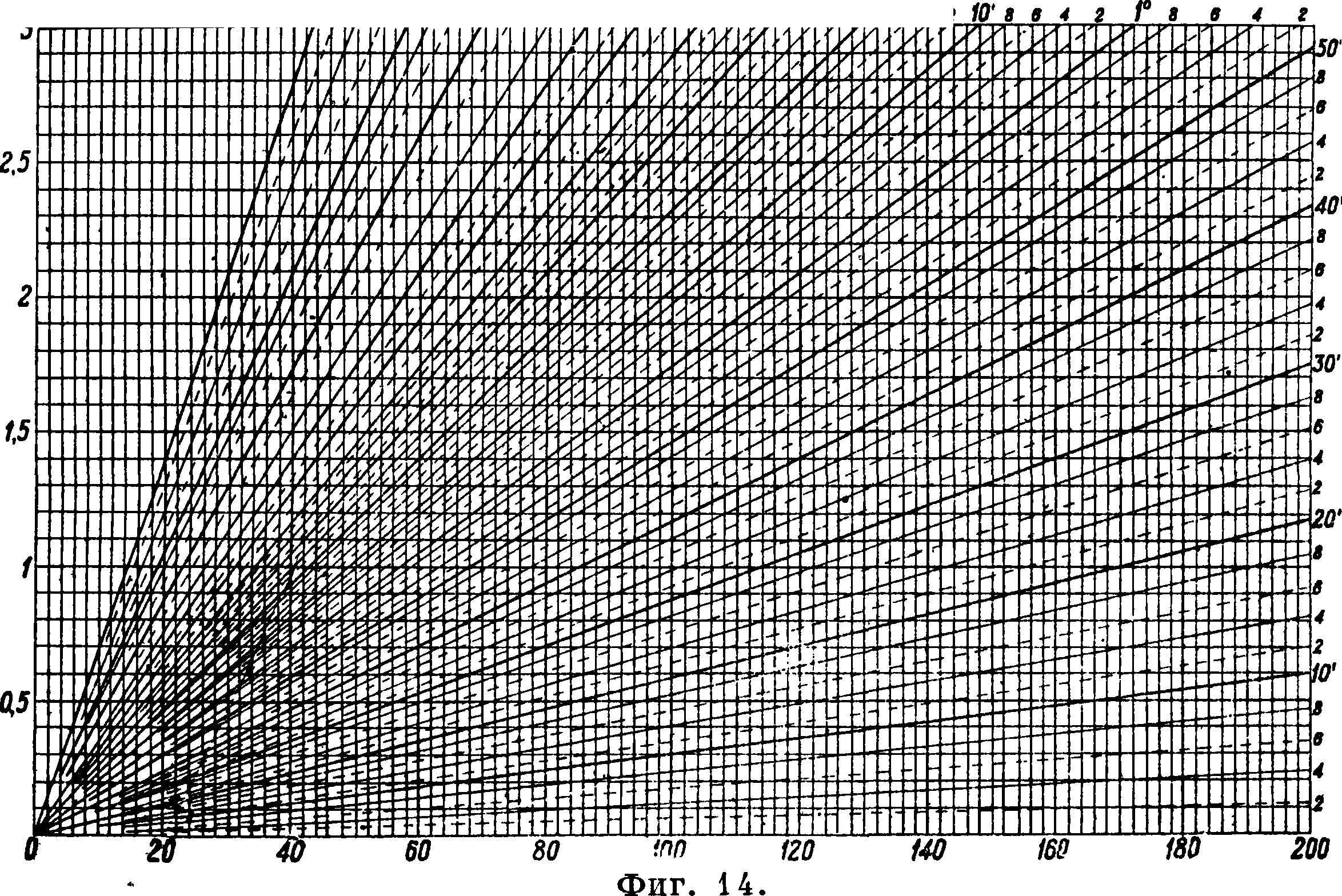
с началом координат. Т. о., имея расстояние и угол, находят пересечение соответствующего наклонного луча с вертикальной линией и на оси×отсчитывают разность высот h. Она суммируется (в уме) с соответствующим знаком с высотою Н точки стояния; и полученная высота реечной точки надписывается карандашом на плане около накола. Если рельеф крупный, с ясными очертаниями хребтов, лощин и оврагов, то сначала намечаются легкими пунктирными линиями водоразделы и тальвеги. Таким путем получается общий «скелет» рельефа, пользуясь которым и надписанными высотами затем проводят горизонтали. Высота сечения сообразуется с масштабом и видом рельефа и обычно указывается в инструкции по С. Горизонтали, выражающие рельеф, в окончательном виде наносятся на планшете мензулы в поле с натуры, чтобы получить вполне правильное живое и наглядное изображение рельефа. Проведение горизонталей по отметкам дома ведет к пропускам и искажениям форм рельефа.

После зарисовки контуров и рельефа вокруг данной точки стояния выбирают новую, т. н. переходную точку, куда посылается вперед рейка. Эта точка определяется так же, как и реечная, но по приходе туда и установке на ней мензулы расстояние до предыдущей точки и разность высот поверяются обратным визированием трубы при одном положении круга. Переходные точки можно определять также по задаче Потенота, ориентируя мензулу, устана-

ближайшей вехи при двух положениях круга или с двух вех при одном положении круга; расстояние берут по масштабу. Высоты переходных точек записывают в журнал, т. к. они впоследствии могут понадобиться для привязок от соседних точек. Далее работа продолжается описанным порядком, причем как общее правило С. ведут без пропусков и перерывов, наращивая чертеж чешуйками одна к другой. Вопрос о расстояниях До реечных точек и расстояниях между переходными точками разрешается видом рельефа: наносить горизонтали можно только до“ первого «хребтика», так как за ним получается «мертвое» пространство, невидимое от мензулы; следовательно ближайшая переходная точка перебрасывается именно на этот хреб-тик (фигура 15). Опыт показал, что расстояния между переходными точками в зависимости от рельефа, а также и масштаба плана колеблются от 100 до“ 500 метров Во всяком случае их нужно выбирать с таким расчетом, чтобы все снимаемое пространство было видно, и не следует скупиться на их сгущение,т.к. благодаря этому заметно сокращается число реечных точек, а работа идет быстрее и выигрывает в полноте и точности. Через две-три переходные· точки, подходят к какой-либо точке геометрич. сети и для контроля привяз&ваются к ней как в плане, так и по высоте. При С. закрытых пространств (лес, очень большие селения) прокладывают инструментальные ходы по всем дорогам „

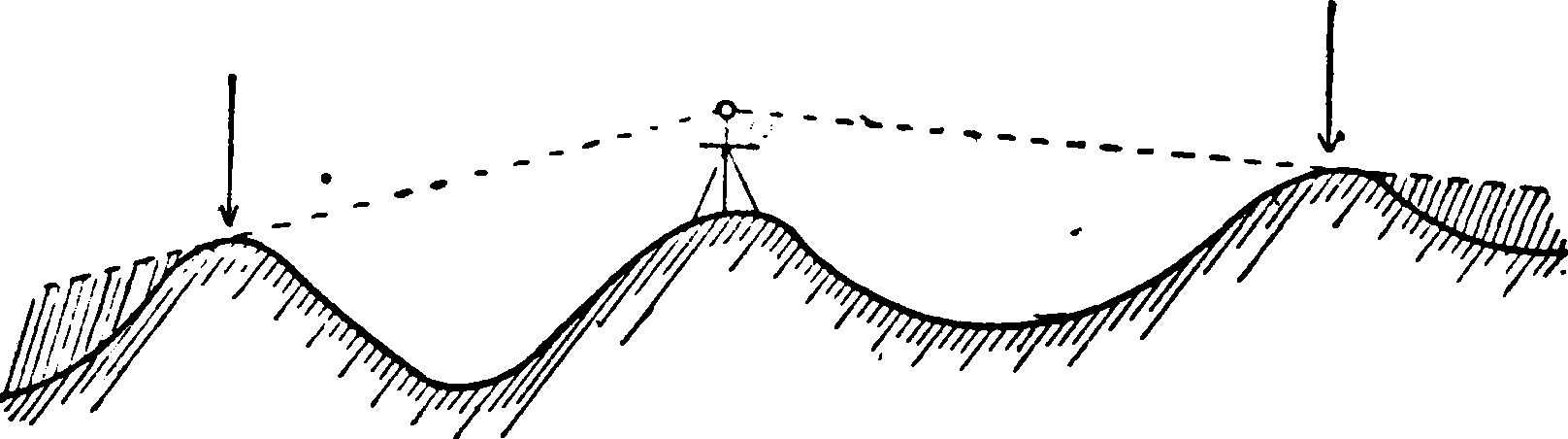
Фигура 15.

вливаемую в искомой точке, по буссоли, и засекая ее затем обратными засечками с окружающих вех (способ Лемана). В этом случае высота определяемой точки получается из измерения вертикального угла обратным визированием с

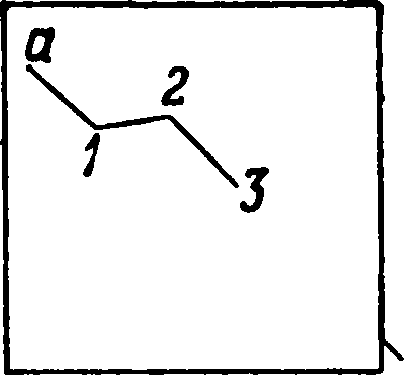
Фигура 16.

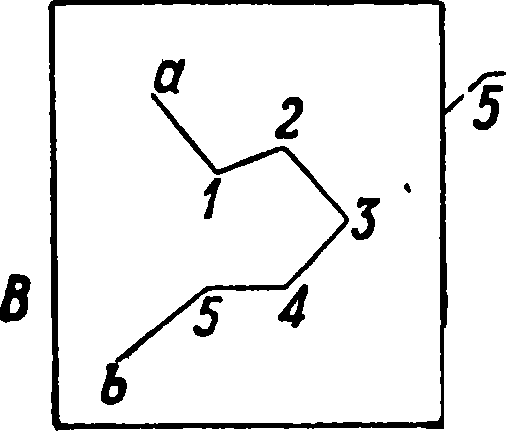
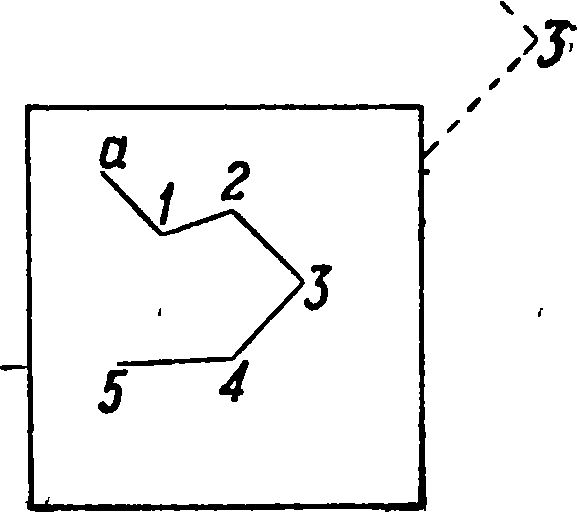
просекам и прочие, применяв. способ «хода с буссолью“ через точку»(фигура 16):мензула в этом случае устанавливается не на каждой точке хода, а через одну. Т. о. положение точки стояния получается как бы обратною засечкою (визирование назад), а положение рейки, высланной вперед, визированием вперед. В том и другом случае расстояния определяются дальномером и сейчас же“ откладываются на плане“ циркулем по масштабу; углы наклонения измеряются назад и вперед, берутся превышения па-масштабу высот и вычисляются высоты точек хода. Схема вычисления и увязка такая же, какая была приведена для полигона геометрич». сети. Эти ходы привязываютсяна опушках леса·к точкам геометрич. сети, а внутри к основным инструментальным ходам. При встреча с водными пространствами (реки, озера) контур их снимается обычным порядком по урезу воды. Высота поверхности воды определяется по рекам через 1—2 км, по озерам в двух-трех местах для поверки; за окончательную берется средняя, которая и выписывается на озере. Обрывы„ террасы и крупные овраги, где это только возможно, изображаются горизонталями. Если же скаты настолько круты, что всех горизонталей поместить нельзя, таковые проводятся через одну, а затем при вычерчивании зимою подобные обрывы обозначаются штрихами. Т. о. вся вырисовка местности на мензульном планшете горизонталями происходит в поле, в чем и заключается преимущество этого способа работы перед С. угломерными инструментами, когда в поле получается только материал для составления плана, к-рый затем обрабатывается камерально; в случае обнаружения промахов или пропусков приходится вторично выходить в поле и совершать нередко большие переезды. Вычерчивание планшета и отделка его условными знаками начинаются с печатания подписей черной тушью или пером—от руки пли особою машинкою в виде штампа; надписи же, набранные в типографии и отпечатанные на ручном станке, вырезаются и наклеиваются на планшет. Последний прием чаще применяется в картографич. работах и не рекомендуется для надписей внутри подлинных планшетов мензульной С., т. к. от времени клей пересыхает и надписи отскакивают. Наоборот, стандартные надписи вне рамок планшета чаще всего наклеиваются готовыми. Далее вычерчиваются, или, как говорят, вытягиваются, горизонтали пером от руки или особым вращающимся рейсфедером-кривоножкой. Цвет горизонталей—сиенна жженая; если издание предполагается одноцветным, то и горизонтали вытягиваются черной тушью. Последними на плане вычерчиваются контуры и заполняются соответствующими значками или иллюминуются красками; затем очерчивается рамка, наклеиваются или печатаются заглавные надписи; далее строится масштаб, и планшет“ подписывается лицами, ответственными за работу. Успех работы одного съемщика за шестимесячный летний полевой период для местности средней трудности по инструментальной мензульной €. выражается следующими цифрами: для масштаба 1 : 10 000 около 30 км², 1 : 25 000— 120 км², 1 : 50 000—250 км².

2. Мензульная полуинструмен-тальная С. отличается от инструментальной тем, что контуры снимаются без применения дальномера (засечки и глазомер) и рельеф зарисовывается без определения высот; геометрия, сеть прокладывается обычным порядком, но тоже без вцеот. Инструментами служат легкая мензула с алидадою или малым кипрегелем без вертикального круга. Порядок работы отличается от инструментальной мензульной С. тем, что геометрия, сеть не прокладывается одновременно на всем участке, подлежащем С., а развертывается постепенно и попутно с самою С. Поэтому точки геометрия, сети лишь изредка отмечаются вехами; в большинстве же случаев засекаются выдающиеся местные предметы. Масштаб С. разумеется мелкий, начиная от 1 : 42 000 и мельче.

Полуинструментальная С. применялась в России до 80-х годов прошлого столетия. Затем с появлением кипрегеля-дальномера-высотомера практиковалась исключительно инструменталь ная съемка, а далее под давлением обстановки Манчжурской войны 1904—05 гг. вновь появилась полуинструментальная съемка, но видоизмененная в соответствии с современными условиями и требованиями. В этом виде полуинструментальная С. практикуется и в настоящее время; особенно широко она применяется в малонаселенных районах Азиатской части СССР, в которых производятся работы для обеспечения различных отраслей народного хозяйства, требующих освещения обширной территории, например геолого-разведочные, краеведческие и др. В настоящее время полуинструментальная съемка производится чаще всего в масштабе 1 : 100 000. Инструментами служат мензула облегченного типа и такой же кипрегель-даль -номер-высотомер. Они укладываются в один небольшой ящик и в таком виде составляют комплект малой мензулы с кипрегелем. На месте работы к ним обыкновенно изготовляются под наблюдением производителя работ две или три легкие рейки. С. опирается на геометрич. сеть, распространяемую попутно со С. от специального измеренного лентою базиса. Если в данном районе есть астрономия, пункт, то сеть привязывается к нему дополнительными треугольниками, а в закрытой местности мензульным ходом. При таком условии рамки планшетов получают география, координаты и ориентировку по истинному меридиану. Точками геометрич. сети служат гл. обр. местные предметы: вершины гор и отдельных сопок, выдающиеся деревья в лесу и отдельные в поле, заметные камни; но вместе с тем ставятся и вехи, чаще же всего складываются конусы из камней или дерна. Высоты точек геометрич. сети определяются с помощью кипрегеля, равно как и всех дополнительных к ним точек стояния мензулы, положение которых определяется простейшим решением задачи Потенота (первичная ориентировка по буссоли); для той же цели пользуются створами; в закрытых лесом участках планшета применяется дальномер. Контуры наносятся на план исключительно засечками с применением глазомера и только в самых общих очертаниях, опуская мелкие подробности. Затем намечается пунктирными линиями «скелет» рельефа, то есть расположение вершин, водораздельные линии, тальвеги, седловины, террасы и т. д., после чего проводятся горизонтали с выражением градации крутизны скатов и общих их очертаний. Горизонтали ведутся не сплошными линиями, как на инструментальной С., а отдельными обрывками в необходимых местах по хребтам, лощинам, у седловин и т. д., которые затем в порядке камеральной обработки плана по возможности сводятся в виде сплошных горизонталей, чему помогают высоты точек геометрич. сети и дополнительных точек стояния мензулы. В случаях закрытой местности на пространстве целых планшетов опорою полуинструментальной С. служат мензульные ходы, пролагаемые по просекам или дорогам и тропинкам в виде сети сомкнутых полигонов. Зарисовка рельефа здесь совершается одновременно с работою по выполнению хода влево и вправо, насколько позволяет видимость. Пространства внутри полигонов зарисовываются глазомерно, причем в этом случае хорошим пособием служит ацероид, к-рый дает быстро и непосредственно высоты главнейших точек рельефа относительно точки стояния мензулы; точность определений разностей высот анероидом, вполне достаточная для такого вида работы. Для ориентирования побочных ходов, ответвляющихся влево и вправо от главных, служит ручная буссоль или компас; линии этих ходов измеряются шагами. На старых полуин-струментальных С. рельеф на планшетах выражался в окончательном виде штрихами, т. к. высот никаких не было и потому провести сплошные горизонтали не. представлялось возможным. Теперь штриховка на планах совершенно не практикуется, а потому и планшеты полуинструментальной С. вычерчиваются по условным знакам инструментальных С. Если работа привязывается к астрономии, или тригонометрии. пунктам, то планшеты очерчиваются рамками с соответствующими надписями планшетов государственных С. Успех работы полуинструментальной С. в масштабе 1 : 100 000—от 800 до 1 500 км² площади в лето в зависимости от условий местности, кдимата, а также в большой мере от опытности производителя работ.

3. Глазомерная съемка производится в целях предварительного освещения местности обычно там, где инструментальных и другого рода С. никогда не было. Инструментами служат буссоль и записная книжка или легкая мензула с компасом или наконец картонная папка с компасом. Необходимо отметить, что целью этого рода работ в большинстве случаев является получение сведений по гидрографии района и орографии его, то есть рельефа. С. контуров угодий является излишней кроме лесных и горных тропинок, полян, обширных заливных лугов и прочие, которые легко зарисовываются попутно. Для зарисовки рельефа наглаз необходимы опыт и уменье быстро разбираться в его строении, в расположении вершин, направлении хребтовых линий, тальвегов и скатов, в очертаниях подошв, уступов и т. д. На этом основании глазомерную С. нельзя считать более «легкою», чем прочие виды инструментальных С.; наоборот, глазомерная С. требует весьма опытных съемщиков. Начинающие съемщики в этой работе встречают большие затруднения и особенно в рисовке рельефа. Т. к. определение углов и ориентирование ходов при глазомерной С. ведутся по буссоли или даже по компасу с точностью, не большей одного градуса, то и в измерении линий нет надобности достигать большей точности; поэтому глазомерной С. измерение линий производится не только шагами, но и глазомером. При измерении линий шагами обыкновенно их считают парами, а еще лучше тройками, для которых затем строится особый масштаб шагов, чтобы можно было откладывать расстояния непосредственно в м. Для этой цели съемщик должен прежде всего установить .размер своего нормального скорого, но не деланного шага, выбрав на местности какое-либо измеренное расстояние, пройдя этот путь несколько раз со счетом троек шагов. Положим съемщик отмеривает км пути 440 тройками шагов. Масштаб плана задан 1 : 25 000. Т. к. в этом масштабе 2 сантиметров основания соответствует 500 метров на местности и следовательно 220 тройкам шагов, то по следующей простой пропорции отыскивается основание масштаба для круглого числа троек шагов, например для 500, тогда х : 2 сантиметров=500 : 220,

или

Следовательно, если построить поперечный масштаб обычного типа, но с основанием в

Т. э. т. XXII.

4,54 см, что будет соответствовать 500 м, то с него можно будет брать непосредственно метры для данного масштаба. Для контроля общего счета числа шагов, если нужно проходить большие расстояния, весьма практично применить шагомер. При пользовании шагомером его н^-жно прицеплять к одежде так, чтобы он имел отвесное положение. При каждом шаге молоточек опускается и передает свои движения механизму. Шагомер перед пользованием нужно проверить, для чего должно пройти с ним несколько раз известное расстояние; показания шагомера можно регулировать. Пользуясь шагомером, следует время от времени проверять просчитанное число троек шагов, суммируя записи длины пройденных сторон хода. Кроме того при глазомерной С. можно измерять расстояние временем, затраченным на проезд пути в повозке или верхом. Для этого записывают по часам время начала и конца движения, а затем по масштабу времени откладывают соответствующее расстояние на плане. Масштаб времени строится подобно масштабу шагов для данного масштаба плана, для чего предварительно необходимо с рабочей скоростью проехать какое-либо известное расстояние. Глазомерное определение расстояний основано на физиологии, особенностях, бинокулярного зрения. Ощущение глубины тем сильнее, чем расстояние между зрачками больше и дальность до предмета меньше. Однако сетчатая оболочка глаза воспринимает различие в глубине не более как на 500 метров Далее уже все предметы кажутся плоскими на одном расстоянии. Только опыт дает возможность оценивать расстояния при большей удаленности до предметов по различию в окраске их, по сравнению с размерами известных предметов и т. д. Поэтому при глазомерной съемке описанным свойством бинокулярного зрения глаз именно и пользуются для зарисовки контуров и рельефа на близких расстояниях. Дальние же предметы легко получаются засечками.

Наибольшие удобства дает при глазомерной С. легкая мензула с алидадой или даже просто с линеечкой, причем компас для ориентирования планшета к нему привинчивается. С. ведут замкнутыми полигонами, пристраивая их один к другому, что и дает надежный контроль в работе. Стороны полигонов .удобно брать по дорогам, направляя их вне дорог там, где мало дорог. Чтобы не допустить значительного накопления погрешностей, рекомендуется вести работу небольшими полигонами; чем они короче и чем следовательно больше узловых поверочных точек, тем работа будет точнее и искажений будет меньше. Азимуты направлений не отсчитываются и не записываются, а направления непосредственно прочерчиваются по линейке сейчас же вслед· за визированием, так как планшет ориентирован по компасу. Стороны полигонов измеряются шагами и откладываются по масштабу; общее расположение местных предметов получается засечками, а очертания их зарисовываются нагл аз. Как уже было сказано, главное внимание в этой работе уделяется зарисовке рельефа. Для этой цели предварительно наносится также по засечкам и глазомерно скелет его, то есть расположение вершин, направление хребтов и скатов, тальвеги, подошвы скатов, седловины ит. д.,а также реки, ручьи. Затем намечаются обрывки горизонталей, вырисовывающие формы рельефа, причем число их и расположение

20

соображается с крутизною скатов. Впоследствии при отделке плана проводятся горизонтали, причем не стремятся к тому, чтобы счет их сошелся по всем направлениям: это невозможно при глазомерном определении разностей высот и крутизны скатов. Следят лишь за тем, чтобы рельеф был выражен правильно и наглядно, хотя бы и не сплошными горизонталями. Предварительные наброски скелета рельефа гарантируют съемщика от пропусков лощин, оврагов, промоин и т. д. Если желают достигнуть более надежной общей связи горизонталей на всем плане, то прибегают к определению высот главнейших характерных точек рельефа с помощью анероида. Во йсяком случае в окончательном виде на плане горизонтали, особенно на крутых скатах, можно не объединять, а оставлять концы входящими в промежутки встречных с ними горизонталей. Если время позволяет, план глазомерной С. вычерчивается затем штрихами. При отсутствии легкой мензулы ее планшет заменяют папкою из картона, к которой привинчен небольшой компас. Папка держится в руках и кроме того подвешивается на ремешке, перекинутом через плечо. Порядок работы остается тем же, но точность С. заметно пострадает, т. к. ориентирование на руках не столь надежно. Такого рода глазомерные С. с папкою обычно производятся в виде вытянутых маршрутов, когда не представляется даже и возможным вести работу замкнутыми полигонами. Чтобы такие маршруты, если они тянутся на десятки км, можно было увязать, а затем и перенести на карту, их необходимо обосновать на астрономия, пунктах, которые определяются попутно специальной партией. Связь по высотам в этом случае хорошо выполняется, если производителя работ снабдить анероидом. При маршрутных глазомерных С. на полях плана зарисовываются наиболее заметные характерные местные предметы, встречающиеся по пути следования, например торчащие скалы и большие валуны, отдельные деревья замысловатого изломанного очертания, обелиски, отдельные здания и прочие Это делается для облегчения ориентирования по плану, т. к. мелкие масштабы, которые чаще всего применяются в глазомерной С., дают настолько обобщенный рельеф и контуры, что ориентироваться по ним на местности далеко не просто. Выноски с рисунками помогают совершенно точно опознавать место стояния при пользовании готовым планом. Планшеты глазомерной С. вычерчиваются и отделываются карандашом по условным знакам применительно к планам инструментальных С. Рельеф изображается горизонталями или штрихами; этот последний способ выражения рельефа в глазомерной съемке дает наибольшую наглядность форм и общую связь всех его очертаний. Надписи выполняются также установленными шрифтами, но карандашом. Успех работы глазомерной С. во многом зависит от опытности съемщика. Однако, если иметь в виду, что он ходит пешком, объём работы ограничивается вполне определенными возможностями: в один день обычно заснимается около 10 км², если дорожная сеть густая и всю ее нужно нанести; успех работы повышается до 25 км² в день в местности не населенной, открытой и бездорожной.

Лит.: Б и к А., Курс низшей геодезии, ч. 1—3,

М., 1891—92; Витковский В., Топография, 3 изд., М., 1928; Курс геодезии, под ред. Ф. Красовского, т. 1—2, М.—Л., 1930; Бон ч-Б р у е в и ч М., Аэрофотосъемка, М., 1931; Jordan W., Handbuch d. Yermessungs-kunde, В. 2, 8 Anil., Stg., 1923. О. Дитц.

Простейшие случаи практического применения теории ошибок (смотрите Ошибки измерений и наблюдений и Практическая математика). При всяких измерениях и наблюдениях, возникающих в процессе С., происходят ошибки систематические и случайные и могут происходить грубые ошибки. Систематич. ошибки должен быть исключаемы приемами измерений и наблюдений; случайные ошибки, которые не устранимы, должен быть доводимы до наименьшей величины и наконец грубые ошибки должен быть вовсе устраняемы путем их обнаружения с помощью контрольных измерений и наблюдений. Факт неустра-нимости случайных ошибок приводит к заключению, что всякие измерения и наблюдения не дают истинного значения измеряемых величин и наблюдаемых явлений; отсюда ясно, что при С. возникает практич. вопрос—с какою именно степенью точности должны производиться измерения и наблюдения/чтобы результаты С. соответствовали по своей точности той цели, ради которой данная С. производится. Практич. решение такого вопроса требует ясного представления об ошибках и об устранении их вредного влияния на результаты С., а также об уравновешивании (увязке) тех ошибок, избежать которые не представляется возможным даже при самом тщательном выполнении С.

Опираясь на теорию ошибок, можно предвидеть точность результатов измерений, даваемых данным инструментом в определенных условиях производства. Так например, измеряя углы одноминутным теодолитом при двух положениях зрительной трубы и беря каждый раз среднее арифметическое из обоих результатов, можно путем многократных наблюдений установить, что-средняя квадратич. ошибка одного угла при указанных условиях будет близка к dt0,5. Отсюда предельная ошибка равна ^1,5. Зная это, можно предвидеть, что угловая невязка в сумме-углов п не должен быть более ±1,5 I/п.

Точность измерений неодинакова для различных измерительных приборов. Она изменяется также с изменением условий измерений. В частности при измерении линий стальной 20-м лентой большое влияние на точность оказывает характер почвы. В этом отношении принято различать три класса местности: к первому классу относят местности, благоприятные для измерений, когда линии идут по ровной и твердой поверхности, как например шоссе, ко второму классу относят местности, представляющие средние-условия для измерений, и к третьему классу— местности, неблагоприятные для измерений, когда линии идут по кочкам, песку, болоту или кустарнику. Конечно эта классификация довольно расплывчата и представляет собой только первое приближение в этом направлении. Однако, когда называется точность измерения линии стальной лентой, то принято указывать, для какого класса местности или просто для какой местности—благоприятной, средней или неблагоприятной—она дана. На точность результата измерения оказывает большое влияние также способ измерения. Если производить измерения, как это принято в массовой практике, то есть каждую линию измерять дважды и из. обоих результатов брать среднее арифметическое, то для линий различной длины и на разных классах местности точность полученных таким образом результатов, измерений м. б. представлена табл. 2.

В этой таблице D—длина линий, т—средние“ квадратич. ошибки результатов измерения та-

Таблица 2.—Твчност-ь результатов измерений для различных линий.

Длина линии D в м	I		II		III
	т в м	т : D	т в м	т : D	т в м	т : D
50	0,026	1:1928	0,032	1:1563	0,036	1:1389
100	0,088	1:2631	0,016	1:2174	0,053	1:1887
200	0,056	1:3570	0,068	1:2 941	0,079	1:2 531
S00	0,072	1:4167	0,088	1:3 409	0,102	1:2 941

ких длин, ^ — соответствующие им относительные ошибки, то есть отношение ошибки к измеренной величине. Это отношение представляют дробью с числителем единица. Так, для линий I класса длиною в 50 метров из таблицы находим, что средняя квадратич. ошибка результата, полученного как среднее арифметическое из двух измерений, т= ±0,026 м, откуда относительная ошибка:

0,026 1 ^Ш~~ 50 “ 1923 *

Эта дробь показывает, что в данном случае точность измерения такова, что на 1 923 метров расстояния средняя ошибка приходится в 1 метров Для линий той же длины, но измеренных по II и III классам, найдем ш=±0,032 и т=±0,036,

= Ш ¹¹ Ζ/“ΤΪ89· Приведенная таблица со-ставлена на основании многочисленных опытов, произведенных в Германии. Из этой таблицы мы видим, что для различных длин относительная ошибка измерения получается разной. Следовательно, называя относительную ошибку измерения линии стальной лентой, необходимо указать: 1) для каких длин она получена, 2) при каком способе измерений и 3) на какой местности: благоприятной, средней или неблагоприятной. Т. к. на практике линии короче 50 метров почти не бывают, то обычно инструкции требуют, чтобы при массовой С. точность измерения линий была не ниже 1 : 2 000 при благоприятных условиях измерения и не ниже 1 : 1 000 при условиях неблагоприятных.

Если углы полигонов измеряются со средней квадратич. ошибкой ±0,5, то нетрудно установить, какая при этом должен быть точность измерения линий. Пусть ошибке угла в 0,5 соответствует поперечное отклонение вехи на величину q. Сравнивая величину этого отклонения с длиною стороны d, мы можем выразить точность измерения угла относительной ошибкой. По малости угла отклонение q можно рассматривать как дугу радиуса d. Но отношение дуги к радиусу, то есть равно соответствующему этой дуге углу, выраженному в радианах. В одном радиане содержится приблизительно 206 265", или 3 438. Следовательно число радианов, соответствующих углу в 0,5, будет 3±g =

или, круглым числом, Отсюда ясно, что^ для соответствия точностей измерение линий должен быть произведено с точностью не ниже —j^·.

Теория ошибок служит также основой и для уравновешивания наблюдений; она указывает пути целесообразного устранения невязок, возникающих при избыточных измерениях. Так например, если в плоском тр-ке для контроля были измерены 3 угла: А=60° 02", В =60°0^,6^, и С=60° 04", то сумма их, равная 180° 0Ί2", отличаясь от теоретической на 12", содер жит невязку /= +12". Если эта невязка допустима, то есть не выходит за пределы, соответствующие заданной точности измерений, то все результаты д.«б. исправлены так, чтобы, во-первых, сумма исправленных углов была равна теоретической, и, во-вторых, чтобы каждый из результатов потерпел при этом наименьшее искажение. В данном случае для каждого угла мы имеем по два значения: одно находим из непосредственных измерений данного угла, другое значение этого же угла получаем посредством измерения двух других. Напр., для угла А будем иметь: одно значение А=60°02" с некоторой средней квадратической ошибкой ±т и другое значение П"=180° — {В + С)== 59°5950" со^ средней квадратич. ошибкой ±mj/2, предполагая, что все углы (равноточны. Если принять вес угла, измеренного со средней ошибкой ±т, за единицу, то веса упомянутых двух значений 4и4" для одного и того же угла А будут:

Р= 1 и Р"=+

Последний получим из пропорции Р" _ m2 __ i Р ~ m2.2 “2

согласно определению веса. Составив теперь из обоих значений весовое среднее, получим окончательное значение для угла А.

2".1-10”J

(.4)=60°00" -I-—=59°5958"

¹⁺2

с весом ³/₂. Подобными рассуждениями придем к окончательным значениям для углов В и С:

	6	•1-8"	1
(В)=60°00"	+ -	1	2
		1+2
с весом 3/а “
	4	•1-8"	1
(О)=60°00"	+ -	1	2
		*+1

с весом ³/₂.

Контролем вычислений служит равенство 180° суммы окончательных значений углов:

(+) + (£) +(С) =180°.

Из сравнения окончательных значений углов со значениями,*полученными для них из измерений, видим, что каждый измеренный угол в результате получил одну и ту же поправку: —4". Если бы измеренные углы были неравноточны, то и поправки к ним получились бы разные. Сумма квадратов поправок, полученных указанным здесь способом, меньше, чем сумма квадратов уклонений тех же измерений от“всякой другой, произвольно взятой величины. Поэтому и самый этот способ получения окончательных исправленных значений измеренных величин называют способом наименьших квадратов.

Итак, теория ошибок позволяет на основе произведенных измерений делать оценку этих измерений. Пусть например по угловым невязкам пяти тр-ков была получена средняя квадратич. ошибка суммы углов одного тр-ка:

m_s=± УЩ=± γΐψ-± 3".

Т. к. средняя квадратич. ошибка одного слагаемого меньше средней квадратич. ошибки суммы трех слагаемых в]/3 раза, то отсюда средняя квадратич. ошибка одного угла т=±]/^Γ[ΐ^Αι=± ι/ϊϋ:=± ι,7".

г Зп. г х5

Последняя формула известна в геодезии, литературе под названием ф-лы Ферреро; она позволяет определять среднюю квадратич. ошибку одного угла по угловым невязкам Δ_1? Δ₂, Δ^ в отдельных тр-ках и этим дает критерий для оценки точности сырого материала, получаемого из измерений. Если сырой материал оказывается по оценке пригодным для дальнейшей обработки, то очень часто в геодезии, работах, связанных геометрии, условиями, его приходится приводить в соответствие с эДими условиями или уравновешивать подобно тому, как это было сделано в примере с одним тр-ком. В результате уравновешивания не только удовлетворяются геометрии, условия, но в некоторой степени улучшается и качество продукции в том смысле, что при этом преодолевается влияние случайных погрешностей измерений, но не больше. Показателем степени преодоления случайных погрешностей измерений в результате уравновешивания служит вес окончательного значения. Так, при уравновешивании углов тр-ка веса измеренных значений были приняты равными между собою и равными каждый единице. В результате же уравновешивания веса также получились равными между собою, но уже каждый оказался равным ³/₂, то есть на 50% выше, чем был до уравновешивания.

Лит.: Шилов П., Геодезич. работы при земле устройстве, ч. 1, Рязань, 1929; Чеботарев А., Способ наименьших квадратор, 2 изд., М., 1928; И в е р-н о в И., Способ наименьших квадратов, М., 1927; Боярский А. идр., Теория математич. статистики, 2 изд., М., 1931. П. Шилов.

С. магнитная, измерение элементов земного магнетизма (смотрите) на нек-ром участке земной поверхности, имеющее целью изучение распределения этих элементов на данном участке. Смотря по характеру тех задач, которые преследует магнитная С., можно различать следующие виды С.: 1} С., имеющие своей задачей выяснение общего характера распределения геомагнитных элементов на поверхности земли в целом. Магнитные С. этой группы могут иметь значение не только для выяснения территориального распределения элементов земного магнетизма, но и для решения .вопросов, связанных с изучением изменений этого распределения во времени. 2) С. для детального изучения магнитной картины какого-либо определенного участка земной поверхности как для целей общего учения о земном магнетизме, так и для установления связи между распределением геомагнитных элементов и тектоникой района. 3) С. прикладного характера для целей разведки полезных ископаемых (смотрите Разведки геофизические), для военного дела и тому подобное. В зависимости от задач С. требования, которые к ней предъявляются в отношении точности и детализации, бывают различны. В особенности это имеет место для С. прикладного характера. Непосредственной целью общей магнитной С. является составление магнитной карты всего земного шара. Требования в отношении точности измерений и густоты сети пунктов наблюдений определяются масштабом карт, на которые намечено нанесение материалов съемки. Общая С. на основании международных соглашений и на основании работ специальной магнитной комиссии, ^существовавшей прежде при

Академии наук СССР, а теперь при Гидрометеорологии. комитете, должна дать материал с точностью: для склонения ±2, для наклонения+3, для горизонтальной составляющей ±0,001 Н. В силу таких требований расстояние между пунктами наблюдений определяется в нормальных областях величинами порядка нескольких десятков км. Существующие по вопросу об удаленности пунктов С. постановления определяют это расстояние в среднем величиной 20—25 км. Т. к. кроме общих задач общая магнитная С. имеет целью выявление аномальных в магнитном отношении областей, то принятой сетью пунктов будут обнаружены все магнитные аномалии (смотрите), имеющие достаточно большие размеры в отношении занимаемой площади. Осуществление этой магнитной С. еще далеко не закончено. Проводится С. средствами и силами государства, на территории которого находится намеченная сеть пунктов наблюдений. Малодоступные области обычно изучаются путем специальных маршрутных С. по путям сообщения, которые хотя и не удовлетворяют общим требованиям, но все же дают нек-рый материал для суждения о распределении геомагнитных элементов в изучаемом районе. Т. к. по самому масштабу работ съемка захватывает промежуток времени в несколько лет, то при составлении сводки необходимо учитывать временные изменения геомагнитных элементов и приводить все наблюдения к определенной эпохе. Последнее требует знаний этих временных вариаций, что возможно в тех случаях, когда страна располагает достаточно мощной сетью магнитных обсерваторий (смотрите). Для учета вековых вариаций, из года в год изменяющих расположение магнитных изолиний на данном участке ззмной поверхности, м. б. использован материал самой С. Для этой цели из ее пунктов выбирается особая сеть точек наблюдений, на которых регулярно через 3 года производятся магнитные измерения. Материал этих наблюдений позволяет составить представление о территориальном распределении вековых вариаций. Точность наблюдений на таких опорных пунктах требуется несколько выше, а именно: ддя склонения ±0,8, для наклонения ±0,5 и для горизонтальной составляющей ±0,001 Н. Для детализации магнитной карты какой-либо ограниченной области, за исключением районов крупных магнитных аномалий, съемка которых ведется но особому плану, густота сети пунктов наблюдений может быть увеличена в нужной степени.

Аппаратура, применяемая при общих С., м. б. любого типа, обеспечивающего требуемую точность. Обычно это магнитный теододит и стрелочный инклинатор (смотрите Земной магнетизм). В целях увеличения точности определения наклонения последний иногда заменяется индукционным инклинатором, применение которого в полевыхусловиях представляет однако «большие трудности. Весьма удобным для съемочных работ является электромагнитометр. Для детализации магнитной картины небольших участков чрезвычайно полезными представляются магнитные весы Шмидта (смотрите Разведки геофизические). Для работ в районах, не имеющих детальных топографии, карт, где определение местоположения пункта наблюдения и истинных азимутов геодезическим способом маловозможно, магнитные теодолиты снаб каются специальной астрономии, частью для не обходимых наблюдений.Что касается специальных

С., имеющих прикладной характер, то здесь и густота сети пунктов наблюдений и точность их определяются задачами С. в каждом отдельном случае. При съемке разведочного характера расположение пунктов наблюдений определяется формой и размерами изучаемой аномалии. При отчетливо выраженном простирании ее целесообразно располагать пункты наблюдений вдоль линий, перпендикулярных этому простиранию, причем расстояние между линиями промера обычно берется большим, чем расстояние между пунктами на линии. Последние определяются глубиной объекта, вызывающего аномалию; при небольших глубинах эти расстояния берутся малыми (от 10—20 метров и выше), при значительных глубинах рационально их увеличивать. Области с большими изменениями магнитных элементов как правило приходится снимать с более густой сетью пунктов, чем области с небольшими градиентами. В случае гнездо образных аномалий без ярко выраженного простирания * пункты наблюдений располагаются обычно в шном порядке. Аппаратура таких С.: специальные магнитометры (смотрите) и весы Шмидта.

Магнитная съемка на море ведется главным образом институтом Карнеджи и имеет целью изучение распределения элементов земного магнетизма на поверхности моря. Институтом сконструированы специальная аппарату ра и специальные суда, предназначенные для таких измерений. Основная трудность таких наблюдений заключается в исключении возмущающих действий железных масс корабля и в борьбе с влиянием качки.

Лит.: см. Земной магнетизм.—^^ιΡ огеН.и Трубят-чинский, Краткое руководство для работ по магнитной съемке, Л., 1931; Hellmann G·., Magnetische Kartographie in Mstoriscb-kritischer Darstellung, «Yeroff.d. Preuss. Meteorol. Tnst.», B., 1909, 215. А. Заборовский.