 > Техника, страница 84 > Тела равного сопротивления
> Техника, страница 84 > Тела равного сопротивления
Тела равного сопротивления
Тела равного сопротивления, такие те ла, в которых напряжения от приложенных к ним сил во всех их точках одинаковы.
Лишь очень редко можно достигнуть того, чтобы напряжения были действительно одинаковы во всех точках тела (растяжение, сжатие) и тело строго удовлетворяло поставленному выше определению. Обыкновенно довольствуются таким подбором формы тела, чтобы наибольшие напряжения в различных поперечных сечениях его были одинаковы, и такое те го тоже называют Т. р. с. Если это одинаковое наибольшее напряжение равно предельному допускаемому, то Т. р. с. ^ является вместе с тем телом наименьшего веса. Это последнее обстоятельство и побуждает применять в инженерше
—1---/--Ffm
| 1 i | •И | |
| - : | 1 | |
| 1 :
1 |
I | |
| ! 1
A -L L— |
* L |
Фигура 1.
Р
Фигура 2.
ных сооружениях Т. р. с., хотя изготовление их сложнее и дороже. Рассмотрим главнейшие случаи Т. р. с. при различных нагрузках.
Растяжение. Прямолинейный вертикальный стержень (фигура 1) растягивается нагрузкой Р, равномерно распределенной по его нижнему сечению, и собственным весом. Вес единицы объёма материала стержня обозначим γ. Чтобы растягивающие напряжения сг в любом сечении стержня были одними и теми же, необходимо, чтобы площадь сечения стержня на расстоянии х от нижнего конца возрастала по закону:
| F(x) | 11
о |b сь, ч“ |
(1) |
| Вес такого Т. р. с.
J |
( у1 | |
| Q=P | «"-О. | 09 |
Площадь сечения и вес для призматич. тела той же прочности определятся соответственно по ф-лам:
| F°=^y, · | (3) |
| Q=F о yl. | (4; |
Из (3) видно, что стержни постоянного сечения можно применять лишь при I <. При длине I > * напряжения от одного только собственного веса превышают допускаемые.
Далее из (2) и (4) следует, что лишь при больших I получается значительное уменьшение веса стержня; если же длина I не велика, то выигрыш в весе ничтожен, то есть формуравно-го сопротивления имеет смысл применять только при очень длинных стержнях. Ради простоты изготовления стержни равного сопротивления часто заменяют ступенчатыми (фигура 2), состоящими изг отдельных частей постоянного сечения. Площади сечений отдельных участков ступенчатого стержня находят по сл. ф-лам:
F1=„_v/. > = (σ-γΙχ) (a-yl2) ’ ^
ο-γΐχ *
для ш-го стержня
(6)
рат -1
(σ-γΙχ) (σ-ylj. (σ-γΐ„,)
Если все участки одной и той же длины, то
ГО
Какой экономии в весе можно достигнуть, применяя Т. р. с., видно из следующего примера. Подъемный канат постоянного сечения для шахты глубиной в 1 000 метров при весе клети Р= 7,8 ш и наибольшем напряжении сг, равном допускаемому. напряжению на простое растяжение Rz=16 килограмм/мм2, весит 13 т; канат равного сопротивления весит 6,7 т, а ступенчатый канат при 5 ступенях по 200 метров каждая весит 7,4 ш.
Все вышесказанное относится также к случаю сжатия прямолинейного вертикального стержня с нагрузкой Р, равномерно распределенной по верхнему сечению его. Площадь поперечного сечения и вес Т. р. с. при сжатии определяются теми же ф-лами (1—4), в случае ступенчатого стержня—формулами (5—7). Форму Т. р. с. часто придают высоким мостовым опорам (фигура 3). Мостовой устой постоянного сечения высотой I=30 метров при нагрузке Р=200 ш, допускаемом напряжении на простое сжатие Rd= 20 килограмм/см2 и удельном весе кладки, равном 2,5, весит 120 W; устой равного сопротивления той же прочности—90 w; экономия в весе 25%.
При изгибе наибольшие напряжения возникают в крайних, наиболее удаленных от нейтральной оси волокнах (смотрите Изгиб). Их величина находится из ур-ия:
м /оч
°=w (8)
Если размеры сечения балки менять вдоль ее длины так, чтобы отношение ~ оставалось пору стоянным, то мы получим балку равного сопротивления при изгибе. Форма ее зависит от закона изменения М вдоль длины балки, то есть балки равного сопротивления при изгибе имеют разные очертания для различных нагрузок.
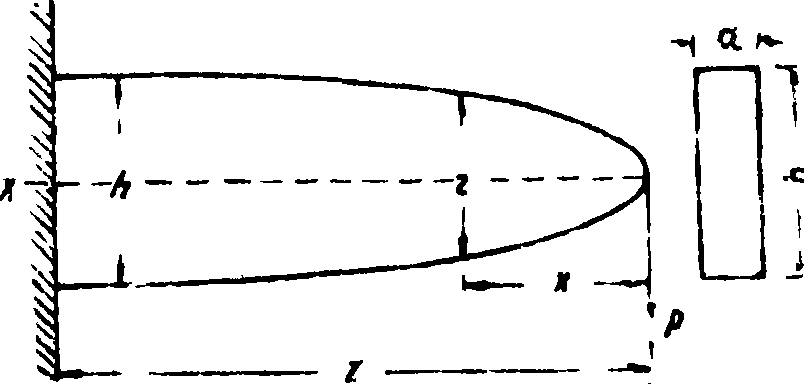
Рассмотрим несколько частных случаев. Балка прямоугольного сечения одним концом заделана, к другому приложена сила Р. Если ширина балки остается постоянной, то высота должна меняться по параболич. закону (фигура 4)
*·-**“- -Рх· (9)
Если высота балки ζ остается постоянной, то

Фигура 3.
ширина а меняется но закону прямой линии (форма балки в плане является треугольной). В первом случае экономия в весе по сравнению с бй постоянного сечения достигает 33%. во втором 50%; прогиб увеличивается в первом случае вдвое, во втором в V/2 раза. Балка прямоугольного сечения постоянной ширины а лежит на двух опорах (фигура 5). Нагрузка Р= ql равномерно распределена вдоль всей длины I балки. Форма балки равного сопротивления ограничена двумя дугами эллипса:
(10>
Экономия в весе около 24%. При определении формы балки равного сопротивления мы не приняли во внимание касательные напряжения, т. к. вообще при изгибе они играют второстепенную роль. Если принять их в расчет, то концевым се- Фиг 4
чеииям надо дать конечные размеры, определив их так, чтобы наибольшие касательные напряжения не превосходили допускаемых.
Примерами балок равного сопротивления являются листовые рессоры, мостовые фермы криволинейного очертания, двутавровые балки переменного сечения и тому подобное. В последнем случае практически невозможно непрерывно изменять сечение балки, поэтому путем наклепки листов изменяют сечение балки скачками, приближаясь к форме балки равного сопротивления. В технике мы имеем еще очень много слу-
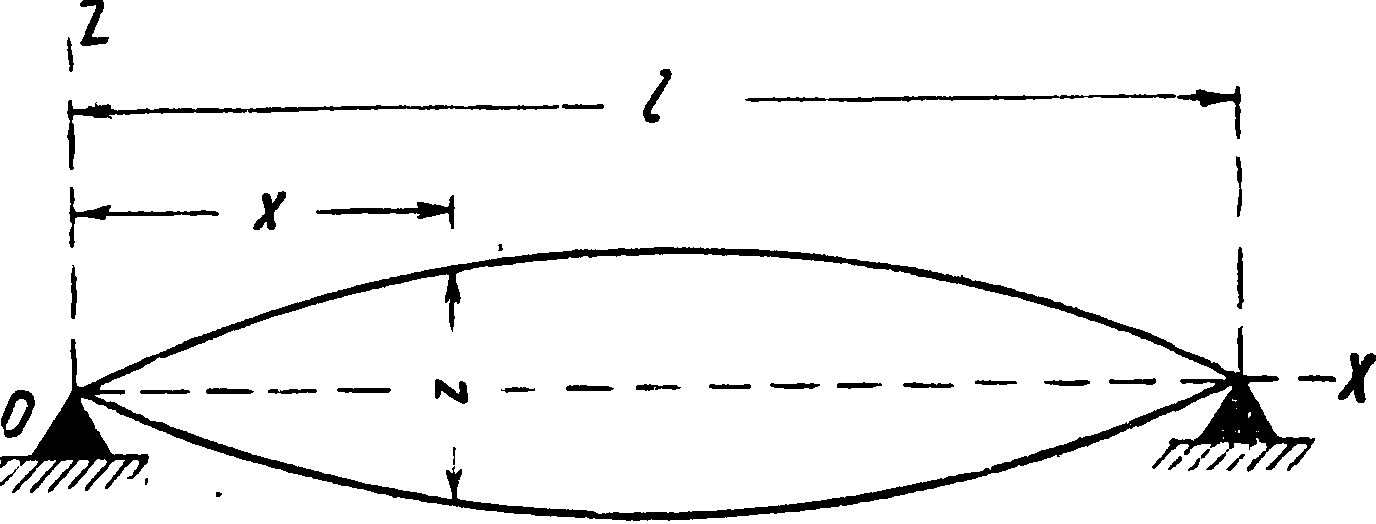
Фигура 5.
чаев применения Т. р. с., например колонны равного сопротивления, подвергающиеся опасности продольного изгиба, быстро вращающиеся под действием центробежной силы турбинные диски, стволы артиллерийских орудий крупного калибра, где помощью системы растянутых колец, насаженных на основную трубу орудия, стремятся приблизиться к стволу равного сопротивления. Еще более приближаются к Т. р. с. в системе Лонгриджа, когда основная труба орудия обматывается проволокой, натяжение которой регулируется так, чтобы при выстреле напряжения в стенке орудия от давления овых газов были равномерно распределены по всей ее толщине.
Лит.: Б о б а р ы к о в И., Сопротивление материалов, М., 1 925; Тимошенко С., Сопротивление материалов, ч. 1, М., 1932; Кирпиче в В., Сопротивление материалов, П., 1918; Прокофьев И., Строительная механика, ч. 1 * Сопротивление материалов, М., 1 923; Худяков П., Сопротивление материалов, Μ., 1Р29; Bach С. u. Baumann R., Elastizitat и. F^stigkeit, 9 Aufl., В., 1924. А.Динник.