> Техника, страница 84 > Телефонная передача

Телефонная передача

Телефонная передача. Теория телефонной передачи, обобщение явлений и законов по восприятью речи в одном пункте и по ее передаче и воспроизведению в другом пункте, находящемся на определенном расстоянии от первого, причем передача происходит электрич. путем по проводной линии. До настоящего времени нет объективного средства, которым можно было бы численно оценить одно телефонное сообщение по сравнению с другим; аналогично дело обстоит в вопросе улучшения телефонного сообщения: мы можем улучшить или ухудшить качество сообщения, но выразить это изменение качества численной величиной мы еще не можем. Иначе говоря, нет общепринятой меры качества передачи речи. Чем же это объясняется? Фигура 1 (S—передатчик, Е—приемник, L—линия) представляет схему Т. п. Микрофон преобразовывает звуковые колебания в электрические; на обязанности линии лежит перенос этих колебаний (по возможности неослабленными и неискаженными) к телефону, и наконец телефон имеет

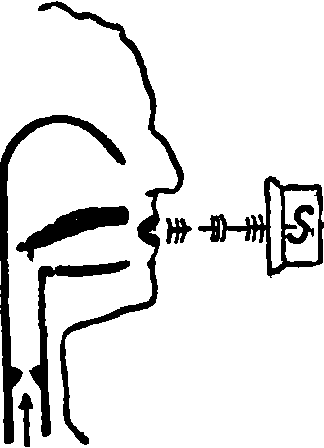
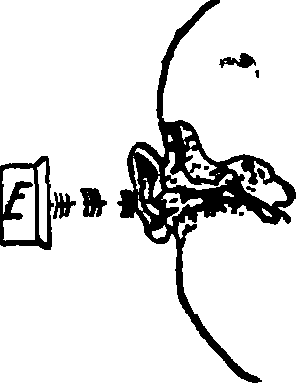
Фигура 1.

только одно назначение—преобразовать воспринятую электрическую энергию в акустическую, причем требуется,чтобы звуковые волны, воспроизводимые телефоном, ничем не отличались от волн, воспринимаемых микрофоном; в это_м случае передачу можно назвать неискаженной. Техника имеет в настоящее время все средства к разрешению этой идеальной задачи. Но чем ближе мы подходим к поставленному идеалу, тем сильнее растут денежные затраты; иными словами: чем качество передачи хуже, тем дешевле устройство сообщения. Поэтому необходимо выяснить, до какой степени мы можем уменьшить стоимость устройства сообщения, то есть ухудшать качество передачи. Какой же фактор является доминирующим при оценке телефонного сообщения? На этот вопрос имеем лишь один ответ: понятливость (артикуляция), то есть в какой мере один абонент понимает другого. Поэтому измерение понятливости должен быть положено в основу при оценке телефонного сообщения. Если бы можно было построить «понятливость-метр» наподобие например вольтметра, с помощью которого измерялась бы понятливость (хотя бы в %), то поставленная задача была бы решена. Но впредь до постройки такого прибора надо идти обходными путями. Если не принимать во внимание того обстоятельства, что один человек поймет с трех слов больше, чем другой после часового объяснения, то измерение понятливости можно производить путем передачи слогов, составленных так, что каждый из них сам по себе не имеет никакого смысла и следовательно не м. б. воспринят по догадке. Для удобства счета искусственные слоги собираются в таблицы по 100 слов, и отношение правильно принятых слогов к общему числу передаваемых м. б. легко выражено в %. Описанным методом был выяснен поставленный выше основной вопрос при проектировании телефонного сообщения: до какого предела телефонное сообщение м. б. ухудшено, причем ответ на этот вопрос дан в косвенной форме, а именно: 1) спектр передаваемых частот должен лежать от /=300 до /=2 400 Hz; 2) полное затухание (смотрите) для средних частот (/=800 Hz) всего телефонного сообщения (от микрофона одного абонента до телефона другого) не должно превышать 3,3 непера; 3) разность между величинами полного затухания сообщения (от микрофона одного абонента до-телефона другого) для любых двух частот в спектре от /= 500 до /= 2 400 Hz не должна превышать 2 неперов.

Неперы идецибелы. В теории Т. п. принята выражать отношения двух величин, имеющих одну и ту же размерность, логарифмом этих отношений. На практике пользуются системой и натуральных и десятичных логарифмов. Если дело идет о двух мощностях Р_г и Р₂>. то пользуются выражениями:

а) в натуральной системе In ^;

2 Р 2

б) в десятичной системе 10 lg

Pi

P2’

Если говорят о двух напряжениях У_г и У₂ или о двух, токах 11 и 1₂> то пользуются выражениями:

а) в натуральной системе In ^ или In —;

у 2 ·* 2

Vi /1

б) в десятичной системе 20lg~ или 20Jg-_r^L·

У 2 f 2

Числа, полученные в результате вычисления по вышеприведенным ф-лам, должны сопровождаться словом «непер» в случае применения натуральной системы и ело— вом «децибел» в случае десятичной системы. Следовательно указания «непер» или «децибел» служат для напоминания о том, какая применена система логарифмов.

Телефонные линии. Постоянные величины, характеризующие линию. Двухпроводная телефонная линия, состоящая из прямого и обратного проводов, имеет четыре постоянные величины, влияющие на передачу разговорного тока, а именно: 1) Омич, сопротивление R_x 1 км линии, измеряемое в Ω, обусловливается размерами и материалом провода; следовательно под величиной R_x подразумевают омич, сопротивление двух км провода (прямого и обратного). 2) Самоиндукция L одного км линии, измеряемая в Н, обусловливается взаимным расположением, размерами и материалом проводов; следовательно под величиной L подразумевается самоиндукция двух км провода (прямого и обратного). Если обозначить буквами г—радиус провода и а— расстояние между проводами, то для меди, бронзы и алюминия при тональных частотах (примерно до /= 10 000 Hz)

i -(9,21 lg у + 1) · ΙΟ^-4.

Для 10 000 Hz коэф. самоиндукции медных, бронзовых и алюминиевых линий несколько понижается, но весьма незначительно. Для искусственной четырехпроводной линии коэф. самоиндукции определяется по следующей ф-ле:

*ч=(2,3 lg+ ο,δ) · 10- НАШ.

Здесь а₁₃, а₁₄, а₂₃ и т. д.—расстояния между проводами 1—3, 1—4, 2—3 и т. д., a d—диам. провода. 3) Емкость С на 1 км линии прямого и обратного проводов по отношению друг к другу, в том смысле, что оба провода можно рассматривать как обкладки конденсатора емкостью С. Величина емкости зависит от размеров проводов, от расстояния между ними и от природы диэлектрика. Если d см—диам. проводов и а см—расстояние между ними, то емкость воздушной двухпроводной линии выразится в F/км сл. обр.:

причем в этой формуле предполагается, что а значительно меньше расстояния между проводом и землей. При подсчетах емкости линии необходимо учитывать емкость изоляторов, которая на 1 км линии м. б. принята равной C_U3t=«= 0,0003 х 1СГ⁶. Для кабелей с достаточной степенью точности можем пользоваться ф-лой:

_п 0,0161е

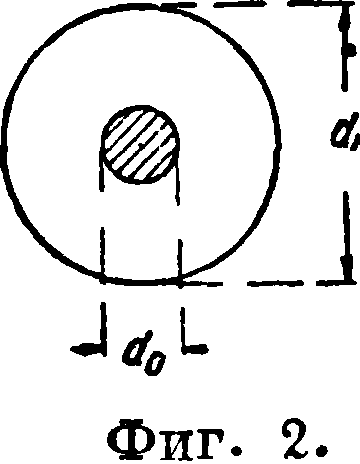
lg

1,2а (2 di — d©)

d₀

1СГ⁶.

Здесь d_x и d₀ усматриваются из фигура 2. Диэлектрическая постоянная в для кабелей с воздушной бумажной изоляцией не является постоянной величиной, а зависит от величины d_x, что видно из данных, приведенных в нижеследующей таблице:

do	di	ε	do	di	ε
0,5	1,03	1,43	0,9	1,25	1,91
0,6	1,15	1,53	0,9	1,76	1,27
0,6	1,39	1,51	•1,3	2,48	1,19
0,7	1,45	1,35	1,4	2,51	1,25
0,8	1,39	1,45	1,4	2,01	1 1,21
0,9	1,64	1,40	1,5	2,79	1,22
0,9	1,82	1,42	2,0	3,15	1,15
0,9	1,88	1,36	2,0	3,09	1,11

Емкость искусственной четырехпроводной линии вычисляется по следующей ф-ле:

^ 0,049×10-10

и=-;--♦

lg 1^αΐ3^α14^α 3^24

α_Χία₃₄d²

Здесь α₁₃, α₁₄ и т. д. —расстояния между проводами 1—3, 1—4 и т. д., d—диам. провода.

4) Проводимость изоляции А на 1 км линии измеряется в мо (сименсах); ее можно представить, вообразив, что вследствие несовершенства изоляции обоих проводов (прямого по отношению к обратному) на длину одного км линии от одного провода к другому происходит утечка тока; проводимость изоляции равна обратной величине сопротивления изоляции прямого и обратного проводов по отношению друг к другу. Для вычисления проводимости изоляции в мо /км м. б. применены сл. ф-лы: а) для воздушных линий

А=1СГ⁶

1 +

20

4 +

1©и б) для кабельных линий (с воздушно-бумажной“ изоляцией)

А= (0,005· ωΟ).

На основании изложенного R, L, С и А не являются в полном смысле слова постоянными величинами и могут (практически) считаться ими только в спектре тональных частот для воздушных медных, бронзовых и алюминиевых линий. Что касается железных воздушных линий, то необходимо подчеркнуть весьма большую зависимость между R, L и частотой переменного тока.

В табл. 1 приведены значения R и L железных линий при различных диаметрах проводов; и при ω=5 000.

Таблица .—3 начения R и L железных линий при ш=5 000.

d, миллиметров	2 *	ar.	R и	3 I	RQ	L Η
3	34	1,79	1,521	1,206	52	0,0082
4	19	2,40	1,97	1,663	37	0,0063
5	12,5	3,00	2,40	2,10	30	0,00525
6	9	3,58	2,80	2,50	25,5	0,0015

* Сопротивление постоянному току.

Для частот, лежащих выше f= 10 000 Hz, можно пользоваться следующей ф-лой:

R=1<Г* Ω/κм.

Для твердотянутой меди ρ=1 800; для железа q=13 500; для алюминия ρ=2 800. Напр~ для медной двухпроводной линии с проводами диам. 4 миллиметров при /= 30 000 Hz получим

R=²^-¹⁸⁰Рр?Л°-А. 1(г⁴=7,35 Щкм.

Симметричные и несимметричные телефонные линии. Симметричной двухпроводной линией назовем такую, в обеих половинах которой R, L, С и А равны между собой. На практике это требование можно считать выполненным, если вся линия является или воздушной или кабельной и если провода на всем" протяжении линии сделаны из одного и того же материала, имеют одинаковый диаметр и расположены на одинаковом расстоянии друг от друга; в этом случае линия будет симметричная и однородная. Равным образом симметричной линией будет например такая, которая состоит из^воздушной линии, к началу и концу которой присоединены кабельные линии равной длины (симметричная неоднородная линия). Как пример несимметричной линии можно привести воздушную линию, которая одним своим концом переходит в кабельную. Несимметричные линии однородными быть не могут. Ур-ия, определяющие законы, которым подчиняются распространение тока и напряжения вдоль проводов, при установившемся режиме имеют следующий вид:

V + JZ^eVl-^

^у а ^у с о о т т eV^l + e-V^l, V_e еУ¹-е~У^{1 1}а~¹е 2 ‘ z 2

(1)

Здесь Vа и 1_а—напряжение и сила тока в начале линии, V_e и 1_е—напряжение и сила тока в конце линии, у=У (R + ?o>L) (А + jcoC)—π о-•стоянная распространения, Ζ=

— волновое сопротивле-

A+ja)C - ¹

н и е (характеристика) линии. Ур-ия .(1) можно представить иначе, а именно:

Ύ ~ УусУЦУУ £,γΙ _|_ Vе~1е% p~vl

т _Ру1_Vg-Z/p -γΐ

^±а ~ * 2Ζ ~ ^е 2Ζ ^β

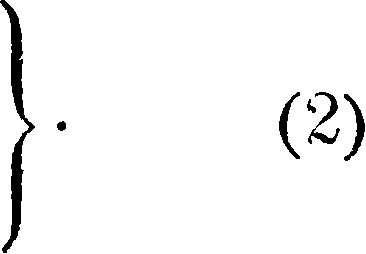
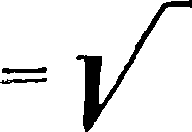
Первый член правой части ур-ий является падающей волной, а второй член—отраженной; .ур-ия (2} можно переписать так:

V_a=V_ne^vl + V_l>e~^vl,

I

а

У ^}1 рУ¹ z ^е

Ул р~у^[

Z

(3)

.Для какой-либо точки, отстоящей от конца .линии на длину х, получим:

F.-F^+F₀e~^YX

1_Х=Тл e^vx — ~-c~^vx j

Волновое сопротивление. Отноше-шие падающей волны напряжения к падающей волне тока и соответственно отношение отраженной волны напряжения к отраженной волне -тока является волновым сопротивлением ли-лши; действительно

i -yi

P+IfZ _γ1 Ye-lfZ

_2 „ ₌ у _и ²

Ve + ZI_{e γ}ι * Ve-Zl_e

2 Ζ 2Z

Преобразуем ур-ие для Z сл. обр.:

yl

= Z.

Z

R+j<oL A + jcoC

RA + w²LC _J_ ct»2C²

= Ze~^i<pK.

JO)

LA -{-C R A ² -f- ω²0²

T. к. для всех существующих линий LA < CR, то мнимая часть отрицательна, что указывает на то, что угол φ_ζ имеет отрицательный знак. Если постоянные линии таковы, что R<<x>L и А<соС, то приближенно имеем: ry, - -ja)L ^ L

A+jtoC-V c

Поэтому для воздушных медных, бронзовых и алюминиевых линий

Z=120 У ln^[lnf + i]Q,

где 2 г—диам. проводов и а—расстояние между проводами. Наир, для алюминиевой, медной и бронзовой линий при α= 20 сантиметров Z=600; 552; 524 при 2г соответственно равных 3; 4; 5 см. Для кабельных линий, для которых coL прибли женное значение вычисляется по следующей формуле:

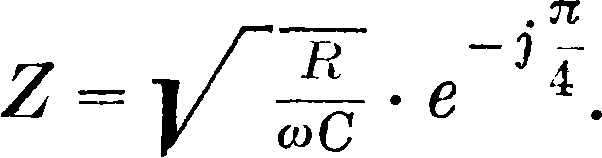
Постоянная распространения у, кило метрическое затухание/? и угловой измеритель а.

y=V(R + jcoL) (A -j- jwC)=β + ja,

β (километрич. затухание) определяет собой затухание волны тока или напряжения, то есть уменьшение ее амплитуды на единицу длины линии (на 1 км) а определяет собой фазный угол и скорость распространения волны вдоль линии, причем

β=j/~^ y^L²AR²)(M²A-A²) - (α)2 CL — AR)], (4)

a=|/^rL[V^r(io2L2+_JR2)(_i0iiC2+A2) + (o>²CL-Ай)]. (5)

Эти ф-лы м. б. упрощены в зависимости от характера линии. Для воздушных бронзовых, медных и алюминиевых линий, то есть при

^А <1.

а>С

o-f/I+i/!·

α= ω LC.

Для кабельных линий, то есть при^< 1 и -^< 1,

R А

Обозначая tge=^- “ tg^=^r, можем ур-ия (4) и (5) представить сл. обр.:

β=ω ]/LCv/~ — ¹ - -г · sin

^г ψ COS ε · COS δ 2 ^0·^

a=ω VL/Ci/~---τ· cos⁶-^— (

У COS ε · COS <5 2 )

T. к. для всех видов линий а>С>Д, то как для кабельных, так и для воздушных линий получим:

β^ωΥοΣ

V·

z-Vi-VA

; α=со VLC

К¹-**·!

СО

Абсолютное затухание βΐ. Обычная междугородная телефонная цепь состоит из сле-

ЦТС МТС Гр, ТРгмге ЦТС Д

: №-ДНХН—ШЬ—

Ч ¹ А

I ¹ ----------

I μ «·ι? μ, ·

--в ^ 3.3 -ч

Фигура Ч.

дующих составных частей (фигура 3). В районе города А: 1) Т—телефонный аппарат, 2) ЦТС— центральная телефонная станция, 3) МТС— междугородная телефонная станция, 4) кабельная линия между Т и ЦТС, 5) кабельная линия между ЦТС и МТС и в) трансформатор Тр_г. В районе города В имеется то же самое. Междугородная станция в городе А соединяется с междугородной станцией в городе В междугородной телефонной линией, которая начинается от первичных клемм трансформатора Тр_г и кончается первичными клеммами трансформатора Тр₂. Полное затухание b между микрофоном одного аппарата и телефоном другого (практически—между телефонными аппаратами) для средних разговорных частот (ω=5 000) не должно превышать: 1) для магистральных линий &< 3,3 непера, 2) для второстепенных линий &<4,5 непера. Величина b=3,3 непера распределяется сл. обр.: а) затухание линии Ь_л= βΐ (называемое абсолютным затуханием) не должно превышать /И= 1,2 непера, Ь) затухание междугородной станции не должно превышать &^<0,15 непера, с) затухание центральной станции не должно превышать b_ц<0,2 непера, d) затухание трансформатора не должно превышать &_w<0,05 непера,

е) затухание городской линии (в районе одного города) не должно превышать Ь_л=0,65 непера. Следовательно

3,3=2 (0,2 + 0,15 + 0,05 + 0,65) + 1,2.

Если Ь=4,5, тр абсолютное затухание βΐ м. б. увеличено до /И<2,4 непера. Для железных линий при вычислении β и а можно пользоваться лишь ф-лами (4), (5), (6) и (7).

В табл. 2 приведены значения Ζ, β и а железной и биметаллической линий, полученные измерением.

Таблица 2.—3 начения Ζ, β и а для железной и биметаллической линий.

	z !	<Ρ°ί	г	β Ю-з	alo-3	R	L-10-з
Ж е л (	з з н а я	двух		П р О В (	)дная	ЛИН	ИЯ с
	пре	) в о ί	{ а	ми д н	[ а м. 4 миллиметров
! 300	1 560	-24°	37	7,19	14,44	19,43	8,32
500	1 415	-22°	02	9,75	24,00	26	8,23
800	1 279	-19°	06	12,63	34,2	28,85	6,93
1 200	1 199	-17°	40	18,11	47,35	38,85	6,15
1 600	1 130	-17°	22	19,35	60,0	42,65	5,655
2 400	1 037	-17°	06	25,19	83,90	52,4	4,85
Биме	талли	ч. д	В у×II р О		водная линия
	с п р	о в о	д а м и д ]		нам. 4	мм
300	871	-26°	39	3,65	7,88	5,8	0,0025
600	772	-16°	Ю	4,4	13,78	6,20	0,0025
800	735	-13°	09	4,6	18,10	6,31	0,0025
1 200	717	-10°	00	4,8	26,46	6,7	0,0025
1 600	696	- 7°	14	4,95	35,0	6,72	0,0025
2 400	683	- 5°	32	5,0	52,15	6,94	0,0025

Зная километрич. затухание β и абсолютное затухание βΐ, найдем длину междугородной линии В табл. 3 приведены ориентиро вочные величины дальностей телефонирования по различным линиям при /П=1,2.

Таблица 3.—Величины дальностей телефонирования при βΙ= 1,2.

Медные воздушные линии		Дуралюми-ниевые возд. линии		Железные возд. линии		Биметаллич. возд. линии
*1	*2	*1	*2	*1	*2	*1	*2
2,0	180	2,0	100	2,0	55	2,0
2,5	240	2,5	150	2,5	65	2,5	—
3,0	320	3,0	220	3,0	75	3,0	—
3,5	400	3,5	280	3,5	—	3,5	—
4,0	500	4,0	350	4,0	94	4,0	320
5,0	700	5,0	500	5,0	109	5,0	440

*ι Диам. проводов, миллиметров. *² Дальность, км.

V,

При βΙ=2,4 дальность телефонирования увеличивается вдвое. Если телефонные аппараты включены непосредственно в междугородную линию, то полное затухание b надо приравнять абсолютному затуханию βΐ, которое не должно быть больше 4,5 непера. При расчете дальности телефонирования нельзя исходить лишь из величины допустимого полного затухания; необходимо принимать во внимание также величину допустимого искажения речи.

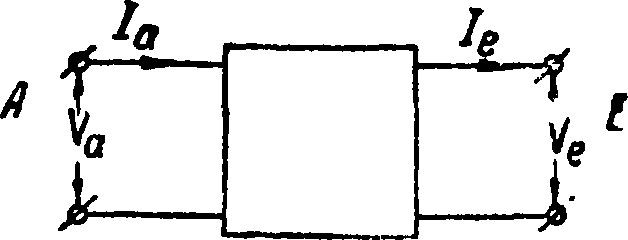
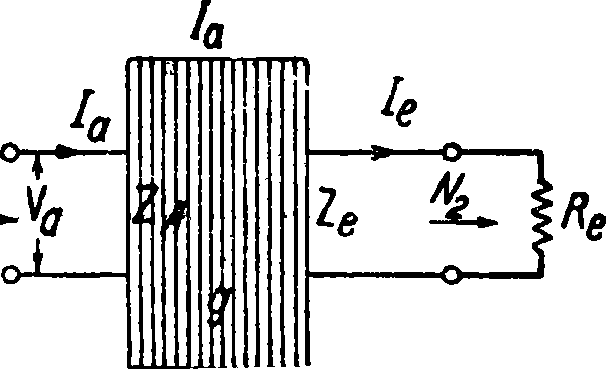
Теория четырехполюсников. Определение. Под четырехполюсником (фигура 4) подразумевается любой электрич. контур, к-рый служит для передачи электрич. энергии; необходимым ограничительным условием является наличие двух входных (начальных) и двух выходных (конечных) клемм (полюсов); с по- _{фиг 4}

мощью первых двух энер- “ ‘

гия подводится к четырехполюснику, а от последних направляется из четырехполюсника далее. Совершенно очевидно, что сила тока 1_ги напряжение V_г у входных клемм четырехполюсника находятся в определенной зависимости от силы тока 1₂ и напряжения V ₂ у выходных клемм, иначе говоря TW(F₂, h),

Ιί=F (F₂, h).

В дальнейшем рассматриваются только такие четырехполюсники, в которых между V_l9 V₂, Ι_λ и 1₂ существует линейная зависимость. Поэтому из рассмотрения исключены четырехполюсники, содержащие: 1) катушки с железным сердечником, работающие на криволинейной части кривой намагничивания; 2) электронные лампы, работающие не на прямолинейной части характеристики, и 3) механические реле. Т^аким образом можно написать

V_±=AjV₂ -f BI₂. I₁=CV₂ + A₂1 где А_г, A₂, В и С—нек-рые комплексные коэф-ты, зависящие от частоты переменного тока, но независящие от V_ΐ9 1_г и V₂ и 1₂. В общем случае эти коэф-ты независимы друг от друга; но мы сперва рассмотрим такие четырехполюсники, коэф-ты которых находятся в определенной зависимости между собой. Назовем симметричными четырехполюсниками такие, которые характеризуются тем, что в их ур-иях (8) коэф-ты А_г и А₂ равны между собой, то есть А_г=А₂=А₉ и кроме того детерминант ур-ия i АВ СА

а)·

(8)

Δ =

= А*-ВС=1.

Е-сли же А_гф А₂, но Δ=А_гА₂ — ВС=1, то такие четырехполюсники называются несимметричными.

С и м м е т ричный четырехполюсник. Ур-ия симметричного четырехполюсника V_a=AV_e + BI_e,

I_a=CV_e + AI_e.

Кроме того детерминант ур-ий равен единице, то есть д= I д® I=а“-вс=i.

Эти ур-ия можно представить в следующем виде: обозначим А=ch д и VВС=sh д и найдем с помощью ур-ий такую величину Z, которая равна

Z __ Ya — YjL ; l е la

T. Э. m. XXа.

25

тогда _

z-Vl

следовательно

A=6hg; B-=Zshg С=^ sh g. Поэтому

V_a= V_ech g + ZI_e shg,

I_a=^ sh g + l_e ch g.

Сравнивая эти ур-ия с ур-иями (1) однородной линии, находим, что величина д является постоянной распространения четырехполюсника, a Z—волновым сопротивлением его. Для определения д и Z имеем следующие выражения:

U₀=Zthg=^; U„=Zcthд=^А

V

щ=th g=th (b + ja) th2и tg2a =

c ’

=

2 M sin φ 1—М2 ’

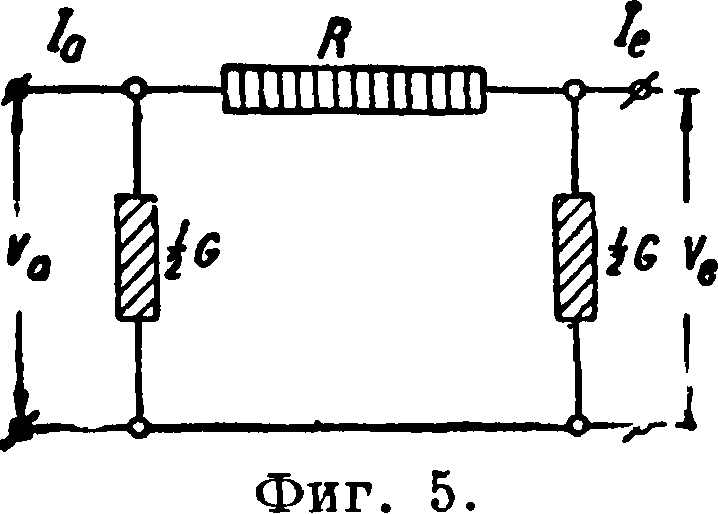
Примеры. Дан четырехполюсник (фигура 5), в котором R — кажущееся сопротивление,

h /₂ ^R/t te

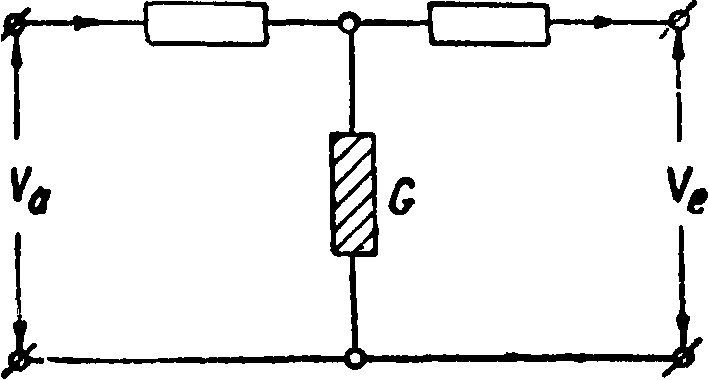
Фигура 6.

a G—кажущаяся проводимость. Ур-ия имеют следующий вид:

Va=v_e(l + i GR) + l_eR=V_eA + I_eB;

I_e( 1 + 5 GR) + V_eG (l + ™)=I_eA + CV_e;

l.

T. o.

A=t+{ GR·, В=Л; C=G (l + ~);

1+-GR

U — — — ^U°~ A~

Z

vi

(ι + ί»«)

sh f

thgf =

1+-GR

RG

(^{1 +}

GR

V RG.

2 2

Если .R=r -f jcoL и G=-4 + ?ω(7, то sh f=ί КО + jcol/) (Л + ;coC) ;

i

R -f" 3^ω t->

(R-j-jtoL) (A+jcoC) 1

1 +

B том случае когда четырехполюсником является однородная линия, то постоянная распространения

У=V(R + jcoL) (А + jcoC₁, а волновое сопротивление

R 4-

A + jojC

T. о. в зависимости от того, являются ли «постоянные» величины R, L, С и А сосредоточенными или распределенными величинами, для постоянной распространения и для волнового сопротивления имеют место различные величины, а именно: в случае сосредоточенных постоянных

sh I=V(R + job) (А +1тСу,

7 ₌ лГ^R+i“>L ^ V А 4- jtoC

14-

(R (Α4^-3^ω^’)

]’

в случае распределенных постоянных

У= VIR + ja>L) (Л + jmC)· Z= yf При малом значении д имеем γ=д. Пусть теперь R= R и G=i·, где R и W—омич, сопротивления. Тогда

z=vTrw· —Д==; вь|-§1/#,

V¹⁺Jw

откуда

R=ZshL; W=fch|·

Проведя аналогичные расчеты для четырехполюсника по фигура 6, получим

R=2Zth% ; W=-^-·

2 ’ Sh b

Несимметричные четырехполюсники.

Несимметричные четырехполюсники в направлении отАкЕ (фигура 7) характеризуются следующими ур-иями:

У α= A_XV + BI;; 1_а=cv_e + А₂1_е, причем детерминант Д_а равен

Д_а=| ^Aca,=_AiA₂-BC=1,

откуда

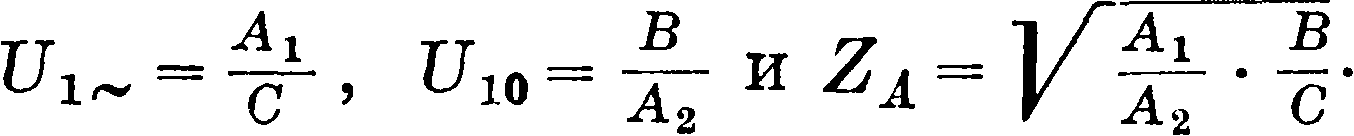
Для обратного направления, т. е’ от Е к А (фигура 7), имеем:

У e — V_aA ₂ + BI_A; I_E=AJ_a + V_A С;

Δ*=Δ_α=А,А₂ — ВС=1;

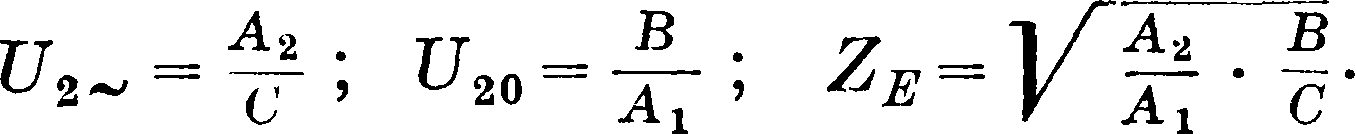
При замыкании зажимов Е сопротивлением, равным волновому сопротивлению Ζ_Ε, входное сопротивление U_a у зажимов А будет равно U_a=Z_A. Обратно, если замкнуть зажимы А сопротивлением, равным Z_A, то входное сопротивление U_e у зажимов Е будет равно Z_E. Ур-ия несимметричного четырехполюсника можно представить также в следующем виде:

У а - Я. [F.chtf + Z_EI_eshg],

¹α= }е 9 + ^ Уе <?],

= ch i? + Z_E qI_A sh g,

Ie= aiAthg +

где q=|/"~=j/Ί^ и g—постоянная распространения. Из ур-ий видно, что несимметричный четырехполюсник можно рассматривать состоящим из симметричного четырехполюсника и нек-рого устройства, к-рое, имея постоянную распространения д= 0, соединяет два различных сопротивления т. о., что ни на одной стороне не получается отражений. Это устройство в отличие от идеального транс-

Фигура 7.

форматора называется идеальным преобразователем. Величины д, Z_E и Z_A м. б. определены измерениями входного сопротивления холостого хода и короткого замыкания

Z_A=; и thд=yifc;

Z_E= УШЖ» И th g =

Так как

J/lO-

Uir~

U 20 и₂„

Следовательно постоянная распространения несимметричного четырехполюсника в обоих направлениях одна и та же.

Четырехполюсники с независимыми коэфициентами характеризуются следующими уравнениями: в направлении от А к Е

V_a=AxV_e + BI_e Ια ⁼ GV_e + A₂I_e Α^Α,Αι-ВСф 1;

в направлении от Е к А

У_Е=(V_aA₂ + BI_A)

I_e=(V_aC+-A₁1_a)^·,^^^·

Следовательно Δ^ · Δ_α=1.

Эти ур-ия м. б. представлены в следующем виде: v_a=qe^s [V_e chg + Z_EI_e sh д],

^J“ ⁼ !^e4&^{Shi? + I}‘^Chfl]’

V_E=e~^s {V_Achg + Z_AI_A shgr],

I_E=^e~^S 3 [|jsh g + I_Ach

где <5=^9l ~⁹? ; ^ ^T ° ^четь1Р^{ехполюс}

ник с независимым коэф-том также м. б. заменен симметричным четырехполюсником и идеальным преобразователем. Ур-ия отличаются множителями е^б и е~⁶. Здесь выясняется физич. значение детерминанта Δ^, так как

1п Δ^ — 2 (5 д₂₉

то есть равняется разности постоянных распространения д_г и д₂ для различных направлений передачи энергии в четырехполюснике. До сего времени известен только один четырехполюсник с независимыми коэфициентами— это электронная лампа в качестве одностороннего усилителя.

Неполноценные четырехполюсники. Типичными представителями этих

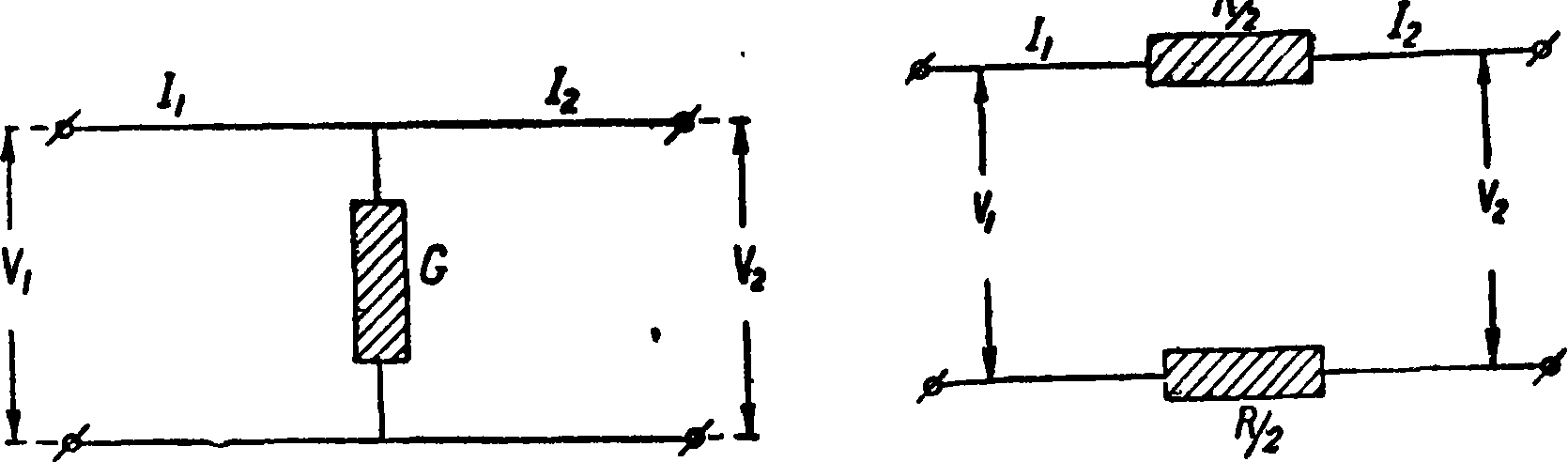
Фигура 8. Фигура 9.

четырехполюсников являются такие, которые не имеют продольных сопротивлений (фигура 8), или, наоборот, не имеют поперечного ответвления (фигура 9). Для первого типа имеют место следующие ур-ия:

V₁=V_2Jh - V₂G + I₂.

Сравнивая эти уравнения с уравнениями четы рехполюсника с независимыми коэфициентами, видим, что

А₁=А₂=1₉ В=о и G=G.

Отсюда получаем, что постоянная распространения д= arc ch 1=0. Для четырехполюсника по фигура 9 имеем:

Vi=V₂ + RI₂,

Il=h.

В этом случае А₁=А₂= 1, В= R и 0= 0; очевидно, что и здесь д= 0.

Практические измерители Т. п. При сравнении четырехполюсников (н’апр“. двух систем Т. п.) между собой для оценки качества передачи необходимо иметь определенную единицу меры. Выясним, не может ли этой мерой быть затухание в четырехполюснике. Включим генератор, эдс которого равна Е, а внутреннее сопротивление равно R_A, к клеммам А несимметричного четырехполюсника, а клеммы Е замкнем сопротивлением R_e тогда сила тока в сопротивлении R_e будет

U.I-

--Ь__I Е [ · I 2 Yz_Az_E I__

{Z_A+ R_A) (Z_E+ Re)-(ZJL-R_A) (Z_S-R_e) e-*9 W В том случае, когда Z_A=Z_E=> Z, будем иметь:

I ίβΤ _р-ъ____2_LZJ_

E ^C I iZ+R_A){Z+R_e)-{Z-R_A) iZ-Be) e-*9 |*

Даже если бы R_A=R_e=Z, т. e. при то и в этом случае величина b не характеризует передачи, т. к. отношение | ~ | находится еще в зависимости от Z. Только в том лишь случае, если бы Z для всех четырехполюсников было выбрано раз навсегда и для всего спектра частот имело бы одно и то же значение, при данных R_a и R_e, величина | ^ | зависела бы исключительно от Ь, и величина b являлась бы величиной, характеризующей передачу речи как по громкости, так и в отношении ее искажения. Но волновое сопротивление Z, во-первых, неодинаково для различных линий, и кроме того его величина изменяется в зависимости от частоты. Следовательно величина Z за постоянную величину принята быть не может, а потому и величина собственного затухания четырехполюсника b не характеризует качества передачи. Очевидно, что коэфициенты А₁₉А₂, В и С, постоянная распространения и волновое сопротивление также не могут характеризовать качества передачи, т. к. они являются параметрами передачи. Отсюда следует, что нам надо изобрести меру качества передачи. Выясним, каким требованиям она должна удовлетворять. 1) Эта мера качества должна характеризовать способность четырехполюсника к передаче установившихся процессов. 2) При одной определенной частоте она должна служить для оценки силы звука. 3) Для всей совокупности разговорных частот показать, в какой степени передается полоса частот и с какой равномерностью звука. Мерой этой будем пользоваться, сравнивая испытуемый четырехполюсник со стандартным, в качестве которого выбираем идеальный преобразователь, соединяющий между собой вполне определенные сопротивления. Меру качества передачи назовем эффективным затуханием. Т. о. имеем две системы (фигура 10). В первой—генератор (Е, R_a) работает на четырехполюсник, замкнутый сопротивлением R_e; во второй системе вместо четырехполюсника включен идеальный преобразователь, что соответствует тому, что генератор замкнут внешним сопротивлением, рав-

Фигура 10.

ным своему внутреннему сопротивлению. Тогда эффективное затухание определится следующим образом: эффективное затухание к четырехполюсника, замкнутого с обеих сторон соответственно сопротивлениями R_a и R_e, равно половине натурального логарифма дроби, числитель которой равен кажущейся мощности N₀, отдаваемой генератором (с внутренним сопротивлением R_a) внешнему (приемному) сопротивлению, равному также R_a, а знаменатель равен кажущейся мощности N₂, к-рую отдает тот же генератор, но внешнему (приемному) сопротивлению, равному R_e, причем между генератором и приемным сопротивлением включен четырехполюсник. Следовательно

(10)

Обозначим входное сопротивление на первичных зажимах четырехполюсника буквой W в том случае, если вторичные зажимы замкнуты сопротивлением R_e (фигура 11). Тогда кажущаяся мощность N_l9 воспринятая четырехполюсником. будет равна

,_т I Е |М w ! _ I Е j* _1 __

I R_a + W I* 4 I R_a I I Rg + W

I 2YRaW

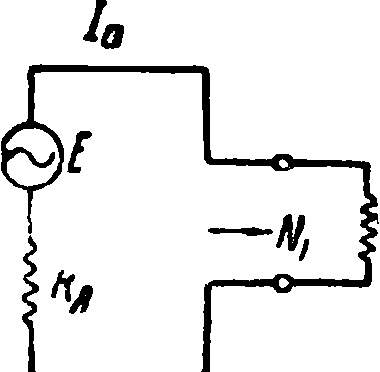
Обозначим

I ^Ra+^W I == μ 2YR0W

Если R_a=W, то M=1 и Nj_=N₀ =

1 E i² 4 (Да)

В общем же случае, когда R_a=^W, 1 JV,

Νι=^Ν°Μ

откуда по аналогии с ур-ием (10) напишем

fc - - In —=¹ In I —I; ^Л “ 2 ^[nN, 2 ^Ш ₂утш

величину к назовем затуханием вследствие отражения, которое имеет место при R_a=^W. Теперь проследим распределение энергии между четырехполюсником и приемным сопротивлением R_e (фигура 12). Четырехполюсник воспринимает кажущуюся мощность N_l9 а отдает приемнику N₂. Отношение кажущейся мощ- _фиг. ₁₂.

ногти N₂ к кажущейся мощности N_± является кпд η четырехполюсника. Для вывода η воспользуемся ур-иями несимметричного четырехполюсника, замкнутого на сопротивление R_e:

^F«=/|(^ch»+f7-^sh^)^F-

^I‘-V^rk(^cha+ %.?^ЬзН·

Умножая эти уравнения друг на друга и огра ничиваясь абсолютным значением, получим: |Г_я|.|2_в|-| (chff + gshff).

(chg + gsh^j-IKM-U·

Т. к. I v„ I · I I_a I=и I v_e I · | I_e |=JV“, то пвсле простых преобразований

¹=’ е²» ( ^κ + ^ζ_:γ ι

*1 2 YR_eZJ L

Νι

JV₃ " Так как

Re ~b Z_e ² ^ — 2g Re~Z_e

lip- -Z_€

][

e~^lg

то

Re~ Ze ReYZ_e

W-Zg

w+z_a

Nl

No

_e2Q ^Re + ^Ze y 2 Y R_eZ_e

откуда но

fW+Zg V» ]

i 2 YwzJ I

	= ъ-	In	W + Zg i
2 N2 Λ			2 Ywz^r 1
J	No	N,	_ e2k. e2k‘
	N i *	n2

ln

Re~ ~ Z_e

I 2V R_ez_e I

— g2 <* + *">

fc=fc + fc.

• Следовательно эффективное затухание равно к=b + In

In

R e~l· Z_e

Rg + W 2 YRaW

+

•ln

W + Z_a

2VR^e ~“ 2VWZ~~

Рассмотрим несколько частных случаев: 1) Если R_a^W, то

fc =

R_e -j- Z₍

In - — In

W+Zg

= k".

R e~l· Z_e2YR7-Z_e

2V~R_eZ_e “I 2VW-Z_a

2) ЕСЛИ Rg=Zg, TO

Тс=b + ln j

3) W=Z_a.

T. к. в этом случае должен быть R_e=Z_e, то

Ra-z_a

4) Если R_a= Z_a и R_e= Z_e, to к=Ь.

5) B_a=I R_a I=r_e*+ jS_a·, R_t= R_t J*~

Если

r_e + jS_e; Z_a^ Z_a e^^X_a + jY_a;

Z_e= Z_e j^a‘=X_e + jY_e.

TO

R_P

I 2 YZ_e R_e

r_a=xy,

$ a ~ a>=COS Ψ_€ и

Ί e~

Rg + Zg

= COS φ_α.

I 2YZgRg

В условиях T. π. cos φ_α и cos<Pe всегда меньше единицы; следовательно lncos<p_a и lncos^g являются отрицательными величинами; т. о. в этом случае благодаря отражению происходит усиление, т. к. эффективное затухание системы будет меньше собственного затухания четырехполюсника. Пользуясь ур-ием (9), можно вывести выражение для эффективного затухания в другом виде, а именно:

к=b₀ + In + In

Re ~Ь Ze

+ ln

Ra+ZaY

zVraZaI

-y_q~29 ^lxe~ _г R A ~~ Z

2 Y R_eZ_E

R_e~ZE Ra-Za

До сих пор мы рассматривали систему передачи в виде одного четырехполюсника; на практике лее приходится иметь дело с рядом последовательно включенных четырехполюсников;

поэтому выведем выражение для эффективного затухания при любом числе последовательно включенных четырехполюсников (фигура 13). Пусть первый четырехполюсник воспринимает кажущуюся мощность N_l9 второй—N₂, последний—N_r и наконец приемное сопротивление— N_r+1. Попрежнему обозначим буквой N₀ мощ-

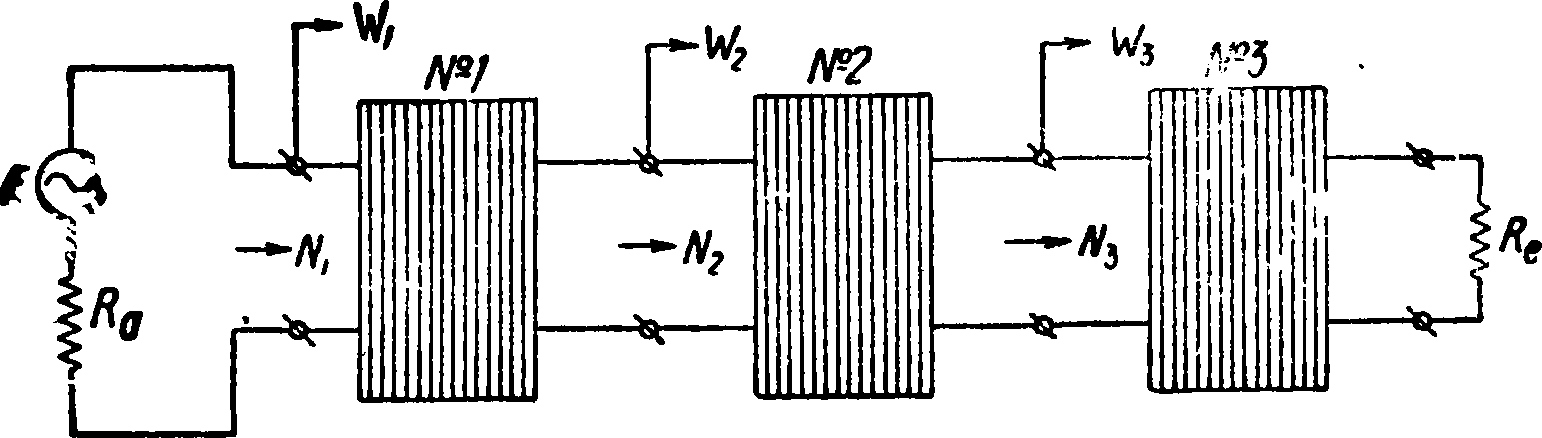
Фигура 13.

ность, отдаваемую генератором в том случае, если он нагружен сопротивлением R_a, равным“ внутреннему сопротивлению генератора. Тогда эффективное затухание всей системы определится из ур-ия:

_РгП- ^νά„. ^е ~N_r+1

Это ур-ие можно переписать так: _в2* ₌ 1L!».=02«. 02 «"=е²

Но е²*" =,

No	= e2lc. e5
N i
Νι	Ni iV2 iV3
Nr + i	iV2 ‘ JV3 ‘ iV4 “
	= · e2^2 · e2

N_k

tfft+i

N_r

N_r+i

Следовательно

/с"=/cj + fcg + /с₃ -f-. причем

Щ=Ь_к- In

tin +

! W_n

• + К,

+ %еп I

W_n- -Zfig I _____

zYWnZ^nl^ I 2 YW_{n +} iZen

где W_n—входное сопротивление η-го четырехполюсника при нагрузке его (п + 1)-ым четьт-

го° зо° 40° за⁰ Фигура 14.

рехполюсником ит.д.; последний же четырехполюсник нагружен приемным сопротивлением R_e. Что же касается затухания то таковое попрежнему равно

fc ₌ in|-gg±gi.|.

I 2YR_a-W 1 I

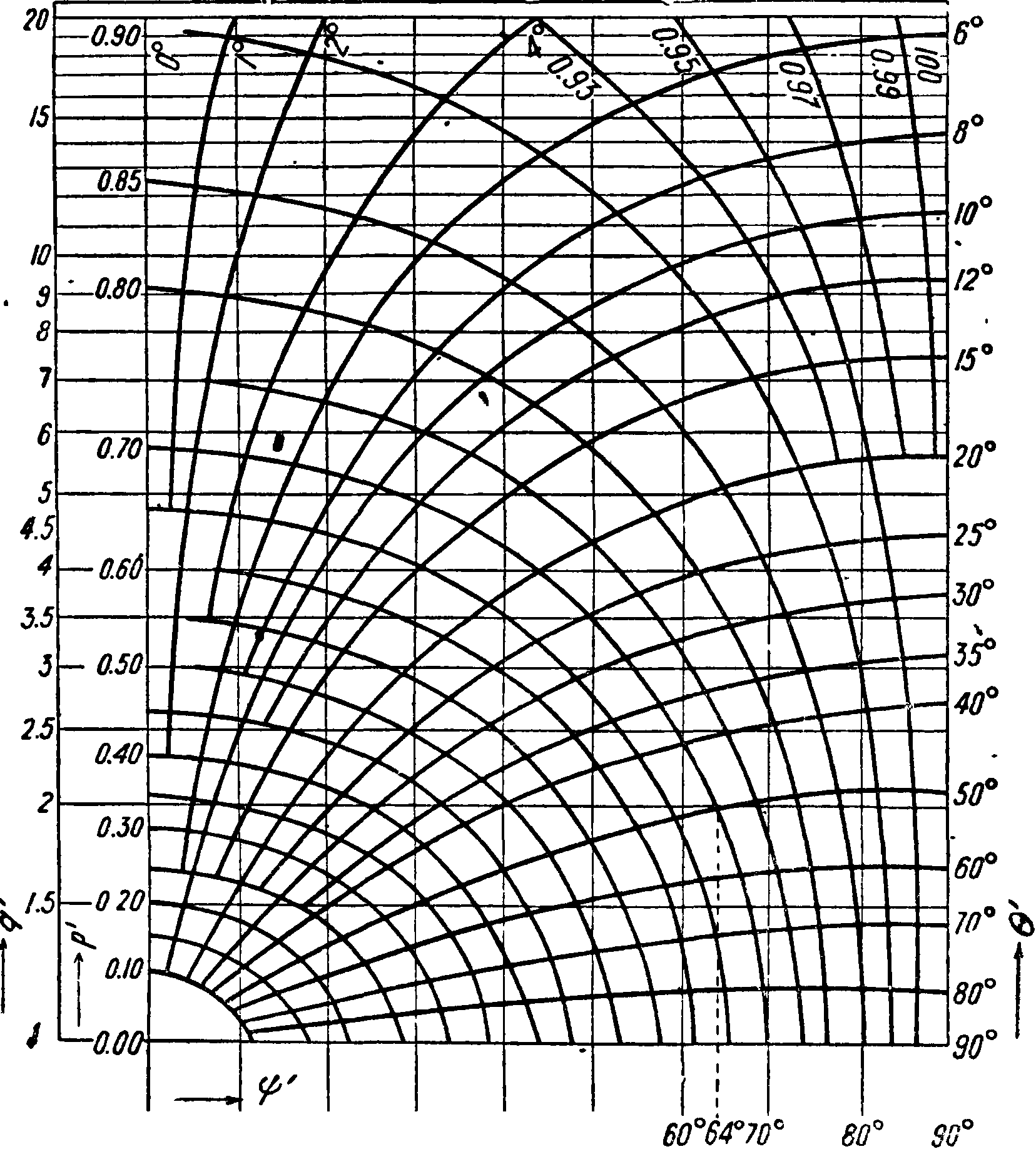
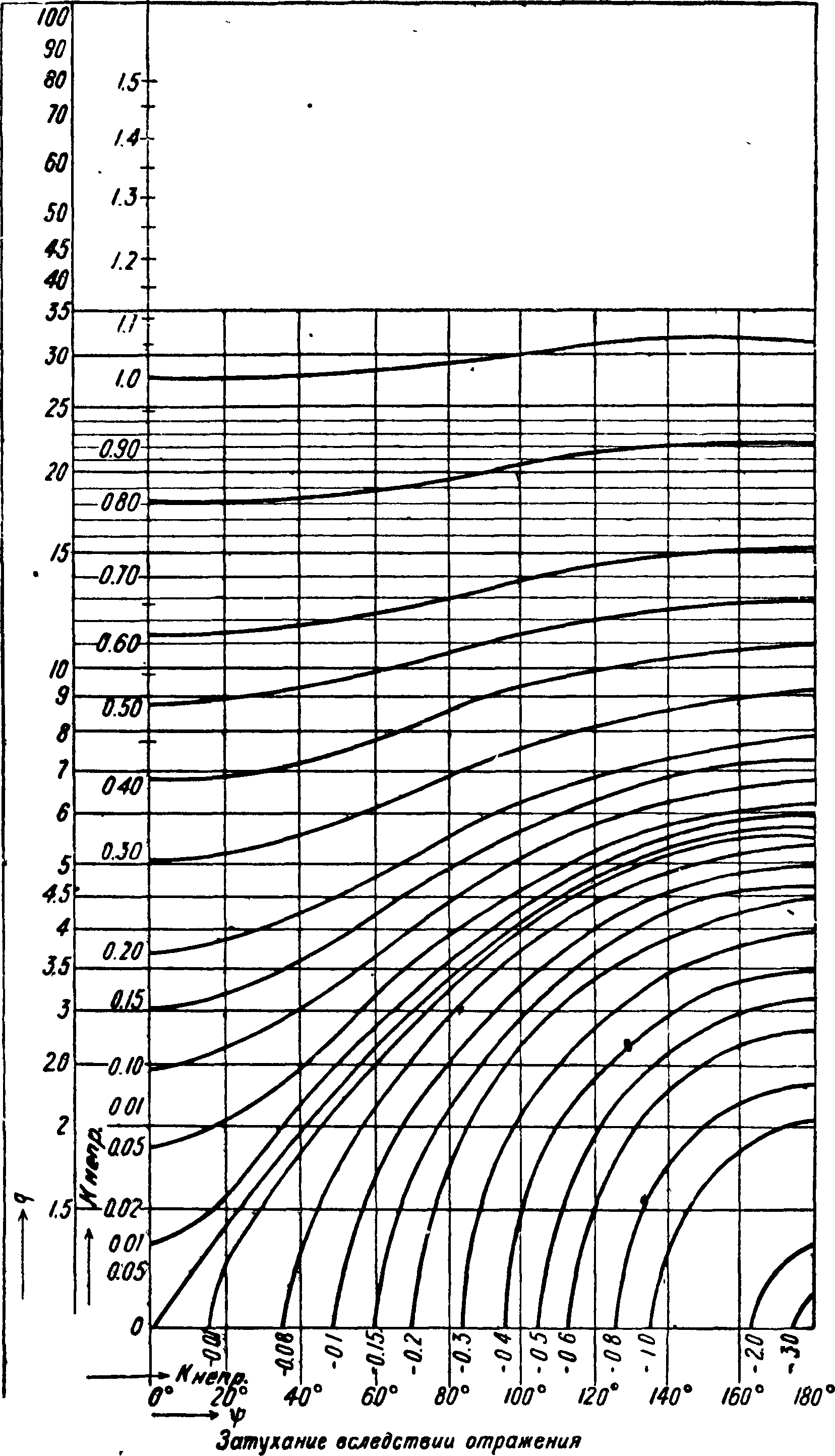
Для облегчения расчетов служат фигура 14 и табл. 4 и 5 для перехода от^и^кри^и для перехода от р и # к q и ψ.

Таблицы построены на нижеследующем расчете. Коэф. отражения в общем виде м. б. представлен в виде:

р=*1Г**.

Так как

Ri+R 2

,1 к--к ·*

^th*“ii+TT5

где х—любое действительное или комплексное число, то

th (In х) =

Пусть тогда

*2-1

X*+l

th

^X-Vw_t·

(in/g-»-»·

= p.

R₁ + R₂

Следовательно коэф. отражения можно написать также в такой форме:

p=th [ш §]

Так как

Bi-IBHe*¹; В_г= В_г |е^3>а;

й.

ТО

Я*

и ψ= ψι - φ₂тогда

<?^v,

i i I R i I

¹ « ¹=I Ri I

Обозначим p=I p I е^]в,

p I e^jS=th (in Vq)=th^ln V q | + j,

откуда

Ip I=l/* ch (In 1 g D-COS ψ ₊ n _ sin у. V ch (In I q p.+ cos φ sh (In | <? |) ’

выражение для (p) можно еще упростить:

I P j² — 1 _ COS Ψ

р ²+1

ch (In J q )’

следовательно

th (In I p 1)--

COS ψ

ch (In j q I)

T. о. для I p I и θ, T. e. для модуля и угла ко-эфитщента отражения, имеем два независимых ур-ия. С помощью этих ур-ий построена система кривых (фигура 14) для модуля 1291 и угла Θ коэф-та отражения в том случае, когда I q I > 1 и угол ψ лежит в первом квадранте (0° < < 90°); ось абсцисс является осью ж-ов;

она дана в линейном масштабе; по оси ординат нанесены деления q в логарифмич. масштабе. Напр. при у>= 64° и q= 2 получим Θ=50° и |р I=0,70, то есть

p=0,70^J50°.

Для того чтобы воспользоваться этой системой кривых для I q < 1 и Θ > 90° (см._табл. 4), приведем пример. Пусть R₁== 360е^-<?45°; R2== 1260e^J80°; найти коэф. отражения р.

Находим г)=i p i _e^je =

_360_

^: 1 260 ^:

JL_. ¹ 3,5’

I (7 I=¹J :

^{14 1} I й₂ I

ψ=— 45° — 80°=— 125°.

Итак I q | < 1 и ζ.ψ лежит в третьем квадранте (111 кв.). Сперва мы должны обратиться к табл. 4.

Для третьего^квадранта и при | q < 1 имеем: I q I== 3,5; v>=180° + у>=180“ - 125°=55°.

ψ q	III кв.	IV ΚΒ.	I ΚΒ.	II ΚΒ.
	L80° < ψ < -	90° <γ>< 0	3<V»<+9 0“ 1 1	180° 1
<t> 1 1	q=q V»,=180°4-v» 1 ρ=—, Ρ δ—δ	q=Q ψ* — — ψ Ρ=Ρ# <5=<5	q=q v-V Ρ=ρ <5=<5	q=q γ>=180° — ψ 1 (5=0
Q<i j	, 1 q ~ q y>=180°+V 1 Ρ~ ΖΓ7 Ρ <5=-(180° — -V)	, 1 ν=-ν P=P <5=180°--<5	, 1 q=-« ψ=ψ Ρ=Ρ’ <5=180°- -δ	, 1 y>/=180° — ψ 1 Ρ=— Ρ <5=180°--6

Для этих значений q τι ψ находим I pI=0,73 и θ =27°,

откуда

^ΙρΜϊΗ ^{= 1,37; е}=-(180-0) =-153°,

следовательно р=1,37 е— у¹⁸³°.

В том случае, когда даны значения р и 0, а требуется найти | ^ | и служат та же система кривых (фигура 14) и табл. 5.

Таблица 5.— Переход от р и#к g и ψ.

&	III ΚΒ.	IV ΚΒ.	I кв.	II ΚΒ.
ρ 1	L80° < δ < - 1	90° < <5 < ( 1	)<<5<+90‘ ί	1 *<(5 <+180° 1
(	Ρ=Ρ	Ρ=Ρ	Ρ=Ρ	ρ=ρ
	<5=180°-Η	<5=—<5	<5=-<5	δ=180°-ό
Ρ<! <	1 q~q	q^q	q=q	1
ι	v=-v	v=-v	ψ=ψ	ψ=ψ
	, 1	, 1	, 1	1
(	Ρ= —	ρ=—	Ρ — —	ρ =—
	Ρ	Ρ	Ρ	Ρ
	#=180°+<5	<5=<5	<5=<5	<5=180°-<5
ρ>1	1 q~q	q=q	q~q	1 «“Τ
1	y>=— (180° — -ψ)	ψ~— (180° - *2 -V) H	•β II Η»· 00 Ο Γ ·€	у>=180с—V3

Теперь перейдем к построению системы кривых для нахождения затухания вследствие отражения. В общем виде величина затухания вследствие отражения выражается т. о :

= In I —1.

I 2YR₁R₂ I

Преобразуем это выражение.

Т. к. сЬ®=|(в“ + е-*) и ch (In х)=~ [х + ^,

то, обозначая х=j/"^, получим:

<4·ηΚ0=^|;

откуда при - q I R ~ ~ R₂ I

- q jv

H^{ch ln}(K|)]|=

I 2YR_XR_Z

= I ch (in -+- ? I) !,

fc=In I I=In H- (ch In ! q | + cos y)l,

2YR₁R₂ ² l² j

2 e^zk=ch In I q | + cos ψ.

T. к. cos ψ=cos (— y>), to Jc зависит только от абсолютного значения разности углов 9>ι—9>₂, то есть мы можем положить

v= I Ψι-Ψί Ι·

Так как

ch (In j qr I)=ch (— In I <71)=ch (ln^),

to Jc остается без изменения при замене | q своей обратной величиной | ~ |. Поэтому для определения величины Jc достаточно иметь один график, на котором даны значения | q | ^ 1 и для

Фигура 15.

углов ψ от 0 до 180°. Такой график^изображен на фигуре 15. Напр. при

R_±=I В_г e^j<Pi=I 630 I e“^J*¹⁰⁰ и й₂=I Д₂1 е³’’²=11 400 I e^-320,

найдем

₇=|_?|е1(л-^=|^[_е+^°·,

следовательно | q |=0,43 и ψ=10’ или j-K=2,3, Ψ=10° и h=0,085.

Эффективное затухание неполноценных четырехполюсников. Четырехполюсник по фигура 16 будем для сокращения называть «поперечным» четырехполюсником, а по фиг, 17—«продольным». Обозначим буквой N₀ кажущуюся мощность, отдаваемую генератором в том случае, если он нагружен сопротивлением R_a, равным внутреннему сопротивлению генератора, а буквой N₂—кажущуюся мощность, воспринимаемую приемным

Л.

Фигура 16.

Фигура 17.

сопротивлением R₂, если между генератором и этим сопротивлением И₂ включен четырехполюсник. Тогда эффективное затухание определится из ур-ия

_р%к _

^N»

Так как

Ν_Λ

N₂

Е ² ~MRa I |Е|²Ч 1

R + Ra + Re I² для продольного четырехполюсника и

R(R_a + R_e) + R_aR_e I»

для поперечного четырехполюсника, для продольного четырехполюсника:

поэтому

No ₌

n₂

Тс=In

Ra + Re I²

2 V R_aR R,

2 VR_aR

1 -

R

Ra + Re

I + In I

1 +

. R

Ra + Re

для поперечного четырехполюсника

n_{q =}n₂

Jc=In

Ra + Re

2 YR_aRe Rg ~f~ Re

2 VR_aRt

RgRe

1 4- -

I ^ R Ra + Re

R_aRe

R Ra+Re I

Если R_a= R_e=R, то в обоих случаях к=In | =0,405.

Ур-ия для Тс можно преобразовать сл. обр. Введем понятие о входном сопротивлении W поперечного и продольного четырехполюсников при нагрузке их сопротивлением R₂. Нетрудно видеть, что для поперечного четырехполюсника W= R+ R₂, а для продольного

W =

R>R 2

четырехполюсника „ — _{R + R}формулы для Тс соответственно

Подставляя в значения R =

= W-R₂ и R =

ReW

R_e-W

ного четырехполюсника ft=in I ^Ra+W I

получим: для продоль-

_I l_n| I

2 ¹¹¹ W

Re

W

I 2VR_aW

для поперечного четырехполюсника

Л-1п|^±Ж|+[1п

I 2ΫR_aw I ²

Влияние отражения на входное сопротивление и на затухание линии. Падающая волна напряжения V_n и падающая волна тока 1_п, распространяясь вдоль линии, находятся в определенном соотношении друг к другу, а именно:

v_n

i

= z,

где Z—волновое сопротивление линии. Если линия на своем конце замкнута нек-рым сопротивлением R_e=£Z, то между напряжением V_eи током 1_е в конце линии будет уже другое

V_e η

соотношение, а именно: j^=R_ei причем из ур-ий (3) для конца линии, то есть при ж=0, получим:

l_eR_e=V_e=V_n + Vо I

z

Vo

Z

(11)

⁷ⁱe¹e___ β __ Уп + Уо β

-у о

Иначе говоря, в результате несогласованности Ζ и R_e в конце линии возникают отраженные волны тока и напряжения. Деля одно ур-ие на другое, получим

Re^e

и или

V_n(R_e-Z)=V₀(R_e + Z).

Назовем отношение отраженной волны к падающей коэф-том отражения и обозначим буквой р: тогда

Уо₌ Re-Z E Vn Re + Z

при R_e=Z, ρ=0; при R_e= 0, р=— 1; при R_e=оо, р=1. В случае несимметричной линии п — ^e~ZE. Rq-Za

Ее R_e + Z_E’Ea R_{a +} Z_A

Явление отражения сказывается на входном сопротивлении линии и на ее затухании, Сперва разберем влияние отражения на входном сопротивлении линии. Из ур-ий (2) имеем

V_a=V_ne>4l +Ve~^iyl) и 1_а=1(1 -ρβ~²*¹), откуда входное сопротивление равно

u_a=X*-z ^1+pe--^w

Ia

1 -pe

-2γΙ

T. κ. γ=β + 7^α, ^το входное сопротивление зависит от частоты и имеет максимум, когда 2а I является кратным 2π. Обозначим

Р-

С другой стороны, р=- 2 8

Re-Z _ — 2т __ -2(г + гв)

Ίΰ+ζ ~^е ~^е

Ιφ

ИЛИ

ИЛИ

е~^2г· е“

-2г.

IV

р е

= I р I

И 2s=φ

поэтому

Ιφ

Тогда

Α_α=Ζ

I р=gi?·

_{1 + e}-2m-2yl _ 1-f e² (^т + У0

₁__e-2m-2yl~ i__e-2(m + y0

Обозначим m + γϊ= g, тогда

‘9 „еО + е^-д -e

_л r? 1 + e *y r? eu -f-e у _r/ „

An ~Z₁__e-_2g Z _pg__e~_g — Z oXYi g.,

Это ур-ие можно представить в несколько более удобном виде для вычислений. Так как д== (Ь + га), то

A_a=Zcth(b+ia)=Z°^{h(b + ia)}-

_ γ ch b cos a + i sh b sin a _ g

s h(b + ia)

sh 2b-i sin 2a

sh b cos a + i ch b sin a

ch 2b-cos 2a

ИЛИ

Ад

Z

sh 2b-i sin 2a

ch2b-cos2a

Построим графически это ур-ие в зависимости от частоты. Прежде всего выясним, чему будет равно отношение при изменении а. Если 2α= 0, то

А_а _ sh2b __ Sh2b 2shbchb , η

ΊΓ ~ сьггь^т 2 sh² ь 2 sbT*~b “ ^{ctn 0} *

Если 2α=2, то

I A J _ I Sh 2b-i l/~ Sh² 2b + 1 -j

~Z I |"ch2b ~ V ch² 2b “ ^A*

Если 2α=тс, то

Α_η Sh 2b 2shbchb _ г

Z “ch2b + l ^cKab^-

и T. д.; дальнейший расчет приведен в следующей таблице, где также вычислен угол между

2 а—>	0	π ~2	n	3 -5*	2 π	5 2 π
а->	0	4	4		4	4
Ι^αΙ-*·	|Z[cth b	z	1Z1 th b	|Z|	|Z|cthb	z
tg e	0	1	0	, i	0	1
		sh 2b		^ Sh 2b		Sh 2b

векторами А_а и | Z |*по ф-ле

, sin 2а

^ ^ε shTT

Величина | А_а |=| Z | cth Ь больше, чем Z|, а величина |H_a|=|Z|thb меньше, чем Z. Т. о. ния при различных величинах коэф-та отражения |р|. Выясним например, как изменяется модуль входного сопротивления в зависимости

от частоты при | р |=0,2 и при | р |=0,4. Выше мы имели д=ш + γΐ=г + is + βϊ + ial =

= v -f- βϊ i (s -f- clV) — b ia

следовательно b=r + βϊ, T. к. | p |=^, то

Табл, 6.—Данные для вычисления |А_Я|.

ω	z	βϊ	τ,+βΐ	τ 2,-{βΙ	th bx	cth b i	th b2	cth b2	j Z| th b i	1Z j cth bi	Z th b2	|Z[cth b2
2 000	1600	0,88	1,68	1,29	0,926	1,08	0,88	1,13	1 480	1 740	1 380	1 860
4 000	1645	0,87	1,67	1,33	0,93	1,078	0,8693	1,15	•1 540	1 780	1 440	1 900
6 000	1 700	0,90.	1,70	1,36	0,9354	1,07	0,8764	1,142	1600	1 820	1 500	1 940
8 000	1 800	0,95	1,75	1,41	0,94	1,06	0,8875	1,12	1 700	1 900	1 600	2 000
9 000	1 875	0,97	1,77	1,43	0,944	1,055	0,8917	1,118	1 760	1 980	1 680	2 100
10 000	2 000	1,00	1,80	1,46	0,947	1,05	0,8977	1,10	1 900	2 100	1 800	2 200

входное сопротивление в зависимости от частоты колеблется около значения волнового сопротивления, становясь то больше то меньше его. Что же касается угла ε, то таковой колеблется около нулевого значения, принимая величины j- arc tg _Ь*_2Ь. Для того чтобы представить графически взаимное расположение век-, торов М_а| и Ζ, от-

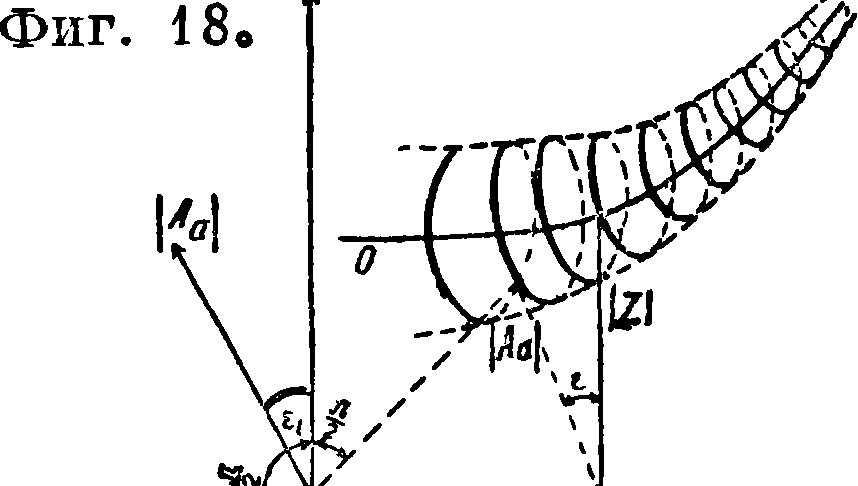
ложим по оси ОХ частоты; на плоскости ΥΟΧ—вектора Ζ, а на плоскости ΥΟΖ— вектора | А_а | (фигура 18), Кривая 00 показывает как изме-уо V^х няется I Ζ | в зави-

симости от частоты,

Как"видно, конец вектора А_а опи- сывает в зависимости от частоты вин-⁷ тообразную кривую в плоскостях, па раллельных плоскости ΖΟΥ, вокруг линии волнового сопротивления. Отдельные витки этой винтовой линии с увеличением частоты уменьшаются, т. к. вследствие увеличения затухания b^thb и cth b приближаются к единице, а угол ε—к нулю. С помощью ур-ия (12) очень легко выяснить форму кривой входного сопротивле-

при р 1=0,2 получим 0,2 или г“ 0,8.

Если I p I=0,4, то г=0,46. Для отличия обозначим г_г=0,8 и г₂=0,46. Задаваясь | Ζ | и βϊ, теперь можем вычислить А_а (табл. 6).

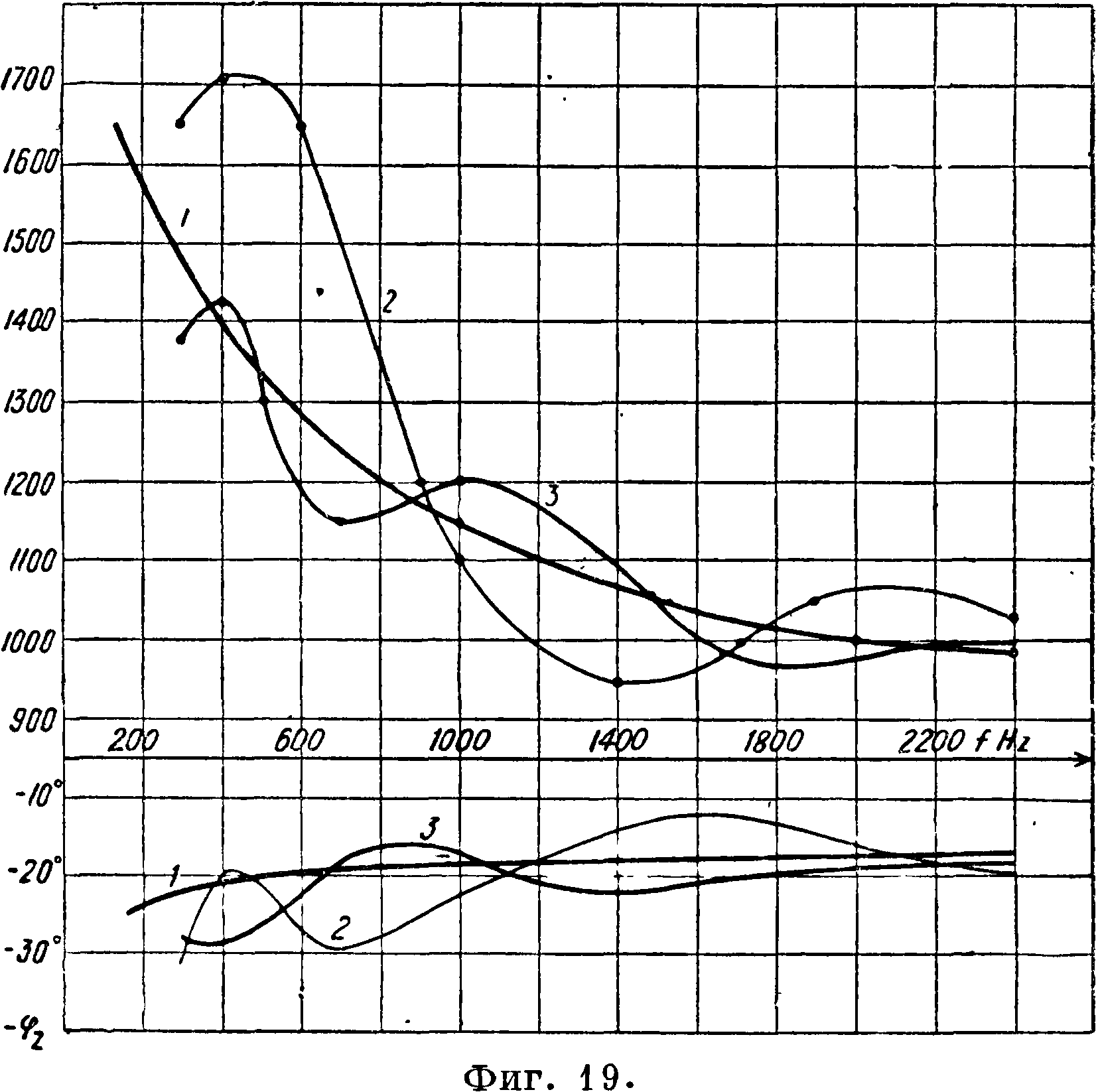
На основании изложенного мы можем вывести следующие заключения: 1) Входное сопротивление однородной телефонной линии в зависимости от частоты носит плавный характер и постепенно изменяет свое значение только в том случае, если линия замкнута-на своем конце сопротивлением, равным волновому сопротивлению линии. В этом случае входное сопротивление равно волновому сопротивлению. 2) С большой степенью точности приближения заключение предыдущего пункта относится также к электрически длинным линиям, то есть к таким, абсолютное затухание которых превышает 1,5 (βΙ> 2). 3) При наличии отраженной волны, то есть при наличии стоячих волн в линии, входное сопротивление в зависимости от частоты теряет свою плавную форму и принимает волнообразную форму; волна эта колеблется около значений Ζ, как около нулевой линии. Чем больше коэф. отражения р, тем больше «амплитуды» волнообразной кривой входного сопротивления. Выше приведены (фигура 19: 1—волновое сопротивление железной

Так как линии, 2—I=60 км, 3—I=100 км) результаты вычислений входного сопротивления неоднородной линии, состоящей из железной линии и кабеля, замкнутого своим волновым сопротивлением, причем входное сопротивление вычислялось при изменении длины I железной линии. Чтобы выяснить влияние отражения на затухание, воспользуемся выражением для эффективного затухания:

к= + inI 1 + inII +

2Y R_eZ_E 2Yz_ARa

-2 γΐ Et_e~Z_{E t} Кд~%А I.

E._e + Z_E Ra+Zl I ’

-f In 1 -

где

+ In 11-k= b

^σΐ “ 2 ^ln Ϊ

Pa

+

2 yl

PaPe^e - ^ал + σ,

i-p|

² ~~ I I σ₂=ln I 1 - e~^2v!p_ap_e.

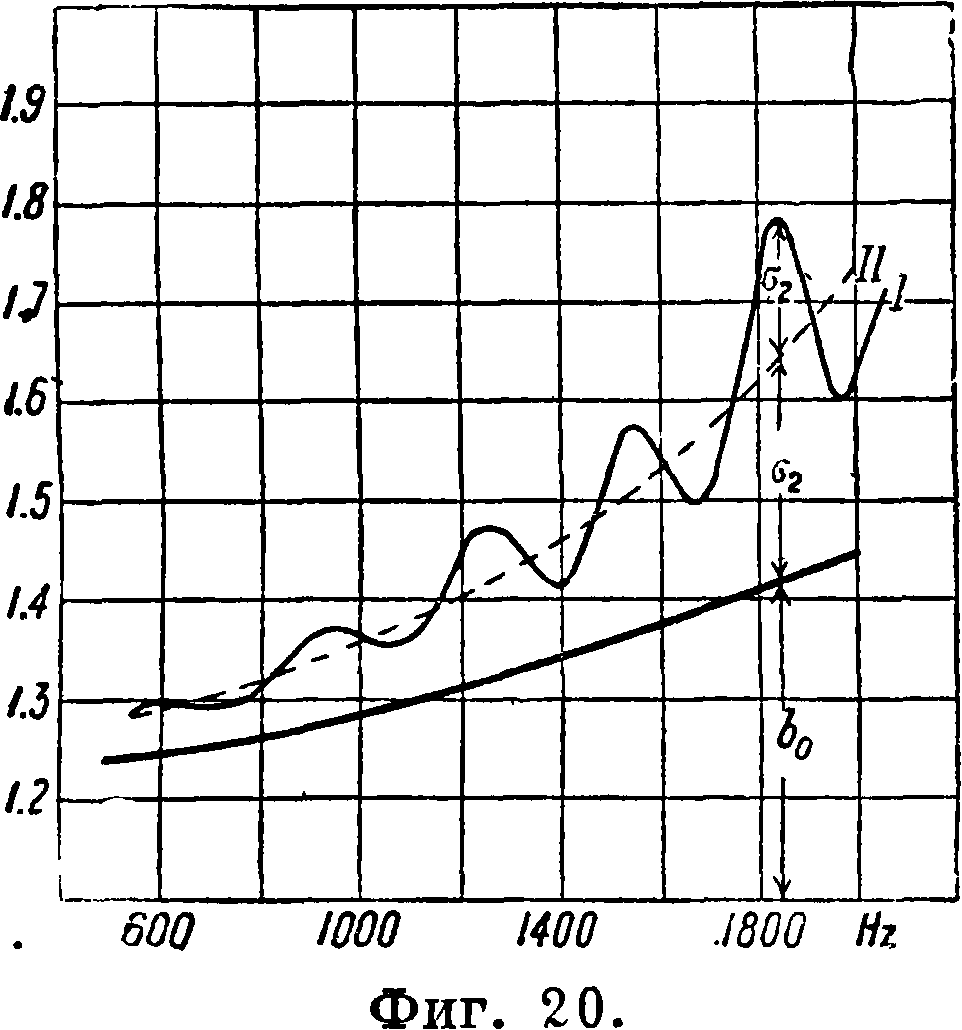
Величины σ_λ и σ₂ являются затуханиями вследствие отражения, причем первый член од в

b (непеоьп ЗаВИСИМОСТИ ОТ ЧИ

СТОТЫ изменяется по плавной кривой (фигура 20, кривая II), а второй член σ₂— по волнистой кривой I, причем максимумы соответствуют тем частотам, при которых 2а I является кратным 2л. Особенное значение явление отражения имеет в линиях, оборудованных промежуточными усилителями; в этом случае вф-ле коэф-та отражения под величиной R_e подразумевают входное сопротивление линии U, то есть р=·_{υ + ζ}. Как известно, коэф. точности настройки промежуточного усилителя <5, равный υ-ζ

0=2

U + Z’

обусловливает собой явление эхо, для измерения которого введено понятие об эхозатухании Ь_Е, причем

е^-Ь*=Ц |=|Р|,

откуда

b_F=In

I v

= ln

U + Z I

u-z

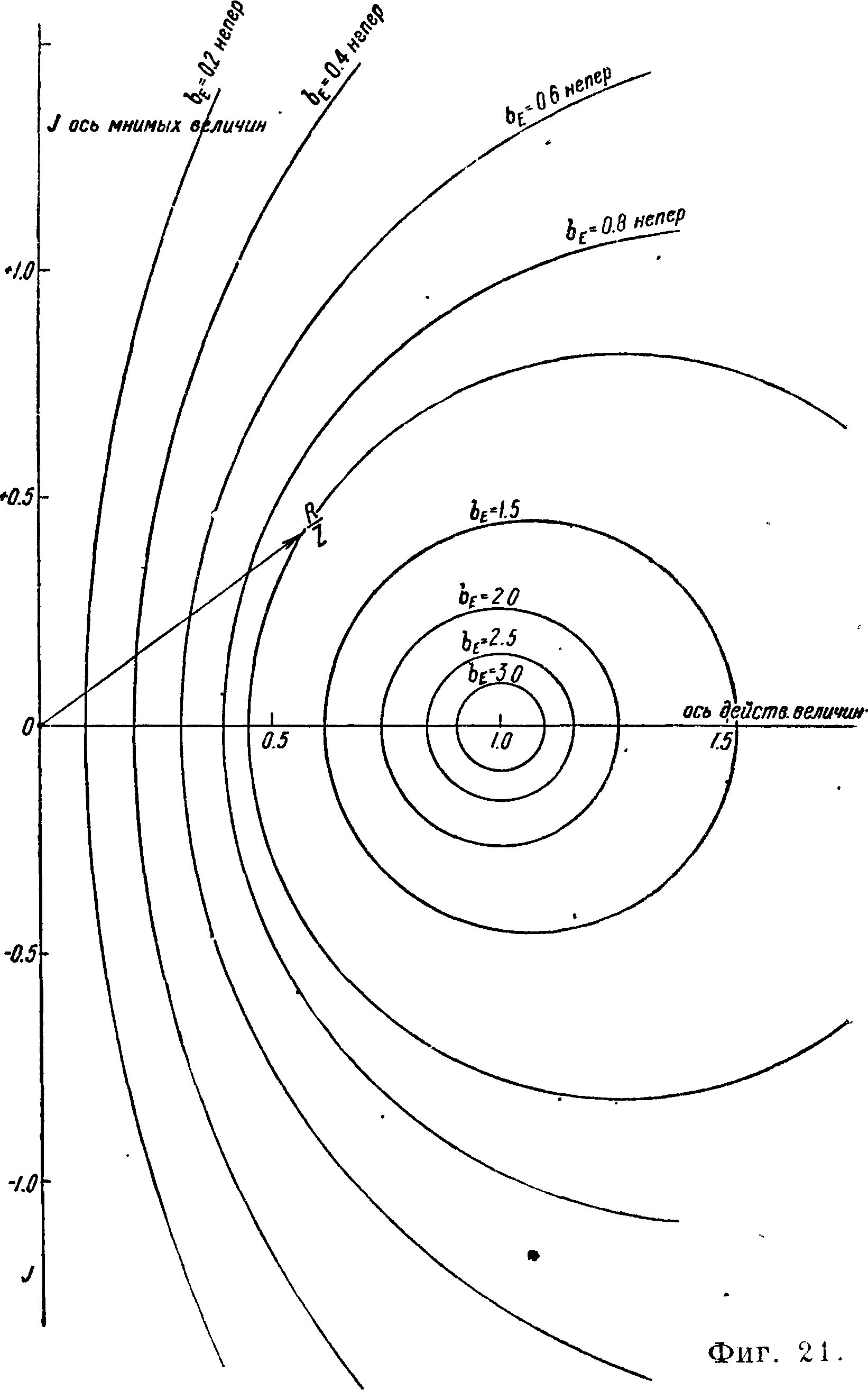
Кривые постоянных значений эхозатухания 7 и

Ь_Е в плоскости γ являются окружностями

(фигура 21), положение центра которых определяется из ур-ий:.

1-4-1 р I²

^ХЦ 1-1 р [2

и Уц ⁼ 0,

радиус же окружностей находится из ур-ия

Г=;

Действительно тт

-1

2|р|

1-J v I²

-ь_Е _

το

у х jy,

IР1

(х-1 )² + У²

(Х-1)2+у2 ’

откуда получаем ур-ие окружности:

Γΐ+1^12-13 Г 2|р| -12

Li-|p|²J Li—J Р |²J

Искажение речи. Искажение первого рода. Изменение формы кривой разго

ворного тока вследствие неодинакового затухания различных частот называется искажением первого рода. Мерой искажения первого рода служит разница Аb между величинами полного затухания при различных частотах, а именно при ω₁= 15 000 (f=2 400) и ω₂== 3 000 (/= 500), то есть

АЬ < Ьо) — 15000 — bш=3000.

Эта разница для первостепенных сообщений не должна превосходить двух неперов. Величина искажения Δ&< 2 непера распределяется сл. обр.: а) величина искажения, обусловливаемая междугородной линией, не должен быть больше 0,7 неперов; Ь) величина искажения, обусловливаемая городскими линиями (в обоих городах), не должна превышать 1,3 непера; с) искажениями, обусловливаемыми МТС и ЦТС, можно пренебречь. Необходимо иметь в виду, что воздушные медные, бронзовые и дуралюминиевые линии практически не вызывают искажений речи; поэтому при применении перечисленных линий в качестве составных частей телефонной цепи искажениями, обусловливаемыми ими, можно пренебречь. Например рассчитаем искажение, имеющее место между двумя абонентами различных городов, связанных междугородной медной линией; в обоих городах связь абонентов с ЦТС и МТС осуществляется кабельной линией с жилами диам. 0,5 миллиметров. Расстояние наиболее удаленного абонента от МТС как в одном, так и в другом городе равно 5 км. Следовательно искажение, обусловливаемое кабельной линией в районе обоих городов, равно Δb=I (β._ί5 ооо βζ ооо) ⁼ Ю×(0,23 0,10)=1,3.

Отсюда видим, что длина I ж. б. увеличена до то есть по 7,5 о в каждом городе. Для второстепенных сообщений величина искажения, обусловливаемая междугородной линией, м. б. увеличина до 1,5 непера. Ниже приведена разность Δβ=β ₅ ооо — β₃ ооо для различных линий:

Название линий	Диаметр, | ММ 1	Δβ
Медная (бронзовая). j	в 4	0,00023 0,00009
Железная.·	4	0,008
j	2	0,0089
Обыкновенная кабель- ) ная..j	0,8 0,7 0,6	0,0255 0,035 0,045
ί 1 1	0,5	0,057

Искажение второго рода. Если какое-либо периодич. колебание дойдет до уха, то оно в нем разлагается по закону Фурье. Ухо сортирует основное колебание и гармоники по их амплитудам, но не может различать

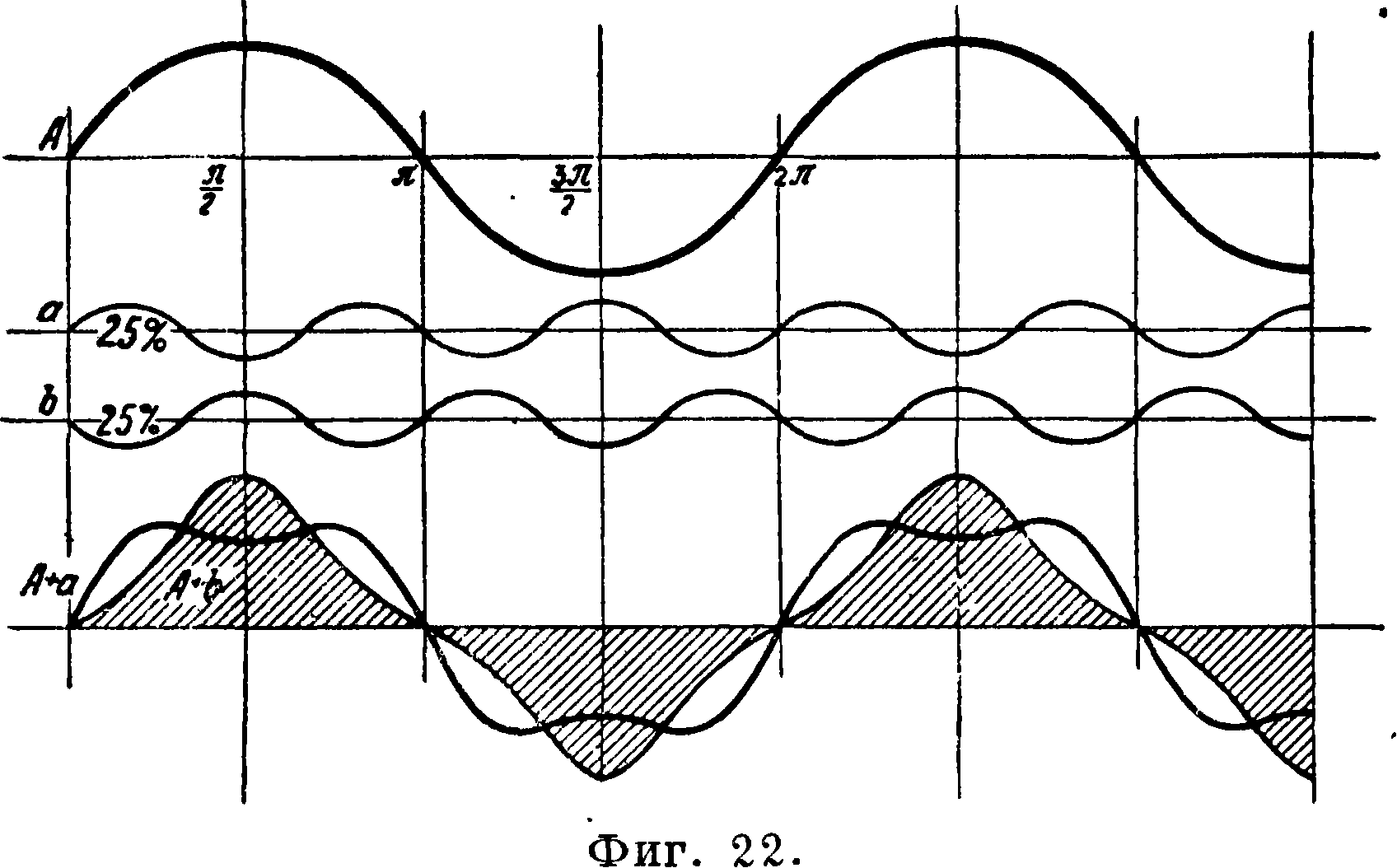
их по сдвигу фаз. На фигуре 22 изображено основное колебание А и ее третья гармоника а, амплитуда которой равна 25% от основной. Результирующая кривая обозначена (И + а). Если по какой-либо причине третья гармоника будет сдвинута на 180° (смотрите кривую b), то результирующая кривая будет (А + Ь). Как видим, форма кривой совершенно различна, но ухо не в состоянии различить эти кривые. Ухо слышит (А- - а) так же, как (А- - b). Т. о. сдвиг фаз не вызывает искажения речи. Искажение же второго рода вызывается удлинением передаваемого сигнала,что вызывается различными групповыми скоростями, то есть скоростями, с к-рыми двигаются группы волн различных частот. Мерой искажения второго рода принимается разность

^Δί=^ι(^-^)^{<30χ10_3(;κ}·> где I—длина линии в км, а₂ и а_х—угловые из мерители волн при двух любых круговых частотах ω ₂ и ω! в спектре от со=2 000 до со=15 000.

Искажения третьего род а—н ели-нейные искажения. Основные уравнения телефонной линии были выведены в том предположении, что постоянные линии зависят только от частоты, но не от величины (амплитуды) тока. Это условие означает, что постоянные электромагнитные поля линии, в частности магнитная проницаемость μ, не зависят от силы тока. Этому условию удовлетворяют телефонные линии, если в них не включены например катушки с железным сердечником, усилители, характеристика которых имеет лишь приближенно прямолинейный характер, и тому подобное.; в противном случае параметры передачи безусловно зависят от силы тока. Вследствие такой зависимости на линии возникают кроме разговорных частот еще новые частоты, т. н. комбинированные колебания. Следствием этого является искажение речи, называемое нелинейным, или искажением третьего рода. Т. к. искажение третьего рода в линиях практически возникает лишь при значительной силе тока, то считаться с ним приходится при телефонировании с усилителями по пупинизирован-ным кабелям (смотрите Пупииизация).

Искажение четвертого рода вследствие отражения. Даже при передаче по линии, свободной от искажений, речь искажается также в том случае, если кажущееся сопротивление приключенного к линии аппарата не равно волновому сопротивлению линии. Как известно, в этом случае в конце линии возникают отраженные волны, величина которых изменяется с частотой; благодаря этому изменяется воспринимаемая приемником мощность в зависимости от частоты. Равенство сопротивления аппаратов волновому сопротивлению отнюдь не совпадает с условием максимальной отдачи мощности линией аппарату. До введения усилителей при передаче на большие расстояния нужно было считаться с кпд линии и мириться с искажением передачи. В настоящее время отсутствие искажений является главным условием, тем более, что при наличии усилителей кпд линии значения не имеет. По этой причине стремятся посредством уточнения соответствия между аппаратами и волновым сопротивлением линии уменьшить отражение на конце и зависимость его от частоты. При неоднородных линиях этого нельзя достигнуть вследствие большого и совершенно незакономерного колебания кажущегося сопротивления линии от частоты; для устранения этого необходимо включать в месте соединения линий надлежаще подобранные переходные трансформаторы.

Лит.Г Юрьев М., Теория телефонной передачи, М., 1931; Ковале н ков В., Основы теории связи, М., 1931; Цимбалистый М., Основы теории телефонной передачи, М., 1932; В г e i s i g F., Theoretische Te-legraphie, 2 Aufl., Brschw., 1924; Hill J., Telephonic Transmission, L., 1920; Hoick e О., Zur Theorie u. Berechnung d. Betriebsdampfung in einfachen u. zusam-mengesetzten Dbertragungssystemen, «ETZ», 1932, 3;

Fiihrer R., Stossfaktor u. Stossdampfung, ibid., 1932, JO; Schmidt К., Neubildung von unterdriickten Sprach-frequenzen durch ein nichtlinear verzerrendes Gdied, ibid., 1933, 1. M. Юрьев.