> Техника, страница 84 > Теория вероятностей

Теория вероятностей

Теория вероятностей, отдел математического анализа, изучающий случайные явления, то есть явления, происходящие под действием причин, носящих неопределенный характер. Случайное явление может иногда произойти, иногда не произойти. Ожидаемое, но не наблюдавшееся явление называется вероятным. Для того чтобы выразить математич. вероятность ожидаемого события числом, надо определить благоприятствующие и неблагоприятствующие статочности, то есть обстоятельства, осуществление которых ведет к осуществлению или, наоборот, к неосуществлению события. Все статочности должны удовлетворять трем условиям: 1) должен быть несовместимы, т. е“. при осуществлении одной статочности невозможно осуществление в том же испытании какой-либо из остальных; 2) должен быть все возможны, то есть при данном опыте одна из этих статочно-стей должна осуществиться; 3) равновероятны (равновозможны). Приведение событий к равновозможным основывается на следующих положениях. Два события равновозможны, если они разбиваются на одинаковое число равновозможных событий; два события не равновозможны, если они разбиваются на неодинаковое число равновозможных случаев. Наоборот, если два равновозможных события разбиваются на неодинаковое число различных событий, то эти последние не м. б. равновозможными. Если ш—число всех несовместимых, всевозможных и равновероятных статочностей, п₁ и п₂—числа статочностей, благоприятствующих соответственно событиям Е_г и Е₂, то вероятности данных событий будут:

Итак, вероятность явления есть отношение числа статочностей, благоприятствую щ их данному событию, к числу всех статочностей. При этом различают случаи:

1) п > ™, то есть р>|,— событие вероятное;

2) η < ™, то есть р < I,—событие сомнительное;

3) п=0, то есть р=0 ,—событие невероятное;

4) п=т, т. e. р= 1,—событие достоверное. Если —=q, то первое событие в q раз веро-

Π·2

По 1

ятнее второго, или—=-, то есть вероятность щ Q

второго события составляет - от вероятности первого. Если р=~— вероятность данного со-

бытия, то р — ——-вероятность противопо ложного события, и следовательно V + р= 1,

то есть сумма вероятностей противоположных событий равна 1. Согласно определению вероятность представляется рациональным числом, лежащим между нулем и единицей. Определяя же вероятность нек-рых событий как пределы вероятностей других событий, мы введем иррациональные числа. Бывают случаи, когда события можно назвать предельными для других событий подобно тому, как касательная называется предельным положением секущей.

! Если событие Е м. б. названо предельным для

1Шдаг₁.со(|ь5ГИ^_!)^н1?1«ЗМ. ft» ···> вероятности которых образуют ряд чисе^_л{р₁₍ р₂. ···· Р», ···. ТО; ^роят^Чт^фб^з^^^-дерределится как предал ойL«TRP¥iYj^cliitfiW-ffi?#/e»t при возрастании задача не-

ср«^^тйдйад#о=[1ййщо|_нй@р§н, числитель ц.11?дамедгайьн^рда!ж?рч§?»^даур^а11у· ^Рас-^№.Ш»й№$^ВЙШШЙЬ1Р0йВДгЙ11 ^{на какое} даед^да^ВР.ФШ^ШРйТМадТй ер_;да^{а чл}ены pH^^jnpp^wpMeilWra&i’nfiafTWSoWi^ii.- ^иск°-ьЖВДоР^&Рдайй^&тШРЭйЧк¹ ^йшаддамьн.ым чи-едш.^т^Дбйдавй^еяв!!^ ,® ®ойеешроедам во-

тштш^гк^!ттзм

ВД iaoPSOT^T^rf, ТШтЯЙЙ

дМбй.НТ^о? ^^т1Шё^ё^г^№^Шнб^^ fmWWmh, ,· &<ЬВДо£ёкё ЩйШвйШ Ш ШШ) J3H котилвияанэо миллиметровмсомяоао лш“ст л йн гыбоч

ВДШ^патТШю да°ШШЬоШ ЭДЮРЙ

яшрш ныщт&тш& ч^тмм чаооо ,вщ; ; нптыооо хыижтлгюяоняйг? ог.энн воя 9 $г?Ш)

и. сшопй&е; i н Щ

ад.Ы>йАемсб8§нЩ т, iT^^et¥6qS8^peg]^

β ёй^{0 Д}§й“ Abroi л η 11 д се q к ϊ гпл о

.0 .Μ 0Ιΐ/ώΙΠϊ3γΐβρΓΙ_ ТЭД <рту JUlf 1|%^!1 ЩЛ И V м г. г; .ГЩ

-эн хэяк¹ о Ш я А—мо² i i v.b Я ьАшлпЖонАяткпщ ШЖТЯ5ШШ§адлВДйй^

ЙШввйЯ^

ммтиооо онлвятотэатооо У ЩI! сяуятотки q Π ( л Я I о :т?дуо I штидр^ыфцш#^9®ftTfUiq‘ a от ,₂Ή н _t^rA

получим: ^ -^_tⁿ ч ^iCi

-т о а т о (Ап к и^й“ п~п“²нт-У о~н⁵!’ к"6 q о ч улстП i?p&$a яйцДётТ °эйбё О b и ^ШкОййЯ ,“ ьРа к! ^eeOtHO· fg Ь о о^у ^{0 тонн 1111} Ч ^{и 0 1}

о IT ‘А Чл?. о N 1^Т Л ,01 IT Т

Основными теорёй&йяРТР№.^1ГйМйФт£&#^гФеОре·*

f .ϊρορ^β“^β w>?p-

кие вероятностей. С л с£ж екие в ё р о я т н о-

Ь^в^ЫШо^Шт₍ *щт“ф™фф (™-

Ьовместимые статочности-n_l,n₂, w₃, А., то ве-рштгжос|гь1 bcd б вхтияоф авца) -с даме вер/ШтнеоЩзй вШцШйй^д отдаАШ^еЧ-рей^трит^н^ Д

-о тea фщ^^Ыа^ЫЬт ^з2кд Щ1 Логц f *=J=A π··,Τ^;ϊ т i,l т ¹ т т ί?^Γ

ШЩчквогуя .9 .т пот

Ρ=Ϊ Vi +А2 +⁽Рз +

ЮООТУТ 09К1

ИТООПТПОПВЯ ТО ТОП!. ПТТООЭ nit l.I< .00 ОЧСЦОО

где m—^:число в®ех статочностеи при данном адэ&й rcj?i щ^ёЬт1фт^^ттщт можных несовместимых яв^ец^й данной груп-йшдаяждо оеущес’вквдьсяупричем^νρ_г,«р₂,#зг“-.Д

p_w—вероятн(^т.¥кШ1?)ддаейи%«^0‘.ч .то .-. о

Pi + Рз ч1 Рз f-iv+Pw ⁼ 1*

^pp^jTgoсрбыг

Р0Ж«^^т)РШШ9!)11()1ГДса котвиг.автад-ю11 ото“;.;im

ббэЬ-Ш »*йЧ13т(3«.| Хай-й^Р^йк^РЭД:

шяс^кмттщътыш⁰

Ш^Тп a fe и 9 « о й) Wii⁰ oJie^-^pfiTftip,

ЙР^ТШШ^^бдаЯб!^ 9«^У.1Й

вероятностей искомого и остальных событий, среди которых рассматривается первое. Если из общего числа m статочностей п_г и п₂—числа благоприятствующих статочностей соответственно явлений Ε_±ηΕ₂, то относительная вероятность первого явления будет:

ril. Πι + П₂ _ _п_г

m m п_г + п₂ ’

Теорема умножения вероятностей. Вероятность сложного события, состоящего в совпадении двух простых событий, равна произведению абсолютной вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие имело место.

Пусть из m всевозможны^, несовместимых и равновозможных случаев

2, ^1» -^-2) ··· > Άη9 A-n+ll ··* J *·· »

§р,рвые Πχ случаев благоприятствуют событью Ёц$ а первые п случаев благоприятствуют Е₂.

Шш^тность события Е_г будет—·; вероятность ^;у(|ытия Е2 при условии, что событие Е_гймё^й’^то, равна, т. к. случаи t!_w1+1, ., A_mфддздают. Наконец вероятность появления обо-^^бытий^х и Е₂ равна Следозательно м.м. ооа. ьп:/:^г‘Т·) _

»,??. 008. Jh. 1L - - ”.

а };атчг!/1 m ?i_L m

p - О

Тее^ема k. б: кьфажена ф-лой: z> (^2>-№)№₂, E₁)=(E₂)(E_l,

?Цё¹ iE₂)—вероятность появления событий

^£^г;й “(Е{У¹ и (£/₂)—соответственно

Е₂),

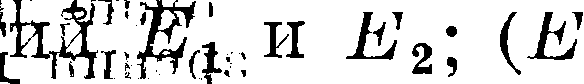
, Ε^χ)—веро-

ятммь-$обышя])-Ь^тя, ддогда известно существование Е_х (Е_г,Е₂)—вероятность события Е’,

Е_г. Правильность обобщенной теоремы, выражаемой ф-лой (Е,Е₂.:. Ед - (ЕМЕцчВх) (Е?„ Е,Е₂).

(Е_{, E_lE._z. E_U1), (А)

легко обнаруживается заключением от η к n+ 1 (методом математической индукции).

События,.Εχ и Е₂ называют независимы-м и, если &езуслоцная вероятность одного из них равна условной вероятности его, вычисленной в предположении, что другое событие имело место, т. ел события^ Εχ и Е₂ независимы, если вероятность одного;Аз них не- изменяется от τατχν, имело ли место другое событие или нет. Теорема о вероятности сложЩйх событий для случая независймых_ событии; выразится так: вероятности _Τί ср&Ш0*№т ЩО^ьрц^у состоящего из< "совпадения? миллиметровдашадх· простых независи-

^Й !§Й Μ!»»® абсолютных вероятностей эт^двдоотьцх^орбцТци. Ф-ла (А) ПХШЖ&П ВЩ9Ь?^ГТ 0Ч7>1. О Г τι я ’) а о ‘)

w5« (В)

. *а белых и ί и :мернмм?шарову извявекают ^наудачу после-

^пР^ичем

кД.жш«Льдат¥Й;#1^ извле-

ченйек ,вОзвращаготм^г©< яшщки < ’©пределить ве-

^бе-

лыМыоН.гОА^адцнь^ д?а иейць^и^рдесь слоя^-Η0βί^^άιτΗθ !€0ό^№Τ^ρϊΜ3ί Φρ@®) πρίχίΦί,ϊχ н е з а-k,Ϋ% :_t f/^бдмуТ йй_{f {};появле-HHHbeiriVk tiiymb· 4Μ9Γο:,ρ|ρ4ί&^ίΓι

Ά

bj-if ,-/,[

t*онq«м3 .Η

^и,®^Г<. а *4-

’D и¹2ц ι .π-

obon ! * iϊΐ< ρ

вероятность появления во 2-м случае черного шара:

а + Ь ⁹

вероятность появления в 3-м случае черного шара:

ь а~+b ’

следовательно по формуле (В) искомая вероятность сложного явления будет:

_ а b _Ь _

Р ~ a+b a+b a+b ~ (α+ b)³ *

Если условия задачи изменить—1-й и 2-й шары не возвращать в ящик, а откладывать в сторону, то сложное событие будет состоять из трех простых зависимых явлений, вероятности которых соответственно будут:

а _b_ _ь - 1

cl -f- b * о, b — 1 а + Ь — 2 Вероятность сложного явления теперь согласно формуле (А) выразится так:

«=^ь-___

^ cl b a -f- b - 1 cl b — 2

Полная вероятность. Если q_ifq₂, ., q_n—вероятности всевозможных и несовместимых гипотез, свойственных данному испытанию, a p_lf р₂, ., р_п—условные вероятности события Е при допущении соответственных гипотез, то полная вероятность события Е выразится так:

Р ⁼ Pi^i ~Ь Р₂#2 +. + PnQn-Здесь имеет место ряд сложных событий, состоящих в совпадении осуществления события Е и одной из гипотез, причем вероятности этих сложных событий (по теореме умножения) будут: Ρι?ι,ρ₂?2, --чРпЯп, а т. к. эти сложные события несовместимы и всевозможны, то полная вероятность (по теореме сложения)

Ρ=Ρι?ι + Ρ222-τ. + РпЯп·

Вероятность сложных событий при многократном повторении опыта и закон больших чисел (теоремы Я. Бернулли и Чебышева)— см. Статистика.

Математическое ожидание. Если Pi, Рг> Р₃> .» Рп—вероятности данной группы несовместимых и всевозможных явлений и если переменная вещественная величина может принимать только значения х_г, х₂, х₃, ., х_п в зависимости от того, какое из явлений данной группы осуществляется, то вероятность того, что х получит значение ж_г·. равно вероятности Pi соответствующего события. Выражение Ρι^ι + Рг^ж2 +. + Рп^хп называется математич. ожиданием переменного х. Оно занимает некоторое среднее положение между наибольшим и наименьшим значениями х в ряде х_и х₂, ., х_п. Если переменное изменяется непрерывно, то математич. ожидание этого переменного представится определенным интегралом.

Вероятностна posteriori. Если опыт состоит из двух частей, причем в первой части, которая была наблюдаема, произошло событие Е_г, то вероятность возможного события Е₂ в подлежащей наблюдению части опыта называется вероятностью a posteriori. Этот отдел Т. в имеет многочисленные приложения в .опытных науках и в статистике. Основной теоремой вероятностей a posteriori является теорема Бейеса (J. Bayes). Если q_u #₂,., q_n—вероятности несовместимых и всевозможных гипотез C_lt С₂, ., С_п, свойственных дан ному опыту; Pi, р₂, ., р_п—условнЬ1ё!&ё$ЬМ1¥№ сти события Е при допущении соотвё№^ШнМА&: гипотез, то при условии, что событиёЖейо^бй¹· лось, вероятность a_t гипотезы С* a jDosliteHoii выразится так: ^тг * ^т?^гп

₌_vm___

^г PiQi ~Ь PzQi ~Ь ··· ~Ь PnQn ол⁽>.0

Действительно искомая вероятность×ЙbЙ-ного события, состоящего в совпадении бЩ-ществления события Е и гипотезы С_г·, выразщтся по теореме умножения двояко: 1)×=

2)×= 1? i a_it где Р—априорная полная вероятность сооытия Е, следовательно

₌ PiQi ₌_PiQi _

^г Р PiQi + PiQz- ~. + PnQn

Эта формула м. б. получена на основании т. н. теоремы деления вероятностей.

Пример. В одном ящике находятся 1 черный шар и 2 белых, в другом—1 белый и 5 черных шаров. Переложив из первого ящика во второй 1 шар и вынув затем из второго ящика

1 шар, обнаружили, что этот последний шар белого цвета. Определить при этих условиях вероятность предположения, что шар, переложенный из первого ящика во второй, был черного цвета. Вероятность р_х гипотезы, что был переложен черный шар, равна ¹/₃, вероятность р₂ гипотезы, что был переложен белый шар, равна ²/₃. Вероятности q_x и q₂ появления белого шара при допущении этих гипотез соответственно ^ и |. Следовательно

i 1

3*7 _ 1

^α1“. 1 1 2 2 5’

3*7+3* 7

Приложение Т.в. к исследованию результатов измерени й—см. Ошибки измерений и наблюдений.

Гауссова теория способа наименьших квадрато в—см. Практическая математика.

Лит.: Марков А., Исчисление вероятностей, 4 изд., М., 1924; Лахтин Л., Курс теории вероятностей, М.—Л., 1924; Некрасов П., Теория вероятностей,

2 изд., СПБ, 1912. В. Никаноров.