> Техника, страница 84 > Теория корабля

Теория корабля

Теория корабля, специальный отдел прикладной механики, рассматривающий внешние силы, действующие на судно, и поведение последнего при различных условиях. Т. к. рассматривает вопросы, связанные с пловучестью (смотрите) судна, с его остойчивостью, с сопротивлением его движению в воде (смотрите Ходкость), с поведением судна при волнении—т. н.к а ч к а суды а,—с его поворотливостью (смотрите ниже) и т. д.

Качка судна. Изучение качки судна имеет целью выяснить поведение судна на взволнованном море, его мореходные качества при этом и меры, коими можно их обеспечить при проектировании судна. При качке возникают добавочные напряжения в корпусе судна, которые должны быть учтены при расчете продольной и поперечной прочности. При качке возникают в отдельных частях судна, например в мачтах, котлах и тому подобное., силы инерции, которые должен быть приняты во внимание при расчете мачт, фундаментов под котлы и других механизмов.

Характер качаний на волнении находится в зависимости от качаний судна на тихой воде, поэтому изучение качки начинается с изучения таковой на тихой йоде. Если судно, находящееся на тихой воде, накренить на один борт и затем предоставить себе, то под действием вы-

прямляющей пары (смотрите Остойчивость судов) оно начинает возвращаться в прямое положение, перейдя к-рое накренится на другой борт, и т. д. Оно начинает совершать колебания около своего положения равновесия до тех пор, — пока колебания не поглотятся сопротивлением воды. Колебания, происходящие около продольной оси, называются боковой качкой, а колебания около поперечной оси—к илевой качкой. Вращение судна около вертикальной оси называется

Фигура 1.

рысканьем. Оно в исследовании качки не рассматривается, т. к. относится больше к поворотливости судна.

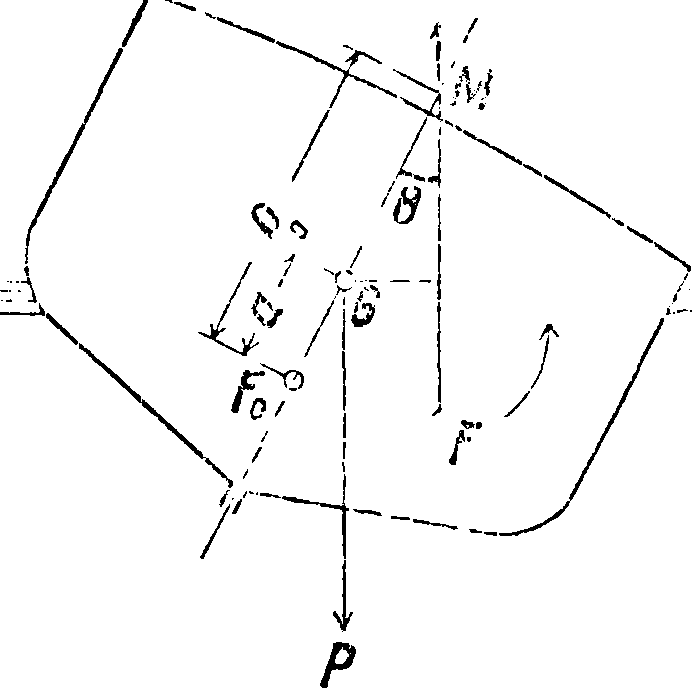
Применяя ур-ие вращательного движения к случаю качающегося судна около продольной оси (фигура 1) и пренебрегая сопротивлением воды, получим

^КЖ2 + ^р(е~^а) sin 0=0.

Здесь К ·— момент инерции массы судна, Р (ρ —a) sin Θ—момент восстанавливающей пары, Θ—угол наклонения, а—возвышение ц. т. судна над центром величины. Предполагая наклонения судна незначительными, можно считать метацентрический радиус ρ величиной постоянной и равной ρ₀, a sin Θ заменить самим углом Θ. Тогда

Κ^ + Ρ(ρ₀-α)θ=0.

Обозначая —?%= ^а-=п², получим альное ур-ие к движения т + »^в=о“

диференци-

Общий интеграл его будет

Θ=С i cos nt + С₂ sin nt. Начальными условиями принимаем при t=0 Θ=0₀ и -jI=0, отсюда С₁=0₀ и С₂=0. Следовательно

Θ=θ₀ cos nt.

Угол наибольшего отклонения θ₀ называется амплитудой качаний, а время Т, необходимое для отклонения судна из одного крайнего положения в другое и обратно, называется естественным, или свободным, периодом качки судна. Время Т определяется из ур-ий п (£_х + Т)=nt_x + 2π,

<*>

Из ур-ия (1) видно, что период качки не зависит от величины размахов судна, если они невелики, то есть качания судна изохронны, кроме того, что период качки увеличивается с уменьшением метацентрической высоты и уменьшается с ее увеличением. Остойчивое судно качается быстро; ве,неостойчивое—медленно. Очень медленные качания показывают на весьма малую начальную остойчивость. Период качки возрастает с увеличением момента инерции судна, то есть большие суда качаются медленнее малых.

Если принять во внимание сопротивление воды, то в ур-ие движения необходимо ввести добавочный член. Принимая сопротивление воды пропорциональным первой степени угловой скорости, получим

άθ

Здесь N — момент сопротивления воды. Обо значая ^=2h, -~^-=п², получим диферен-

циальное ур-ие движения (попрежнему полагая sin θ Θ)

^ά2θ + 2 h

di* "Г

άθ

dt

+ η²θ=0.

Общий интеграл его будет где в=е ^м (С_г cos n_Lt + С₂ sin nj), п=η² — h² > 0.

При тех же начальных условиях имеем:

Οχ-βο, С₂=^0„,

угол наклонения

Θ=в₀е~^м (cos n_Lt + — sin n_xt).

(?)

Последнее ур-ие изображает колебательное движение с постепенно уменьшающимися амплитудами. Период его колебаний несколько больше, чем без сопротивления воды. Он определяется выражением

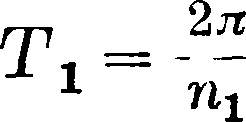
(ι~ Ζ²)

Времена, потребные на наклонения и выпрямления, несколько отличаются друг от друга:

чтобы судну встать, нужно на ~ времени больше, чем для того, чтобы лечь, где φ== arctg^-. Если принять сопротивление воды пропорциональным второй степени угловой скорости О² или пропорциональным двучлену, один членк-рого выражает пропорциональность первой, а второй—квадрату угловой скорости (вида 2Ь6-{-кв^/2), то получится для угла отклонения более сложное выражение. Период качки остается весьма близким к периоду качаний без сопротивлений, то есть качка обладает изохронностью. Для более интенсивного погашения амплитуд размахов качающегося судна увеличивают момент сопротивления воды, для чего применяют боковые кили. Относительно большие боковые кили делаются на малых судах с меньшим коэф-том полноты мидель-шпангоута. На больших судах с почти прямоугольным мидель-шпангоутом действие их по сравнению с сопротивлением скул незначительно, т. ч. от них можно отказаться. Большие боковые кили могут оказать вредное влияние на ход судна. На ходу влияние боковых килей заметнее (смотрите Успокоители качки).

Для рассмотрения общего случая качки судна на тихой воде необходимо решить систему диференциальных ур-ий, представляющих собою общие ур-ия движения твердого тела. Движение твердого тела известно, если определено поступательное движение ц. т. и вращательное движение около ц. т. Составляя подобные ур-ия, придем к выводу, что ц. т. судна будет двигаться только по вертикальной линии, а вращение относительно вертикальной оси будет равно нулю, то есть рысканья не будет.

Рассмотрению подлежат лишь следующие три уравнения:

yK + fl^of„=-04SoJv; (3)

Кб" + Р (о₀ - а) Θ=0; (4)

Κ_ιΨ" + [Р (В - а) + S/lSol²] Ψ=- <^£₀1£₀. (5)

Здесь fo — вертикальное перемещение ц. т., Р—вес судна, д—ускорение земного притяжения =9,81 m[ck^z, А—масса единицы объёма, дА=γ—вес единицы объёма, S₀—площадь грузовой ватерлинии, I—расстояние ц. т. грузовой ватерлинии от ц. т. судна, причем I считается положительным, когда ц. т. грузовой ватерлинии расположен в нос от ц. т. судна, R—продольный метацентрический радиус,(Р|-а)—продольная метацентрическая высота, К—момент инерции массы судна относительно продольной оси инерции, проходящей через ц. т. судна, К_г — то же относительно поперечной оси, Θ— угол крена, ψ—угол диферента, считающийся положительным при диференте на нос. Из ур-ий (3) и (5) видим, что если 1ф 0, то вертикальные колебания ц. т. судна сопровождаются килевой качкой. Вэтихур-иях сопротивление воды не учитывается. Решая эти ур-ия

при	1=0, придем к выражениям
	£о =	Z0 cos nxt --	r 2 ль - z0 cos —;	(6)
	0 =	θ0 cos n2t =	л 2 nt θ0 cos jr;	(?)
	гр =	ψ0 cos n3t =	2 nt Vo cos -Гз,	(8)
где	при t =	0? Co — z0,	в=ea и ψ=v>„
	η^9ψ;	n!=P(e£	-a). P(H-a), ni~ Kl	J
Т i	= —=2π1 щ У	Λ“. · T gyS0 ’	= — — 2π f K n2 VP (ρ0 -	a)’

Т

з ~

2л п₃

Кг

Р(К - а)

Видно, что каждое из движений периодическое и имеет свой определенный период. Периоды вертикальных колебаний Т_г и килевой качки Т₃ по величине близки друг к другу

Т,- 1,9 1/Я; Г₃=1,8|/Я,

где Н—углубление судна. Период боковой качки Т₂ обычно больше. От его величины зависит характер боковой качки на волнении. При I ф 0 неизвестная Θ входит лишь в одно ур-ие (4), свободное от других неизвестных и дающее простое гармонии, колебание с периодом Т₂, приведенное выше. Для интегрирования системы совокупных ур-ий (3) и (5) необходимо исключением одной неизвестной составить диференциальное ур-ие, заключающее лишь вторую неизвестную. Проделав соответствующие математич. выкладки, придем к выводу, что вертикальные колебания судна будут сложными колебаниями, слагающимися из двух гармонии, колебаний. Периоды этих колебаний будут весьма близки к периодам Т_г и Т₃ вертикальных колебаний и килевой качки, когда эти колебания не связаны между собою. Влияние сопротивления воды сведется к затуханию колебаний и к незначительному увеличению тех или иных качаний.

Качка на волнении. Исследование качки на установившемся волнении показывает, что качка судна м. б. уподоблена качаниям маятника в сопротивляющейся среде, причем на маятник действуют возмущающие силы, изменяющиеся периодически с течением вре мени. Колебания такого маятника состоят из свободных и вынужденных. Первые происходят из-за первоначального отклонения маятника от положения равновесия под действием восстанавливающей силы, стремящейся привести маятник в положение равновесия. Вынужденные колебания происходят от действия внешних возмущающих сил. Амплитуды колебаний маятника, даже незначительные при статическом действии возмущающей силы, достигают значительной величины при приближении периода изменяющейся возмущающей силы к периоду естественных, или свободных, колебаний маятника. Обращаясь к качке судна на волнении, отметим, что восстанавливающей силой будут момент восстанавливающей пары и избыток пло-вучести, а возмущающей силой—раскачивающее действие волн. Волны оказывают наибольшее действие на судно, когда период волны равен или близок к периоду собственных колебаний судна. При боковой качке совпадение указанных периодов, или резонанс, а следовательно опасный характер качки, будет-иметь место лишь в случае волн очень большой длины по сравнению с поперечными размерами судна (порядка 400 метров при ширине судна ок. 30 м). Поэтому при исследовании ограничиваются рассмотрением боковой качки судна, идущего лагом (параллельно гребням волн) к большей сравнительно с миделем волне. При рассмотрении килевой качки при ходе судна перпендикулярно к гребням волн подобного ограничения делать нельзя, т. к. длина волн в этом случае будет порядка длины судна.

А. Боковая качка. Теория боковой качки на волнении была разработана в 1861 г. Фруд-jM, положившим в основу следующие предположения: а) волнение установившееся; б) судно стоит лагом к волне, и поперечные его размеры малы не только относительно длины волны, но и относительно ее высоты; в) вода не оказывает сопротивления качаниям судна. Позднее было учтено и влияние сопротивления воды. Академик А. Крылов дал общую теорию качки. Необходимо еще ввести предположение, что присутствие судна не изменяет распределения давления среди жидкости, то есть что на каждую точку погруженной поверхности действует такое же давление, к-рое было бы в этой же точке в отсутствии судна. Волны (смотрите) принимаются образованными по трохоиде. Частицы жидкости в трохоидальной волне описывают окружности нек-рого радиуса г с постоянной угловой скоростью ω. На основании положений теории волн и принятых малых размеров судна по отношению к волне можно считать, что сила поддержания всего судна направлена по нормали к волне, а само судно описывает ту же орбиту, что и частицы волн. Если принять момент сопротивления воды пропорциональным относительной угловой скорости (по отношению к воде), то диференциальное ур-ие вращательного движения судна будет

ΚΘ" + АГ0 + Р (ρ₀ — а) Θ=Р (ρ₀ — а) а₀ sin +

-Г Ka^—cos (9)

Здесь а₀=— —угол наибольшего волнового

2 л1, ,

склона, —=ψ — фаза, г—период волны, h—

высота волны, Я—длина волны. Связь между высотой h, длиной Я, периодом г и скоростью V

волны, скоростью ветра Ve и отношением h : λ на основании около 200 различных наблюдений сведена Циммерманом в графич. таблицу (фигура 2). Левая часть ур-ия (9) та же, чт® и при качке на тихой воде. Правая часть есть резуль

тат действия возмущающей силы, то есть волн. Соединяя оба члена правой части, получим Кд" + Νθ + Ρ(ρ₀-α)Θ=*

₌ Р(^-оН_д._п,Ы×cosy V×^f ) ’

где

2л N

(10)

у=arc tg

Введя обозначения

Г Р (ρ₀ - а)

N

= 2 h;

P(Qo-a) ₌ Т.2- Р(бо-а) «о _sК ’ К cosy

₌=2» cosy ’ т получим

0" ₊ 2т + т=Н sin (pt + У). (11)

Это ур-ие можно рассматривать, как ур-ие движения маятника, совершающего малые колебания в среде, сопротивление которой пропорционально первой степени скорости, причем постоянно действуют возмущающие силы, изменяющиеся периодически с течением времени. Общий интеграл будет

0=е~^м [Οχ cos n_xt + С₂ sin %ί] + Ω,

причем n =№ — h², τ. к. всегда № — h²> 0. Частное решение Ω определяется из ур-ия

Ω=A sin (pt + у + <5)_? (12)

где А и δ—неизвестные постоянные. Подставляя значение Ω в ур-ие движения, имеем

А-

cos δ — sin <5 =

V(k² _p2)2_|_4h2p2 *

k² — p²

V(k² - p2)2 ₊ 4h2p2 ’

- 2hp

’ Y(h²- p²)² -j- 4h2p2

Входящий в состав общего интеграла член

e~^ht (Ci cos %ί + С₂ sin %(), ^в к-ром и определяются по начальным условиям, представляет собою свободные колебания с периодом — ’ свойственные боковой качке на тихой воде. Член Ω=A sin (pt + у + δ) представляет вынужденные колебания, происходящие от действия волн. Полагая в предыдущем уравнении

Ci=e_osⁱⁿ0; c₂=0„cos/s,

выражение свободных колебаний можно переписать так:

в„е~^мsin (n_Lt + β)= в₀е~^м sin + β}·

Здесь Τ—период свободных колебаний, 0_О— начальная амплитуда, β—начальная фаза. Присутствие множителя е~^ы показывает, что свободные колебания с течением времени затухают и остаются одни лишь вынужденные

О=Ω=A sin + у + δ ^

с периодом, равным периоду волны. До полного затухания свободных колебаний - судно имеет неправильные качания, полученные в результате наложения двух независимых колебаний: а) с постепенно убывающей амплитудой д₀е~™ и периодом Т и б) с постоянной амплитудой А и периодом г. По мере погашения свободных колебаний движение приближается к гармоническому. Определим 0_О и для случая, когда начальное наклонение и угловая скорость равны нулю в момент прохода подошвы первой волны, то есть при t=0, 0=0 и 0= 0. Из общего интеграла после подстановки начальных условий имеем

« 2π ¹

^Р Т h + ctg(y-M)’

А=-=^^н____.

Y{k² - p²)² -j- 4h²p²

Величина Я, входящая в состав первой части диференциального ур-ия, может быть охарактеризована как амплитуда того статического отклонения (0_ο)ι, к-рое произвел бы постоянный момент соответствующей величины. Это отклонение определяется из диференциального ур-ия, делая в нем 0=(0_ο)χ=Const, т. e.

из ур-ия к² (0_О)_Х=Я. Следовательно (0_ο)χ=~ =

⁼ cSy—величина, близкая к максимальному волновому склону. Сравнивая это отклонение с амплитудой А колебания, производимого моментом Hsin(pi-fy), видим, что отношение N : (0_ο)ι=V выразится ф-лой:

к² 1

V=----- =----------- ----.

V(k² - р²)² + ih²p² i р²у ±h² р²

V к²) ⁺ к² Ί²

Видно, что указанное соотношение зависит только от двух переменных р Т

Величина д= ^=—равна отношению периодов свободных колебаний судна без сопротивления к периоду возмущающей силы или раскачивающего момента. Следовательно изучение величины отклонения, производимого действием волн, сводится к изучению величины 1

V =—====·

Y(l~ д²)²-f-c²q²

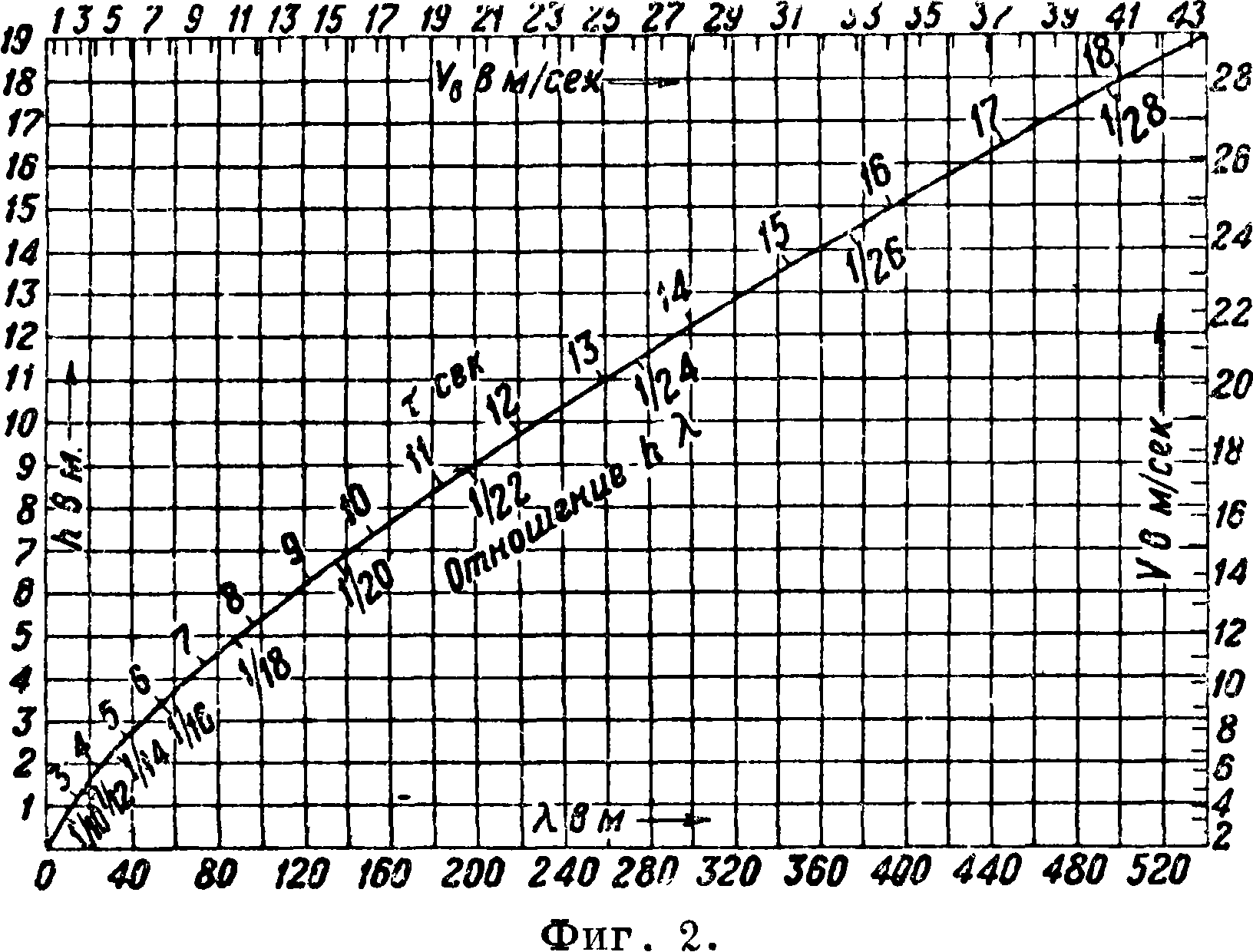
При малых значениях с то есть при малом сопротивлении и при величине q, чувствительно отличающейся от 1, величина v будет близка к где 11 — q²| означает абсолютную величину разности (1— q²). На фигуре 3 приведен график изменения величины v (к-рую можно считать как бы мерою динамич. восприимчивости колебаний) в зависимости от q для различных значений коэф. сопротивления с. Величина δ в ур-ии (12)

представляет опаздывание в фазе, или разность фаз между отклонением и силой, его производящей. Рассмотрение фигура 3 показывает, что величина отклонения, производимого данной периодич. силой по мере приближения периода свободных колебаний системы к пе-

с=0 с-0

Фигура з. риоду вынужденных, быстро возрастает и при равенстве обоих периодов (резонансе) достигает значения ^, к-рое при малой величине с весьма велико. Вместе с тем в этом случае разность фаз равна ~ или опаздывание отклонения составляет ~. Обыкновенно величина с

4

невелика. Лишь только q отклонится от 1, то есть периоды свободных колебаний и силы отклонятся от равенства хотя бы на 10%, то v становится значительно меньше своего максимума, причем по мере приближения q к 0 величина v приближается к 1, по мере же возрастания q сверх 1 величина быстро убывает до нуля. Разность фаз быстро доходит до —π

или опаздывание отклонения происходит на|·

Следовательно если изменять период волн, раскачивающих судно, то при приближении периода г к Т качка судна быстро возрастает, отклонения достигнут некоторого максимума, и судно без достаточной динамич. остойчивости может перевернуться. Остойчивое судно, способное выдержать значительные наклонения, не перевернется, т. к., с одной стороны, сопротивление ограничивает раскачивание, с другой же, при больших углах крена судно будет иметь другой период. Судно с очень большой остойчивостью на большой волне обладает малым периодом собственных колебаний по сравнению с периодом волны; при этом при-близительно v=l и <5=0. В этом случае выражение вынужденных колебаний может быть написано в виде:

Θ=(е₀ sin + у)=sin (^ + у)=cosy V τ * )

Вследствие малости γ приблизительно

_д. 2 πί

Θ=a₀sm—=a,

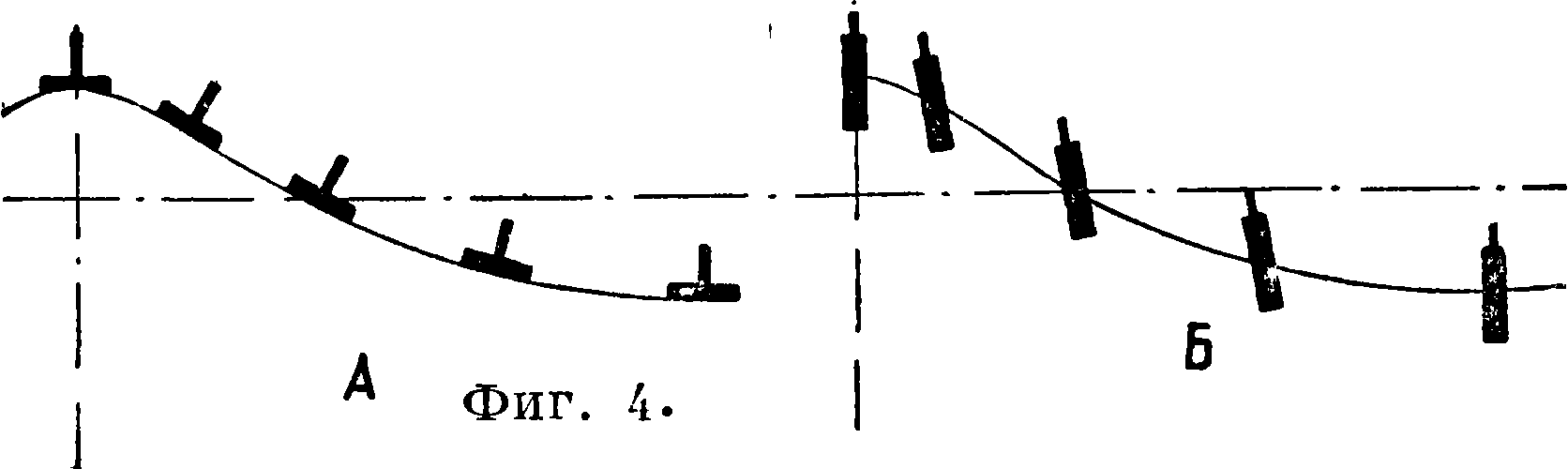
где a—действующий угловой склон волны. Мачты чрезвычайно остойчивого корабля таким образом будут оставаться перпендикулярными к поверхности волны, или судно будет следовать покатости волны. Такого рода качку испытывает плот (фигура 4,А). Наоборот, в случае весьма малой метацентрической высоты, то есть у мало остойчивого судна, когда ^достаточно велико,

можно считать v=Амплитуда колебаний бу дет А=^°₂, что при незначительности а₀ дает малую величину, то есть судно почти не будет испытывать качки (фигура 4,Б). В случае нулевой остойчивости раскачивание судна происходит исключительно вследствие трения воды о борт.

В предыдущих выводах рассматривалось действие на судно идеально правильного волнения, какового в действительности не наблюдается. Последовательно набегающие волны могут быть различного периода и различных элементов. Множитель e~^hl в выражении для амплитуды свободных колебаний не будет беспредельно уменьшаться, т. к. значение t при проходе каждой новой волны будет меняться от 0 до соответствующего t_K, т. ч. свободные колебания уже не погашаются и качка не становится однообразной,^представляя наложение двух систем колебаний (свободных и вынужденных) с различными периодами. Для расчета качки необходимо знать не только средний размер периода волн, но и самую систему волн. В этом случае наибольшая амплитуда колебаний определяется из амплитуды вынужденных

колебаний, для чего достаточно знать наибольший волновой склон системы и отношение периодов собственных колебаний судна и волн. Пока периоды судна и волн значительно разнятся между собою, можно при этом пренебрегать сопротивлением воды. Амплитуды свободных колебаний м. б. в 1,5—2 раза больше вынужденных, какими их и считают, т. e. 0_О= 2А; тогда

^Λ=ν (^θο)ι=να₀=—^1 Л.

У больших судов период собственных колебаний достигает 16—18 ск. Период весьма большой волны составляет не более 9 ск. Следовательно q ^ 2 и γ=Полагая j=—, полу-

лучим амплитуду вынужденных колебаний не-более 3°. Наибольшие размахи будут достигать в редких случаях 9°, качка будет плавной. Для малых судов или судов излишне остойчивых q ^ 1. Амплитуда вынужденных колебаний будет достигать 9°. Если на таких судах отсутствуют сильно развитые дейдвуды или кили, погашающие свободные колебания, качка будет весьма стремительной. У судна малоостойчивого вынужденные колебания незначительны * собственные же колебания при подходящей системе неоднообразных волн м. б. весьма значительны. Подобное судно может испытывать весьма плавные качания, но с большим раз-

махом совершающиеся в течение промежутка времени, равного нескольким периодам волны. Для учета влияния отношения ширины судна к длине волны в выражение амплитуды вынужденных колебаний вводится множитель о - ’· »·

А=dvc,

тде β=и В—ширина судна.

Б. Килевая качка. Килевая качка разработана академиком А. Крыловым. В основу положена гипотеза, что на каждую точку погруженной поверхности судна действует такое ;же давление, какое было бы в этой точке жидкости в отсутствии судна. Без этой гипотезы при современном состоянии гидродинамики вопрос решен быть не может. Предположим, что судно расположено поперек гребня волны носом по направлению бега волн. Неподвижные в пространстве оси Οξ и Οζ берем в направлении бега волн и вертикально вниз, приняв за начало координат проекцию ц. т. судна на горизонт воды в состоянии покоя. Подвижные оси, связанные с корпусом судна, направим через ватерлинию на спокойной воде в нос, а ось ординат—через ц. т. судна вниз. В состоянии покоя обе системы совпадают. Качка состоит из поступательных движений ц. т. судна и вращательных движений судна около его ц. т. Значение имеет вертикальная составляющая поступательных колебаний,определяемая ординатою Со Ц· ^т· судна, считая от оси Οξ. Вращательное движение (собственно килевая качка) определится углом гр наклонения судна около поперечной оси, проходящей через ц. т. При увеличении диферента на нос у> считается положительным. Волна принимается для упрощения рассмотрения по синусоиде. Ее ур-ие:

С=r₀ cos 2π cos Θ.

Значения букв—принятые раньше, ζ—добавочная высота воды над нормальным уровнем,

r₀= I=полувысоте волны. Ур-ия движения: у Со * (поступательного),

K_lW"=£ {Zx — Хг) (вращательного),

где через большие буквы Z и×обозначены проекции всех сил на соответствующие оси.

На судно действуют силы: 1) Вес судна ρ=γν_ο, где V₀—объёмное водоизмещение на тихой воде. Проекции этой силы на оси будут Z=Р; Y=0; Х= 0, а координаты точки приложения ж=0; у= 0; 2=0.2) Сила поддержания Q. 3) Сопротивление воды качаниям судна. Сила поддержания элементарного объёма dv в первом приближении равна

dp=У (1 + cos Θ) dv.

Здесь R—радиус катящегося круга; значения остальных букв указаны выше. Проекция силы поддержания на ось

dZq=— dp cos а ^ — dp) Zq =

= — у f (1 + 5cosΘ) dv,

V

где интеграл распространен на весь подводный объём судна, ограниченный волновой поверхностью. Окончательно получим:

Z_g=-[yV₀ + yv + у^ J cos θάν], ι*ο

В начале счета времени волна расположена своей подошвой против начала координат. Если F_XF—естественная грузовая ватерлиния

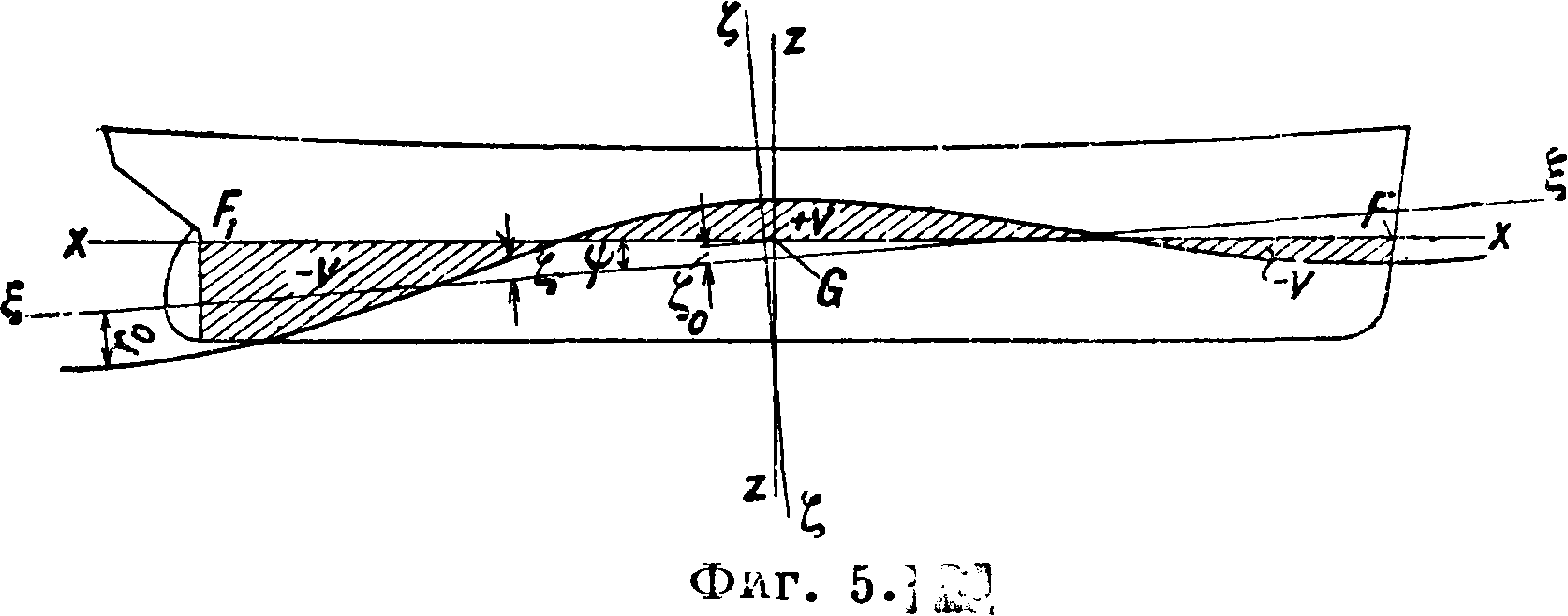
(фигура 5), то в момент времени t погруженный объём судна отличается от водоизмещения F₀

на объём v, заключенный между гру-- $ зовой ватерлинией и положением вол-Г ны в этот момент. Если принять об-Фигура 6. воды судна вблизи грузовой ватерлинии прямостенными, то добавочный объём v м. б. выражен интегралом (фигура 6):

1

v=2 [ у ND dx,

-ь_а

где у—ордината грузовой ватерлинии, соответствующая значениям абсциссы ж, и L_x=GF, L₂= GF₁. В виду малости угла ψ принимаем COS Ψ ££ 1, sin ψ ^ Ψ И ζ=X.

Из фигура 6 видно, что при этом допущении

NJD-

: ΗΝ — НЕ=Со + %V> — ^ro cos 2п ^ — ί j.

Добавочный объём

Li Ь_г

v=2ζ_ύ jydx А 2ψ f yx dx —

-U

/a ^7lt f* 2jC 0C 7

-2r₀cos-_T- I ycos-j-dx —

^T-l,

2 πχ 7

! sin —аж;

. 2 nt Г

,sin — J у SII

-L,

t. к. 2 J ydx=S₀, t. e. площади грузовой

*

ватерлинии, то 2 J ух dx=S₀l равно статичес--l₂

кому моменту площади грузовой ватерлинии относительно поперечной оси, проходящей через проекцию ц. т. судна. Для остальных интегралов введем обозначения

Li Щ

/QtzOC (*

у cos -у- dx=α₀; 2 у sin -l₂ -l₂

2πχ

dx=b_в.

Величины а₀ и b₀ постоянные для данного судна и для данной волны. Они сразу вычисляются по одной из приближенных ф-л квадратур, причем ординаты у берутся с теоретич. чертежа. Подставляя, получим

v=5<ьо + S_al4>—r₀ (α„ cos ^ + b„ sin ·

Момент добавочного объёма v относительно оси у будет

Li_ Lx

M_v=2 I NO yx dx=2ζ₀ f yx clx +

— Lo

Li ^ L_l ^

+ 2ψ J yx² dx — 2r₀ cos ~-_τ I yx cos ^ dx — -L -L,

Li

~ 2л t Г · 2πχ j

— 2r₀ sm — J yx sin -г- аж.

^T-l₂

2 J" yx² dx=I — момент инерции площади грузо-

— l₂

вой ватерлинии относительно поперечной оси, проходящей через проекциюц. т. судна. Заменяя

Li

2 J ух cos²— б£ж=а_х; 2 J ух sin у- dx =

—ь₂ ~

получим м„=S₀lCo + - Г„ cos + 6_г sin У) ·

Датее, т. к. dv=a₀dx, т.о

^Ll

J cos Θ dv=2 J* <τ₀ cos Θ dx,

V₀ -L_ti

где <т₀— половина площади шпангоута от киля до грузовой ватерлинии. Подставляя

n _n /х ί 2πχ 2πί

cos Θ=cos 2π I _я — - J=cos -у cos — +

. 2лх. 2л ί

- sm -г sm —,

λ τ

получим

J*<τ₀ cos θ dx= 2 cos ²ψ j σ₀ cos dx -f

Vo -Li

Li

,. 2nt (* 2ях 7

+ 2 sm — I <t₀ sm -у аж;

-L>

полагая:

Li Li

2 J a₀ cos ²-ψ dx=A₀ 2 J σ₆ sm ²ψ dx=B_u,

-Li -Li

для Zq окончательно имеем

^z4 ⁼ - у { ^F0+ -S„Co+ S₀ly> - r₀ [(a₀- У) cos ²Д +

+ (^&0-7г) ^s:nvJ}·

Значение г“

I жсоввйг“

г’о определяется ур-ием:

Lx

J x cos Θ dv=2 cos y- j a₀ x cos ~-ψ dx -f-

Vo -Li

, о · 2 nt r. 2nx

+ 2 sm — I <т₀ ж sm —

dx.

Обозначаем

Li Li

2 j σ₀χ cos ^ dx=и 2 | σ₀ ж sin у- сйж =

— Li —Li

Момент силы поддержания относительно оси у

Mqv ⁼ ZqX — Хд ζ=γ{ν ₀ау> — Β₀1ζ ₀ — Ιψ +

+[(^β* - If)^cos T + Щ - £)^sui T]} >

где a—расстояние между ц. т. и центром величины. Принимая сопротивление воды пропорциональным первой степени скорости и обозначая ^=jRi, где —условный продольный метацентрический радиус, имеем уравнения движения в форме:

— Со + 2iV_хСо + yS^o=уг₀ |^a₀— cos ~ +

+ (^?,o-§)siny]-y£₀i_v;

КУ + 2jΝ₂ψ + P (j— a) ψ =

= Vo[(a_L - У) cos ~+(b₁- И) sin ψ]-yS₀K.

Коэф. при cos и sin в диференциальных ур-иях можно представить так:

1’ ·[{»

L

С 2πχ ₇,

= J Ui cos -_А- dx=а’₀;

-i.,

>0-%-f(tr-%)8in^a-?dx =

u^Li

V 2πχ ₇

= J Vi sin -j- clr =

— L2 ^

^a!^-7T ⁼ ,i (г/-^)жсо8²-уйж =

-Li

Li

= J у_га cos -_A- da;=aj;

-Li

Li

= f y_lxsia~dx=bl,

еде У!=у-^.

При вычислениях на практике начало координат не совпадает с миделем теоретич. чертежа.

— X, — Чт -X

Фигура 7.

Тогда вносятся такие исправления (фигура 7): J у! CCS с7ж=f у, cos²-^yi) ^ ₌

-Li -Li

^{= C0S} Т »1008^^ +

-L,

+ sin

2лг

J У_г Sin

-L₂

J ^

-L,

Sill

2 πχ

= J’2/1 sin _{dXi =}

— Li

Ll

= cos j^sin^i“,-

-ii

-sin²yi J‘ y_L 005²-ψ cl_Xl.

-L,

Обозначая

^2jT ^{= fi}’ 2/i cos=α₀;

-U

U

Г · 2πΧι ₇ а

J sin д~ ύΧι =

- L₂

получим

^αό=^ао COS μ + β₀ sin μ; b_Q=β₀ COS μ —a-о sin μ. Точно так же

L_x Lx

/2~х ₇ /* .₄ 2π(χ_Ύ — ΐ)

хух cos — clx=I {Х1 — г)у_г cos-j—ах_г=

— L₂ — l₂

b

= cos ²-ψ J x_Ly_x cos clxx 4-

-L,

L

,. 2 πί i. 2πΧι ₇

4- sin — I ХхУх^т—^ clx_L —

-L_a

La

. 2πΐ Г 2πΧι ₇

— г cos — I уi cos «Ж! —

-u

Lx

. 2 лг Г. 2πΧι _Ί.

— г sin— J Уг sin -у-¹ ажт,

— l₂

Г sin ^=f (ж_х — г) г/_х sin ^2πΦ--·-9- c?34 =

-l, -l₂

Lx

2 πί Г. 2 πΧι 7

= cos -- I х_гу_г sin -y-^ аж_х —

-L • ^L.¹

— sin ^ j ж_х2/_х cos —

-L_a

L_x

• 2 ni P · 2яхi ₇ i

— icos-y- I Ух Sin yP <2ж_х 4--l₂• ^L1

4- г sin ^ j Ух cos²-*™ c?®!.

-L_a

Обозначая

L

(* 2 πΧχ j

ХхУх cos -j-¹ αΧχ=α_χ;

-l₂

L

f x,yx sin б7ж_х=/?!,

-La

получим:

α|=α_χ cos μ 4- βχ sin μ — »0г;

= βχ cos /-ί — α_χ sin μ — Ь<^· Интегралы α₀, /?₀> α_χ и βχ проще всего вычисляются по правилу трапеций. Полагая все коэф-ты, вошедшие в диференциальные ур-ия известными, последние можно представить в следующем виде:

Со + 2 hCo + η*ζ₀=^γ-ψ (αό CCS — + &ό sinЦ¹),

ψ" + 2 Tcy> + р^гу>=~ (αί cos ²-^- + ^δί ^sin ~)

При l=0 общие интегралы их будут:

ίο=^е~^М Wl COS ΎΙχί + 6₂ Sin ΎΙχί) 4

4- H cos-- - F sin —,

¹ τ r

Ψ=β“^Λί (C₃ cos p_xi 4- C₄ sin pxt) +

4- M cos--h N sm — »

¹ τ τ

где

w_x=Vn² — /?²; px=Vp^% — /с².

Коэф-ты 6, 62, 6₃ и 6₄—произвольные постоянные, определяемые из начальных условий, Н, F, М и JST—постоянные коэф-ты, определяемые так, чтобы удовлетворить диференциаль-ным ур-иям. Члены с множителем е~^ш определяют свободные колебания, которые весьма быстро убывают и через несколько секунд после начала движения погашаются. Вторые члены решений представляют собой вынужденные колебания, не зависящие от начальных условий. Нет надобности определять коэф-ты свободных колебаний в виду быстрого затухания последних. Достаточно определить постоянные H, F, М и N путем подстановки частных решений в диференциальные ур-ия и сравнения коэф-тов. Амплитуды размахов соответственно будут

C_omax=VH* + F* и vw =VM* + N“. Амплитуды размахов штевней будут

(ίο 4- Lxw)_max=[/(Н ± LxM)² + (F± LjN}², где Lx—длина носовой или кормовой части, считая от ц. т. судна. Если судно имеет ход, то меняется только видимый период волны. При :ходе судна со скоростью v в направлении бега волн, скорость распространения которых V_Ускорость бега волны по отношению к судну будет V — v и видимый период волны

_ ^λ _^λ·ι_^ν — ^τ

^Tl~ V — v ~ V * ¹ ~ V ~ iF V

Когда волна встречная, то видимый период

Вместе с тем, т. к. нос судна направлен в отрицательную сторону оси £,то в ур-ие волны х д.б. заменен —ж, то есть

С-г₀сов2*(£+1).

То же необходимо сделать во всех интегралах а<4 b’, а[, Ь’х, т. ч. интегралы, содержащие нечетную ф-ию х — а, переменят свой знак, а содержащие четную ф-ию х—а не изменят знака. К первым относятся интегралы b₀ и а[, ко вторым—αό и b. Так как от а и b зависят разности фаз, то с переменой курса меняется характер качки. Меняется также отношение периодов собственных колебаний судна к видимому периоду волны, от чего меняется и величина размахов судна:

д _ уго ^ъ _ УГрb.Т* 1

^ ~ Κχ “, 4π* 4π2Κχ * Т2*

Обычно при перемене курса навстречу волне качка становится сильнее, при попутной же волне амплитуды размахов становятся меньше. При косвенном курсе к волнам вместо истинной длины волны λ необходимо ввести действую-

щую длину (фигура 8), равную А₁=^С_, с видимым периодом т_х=—^-. В этом случае

1- Lr sina

килевая качка сопровождается боковой. Действующей волной, вызывающей боковую качку,

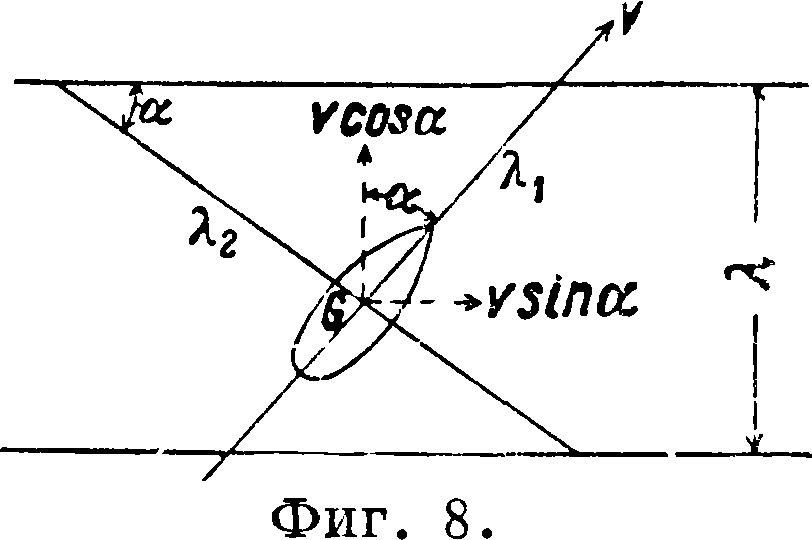
можно считать волну длиною λ₂=с видимым периодом τ₂ =—При изменении

1— cosa

курсового угла от 0 до 90° угол действующего волнового склона будет все время уменьшаться, дойдя до минимального значения. При дальнейшем увеличении курсового угла от 90 до 180° килевая качка будет опять усиливаться, дойдя до максимума при ходе судна вразрез волны против направления ее бега. Так как увеличение хода при курсовых углах до 90° увеличивает видимый период волны, а при курсовых углах больше 90° уменьшает его, то для случая, когда период свободных килевых колебаний судна меньше истинного периода волны, размахи при курсовых углах а < 90° будут меньше, а при а > 90° будут больше соответственных размахов судна, стоящего или идущего меньшим ходом. Если период судна больше периода волны, то будет иметь место обратное явление. Для судна без хода боковая качка достигает своего максимума при a=90°, то есть при положении судна лагом к волне, и соответственно уменьшается до 0 при a=0° и α= 180°. При ходе на волне, период которой меньше периода свободных колебаний корабля, размахи судна при курсе 0 < a < 90° будут больше соответственных размахов судна без хода, т. к. отношение периодов судна и волны будет приближаться к 1. При 90 < a < 180° видимый период волны меньш^истинного, отношение периодов увеличивается, удаляясь от синхронизма. Следовательно на ходу боковая качка становится наиболее сильной при косвенном курсе судна. Увеличение хода вызывает наибольшую качку при более острых курсовых углах.

Момент инерции массы судна относительно поперечной оси, проходящей через ц. т., приблизительно м. б. определен по формуле К_г= 0,01 v; шх 2.

Сопротивление воды можно определить по следующей приближенной ф-ле:

R=— TcS^q — JcS₀ Ιψ

Мэмент сопротивления воды

Мл — — RSoKo TcJxp.

Значение букв—принятое выше. Коэф. /с колеблется от 0,010 Vh до 0,012J/L. Для вычисления коэф-тов Я, F, М и N подставляем в диферен-циальные ур-ия качки ур-ия

£о=Я cos----F sm —»

τ τ

, 2 πί, ,_τ. 2 nt

ψ=Μ cos---у N sm —

^Τ τ τ

и сравниваем коэф-ты при cos и sin. Получим систему 2 линейных ур-ий с 4 неизвестными. Проще всего эту систему решить методом последовательных приближений вычисления как боковой, так и килевой качки; все удобно располагается в таблицы.

Определение сил инерции при качке. Предполагая, что поперечные размеры корабля малы по сравнению с размерами волны и сохраняя принятые обозначения, можно написать ур-ия движения при боковой качке:

. 2nt

Vo — ^ro ^Sin ’

c. 2 πί

io=U cos --,

ΰ ==A sin + у + <5^ + 0_Ge~^ht sin + β^ ·

Рассматривая случай качки, отличающийся от синхронизма, можно считать величины у, δ и β малыми, т. ч. последнее ур-ие примет вид

0=4 sin — + в₀е~^м

sin-

2 nt

Ускорения этих движений после отбрасывания пренебрежимо малых величин и упрощения последнего ур-ия будут:

Vo — ~ ~2~ Vot ίο--ίο

η, Ιπ² ~ ,. 2π

θ =---₂- (3 + a₀ sin — J

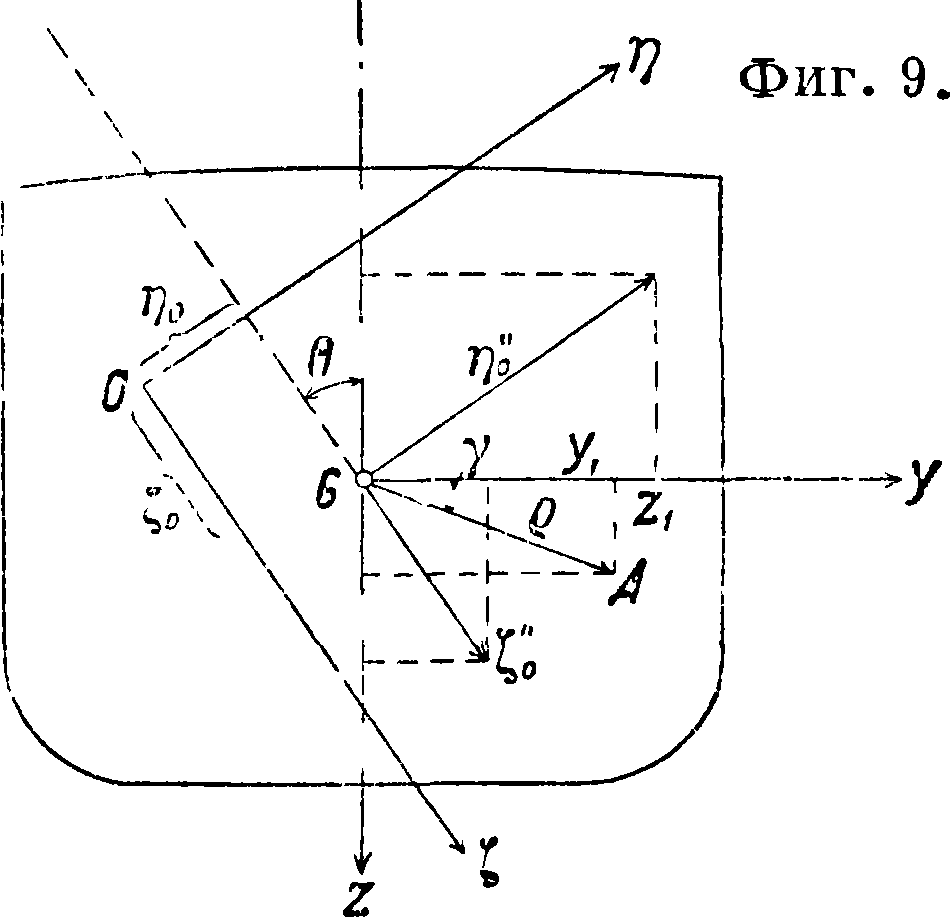
Здесь a₀—угол наибольшего волнового склона. Ускорения точки А (ад, у_и ζβ) от поступательного движения будут те же, что и для ц. т., то есть Vo и ίο. Разлагая эти ускорения по направлению осей у и ζ (фигура 9), получим для составляющей ускореыияпо оси у: ы_у=г/q cos 0 -f -Ь iSsinfl, по оси ζ: ω_ζ=— г/" sin 0 +

+ ίό COS 0.

Ускорение от вращательного движения судна около оси х будет равно произведению углового ускорения этого движения на расстояние ρ точки до оси вращения и направлено перпендикулярно к ρ, т. e. w=0"q. Составляющие этого ускорения по направлению осей у и ζ будут

Wy=— w sin γ=— 0"ρ ~=— 0"*1, ιν_ζ=ιν cos γ=0"ρ ^=Q"y_L.

Суммируя ускорения от вращательного и поступательного движений, получим:

Wу=w_y -f w_y=Vo cos 0 + ίο sin 0 — 0"^_1?

W_e=+ w_z=— η”₀ sin 0 + ίο cos 0 + в"у_1а

Применяя к килевой качке те же рассуждения, найдем составляющие ускорений по осям х и ζ: W_x=ω_χ + w_x=fj cos ψ + ίο sin ψ - ψ"ζ_ΐ9Wi _s= ω_ΐ2 + м;_1в=—Й siny> + ίο COS ψ + ψ"χ_ΐ3

При одновременном действии боковой и килевой качек ускорения по оси ζ будут складываться алгебраически. Имея численные значения ξρ,νο,ζο,θ",ψ",θ и ψ, нетрудно определить в любой момент качания ускорения любой точки судна. Т. к. ускорения меняются с течением времени в нек-рых пределах, то ф-лы для наибольших величин ускорений будут иметь вид:

/ТТ7- 4 П²Гп. in²

л)max ~ Ψ max 4“ ЩГ Ψmax Ή’

{W_v)_max=cos в_тах + ^ (Q_mnx + 0_O) s_it

(WOmax=sm в_тах + --_s- (6_max + 0_O) y_x,

/ттт 4 п²Гп. .4 π²

(^1 z)max~ _τ2~ Sin^„_m3j -p ~_τ2~ Wnax^ 1*

Для расчета необходимо задаться величинами углов у_тах и Θ_ηιαχ. Все слагаемые в последних ф-лах должен быть взяты одного знака. Имея ускорения, можно определить и силы инерции но соответствующим направлениям, для чего умножаем их на массу тела.

Поворотливость. Управление судном при помощи руля имеет в виду повороты его в горизонтальном направлении для плавания по определенному курсу и для изменения последнего при свежей погоде, при встрече с течениями, а также для плавания в гаванях, протоках и для избежания столкновения со встречными судами. В понятие «управление судном» входят два взаимно противоположных понятия: способность судна изменять свой курс при отклонении руля, называемая поворотливостью, и способность судна сохранять свой курс неизменяемым, называемая устойчивостью на курсе. Когда руль судна находится в прямом положении, то есть в диаметральной плоскости, то, не принимая во внимание внешних сил (течение, волнение, ветер), судно должно двигаться прямолинейно. При отклонении руля частицы воды или струи начинают давить неравномерно на обе стороны пера руля. Пусть равнодействующая всех давлений, нормальных к поверхности руля (фигура 10), сведется к силе Е,к-рую можно разложить f на составляющие:

продольную Rl и	V я г
	— д----
^ Т. п dv	J___

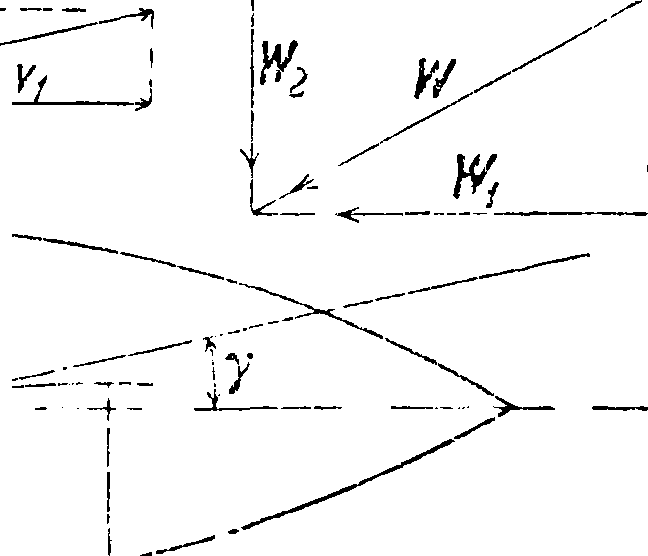
Фигура 10.

поперечную R₂. Продольная составляющая вызовет уменьшение скорости судна до величины v_u а поперечная R₂—появление скорости в поперечном направлении v₂ (скорости дрейфа). Равнодействующей этих скоростей v соответствует определенное по величине и положению сопротивление воды W, разлагаемое на составляющие W₁ и W₂. От действия сил R и W одновременно получаются вращающие моменты, заставляющие судно изменить прямолинейное направление движения. На судно постоянно действует сила упора винтов Т, а во время вращения—центробежная сила F. Под действием всех этих сил диаметральная плоскость при вращении составляет нек-рый угол с касательной к траектории γ. Этот угол называется углом дрейфа. Он обычно равен 5—8° и будет тем больше, чем меньше диаметр кривой перемещения судна (диаметр циркуляции) и чем лучше поворотливость судна. Для движения судна параллельно его продольной оси и перпендикулярно к ней можно написать следующие диференциальные ур-ия движения

Р dvо

— ~ COS V a dt *

Р dv₀.

—7 sin γ +

a at ¹ g

P о

cos γ=W₂ — R₂

Для вращательного движения имеет местоур-ие

Здесь г—радиус циркуляции, М—момент вращения от давления воды на руль относительно ц. т. судна, M_w—момент вращения от сопротивления воды, v₀—скорость движения судна,

Р—вес судна, a—ускорение земного притяжения =9,81 м/ск², 0—угол, составляемый продольной осью судна в момент времени t с направлением ее в начальный период и определяемый из соотношения б=у+

о

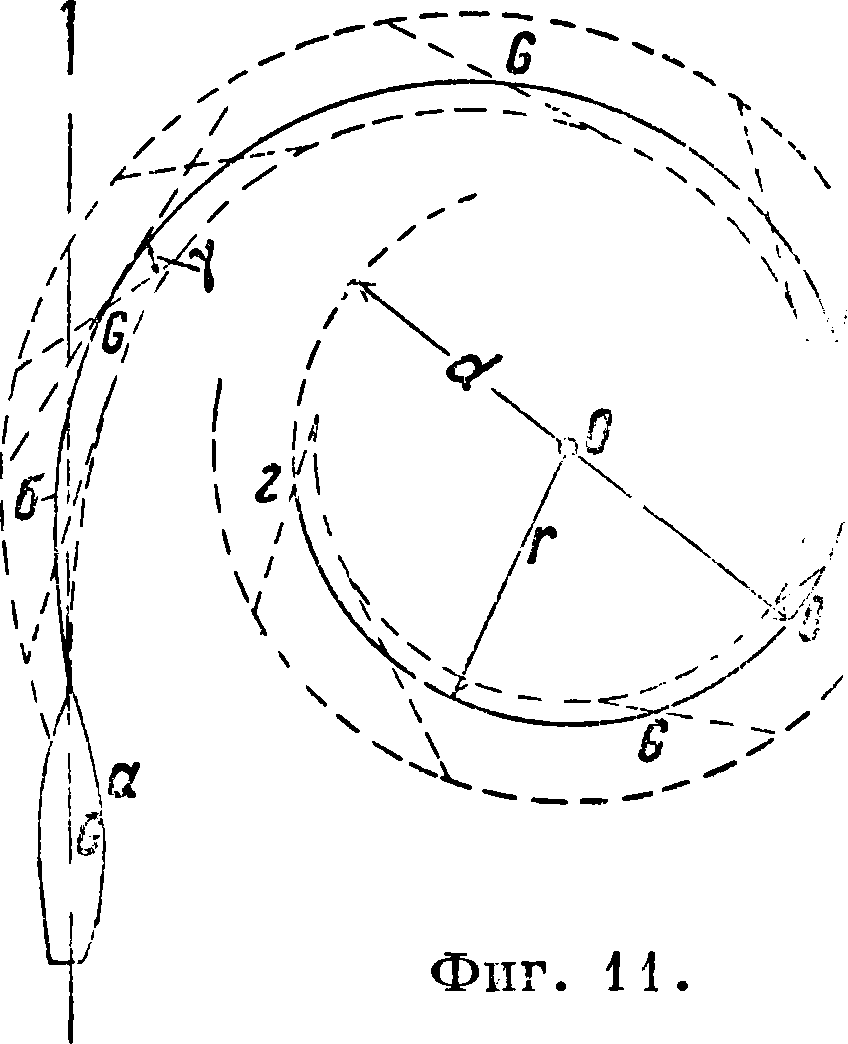
J—момент инерции массы судна относительна вертикальной оси, проходящей через ц. т. суд· на. Практйч. решение ур-ий возможно только при допущении ряда упрощений. Это тем болео необходимо, что действие гребных винтов изменяет в значительной степени давление воды на руль. Если судно на прямом курсе двигалось с постоянной скоростью v и в нек-рый момент времени его руль отклонен от прямого положения на угол а, то при дальнейшем движении можно различить три фазы движения. Первый период охватывает время с момента прямого положения руля до его отклонения на угол а. Этот период охватывает всего несколько секунд. Вращающий момент от действия давления воды на перо руля достигает полной своей величины, равно как и составляющие этого давления R_t и R₂, тогда как момент сопротивления воды М^возрастает на незначительную величину. Вследствие большой инерции судна движение его в этот момент лишь незначительно отклонится от первоначального прямого курса и то в сторону, противоположную требуемому направлению вращения a-^б (фигура 11). Во вторую фазу (б—в) движения момент сопротивления воды возрастает до полной своей величины, и судно приводится в требуемое вращательное движение. В третий период (в—г) движения вращающие моменты от давления воды на перо руля и от сопротивления воды сравниваются.

1 dv

угловое ускорение - · ^ делается равным нулю,

и судно приводится в равномерное движение по окружности с центром в О. Оба диференциаль-ных ур-ия при этом упрощаются, т. к. касательное ускорение ~ в этот период равно 0.

Угол дрейфа и радиус г становятся постоянными величинами. Вследствие дрейфа наблюдателю, находящемуся на палубе, будет казаться, что судновращается невокругсвоего ц. т., а около какой-то точки, лежащей впереди ц. т.

Расстояние d между обратными курсами при повороте на 180° называется тактич. диаметром циркуляции. Величина его зависит от длины судна, поэтому поворотливость обычно определяется этим диаметром, выраженным в длинах судна. Чем меньше отношение ^, тем лучше поворотливость. При одинаковых величинах отношений поворотливость улучшается: 1) с увеличением угла отклонения руля до некоторого вполне определенного значения (приблизительно до а=35°); 2) с увеличением отношения поверхности пера руля к площади погруженной в воду части диаметральной плоскости;

3) с улучшением обводов кормы, способствую-

щих наивыгоднейшему подтеканию воды к перу руля; 4) с выпрямлением струй воды, отбрасываемых лопастями винтов.

При циркуляции получается угол крена, приблизительная величина которого определяется формулой

4β=

_ν*α

gr (Qo^a)

COS γ.

Здесь a—расстояние между ц. т. судна и его центром величины, β—угол крема при циркуляции, V—скорость судна при циркуляции, ρ₀ — а—метацентрич. высота; значение остальных букв—принятое выше, все величины в ражены в метрич. мерах. Если желательно ν выразить в узлах, то формулу ее нужно поставить со множителем 0,514. Выражая β в градусах, а ν в узлах, получим

β° ^ 1,54°

ν²α

Ноо-а)

* COS

У*

Для,давления R на перо руля различные исследователи дают разные ф-лы: Наиболее применимой является формула Жосселя:

Л — kSv² SITI а

0, l^lJ5 -j- 0,о05 Sin а’

где к—коэф., равный 20—25 для скоростей, близких к 20 узлам, S—площадь пера руля в м², ν—наибольшая скорость судна в м/ск, а— наибольший угол отклонения руля от прямого его положения. Отстояние I центра давления воды от задней кромки руля по Жосселю равно I=&(0Д95 + 0,305 sin α),

где b—ширина руля в м. В Германии пользуются ф-лой Эйлера:

R=13,5 £ν² sin² α

и Вейсбаха:

R=34,5 Sv² sin α (1 - cos α).

В Англии пользуются ф-лой Ранкина:

R= И Sv² sin α,

Имеет применение также формула Релея:

R =

4л sin а 4- -л sin а

-SvK

Отстояние центра давления от передней кромки по Релею:

ь

2

_ JCOS а

~4 + π Silia *

По высоте положение точки приложения давления принимается на уровне ц. т. площади пера руля. Момент давления воды на руль относительно оси баллера будет M=Rl. По нему рассчитываются как размеры рулевых приводов, так и мощность рулевой машины. Напр. диаметр головы руля d₀ определяется выражением

16 м где т—допускаемое напряжение на кручение. Если применять формулу Жосселя, то М=Rl=kSv²b sin a.

Для расчета рулевой машины можем воспользоваться следующим выражением для работы давления на перо руля при отклонении его от прямого положения до угла а по Жосселю:

a

A=kSv²b j·sin a da=kSv²b(l — cos a) кгм

b

отсюда мощность рулевой машины дт_ Λ. _ Sv²b{4— COS a) tt>

^iV “ 75η t 75η t ~~ *

где η — кпд рулевой машины, t—время, потребное для отклонения руля на борт. Последние исследования выяснили, что при отклонении руля сила давления воды на его перо состоит из 2 слагаемых:

R=R + R",

где R—увеличение давления с передней (рабочей) стороны и R"—уменьшение давления с задней (нерабочей) стороны. Доминирующее значение имеет составляющая R", величина которой при углах, не превышающих 20°, составляет ок. 0,8 R (опыты Эйфеля). Опыт и теория подъемной силы аэропланного крыла также устанавливают преимущественную роль очертания задней поверхности крыла. Вследствие указанных причин в последнее время обращена внимание на очертание пера руля (руль Эрца, Вагнера, сист. Симплекс и др.), чем осуществляется лучшая поворотливость судна, уменьшаются мощность и вес рулевых механизмов и несколько увеличивается скорость самого судна (смотрите Судовые устройства). Устойчивость судна на курсе обеспечивается действием руля и поддерживается потоком, отбрасываемым гребными винтами. Новейшие формы рулей способствуют также большей устойчивости на курсе. Начинают находить применение автоматические приборы, удерживающие судно на курсе (Аншюца, Сперри),

Лит.: Невражин В., Теория корабля, ч. i, СПБ, 1911; Крылов А., Теория корабля, ч. 2, СПБ, 1908; Яковлев С., Кораблеустройство и трюмное-дело, ч. 1, Теория корабля, Л., 1928; III е р ш о в А., Устройство и теория корабля, Л., 1930; Horn F._yTeorie des Sehiffes, Handbuch der physikalischen u. tech-nischen Mechanik, hrsg. v. F. Auerbach u. W. Hort, B. 5, Lief. 2, Leipzig, 1928; J о h о w-F о e r s t e r„ Hilfsbuch fur den Scniffbau, В. 1—2, 5 Auflage, Berlin, 1928. С. Яковлев.