Теория подобия

Теория подобия, учение о методах обобщения данных опыта путем представления рр-зультатов эксперимента в форме таких зависимостей, которые по своей структуре отвечают механизму исследуемого явления. Исходными понятиями Т. п. являются следующие. Диферен-циальное ур-ие (или система диференциальных ур-ий) представляет собой математич. модель механизма, общего целому классу явлений. Индивидуальные различия отдельных явлений одного итого же классаобусловленыобстоятельствами произвольными и посторонними по отношению к их механизму—состоянием физич. области, охваченной процессом (системы) к моменту его возникновения (начальные условия), и взаимодействием между системой и окружающей средой (граничные условия). Кроме того различия вносятся неодинаковостью физич. свойств тех тел, из которых образована система. Данные, которые в своей совокупности исчерпывающим образом определяют все эти особые обстоятельства, имеют значение условий однозначности, т. к. присоединение их к основным ур-иям выделяет нек-рое единичное явление из класса ему подобных. При сравнении явлений, принадлежащих к одному и тому же классу, обнаруживаются весьма глубокие различия их свойств. Поэтому возможность распространения результатов, полученных при изучении конкретного явления, на все другие явления того же класса исключена. В этом смысле класс явлений — область очень широкая.

В Т. п. устанавливается понятие труп-п ы явлений как области, в пределах которой обобщение закономерно и плодотворно. Группы выделяются из класса на основе расширенного понимания условий однозначности. Задание условий однозначности для единичного явления заключается в определении частных значений ряда физич. величин, характеризующих особые его признаки. Применительно к группе явлений те же признаки выражаются в виде произведений из соответствующих величин на постоянные численные множители (м н о-жители преобразования), которые принимают различные частные значения для отдельных явлений, входящих в состав группы, но сохраняют неизменные значения в пределах каждой данной системы. Умнояюние совокупности величин на один и тот же численный множитель есть подобное преобразование и х. Следовательно условия однозначности всякого явления получаются из условий однозначности любого другого явления той же группы непосредственно с помощью подобного преобразования всех величин, входящих в их состав. Так, поверхности взаимодействия между •системой и окружающей средой во всех явлениях одной и той же группы между собой подобны (геометрическое подобие «систем). Физич. константы образуют подобные поля (физическое подобие систем). Векторы всех величин в начальный момент и на границах систем также между собой подоб-ны(подобие начальных и граничных условий). Т. о. условия однозначности для различных явлений одной и той же группы по существу представляют между собой одну и ту же систему условий, данную в различных масштабах (в широком понимании этого слова имеется в виду не только геометрии, масштаб, но также масштаб всех физич. величин: скоростей, перепадов давлений, £°-ных градиентов и тому подобное.). Но условия однозйачности в совокупности с основными ур-иями определяют все свойства явления. Поэтому явления одной и той же группы, отвечающие одинаковым ур-иям и подобным между собой условиям однозначности, представляют со-«бой одно и то же явление, данное в различных масштабах, то есть образуют группу подобных между собой явлений. Этот вывод выражает содержание важнейшей теоремы Т. п.: подобие условий однозначности естьдо-•статочное основание для утверждения подобия явлений, определяемых одной и той же системой уравнений. Группа подобных между собою явлений и есть область обобщения данных опыта.

Критерии подобия. Множители преобразования не м. б. выбраны произвольно, так как величины, получаемые в итоге преобразования, должны удовлетворять основным ур-иям. Допустимы только такие подобные преобразования условий однозначности, по отношению к которым основные ур-ия инвариантны. Условия, ограничивающие свободу выбора множителей преобразования (обусловливающие уравнения), заключаются в требовании равенства единице нек-рых их комбинаций, составляемых по определенным правилам. Но если множитель преобразования какого-либо выражения равен единице, то выражение это при преобразовании не изменяется. Следовательно, подобные между собой явления отличаются той особенностью, что известные комбинации из ве личин, входящих в состав основных ур-ий, имеют для них одинаковые значения. Эти комбинации называются критериями подобия. Очень существенно, что критерии подобия м. б. составлены непосредственно по виду диференциальных ур-ий без их интегрирования, почти во всех случаях невыполнимого. Критерии подобия принято обозначать первыми двумя буквами фамилий исследователей, прославившихся своими работами в данной области знания. В гидродинамике особо важное значение имеют следующие критерии:

~^d=Re (Reynolds),

= Eu (Euler),

g- Er (Froude),

~=Ba (Bairston).

В теории теплообмена приходится кроме того рассматривать нек-рые другие критерии, из которых важнейшими являются:

-_а^,!=Ре (Peclet),

^=Pr (Prandtl),

~=Nu (Nusselt),

= Gr (Grashof),

где ρ — плотность жидкости, ν, Я, а и β — коэфициенты кинематич. вязкости, теплопроводности, температуропроводности и объёмного расширения, д—ускорение силы тяжести, w— скорость жидкости, с—скорость распространения звука в жидкости, Δρ—перепад давления, d—определяющий размер (например диаметр канала), а—коэф. теплоотдачи, ΔΤ—1°-ный напор (разность t°). Отдельные типичные случаи движения и теплообмена характеризуются различными совокупностями этих критериев. Так, если работой силы тяжести молено пренебречь (например движение по горизонтальному каналу), то выпадает из рассмотрения критерий Fr. Критерий Ва приобретает значение только при весьма больших скоростях жидкости, приближающихся к скорости звука. При весьма малых скоростях (а также и при весьма больших) несущественным становится критерий Re. Для процесса теплообмена при вынужденном дви-леении жидкости (например теплоотдача от продуктов сгорания поверхности нагрева котла) характерным является критерий Ре. Наоборот, в условиях свободного движения (например теплоотдача калориферов, печей домашнего отопления) критерий Ре несущественен, и определяющее значение приобретает критерий Gr.

Форма обработки данных опыта. Из предшествующего следует, что к подобным явлениям приводят только такие подобные преобразования условий однозначности, при которых критерии, составленные из преобразуемых ве-, личин, сохраняют неизменное значение. Никакими иными требованиями свобода преобразования условий однозначности не ограничивается. Поэтому равенство критериев, построенных только из тех величин, которые входят в состав условий однозначности, есть необходимое и достаточное основание для утверждения подобия явлений как прямого следствия подобия условий однозначности. Не все величины, содержащиеся в ур-иях, входят в состав условий одно значности. В связи с этим критерии разбиваются на две группы: к первой относятся критерии, построенные исключительно из тех величин, которые входят в состав условий однозначности, ко второй—все остальные. Только критерии первой категории выражают требования, ограничивающие свободу преобразования условий однозначности. Им присвоено название определяющих. Этим термином подчеркивается то обстоятельство, что данной совокупности критериев первой категории отвечает одна определенная группа подобных между собой явлений. Но если явления подобны между собой, то одинаковые значения имеют все критерии, а нс только определяющие. Итак, различие критериев обеих категорий заключается в том, что равенство определяющих есть предпосылка подобия явлений, а равенство всех остальных—его следствие. Это противопоставление означает, что каждой данной совокупности определяющих критериев отвечает одно только возможное значение любого критерия второй категории. Полученный вывод выражает вторую основную теорему Т. п. Неопределяющие критерии суть однозначные функции критериев определяющих. Так, для случая движения жидкости по горизонтальному каналу с обычными для техники скоростями ур-ия гидродинамики приводят к двум критериям Re и Ей. Но в состав критерия Ей входит величина Δρ, которая не содержится в условиях однозначности. Поэтому определяющим является один только критерий Re. Критерий Ей есть его ф-ия. Если какому-либо конкретному случаю движения (например движения воды по прямой цилиндрич. трубе со спокойным входом) отвечает определенное значение критерия Re, то любое другое движение, происходящее в геометрически подобном канале с подобными условиями входа, будет ему подобно, если оно характеризуется тем же значением Re. Отдельные величины, входящие в состав критерия, могут иметь самые разнообразные значения, движущимися средами м. б. жидкости с самыми различными свойствами (воздух, дымовые газы, керосин, глицерин); но, если только значения Re одинаковы,—движения подобны. При вычислении Re можно вводить значения скорости в любых геометрически сходственных точках входного сечения (например по оси) или среднюю по сечению скорость (определенную по расходу). Подобные движения характеризуются одинаковыми значениями критерия Re. Поэтому каждому данному значению Re отвечает одно только возможное значение Ей. Иными словами Ей есть однозначная ф-ия от Re. Т. о. если при исследовании какого-либо конкретного случая (например движения воды в трубе данного диаметра) найден вид зависимости Eu=f (Re), то полученный результат непосредственно распространим на все подобные движения. Вид этой ф-ии изучен для многих технически важных случаев (движение по прямым и криволинейным каналам, обтекание шаров и цилиндров, обтекание тел со специальными профилями и т. и.). Все эти системы характеризуются при помощи коэфициен-тов сопротивления, которые представляют собой удобные для практики модификации критерия Ей и следовательно являются однозначными ф-иями Re. Весьма обширный экспериментальный материал, которым располагает гидродинамика, полностью подтверждает вывод о существовании однозначной связи между Eu и

Re. Такого рода зависимостям, в которых неопределяющие критерии выражены в ф-ии от определяющих, присвоено название уравнений связи между критериями. Уравнениями связи и устанавливаются те общие формы, в которых надлежит обрабатывать данные опыта. Так, результаты исследований по теплообмену между твердыми телами и жидкостями должен быть представлены в виде ур-ий:

Nu=φ (Ре, Ру)

для случая вынужденного движения и Nu=ψ (Gr, Ру)

для случая свободного движения. Ур-ия связи не только являются основой для закономерного обобщения данных опыта, но и содержат в себе известную программу исследования, которое прежде всего заключается в определении вида ф-ий, входящих в состав ур-ий связи.

Моделирование. Одновременно с задачей о методах закономерного обобщения данных эксперимента Т. п. решает также задачу о методах закономерного замещения объекта эксперимента. Все подобные между собой явления качественно совершенно тождественны друг другу. Вместе с тем величины, характеризующие их количественные признаки, находятся в очень простых, заранее известных соотношениях. Поэтому непосредственное исследование данного конкретного явления вполне возможно заменить изучением любого другого явления той же группы. Такого рода замещение основного явления— о б р а з ц а—другим подобным ему явлением— моделью — называется моделированием. Применение метода модели оказывается чрезвычайно плодотворным во всех тех случаях, когда исследование основного явления представляет какие-либо специфич. трудности (невозможность непосредственного наблюдения, недоступность объекта для измерений и т. π.). Т. о. моделирование есть воспроизведение явления, подобного нек-рому другому основному явлению. С точки зрения Т. п. это—частная задача, которая непосредственно разрешается с помощью ее общих методов. Для того чтобы воспроизвести явление, подобное образцу, достаточно удовлетворить следующие требования:

1) геометрии, подобие обеих систем, 2) физическое подобие сред, 3) подобие начальных и граничных условий, 4) равенство определяющих критериев. Если все эти требования выполнены, то можно с полной уверенностью утверждать, что картина, наблюдаемая в модели, совершенно точно воспроизводит действительную обстановку процесса и что измеренные величины после умножения на соответствующие множители преобразования определяют условия в образце.

Изложенные соображения приводят к заключению, что метод модели применим—по крайней мере в принципе—во всех тех случаях, когда для явления-образца м. б. заданы все условия, составляющие содержание основных требований подобия. Моделирование широко практикуется в судостроении, гидротехнике, воздухоплавании и других областях техники, связанных с приложением механики сплошной среды. За последние годы моделирование получило широкое развитие в теплотехнике. Здесь метод-модель применяется, с одной стороны, для изучения картины движения газов в котлах, печах и других тепловых аппаратах, а с другой,—для исследования чисто тепло-

7. Э. m. XXII.

бых явлений, например распределения t°, потоков тепла и тому подобное., в изоляции теплопроводов, обмуровках, грунтах. Вообще приложения метода модели весьма многочисленны и разнородны (например изучение акустических свойств помещений). Применение его всегда оказывается весьма плодотворным, в особенности же при изучении новых конструкций, их критич. освоении и усовершенствовании (легкость и дешевизна изготовления моделей, простота переделок и тому подобное.). В некоторых случаях не представляется возможным реализовать все требования, необходимые для строгого осуществления подобия. Так, при движении газов по дымоходам котла происходит теплообмен с поверхностью нагрева, вследствие чего плотность их изменяется. При моделировании рабочей жидкостью служит обычно среда постоянной плотности (холодный воздух, вода), и следовательно одно из основных требований—подобие полей физич. констант—не удовлетворяется. Во всех таких случаях имеет место приближенное подобие явлений. Теория приближенного моделирования находится еще в начальной стадии своего развития.

Видоизменением метода модели является метод аналогий, основанный на формальной тождественности ур-ий, определяющих различные классы процессов (например уравнение t°-ного поля и поля электрич. потенциала, уравнения диффузии и распространения тепла). В этом случае явление-образец моделируется при помощи явления другого класса. Все основные соображения, изложенные применительно к простому моделированию, остаются в силе и здесь с той только разницей, что переход от образца к модели связан не с изменением масштаба, а с изменением физич. природы величин (например изо-термич. поверхности моделируются эквипотенциальными поверхностями, количеству теплоты в образце отвечает количество продиффунди-ровавшей жидкости в модели). Замещение величин, подлежащих измерению, величинами другой природы во многих случаях представляет большие преимущества, т. к. позволяет применить совершенно иную экспериментальную методику.

Приложения Т. п. Наибольший интерес представляют те приложения Т. п., в которых она применяется как основа для обобщения данных единичного опыта. Метод обобщения заключается в том, что данные опыта обрабатываются в форме ур-ий связи между критериями, причем неопределяющие критерии выражаются как нек-рые однозначные ф-ии от критериев определяющих. Нахождение вида этих ф-ий и является основной задачей эксперимента. Ниже приводится несколько характерных примеров приложений Т. п.

Одной из важнейших задач аэро- и гидродинамики является исследование стационарного взаимодействия между жидкостью (упругой или капельной) и твердыми телами, движущимися по отношению к ней. При этом различают два основных случая: обтекание твердого тела потоком жидкости (внешняя задача) и течение жидкости по руслу, ограниченному твердыми стенками (внутренняя задача). Рассматриваемым процессам отвечает ур-ие связи

Eu=f(Re) или ^i=f{~)·

Величина Δρ является количественной мерой той потери энергии, которая обусловлена взаимодей ствием между твердым телом и потоком. В условиях внешней задачи это взаимодействие характеризуется силой сопротивления W, то есть силой, которая должен быть приложена к телу для того, чтобы удержать его на месте в потоке жидкости, движущейся со скоростью w (или, что то же самое, сообщить ему скорость w по отношению к неподвижной жидкости). Здесь

A w

величина Δρ находится как отношение у, где

F—характеристическая площадь (площадь поперечного сечения). Ур-ие связи приводится к выражению

W=f_x (Re) Fqw²

или

w=2f_x (Re)F^f,

к-рым сила сопротивления определяется через кинетич. энергию единицы объёма жидкости. Эту зависимость обычно представляют в виде где С=2 f_x (Re) — коэф. сопротивления. В условиях внутренней задачи взаимодействие между потоком и стенками характеризуется уменьшением статич. давления в потоке жидкости. В случае канала с постоянными геометрии. свойствами (прямая труба неизменного сечения) характерной величиной является падение давления на единицу длины. Следует только иметь в виду, что рассматривать надо не абсолютную длину I, а относительную по отношению к определяющему размеру d. Соответ ственно ур-ие связи приводится к виду

= f₂ (Re) qw² или Δρ=2/₂ (Re) J

Так же как в случае внешней задачи принимается обозначение

2П (ite)=f,

причем для величины ξ сохраняется название коэф-та сопротивления. Ур-ие приводится к известному выражению:

Ap-ia⁴?· W

Т. о. необратимые преобразования энергии в условиях внешней и внутренней задачи определяются аналогичными ур-иями, в сосуав которых входят особого рода безразмерные коэфи-циенты, существенная особенность которых заключается в том, что они представляют собой однозначные ф-ии от критерия Re. Ур-ия (1) и (2) являются основными расчетными ф-лами при решении разного рода задач о механич. взаимодействии между твердым телом и потоком жидкости.

Определение коэф-та С сводится к измерению силы W при разных скоростях относительного движения жидкости с известными физич. свойствами (с известными ρ и ν). Сила сопротивления измеряется с помощью динамометров (смотрите Аэродинамические весы). Результаты опыта обрабатываются в форме зависимости коэф-та С от критерияРе. На фигуре 1 приведена в логариф-мич. системе координат кривая зависимости коэф-та С от критерия Re для шара. Из рассмотрения ее видно, что все экспериментальные точки, полученные разными исследователями при существенно различных условиях (обозначенные на фигуре 1 различным образом), хороша укладываются на одной кривой; это является весьма убедительным доказательством правиль-

ности утверждения, что коэфициент С—однозначная функция от критерия Re.

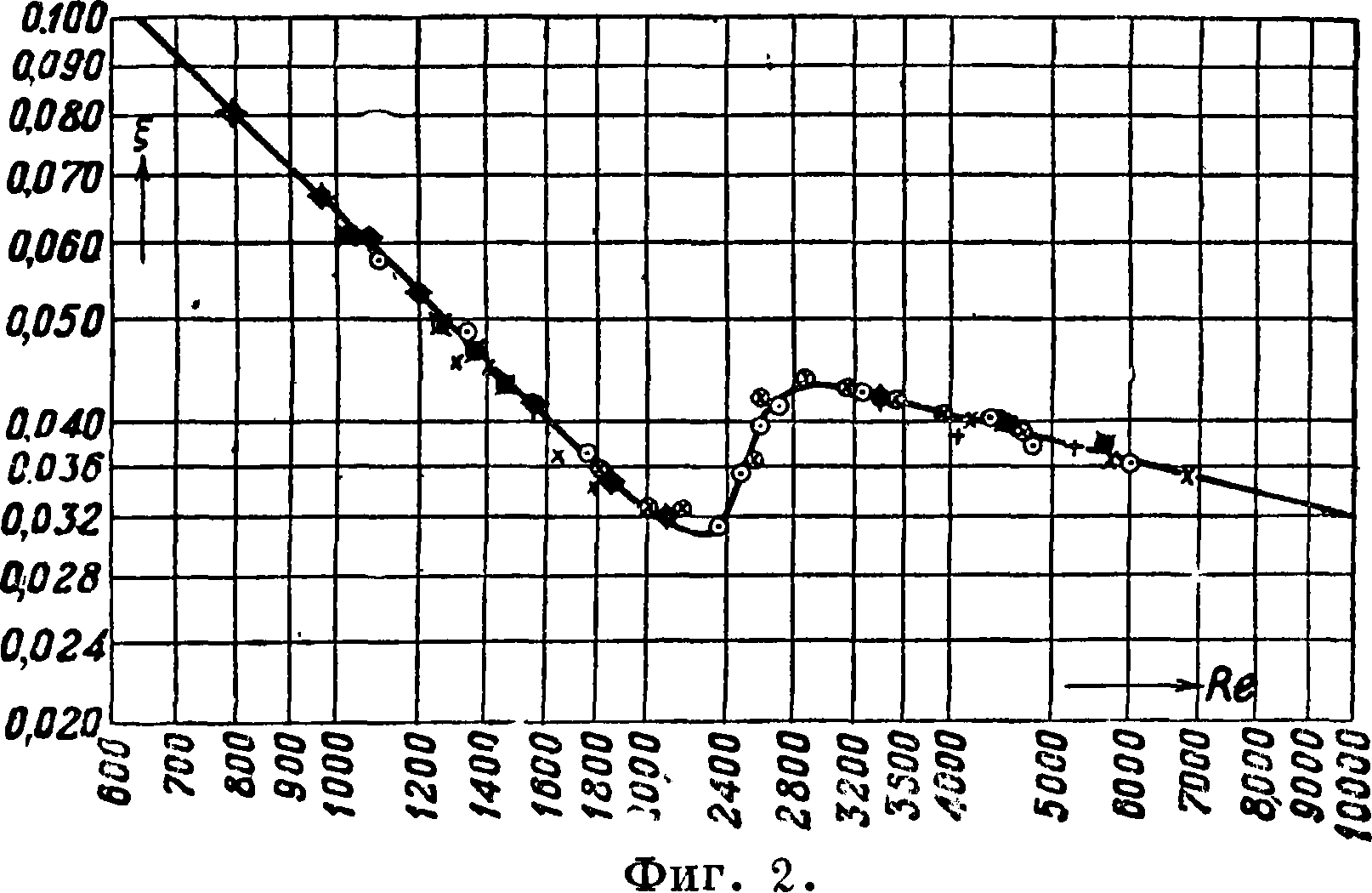
Определение коэф-та ξ сводится аналогичным образом к измерению разности статич. давлений в двух сечениях трубы при разных скоростях течения жидкости. На фигуре 2 пред-

с^ t
1
1
1
								— Re

_fwl - _____

«Г¹ 10⁰ 10 10² Ю³ 10⁴ Ю⁵ 10^е ю⁷

Фиг, 1.

ставлена кривая зависимости ξ от Re. И здесь с полной очевидностью обнаруживается однозначность рассматриваемой связи. Особого внимания заслуживает перелом кривой, свидетельствующий о резком изменении закона сопротивления при Re =2 300. Это изменение обусловлено реконструкцией потока—переходом от ламинарной формы течения к ту р-булентной (смотрите Ламинарное и турбулентное движение води и Турбулентное движение). Значение Re=2 300, представляющее собой границу областей устойчивости ламинарного и турбулентного движения, называется критическим. В полном соответствии с выводами Т. н. критич. значение остается неизменным независимо от физич. свойств жидкости, диам. трубы и других индивидуальных признаков явления; при Re < 2 300 всякое возмущение потока затухает, и он приобретает ламинарный характер, при Re>2 300 раз возникшее возмущение нарастает и турбулизирует поток. Из

рассмотрения фигура 1 выясняется, что в условиях внешней задачи также происходит внезапное изменение закона сопротивления при Re=^ 2,5· 10^б. И здесь причиной изменения является реконструкция потока—перемещение места отрыва струй и сужение вихревой области (смотрите Турбулентное движение). Существенно, что реконструкция происходит при определенном значении Re независимо от свойств жидкости и размеров обтекаемого тела.

Кривые сопротивления в равной мере относятся ко всем геометрически подобным между собой телам при движении жидкости с любыми физич. свойствами, Каждое явление, исследование которого дает экспериментальную точку на кривой, есть модель всех других явлений, характеризующихся тем же значением критерия Re. Если возникает вопрос о законах сопротивления в некотором конкретном случае (например движение определенного тела в определенной же среде), то вовсе нет необходимости исследовать именно этот случай. Достаточно исследовать модель явления, то есть изучить движение тела, геометрически подобного (в произвольно измененном масштабе) в любой среде одинаковым значениям Re в образце, и модели будут отвечать одинаковые значения коэф-тов сопротивления и качественно тождественные картины течения. Пусть напр, поставлена задача изучить на модели распределение сопротивления и картину движения для котла, модель которого В V15 натуральной величины представлена на фигуре 3. Количественные требования, обеспечивающие подобие сводятся к условию

Re"=Re, или

»"d" v"

отмечены величины, относя-

где значками щиеся к модели и образцу.

Рабочей жидкостью модели служит вода.

Масштаб выбран Таким образом условие Re"=Re служит для выбора скорости воды в модели. Данные для образца: скорость газов w= 13,0 м/ск определяющий раз-. мер (в качест-ве характерного размера выбрано расстояние от верхнего края перегородки, разделяющей первый и второй дымоходы, до барабана) d=l,72M-₁ коэф. кинематич. вязкости (газы при t° 1 065°) v=175· 10^_6 м²/ск,

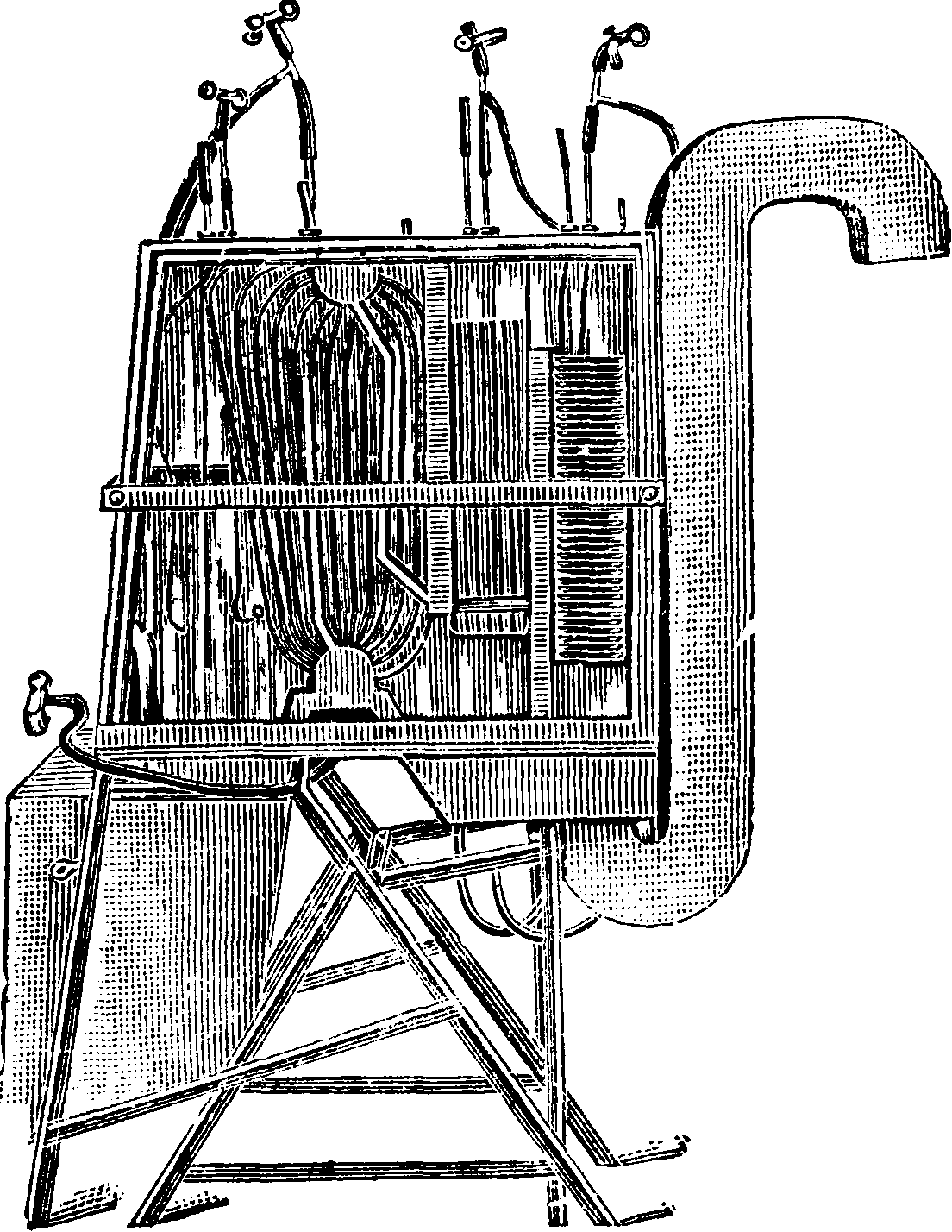
Фигура 3.

Re =

13,6 · 1,72 175·10-6

= 133 500.

Данные для модели:

d"== 0,115 м,

v"=1,23 · ПТ⁶ мЧск,

w"=Re=133 500 ·=1,43 м/ек,

Т. о. для воспроизведения картины движения газов на модели необходимо осуществить такой расход воды, чтобы скорость ее в соответственном сечении равнялась 1,43 м/ск. Существенно, что скорость в модели составляет только ок,.

^ скорости в образце; это значительно облегчает непосредственное наблюдение. В противоположность этому перепады давления в модели значительно больше, чем в образце. Действительно из условия

Ей"=Ей, или -У7,

’ ρ W 2

получается

Ар" __ ρ" /гс" 2

Ар ~ ρ * J ⁹

Ар

ρ ν²

откуда ясно, что перепады давления в модели в несколько десятков раз больше сходственных перепадов в образце. Это обстоятельство также существенно упрощает технику эксперимента, т. к. вместо весьма малых разностей давления (порядка миллиметров вод. ст.) в образце объектом измерения при исследовании модели являются разности порядка нескольких десятков миллиметров.

Лит.: Н ь ю т о н И., Математич. начала натуральной философии, пер. с лат., П., 1915; Г у х м а н А., Физические основы теплопередачи, Теория подобия и ее приложение, т. 2, Л. (печат.); Кирпичев М. и Гух-м ан А., Теория подобия, «Труды Государственной фи-зико-технич. лаборатории», М., 1929, вып. 9; их же, Приложение теории подобия к опыту, 1931, вып. 1; В г i d-gman Р., Theorie d. physikalischen Dimensionen, Lpz., 1932; GroberH., Die Grundgesetze d. Warmeleitung u. des WcLrmeuberganges, B., 1921; S chack A., Der indu-strielle Warmeiibergang, Diisseldorf, 1929; Ehrenfest-Afanassiewa, Der Dimensionsbegriff u. d. analy-tiscbe Bau physikalischer Gleichungen, «Mathematische Annalen», B., 1916, B. 77, H. 2; W e b e r M., Die Grund-iagen d. Ahnlichkeitsmechanik u. ihre Verwertung bei Mo-dellversucbe, «Jahrbuch d. Scbiffbautechniscben Gesell-scbaft», B., 1919, B. 20; Weber M., Das allgemeine Ahnlichkeitsprinzip d. Pbysik u. sein Zusammenhang mit d. Dimensionslehre u. d. Modellwissenschaft, ibid., B., 1930, B. 31; H e r r m a η n W., Ueber die Bedingungen f. dynamiscbe Ahnlichkeit, «Z. d. YDI», B., 1931, B. 75, 20; Nusselt W., Grundgesetz des Warmeiiberganges, «Gesnndheits-Ingenieur», B., 1915, B. 42; Weber M., Abnlichkeitsmechanik oder Theorie d. Modelle, Hutte, des Ingenieurs Taschenbuch, 25 Aufl., В. 1, Berlin, 1931; PrandtlL., Einfiihrung in die Grundbegriffe d. Stro-mungslehre, Handbuch d. experimental Physik, brsg. v. W. Wien u. F. Harms, B. 4, T. 1, Lpz., 1931; Busemann A., Gasdynamik, ibid., Lpz., 1931; Ackeret J., Gasdy-namik, Handbuch d. Pbysik, hrsg. v. H. Geiger u. K. Sche-el, B. 7, B., 1927. А. Гухман.