> Техника, страница 84 > Тепловая инерция

Тепловая инерция

Тепловая инерция, теплоустойчивость, свойство всякого тела сохранять постоянной свою t°, если оно не будет выведено из этого состояния Г-ным воздействием окружающей среды или какого-либо другого вида энергии, переходящей в тепловую. При этом роль силы играет количество тепла, роль скорости—1° и роль массы—объёмная теплоемкость. Отсюда следует: 1) при перенесении тела в среду с постоянной t° оно не принимает ее мгновенно, но асимптотически приближается к ней; 2) при колеблющейся t° среды будет колебаться и t° тела, но с меньшей амплитудой. Первая проблема является хорошо изученной под названием теории остывания; вторая является еще недостаточно разработанной и преимущественно называется в технич. литературе теплоустойчивостью тела.

Ряд основных вопросов жилищного строительства тесным образом связан с теорией теплоустойчивости. Одним из главных требований, предъявляемых к жилищу, является сохранение в нем б. или м. постоянных t° независимо от сильных колебаний наружных t° и неравномерного притока тепла от отопительных устройств. Старое строительство, применявшее толстые теплоемкие или нетеплопроводные стены, могло не считаться с этой проблемой. Новое строительство при применении тонких нетеплоемких конструкций должно тщательно учитывать теплоустойчивость зданий для определения характера и режима обслуживающих их отопительных устройств. Особенно резко значение теплоустойчивости зданий можно наблюдать на временных построй ках типа бараков. Если эти здания будут отапливаться нетеплоемкими железными печами, притом с перерывами на ночь, то при сильных морозах, несмотря на высокие дневные t° внутри помещения, за ночь здание успевает так охладиться, что его 1° в нек-рых случаях доходит до 0°. Это явление может устраниться либо соответствующим режимом отопления, например непрерывной топкой, либо установкой теплоемких отопительных устройств, дающих сравнительно равномерную подачу тепла. Таким образом в применении к жилищному строительству проблема теплоустойчивости м. б. формулирована сл. обр. Дано помещение, ограниченное вполне определенными наружными и внутренними поверхностями ограждений; требуется определить зависимость между колебаниями наружной t°, внутренней t° и притоком тепла от отопления. Введем обозначения: z—время, z₀—период колебания притока тепла и наружных t° (обычно можно принять z₀=24 час.; для нек-рых проблем принимаются другие периоды), х(^т)—расстояние от наружной поверхности, —расстояние от на ружной поверхности &-го слоя m-го ограждения, hi#)—темп-pa вну треннего воздуха, t_t—средняя темп-pa внутреннего воздуха

U=<»<*) de,

О

t_e(z)—темп-pa наружного воздуха, t_e—средняя темп-pa наружного воздуха, И^щ(х, z)—темп-ра внутри m-го ограждения, И^т х)—средняя темп-ра внутри m-го ограждения, V^m)—толщина m-го ограждения, Д_А—толщина lc-το стоя, -Е^(Ш>—поверхность m-го ограждения, F—об-

щая поверхность ограждений ( F=2 ^^(Ш) ),

т-1

F_s—поверхность отопительного устройства, с или —объёмная теплоемкость, λ или —

теплопроводность, К или К^(Ш>—общая теплопроводность, —поток тепла через 1 м²

m-го ограждения, wffi—средний поток тепла через 1 м² m-го ограждения, w_s(z)—выделение тепла 1 м² отопительного устройства [не учитывая теплоемкость обстановки, F_sw_s(z)== 2 F^(m)w(V^m z)], w_s—среднее выделение тепла 1 м² отопительного устройства, а_г—коэф. тепловосприятия, а_€—коэф. теплоотдачи, Т— амплитуда колебания t°,W—амплитуда колебания гг, τ—фаза t, β—фхза w. В дальнейшем ф-ии

1_е(#) ^{и w}s(z) будут считаться периодическими с периодом z₀.

С математич. точки зрения проблема теплоустойчиво сги сводится к решению системы ур-ий:

а4 ^<<я,<*’ *> - ^ £ te Ш “^я>(“. 4 (1)

te ш ^4<Ж)(*· *)]х-«"> ⁼

> (2)

te Ш *)]*-» - «Л ^<я,)(0,О - 1Ш I ’

м

g l^Ft^ -2 4=«м)· (3)

⁶ 771=1

Из этой системы ур-ий нужно найти зависимость между ti(z), t_e(z) и w_s(z). Разложим получаем

t,{z), t_e(g) и w_s(g) в ряды Фурье:

оо

1,(2)=U + 2 » ^C0S {^ηϊο^Ζ~ ^{Ti п}) ’

п=1

оо

h(2)=t_e + 2 ^Те, п COS {п ²^g - Т_е, „),

^— βs» и)

η=1

w_sO) - тонн.

+ 2 ^s, n COS (

n=l

2π

n-z-

^zo

(4)

(5)

(6)

и будем искать зависимость между соответственными коэф-тами рядов, то есть между

^и п> м» ηι пу ^τ€-»η ^ βδ, η·

Из дальнейшего будет видно, что если задаться двумя парами коэф-тов с одинаковыми индексами, то третья пара с теми же индексами определяется однозначно. Следовательно коэф-ты с разными индексами не влияют друг на друга. Положим далее

t<^m x, z)=^^тЧх, г) + f₂^(W)(z, *) 00

и соответственно

w_s(z) =

,(2) + w_St ,(z),

причем оба слагаемых удовлетворяют ур-ию (1), а вместо (2) положим:

№ £ *1^<м>(®. *)],_,<»>=j

[^Α(ί *)]*=!<««> =-%а^<ж>.*)

[λ$ £ *)]_х=0=а_е <^>(0,*)

[^А<£ 1“,<“>(“, *)]*₌₀ - «. [V^mK0,z) - i_f(*)] j

Кроме того из (3) и (7) получаем: м у·.?#,(*)- 2 *)]-

! (го

2LI

т=1

М

- ^ 2 ^‘"WV)=»1, Л») + _s(z).

т=1

(3)

sin [г$-т(г<»*>)] _ S(K™)) Ч

8ϊη[τι-τ(1<™))]-δ{1(™)) “ α* I

Щрт>)=аДУ

Из ф-лы (3) получаем

Sin [τ/-τ(/(™))] бш<5(И™))

(9)

Физический смысл каждого из этих двух частных решений следующий: Ι^ζχ,ζ) является общим интегралом ур-ий (1) и (2) при предположении /Д£)=0, t₂^(m)(x,z)—при предположении ί_ζ(ζ)=0; каждое из этих двух решений м. б. определено самостоятельно, а общее является их суммой. Т. о. для решения общей задачи достаточно решить серию частных: решить ур-ия (1) и (2) при предположении, что i_€(z) и t_t(z) являются гармонии, ф-иями с периодами z₀; Ц ; Ц ;.; В таком случае w_s{z)

определится непосредственно из (3) и (6).

1) Определение w_{u s} (z). Согласно закону Ньютона мы можем написать

w 0™, (8)

Полагая все ф-ии, входящие в ур-ие, гармоническими, получаем

Ж(1<™>) cos z - /S(l<^m>)] =

= ^аг [Ό COS g - ti ) -

- T(l‘^m>) cos g - r(l<^m>))] ·

Обозначив

= S(V^m>) и β(1<"·>) - т(г‘^И1>)=<5(ί<“>),

_1_

F_s

Μ

У] F^w[V^m z]=w_us(z).

Из ур-ия (9) видим, что т_г· — является ф-ией —^(W))· и

Обозначим

sin[r/-r(/(^m))] __ Sin[r_?— τ(Κ™))-δ(Κ™))] _

S(l(^w>) sin ό(1(^ηι)) sin<5(Zc™))

= ^Т£“

Sin [гг—КП”¹))] sin ί(ί(“))

= /ι,

sin [τ —τ(lc^w0)] sin <5(£(™))

r, - τ(1<™>)]=/„ Sin [ji(l<">) - T₍] =

= UW^m), r_t-T(l‘">)]-/₄.

При этих обозначениях мы получаем окончательно

T(l^)=TiU, W(l‘^m>)=OfTift, W,s=^a4i.

(10)

(П)

Μ 2 Μ 2

• | 2^f4"^,faj +(^ 2 ^2!,<m4«J >

(12)

M

2^ip,m4.

tg (^_1)S - T,·) =

T. о. при известных

Μ

2-^р’^<тл₁

m=1 S(IW)

(13)

и 0(l^^w>), пользуясь этими ф-лами, можем по Т⁷*· и т_г· получить ^wi,s(^) ^{и П}Р· Для удобства пользования этими ф-лами служат табл. 1,2, 3, 4 и 5.

Итак, наша вспомогательная задача сводится к определению S(V^m}) и <5(l^(W)) в зависимости от характера рассматриваемого ограждения. Рассмотрим стену, состоящую из нескольких однородных слоев. Внутри каждого слоя коэф-гы λ{χ) и с(ж), входящие в ур-ие (1), постоянны, и для А;-го слоя оно преобразуется

£«*>*)=% £.-*(*.*), (Т)

вместе с тем на границе ft-го слоя должно соблюдаться равенство

t (х_к + О,z)=t(x_k- 0,g); (14)

w(x_k 4- 0,0) -= w(x_k - 0,ζ) или

<*’*)]*-*»+о “

(^l5>

Согласно Фурье общий гармонии, интеграл ур-ия (1) имеет вид

t (χ,ζ)=А_хе~^у sin ^ ζ - у + +

+ А_ге“^у sin g + у + 0₂), (16)

S<^m>

Таблица 1. — Зависимость для ш-й поверхности стены между т_г- - т(»о, о(^т) и ]g--

ό (»«)

0

-15

-30

-45

-60

-75

-90

-105

-120

-135 i

-150

-185

-180

τΐ — т(т)

0

+ 15

+30

+45

+60

+75

+90

+ 105

+120

+135 1

+ 150

+165

+ 180

1

НЬг. 1 ! !

— оо + оо

— оо 0,000 + оо

— оо -0,286 +0,286 + оо

— оо -0,438 0,000 +0,436 ! + оо 1 ! ί !

— оо -0,524 -0,150 +0,150 +0,524 + оо ί

— оо -0,572 -0,239 0,000 +0,239 +0,572 + оо

— оо -0,587 -0 + 83 -0,088 +0,088 + 0,283 +0,587 —|— оо

— оо -0,572 -0,301 -0,135 0,000 +0,155 +0,301 + 0,572 —оо 1 1 1

— оо -0,524 -0.283 -0,150 -0,047 +0,047 + 0,150 +0,283 + 0,524 + оо ;

1 ! - оо 1 -0,438 -0,239 -0,135 -0,062 0,000 +0,062 +0,135 +0,239 + 0,436 + оо

— оо -0,286 -0,150 -0,088 -0,047 -0,015 +0,015 +0,047 +0,088 + 0,150 + 0,286 i + оо 1 1

НЬг. 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 11 Ьг.

0 ± 15 ± 30 ± 45 ± 60 ± 75 ± 90 ±Ю5 ±120 ± 135 ±150 ±165 ±180

* При <5 > 0

т{-:(«) > 0, п;:

Ж δ < 0

тг—τ(™> < 0.

Таблица 2. — Значения/!·

δ (т)
0	-15	-30	-45	-6Э	-75	-90	-105	-120	-135	-150	-165	-180	Tj-rW
0	+15	+30	+45	+60	+75	+90	+ 105	+ 120	+ 135	+ 150	+ 165	+180
libr.	1,000	1,000	1,000	ι,οοο	1,000	1,000	1,000	1,000	1,000	1,000	1,000	I libr.	0
	0,000	0,5i8	0,707	0,817	0,897	0,963	1,035	1,115	1,225	1,414	1,932	оо	± 15
		0,000	0,363	0,577	0,732	0,863	1,000	1,155	1,363	1,732	2,732	оо	± 30
			0,000	0,299	0,518	0,707 0,500	0,897	1,115	1,414	1,932	3,343	со	± 45
				0,000	0,268		0,732	1,000	1,336	2,000	3,732	со	± 60
					0,000	0,259	0,518	0,817	1,225	1,932	3,835	со	± 75
						0,000	0,268	0,577	1,000	1,732	3,732	со	± 90
							0,000	0,299	0,707	1,414	3,346	со	±105
								0,000	0,363	1,000	2,732	со	±120
									0,000	0,518	1,932	со	±135
						1				0,000	1,000	со	±150
											0,000	со	±165
			i							1		libr.	±180 i

Таблица 3. — Значения /₂.

д(П1)

0	-15	-30	-45	-60	-75	-90	-105	-120	-135	-150	-165	-180	тг--т(»0
0	+15	+30	+45	+ 60	+75	+90	+ 105	+ 120	+ 135	+150	+185	+180
libr.	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000	libr.	0
	1,000	0,518	0,363	0,299	0,268	0,259	0,268	0,299	0,333	0,5x8	1,000	со	± 15
	!	1,000	0,707	0,577	0,518	0,500	0,5-1.8	0,577	0,707	1,000	1,932	оо	± 30
	1		1,000	0,817	0,732	0,707	0,732	0,817	1,000	1,414	2,732	со	± 45
				1,000	0,897	0,833	0,897	1,000	1,225	1,732	3,346	оо	± 63
					1,000	0,933	1,000	1,115	1,333	1,932	3,732	оо	± 75 !
						1,000	1,035	1,155	1,414	2,000	3,855	оо	± 90 !
							1,000	Ι,ΐιδ	1,335	1,932	3,732	оо	±105
	1							1,000	1,225	1,732	3,345	оо	±120
									1,000	1,414	2,732	оо	±135
										1,000	1,932	оо	±150
											1,000	оо	±165
			1									libr.	±180

Таблица 4. — Значения /₃.

<5(^W)

0

-15

-30

-45

-60 -75

-90

-105

-120

-135

-150

-165

-180

τΐ-τΟη)

0

+15

+30

+45

+60 +75

+90

+ 105

+ 120

+ 135

+ 150

+ 165

+ 180

libr.

0,000 +1,000

0,000 +0,500 + 1,000 •

0,000 +0,252 +0,383 +1,000 J

0,000 + 0,211 -1-0,452 + 0,789 + 1,000

0,000 +0,158 +0,323 +0,334 +0,863 + 1,000

0,000 +0,057 +0,250 ±0,500 +0,750 +0,933 + 1,000

0,000 0,000 +0,134 +0,353 +0,634 + 0,833 +1,000 + 1,000

0,000 -0,077 0,000 + 0,211 +0,500 +0,789 +1,000 + 1,077 + 1,000

0,000 -0,183 -0,183 0,000 +0,317 + 0,683 +1,000 +1,183 +1,183 + 1,000

0,000 -0,353 -0,500 — 0,333 0,000 + 0,500 +1,000 +1, з 3 3 + 1,500 + 1,333 +1,000

ο,οοο libr. — 0,830 1 — оо -1,330 - оо — 1,3 30 i — оо — 0,830 — оо 0,000 1 - оо + 1,000. libr. +1,830 + оо +2,330 + оо +2,350 J + оо +1,860 ; + оо + 1,000 ; + оо libr.

0 ± 15 ± 30 ± 45 ± 60 ± 75 ± 90 ±105 ±120 ±135 ±150 ±165 ±180

T а Г) л. 5. — Значения /₄.*

<5(ш>

ί

0

-15

-30

-45

-60

-75

-90

-105

-120

-135

-150

-180

I -180

тг--т<»и> !

0

+ 15

+30

+45

+ 60

+75

+90

+ 105

+ 120

+ 135

+ 150

+ 130

+ 180

I

0,000

0,000 0,000 1

0,000 ±0,134 0,000

0,000 ±0,183 ±0,183 0,000

0,000 ±0,211 ±0,289 ±0,211 0,000

0,000 ±0,232! ±0,363 ±0,383 ±0,232 0,000

0,000 ±0,250! ±0,4831 ±0,500! ±0,433 ±0,250 0,000

0,000 ±0,238 ±0,500 j ±0,834 ±0,334 ±0,500 ±0,238 0,000

^ 0,000 ±0,289 ±0,577 ±0,789 ±0,833 ±0,789 ±0,577 ±0,289 0,000

1 0,000 ±0,317 1 ±0,383 ±0,000 ±0,183 ±0,183 ±0,000-±0,883 ±0,317 0,000

0,000 ±0,383 ±0,8 53 ± 1,3 a j ±1,732 ±1,837 ±1,732 ±1,837 ±1,732 ±1,383 0,000

0,000 ±0,500 ±1,363 ±2,363 ±3,232 ±3,732 ±3,732 ±3,232 ±2,363 ±1,386 ±0,500 0,000

libr. ±оо ±оо ±оо ± со ± со ±оо ±оо ±оо ±оо ±оэ ± со libr.

ί 0 ± 15 ± 30 ± 45 ± 60 ± 75 ± 90 ±105 ±120 ±135 ±150 ±165 ±180

I * При δ > о /₄ > о, при ό < о /₄ < о. где

»“(*-**) V т&>	(17)
w (х,я) =
= Κ^[-^Βΐη(ϊ^-» + β’+Γ	) +
+ Аг& sin г + у + + тонн)] i	(IS)
как t (ж, я), так и w (ж, я) зависит от четырех независимых постоянных Аи П2, дг и θ2. Преобразуем i и w так, чтобы они имели вид
t(x,e)=Ts cos(f-^-r,) = = Т„ ~ξ cos [ψοΖ~ (ту - τ„) - τ0] ;	(19)
W (X, Ζ) =Wy COS [ψ^Ζ - βν) = = Tr0^cos[2^-(^-^)-^o]	(20)

и зависели от новых независимых постоянных Т₀, Ж₀, г₀ и β₀. Из ф-т (16) и (18) мы можем заключить, что, если для какого-либо значения ж мы одновременно увеличим t (х, я) и w (х, я) в одинаковое количество раз и сдвинем их фазы на одну и ту же величину, то и для всех других его значении t (ж, я) и w (ж, я) увеличатся в то же число раз и сдвинутся на ту

Следовательно

VV о vv о же величину.

Р_у — β₀ будут зависеть не от четырех постоян но _ о ных, а только от двух:

Вместо $₀ мы введем новую определяемую равенством

Do- ^S°

βο ^το⁼

постоянную

= <5ο Do

Ί Γίπολ

V Ζ₀

(21)

и будем определять D_y и д_у как ф-ии В₀₎ <5₀и у. Положим сначата D₀=l. В таком случае путем многочисленных переделок можно получить

sin 2у

; cos (<5₀ + 15°)

1+th 2у sin (<5₀+ 45^е) ’

lg

где F=pJ^y

cos 2у

^{ig tg} ^ ⁼ l^g ΐ+G > ^{Где G =} l+5tF2!/sin (ίο+45°)

COS (<5q + 15°)

-. (23)

Положим, с другой стороны, <5₀=45°. В таком случае

COS 2у D$-l

ig Dy=i lg i+f, где F lg tg δ_ν=lg ~, где G

ch iy D g+i

O _

1+th 2у

,(22)

sin 2у jDq —1 Sh 2y Dg+1

1 + cth 2y

i + ^O²

Эти ф-лы позволяют установить зависимость между В_у и д_у, с одной стороны, и D₀, <5₀ и 2/,—с другой, в графич. форме. Построим на плоскости оси координат, причем за ось абсцисс примем δ, а за ось ординат—lg В. Положим lg D₀=0 и

<5₀=— 135°; — 130°; — .; — 5°; 0°; +- 5°; .;+45° и будем давать у последовательно значения:

У=-~ — 0,95~ ;. — 0,05-^-; 0;+

+ 0,05 ~ ; .·.; + 0,95 ; +-£.

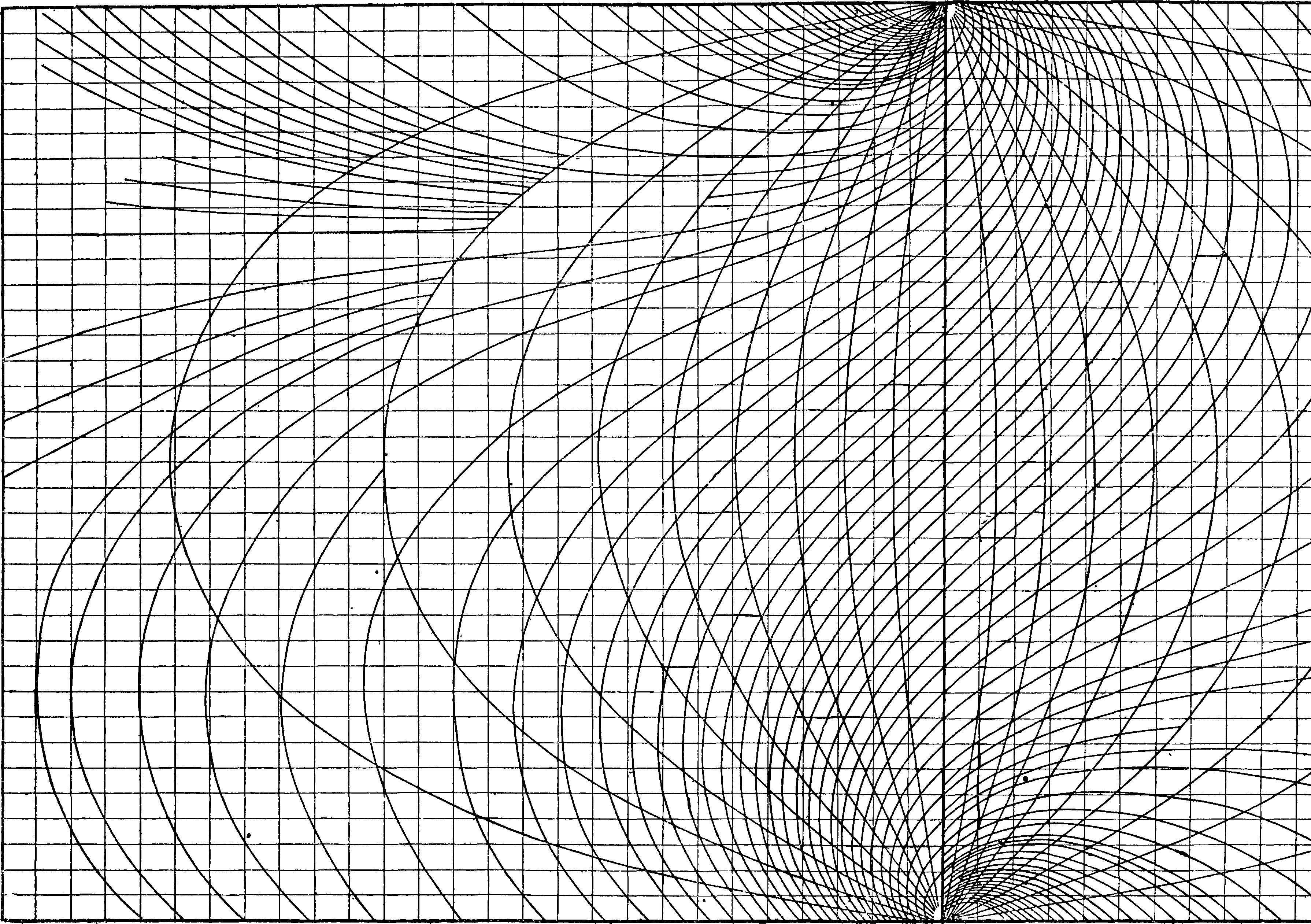
Подставив эти значения <5₀ и у в ф-лы (22) и (23), мы получим ряд значений lg В_у и д_у, которым на нашей плоскости будет соответствовать ряд точек. Соединим серией кривых точки, имеющие разные значения у и равные <5₀, и другой серией точки, имеющие равные значения у и разные <5₀ (фигура 1). В тех местах, где кривые слишком далеко отстоят друг от друга, мы дополнили их по ф-лам (22) и (23). При помощи этой диаграммы расчет В_у и б_упроизводится совершенно автоматически. Пусть мы имеем начальные значения В₀ и <5₀. Этим значениям соответствует точка с соответственными координатами. Из этой точки будем продвигаться вдоль первой серии кривых на число шагов, соответствующее значению у, считая,

что каждый шаг соответствует 0,05-γ. Следо вательно 1 сантиметров стены соответствует 0,4 1 —^c,i

Г л λ]·ζ₉

шага (смотрите табл. 6).

Для окончательного решения 1-й вспомогательной задачи остается показать, как, зная значения В и δ для конца к-го слоя, получать их для начала (к +- 1)-го и наконец как определять значение этих величин на наружной поверхности. Но это не представляет никакого

Д ИА Г Р А Μ М А

для расчета теплоустойчив осте

-

-1,3 1,2 -1,1 -1,0 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3 -0,2 -0,1 0,0 *0,1 *0,2 *0,3 *0,4 *0,1

Название материалов	Коэф. теплопро водности fa А	Объем ная теплоемкость с	Период колебания в час Zo	Число шагов диаграммы, соот-ветств. ,1 сантиметров стены	lg У с А	на наружной поверхности стены	J S(!<«*>)_ ! ai I -1 gD(h™))
Бетон литой.	1,00	380	24	0,90	1,290	0,302	+ 0,124
Железобетон набивной. Шлакобетон набивной в наружных огражде	1,33	440 i	24	0,84 J	1,384	0,208	+0,218
ниях .. Дерево поперек волокон в наружном огражде	0,50	250	24	j 1,03	1,048	0,544	-0,118
нии .. То же во внутренних	0,15	390	24	2,35	0,881	0,708	-0,282
конструкциях.	0,12	390	24	2,65	0,835 1,154	0,757	-0,331
Кирпичная кладка. Торфяные плиты, сма	0,70	357	24	1,04		0,393	-0,033
чиваемые.	0,07	200	24	2,46	0,573	1,019	-0,593
То же, несмачиваемые. Обыкновенная известковая штукатурка на	0,06	175	24	2,49	0,511	1,081	-0,655
внешней поверхности То же на внутренней	0,75	320	24	0,95	1,190	0,402	+0,024
поверхности.	0,60	320	24	1,03	1,142	0,450	-0,021

труда; из ф-л (14) и (15) заключаем, что

S(x_k + 0)=S(x_k-0),

9(х_к + 0)-Я(х_к-0),

следовательно

УВ (ж,. -0)=У²—j) (χ_:, ₊ о)

ИЛИ _

lg В(х_к + 0)=В (х_к - 0) + lg Ус_кХ_к -

- ig V+₊i^₊₁ ·

Т. о. для перехода от конца к-го к началу (к + 1)-го слоя нужно сохрани гь значение абсциссы и продвинуться по вертикали на отрезок (табл. 6):

igVcA-ig V4+ι4₊ι ·

Для определения Ό (0) и δ (0) воспользуемся вторым ур-ием (2)· Из него следует, что w₁ (0, z)=a_et_x (0, z).

Отсюда заключаем, что

$(0)=а_в и δ (0)=0.

Следовательно (табл. 6)

lgJD(0)=lg

к

2 лс₁Л₁Zo~

(24)

Т. о. по значениям на наружной поверхности стены lg I) и δ мы можем, переходя от слоя к слою по диаграмме фигура 1, определить эти величины и на внугренней поверхности стены,

затем, прибавляя к lg D(l^(m)) lg

Vϊ

ясШ

*0

МЫ

получаем, lg ^Sjl — и по табл. 1, 2, 3, 4 и 5 определяем все нужные нам величины.

2) Определение w₂, _s(z) и t₂(l₃z). Для определения w₂,_s (z) мы не можем воспользоваться приведенными выше таблицами, т. к. по первому условию (2)

= 1 И δ О^т)=о. (25)

Однако, пользуясь нашей диаграммой, мы можем подобно предыдущему случаю от внутренней поверхности перейти к значению этих ве личин на наружной и затем по таблицам определить Т (0) и т(0), причем в ф-лах (10), (11), (12) и (13) индекс г нужно заменить через e. Т. о. для решения второй вспомогательной задачи мы по JD (0), δ (0), Т (0) и т (0) должны определить две последние из этих величин на внутренней поверхности стены. Для этого достаточно определить в формуле (19) неизвестные величины: значения ^ и г_у — т₀ как ф-ии JD₀ и δ₀ я у. Эту задачу можно решить также графич. методом: положим для ό₀=45° т₀=0. Давая различные значения lg JD₀ и у, мы будем получать различные значения lg D_v> д_у и т_у. Каждому значению lg D_y и д_у соответствует на плоскости определенная точка; следовательно каждой точке соответствует значение Ту; соединим точки, соответствующие равным значениям т_у) новой серией кривых;

аналогично поступим для lg : положим для

lg J)_Q=О и lg jP₀=0 и, давая различные значения д₀ и 2/, будем получать lgJD^, д_у и lg Ту> соединяя точки, имеющие координаты lg и ду и соответствующие равным значениям lg Ту, получим еще одну серию кривых. Формулы, определяющие т_у для <5₀ =45° и lgT_y для lg Х>₀=0, можно получить путем длительных но не представляющих принципиальных трудностей переделок:

причем и

^τ2 ^{= Δ}ι^τ + ^Δ2^τ> tg Δ_χτ=th у tg у

tg Δ₂τ

sin2 у _

ch2 у -у cos2 у

7~, п ^sh2^

⁰ Ch2y + C0S2y

И

Ту=ch 2у -f (sh 2у + sin 2у) cos ό₀ -f

-f (sh 2у - sin 2у) sin δ₀.

При помощи этих кривых и вторая вспомогательная задача решается автоматически. Каждой паре чисел lgD и δ или каждой точке нашей плоскости соответствуют два новых числа lgT и т. Пусть началу &-го слоя соответствуют lg-Z)^, <S*__M lg Т_к-__х и т_к__1Уа концу его—lgJD_A, δ,., lg T_k и т_к. Для того чтобы определить, насколько при переходе от начата к концу слоя изменяется lgT и τ, достаточно взять и Ig^-lgTi-i (26)

Ч~Ч-1 ^J

Зная Т₀ и т₀ на наружной поверхности стены, мы шаг за шагом по формуле (26) можем определить их и на внутренней. Отсюда W (£^(Ш)) и β (V^m)) получаются по ф-лам:

lg W (V^m))=lgS (Ιί^,η>) + lg Τ (Z<^TO>)

^И β (V^m))=δ (V^m)) -f- τ

Ho lg £a^(m))=^a* и d(V^m>) =0 согласно (25), следовательно

lg W (V^m))=lg a_t + lg T (U^m))

T. о. и вторая вспомогательная задача решена. Следовательно решена и общая. Определим например T_iy зная из метеорология, таблиц t_e(z) и из экспериментальных наблюдений над отопительной системой данной конструкции w_s(z). Эту задачу можно решать в следующем порядке: 1) определяем для каждой наружной поверхности ограждения w₂ (V^m),z);

2) определяем w_2fS(z) по ф-ле

«>,.(*)Σ ^{Fim) w}* i¹¹"⁴.*);

3) определяем w_us (z) по формуле w_bs (z)=w_s(z)—

— w₂^{z) 4) определяем lg _и <5₃ (V^m))

для каждой поверхности ограждения; 5) определяем f_ls f₂, /₃ и f₄ для каждой поверхности ограждения; 6) определяем Т_г· из у-рия (12) по ф-ле

τΥ{Σ ^F<m> f·)· + (Σ

Практически, ограничиваясь периодами колебания £Дг) и w_s(z), меньшими или равными 24 част., мы можем считать, что наружные темп-рные волны затухают в толще ограждений, не доходя до внутренней поверхности их для всех ограждений, кроме окон. Для этих последних можно положить; считая их абсолютно нетеплоемкими,

w₂(U° z)=K™ [f_e— следовательно

K‘°> [i,-i, (*)].

Мы ограничились в этой статье изложением общей теории теплоустойчивости без приведения употребительных практич. ф-л, т. к. все они крайне несовершенны и имеют лишь временный интерес.

Остывание тел. Темп-pa в каждой точке всякого физич. тела, граничащего различными частями своей поверхности со средами, имеющими постоянные, хотя и различные, t°, асимптотически приближается к некоторому пределу, различному для различных точек. Т. о. возникают две задачи: определить для каждой точки тела предел, к к-рому стремигся ее t°, и определить, с какой скоростью t° приближается к этому пределу. Первая из этих задач встречается гл. обр. как вспомогательная для определения теплопередачи: через ложные тела; вторая начинает приобретать применение как в вопросах строительной теплотехники, так и во многих производственных процессах. Введем следующие обозначения: z — время, х, у, и— координаты точек тела (для стены х=0 для одной из ее поверхностей), г — радиус, х_к и г_А. — расстояния /т-го слоя в многослойных телах от поверхности или от центра, t_lt t₂, .—темп-ры окружающих сред, Цх, у, и, z)—темп-pa точек тела (если t° не зависит от нек-рых координат, то они не пишутся), t₀(x, у, и)—начальное распределение темп-p, t(x, у, и)—предельное распределение темп-p, w—поток тепла (w=— ),

λ(χ, у, и)—коэф. теплопроводности, с(х, у, и)— коэфициент объёмной (вместо су) теплоемкости, «i, а_?, .—коэф-ты теплоотдачи (или тепло-восприятия), К — число слоев многослойной стенки,×— толщина всей стены, R—общий радиус цилиндра или шара (значения коэфициен-тов см. Спр. ТЭ, т. VII). По методам решения указанные общие задачи распадаются на следующие частные. 1) Установившийся поток тепла через однородную или состоящую из нескольких слоев плоскую, цилиндрич. или сфе-рич. стенку. 2) Остывание однородных или состоящих из нескольких слоев стен цилиндра и шара. 3) Установившийся тепловой поток через однородное тело, ограниченное двумя цилиндрическими поверхностями, основания которых м. б. практически конформно отображены на две параллельные прямые или кон-центрич. окружности. 4) Остывание и установившийся поток тепла для произвольных тел однородных или состоящих из нескольких однородных. С математич. точки зрения решение этих задач сводится к нахождению ф-ии, которая внутри однородных частей тела удовлетворяла ур-ию теплоты, а на границах разнородных частей и на поверхности тела—следующим пограничным условиям:

t (х + dx, у -f dy, и + du, z) =

= t(x — dx, у — dy, u — du, z), (27)

w (x -f dx, у -f dy, и -f du, z) =

= w(x — dx, y — dy, u — du, z) (28)

при dx=0, dy=0, du == 0.

Выразим ур-ие (28) в конечных разностях, предположив, что направление dn совпадает с дх,

- t (х + Δ_χχ, у, и, z) — t (х, у, и, z)

¹¹ L_xx ~~

Q t(x, у, и, z) — t(x—к_гх, у, и, Z)

ИЛИ

t(X,y,U,g) =

Λ₃ Δ₂×Λο Δι x

t(x-}~ A₁x,y,u,z)- -t(x-k₂x,y,u,z)

1 +

λi Δ₂×λ₂ Δ_χχ

-(29)

и на поверхности тела

^аг [ t (X, у, и, Z) - *<] - + А (ж, у, и) ~ t(x, у, и, г) (30)

для х, у, и, лежащих на поверхности тела. Если направление dn_{ совпадает с дх, то ур-ие (30) можно заменить ур-ием в конечных разностях при условии, что Аж не выходит из однородного слоя,

o.i[t{x,y,u, £)-«,·]= +

+ λ (X, у, и) *⁽*^+д*· ^у’

или

t(x,y,tc, s)={,· +

t (x + Δ χ, у, и, z)-tj

1 +

α^Δχ Я {X, у, и)

(31)

Общее ур-ие движения тепла имеет вид Для однородного тела оно преобразуется в

£‘-Нё‘+£.<+£·] «

В случае установившегося состояния очевидно 4- £=о. Следовательно ур-ия (32) и (33) преоб-

OZ

разуются в

⁺^[^А1Д+^[^А1г(|^{=0 (34)}

+ <³⁵>

Из ур-ий (29), (31) и (32) заключаем, что t (ж, 2/, и, %) — t (ж, 2/, и) + t_x (ж, 2/, и, я),

причем t_x удовлетворяет *ур-ию (33) и (30) при предположении, что все ^-=0. Т. о. вопрос об остывании и об установившемся состоянии можно изучать отдельно.

1-я з а д а ч а. В этом случае для стенки плоской

^ [а (*)έ *(*)]- о,

цилиндрической (в цилиндр, коорд.)

57 [гЧг)^Чг)]=0,

сферической (в сферич. координатах)

£ [г“А (г) £ί·(>-)]=0.

Решая эти ур-ия, получаем поток тепла для стены с 1 м²

t —t 2

w =

JL_i- V ^χ*^+ι~^χΐί i ¹ *

«1 ⁺ ZA Я_к α₂

для трубы cl η. Μ

W =

2 7Г ( ί 1 — 12 )

fe=l

lnrjf+ι -In r_kЧ

^a2^rK+l

для шара через всю поверхность inlh-t ₂)

- +

Vr »7; ^fH^r2K +1

(36)

Ί ¹ ЛГ+1

и темп-ры для стены

_i=ii__wjJ + 2 *шгЗ ₊ *=5г для трубы

_Λ j "W i 1, VI lnrK₊i-ln5r/_;, 1пг-1пгр

^ί_Η”2π a.r+Z^ - ^

k=l

для шара

(37)

2-я задача. Для решения этой задачи ищем частное решение ур-ия (32) в виде

t (ж, у_t и, z)=y (0) /(ж, у, и).

Подставляя это выражение в (33), разделив переменные из равенства ф-ий от 0 и от ж, у, и, заключаем, что они тождественны некоторой постоянной —μ. Следовательно

Ψθ) =

д_

дх

[Φ]+1,Ηι]⁺Ά>Μ+^-»·

Т. Э. т. XXII.

В частных случаях ур-ие (36) преобразуется: в однородном слое плоской стенки

d² dx ²

/(®) +

μθ

λ

fix)

= 0,

для цилиндра

dr^{2 7}

для шара

^/(г) + “-Д-/(г) + А*!Нг)-0.

Эти ур-ия имеют соответственно решения

(ж)=И cos ]/"/г I ж + В sin ]/" μ | ж,

(^r) ⁼ AJ„ (^/~ /i I ж)

[J₀ — Бесселевы функции (смотрите)],

i] μ χ

fir)-Α

ν

С

На поверхности для ж=ж,.₊₁ или г=г_к+1 иэ (29) получаем, положив ]/*μ^ν_1ί+1=ν,

, f(у) f(y)

C₁R²

Это ур-ие имеет бесконечное множество корней v_h. Т. о. получаются частные решения, удовлетворяющие ур-иям (31) и (29). Общее решение должно удовлетворять еще условию t₀ (ж, 2/, w) —произвольной функции. Можно доказать, что это решение имеет вид

^ -у^{2 λζ}

t=2

к

А_к зависят только от t₀(x, 2/> я), v—от | Е. Следовательно

^[д л, ^f0 (ж,

Положим t₀ (ж, у,и)= /₀,

‘=г)·

К”* π)·

Точно так же потеря тепла телом за время 0 w=w_o0(}R, ^ϊ)·

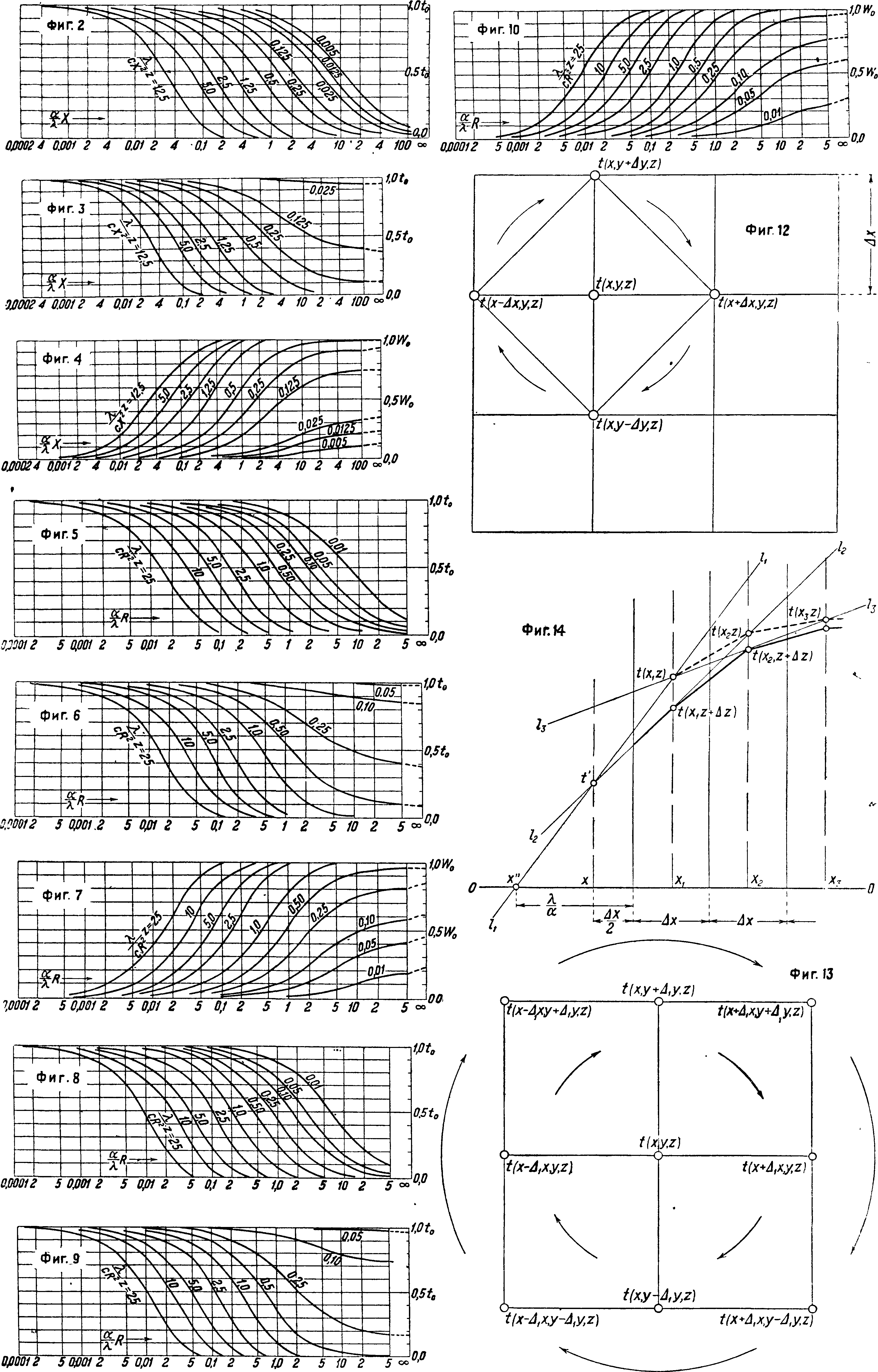
Ф-ии F и Ф представлены графически Гребером для г=0иг=Л или ж=у и ж =×(фигура 2, 5 и

В дают ί° поверхностей соответствующей стенки цилиндра и шара, фигура 3, 6 и 9—1° середины, фигура 4, 7 и 10—потерю тепла).

3-я задача. Эта задача обыкновенно решается при заданных ί° на обеих поверхностях. При условии (30) для получения приближенного решения нужно увеличить тело на слои тол-λ λ

щиной -- и — и считать на поверхностях нового увеличенного тела темп-ры t_x и t₂. Отобразим конформно основания границ на две концентр ич. окружности или параллельные прямые. Пусть при этом ж=ж(м, v) у=у (и, v). Распределение темп-p между окружностями и параллельными прямыми при темп-pax на поверхностях t_x и ί₂ дается ф-лами (36) и (37)

при предположении ~=0. Из теории конформного отображения известно, что если на плоскости (w, v) в точке с координатами (щ, г>₀> имеется темп-ра /, то ту же темп-ру имеет точка с координатами ж₀=ж(^₀, г>₀), у₀=у(и₀, ?о₀) на плоскости (ж,.у). Зная темп-ры, не трудно

определить и поток тепла. Таким способом можно получить поток тепла от трубы или туннеля, заложенных на глубине h (фигура 11),

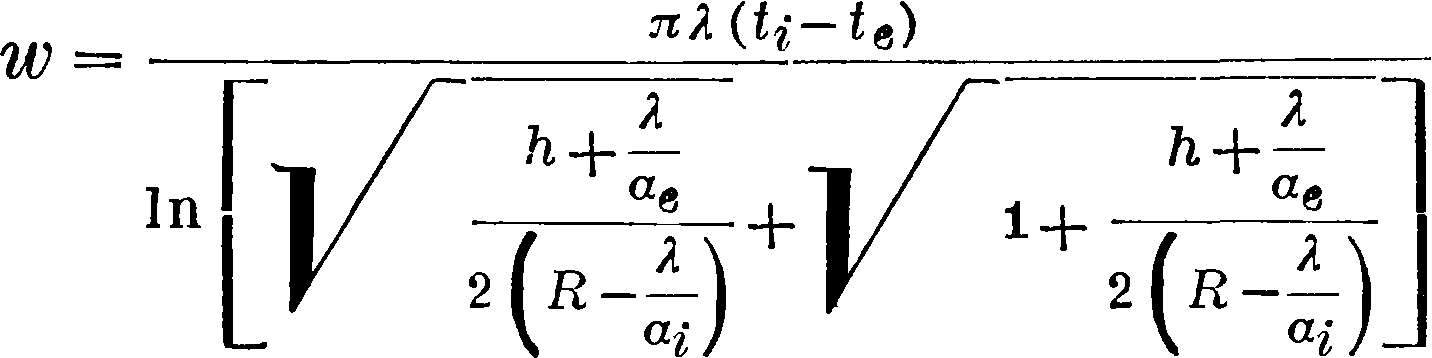
Методами конформного отображения можно также отобразить угол стены на параллельные прямые и прочие.

4-я задача. Эта задача самая общая, решается методом Либмана. Ограничимся плоским (то есть ограничен-Фигура и. ным цилиндрич. поверхно стями) телом, т. к. обобщение на пространственное не представляет труда. Возьмем однородную часть тела и разобьем ее на равные квадратики со сторонами Ах. Положим. с Ая²

и, заменив в ур-ии (27) производные конечными разностями, получим

Вместо ф-лы (38) можно пользоваться ф-лой Селиверстова-Поллок, которая экономит вычисления в два раза, давая тождественные результаты. Берем А_хх — |/2 Ах и, сохраняя прежнее значение Az₉ имеем (фигура 12):

t (X, У, г + 2 Аг)=~ [ t(ж, у, г) +

+ Н t(x + A,x, у,г) + Цх,у~А, у, г) +

+ Цх-А,х, у, z) + t(x, у + А,у,е) +

+ С*(яг + Δ, х, у + Δ, у, г) +

+ £(х + А, х, у — Δ, 2/, z) + t(x — А, х₉ у —

- А, ж, у - Δ, 2/, z) + t (х - Δ, х, у + Δ, у, $)]} ].

Для остывания стены можно пользоваться как методом Либмана, так и графическим методом

, Шмидта. Положив Az=~ ~, получаем (фигура 13)

t (х, z + Δ*)=1^(х-± ^Ах> *) + *(«-*“. *).

Для определения t (х, z + Az) графически разбиваем стену (фигура 14) на полосы Ах. Из середины каждой восставляем перпендику-

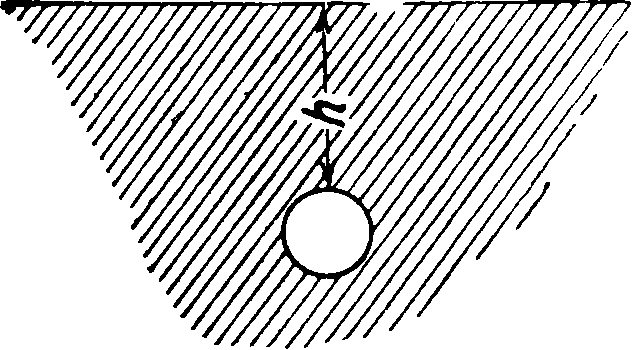
t (ж, 2/, z + Az) =

t (зс4 А%, у, z) + t(x, у-Ay, z) + t(x-Ax, у, z) + t(x, У + Ау, z) 4

(38)

Получив т. о. значения t (ж, у, ζ + Az) для всех точек кроме пограничных, получаем для последних по ф-лам (29) и (31). При этом для неоднородного тела необходимо соблюдать условие d Ая² __ с₂а₂х² __ л „

4 Д₂4 ··· ^

к-рое определяет соотношение между Δ^, А₂х и т. д. Т. о. шаг за шагом определяются скорость остывания и предельное распределение темп-p в любой точке и в любой момент. Полученные значения являются приближенными, но будут тем точнее, чем меньше Ах, если с уменьшением Ах увеличивается число десятичных знаков при вычислении t (х, у, z). В качестве примера на расчет по методу Либмана ляр высотою t (ж, z). Температура в момент z изобразится графически ломаною t(x_l9 z) t(x₂₎ z) t(x₃₎z). Соединим прямой l₃ точки t (x_l9 z) и ί (ж₃, z). Пересечение прямой 1₃ с вертикалью х₂ определит точку t (х₂, z + Az). Точно так же, соединяя t(x₂,z) и t(x^z)₉ t(x₃,z) и t (ж₅, z) и т. д., получаем t (х₃, z + Az), t (ж₄, z + Az) и т. д. Для определения t{x_Xi ζ + Δ#) откладываем отрезок длиной £, который определит ж",

и отрезок γ-, который определит вертикаль х.

Пересечение прямой 1₁₉ проходящей через ж" и t (ж_1} z), с вертикалью х определит t. Пересечение прямой l_2t проходящей через t и t(x₂, z),

Таблица 7. —Распределение t° в углу кирпичной стены в i/_a кирпича.

Ц=+ 20

4-13,40 413,39 413,38 413,34 413,26 413,17 413,01412,75 412,33 411,67 410,50

4 8,24 4 8,24 4 8,20 4- 8,12 4 8,00 4 7,84 4 7,55 4 7,10 4

4 3,10 4 3,08 4 3.03 4 2,93 4 2,80 4 2,60 4 2,20 4 1,67 4

- 2,05 - 2,07 - 2,12 - 2,22 - 2,38 - 2,60 - 2,95 - 3,50 -

- 7,20 - 7,22 - 7,27 - 7,35 - 7,50 - 7,70 - 7,99 - 8,43 -

-12,36 -12,37 -12,40 -12,46 -12,55 -12,70 -12,90 -13,17 --17,53 -17,53 -17,54 -17,56 -17,58 -17,64 -17,70 -17,78 -

t_e =

приводим остывание (табл. 7) и предельное распределение темп-p (табл. 1 и 8) в углу однородной кирпичной стены при ж=0,375 м, λ== 0,6,0!=7,5, α₂=20, Ах=Ау= 6,25 см.

Этот пример заимствован из работы Д. Панова. Начальные темп-ры были положены равными — 20,000000.

Таблица 8 .—С корость приближения к установившимся температурам.

п	i(0,ybnAz)	t(X, Vi, nAz)
0	-20,000000	-20,000000
1	-20,000000	4 8,037383
2	-18,066380	412,229883
3	-17,643897	413,145936
4	-17,551584	413,346092
5	-17,531414	413,389825
6	-17,527007	413,399381
7	-17,526044	413,401469
8	-17,525833	413,401926
9	-17,525787	413,402025
10	-17,525777	413,402047

6,35 4 5,17 4 3,10 4 9,03 0,82 - 0,43 - 2,29 - 4,93 - 7,88 4,28 - 5,35 - 6,80 - 8,68 -10,76 -12,89 9,04 - 9,81 -10,87 -12,14 -13,53 -14,99 -16,45 3,55 -14,04 -14,65 -15,37 -16,18 -17,03 -17,89 -18,75 7,91 -18,07 -18,27 -18,50 -18,76 -19,04 -19,32 -19,60 -19,88 - 20

с вертикалью х_х определит искомую t (x_l9 z + + Az). T. о. получаем новую ломаную t (x_l9 z -f

t (ж, z + Az) около границы двух слоев опреде-

*29

ляются следующим построением: проводим через (ж₃, z) горизонталь Пересечение ее с вертикалью х, отстоящей от границы на

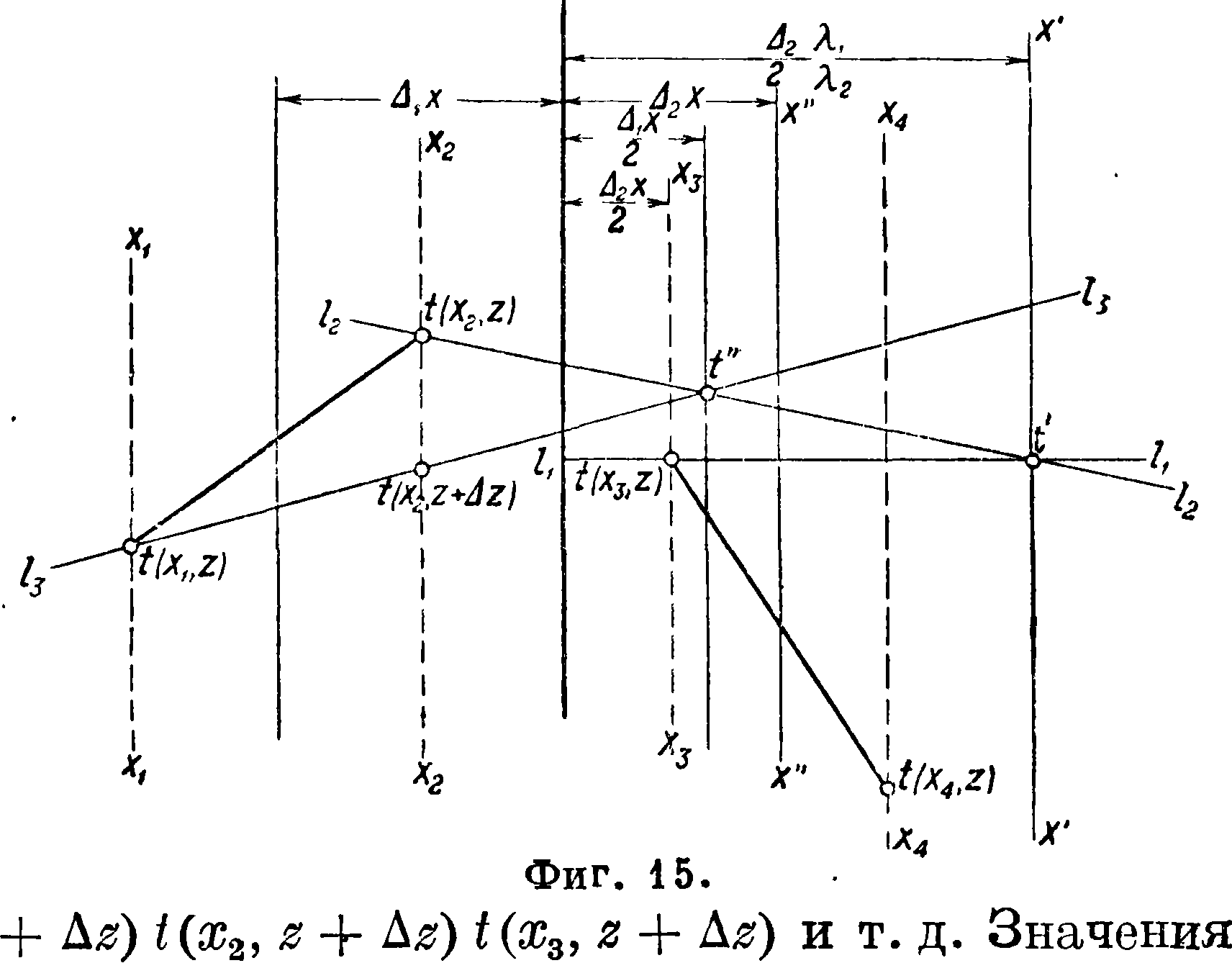
^ определит V (фигура 14). Проводим через V и t (х₂, z) прямую 1₂. Пересечение ее с вертикалью ж", отстоящей от границы на,-~₉ определит t". Наконец пересечение прямой l_s, проходящей через t" и t (x_l9 z), с вертикалью х₂определит t (х₂, ζ + Δζ). Подобным образом получается t (ж₃, ζ + Δζ) (фигура 15).

Лит.: Власов О., Плоские тепловые волны, «Известия Политехнич. ин-та», 1927; Гребер Г., Введение в теорию теплопередачи, пер. с нем., М.—Л., 1933; Мачин-с к и и В., Теплотехнич. основы гражданского строительства, М.—Л., 1933; Селиверстов Г., К вопросу тепловой инерции зданий, М.—Л., 1933; Fourier J., Theorie de la chaleur analytique, «Ann. Chim. et Phys.», P., 1816,

t. 4; G-rober H., Die G-rundgesetze der W&rmeleitung

u. des Warmeiiberganges, 2 Aufl., B., 1933. Г. Селивэрстов.