Теплопередача

Теплопередача. Понятие Т. охватывает всю совокупность явлений теплообмена между телами. Получение и отдача тепла физич. телами могут происходить тремя различными способами: путем кондукции, или теплопроводности, конвекции, или теплопереноса, и радиации, или лучеиспускания. Кроме того она может конечно происходить и через другие промежуточные формы энергии.

До 40-х гг. прошлого столетия теплота считалась особого рода невесомым веществом—«теплородом». Работы Роберта Майера (1842 г,), Джоуля (1843 г.) и Гельмгольца (1847 г.) разрушили этот взгляд и привели к представлению о теплоте как о беспорядочном движении частиц тела. При этом представление о тепловых явлениях, охватываемое в просторечии одним словом «теплота», расчленилось на два понятия: 1) внутренней тепловой энергии в определенном состоянии и 2) теплообмена, то есть получения и отдачи телом энергии при различных изменениях его состояния. Последнюю и принято называть в термодинамике теплотой. Подробнее см. Термодинамика.

Внутренняя энергия тела представляет собой кннетич. энергию беспорядочного интрамолекулярного движения частиц тела. Внутренний строй тела определяется, с одной стороны, интенсивностью теплового движения частиц, с другой, теми не вполне разгаданными еще причинами, которые действуют между частицами и которые носят название сил сцепления. Под влиянием этих сил сохраняется нек-рое среднее расстояние между частицами тел твердых и отчасти жидких. Эти силы убывают с увеличением расстояния между частицами, и тела переходят в газообразное состояние, при к-ром частицы свободно двигаются по всем направлениям. Для газообразных тел достаточно немногих предположений относительно движения и природы молекул для вывода всех их физич. свойств. Кинетическая теория (смотрите) газов т. обр. сводит все тепловые величины—внутреннюю энергию, t°, теплопроводность и т. д.— к чисто механич. представлениям. Ее воззрения являются одним из наиболее важных завоеваний материалистич. мировоззрения. Попытки аналогичных выводов для твердых тел наталкиваются на большие трудности. Однако Дебаю в 1912 году удалось заложить основание упру гост-ной теории тепла. Дебай принимает, что тепловые движения частиц твердого тела тождествен-

ны с упругими колебаниями тела и что внутренняя тепловая энергия· есть не что иное, как сумма механич. энергий этих колебаний. Вводя гипотезу, что число возможных колебаний тела не м. б. больше числа степеней свободы тела, сохраняя лишь более медленное колебание и отбрасывая все остальные, Дебай получает ф-лы, хорошо согласующиеся с опытными данными относительно теплоемкостей запаса тепловой энергии и других свойств тела. Упругостная теория тепла Дебая относится к одноатомным телам и, прилагая законы упругих колебаний, он рассматривает твердое тело как сплошное. Появившаяся в том же году работа Борна и Кармана исходит из представления о молекулярной структуре вещества и рассматривает возможные колебания одноатомного твердого тела, образованного из атомов, расположенных в вершинах кубической решетки. После них появился целый ряд работ, связывающих тепловые свойства с учением Планка о колебаниях электронов или заряженных молекул (ионов) как источниках лучистой энергии. Т. о. физика в последнее время твердо стала на путь материалистич. понимания тепловых явлений и рассматривает передачу тепловой энергии в твердом теле как следствие колебательного движения его частиц. Если в соседних слоях тела энергия частиц различна, то непрерывные взаимодействия частиц между собой повлекут увеличение энергии в тех слоях, где она меньше, причем передача энергии может происходить не путем столкновений частиц, а передачей частицами лучистой энергии (передача через окружающее молекулы и атомы пространство). Однако механич. теория тепла не настолько разработана, чтобы можно было ей пользоваться для вычисления различных случаев Т., и в настоящее время теория Т. остается на феноменологии, точке зрения, не вникая в материалистич. сущность тепловых процессов, а рассматривая их как некоторые закономерности, могущие быть подвергнутыми математич. исследованию. Такая формальная математическая теория теплообмена была создана еще Фурье (1828 г.) и Пуассоном (1835 г.) и в результате трудов многочисленных ученых в нас-^х тоящее время представляет целый отдел математич. физики. Связь между величинами, характеризующими различные случаи Т., обыкновенно в виду сложности явления м. б. получена лишь в диференциальном виде, в форме диференциального ур-ия. Содержание теории Т. заключается в интегрировании диференциального ур-ия Т. на основе заданных начальных и граничных условий, к-рыми выделяется данный конкретный случай.

I. Кондукция. Выведем ур-ие Т. в однородном, изотропном (имеющем по всем направлениям одинаковые свойства) твердом теле для случая нестационарного, т/е. меняющегося во времени, теплового потока. Выделим из тела элементарный параллелепипед abcdabed (фигура 1) с ребрами dx, dy, dz, параллельными осям координат, которые выбраны прямоугольными и расположенными так, что плоскости параллелепипеда dz-dy совпадают с изотермич. плоскостями. В таком случае поток тепла будет

~<ta,

Фигура 1.

направлен параллельно оси×и проходит только через плоскости параллелепипеда, параллельные XOZ. Количество тепла dQ_b вошедшее через заднюю плоскость· abed в параллелепипед, будет пропорционально градиенту темп-ры дТ

, коэф-ту теплопроводности А, величине поверхности abed, равной dy · dz, и времени dt. dQ^-X^-dydz-dt.

Одновременно вышедшее из передней плоскости abcd количество тепла dQ_n пропорционально тем же величинам, но градиент темп-ры дТ

при переходе от изотермы Т к изотерме Т + dx,

лежащей на расстоянии dx от первой, изменит-дТ. д“Т у СЯ В -Н7, + ^Х.

дх дх²

Следовательно

^Qn=- * (% + ^ <0 · ^dV dz-dt.

Знак «—» указывает, что положительный поток тепла направлен в сторону уменьшения темп-ры, то есть отрицательного ее градиента. Разность д%Т

dQi — dQji=А — · dx · dy dz · dt

представляет количество тепла, накопившееся в параллелограмме за время dT. Оно очевидно равно с-о· aT-dV,тде с—теплоемкость, ρ—плотность вещества, dV=dx dy dz—объём параллелепипеда, a dt—повышение его темп-ры, вызванное притоком указанной теплоты. Приравнивая друг другу оба выражения для накопленного в параллелепипеде количества тепла, получим после сокращения на dx dy dz:

д“Т дх“ ^:

дТ

При выводе коэф. теплопроводности принимался постоянной величиной. В общем случае, когда направление потока не совпадает с осью OX, dQi~ dQn представит составляющую потока по оси ОХ, и для составляющих потока по направлению осей OY и OZ получится аналогичное выражение, а накопление тепла в параллелепипеде представится суммой трех таких членов, т. ч. в общем случае ур-ие (1) примет вид:

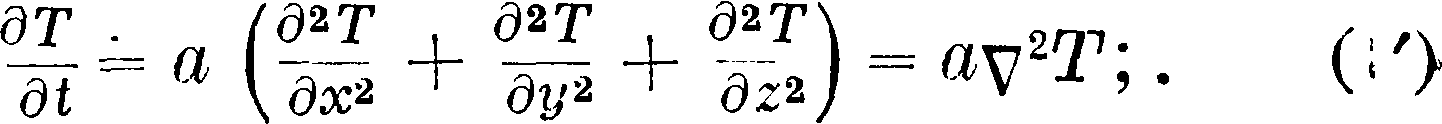
а= ^ называется коэф-том температуропроводности тела, т. к. скорость повышения темп-ры в теле пропорциональна ему.

В качестве примера интегрирования полученного ур-ия рассмотрим решение следующей задачи: «плоская плита,толщина которой 2Х,имевшая первоначально темп-ру Т_с, внезапно перенесена в среду с t°, равной 0°. Найти закон ее охлаждения, в частности изменение темп-ры Т в любом расстоянии от середины плиты, в функции времени £». Размеры плиты предполагаются достаточно большими, для того чтобы можно было пренебречь влиянием краев. Условия однозначности данной задачи, выделяющие из множества решений определенный заданный случай, суть: 1) начальные условия: для времени £=0 все точки плиты имеют одну и ту же темп-ру Т_с; 2) граничные условия: а) соприкасающаяся с обеими сторонами плиты окружающая среда сохраняет все время постоянную температуру 0°; б) отдаваемое в единицу времени с единицы поверхности количество тепла а — — А отводится окружающей средой.

Его поэтому можно приравнять произведению из разности темп-p плиты и среды Т на коэф. теплоотдачи а с поверхности плиты:

<2>

3) физич. величины а, Я, с ρ должны быть численно заданы.

Располагая систему координат так, что ось ОХ совпадает с направлением потока тепла, будем иметь, диференциальное ур-ие вида от _ д“т

dt “ ^а дхг *

Решение ур-ия (1) имеет вид: Т=е ~^ψ(χ). Подставляя его в (1) и придавая в целях дальнейших упрощений константе С_г вид: _п <52 а

A2’

получим т. н. ур-ие Покеля:

; ^+ -£**)=о, (п

к-рое удовлетворяется значением φ{χ)=С · cos (^·

Т. о. решение ур-ия (1) есть

-~at

Т=С · е сов (if), (3)

что легко ^проверить подстановкой. Значение постоянной δ определяется граничным условием (2), а постоянной С — начальным условием. Подстановка выражения (3) для Т в (2) дает:

= <5 · tg <5 (20

при допущении, что все физич. константы—постоянные величины. Это ур-ие имеет бесконечно большое число корней <5_Х, <5₂, б_п, и следовательно полученное решение (3) распадается на бесконечное число частных интегралов. Общий интеграл есть их сумма. Постоянные С находятся из условия,что в начальный момент времени t=0 темп-pa тела равна Т_с. Прием для определения постоянных С интегрирования состоит в т. н. гармонии, анализе. Нахождение общего интеграла ур-ия (1) по данным частным решениям его и при условии удовлетворения в начальный момент t=0 заданному распределению темп-p в теле в общем случае сводится к разложению в ряд Фурье ф-ии, удовлетворяющей т. н. условию Дирихле. Для частного случая, когда в начальный момент (t=0) плита во всех точках имеет одинаковую Т_с, общее решение поставленной задачи получается в следующем виде:

п=оо

<5_w + sin<5_w QOSdf

-· COS

Μ)·

_д“

X ²

•(4)

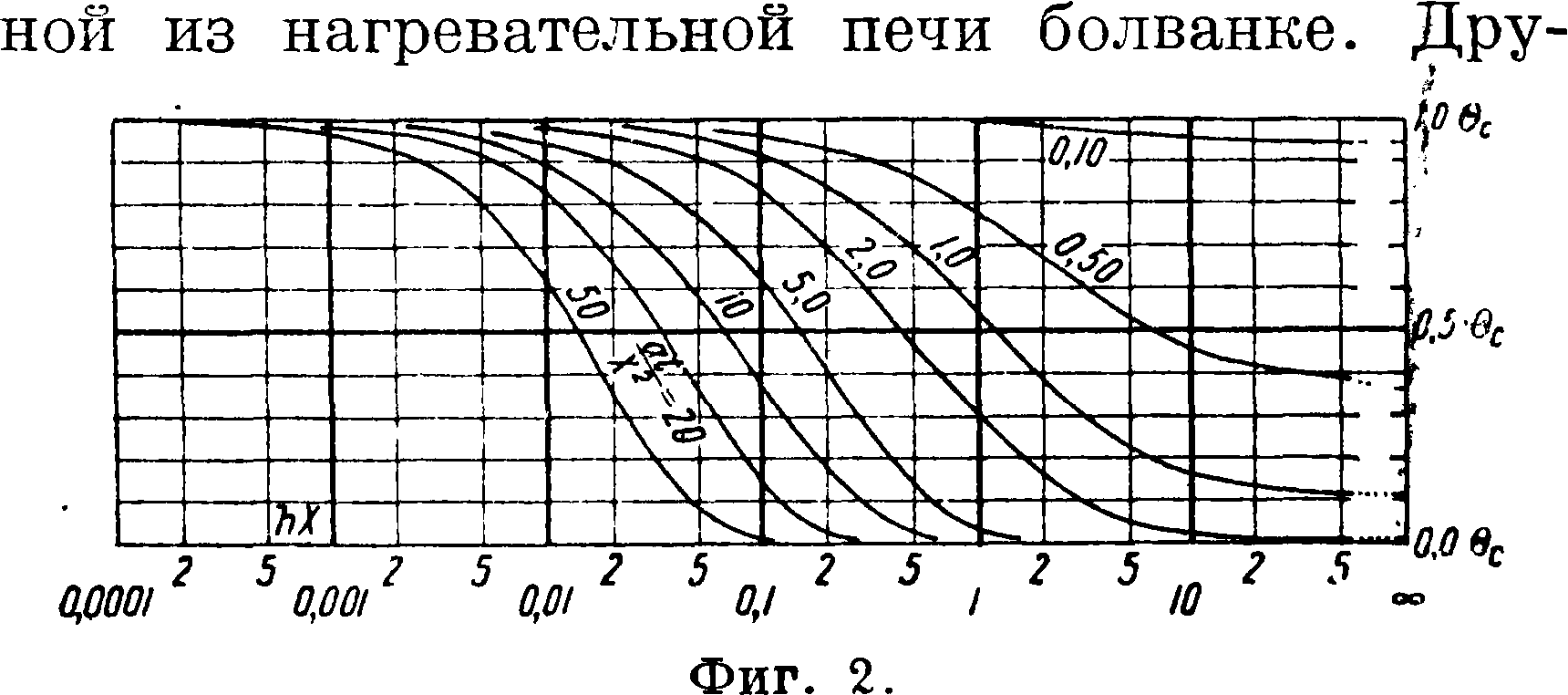
Для нахождения темп-p через нек-рый проме-жуток времени после начального момента достаточно сохранить только первые 3—4 члена ряда, т. к. влияние остальных почти не сказывается. Буссинек называет тепловой режим, при к-ром достаточно ограничиться одним первым членом, отрегулировавшимся (regularise), или, как принято его называть по-русски, регулярным режимом. Ф-ла (4) позволяет найти изменение темп-ры с течением времени в любом сечении плиты, находящемся на расстоянии х от ее середины. На фигуре 2 представлен графич. результат вычисления темп-ры в середине плиты (х^О) для различных толщин плиты (2-Х) и коэф-тов температуропроводности а и теплопроводности Я, материала плиты и коэ-

фициента теплоотдачи а от наружной поверхности плиты к окружающей среде. Подобные же решения задачи можно было бы произвести для случаев охлаждения цилиндра, шара, куба, параллелепипеда и прочие Решение этих задач имеет технич. значение, т. к. позволяет найти внутренние напряжения, возникающие при остывании в различных предметах, например в выдан-

гой весьма важный случай Т. представляет пе-риодич. нагревание и охлаждение тел окружающей их средой, составляющие рабочий процесс многих тепловых аппаратов, например регенераторов промышленных печей, воздухоподогревателя Юнгстрема и прочие Подобные же колебания темп-ры происходят в стенах зданий при суточном колебании наружной темп-ры, в стенках цилиндров.и поршней паровых машин, двигателей внутреннего сгорания и других машин. Во многих подобных случаях также возможно математическое решение задачи, позволяющее вычислить изменение темп-ры.

Аналогичным образом разрешается и задача о количестве тепла, отданного телом за известный промежуток времени.

Из ур-ия (1) нестационарного теплообмена в теле как частный случай получается стационарное распространение тепла, если в нем положить дТ

jj=0. В этом случае распределение темп-ры в теле не меняется с течением времени. Ур-ие (1) переходит при этом в ур-ие Лапласа:

W, д“т о“т _п

0χ2 “Г ду2 Т 022 УР)

или в векторном обозначении у²Т=0 (div. grad T — 0). В такой форме ур-ие (5) не зависит от выбора системы координат. Наиболее часто встречающимися в технике случаями стационарного потока тепла являются Т. через поверхность нагрева котлов (барабаны, плоские днища, дымогарные и кипятильные трубки котлов), трубопроводы, трубки конденсаторов, теплообменных аппаратов ит.п.Во всех этих случаях поток тепла проходит через плоские или свернутые в цилиндр стенки постоянной толщины в направлении, перпендикулярном к их поверхностям. Для плоской стенки, направляя одну из осей прямоугольной декартовой системы координат параллельно направлению потока тепла, получим ур-ие Лапласа в виде дх2 ^U’

откуда непосредственно следует, что

U-СхиГ-СхЯ + С,.

Ставя граничное условие, что для х=0, T=T получим

-¹=С_±=Const, (6)

т.е. прямолинейное падение темп-ры через стенку. Отсюда количество теплоты, проходящее в единицу времени через единицу поверхности се-

чения, перпендикулярного к изотермич. плоскости, равно

ο=-^λΖ=^λΤ-Ψ· w

По формуле (7) обычно и производят все технич. расчеты стационарного теплообмена в тепловых устройствах. Однако она неприменима в случае, когда Я меняется вместе с темп-рой тела. Это имеет например место в огнеупорных материалах, коэф. теплопроводности которых значительно больше при высоких темп-рах.Ур-ие(б) при этом становится неверным. В случае стационарного теплового потока внутренняя энергия нигде в теле не скапливается и не расходуется, и через все изотермич. плоскости в единицу времени через единицу поверхности проходит одинаковое количество теплоты Q:

@=-Д^=Const.

В этом ур-ии Я=/(Т). Если тело составлено из двух или нескольких материалов разной теплопроводности и их поверхности раздела суть изотермич. плоскости, будем иметь:

Q=К

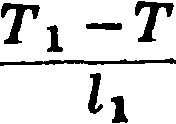
т_г-т₃Т, ’

откуда

q|l_=Ti-T₂ и ρ£=Τ₂-Τ₃.

Складывая полученные два равенства почленно, получаем с=ттЬг^(Т1‘^Тз)· ⁽⁸⁾

λχ Л₂

Теплопроводность плоской плиты пропорциональна отношению ~. Величина, ей обратная,

$=j, пропорциональна сопротивлению, к-рое плита оказывает прохождению тепла. Согласно выведенной формуле сопротивление тела, составленного из нескольких тел, равно сумме сопротивлений этих тел о __ о » о _ i h _h + h

S-Sl+S₂- —+ ——,

где Я—условный общий коэф. теплощ оводно-сти, или в общем случае:

k=1

где Т_а и Т_г—темп-ры на поверхностях, ограничивающих рассматриваемую составную плиту. Значение коэф-та теплопроводности твердых тел для различных материалов см. Спр. ТЭ, т. III, стр. 141 и т. VII, стр. 448. i

Ур-ие (7) неприменимо также и в том случае, когда рассматриваемая стенка не плоская, а криволинейная. Легко показать, что для цилин-дрич. полого тела—трубы со стенками постоянной толщины—выражение перехода тепла через стенку получает следующий вид:

Q=—Sr (^т« ~ ^т*)· (⁹)

Д Inite

Здесь R_a и И_г—расстояния от центра трубы наружной и внутренней ее поверхности, a Q— количество тепла, проходящее в единицу времени через единицу цилиндрич. поверхности трубы, отстоящей от центра трубы на расстоянии R. Очевидно при переходе к цилиндрич. поверхности, находящейся на другом расстоянии, плотность теплового потока должна измениться обратно пропорционально отногае-

Т. Э. m. XXII.

нию расстояний их от центра трубы. Для случая, когда толщина стенки трубы <5, равная Ra—Ri, весьма мала по сравнению с R_ir

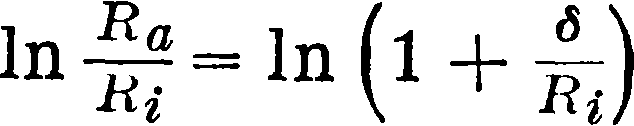
можно разложить в ряд и ограничиться первым членом ряда:

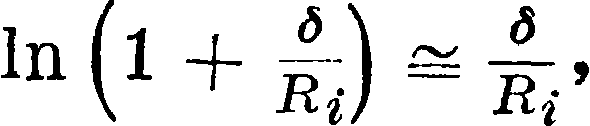
a R принять равным Rj. В таком случае выражение (9) преобразуется в

Q - (Т_а - Ti),

то есть превратится в ур-ие (7) для плоской стенки. Т. о. рассчитывать теплообмен в трубах по ф-лам, выведенным дляслучая плоской стенки, можно только в тех случаях, когда сохранение только одного первого члена разложения в ряд In ~ не связано с большой погрешностью. В противном случае надо всегда применять выражение (9).

Во всех предшествующих выводах предполагалось, что в теле нет источников тепла. Если же теплота возникает в теле вследствие превращения в нее каких-нибудь иных видов энергии, например в результате прохождения через тело электрич. тока, то ур-ие (1) перейдет в такое:

Ж ⁼ «V^2r + jrc^w’ (¹⁰>

где w—количество тепла, развившееся в единицу времени в единице объёма тела.

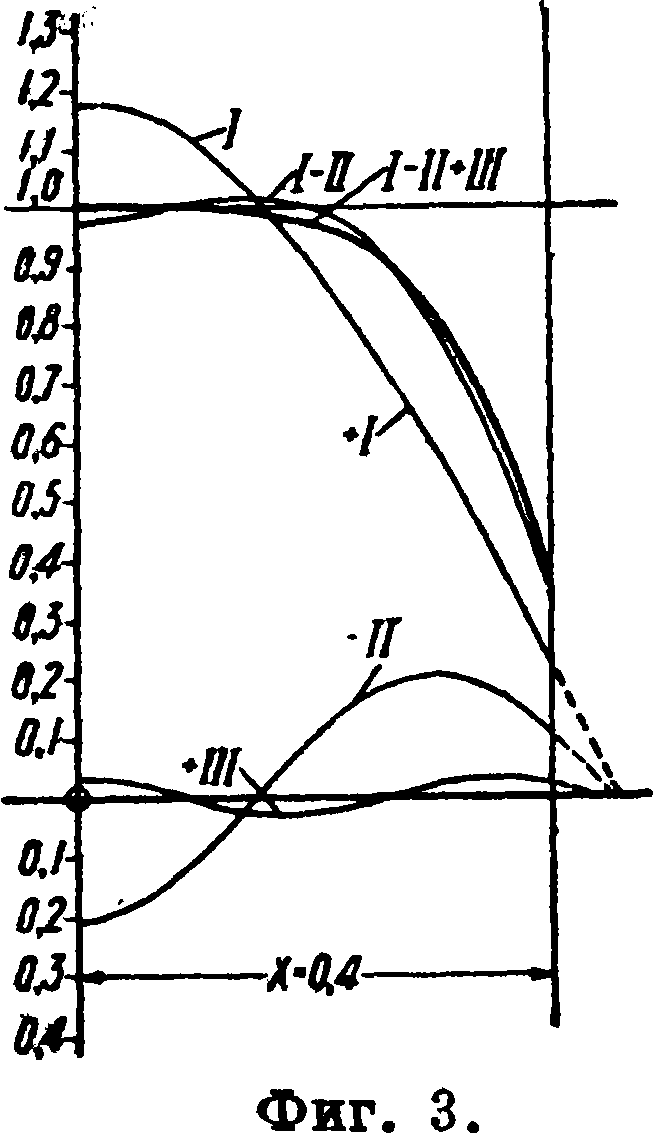
В заключение следует сделать два замечания о характере выводов математич. теории теплообмена. Теория рассматривает тела как непрерывные континуумы, которые сплошь заполнены материей. В действительности же материя распределена в пространстве дискретно и состоит из отдельных молекул и атомов, находящихся на значительных, по сравнению с заполненны- ми ими частями пространства, расстояниях друг от друга. Поэтому под диференциалами величин (dx, dy, dz) надо подразумевать не произвольно малые величины, а выбирать размеры рассматриваемых элементарных объёмов dx· dy-dz так, чтобы в них находилось достаточно большое количество молекул для того, чтобы можно было рассматривать материю в этих объёмах, как континуум. Это условие за исключением специальных случаев (уплотняющий удар в сопле и тому подобное.) всегда м. б. удовлетворено. Второе замечание относится к тому, что математич. теория теплообмена стоит на формальной феноменологии. точке зрения на природу теплоты и в ее ф-лах не содержится никаких ограничений в отношении скорости распространения тепла в теле. Из ф-лы (4) например вытекает, что через самый малый промежуток времени с момента соприкосновения плиты, нагретой до первоначальной темп-ры Т_с, со средой, имеющей отличную от нее темп-ру, изменение темп-ры скажется во всех точках плиты, как бы велико ни было расстояние 2Х, то есть толщина плиты. Однако это не имеет большого значения, т. к·, при вычислениях почти всегда берется приближенное решение, и в формуле (4) отбрасываются все члены кроме первых 3—4. На фигуре 3 изображено распределение темп-ры (выраженное в отношении Т: Т_с) от середины плиты до ее края через промежуток времени t=5. Толщина плиты 2Х== 0,8 м, материал ее—бетон (А=*0,€> кг1мч°С, у=2 000 килограмм/м³ и с=0,27 cal/кг °С). Как видно из фигуры, члены ряда (4) быстро убывают, и

трех членов его Ь-П+Ш достаточно, чтобы представить картину распределения темп-ры, близкую к действительности.

II. Конвекция. Если жидкость находится в покое, то частицы ее передают свою энергию друг другу путем ряда взаимных столкновений.

Эти столкновения вызывают беспорядочное движение частиц жидкости взад и вперед, благодаря которому они постепенно перемещаются из своего первоначального положения, проникая между соседними частицами, смешиваются с последними и т. о. путем диффузии осуществляют также передачу тепла в жидкости. Таким же образом передается тепло и в том случае, если жидкость движется ламинарно, параллельными слоями, не перемешивающимися между собою. Т. происходит при этом по законам, аналогичным твердому телу, и выражается той дТ

же ф-лой Q=— Λгде λ—коэф-т теплопроводности жидкости. Условия Т. совершенно меняются, если жидкость движется турбулентно (смотрите Турбулентное движение). В этом случае можно представить жидкость как бы разбившейся на осколки, которые беспорядочно двигаются, вращаются и перемешиваются друг с другом. Благодаря такому беспорядочному движению отдельные части жидкости быстро смешиваются между собою, и вместе .с этим осуществляется перенос внутренней энергии частиц из одной части пространства в другую. Если при этом температура жидкости в разных точках пространства’различна, то таким образом путем конвекции осуществляется перенос тепла в жидкости. Одновременно конечно сохраняется и передача тепла при помощи теплопроводности, и интенсивность ее даже значительно увеличивается, т.к. конвекция сближает и перемешивает частицы, сильно отличающиеся друг от друга по темп-ре. Т. о. тепло передается в жидком теле теплопроводностью и переносом тепла движущимися частицами. Кроме этих способов передачи тепла, которые можно назвать внешними причинами теплообмена, внутри потока жидкости может возникнуть тепловая энергия благодаря внутреннему трению жидкости, поглощающему часть живой силы видимого движения частиц и переводящему ее в молекулярное движение, то есть тепловую энергию. В разных местах потока могут существовать различные давления, и если жидкость упругая и объём ее заметно изменяется с изменением давления, то работа сжатия в силу первого закона термодинамики может также пойти на изменение внутренней энергии жидкости.

В большинстве теплообменных аппаратов обеими внутренними причинами выделения тепла можно пренебречь, и только в том случае, когда рабочая жидкость имеет особо большие скорости (теплообмен газов, движущихся по охлаждаемым лопаткам газовой турбины, или теплопередача в котле «Велоке», горячие газы которого в дымогарных трубках имеют скорость порядка 200 м, и тому подобное.), величина их становится настолько значительной, что нельзя не принимать их во внимание.

Рассмотрим теплообмен в потоке жидкости при следующих упрощающих вопрос допущениях: 1) движение потока стационарно; 2) его, темп-рное поле также стационарно; 3) жидкость может считаться несжимаемой (ρ=Const); 4) теплотой, возникающей от внутреннего трения, можно пренебречь. Подобно тому как это делалось раньше при выводе ур-ия Т. твердого тела, выделим в жидкости элементарный объём с гранями dx, dy и dz. Количество тепла, полученное им при помощи теплопроводности, уже было выведено ранее. За время dt оно равняется λ-^Τ -dx-dy-dz-dt. Т.к. процесс Т. по предположению не меняет темп-рное поле, то как-раз такое же количество тепла уносится за эго время потоком, протекающим через выделенный объём. Назвав через w скорость потока и через w_x, w_y и w_z ее проекции на оси, будем иметь, что через площадку dy-dz входит за время dt количество жидкости q-w_x-dy-dz, обладающее внутренней энергией, равной e-g-w_x- dy-dz-dt. Здесь ρ—плотность жидкости, а е—внутренняя энергия единицы массы. Выносимое из противоположной грани количество энергии выразится так же, но множитель s-w_x изменится на ве-

личину --Q— · dx. Для остальных двух пар граней напишутся аналогичные выражения. В результате прошедшее за время dt через объём dx-dy-dz количество жидкости унесет из объёма энергию, равную

Приравнивая друг другу количество внутренней энергии, переданное рассматриваемому объёму теплопроводностью и унесенное потоком, получим:

ИЛИ

+ е^е№+Ф+ж)· <^п>

Если жидкость не претерпевает изменение агрегатного состояния, то de=ρ-e- dt, а следовательно дх дТ.

дх⁹

δε

а?¹

C-Q

дТ

ду

δε

дТ

И is-=С · ρ -_я -δζ " δζ

С другой стороны, длястационарного потока жидкости, протекающего через элементарный объём dx-dy-dz, алгебраич. сумма входящих и выходящих через его грани потоков должна равняться нулю. Совершенно аналогично только что приведенному доказательству получим, что через площадку dz- dy за время dt втекает количество жидкости q-iv_x-dy-dz, а через противоположную площадку—

q-w_x- dy-dz + ρ dx · dy · dz ит. д.

Алгебраич. сумма потоков через все 6 сторон элементарного параллелепипеда будет следовательно равна:

(dv?x V дх

ду>у ду

dwv

δζ

)·

По устовию стационарности потока накопления "или расходования жидкости ни в каком объёме жидкости не происходит. Следовательно

i dyfz __ л дх ду δζ

(12)

Это—т. н. ур-ие стационарности потока для случая несжимаемой жидкости. Подставляя вы-

ражения для ^ит.д.в ур-ие (11) и принимая во внимание равенство (12), получим окончательно ур-ие Т.

A. v²T=ce(w_x.^ + wv ξ + (13)

или, применяя для правой части векторное обозначение,

Я · _v²i=cq · wQx/T. (13)

Т. о. для нахождения интеграла этого ур-ия надо знать распределение скоростей в жидкости. Этот результат м. б. предсказан заранее, т. к. очевидно Т. конвекцией тесно связана с характером движения жидкости. Следовательно ур-ия теплопередачи в жидкости надо решать совместно с ур-иями гидродинамики. Одно из ур-ий гидродинамики, ур-ие (.12), было уже использовано для упрощения ур-ия (13). Остается присоединить к нему основное ур-ие движения вязкой жидкости, т. н. у p-и е Навье-Стокса. Оно представляет собой применение второго закона Ньютона (действующая на тело сила пропорциональна массе тела и его ускорению) и для стационарного потока несжимаемой жидкости имеет вид в декартовых проекциях:

(«я дх У ду

"у

(d*vj_T,

dz ₄

Q9-

dp, dx

. U“ W_T,

+^μ 0** +

o*y>x,

dy* "T" )

(14)

для оси OX и аналогичные два ур-ия для проекции на оси OY и OZ, или в более наглядном виде, в векторном обозначении (Прандтля) получим ур-пе бедующего вида:

ρ · wQyw=Q9 — VP + μψν). (14)

Здесь, кроме встречавшихся прежде обозначений, р—давление, g—ускорение силы тяжести, μ—коэф. вязкости (внутр. трения) жидкости. Левая сторона представляет произведение массы (единицы объёма жидкости) на ускорение; первый член справа есть сила тяжести, действующая на единицу объёма, второй—оказываемое на него остальной жидкостью давление и третий—взаимодействие с жидкостью, окружающей единицу объёма вследствие наличия внутреннего трения.

Если под р понимать пьезометрич. давление, представляемое высотой столба жидкости, и если жидкость течет под напором (нет свободной поверхности уровня), то член, представляющий силу тяжести, из ур-ия (14) исчезает.

Т. о. задача Т. в жидких телах даже при всех тех упрощениях ее, которые были приняты выше, является очень сложной и в общем виде не поддается решению. Еще более сложной она становится, если отбросить принятые выше упрощающие допущения. Ур-ие Т. превращается в ^р-ие энергии, гласящее, что изменение энергии в нек-ром объёме жидкости за некоторый промежуток времени слагается из: 1) теплоты, переданной кондукцией, 2) теплоты, принесенной конвекцией, 3) работы, произведенной внешними силами. Для определения последней ур-ие Навье-Стокса преобразовывается в ур-ие механич. энергии, к-рое в форме, приданной ей В. Томсоном-Рейлеем, показывает, что работа сил тяжести и сил гидродинамич. давления преобразуется в увеличение живой силы жидкости, в работу сжатия жидкости и рассеивается вследствие внутреннего трения, превращаясь в теплоту.

Разрешение такой системы сложных ур-ий представляет непреодолимые трудности. Ме жду тем наиболее важные для техники случаи не м. б. сведены к простейшим схемам, а представляют сложный комплекс каналов переменного сечения с весьма развитой поверхностью, частью представляющей ограничивающие поток стенки, частью находящейся внутри канала в виде пересекающих его трубок и тому подобное. Поэтому изучение законов Т. идет гл. обр. в направлении экспериментальных исследований по Т. Для правильного расчета и рационального конструирования теплообменного аппарата особенно важно знать законы отдачи тепла от рабочей жидкости стенкам аппарата, знание же распределения темп-ры и теплообмена внутри жидкости является лишь вспомогательной задачей. Поэтому наибольшее число экспериментальных исследований относится к нахождению коэф-та теплоотдачи, определяемого из ф-лы

ρ=α·Δί, (15)

где Q—поток тепла, проходящего в единицу времени через единицу поверхности, Δ/—разность между средней t° жидкости и температу-р о ΐ стенки. Ф-ла эта ведет свое начало от Ньютона^ первоначально предполагалось, что коэф. теплоотдачи а—величина, не зависящая от температуры. Однако позднейшие опыты установили, что а меняется в зависимости от темп-ры, плотности рабочей жидкости, ее скорости, линейных размеров и конфигурации тепловоспринимающей поверхности и т. д. Величина полученного из опыта над теплообменным аппаратом коэф-та теплоотдачи является результатом совокупного действия всех упомянутых факторов, причем бывает весьма трудно раскрыть влияние каждого из них. Перенести данные опыта на другой аппарат, отличный по размерам, по геометрич. формам или по скорости и плотности рабочей жидкости, оказывается уже затруднительным. При определении коэфициен-та> теплоотдачи применяется общий метод экспериментальной физики—разделение влияния отдельных факторов и постановка опыта, позволяющего элиминировать влияние ряда их и выделить один определенный фактор, действие которого изучают в чистом виде. Следуя этому методу, к-рый м. б. назван методом рафинирования явления, физико-технич. лаборатории ставят исследование наиболее простых геометрии. тел, например теплообмен между стенками прямых круглых трубок и протекающей в них водой, воздухом и другими жидкостями. Исследуется отдельно влияние на коэф. теплоотдачи скорости жидкости в трубке одного и того же 0, затем влияние 0 трубки, затем .меняют температуру жидкости, степень завихренности ее движения и т. д. Для таких простых случаев оказывается возможным подметить из опыта оп-. ределейную закономерность. После этого естественно рождается вопрос, на какие случаи из практики можно распространить полученные в лаборатории результаты? Очевидно только на те, которые подобны этим последним. Вследствие этого возникает задача—найти признаки, по которым можно узнать, подобны ли друг другу явления. Учение о подобии дает определенные указания в этом направлении. Одним из его выводов является утверждение, что существуют инварианты подобия, то есть такие величины, которые во всех подобных явлениях имеют одинаковую величину. Теория подобия дает и способ нахождения этих величин, т. н. критериев, представляющих произведение из наблюдаемых в опы-

те величин—скорости, плотности, коэф-та теплопроводности и тому подобное. Эти выводы теории используются при обработке данных опыта в том направлении, что дается зависимость не между самими наблюденными величинами, а между соответствующими произведениями их, составляющими критерии подобия. Напр. дается не зависимость коэф-та теплоотдачи а от 0 трубки d_t скорости газов гг, плотности ρ и коэф-та температуропроводности a, a связь между этими величинами представляется в виде зависимости a - d · d

между комплексами — и ——, то есть в виде функциональной зависимости между двумя критериями подобия. Достаточно установить, что в каком-нибудь тепловом аппарате явление подобно тому, к-рое наблюдалось в лаборатории, для того чтобы иметь право распространить найденную формулу на данный аппарат.

Теория подобия выполняет т. о. роль метода обработки данных лабораторного исследования. Однако значение ее гораздо больше. Она одновременно дает правило для моделирования тепловых аппаратов. Конфигурация каналов тепловых аппаратов бывает обыкновенно так сложна, а поверхность, воспринимающая тепло от газов или жидкости, протекающих через них, так развита, что во многих случаях на них почти невозможно перенести данные лабораторных опытов. Для этого приходится синтезировать слишком много составляющих, взятых из отдельных рафинированных исследований. Например в лабораториях хорошо изучена теплоотдача жидкости, текущей по трубе, менее полно исследован теплообмен жидкости с пучком труб, расположенных поперек потока, еще меньше данных есть о теплоотдаче труб, расположенных под нек-рым углом к направлению потока. Но даже имея все эти данные, нельзя из них составить коэф. теплоотдачи пучка труб, например для случая вертикального водотрубного котла. Теплоотдача зависит не только от расположения труб, но и от характера движения газов, к-рые, двигаясь по дымоходам, после поворотов в них текут неполным сечением ходов, образуя вихревые области, так что значительная часть поверхности нагрева находится в застойном мешке медленно вращающихся газов, а остальная поверхность омывается потоком, текущим с повышенной скоростью. Между тем в лабораторных опытах газы двигаются полным сечением. Предугадать, как будет происходить движение газов в разных частях котла, невозможно, т. к. каждой конструкции котла отвечает своя индивидуальная картина распределения скоростей в потоке, поэтому наряду с методом рафинирования опыта возник и развился метод моделирования явлений. При моделировании не выделяются отдельные части котла (трубки, омываемые поперечным или па-, раллельным током, и тому подобное.), а работа всей поверхности нагрева исследуется на модели, то есть явлении, родственном (аффинном) данному. Теория подобия учит, что при соблюдении известных условий можно в уменьшенной по размерам копии какого-нибудь теплового устройства, в к-ром движется даже другая жидкость (например вода вместо воздуха), получить полное или приближенное подобие картины движения жидкости по его каналам. Благодаря такой подмене одного явления, служащего образцом, другим, родственным ему,—его моделью,—оказывается возможным наблюдать и исследовать многое, что недоступно для наблюдения в образце. Напр.,

сделав боковые стенки модели какой-нибудь печи стеклякными, можно изучить подробно картину движения в ней холодных газов, что невозможно осуществить на самой печи из-за высоких темп-p ее и недоступности для осмотра. Если в модели гидравлич. подобие достигнуто для какого-нибудь места котла, то, исследуя теплоотдачу отдельного участка одной или нескольких труб его, можно при соблюдении правила теплового подобия получить результаты, которые м. б. непосредственно распространены на самый котел. В отличие от метода рафинирования явления этот второй метод м. б. назван методом аффинирования явления.

Почти каждый физич. опыт заключает в себе оба метода. Исследование Нуссельтом и рядом других авторов теплоотдачи прямой круглой трубы, через к-рую протекает поток со стабилизовавшейся во входном участке трубы степенью турбулентности, есть пример применения первого метода. Опыты Рейхера над теплоотдачей поперечных труб с выяснением влияния возмущения потока первыми рядами труб на теплоотдачу последующих содержат уже в себе элементы обоихметодов, а исследование моделей печей, котлов, гидравлич. устройств и тому подобное. в модельных лабораториях представляет применение второго метода. В последующем изложении дается краткое понятие об учении о подобии, на основании которого данные опыта выражаются в форме зависимости между критериями подобия и выводятся правила моделирования.

Теория подобия. Учение о подобии явлений было дано Ньютоном в его «Principia», в которых он не только изложил основы кинематич. и динамич. подобия, но и вполне отчетливо формулировал условия, необходимые и достаточные для существования механич. подобия. Только через 200 лет идеи Ньютона получили должную оценку. Начиная с 30-х гг. 19-го столетия, целая плеяда ученых стала разрабатывать теоретически и экспериментально учение о подобии в применении к различным физич. явлениям. Отмечая только немногие выдающиеся работы в этой области, можно назвать: Fourier (1822), Bertrand (1848), Reech (1852), Froude (1872), Helmholtz (1873), О. Reynolds (1883), Rayleigh (1892), Buckingham (1914). Nusselt (1915), Афанасьева (1915). Их трудами теория подобия превратилась в общее учение, охватывающее все явления природы. Теория подобия исходит из математич. выражения тех законов, которым подчиняется рассматриваемое явление. Если присоединить к общим законам т. н. условия однозначности, то из всего класса явлений выделится одно определенное единичное явление. Большинство законов м.б. формулировано лишь в диференциальном виде, в формедиференциаль-ного ур-ия, связывающего различные физич. величины, интегрирование которых возможно только для отдельных простых случаев. Теория подобия позволяет для подобных явлений сделать ряд выводов относительно взаимной связи между характеризующими эти явления величинами без интегрирования уравнений. В этом ее значение. Теория подобия, изложенная в самой общей форме и могущая быть поэтому примененной к любому явлению (течение воды и газов, полет снарядов, движение судна, Т., электрич. явления и тому подобное.), показывает, что в подобных явлениях нек-рые величины одинаковы. Они называются инвариантами подобия, или критериями. Исходя из этого свойства подобных явлений, можно показать,

что· для получения подобия между двумя явлениями достаточно сделать подобными их условия однозначности. В этом и заключается правило подобия, являющееся основой теории моделирования.

Изложим кратко основы теории подобия. Будем называть классом явлений все явления, подчиненные какому-нибудь общему для всех них закону. Этот закон, вообще говоря, м. б. выражен в виде некоторой функциональной зависимости (одной или нескольких)

F {щ, .,м_и}= 0, (16)

где и₁₉ ., и_п—величины, характеризующие данное явление. Присоединение условий однозначности к (16) делает зависимость между и₁₉ ., п_п определенной, отвечающей данному единичному явлению. Будем различать такие частные значения величин значками " и т. д. Равенство (16) после присоединения к нему условий однозначности примет вид:

F {и₁₉ ., <}=0. (16)

Среди множества явлений данного класса встречается ряд подобных данному единичному случаю и ₉ явлений. Подобными называются такие системы, у которых отношения характеризующих явления величин есть постоянные числа. Это определение заключает в себе как гео-метрич. подобие, так и подобие полей физич. величин. Если например скорость в заданной системе (16) имеет величину и, то скорость в геометрически сходственной точке подобной ей системы есть и"=си₉ где с имеет одно и то же численное значение во всех точках системы. В понятие подобия направленных величин (векторов) само собой включается и условие их параллельности друг другу. Т. о. математич. формулировка подобия принимает вид следующих равенств:

ГУ=Са,

= Си

(17)

1 2 П

Сопоставление (16) и (17) позволяет сделать ряд выводов относительно свойств группы подобных явлений, общих для всех них. Рассмотрим две подобные друг другу системы и ₉ .₉и_п и и]₉.₉и^пП9 представляющие определенные единичные явления. Основное равенство (16) для первого есть:

F [и, .,<}=0 (16)

и для второго:

f .,<} =о. (16")

Очевидно, если величины с₁₉ ., с_п известны, то любая из величин первой системы, например и ₉ м. б. определена не только из равенства (16), ной из равенства (16"), используя соотношения (17): и=Ciui. Можно поступить и так: не искать значения и} из (16") и затем подставлять его значения в (17), а, наоборот, заменить сперва в (16") значения и ₉ ., Un через и ₉.,ип посредством равенства (17). Ур-ие (16") получит при этом вид:

F j· =0. (16")

Из этого ур-ия должны получиться значения и ₉ ., ип те же, что и непосредственно из ур-ия (16). Это м. б. в случае, если ур-ие (16) и (16") то кдественны друг другу, то есть если в ур-ии (16") все множители взаимно сократятся. Короче говоря, основное ур-ие (1) инвариантно по отношению к указанной подстановке

(17). Если бы выражение (16) представляло полином первой степени вида а₀ + а{и_х +. 4-+ о>п“п=0, то очевидно каждый из множителей с₁₉.₉с_п должен был бы равняться единице; это значит, что данный класс не содержит подобных между собою явлений. Большинство ур-ий физики представляет собой сумму степенных комплексов из величин и вида Р== · и² · г^з³ и тому подобное., где х₁₉ х₂₉ х_ъ — числен ные величины. После подстановки в такой комплекс вместо и величин си перед ним появится общий множитель N=с ¹ · с“² · с%³9 который так составлен из величин с₉ как сам комплекс Р из величин и. В этом случае для получения инвариантности ур-ия достаточно, чтобы каждый множитель N равнялся единице.

Ф-ий, обладающие тем свойством, что после умножения входящих в них величин на некоторые множители последние можно вывести за знак ф-ии, называются гомогенными (однородными) ф-иями. Другими словами, если

ψ (ΟχΜι, с_пи_п)=ψ (с_г.с_п) * Ψ (и,., и_п),

то ψ есть гомогенная функция. Выражение (1) F Iи₁₉ ., и_п}=0 всегда можно представить как функциональную зависимость ме кду гомогенными ф-иями от и₁₉ ., и_п. Оно тогда получит вид:

ф{п_1г.,Н_т}-0, (16bis)

где H-l =φ₁1щ, u_n J· ит. д.—гомогенные ф-ии. Размерность каждого члена Н₁₉ ., Н_т определяется размерностью входящих в него величин и ВИДОМ ф-ии φ_ΐ9 ., q>_m.

Всегда возможно зайисимость (16bis) привести к безразмерному виду. Напомним, что применяемая в физике система единиц выражает размерность одних величин через другие. Например по 2-му закону Ньютона действующая на тело сила по величине пропорциональна массе тела и его ускорению: f=С · т · а.

С есть коэф. пропорциональности, величина которого определяется выбором единиц для измерения силы /, массы ш и ускорения а. Но если единицу измерения силы выбирать так, что для массы т=1 и ускорения α= 1 сила /== 1, то множитель С делается равным единице и f=т · а. (18)

Обе части этого выражения имеют теперь одинаковую размерность: массах ускорение. Для того чтобы привести это выражение к безразмерному виду, надо разделить его на один из членов, например на та:

1=-П или Я-1=0, (19)

где Н—гомогенная безразмерная ф-ия. Из этого примера видна цель введения гомогенных ф-ий в безразмерном виде: в этом случае получается наименьшее возможное число их. Напр. в ур-ии (18) их былй два, а в ур-ии (19) лишь одно. В дальнейшем будем считать, что равенство (16bis) всегда приведено к безразмерному виду. Подобно тому как это делалось с уравнением (16"), произведем подстановку в ур-ие (16bis) вместо и величин си. Оно превратится в

Ф{я₁я₁,.,я_юя_т}=0.

Поставленное требование инвариантности уравнения (16bis) по отношению к такой подстановке приводит к условиям:

Я_г=1, Я,=1,., N_m=1.

(20)

Величины N так составлены из отношений

. _ b

^1_ «; ’ ^я_ «V

как сами ф-ии Я из величин и₁₉ ., и_п. Имея это в виду, получим для того случая, когда в ф-ии Я не входят диференциальные выражения, условия (20) в следующем виде:

ΗΪ _{= =}

н н₂ нпь или н”=н I _β

Нт=Нт j

Т. о. в этом случае ф-ии Я суть инварианты ур-ия (16^bis) или, что то же, и ур-ия (16): их значения не меняются при переходе от одной системы к другой, ей подобной. Для случая, когда ф-ии Я содержат в себе диференциальные операции, дело несколько меняется. Пусть одна из ф-ий Я имеет такой вид:

(21)

Тогда д“и_г

дик

= я.

d²(ci^i)

[d(c₂u₂)]2

= ~Н=NH.

С ^·|

Требование JV=1 приводим к ~ =1илик-^ =

u,f

На этом примере видно, что инварианты подобия состоят из самих величин, а не их диферен-циалов. Следовательно теория подобия позволяг ет найти для подобных систем нек-рые соотношения между величинами, не производя интегрирования основного ур-ия. Далее, приведенный пример показывает и простой прием получения инвариантов ур-ия (16^bis), к-рый можно назвать образно методом «резинки», или «губки», т. к. инварианты подобия получаются из ф-ий Я путем уничтожения («стирания») в последних всех диференциальных значков. Инвариантам подобия обыкновенно присваивается название критериев. Т. о. мы получили основную теорему теории подобия. В подобных системах все критерии инвариан-т н ы. Это значит, что при переходе от одной подобной системы к другой критерии сохраняют одно и то же значение. Это свойство алгебраически можно записать так:

к=idem.

Итак, мы пришли к выводу, что в подобных системах множители преобразования с характеризующих явление величин не могут выбираться произвольно. Ур-ие (16), представляющее закон, к-рому они подчиняются, накладывает на выбор их определенные ограничения: в действительности могут существовать только такие системы, у которых определенные комбинации из множителей преобразования равны единице или, что равнозначно, у которых все критерии подобия одинаковы. Ур-ия физики обыкновенно имеют вид диференциальных ур-ий с частными производными. Соответственно этому условия однозначности их могут иметь вид функциональной зависимости между граничными значениями величин и. Точно так же физич. параметры системы часто задаются в форме ур-ия, связывающего их между собой. При разыскании критериев все эти ур-ия должен быть присоединены к основному явлению. Т. о. в общем случае надо под ур-ием (16) подразумевать систему общих ур-ий и ур-ий условий однозначности.

Выясним теперь, какой вид имеет общий интеграл этого ур-ия (16). Предположим, что мы нашли критерии подобия уравнения (16) к₁₉., к_т и что число их равно т. Заметим попутно, что в выборе критериев остается некоторый произвол: вместо полученных критериев можно взять нек-рые комбинации из них, которые очевидно тоже будут инвариантами подобия. Напр. вместо двух любых критериев к_х и ft₂можно взять.производные из них fc₃=к_хТс₂ и ft₃== к_±: к₂. Предположим теперь, что ур-ие сперва было проинтегрировано и лишь после этого стали искать критерии подобия. Очевидно интеграл ур-ий можно также представить в виде ф-ии от нек-рыхбезразмерных гомогенных ф-ий. Пусть число их равно г:

У[Я_1#.,Я_Г]=0.

Т. к. это ур-ие не содержит уже диференциальных выражений, то его критерии суть: Н_1#.,Я_Г.

Итак, в результате мы получили две системы критериев ft и Я. Они очевидно не м. б. различными, т. к. это означало бы, что перемена порядка операций нахождения интеграла ур-ия и разыскания критериев может сделать подобные системы неподобными, или обратно. Никаких новых критериев операция интегрирования принести с собой не может, если задача была определенной и все условия однозначности были присоединены к основному диференци&льному ур-ию. Поэтому критерии Я м. б. только производными от ft, и число их г=т. А так как выбор основных критериев зависит от нас, то мы можем критерии выбрать за основные и написать, что интеграл имеет вид:

(22)

^1 ^— Ψΐ (ц> ** ·» 1

(23)

Полученный результат показывает, что интеграл диференциального ур-ия можно получить в форме зависимости между его критериями или в виде «уравнения подобия» (в общем случае— сисгемы ур-ий). Из (22) и (23) непосредственно вытекает, что из ш критериев системы только m — 1 независимы, а т-ный есть их ф-ия.

Ур-ие подобия есть общий интеграл нашего диференциального ур-ия. При определенным образом заданных условиях однозначности оно представляет зависимость между критериями всех подобных систем в любых геометрии, сходственных точках их. Задавая координаты, получим значения критериев в соответствующих местах. Наоборот, можно не менять места в пространстве, а наблюдать изменение критериев в определенной точке системы, к-рое будет вызываться изменением нек-рых из условий однозначности. В этом случае получится изменение критериев в избранном для наблюдения месте системы, и ур-ие (22) представит последовательные группы систем, подобных между собою, но отличных от предыдущих групп.

Всякий эксперимент состоит из серии единичных опытов, представляющих варьирование условий однозначности и нахождение происходящего от этого изменения системы. Уравнение подобия дает право выражать зависимость между отдельными величинами, характеризующими наблюдаемое явление, сразу в форме зависимости между критериями системы и тем самым распространить данные опыта на всю группу подобных явлений.

Однако это право остается чисто формальным, пока не дано способа распознавать подобие явлений. Конечно для этого было бы вполне достаточно проверить существование равенств (17) по всему полю двух систем, но это—путь, фактически нереализуемый. Для того чтобы метод подобия имел плодотворное практич. применение, необходимо уметь находить признаки подобия, реализуемые в опыте. Т. о. мы приходим к постановке вопроса, обратной только что изложенному. До сих пор подобие .мы считали наперед заданным и искали, какие следствия можно извлечь из ур-ий физики для явлений, подобных между собой. Теперь ставится обратная задача: требуется установить условия, необходимые и достаточные для того, чтобы системы стали подобными друг другу. Покажем, что для этого достаточно сделать подобными условия однозначности обеих систем. Представим себе какое-нибудь физич. явление, протекающее в определенных геометрии, контурах, например движение газов по газоходам, теплоотдачу от газов стенкам котла и тому подобное. Пусть известно дифе-ренциальное ур-ие, к-рому подчиняется происходящее в названной системе явление. Пусть также мы умеем установить для него условия однозначности. Назовем эту систему первой. Представим теперь., что имеется вторая система, у которой все величины, входящие в условия однозначности, подобны первой системе. Можно ли утверждать, что эта система подобна первой? По предыдущему если эти две системы подобны, то множители преобразования с их условий однозначности не м. б. выбраны как попало, т. к. среди критериев подобия могут оказаться и такие, которые составлены только из величин, содержащихся в условиях однозначности. Следовательно выбор множителей е для условий однозначности ограничен тем условием, что критерии, составленные из величин, входящих в условия однозначности, у обеих систем одинаковы:

(к)усл. од“.=idem. (24)

Без соблюдения этого условия вторая система не м. б. подобна первой. Наоборот, после выполнения этого условия она наверное подобна первой системе. В самом деле, после выполнения условия (24) подобие систем становится возможным, т. к. всегда можно выбрать осталь-. ные множители с величин, не входящих в условия однозначности, так чтобы и все остальные критерии в обеих системах были одинаковы. Представим себе такую систему и сравним ее со второй. Оказывается, что у них условия однозначности одинаковы. Следовательно по самому смыслу понятия «однозначность» эти системы тождественны. Но одна из них подобна первой системе, значит и вторая система подобна первой. Т. о. выбор остальных множителей с а следовательно и критериев, м. б. произведен только однозначным способом.

Итак, подобное преобразование условий однозначности системы, инвариантное относительно критериев ее, приводит к системе, подобной первой. Или, т. к. условия однозначности есть тоже нек-рая система, составляющая часть рассматриваемой системы, и понятие «подобия условий однозначности» уже должно содержать в себе условие инвариантности их критериев, то можно просто сказать, что «системы подобны, если их условия однозначности подобны». Т. о. надо различать два рода критериев: 1) критерии, составленные только из ве личин, входящих в условия однозначности; инвариантность их есть одно из условий подобия;

2) все остальные критерии; инвариантность их есть следствие, а не предпосылка подобия. Критерии первого рода будем называть определяющими подобие условий однозначности. Условия однозначности м. б., вообще говоря, формулированы различными способами. В зависимости от этого и определяющими становятся другие критерии. Когда при производстве опыта производится варьирование какого-нибудь из условий однозначности, то тем самым меняется определенным образом и соответственный определяющий критерий. Каждой данной величине последнего отвечает определенная группа подобных явлений. А т. к. для каждой такой группы и все остальные критерии приобретают вполне определенные значения, то они представляют однозначные ф-ии определяющих критериев. Представление данных единичного опыта в виде функциональной зависимости одних критериев от других есть метод распространения этих данных на целые группы явлений. Получающаяся таким обр. зависимость между критериями есть очевидно частный случай выведенного ранее ур-ия подобия. Полученное правило получения подобных явлений есть не что иное, как правило моделиро-в а н и я. Для построения модели какого-нибудь явления достаточно найти условия однозначности этого явления и преобразовать их подобным образом. Тем самым будет осуществлена модель явления, подобная натуре, послужившей для нее образцом.

Т. о. теория подобия приводит к следующему методу постановки эксперимента и обработке его результатов в том случае, когда общий закон, к-рому подчиняется исследуемое явление, м. б. дан лишь в диференциальном виде: 1) устанавливаются «условия однозначности», к-рыми данное явление Т. (в котле, печи и тому подобное.) выделяется из всех других случаев; 2) производится эксперимент, состоящий, вообще говоря, в варьировании одного или нескольких из условий однозначности и наблюдении при этом изменения других величин, характеризующих явление;

3) из диференциального ур-ия, представляющего общую закономерную связь между этими величинами, находят критерии подобия;4) результаты опыта обрабатываются в форме функциональной зависимости между ними. Определяющие критерии, то есть те, которые составлены только из величин, входящих в условия однозначности, являются независимыми переменными, изменение которых отвечает варьированию в опыте условия однозначности. Остальные критерии представляют их однозначные ф-ии. Представленные в таком виде результаты произведенного опыта м. б. непосредственно распространены на все случаи, которые подобны исследованному. Для этого нужно лишь подставить вместо критериев их выражение через отдельные величины и придавать последним те численные значения, которые отвечают каждому отдельному случаю.

Применение теории подобия к Т. Изложенное выше учение о подобии привело к следующим выводам: класс явлений, подчиняющихся какому-нибудь закону природы, оказывается возможным разбить на группы подобных между собою явлений. Если рассматриваемый закон природы можно выразить аналитически, в виде связи между величинами, характеризующими рассматриваемый класс явлений, то есть в форме ур-ия, то теория подобия показы-

вает, что для группы подобных между собой явлений данного класса это ур-ие инвариантно, то есть не меняется при переходе от одного единичного случая к другому. Далее теория показывает, что в этом случае существуют инварианты подобия,т. н.критерии, составленные определенным образом из величин, характеризующих класс явлений. Для того случая, когда закон природы не удается найти в виде зависимости между конечными величинами, а он м. б. получен лишь в виде диференциального ур-ия, теория подобия дает способ найти критерии подобия, не производя интегрирования ур-ия. В тех случаях, когда диференциальное ур-ие, представляющее искомый закон природы, не м.б. проинтегрировано, приходится обращаться к опыту и получать искомую зависимость между величинами, характеризующими явление, экспериментальным путем. Теория подобия дает при этом общее указание, что найденную из опыта зависимость надо искать в виде функциональной связи между критериями подобия. Тем самым дается и путь к распространению данных единичного опыта.на все подобные явления.

Применим все сказанное к Т. жидких тел, ограничившись рассмотрением стационарного процесса, и пренебрежем изменением объёма текущей жидкости и изменением t° от работы сжатия и от трения. Установим сперва условия подобия скоростных полей. При сделанных допущениях ур-ие движения жидкости для проекции на ось ОХ имеет, по предыдущему,вид:

е(

ОУ9_х,

^w«-e5r + “’

У ду

+ Щ

d²w

~ду“

дх )

дх

>? I

2 "1“ дх“ ) *

Аналогичный вид имеют два ур-ия для других осей координат. Или в векторном обозначении:

qwQkjw=— VP + μψιν.

Замечая, что стоящие в скобках многочлены суть гомогенные ф-ии (что непосредственно ясно из векторного написания ур-ия), приведем ур-ие к безразмерному виду Делением его на левую часть равенства и применим описанное выше правило нахождения критериев. Оно дает два критерия, которые названы именами Рейнольдса и Эйлера:

= ^ и Еи=Ц.

μ QW²

Здесь I—любой линейный размер, характеризующий поток, например для случая движения жидкости по трубе за таковой можно выбрать 0 трубы d Ар представляет падение давления между двумя точками потока. Оно введено вместо давления р, т. к. абсолютная величина последнего не играет роли в движении жидкости (для упругой жидкости давление сказалось бы на величине плотности ρ). Второе ур-ие гидродинамики, ур-ие сплошности, имеющее для стационарного потока несжимаемой жидкости вид

/d v_x. дчу, д и₂ _{Λ Λ}

Ы + ~ду + ~л) - ^{0 или}=о,

различных скоростях в зависимости от вязкости, плотности ит. п., следует дать зависимость критерия Ей от Re: Eu=f (Re). Этим ур-ием охватываются все подобные процессы движения жидкости. Чтобы иметь право применить это уравнение, найденное на основании исследования единичного явления, ко всякому новому случаю, надо сперва убедиться в том, что имеет место подобие последнего с исследованным явлением. Для этого надо посмотреть, подобны ли геометрии. контуры сосудов, через которые протекает жидкость, и подобны ли во входном сечении кинематич. условия движения. Этого мало; критерий Re составлен из ρ, I, μ и w. Это все величины, входящие в условия однозначности. Следовательно появляется еще одно ограничительное условие Re=idem, то есть величины

~~ во входном сечении должны быть одинаковы для случая, экспериментальное исследование которого привело к формуле Eu=f(Re), и для того случая из технич.- практики, к к-рому хотят применить эту ф-лу.

Перейдем к рассмотрению темп-рного поля. Оно представляется ур-ием:

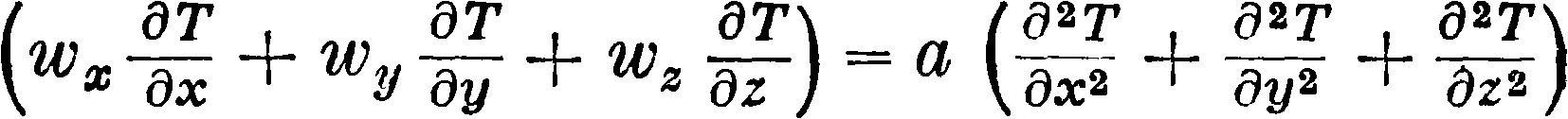
или в векторном обозначении

wQуТ=а · у² * Т.

И здесь поставленные в скобки суммы суть гомогенные ф-ии. Поэтому получается лишь один критерий ~= Ре (Пекле).

Условия однозначности заключаются в задании распределения темп-ры во входном сечении и на границах потока (у стенок) и численного значения величины а. Требования подобия условий однозначности налагают на выбор а ограничительное условие инвариантности критерия Ре, к-рый является определяющим критерием. При исполнении этого требования и темп-рные поля оказываются подобными, т. ч. для любых сходственных точек в потоке t и на стенке Т_с отношение

grad Т ·=idem,

то есть одинаково для всех подобных явлений. Ограничимся частным случаем, наиболее важным для технич. приложений. Именно определим условия, достаточные для того, чтобы имело место подобие на границе жидкости с ограничивающими ее стенками, воспринимающими от жидкости тепло. Пусть стенки имеют во всех точках одну и ту же темп-ру Т_с. Количество тепла, переданного в единицу времени единице поверхности стенки, дается ф-лрй Ньютона

Q=a(T_M-T_c),

где Т_п — средняя темп-ра потока жидкости, точнее—среднединамич. темп-ра, определяемая из условия

Т_п= Jtw da/J w da,

σ et

не дает никаких критериев подобия. Условия однозначности заключаются в задании во входном (или каком-нибудь другом) сечении кине-матич. условий входа жидкости (распределение скоростей, ускорений) и численных значений физич. параметров ρ и μ. Для технич. целей весьма важно иметь характеристику потока н отношении падения его рабочего напора. Вместо того чтобы выражать изменение Ар при где а — площадь поперечного сечения потока. С другой стороны, Q — — Д_с grad Τ, откуда следует, что

^=-т- grad Т y~t~_c=idem.

Т. о. в подобных системах=Nu (Нуссельт)

есть инвариант. Если выражать результаты опыта не как зависимость коэф-та а от ско-

рости w, температуропроводности а, линейного размера I и т. д., а представлять их в виде Nu=f(Pe, jRe),

то такая формула может быть непосредственно распространена на все явления, подобные исследованному.

Вместо -одного из критериев Ре и Re можно ввести производный от них Ре : Re=^, где v =

= ^ — т.н.коэф. кинематич. вязкости. Он обозначается через St (Стентон). В нем. литературе за последние годы этот критерий заменен обратной величиной ^=Рг (Прандтль). Легко видеть, что Рг (так же, как и St) есть ф-ия только физич. параметров жидкости. Итак, формула для коэф-та Т. должна иметь вид Nu=φ (Re, Рг),

для того что^бы быть пригодной для распространения данных единичного опыта, по результатам которого они составлены, на все другие подобные явления. Применение же ф-лы на явления, не подобные образцу, незакономерно и может привести к ошибочным заключениям.

Все изложенное объясняет, почему в настоящее время опыты по Т. всегда обрабатываются в виде зависимости между величинами Re, Ре, Рг, Nu и тому подобное. Напр. последние опыты Краусс-Сольда (1933) представлены в виде:

Nu=0,024 · KeV · Рг⁰,³⁷.

Эта формула объединяет в себе ряд опытов, произведенных различными исследователями над Т. стенкам трубки текущими в ней водой, воздухом, машинным и трансформаторньГм маслами и рядом других тел. Численные данные для различных случаев теплообмена воздуха, воды, пара и других жидкостей см. формулы для коэф-та Т., приведенные в книге Шака (смотрите литературу).

111. Лучеиспускание. Передача тепла телами может происходить не только телами, непосредственно соприкасающимися между собой, но и телами, находящимися на значительном расстоянии друг от друга, посредством лучистой энергии. Природа лучистой энергии и механизм передачи ее через пустое, незаполненное материальными частицами пространство еще не разгаданы. Согласно современным воззрениям распространение лучистой энергии обусловливается электромагнитными волнами, которые вызываются колебаниями электронов, движущихся вокруг положительно заряженного ядра и в совокупности с последним образующих атомы материи. Т. о.· прежнее разделение лучей на световые, тепловые, химические и т. д. является чисто формальным, описывающим лишь различное воздействие лучей разной длины волны на материальные частицы, и лучистая энергия всех родов лучей может при известных условиях переходить в тепловую энергию материальных частиц. Так например, покрытая сажей поверхность твердого тела не отражает падающие на нее лучи, а все их поглощает, превращая в теплоту. Такое тело, поглощающее все лучи любых длин волн, называется, по аналогии со световыми явлениями, абсолютно черным или просто черным. Между поглощательной способностью тела и ее лучеисщ скательной способностью существует связь, даваемая законом Кирхгофа. При каждой данной темп-ре всякое тело излучает только те лучи, которые оно способно поглощать при этой темп-ре. Каждая падающая на тело единица лучистой энергии. вообще говоря, распадается на три части: отраженную—R, прошедшую сквозь тело·—D и задержанную телом, или поглощенную им, А, т.ч. R + D + А=1. Для всех технически важных случаев можно принять, что тела непрозрачны, так что D=0. А характеризует собой лучепоглощательную способность тела и м. б. назван коэфициентом поглощения лучей. Его иногда также называют степенью черноты тела S. Очевидно для черного тела А== 1, соответственно R= 0. Коэф. А, вообще говоря, м. б. различен для разных длин волн. Тело, обладающее таким· свойством, называется цветным. Если А < 1 и одинаков для всех длин волн, то тело называют серым. Большинство тел, встречающихся в технич. практике,— серые тела. Если назвать через E_s лучеиспускательную способность черного тела при определенной темп-ре, то есть количество энергии, излучаемое единицей поверхности тела в единицу времени, то закон Кирхгофа утверждает, что при той же t° излучение серого тела будет Е=А · E_s, то есть что коэф. поглощения

(25)

коэф-ту лучеиспускания серого тела. Для цветного тела закон Кирхгофа верен для каждой длины волны λ:Ε_λ=Α_λΕ_8λ, но Α_λ в этом случае различен для разных длин волн. Коэф. лучепоглощения тела зависит не только от его вещества, но и от степени шероховатости поверхности. Для полированной поверхности он резко снижается. Поэтому обшивка горячего предмета полированными металлич. листами является хорошей теплоизоляцией. Выше 500—600° поверхность почти всех тел теряет полировку и становится матовой, но и выше этих t° А ддя полированной поверхности сохраняет несколько пониженное значение. Абсолютно черного тела не существует, и коэф. поглощения сажи ^0,9. Для получени абс. черного тела Кирхгоф предложил устройство в виде полой камеры с небольшим отверстием. Каждый упавший в это отверстие луч, прежде чем выйти обратно наружу, претерпит многократное отражение от стенок, причем почти вся его энергия поглотится последними, и следовательно полость отверстия обладает свойством черного тела. Такое устройство употребляется в физич. лабораториях для градуирования пирометров. Интенсивность испускания черным телом лучей различной длины волны изменяется вместе с t° тела. В 1900 г. Планку удалось дать, исходя из квантовой теории излучения, по которой электроны атомов испускают лучистую энергию лишь целыми квантами hv (где v — число колебаний, a h — постоянная Планка), общую формулу для интенсивности испускания черным телом лучей всех длин волн. Если представить лучеиспускательную способность черного тела волн длины от А до А -f- άλ в виде άΕ=Ι_λ· άλ, то для Ι_λ—интенсивности лучеиспускания волн длиною А—Планк выводит следующее выражение:

Ι_λ=3,17 · 1(Г⁸ ~~ Г-г-¹-1 · (26)

^{л 9} 1,43 I_м² ч cjuj ^{4 7}

~λΤ i

в —1

Здесь все величины даны в Cal, м и часах кроме длины волны, которая подставляется в сантиметров (подробнее см. Энергия). Графич. изображение ф-лы (26) дано на фигуре 4, на которой длины волн отложены по оси абсцисс в микронах (0,001 миллиметров).

мЗ-ч.

%20000

Из нее видно, что при повышении темп-ры интенсивность лучеиспускания резко возрастает, причем одновременно максимум лучеиспускания передвигается влево, в сторону меньших длин волн. По своему действию на тела лучи различных длин волн могут быть разделены на следующие группы: 0,017 -f-5 ηιμ—рентгеновы лучи и лучи радия (8 октав), 5 7ημ -р 0,02 μ — неисследованная область (2 октавы), 0,02 --0,4 μ — ультрафиолетовые химические л^чи (3,5 октавы), 0,4 -f- 0,76 μ — видимые лучи (1 октава), 0,76 -f-0,34 миллиметров — инфракрасные (тепловые) лучи (8 октав), 0,34 ч-2 миллиметров — неисследованная область (2,5 октавы), 2 миллиметров -у несколько км — электрические волны. Из фигура 4 видно, что при температуре топок котлов и промышленных печей максимум лежит в области инфракрасных лучей. Если в выражение άΕ_λ=Ι_λ άλ подставить вышеприведенное значение Ι_λ и проинтегрировать его от 0 до оо, то получится формула для лучеиспускания черного тела:

(²⁷>

		1
	Р	А
		W
J	L
	¹ (	V ч
J	й

2 }

Длина волны

Фигура 4.

6_ 7 в 9 /0μ

где

Со=4,95

Cal

м?ч аоо) _

Этот закон был найден из опыта еще в 1872 г. Стефаном, а теоретич.’путем в 1884 г. Больцманом, поэтому он называется законом Сте-фан-Больцмана. Для серого тела E=AE_S и следовательно С=И *4,25. Ниже приводятся значения коэф-та С для нек-рых материалов, имеющих технич. применение:

Саша 4,6

Чугун шероховатый, ржавый. 4,6

Железо матовое, ржавое. 4,з

» сильно ржавое. 4,1

» катаное.. 3,7

» полирэранное. 1,3

Известняк матовый, белый. 4,3

Песчаник красный, шлифованный. 3,3

Из приведенных примеров видно, что почти все тела в топочном пространстве и дымоходах имеют С ^ 4.

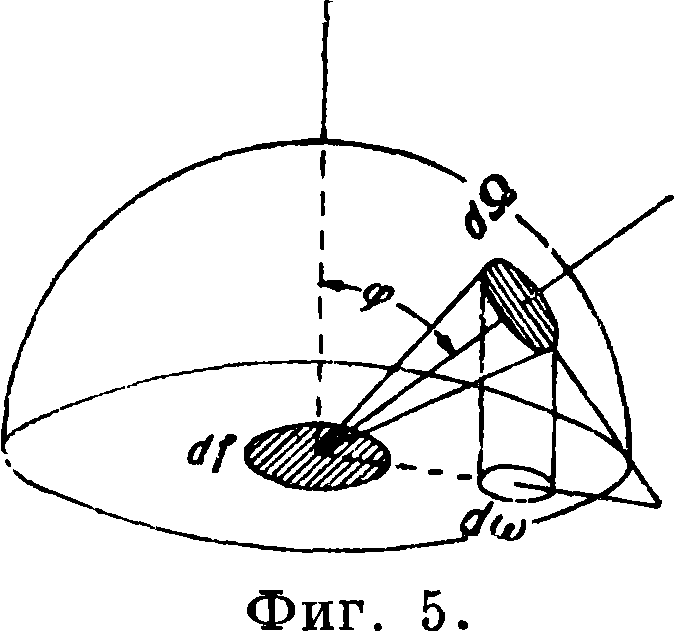
В формуле (2 7) E_s представляет излучение поверхности тела по всем направлениям, или т. н. полусферич. излучение плоскости. Излучение в определенном направлении дается законом Ламберта, согласно к-рому излучение поверхности под углом φ к ее нормали Ε_φ относится к излучению в нормальном к поверхности направлении E_0t как cos φ

Ε_φ=Ε₀- cos φ. (28)

Просуммируем излучение элементарной площадки df по всем направлениям, то есть найдем ее суммарное полусферич. излучение. Для этого построим над ней полусферу радиусом=1 (фигура 5). Пусть пучок лучей, выходящих из площадки df под углом φ к нормали, вырезает на полусфере площадку άΩ. Энергия, излучае мая через эту площадку в единицу времени, равна

Ε_φ · df · άΩ=Е₀ · df ’ cos φ · άΩ=E₀df · άω,

где άω=cos φ · άΩ есть проекция άΩ. Суммируя все излучения через полусферу и замечая, что Σάω=ω есть площадь круга радиуса г=1, получим:

E df=Е₀ · df · ω=Е₀ · df · π.

Но согласно закону Стефан-Больцмана Е== ^С Ш⁴’ поэтому

Яо=1 (тоо)‘ ^{и Е}*=Н-МГ-сов?· (29) Это и есть искомое выражение для энергии лучеиспускания под углом φ к излучающей поверхности. Полученное выражение позволяет сейчас же вывести взаимодействие двух эле

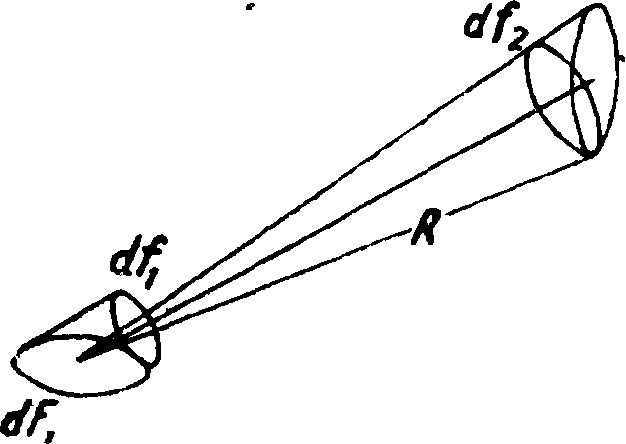
ментарных площадок (фигура 6). Излучение площадки dF_x на площадку dF₂

άΕ_φ=Ε_φ · dF_x. άΩ=Ε₀

dfi - df₂K2 ’

или на основании ф-лы (29)

dE _а

π V

TlA

100

dfi · df₂

К*

(30)

Здесь dfi и df₂ — проекции площадок dF_x и dF₂, видимые в направлении R, а величина R есть расстояние между площадками. Интегрируя (30) по величинам df_Y и df₂, можно найти излучение одного тела определенной конфигурации на другое. Обратно, подставляя в формулу (30) значение С₂ и Т₂ для второго тела, найдем лучеиспускание последнего на первое тело. Т. о. может быть разрешена задача о теплообмене двух тел лучеиспусканием. В общем случае получается очень сложная зависимость. Покажем, как задача разрешается для нек-рых частных случаев.

Наиболее простой метод решения предложен в последнее время Поляком и заключается в определении разницы между приходом лучистой энергии и ее расходом, то есть в нахождении результирующего потока от одного тела к другому. Изложим вкратце этот метод.

Нек-рое тело излучает энергию в окружающую среду и само подвергается излучению со стороны других тел. В этом случае надо отчетливо различать следующие три понятия: ^собственное излучение тела, определяемое за-

коном Стефан-Больцмана (27): Е=С т^ ;

2) эффективное излучение тела E_ef, слагающееся из собственного и из той части упавших на тело лучей, которая отражена им обратно, и 3) результирующий поток лучистой энергии, представляющий разницу между приходом и расходом энергии. Результирующий поток, отнесенный к единице поверхности, обозначим через х. Результирующий поток или «сальдо тела» можно выразить двояким способом. С одной стороны, его можно рассматривать как разность всех поглощенных телом лучей и собственным излучением х=Е₂-Е₁₉ (31)

где через Е_г обозначено излучение, а через Е₂ — поглощенные единицей поверхности лучи. Формула (31) представляет баланс энергии и именно сальдо тела, так сказать, с внутренней стороны поверхности тела. С другой стороны, этот баланс можно составить с противоположной стороны поверхности, вне тела. В этом случае результирующий поток х очевидно равен разности встречных потоков, падающих на тело и уходящих от него:

x=(E_ef)₂-(E_ef) i. (32)

На основании (31) и (32) можно написать, что падающий на единицу поверхности поток {E_ef)₂равен поглощенному телом потоку Е₂=х + Е_х, деленному на коэф. поглощения тела А_х:

(Е_еГ)₂=(32)

Соответственно отраженный поток будет равен

А 1

Полный уходящий от тела поток (E_pf) ₁ очевидно равен сумме отраженного излучения и собственного излучения:

W=ЧгГ & + + ^Ει=ЧгГ ^ж + Ιί

или на основании закона Кирхгофа, подставляя=E_st

A i

= ( ^7 — i) ^ (33)

При выводе принималось, что тело излучает со всех своих точек постоянную лучистую энергию, равно как и получает от других тел поток равномерной интенсивности. В общем случае надо было очевидно рассматривать потоки энергии, отнесенные к бесконечно малым площадкам dF, и затем произвести интегрирование их.

Приложим выведенную формулу (33) к случаю двух параллельных стенок, на столько больших по размеру и близких друг к другу, что влияние концов их не сказывается на равномерности потока. Результирующий поток первого тела х_х очевидно равен и обратен по знаку результирующему потоку второго тела х₂:

х_г=—х₂. (34)

Щ основании (33) имеем:

Χι={Щ - {Щ=[(-ί) ·4 -г B_s2] -

-[Н-Ь+я-]· ⁽³⁵>

Отсюда, подставляя х₂=—х₁, получим

_{Xi =} E_S1 -Е_п (35)

-¹

или, т. к. Е_л=C_s (А) e_s2=C_s (Г|)‘, 4_гС,-

= С_Х и А₂С₈—С₂, после подстановки получим известную формулу Нуссельта, выведенную им путем рассмотрения повторного поглощения и отражения энергии обоими телами:

(Т₂^_(ТЛ⁴

’ 100 f I 100

-= ’~±7±ΖλΓ

Cl С₂ C_s

В такой форме закон Стефан-Больцмана обыкновенно применяется в тепловых расчетах котлов. Эта форма представляет частный случай взаимодействия параллельных поверхностей. Повторяя это рассуждение для двух концентрических шаровых или цилиндрич. поверхностей, легко получить выражение

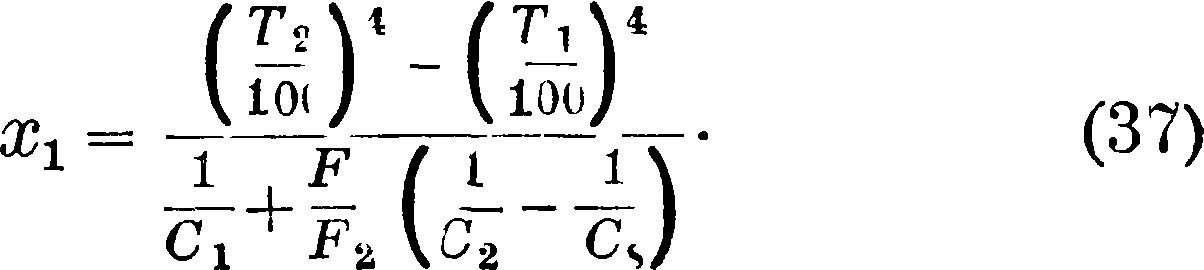
В общем случае задача нахождения сальдо потока приводится к решению интегральных уравнений.

До последнего времени во всех технич. расчетах Т. топочного пространства принималось, что топочные газы прозрачны для лучей. Это верно для двухатомных газов (0₂, N₂). Однако Шак и затем Нуссельт показали, что находящиеся в продуктах горения трехатомные газы С0₂ и Н₂0 обладают цветным поглощением. Поэтому во всех технич. расчетах теплопередачи топочного пространства котлов и печей, а также первого хода котлов приходится принимать во внимание непрозрачность газов для нек-рых длин волн.

Для ознакомления с техническими расчетами теплопередачи следует обратиться к специальной литературе. Основные понятия можно почерпнуть в книге Шака.

Лит.: Хвольсон О., Курс физики, т. 2 и 3, Берлин,1923; Г р е б е р Г., Введение в теорию теплопередачи, пер.с нем·, М.—Л., 1933; Т е н-Б о ш, Теплопередача, пер. с нем.,М., 1930; Schack A., Dor industiielle Warme-iibergang, Diisseldorf. 1929; Grober H., Einfiihrung in die Lelire von der Warmeiibertragung, B., 1926; Grober H., Die Grundgesetze der Warmeleitung Und des Warme-iiberganges, B., 1921; G ro ber H., Warmeiibertragung,

2 Aufl., B., 1927; Encyklopadie d. mat. Wissenschaften, B. 5, T. i, H. 2, B.—Lpz., 1905. M. Кирпичев.

^C[(94L)⁴]· <*o

Теплопередача

; ^+ -£**)=о, (п

+ ее№+Ф+ж)· <п>

+ е^е№+Ф+ж)· <^п>