> Техника, страница 84 > Теплопроводность

Теплопроводность

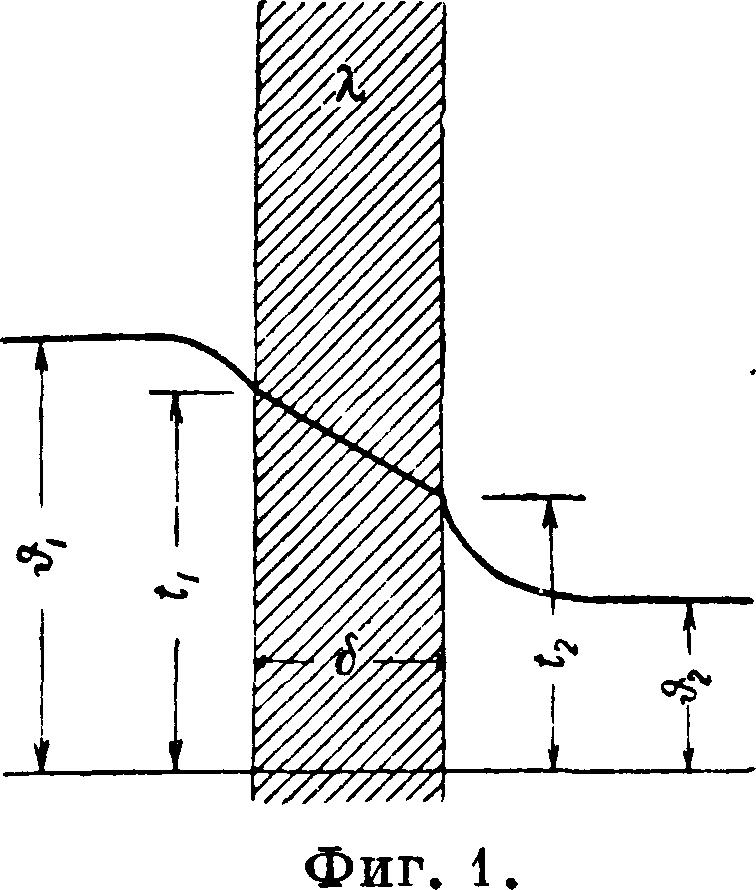
Теплопроводность, свойство среды или системы тел передавать тепло, не участвуя при этом в видимом движении. В процессе такой передачи тепла распределение t° может сохраняться постояннымуили меняться с течением ^ времени. В первом случае имеется установившееся, или стационарное, состояние, во втором—переменный тепловой режим. Основой теории распространения тепла путем Т., разработанной Фурье, служит предложенное Био уравнение, определяющее зависимость между потоком тепла Q, разностью темп-p ii—1₂ и геометрии. размерами тела для простейшего случая плоской однородной стенки (фигура 1) толщиной δ:

Q^XF^r, (1)

где τ—время, a F—поверхность стенки, к^к-рой отнесен поток Q. Коэф. Т. материала Я определяется свойством вещества стенки. Ниже даны переводные коэф-ты для перевода одних единиц Т. в другие:

λ в технических единицах » в физических »

» в электрических »

» в британских » 0,124

Г BTU дм. L фт. ч °F

Г cal Ί

L М ч °с J

• · ³⁶⁰ ["сж^ск^ст]

••••МеШ

Коэф. Т., вообще говоря, зависит от ί°, но в случае малых разностей t° в большинстве задач мы можем принять его постоянным и отнести к некоторой средней t°. Ур-ие (1) легко распространить на любое однородное изотропное тело с произвольным распределением t°. Пусть dF—произвольный элемент какой-либо изотермич. поверхности тела и п—нормаль к этому элементу; если dt бесконечно малое падение t° на элементе нормали dn, то ур-ие (1) напишется в виде:

dQ=-^dFdx (2)

для элемента времени dr; называется градиентом t° и обозначается grad ί. Если элемент dF не совпадает с изотермич. поверхностью, а составляет с ней нек-рый угол, то

dQ_n=-^dF άτ, (3)

7*t

т. e. в общем случае нормальная составляющая теплового потока dQ_n через площадку dF определяется ф-лой (3), где п есть нормаль к этой площадке. Для вывода общего уравнения Т. рассмотрим произвольный параллелепипед (фигура 2), вырезанный внутри тела, с ребрами dx dy dz. Поток тепла, проходящий через параллелепи- £ пед, мы можем разложить на 3 составляющие вдоль осей Χ,Υ, Ζ. Поток тепла вдоль оси×определится соотношением:

-b{rXdvdzdr=-X^_x)_x^_xdyd_Zdr + dt

Фигура 2.

+ су dx dy dz άτ

или дх

(я dx dy dz άτ=су dx dy dz dr;

такие же ур-ия мы можем составить и для двух других составляющих теплового потока вдоль осей Y и Z. Складывая их и сокращая на dx dy dz dr, мы получаем общее ур-ие Т. для изотропного тела без источников тепла:

<⁴>

При постоянном Я ур-ие (4) переходит в

ot _ λ d4 dn, d4- _ »₂,

dx су Idx2 + dy* 4- _az2J an fr*

(5)

Если в элементе объёма выделяется количество тепла dq=f (xyzr) dx dy dz dr, то к правой части ур-ия (5)или (4) нужно прибавить член — f(xyzt). В случае стационарного состояния мы имеем

|*=о дх

d4 d4 dx2 * dy²

(6)

Величина — обозначается обыкновенно через а и называется температуропроводностью, материала. Размерность величины а есть [>²/ч].

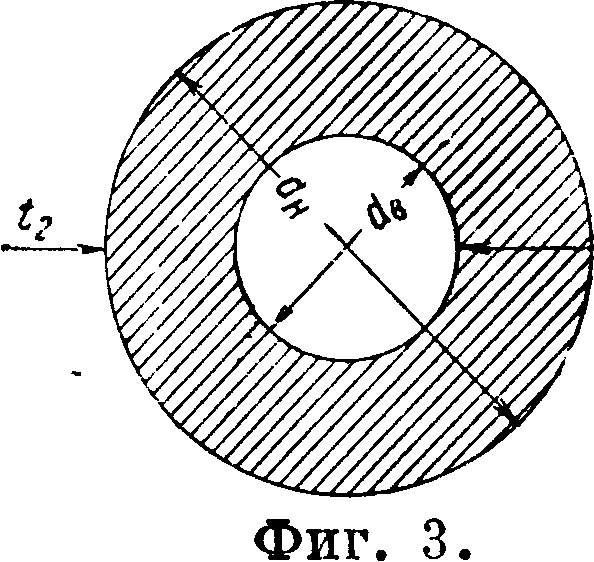
Некоторые простые случаи Т. Для плоской стенки, как мы видели, имеет место ур-ие (1). Для цилиндрич. слоя (фигура 3) бесконечной длины с наружным и внутренним диаметрами d_H и d_e находим решение для стационарного состояния:

ρ=-2πρϊΛ^; Q -~-=-2nUdt;

интегрируя от до t₂ и от d_e до d_H, находим

Q =" ”r^L7-· (7)

_L in 2 λ ^Q d.

Для сферич. слоя тем же способом находим, dt,

do

Q=~ 4λπρ² ^ ; 4nXdt=-Q^·,

интегрируя от ^ d_e до -находим

<2=7

d_H

π ( ί i — fji)

2-fi—1Λ

2 Я d₆ d_M

И ОТ ДО ί₂,

(8)

Оба решения относятся к единице времени. Для иллюстрации нестационарного потока тепла рассмотрим нагревание стержня при следующих пограничных условиях: х=0, t=t₀,

х — оо, t=О, τ=0, t=0.

Пренебрегая потерями тепла от стержня в стороны, получаем дЧ

ду“

=^=°“

= а

^дЛ

дх2’

Решение этого ур-ия напишется в виде:

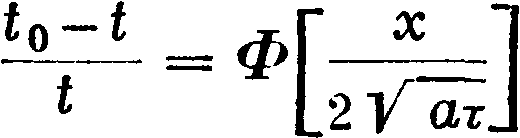
I

где Ф ({)=f е - ϊ4ξ.

о

Т. металлов и сплавов. Один из самых старых способов определения Т., которым пользовался Ингенгус, состоял в сравнении распределения f® в различных стержнях, нагреваемых с одной стороны ц отдающих тепло по всей длине в окружающую среду, причем для простоты t° отмечалась по плавлению воска, которым стержни были покрыты, причем, как показали Депре и Био, Т. различных металлов относятся, как квадраты t, отрезков, на которых воск расплавился. Определением теплопроводности по охлаждению стержня занималось очень много исследователей (Лангберг, Депре); особенно тщательные исследования принадлежат Видеману и Францу, которые помещали испытуемый стержень, нагреваемый с одной стороны парами воды, внутри металлич. цилиндра, охлажденного снаружи водой. Темп-pa стержня измерялась подвижным термоэлементом, спай которого мог быть прижат к произвольной точке стержня. Любопытный способ относительного определения Т. дал Фойгт. Из различных металлов изготовлялись два образца в виде трехугольных пластинок и спаивались так, что линия спая представляла собой диагональ квадрата. При нагревании одной из сторон квадрата линии теплового потока, а следовательно и изо-

tg<Pl λ л термы преломлялись по закону ^, и

следовательно по углам φ₁ и φ₂ можно определить отношение Т. металлов. Изотерма делалась видимой путем покрывания пластинок сплавом терпентина с воском, к-рый давал достаточно резкую изотерму плавления. В других способах измерялось количество тепла, подводимое к стержню, и падение t° вдоль него (Дональдсон, Якоб), причем в нек-рых случаях вместо стержня испытывались пластинки (Хонда и Симиду). Один из самых изящных методов определения Т. металлов был предложен Кольраушем, причем измерялось не Я, а отношение Так как электропроводности κ, то есть ^.

Экспериментально этот метод был разработан Егером и Диссельхорстом. Через испытуемый металлич. стержень диам. 1—2 сантиметров проходит нагревающий его ток, причем концы стержня поддерживаются при постоянной t_x. Измеряя в центре стержня и на его концах разности потенциалов V и t°, мы имеем при условии отсутствия боковых потерь тепла в окружающую среду

λ _ У2

κ 8 (t₂ — ίi) *

Результаты измерения весьма надежны для толстых стержней и при хорошей изоляции. Недостатком метода являются весьма большие силы тока, необходимые для нагревания стержня (до 300 А в опытах Егера и Диссельхорста). Для уменьшения силы тока Симиду предложил пользоваться значительно более тонкими стержнями, устраняя боковые потери тепла при помощи нагрева защищающей стержень трубки, создающего в ней то же распределение ί°,

как и в стержне. Определением ~ занимались

Лангмюир, Анжелл Мейсснер и др. Т. металла лежат в пределах между 1 (сплав Sb+Cd) и 360 (Ag), при весьма низких t° наблюдались величины 1 400 для Си и даже до 10 000 для Си монокристалла. Небольшие примеси значительно· понижают Т. чистых металлов; t° (выше 0°) мало влияет на T. С понижением t° Т. растет и тем быстрее, чем ниже t°. Видеманом и Францем была установлена закономерность, связывающая λ и κ, а именно, что для определенной t° отношение ^ есть величина постоянная для всех металлов. Закон этот является приблизительным (±10%) и относится также и к сплавам и сталям с большим содержанием С. Лоренц установил другую закономерность, а именно, что ^ должен быть величиной постоянной,] не зависящей от t°. Он обозначал 10⁸^=L₀= Const,

Для чистых металлов величина L₀ колеблется незначительно и лежит между 2,2 и 2,5; для сплавов эти числа тоже б. или м. соответствуют действительности. Исключением являются металлы и сплавы с очень малой электропроводностью, для которых (Cd и Sb) L₀ достигает 243. Кенигсбергер высказал предположение, что эти отношения можно объяснить тем, что Т. металла составляется из действительно металлической Т. и Т. неметаллической, причем чем больше первая, тем ближе металл следует закону Видемана-Франца-Лоренца. У металлов с малым κ превалирует 2-й вид Т., что и вызывает большие отклонения. Технич. интерес представляет изучение периодически меняющихся £°-ных полей и вызванных ими напряжений в различных машинах, двигателях и машинах-орудиях, т. к. иногда эти напряжения могут повести к серьезным авариям. С другой стороны, важен отвод тепла по метал-лич. частям различных электрич. установок.

Т. дурных проводников тепла. Почти все основные методы определения Т. дурных проводников тепла, применяемые в настоящее время, сводятся к измерению количества тепла, прошедшего через испытуемое тело, по электрической энергии, израсходованной на нагрев, разности t° и линейным размерам тел. Материалы исследуются в форме плиток цилиндр ич. слоя, сферич. слоя, цилиндров, нагреваемых с торца, и т. д. Приборами с двумя испытуемыми плитками Р_х и Р₂, между к-рыми помещался электрич. нагреватель Н_и пользо-

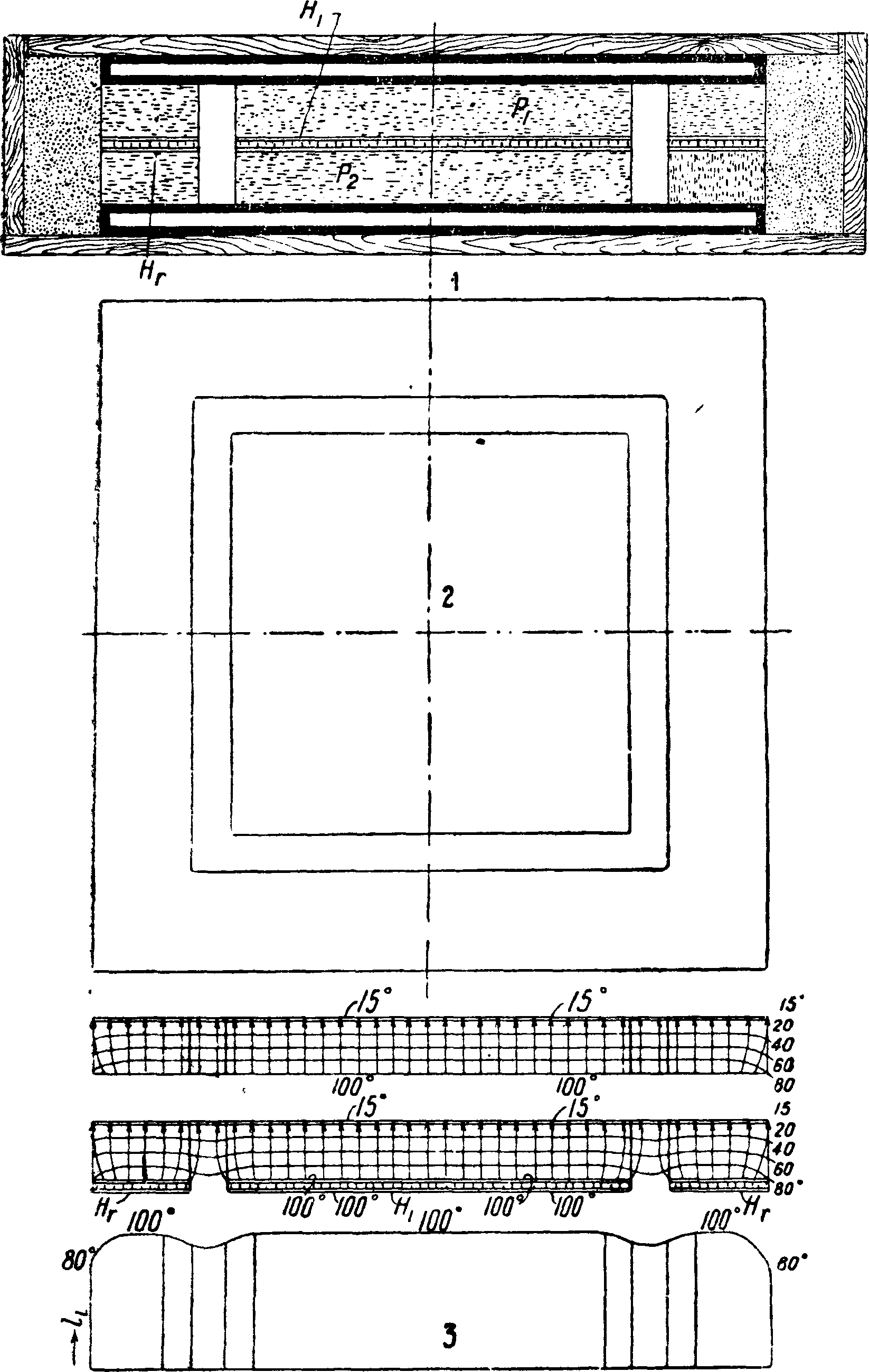
Фигура 4.

вались Поэнсген (фигура 4: 1—вертикальный разрез, 2—вид сверху, 3—изотермы по различным сечениям) и Гребер в Мюнхенской лаборатории технич. физики, в которой и были разработаны основные способы измерения Т. строительных и изоляционных материалов. Недостаток плоского прибора состоит в необходимости устранения боковых потерь тепла при помощи т. н. охранного кольца Н_г) к-рое усложняет регулировку прибора и все же не всегда обеспечивает достаточную точность. Чтобы не встречаться с необходимостью изготовления двух одинаковых образцов, Якоб сконструировал прибор (фигура 5) с одной плиткой Р, а потери тепла от нагревателя Н вверх компенсировал другим нагревателем D, к-рый поддерживался при ί°, одинаковой с первым. Т. о., считая и охранное кольцо G, приходится ре гулировать три самостоятельных нагревателя, что очень осложняет испытание.Подобный прибор установлен и в Физико-технической лаборатории ВТИ.

Нуссельт пошел по совершенно другому пути. Он заключает электрический нагреватель Н

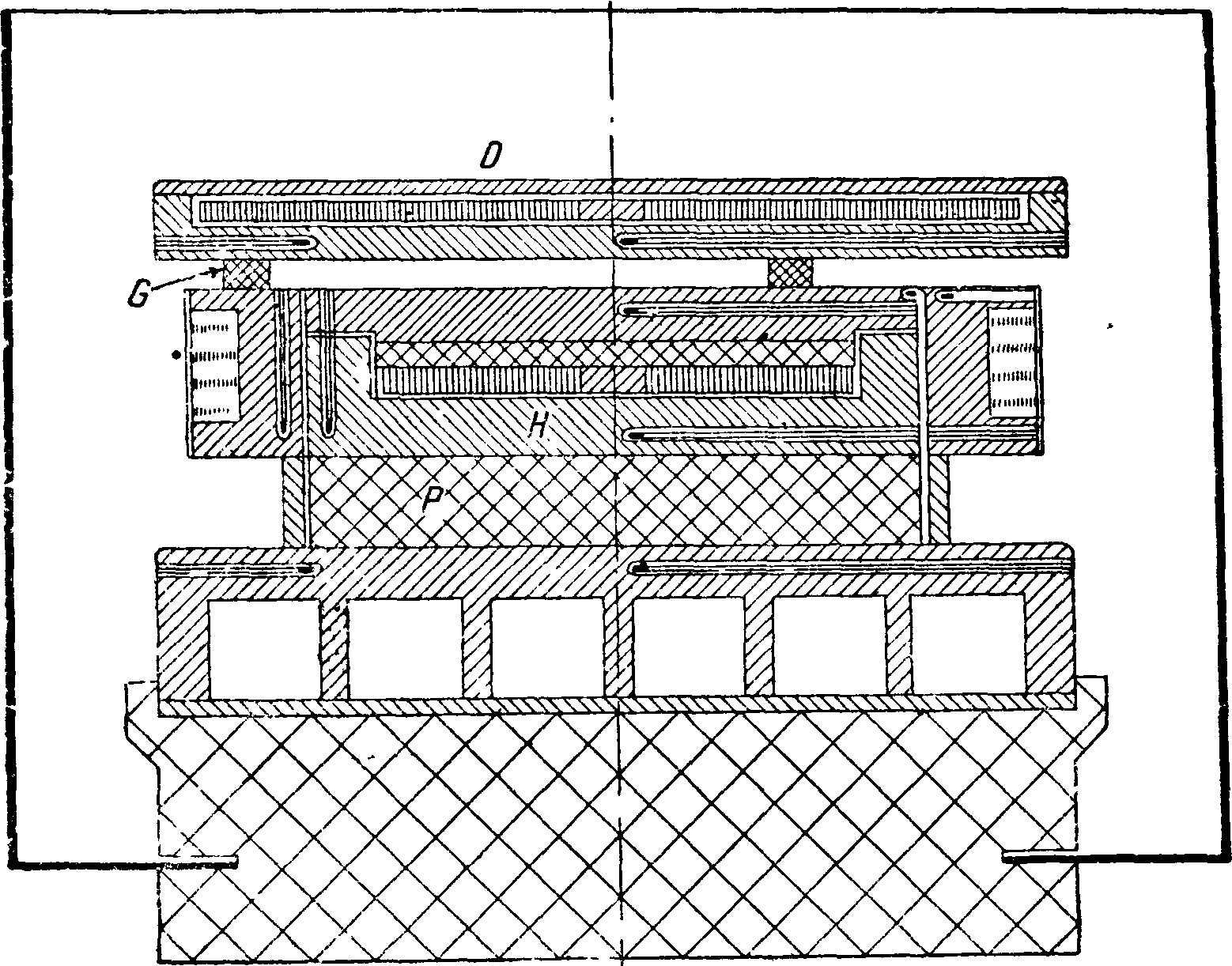
Фигура 5.

Фигура 6.

внутри испытуемого полого тела Р так, что весь поток тепла проходит через испытуемый материал и отпадает необходимость компенсировать боковые потери (фигура 6). При испытании сыпучих материалов для простоты он устраивал свой прибор в виде шара со сферическим нагревателем в центре.

Л ля твердых материалов прибор имел кубическую форму в виду сложности устройства сферич. образцов.

Для увеличения точности прибору давались весьма большие размеры (0,6 м), благодаря чему одно испытание длилось

3—14 дней. Из своих опытов Нуссельт попутно определял вли

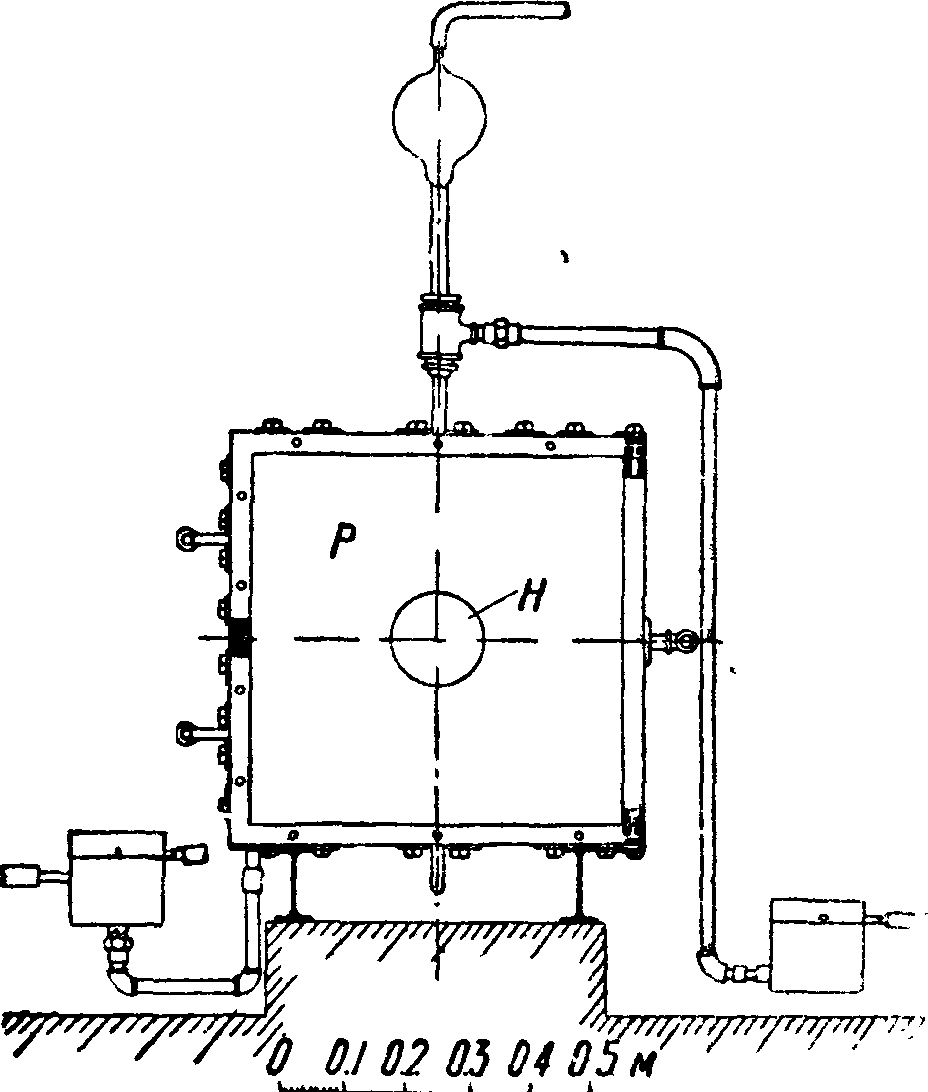
яние t° на теплопроводность. Для испытания изоляции трубопроводов Ван Ринеум устроил прибор в виде длинной трубы, покрытой слоем испытуемого материала, причем потеря тепла концами трубы учитывалась расчетным_: путем на основании

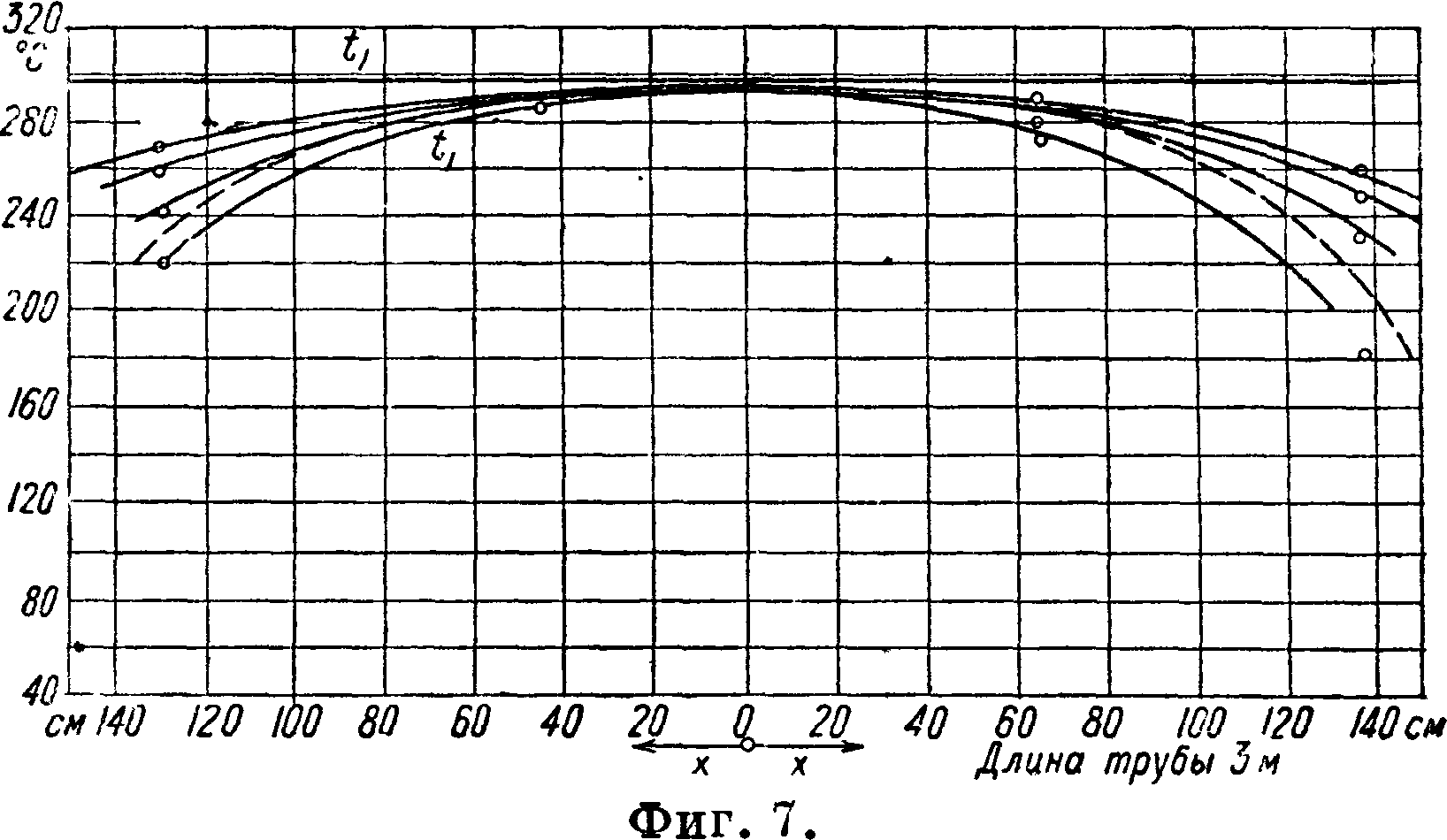
измерений t° вдоль трубы; фигура 7 показывает влияние различной степени охлаждения концов на t° в средней части трубы. Способ, предложенный Тимротом, состоит в измерении Т. цилиндра а, нагреваемого по плоскости основания плоским нагревателем &, смонтирован-

ным на основании другого цилиндра с причем оба цилиндра помещены в холодильник d (фигура 8). Поток тепла—расходящийся. Измерение сводится к измерению тока и разности t° между центром нагревателя и холодильником.

На фигуре 9 дана схема электрических соединений: L—прибор, К—коммутатор, позволяющий при помощи одного гальванометра д производить измерение t°, силы тока и напряжения на зажимах нагревателя, R, С—реле, служащее для поддержания постоянства t° воды, R_x— реостат. В этом способе,похожем на способ плоских пластин, устранена необходимость компенсировать боковые потери, и вместе с тем размеры прибора невелики, что позволяет относительно скоро производить испытания. Прибор установлен в ВТИ и других институтах. Кондратьев и Стаценко разработали ряд методов определения Т. при нестационарном (регулярном) режиме, позволяющем производить определения Я весьма быстро. Степень точности измерений ниже, чем для стационарного режима. Зная Т. материала, можно поставить обратную задачу, а именно— измерения расхода тепла свести к измерению разности ί°. Эту задачу весьма остроумно решил Шмит. На поверхность, отдающую .тепло в окружающую среду, накладывается тонкая

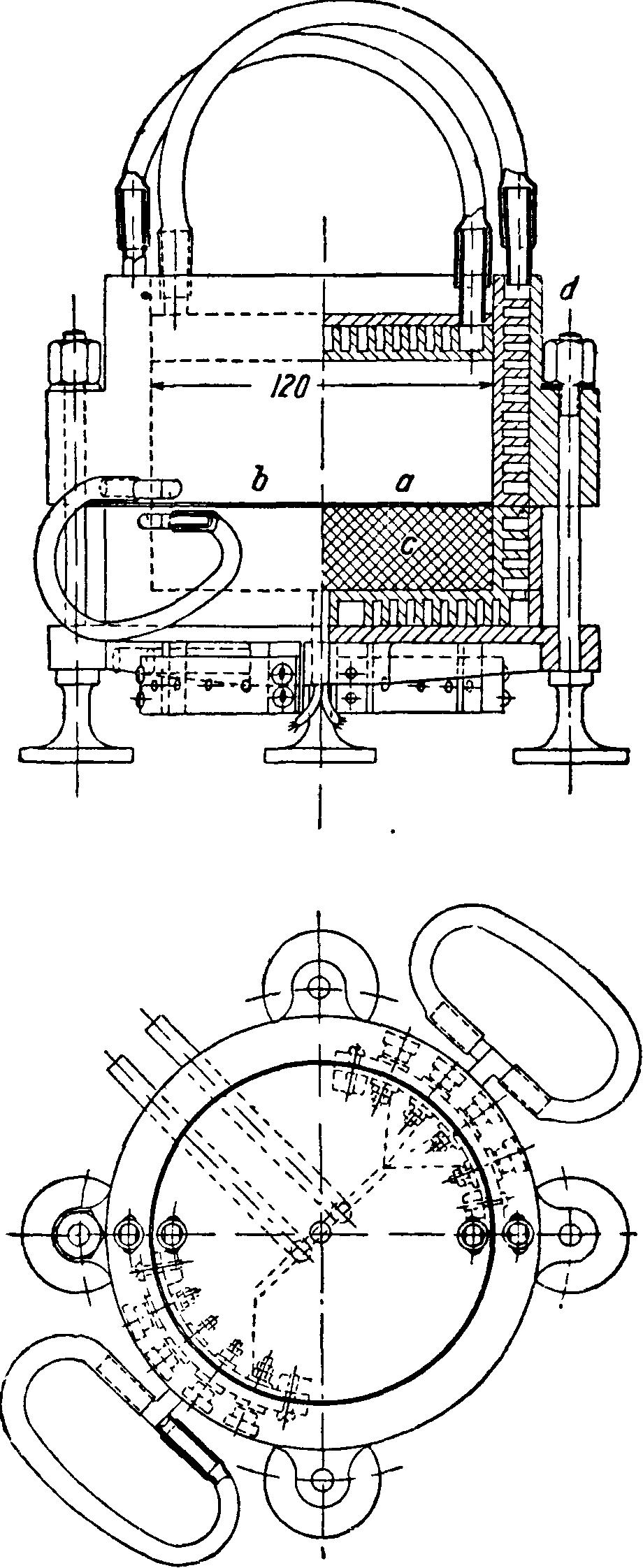
Фигура 8.

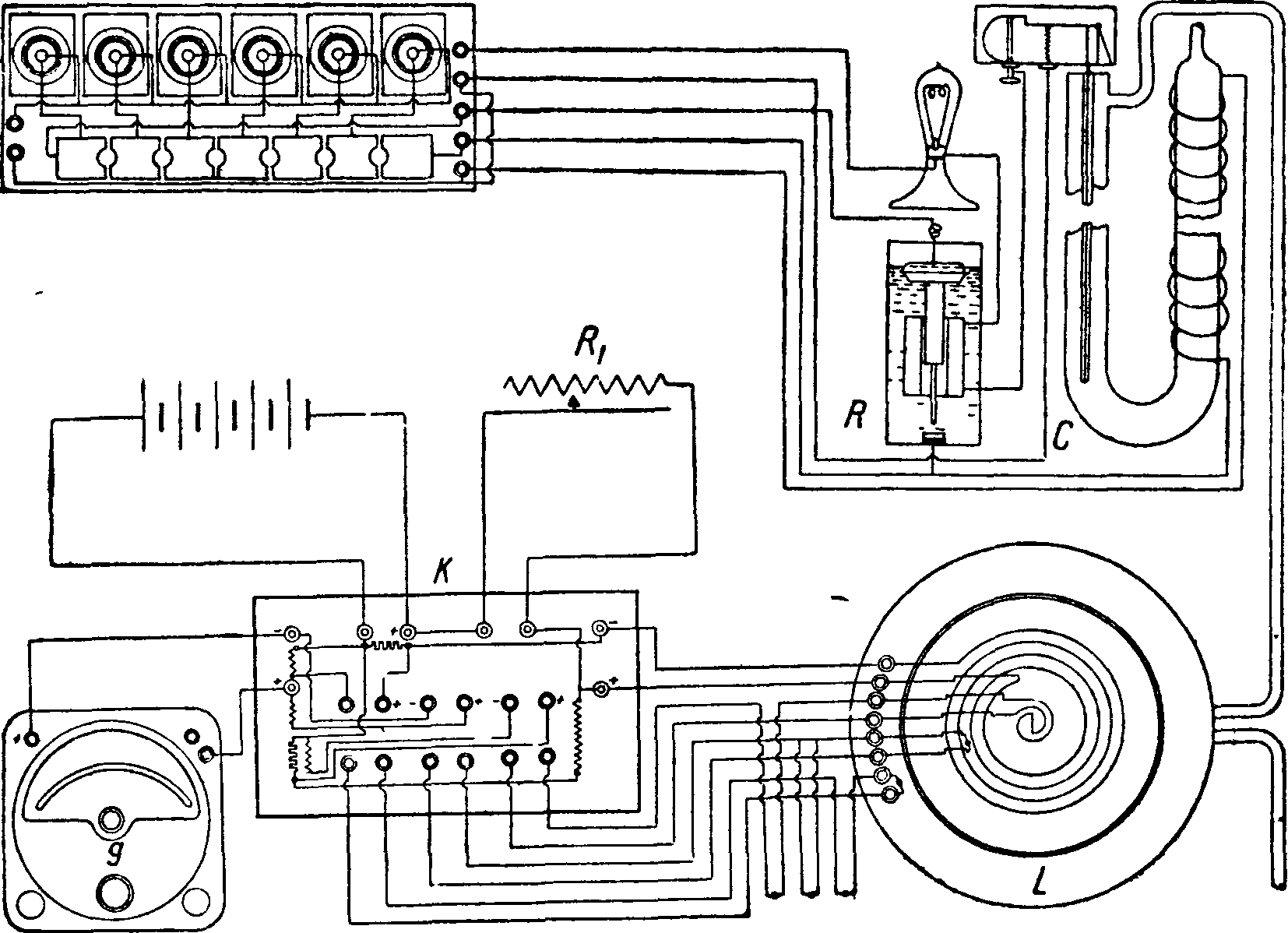
Фигура 9.

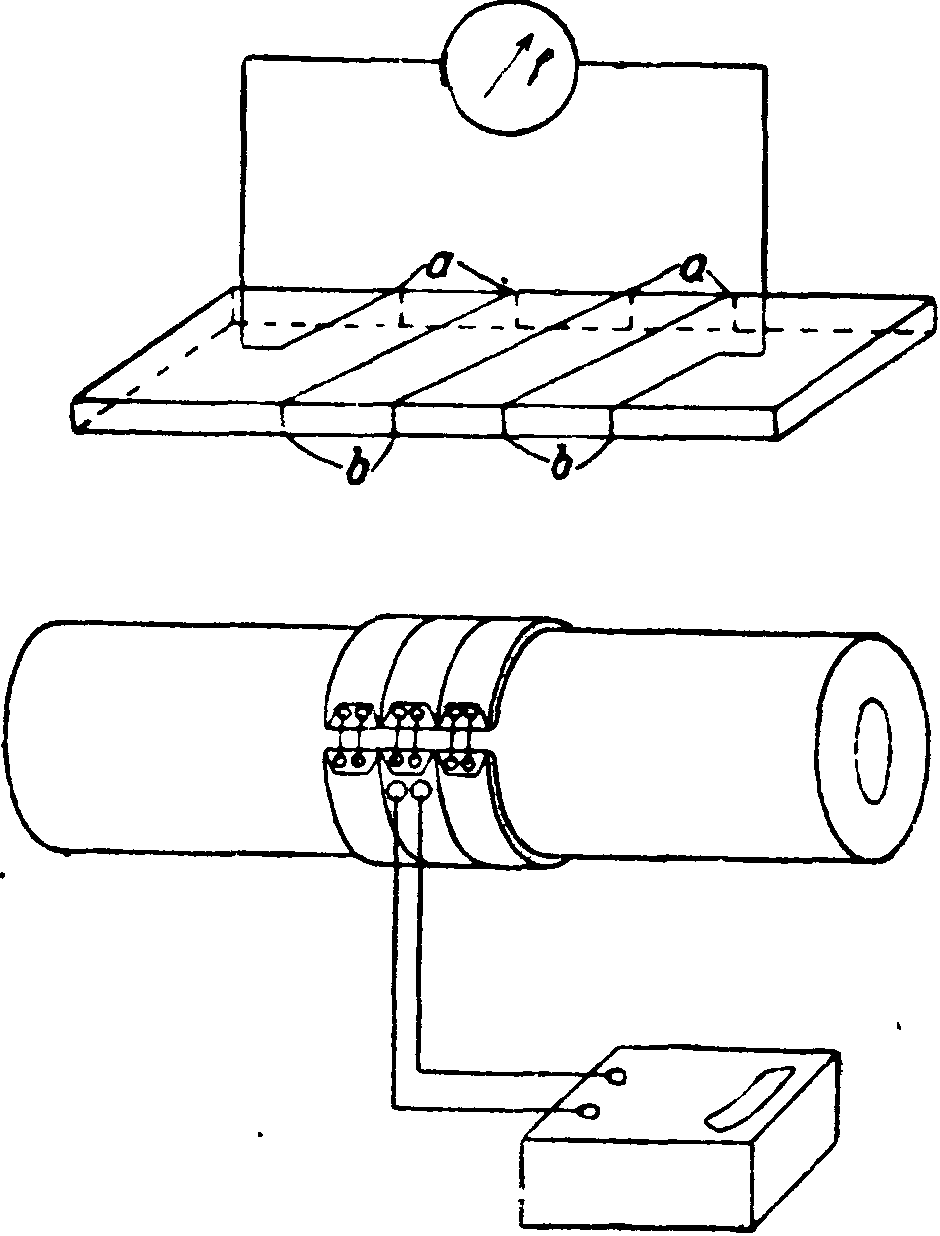
резиновая лента (фигура 10) с установленными на ней 100 диференциальными термоэлементами а и Ь, определяющими разность ί°. ее поверхностей (на фигура 10: 1—расположение термопар в резиновой ленте, 2 и ά—различные споеобь^ накладки на трубу, 3—измерительная лента и две охранные ленты по краям). По эдс этих термоэлементов измеряется пропорциональный ей поток тепла через резиновую ленту. Прибор м. б. проградуирован прямо в калориях. Т. изоляционных, почти^всегда пористых материалов является ф-ией Т. воздуха, заключенного в их порах“ Влияние t° т. о. будет тем больше, чем больше пористость и чем больше объём пор. Впервые на возрастание Я с t° указал Эйкен, но окончательно это было установлено классич. опыуами Нуссель-та. В этом же направлении проводили работу Ван Ринсум, Гребер, Герене и др. Температурный коэф. самого материала мало сказывается, т. к. Я твердого каркаса вообще мало влияет на общую Т. изоляционного материала. Т. материала вообще тем меньше, чем больше его пористость, то есть чем меньше его объёмный вес (вес единицы объёма).

Особенно сильно сказывается влияние объёмного веса на Т. порошков (опыты Тейлора,

Смолуховского и др.), Я которых гл. образом определяется термин, сопротивлениями точек соприкосновения. Огромное уменьшение, Т. с уменьшением дав-

3

Фигура 10.

ления газа было установлено опытами Смолуховского. Влажность материала сказывается также очень сильно на его Я, особенно в случае порошков, т. к. влага прежде всего заполняет самые мелкие поры и конденсируется на местах соприкосновения частиц,^сильно понижавших термин, сопротивление.

Т. жидкостей и газов. Для измерения Т. жидкостей Христиансен, Миллер, Чаток, Якоб и др. пользовались методом жидкой пленки, пропуская через нее поток тепла сверху вниз. Винкельман исследовал Т. жидкостей и газов при нестационарном состоянии, определяя Я в шаровом слое между наружным метал-лич. шаром и внутренним, служащим термометром. При переходе из твердого состояния в жидкое Т. вещества резко уменьшается, особенно большой скачок получается для металлов. Изменение вязкости η играет незначительную роль. Давление сказывается на вязкости жидкости гораздо больше, чем на ее Т. Бриджмен на основании своих опытов, опытов Вакс-мута и теоретич. рассуждений находит для неэлектропроводной жидкости ф-лу

- 2 Rv

^А ~~ <52 ’

где R—газовая постоянная, v—скорость звука, 1

<5= —среднее расстояние между центрами молекул. Значения коэфициента Я для жидкостей по Бриджмену приведены в сл. таблице:

Жидкость	Измерено	Вычислено
Этиловый голь.	0,0043	0,0052
Эфир..	0,0033	0,0029 0,0151
Вода ..	0,0144

Т. газа не зависит от давления до тех пор, пока при уменьшении его средние пути пробега молекул газа не станут одного порядка с линейными размерами сосуда. При не слишком малых давлениях для газов имеем λ=ft С,»?;

взяв для η формулу Сезерланда

η =

С,УТ

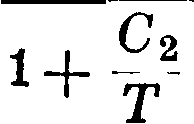
находим

СгУТ

1+^ -г _т

Вопросы Т. газов теоретически разработаны на основе кинетич. теории. Для смесей газов Васильевой было дано соотношение:

χ ₌ jMl__, Р2Я2.

Ρι + Αρ₂ Ρ₂ + βΡι*

Для 0₂ + Η₂ коэф. А=1,379 и В= 3.064.

Лит.: Хвольсон О., Курс физики, т. 3, Берлин, 1923; Тимир яз ев А., Кинетическая теория материи, Μ.—П., 1923; Г р ё б е р Г., Введение в теорию теплопередачи, пер. с нем., М.—Л., 1933; Каммерер И., Термоизоляция в пром-ети, пер. с нем., М.—Л., 1932;

Т и м р о т Д., Определение теплопроводности и теплоемкости строительных и изоляционных материалов, пер. с нем., М.—Л., 1932; Ч а п л и н Г. и Максимов Т., Теплопроводность строительных и изоляционных материалов, «ИТИ», М., 1925, вып. 11—13; Тимрот Д., Приборы для определения строительных и изоляционных материалов, Доклады СССР на международной энергетич. конференции в Берлине, «ИТИ», 1930; GroberH., Die Grundgesetze d. Warmeleitung u. des Warmeuberganges, В., 1921; Handbuch d. Experimentalphysik, hrsg. v. W. Wien ii. F. Harms, B. 9, T. 1, Leipzig, 1929; M i s e s R. u. Frank P., Die Differential u. lntegralgleichungen d. Mechanik u. Physik, 7 Aufl., B. 2, Brscbw., 1927; N u s-s e 11 W., Die Warmeleitfahigkeit von Warmeisolierstof-fen, «Mitt. u. Forschungsarbeiten», Berlin, 1909, H. 63/64. Д. Тимрот.