> Техника, страница 85 > Термодинамика

Термодинамика

Термодинамика. Термодинамика и механика Ньютона. Механика Ньютона получила свое полное выражение в труде Лагранжа [^х]. Здесь она вся была сведена к одному принципу возможных работ, и все остальное было лишь простым аналитич, развитием этого принципа. Принцип возможных работ гласит: «если мы, отвлекаясь от текущего времени, рассмотрим в данный момент какую-либо механич. систему, находящуюся в движении (или равновесии), то алгебраич. сумма бесконечно малых возможных работ всех действующих на систему сил—со включением сил инерции для случая движения—равна нулю». Бесконечно малой возможной работой какой-нибудь силы Р называется произведение Р*<5р. где δρ—возможное перемещение точ щ прило кения силы по линии действия Р, или проекция возможного перемещения ds на направление силы, то есть Р · δρ=Р · ds · cos (5, Р). Но возможное для дан ного момента перемещение не есть действительное перемещение за бесконечно малый промежуток времени, текущий за данным моментом: математич. маятник, длина которого допустим явно изменяется во времени, имеет возможным перемещением элемент дуги окружности определенного для данного момента радиуса, действительное же перемещение вследствие изменения радиуса совсем не будет элементом этой окружности. Итак, когда условия системы явно зависят от времени, действительные перемещения могут не лежать в числе возможных для данного момента; для этого случая δρψ dp.Что касается сил инерции, то по второму принципу Ньютона сила в направлении движения какой-либо точки, потребная для изменения скорости V, будет ~ (mv), и, не выходя из рамок механики Ньютона, мы можем считать массу переменной (Мещерский, Эйнштейн, де-Бройль). Следовательно сила инерции в направлении движения точки равна—(mv). Проекциями ее на оси X, Y, Z будут ™ (mv)J cos (v, х) ит. д., но ^ (mv)J cos (v, х)=v ^cos (v,a?)-f-

. (dv, v dm, av_T d, ₄

^+mUt) ^cos(»>^ж) ⁼ di^+^w-df=di^иT·^д· Поэтому, считая, что работа результирующей равна сумме работ слагающих, и разложив силы по осям X, Υ,Ζ, получим выражение принципа возможных перемещений:

2 - [It (^m»x) ·^δχ +4t (^m + ж 0»г>₂и“] +

+ 2 ΙΧδχ + Ydy + Zbe=0,

и например если мы имеем одну свободную точку, то есть если δχ, δ у, δ z произвольны, то получим ур-ия ее движения, приравняв каждый из множителей при δχ, δρ, δ z нулю:

- Tt (^mv*⁾ + -X=0 и T. д.

Теперь обычно пользуются принципом Гамильтона, то есть тем же принципом возможных перемещений, только в другой форме [*], поэтому мы не будем на нем останавливаться. Мы должны поставить здесь вопрос: в каком отношении механика Ньютона стоит к принципу сохранения энергии, являющемуся основным для Т. и для всей теперешней физики. Мы должны ответить: механика этого принципа не имеет, она имеет лишь принцип живых сил. Если условия системы явно от времени не зависят, то действительные перемещения лежат в числе возможных, можно положить δp=dp и тогда имеем

2 (mv_x) dx +. - dx+Y dy 4 Zdz)=0. Если силы имеют потенциал, то×dx- -Y dy-f-

Ч-Z dz=dF; далее ~-_t (mv_x) dx=v_x ~ (mv_x) dt =*

=v_xd(mv_x) и следовательно v_xd(mv_x)^jrv_yd(mv_y)~ -+ v_zd(mv_z)={vl+vl+vf) dM+m(v_xd*v_x+VydVy-j-+ v_zdv_z)=v^%dm + mv dv=d(mv²) — mv dv.

Если положим массу зависящей φτ скорости, то ш — /(v) и mv dv можно положить равным dd>(y), где Φ(ν) — ff(v) dv, тогда получим Σ [d(mv^z) — dO(v) — dF]=0; интегрируя, имеем Σ [mv* — Φ(ν) — F]=Const. Когда масса от скорости не зависит, то άΦ=·

= mv dv=~ d(mv^z), тогда^ (лр — -£^=Const— обыкновенное уравнение живых сил. Назовем

ΥΥΙΌ2 с. _Λ Т-.Ч

у- кинетич. энергией, h{—F)—потенциаль-

Фигура 1.

ной энергией, тогда имеем: если условия системы явно от времени не зависят и силы имеют потенциал, то сумма кинетической и потенциальной анергий системы остается постоянной за все время движения. Элементарным примером может служить движение гармонич. маятника. Здесь (фигура 1) точка А двигается из А₀ под действием силы из точки О, *сила представлена на диаграмме прямой Οα_γα. В положении А_г точка А имеет ки-нетич. энергию, изображаемую площадью^ аа_гА_ъ и потенциальную,—А_га_гО. Сумма их равна постоянной величине А₀аО за все время движения точки. Если масса зависит от‘ скорости, например т=-β===. > у с2—и²

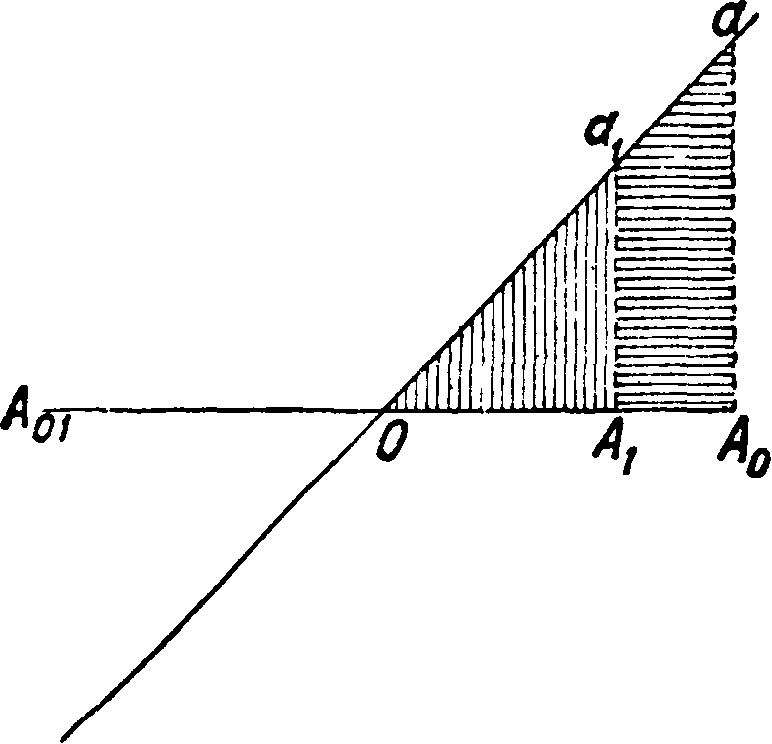
где т₀—масса покоя, ν—скорость точки и с—скорость света [это выражение у де-Бройля (de BiogLe) м. б. получено независимо от теории относительности [*]], тогда

άΦ(ν)=f(y)v dv =,

Vc*-v²

Φ(ν)=— m₀cj/c² — ν², mv³ - Φ(ν)--У°^са·.

K-S

Следовательно

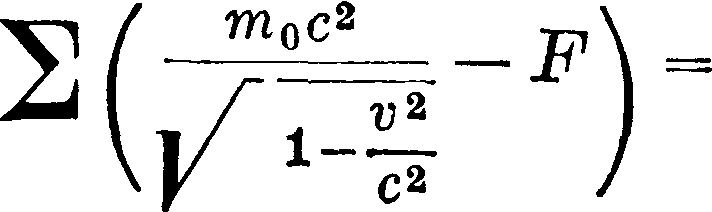
Интерпретация остается та же. Но возьмем движение точки А (гармонич. маятника) с трением постоянной величины, тогда известно, что максимальная кинетич. энергия точки А будет постепенно убывать и точка остановится в т. н. области равновесия. Это хорошо иллюстрируется чертежом, аналогичным фигура 1. Но механика не ставит и не может, выходя из своих ур-ый, поставить вопрос, куда же девается энергия. Она может ответить на это: на работу преодоления силы пассивного сопротивления. Такой ответ с теперешней точки зрения неудовлетворителен. Мы должны найти в чем-то эту исчезнувшую энергию и находим ее в тепле, но уже совершенно выходя из рамок механики Ньютона. Поэтому заранее видно, что все попытки свести опять тепло на движение, описываемое Ньютоновой механикой, не могут иметь успеха, т. к. опять мы встретимся с теоремой живых сил, являющейся лишь частным случаем принципа сохранения энергии, и должны будем опять вводить силы междумо-лекулярного трения и т. д. Но, принимая по принципу сохранения энергии, что видимое исчезновение энергии есть просто переход ее в тепло, мы должны поставить вопрос: оценивая механич. энергию кгм, а тепло—Cal, какое соотношение имеем мы между калорией и килограммометром и от каких условий перехода механич. энергии в тепло или, обратно, тепла в механич. энергию зависит эта оценка.

Принцип эквивалентности. Поставив этот вопрос на основании принципа сохранения энергии, мы можем конечно получить ответ на него лишь из опыта, и ответ формулируется так: при всяких условиях перехода" механич. энергии в тепло и обратно 1 Cal оценивается в 427 килограммм (калория здесь 15°, большая). Это есть принцип эквивалентности, впервые сформулированный Робертом Майером [*]. Как известно, принципы Т. были намечены в общих контурах Ломоносовым, но его попытка не обратила на себя внимания ученых, как это часто бывало и с другими великими начинаниями, и лишь в 19 веке принялись за подробную разработку задач Т. Не нужно думать, что принцип эквивалентности есть лишь следствие принципа сохранения энергии. Попытки доказать непосредственно из принципа энергии одинаковость оценки калорий при всяких условиях основаны на скрытом предположении возможности обратить всякий процесс перехода работы в тепло и тепла в работу. Обратимость эта в действительности может и не существовать. Поэтому принцип эквивалентности нужно рассматривать как самостоятельный опытный принцип. Известно, что Роберт Майер определял эквивалент из соотношения между теплоемкостями для так называемым совершенных газов. Теплоемкость ср при постоянном давлении всегда больше теплоемкости c_v при постоянном объёме. Следовательно можно по принципу сохранения энергии написать для 1 килограмм газа: разность между с_р и c_v эквивалентна работе газа, в первом случае выражающейся в преодолении внешнего давления Р кгм~² и равной и молекулярного сцепления при расширении газа равной Ь₂, т. e. Е(с_р—a_v)=L₁4-L₂, где Е—оценка Cal в килограммахм. Допустим, что гае заключен в цилиндр с поршнем F m^z, тогда L₁=p-F(h₁—h₀)=p-(v₁- v₀), где v₀ и v_x—на-* чальный и конечный объёмы газа; работой L_zможно пренебречь на основании опытов Гей-Люссака, и тогда E (c_p—c_v)=р(^₁— Ч>), но для совершенных газов pv₁=RT₁, pv₀=RT₀ и, т. к. Т_х—Т₀= Г, получим L_X=R, т. о. Е{с_р— —c_v)=R для всех совершенных газов, то есть следующих уравнению Мариотта-Гей-Люссака; можно непосредственно проверить на аргоне, гелии и т. д., что число Е близко к данному выше. С другой стороны, всякое отступление от соотношения Майера указывает на то, что газ не м. б. признан за совершенный, то есть находится не так далеко от области своего ожижения, как нужно для того, чтобы удовлетворить соотношению pv=RT; например для углекислого газа соотношение

E (c_p-c_v)=427 (с_р- с„)=В

не удовлетворяется в достаточной мере хорошо, E (Cp—c_v) в этом случае равно 21,35, между тем R=19,25, для гелия же E (с_р—c_v)=20,9 и R=21,2 (согласие хорошее), для азота—30,3 и R=30,2 и т. д. Для углекислого газа нельзя уже пренебрегать работой молекулярного разъединения, или т. н. дисгрегации, и уравне-ьие pv=RT не представляет достаточно хорошо зависимость между р, ν, Т. Для подобных тел считаются с тем, что в видимом уд. объёме заключен еще объём совокупности находящихся в нем молекул; этот последний не изменяется и если обозначить его через b, то изменению подлежит ν— b (Д. Бернулли); затем кроме внешнего давления считаются еще с силами сцепления, действующими на молекулы, находящиеся на поверхности объёма, со стороны молекул, находящихся внутри. Эти силы можно принять зависящими от объёма и от £°, поэтому вместо р будет в ур-ии р+/(Т, ν) и ур-ие примет вид:

[р + КТ, ν)](ν -Ь)= RT.

К этому роду принадлежат ур-ия Ван-дер-Ваальса, Клаузиуса и др. Далее будет показан термодинамич. прием составления ур-и£ по опытным данным.

Первое основное уравнение“ Т. Всякое тело, подвергающееся действию тепла, изменяет свое состояние. Изменение состояния тела характеризуется изменением параметров р, v, Т. Между ними, как мы видели, можно представить зависимость в виде ур-ия, называемого характеристич. ур-ием. Не всегда конечно мы можем измерить эти параметры дмя всего видимого объёма тела, т. к. в различных местах видимого объёма эти параметры м. б. различны, например воздух или пар, вытекающий из резервуара с высоким давлением, не имеет для каждого момента одинакового давления во всей своей массе, в нем существуют сгущения и разрежения, но при. испытании поршневого двит гателя мы считаем, что давление, показываемое индикатором, относится ко всей массе под поршнем. В первом случае скорость внешнего движения- сравнима или даже превышает скорость распространения упругих колебаний (скорость звука), во втором мала сравнительно с ней. Ряд изменений состояния тела мы называем процессом и потому разделяем процессы на быстрые и медленные. Вторые м. б. изображаемы графически в координатах v, р или Т, v или Т, р; по двум данным на изображении процесса параметрам мы находим третий, зная Характеристич. ур-ие тела. Обычно в изображениях предлагается 1 килограмм тела (иногда 1 г) и удельный объём. g Координаты ν,ρ имеют то преи-^ мущество, что внешняя работа тела за время процесса АВ изображается площадью АВbа (фигура 2), т. к. бесконечно малая работа дается выражением pdv, в чем нетрудно убедиться, если представить себе те-а и ло, заключенное в неко-

_фиг< 2. торый объём (везде на по верхности и внутри давление для данного момента р), и дать объёму измениться на dv=£_idF-dh, где dF—элемент поверхности объёма, a dh—расстояние по нормали, между начальной и измененной поверхностью объёма. Теперь мы можем применить принцип энергии и принцип эквивалентности для участка АВ этого медленного процесса. Пусть здесь участвует тепло в количестве Q Cal, тогда мы напишем: EQ=работе изменения состояния тела на пути АВ-f внешняя работа, которая изобра кается площадью аАВb (эта площадь разумеется дает кгм, так как давление дается в килограммах/м², а объём— в м³). Работа изменения состояния тела называется изменением внутренней энергии; относительно ее можно сказать, что она выражается в работе молекулярного разъединения (дис-грегации) и в изменении t° тела. Последнее может происходить и без видимого изменения объёма; при v=Const мы тратим для повышения t° тела известное количество тепла, что равноценно работе. Положим теперь, что между состояниями А и В произошел другой процесс АС В, количество тепла Q, здесь участвующее, будет уже другое по ур-ию эквивалентности, т. к. внешняя работа—другой величины, но под вопросом стоит изменение внутренней энергии. Когда господствовало механич. воззрение на тепловые явления, тогда говорили, что вну тренняя энергия в своем изменении состоит из двух частей: работы дисгрегации и изменения живой силы молекул; последнее принималось пропорциональным изменению t°. Силы между молекулами считались имеющими потенциал и тогда разумеется выводилось положение, что внутренняя энергия в своем изменении не зависит от промежуточных стадий процесса, а только от начального и конечного состояний системы, т. ч. изменение ее по АВ или по АС В одинаково. Но мы уже видели, что механика даже не имеет принципа энергии, не имеет и понятия t°. Совершенно произвольно и не соответствует фактам принимать t° пропорциональной живой силе молекул. Далее всегда ;с точки зрения механики м. б. поставлен вопрос о существовании силы междумолекулярного трения, работа которой будет несомненно зависеть от путей, пройденных молекулами, то есть от вида процесса. Т. принимает положение о зависимости изменения внутренней энергии только от начального и конечного состояний тела и независимости от промежуточных стадий, но как положение, подтверждаемое опытом. Для совершенных газов, как мы видели, можно принимать работу дисгрегации равной нулю; для них внутренняя энергия, нагреваем ли мы газ при постоянном давлении на 1° или при постоянном объёме на 1°, одинаково изменяется. Следовательно ее нужно считать зависящей только от t° и тем самым независящей от того, каким процессом t° изменилась. Для других тел внутренняя энергия является ф-ией и t° и объёма (или давления), но как ф-ия определенная она в своем изменении зависит только от начальных и конечных значений параметров Т и v (или Тир). Поэтому для бесконечно малого медленного процесса мы имеем ESQ==dU- -p dv; здесь U—f(T, v)—внутренняя энергия, a SQ—бесконечно малое количество тепла в процессе, знак <3 поставлен в отличие от знака d, указывающего на диференциал от ф-ии (или независимого переменного), количество же SQ не есть диференциал ф-ии, т. к. оно зависит от частностей процесса. Если положить |г =И=

= термич. эквиваленту работы и считать, что внутреннюю энергию мы выражаем в Cal, то ур-ие примет вид SQ=dU -f Ар dv — первое ур-ие Т. для однородного тела, совершающего медленный процесс. Для процессов быстрых по принципу энергии мы можем написать SQ=dU + ASL + AdW; здесь опять A3L—бесконечно малая (в Cal) работа преодоления внешних сил и AdW—приращение внешней кинетич. энергии. Оба ур-ия несовместимы, то есть нельзя совместно пользоваться и тем и другим: первое является лишь частным случаем второго, когда количеством dW можно пренебрегать. Тогда, и только тогда“ работу можно выразить через р dv, т. к. давление во всей массе тела можно считать одинаковым для каждого мо-чмента. Одновременное же пользование ими (как это иногда бывает) может привести только к скрытому или явному противоречию с принципом энергии, то есть к получению энергии из ничего. Для медленных процессов можно дать другое выражение для SQ. Можно всякий бес-

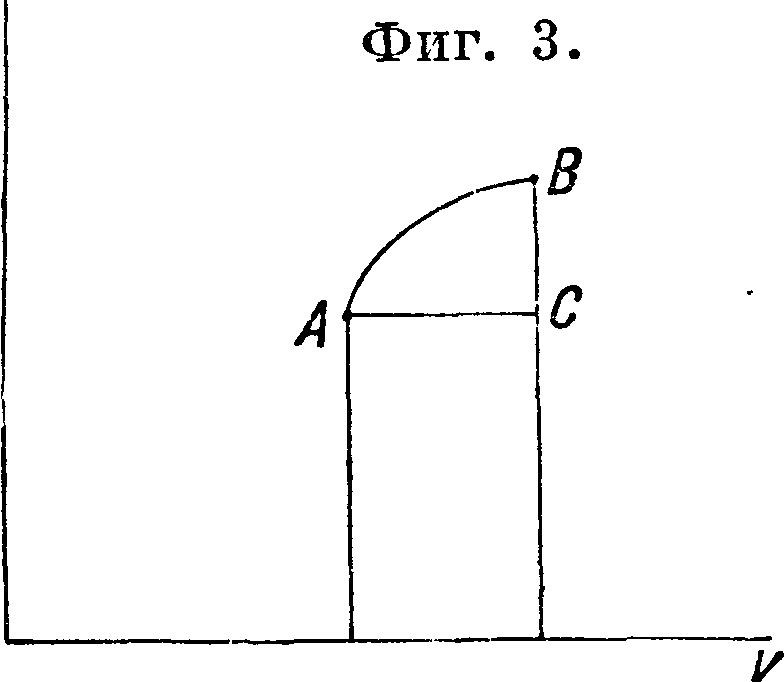
конечно малый процесс АВ заменить процессами АС (фигура 3), где р=Const, и СВ, где v=Const, и если на АС участвовало тепло dQ_±, на СВ—δQ₂, а на АВ—3Q, то можно положить SQ — 3Q_l- -dQ₂, т. к. внутренняя энергия изменяется одинаково на процессе АС В и АВ; во внешней работе разница будет лишь на площадь АСВ, являющуюся уже малой второго порядка, но SQ_l=c_pdT_AC, <5Q₃=b/1Т_пв, где с,

и c_v—теплоемкости и dT_AC=_dOdv(p=Const), dT_CB=^ dp(v=Const). Следовательно

<5Q=Op |f dv + c_v Ц dp=dU + Ap dv, отсюда

^dU= {^ύρ^, ~ ^Ap) ^dv + ^cv%^dp.

Для совершенных газов дТ _ jp. dT^v_ V _л _ JP

aw R ’ dp R’ R R

T. e.

dU=^ (p dv-v dp)=c£T,

что можно было и прямо видеть. Выражение dU указывает, что c_v для совершенных газов является функцией одной только £°,так же по равенству Майера и с_р. Если этого у какого-нибудь газа нет и c_v или с_р зависит и от t° и от давления (или объёма), то ур-ие pv=RT для него уже не годится, и работой дисгрегации пренебрегать нельзя. Для какого-нибудь тела вообще можно положить U=f(p, v) и тогда

^dU= Щ ^dP + Ш ^dv=(^С»И - + ^с» Ipdp>

то есть

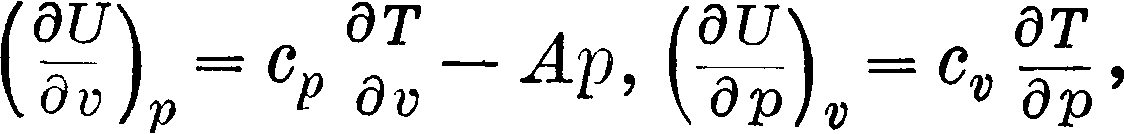
и вследствие того что

_а_ ат ₌ _д_ (ди

dp dv) ~ dv др ) ’

имеем

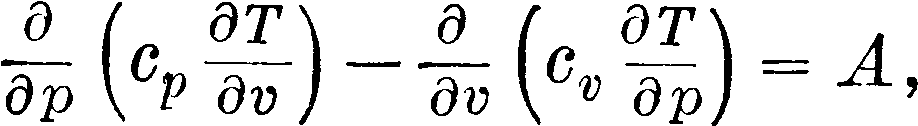
обобщенное соотношение Майера для всякого однородного тела, определяемого в своем состоянии параметрами p, v, Т. Из соотношения для внутренней энергии газа dU=c_v dT получим U=С7₀ + $ c_v dT; положим c_v (как функцию Т) равной

^Gv₀ + clT -f- βΤ* +,

тогда и=Ε7„ + c_VoT + I T² + I T* +.

По механич. толкованию следовало бы, что внутренняя энергия газов сводится к живой силе молекул. Если это принять, то из выражения для U видим, что никакой пропорциональности между t° и живой силой молекул не существует и следовательно, как и было указано, механика бессильна дать определение для t°. Опыт и указывает на зависимость для совершенных газов теплоемкостей от t°. В приложениях обычно полагают cv= cvo+aT, также Ор=Ср₀ + аТ, коэф-ты при степенях Т и в c_vив с_р должен быть одинаковы по соотношению Майера.

Разделение процессов. Второй принцип термодинамики. Процессы мы разделяем на быстрые и медленные. Но их можно разделить на обратимые и необратимые. Если, совершив какой-нибудь процесс с телом, мы можем обратно привести тело в начальное состояние теми же стадиями, но только в обратном порядке, мы называем процесс обратимым; если этого сделать нельзя,—необратимым. Все быстрые процессы явно необратимы: процесс истечения из резервуара с высоким давлением нельзя обратить, но процесс медленного нагревания, наир, при постоянном давлении, обращается в процессе медленного охлаждения при том же давлении. Поэтому первым условием обратимости является медленность процесса, вторым условием—неизменяемость физич. характеристик тела во время процесса, то есть зависимости между p, v, Т и зависимости с_р и от (p, Т) или (v, Т) или Т. Если почему-либо“ на прямом процессе вдруг изменилась зависимость между p, v, Т, то на обратном процессе под теми же давлениями и объёмами мы можем и не получить тех же t°, если не происходит-обратного внезапного изменения зависимости между p, v, Т. Точно так же изменение характера теплоемкостей может дать на обратном пути другие по абсолютной величине изменения внутренней энергии, хотя внешняя работа по абсолютной величине будет та же самая. В обратимом процессе мы всегда имеем: SQ=dU- -Ap-dv или в конечном виде Q=U₂— — U^AL, где L—внешняя работа за конечный процесс. На обратном процессе меняются знаки и у внешней работы, и у изменения внутренней энергии, и у тепла, абсолютные же величины остаются теми же самыми. Для необратимого процесса имеем: SQ=dU+ ASL-{-+AdW или в конечном виде Q=U₂-U₁- -4-AL- -A(W₂—W₁). Мы можем из ряда процессов (обратимых и необратимых)^ составить замкнутую цепь, или цикл, и для него написать. Σ©= U₂—Пх+ДЬ+Д (W₂— ¥_г). Но так как по» условию тело возвращается в начальное состояние, то U₂=U₁ и W₂=Wi, следовательно^ для всякого цикла имеем ^Q-AL, то есть для цикла алгебраич. сумма участвующих в нем теплот есть эквивалент внешней работы. Всякая правильно действующая калорич. машина в идеале должна своим рабочим телом (паром, газом и т. д.) совершать цикл, потому что-1) всякая машина должна работать правильно» периодически, 2) выбрасывание отработавшего» тела и замена новым представляет излишнюю“ потерю. Паровая машина с конденсацией в этом отношении ближе к идеалу, нежели двигатель внутреннего сгорания. Но и в последнем можно усмотреть приближенный цикл, если обратить внимание на то, _рчто главным по весу телом, входящим в состав смеси воздуха и горючего, является азот, а он химически не изменяется. Поэтому мы можем считать, что калорич. машина совершает своим рабочим телом цикл.

И здесь главный вопрос: может ли термин, кпд быть равным 1? Всякая машина, действующая одной механич. энергией, уменьшением трения * то есть потерь на тепло, мол-сет приближаться в своем коэфициенте использования к 1. Можем ли мы и для тепловой машины уменьшением вредных потерь тепла иметь то же самое? Можем ли мы в цикле тепловой машины избежать в идеале тепловые потери во внешнюю среду и только давать тепло рабочему телу исключительно на работу? Представим себе обратимый процесс АВ (фигура 4), здесь со

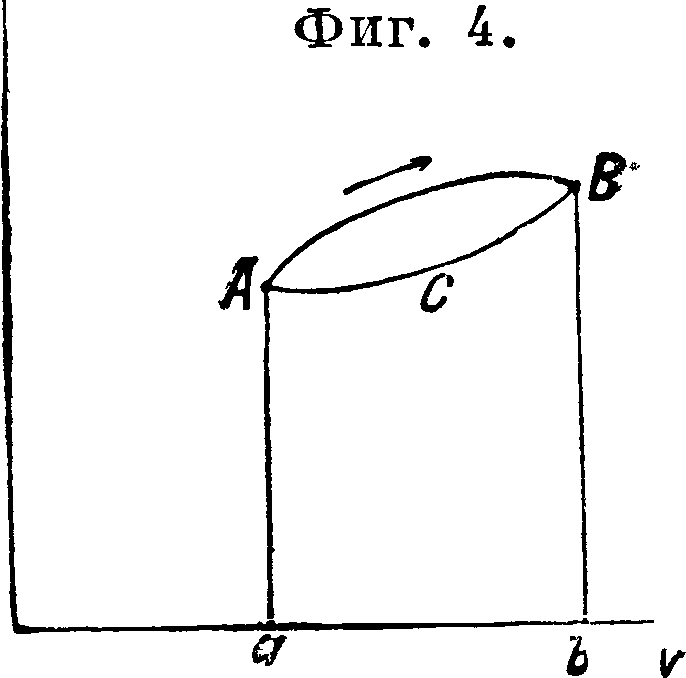
вершается положительная внешняя работа (dv>0) величиной аАВb, участвует некоторое количество тепла Q, изменяется выутрейняя .энергия. Пусть теперь мы имеем процесс ВС А, на который тратим работу (dv< 0) величиной аАСВb, отнимаем от тела тепло и возвращаем внутреннюю энергию в начальное состояние. Тогда имеем £tQ=AL=A-площадь ABCA—Q—Qi. Тепло Q_t бесполезно отдано во внешнюю среду. Можем ли мы его в идеале .положить равным 0? Если бы на процессе ВС А не участвовало тепло, то это было бы возможно.

Процесс, происходящий без участия тепла, называется адиабатическим, и его уравнение «есть 0----dU+Ap dv, из которого видно, что при •затраченной на этот процесс работе (dv<0) внутренняя энергия возрастает, положительная же работа совершается за счет убыли внутренней энергии. -Вопрос следовательно будет такой: можем ли мы из какого-либо состояния тела В привести его в другое какое-либо состояние А путем адиабатным? Адиабатный процесс есть процесс механический, без участия внешнего тепла. Если бы вопрос решился положительно, то между механич. энергией и тепловой не было бы по существу никакой разницы, и из механики мы прямо получили бы учение о тепле. Этого однако нет, и потому вопрос нужно решить в отрицательном смысле (аксиома Кара-Теодори). Но после этого мы теперь должны поставить другой вопрос: в чем эта разница заключается? На это мы должны ответить: разница в том, что тепловая энергия связана с понятием о t°, которого в механике Ньютона нет и к-рое, как мы видим, объяснению механическому не подлежит. О значении t° говорит постулат Клаузиуса: если мы имеем изолированную систему двух тел, теплого и холодного, то невозможен переход тепла с холодного на теплое без затраты энергии. Постулат Клаузиуса утверждает, что не существует такого инструмента, при помощи которого калории, освобождающиеся при замерзании воды, производили бы кипение воды при 100°. Всякое приспособление этого рода требует для своего действия затраты внешней работы, следовательно калории при 0°, хотя бы их было неограниченное число, бесценны для работы калорич. машины, если окружающая среда и рабочее тело имеют t° выше 0°. А между тем калории эти все-таки оцениваются каждая в 427 килограммм работы. Т. о. механич. оценка калории ничего еще не говорит о возможности работать этой калорией в калорич. машине для получения положительной внешней работы. Нужно каким-либо образом повысить t° этой калории. Это происходит наир, при химич. взаимодействии двух тел, где внутренняя энергия компонентов обращается в калории высокой t°, чем мы и пользуемся, •создавая условия для этого соединения, наир, в машине Дизеля—работой. Но устроить тепловой рычаг, к-рый не требовал бы никакой энергетич. затраты на себя, нельзя по постулату Клаузиуса. Тем не менее ни постулат Клаузиуса ни аксиома Кара-Теодори не решают вопроса о возможности или невозможности получения кпд в калорич. машине равным 1. Мы можем представить себе другой процесс— постоянной Г. Здесь тело может брать тепло от источника той же t°; это не противоречит постулату Клаузиуса. При обратном изменении оно может отдавать тепло тому же источнику— спять не будет пр.отиворечия. Этот процесс ^является вполне обратимым, то есть не только по отношению к телу, но и по отношению к тепловому источнику, питающему этот йфоцесс. Теперь допустим, что для какого-нибудь тела адиабатный процесс AJDB имеет для двух своих точек А и В (фигура 5) одну и ту же t°. Проведем

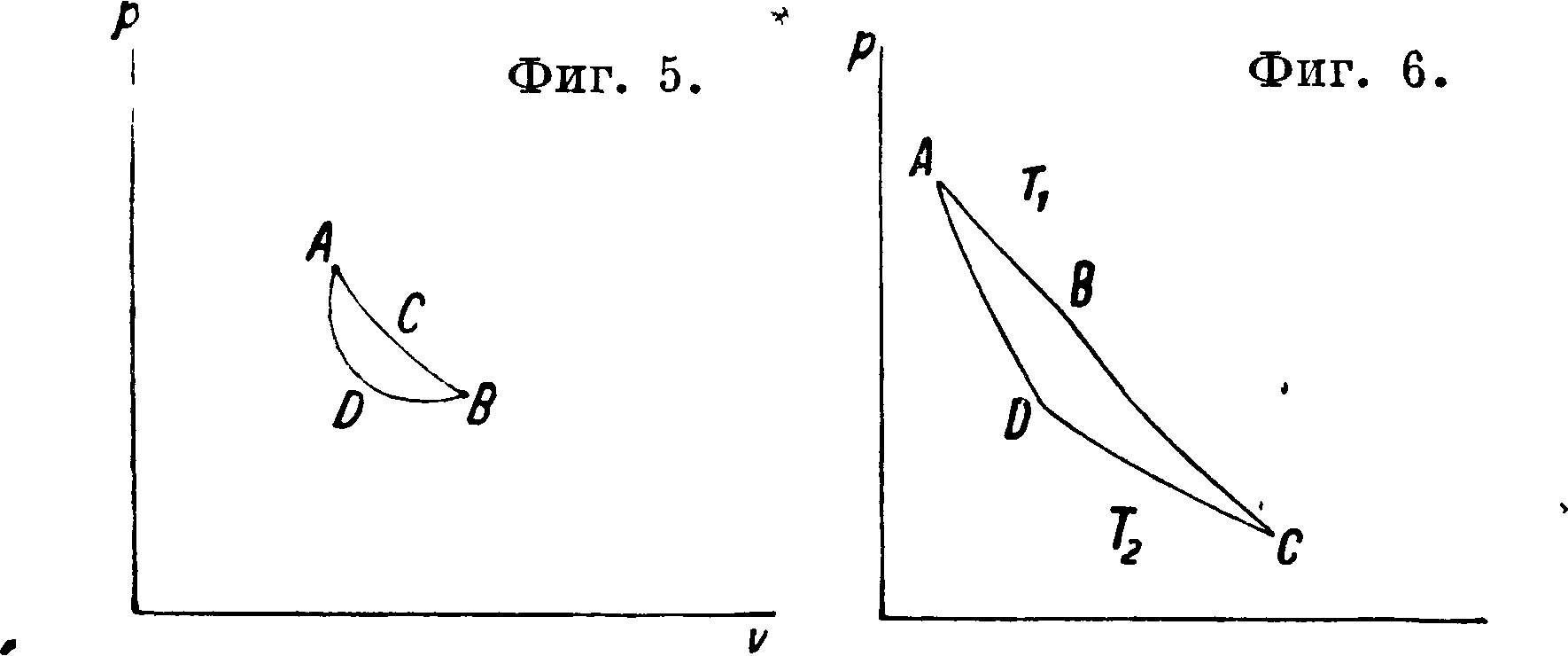
через эти точки изотерму АСВ, и тогда несомненно получаем цикл ACBDA с коэф-том, равным 1. Может ли это быть? Для решения этого вопроса предположим обратное, то есть что существует в природе тело, у которого адиабата не имеет двух точек с одинаковой ί°, и далее, что для такого тела изотермы не пересекаются. Для такого тела, если оно существует, мыслим замкнутый никл из двух изотерм и двух адиабат. Этот цикл будет вполне обратим и по отношению к рабочему телу и по отношению к участвующим здесь источникам—теплому с t° Т_г и холодному с t° Т₂. В случае процесса АВС В А (фигура 6) мы получаем положительную внешнюю работу, причем от источника Т_г взято было тепло Q_x Cal, источнику Т₂отдано Qa Cal и Q₁—Q₂ == А · площадь ABCDA. В случае процесса ADCBA у источника Т₂взято Cal, источнику Т_х отдано QiCal, что произошло за счет тепла Q₂ и добавочной внешней работы АВСВА. Следовательно в этом цикле мы по произволу можем или получать положительную работу или отдавать калории теплому телу за счет калорий холодного и добавочной внешней работы. Это и есть цикл Карно. Теперь только мы можем сказать, что если цикл Карно мыслим хотя бы для одного тела природы, то не может существовать ни одной калорич. машины с использованием тепла большим, чем в схеме Карно, при одинаковых для той и другой машины тепловых источниках. Действительно мы всегда можем представить себе машину Карно одинаковой мощности с данной машиной и обратить машину Карно. Тогда если данная машина выгоднее машины Карно, то она берет меньше, чем машина Карно, тепла у теплого источника и отдает меньше холодному. Спарив данную машину с обратной машиной Карно, мы в результате брали бы нек-рое количество тепла у холодного источника (-[-машина—Карно) и отдавали теплому (-машина-}-Карно), а работы извне на это не потратили бы, т. к. спаренные машины представляли бы собой простой инструмент, не дающий во-вце работу, но и не требующий ее. Это противоречит постулату Клаузиуса.

Иногда возражают, что в действительных тепловых двигателях происходит химич. процесс сгорания и доказательство с источниками никакой силы не имеет. Возражение это имело бы некоторое основание, если бы термодина-мич. принципами нельзя было охватить химич. взаимодействия, как механикой Ньютона нельзя охватить тепловые явления. Но здесь дело происходит как-раз наоборот: Т. дала мощный толчок к развитью физич. химии. Во-вторых, можно представить себе процесс Дизеля например спаренным с обратной машиной Карно той же мощности и между теми же Р, но меньшего кпд, и получить опять нагревание теплого источника машины Карно холодильником, общим у Карно и у Дизеля, без затраты дополнительной энергии. Поэтому нет надобности останавливаться на этих когда-то часто практиковавшихся возражениях против принципа Карно и постулата Клаузиуса.

Теперь далее таким же путем мы докажем, что если машины Карно мыслимы для нескольких тел, то кпд процесса Карно прц одних и тех же источниках тепла не зависит от природы рабочего тела. Далее если процесс Kapfio мьь слим для одного тела природы, то ни у одного тела природы не м. б. двукратного пересечения адиабаты с изотермой, не м.‘ б. пересечения адиабат, не м. б. касания адиабаты и изотермы, не м. б. замкнутого процесса с положительной работой и одним источником тепла (принцип Томсона).Но процесс Карно не только мыслим, но и м. б. осуществлен. Поэтому все заключения будут универсального характера, пока не опровергнут постулат Кдаузиуса. Так. обр. второй принцип Т. формулируется двумя положениями: 1) не существует процесса калорич. машины при данных t° двух источников (нагревателя и холодильника), более выгодного, чем процесс Карно, и 2) кпд процесса Карно не зависит от природы рабочего тела. Особенно важным является второе положение. Это значит, что в выражении кпд цикла Карно не может стоять ни объём ни давление, т. к. тогда неизбежным являлся бы вопрос: объём какого тела? Коэф. процесса Карно может зависеть только от того параметра, к-рый является общим у тела и источников тепла, то есть от t° источников. Поэтому для вывода выражения коэфициента возьмем уравнение в общем виде для газообразных тел lp + f(v, Т)] (v — b)=RT. Оно м. б. сведено к виду р (V — b)=RT — f(v, Т) (v—b). Т. к. участвуют теплоты Q₁ и Q₂, то кпд будет

„_ АТ _ Qi-Q-г _ -i _Q2

Qi ~ Q i Qi

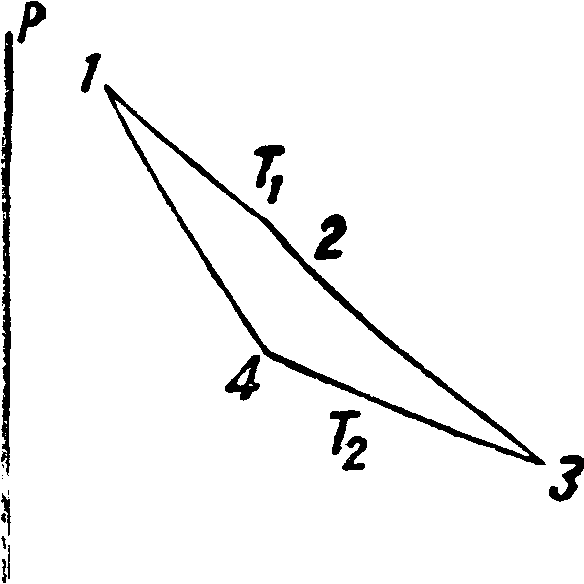
Тепло по изотерме Т_г (фигура 7) связано соотношением Q_x=U₂-U₁- - AL, так же Q₂=U₃ —

Δ 3

• U₄ + AL₂, работα= f p dv, L₂=J p dv, но

L_l=RT₁f f(v,T,)dv, 1

l₂=rt₂ ln - f («, T_t) dv,

4

следовательно

Λ Q 2 _

Qi

-1-

[^{A In T}*> ^d”^{+ ч}шг]

[

A ln

2 А П i HT₁J

f{v, T_±) dv +

U*-U i

UT,

]

T. к. v не может входить в кпд и т. к. v входит в выражение внутренней энергии несовершенного газа, то для всех тел, представляемых дан ным выше ур-ием, должен быть соотношение в четырех точках пересечения адиабат с изотермами

U3 — U4, А т~» 1 „ (У—Ь) 3

-ψ;Ι Uv,T₂) dv =

= AR ln

и кпд цикла Карно η=1 — ~·. Можно было прямо получить его, взяв ур-ие для совершенных газов. Совершенные газы отличаются только отсутствием сил сцепления, но та или иная сила сцепления не может повлиять на выражение кпд по основному свойству процесса Карно. Т. о. для цикла Карно имеем

1_^=1-Qi

Здесь Q₂ взято по абсолютной величине, так же и Q_±. Т. к. при обратном цикле Карно Q_x < 0 и Q₂ > 0, то общее алгебраич. соотношение для прямого и обратного циклов будет ~ + |^=0,

т.	Q 2	т2	тттттт Ql Q2
Тг	ИЛИ ~~ — Ч i	Τι	ИЛИ 7~ — 7гГ-i 1 1 2

из которого ясно, что если одно тепло положительно (дается рабочему телу), то другое отрицательно (отнимается во внешнюю среду).

Теорема Клаузиуса. Энтропия. Тепловые диаграммы. Для какого-нибудь замкнутого процесса вообще можно считать, что он происходит под влиянием нескольких источников различных темп-p Т_г, Т₂, ., Т_п с тепло-тами Q_l9 Q 2,., Q_n, участвующими в этом процессе. Соотношение между теплотами и t° можно вывести т. о. (К. Нейман). Представим себе между каждыми двумя источниками цикл Карно такой, что тепло одного источника, участвующее в процессе, равно и противоположно теплу, участвующему в цикле или циклах Карно, наир, первый источник (какой угодно) участвует в процессе теплом Q_l9 а в цикле Карно q!,тогда наложим соотношение Q₁ + q_llL=>

= 0, далее теперь для Карно=0, чем определяется q_2l, затем для второго источника, участвующего и в первом и во втором циклах Карно,.

©2 + #21 + #22 ^— 0

и для второго цикла 0, чем опреде ляется #₃₂, и т. д. Очевидно, что на последний п-й источник мы уже условия на его теплоты наложить не можем и он участвует теплом Qn + #ю ог-ι) ^{и в} процессе и в последнем цикле Карно. В сложном этом процессе £(Q + #) обратится очевидно в Q_n + #_w(rt_₁₎. Разделив каждое из равенств

Ql + #11 ⁼ 0, Q2 “1“ #21 + #22 ⁼

Q* + #32 + #33 ⁼ 0? ···

соответственно на Т_г, Т₂, Т₃ и т. д., сложив все равенства, прибавив к обеим частям сложного равенства по _и приняв во внимание соотношения Карно, получим

Σ

Qn

Тп

Qn+ Qn(n — 1)

кроме того имеем

Id (Q + #)=AL=Q_n 4- qn(n-1)·

Прабая часть равенства не м. б. положительной, т. к. это значило бы, что весь сложный замкнутый процесс произошел лишь за счет одного (п-го) источника и была получена положительная работа AL, чего, как мы видели_х

быть не может, следовательно мы имеем ^<0

для всякого замкнутого процесса, причем здесь Т—темп-ры источников. Если процесс состоит только из обратимых частей, то в виду его медленности можно считать, что на бесконечно малом отрезке t° тела является определенной для всей массы рабочего тела и что этот бесконечно малый отрезок процесса совершен под влиянием источника, имеющего ту же (с точностью до малых второго порядка) t°, что и тело. Тогда за Т в неравенстве можно считать t° тела и в виду бесконечного множества источников вместо Q взять SQ и вместо ,суммы интеграл, распространенный на весь замкну.-

тый процесс, то есть получим Но про цесс обратим, и если его обратить, то все SQ переменят знаки, и следовательно было бы

fi Q

ψ->0ί, но знак «больше» не может иметь места ни для одного процесса, и потому для обратимого замкнутого процесса всегда имеем

~=0 (теорема Клаузиуса). Это есть тепловая характеристика замкнутого обратимого процесса, аналогичная тепловой характеристике процесса Карно. Если мы теперь замкнутый обратимый процесс ABCDA разобьем на две части АВС и CD А, то имеем

ABC CD А

отсюда

Г δζ) Λ ад ₌ Г 6Q

J т Jr J т’

ABC CDA ADC

то есть при переходе тела из состояния А в состояние С каким-либо обратимым процессом J* ~ имеет одну и ту же величину. Это значит, что ^=dS, где S—функция параметров, определяющих состояние тела. Эта ф-ия называется энтропией. Она является вспомогательной ф-ией, имеет, как видно из соотнощения, измерение теплоемкости (то есть калории на кг и 1°) и дает возможность определять тепло во всяком обратимом процессе. Действительно, представим себе координаты S иТ (фигура 8) и изобразим

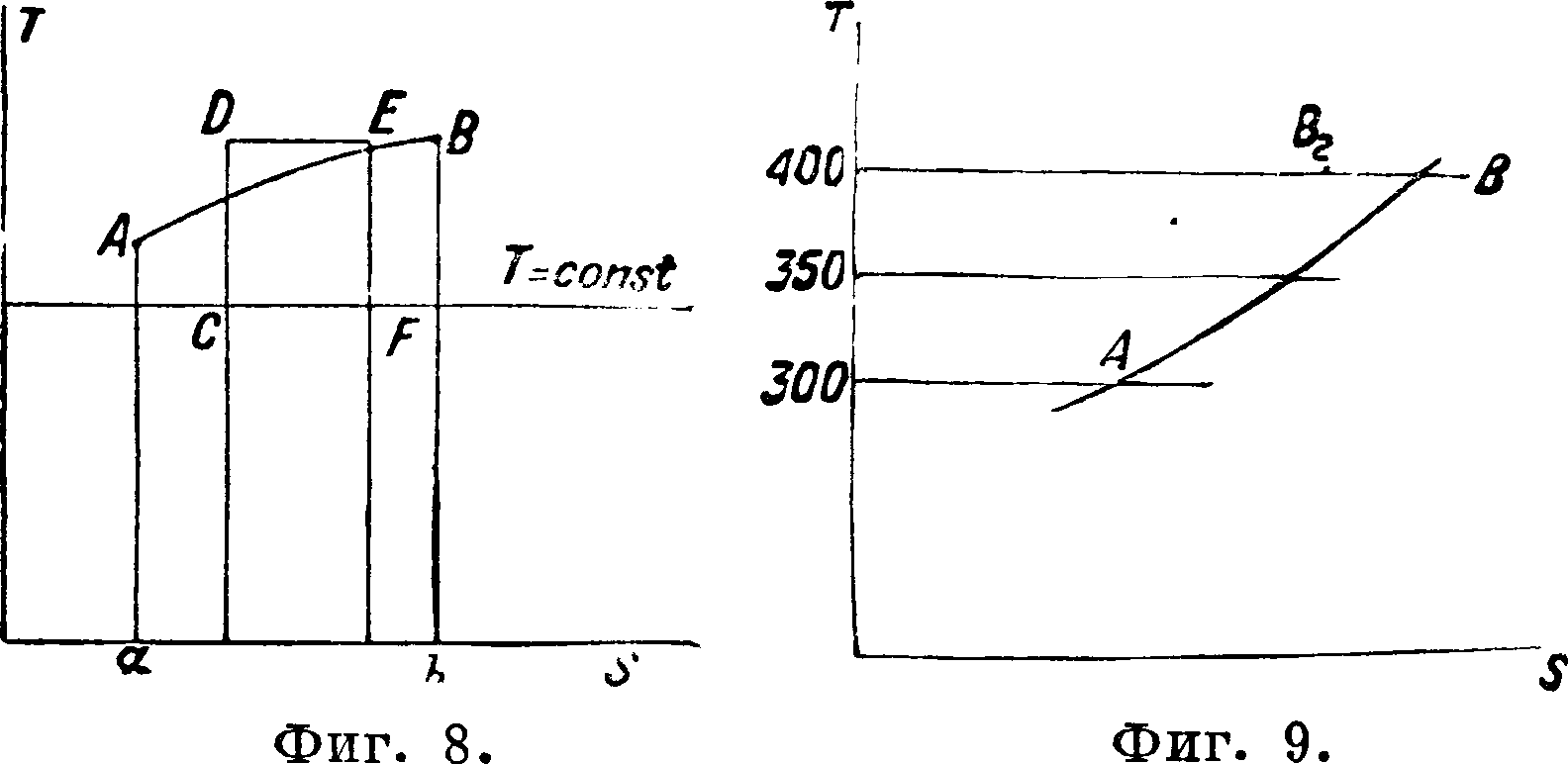
в этих координатах какой-либо процесс АВ; тогда тепло, участвующее в процессе, выразится площадью АВbа по соотношению Q=J Т dS;

изотермы в этой системе координат изображаются прямыми, параллельными оси S (Т=Const), адиабаты—прямыми, параллельными оси Т, т. к. здесь dQ=0 и следовательно dS=О, S— Const, цикл Карно — прямоугольником CDEF. На процессе АВ тело, как видно по диаграмме, получает тепло (dS>0, SQ>0), на процессе ВА (dS< О, <5Q<0) тело отдает тепло во внешнюю среду. Поэтому, изобразив какой-нибудь процесс, извеетный нам из координат V, р, в координатах S, Ту мы увидим не только количество теп ла, в нем участвовавшего, но и знак тепла, что очень важно при исследовании процессов. Предположим, что мы имеем в системе v, р ряд процессов с каким-нибудь совершенным газом, например воздухом; перенесем эти процессы в систему S и Т (фигура 9). Сначала изобразим линию постоянного атмосферного давления. В системе S и Т возьмем на изотерме внешней среды (например Т₀= 300°) точку А и будем считать, что эта точка представляет состояние воздуха при Т₀=300° и р₀=1 atm. Дальше для линии постоянного давления имеем характеристику dQ=c_pdt, допустим, что c_v=c_Pq + aT_rтогда dQ=c_Pq dt + аТ dt,

^r§-~dS=c_Po^f + adT

и отсюда S — S₀=c_Po In + a (T — Т₀). Задав-

шись масштабом для энтропии (например 0,01 Са1/1°=»=2 миллиметров), вычисляем для различных Т (больших Т_с) разность энтр S — S₀ и откладываем их от точки а вправо, в сторону возрастающих энтр, т. к. в этом процессе dQ > 0 при Т > > Т₀. В пересечении ординат, проведенных в этих полученных точках, с соответственными изотермами получаем точки кривой постоянного атмосферного давления. Пусть требуется теперь изобразить состояние воздуха при давлении 2 atm и 400° абс. Проводим изотерму 400° (по масштабу темп-p) до пересечения с кривой р=Const=1^atm в точке В. Эта точка изображает состояние воздуха для р=1 atm и Т=400°; из этого состояния перевести воздух в состояние 2 atm и 400° можно путем сжатия по изотерме, при этом по ур-ию Q=U₂— U₁ + AL имеем (U2=при Т= Const для совершенных газов)

Q=AL= Jpdv=ABT J^-^-ART ln^

и по ур-ию pv=RT для этого случая —=2, то есть

Q=—ART In 2; теперь при Т= Const Q =·=Т (S₂—S_±)=— ART In 2, откуда S₂—S₁== — AR In 2, и, высчитав, откладываем влево от точки В найденную разность энтр. Таким путем переносим из системы V, р в систему S, Т любые точки. Нужно только знать в системе v, р температуры. Но, если известна в этой системе хотя бы одна температура, остальные определятся.*

Предположим, как это бывает на индикаторных диаграммах, нам неизвестно количество газа, участвовавшего в процессе, но известен только его объём и давление, и мы принимаем, что масса его G не меняется за время процесса.

Тогда Gvp=GRT, Gv₁p₁=GRT₁, откуда ~ =

=, и если Т известно, то по отношению давлений и объёмов, читаемых на индикаторной диаграмме, определим Т в любой точке. Нужно только знать мертвый объём в его отношении к объёму, описываемому поршнем, что часто известно по степени сжатия, и далее на индикаторной диаграмме прибавить на линии счета объёмов пропорциональный отрезок. Приложенные здесь диаграмма и таблица объясняют подробности (фигура 10). Нужно заметить, что здесь принималась неизменяемость характера с_р, c_v и R за все время изображаемого процесса и величины эти брались для воздуха; Между тем диаграмма снята была с двигателя Дизеля. Поэтому тепловое изображение лишь приблизительное, но оно дает возможность в общих

чертах судить о тепловом характере процесса, как уже было указано. Общее выражение энтропии для совершенных газов можно получить из ур-ия

dQ dU. Apdv _ c_vdT. ARdv __

T ~ T" T T ¹ v ⁼

^cv₀ + ^aT T

dT +

ARdv

- 9

V

и, интегрируя, имеем:

S — S₀=c_Vg lnf_o + a(T-To) + AR ln^,

или

S-S₀

о(Г-То)

4^ln

T

.To

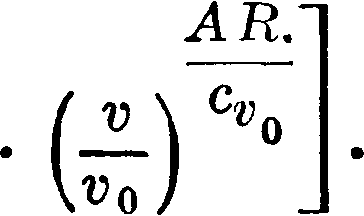
Для одноатомных газов (гелия, аргона) можно принимать c_v=Const=^₀,α=θΗследовательно

S — S₀=c_v In

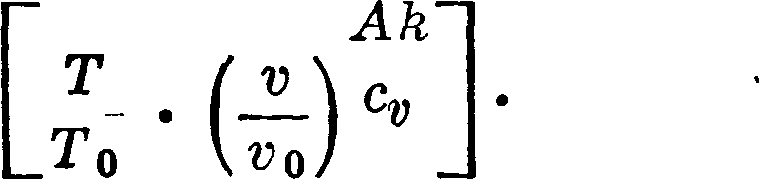
Положив для них &=7с и взяв по ур-ию Май-

c_v

ера с_р — c_v=AR, получим

—=й-1.

Cv

Таким образом

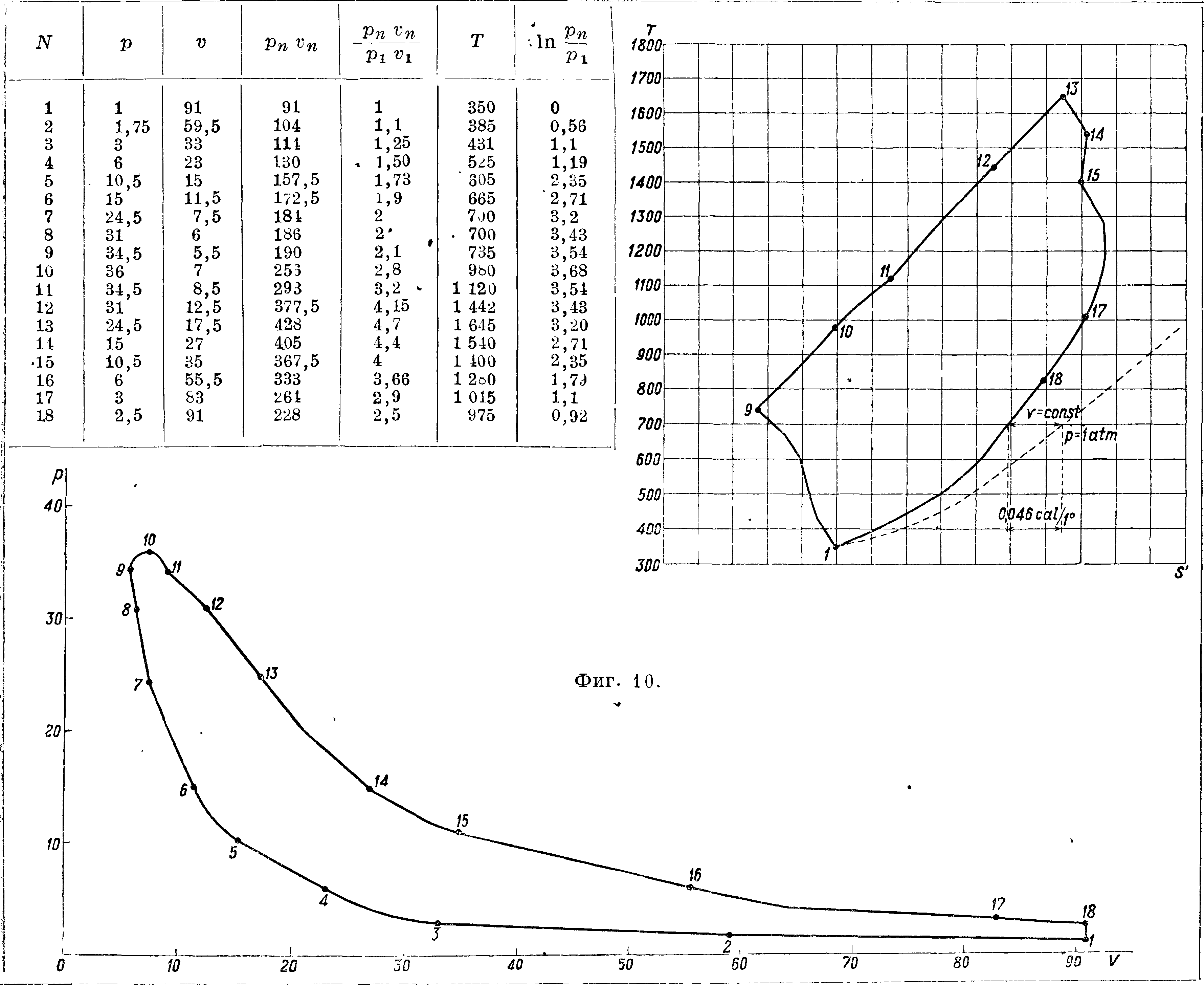
s-s₀=_c,in[£ -(у)·^-1]·

Характеристические функции. Мы имеем теперь два ур-ия Т. для обратимых процессов: 1) <5<2=dU + Ар dv, 2) SQ=T dS. Можно ввести кроме энтропии ряд других вспомогательных ф-ий для термодинамич. исследования как процессов, так и самой природы тела. Ф-ия U + Αρν является так же определенной состоянием тела, как и сама ф-ия U (как говорят, с точностью до произвольного постоянного, заключенного в U). Разность этих ф-ий для двух состояний тела, т. e. U ₂ — U_l + Αρ₂ν₂ — Αρ_χν_γ, вполне определенна (постоянное исчезает) и также не зависит от процесса, которым тело переходило из одного состояния в другое. Ф-ия эта называется энтальпией (Камерлинг-Оннес), или теплосодержанием, и обозначается i (Молве). Последний термин взят из учения о насыщенном паре и там имеет реальное значение. Разность энтальпий в процессе постоянного давления дает тепло, участвующее в этом процессе, что видно из ур-ия Q₂= U ₂— U₁-ⁱrAjpdv;

при р=Const Q₂=U₂— U_l + Ар (v₂— v_±) =*=^₂-i_1(i)==Const). Первое ур-ие Т. теперь м. б. .написано так:

SQ=clU + Ар · dv=d (U + Αρν) — Αν · dp =>

= di — Αν · dp.

При р=Const имеем dQ - c_pdT=di, но вообще di=qy dT + dp и при р=Const получим

Ср =. Точно так же при v=Const из ур-ия

SQ=dU + Ар dv имеем c_v =. Первое соот ношение показывает, как можно определить г, если известны с_р для различных t° и давлений,

путем графич. интегрирования. Из уравнения SQ=di-Av · dp и 6Q=T · dS получим и т. к. dS есть диференциал ф-ии при независимых здесь переменных Т и р, то а /1 метров ₌ _а_ /1_ « di __ Аи ар г·αг] "" от т·αр. т J ’

то есть

i ач _ i дч

Т * ор-дТ~ Т * др-дТ

i ai, Αν A dv

г“ ’ ар г“ “"f·αг ’

или

(Э=^-лт Р—

Это соотношение позволяет определять по энтальпиям объёмы. Т. о., определив опытным путем теплоемкость при постоянном давлении для различных t° и давлений, мы можем по ним определять и объёмы, т. e. Т. дает средство по одним только величинам с_р уже представить зависимость между p,v, Т, то есть характеристич. ур-ие (графически или ф-лой). С другой стороны, вычисляем разность энтр для различных давлений и t°, имея значения с_р, по соотносит ^

шению^$^_=Сошз4=с^ —. Опять можем составить график Ц и определять S — S₀ для какого-нибудь давления. Отсюда видим тесную связь между величинами р, v,T,i,S,U. Можно взять какие-нибудь две из этих шести величин за независимые переменные и подыскать такие ф-ии, которые своими прЬизводными и комбинациями их давали бы остальные четыре величины. Эти ф-ии называются характеристическими (Массье) и служат весьма удобным средством находить по опытным данным основные термодинамич. величины. Напишем ур-йе 6Q=dU +Лр · dv=Т dS. Из него получаем Ар - dv=Т. dS-dU=d (TS) - dU-SdT =

— d (TS — U) — S dT,

или

d (TS — 77)=SdT + Ap· dv.

В левой части равенства имеется диференциал ф-ии, определяемой (в своей разности) состоянием тела, в правой—полные диференциалы параметров Т и v, которые и служат независимыми переменными. Функция TS — U называется свободной энергией и является характеристич. ф-ией при независимых переменных v и Т. Обозначая ее через F, имеем

dF=ψ dv + % dT=S dT + Ap clv.

Отсюда

fv=^A?’

-=S,

_TdF ^x dT

- F

dF_

dv

v=г,

-F=U,

dF

dv

V.

T. о. через две независимые переменные Т и v, ф-ию F и ее производные выражаются остальные 4 термодинамич. величины. Так как (ди _ _т d*F °¹» of)_v ¹ ат²’ то в свою очередь

d*F

( _ гр

dv) т dT*dv~

т а²

ат²

точно так же

(ЮЛ _{= τ}._φ²Ζ_

dvfT dTdv

Ф-ия F была введена Гельмгольцем и названа им свободной энергией (в его обозначении свободная энергия U — TS=— F, здесь взято обозначение Массье как более удобное)· Возьмем теперь независимыми переменными Т и р, имеем

dQ=di-Av-dp=T-dS,

отсюда

d (TS-i)=S dT — Αν · dp; обозначим ф-ию TS — i через Ф (ее называют· иногда термодинамическим потенциалом; введена она была Дюгемом). Тогда имеем

8 dT -и отсюда

Αν · dp --

dT

i=TS —Φ=Τ

дФ ~ dΦ ар^:

- Αν;

dΦ

dT

-ф=Т*

д

dT

и=Т²-

_д (Ф дФ dT Т) dp V’

и так же, как для c_v, находим

. др ¹ дТ*)_р

далее опять можно получить

^ldi-)=-AT^dv

с_р=Т

ffl··

02ф _β

* ат^{2 9}

+ Αν=-ΛΤ*_Θ⁹Γ(Ϊ-)

dp)T дТ ¹ dT

Но в ур-ии SQ= di —Αν · dp можно взять независимые переменные и р. Тогда 6Q _ di Αν-dp dS _л., dS

T

и отсюда за

ds=p~^

dS ,.,

^- ж ^dl +

dp

dp

/0S _ i_ /as ^

j

- — Av

as

ai’

t. e.

T =

1

as

di.

as

«=_ -^a-P as ^:

di

U=i — Apv == г + p

as

dp

~dS

di

Отсюда видим, что в этом случае энтропия является характеристич. ф-ией. С другой стороны^ можно написать

di — TdS=Αν

dp, d_v=%-Ad_S.

Берем i тогда

Αν Αν

8 за независимые переменные

BE

^di + ^dS.

di ¹ as

dp

Сравнивая, получаем:

/0jp 1 dp

[oi)r Av ’ as~

T_

Av ⁹

t. e.

Av --

m;

idp

dSJi

/dp

di J s

©),

Следовательно p является характеристич. ф-иейг при независимых переменных г и S, Точно-так же получаем, что U будет характеристич. ф-ией при переменных v и S; v—при переменных U и S. При переменных S и р характеристической ф-ией будет г:

йг= Т dS + Av-dp=Л · dS + · dp,

di

отсюда

(as)_p ^T’ (dp)^^{- Av и τ}· ^д

Теперь можно и первое ур-ие Т. написать в; формах, иногда более удобных для приложе-

ния, например, взяв за независимые переменные V и Т и введя ф-ию F, имеем

6Q=dU +Ар dv=(§!Д ЙГ + [(|f )_г + Ар] dv,

НО

Ut?/у ⁱ ΟΤΟυ Ου ^JL1 ОТ ™ ^И -Ur/да следовательно

6Q=c_vdT + AT f_T dv.,

ОТ

Точно так же при независимых, переменных Тир получим, выходя из ур-ия SQ=di — —Αν · dp и пользуясь ф-ией Ф,

0Q=c_pdT-AT|р dp.

По первому ур-ию имеем

^{= с}р I? + ^cv 0 =

-(^^p+U^dv)+^ATU^dv·

то есть

с“-«·>(£) г^лт{ШЬ

Но, рассматривая v как ф-ию Тир при р== Const, получим

dv=~dT,

а, считая Т за ф-ию v и р при р=Const, получим

dT=~dv

Ου

и отсюда следовательно

с

аг ₌

dv)_p ~

1

дг>

ОТ

с,-с,-АтЩ1. (§^·

Это—соотношение Клапейрона для теплоемкостей всех тел. Оно пишется также

Ш=^лт·

Можно исключить, именно при р=Const имеем

^=^0иШ₈=-©г-©„^;

отсюда

Но, так же как и раньше, найдем

МЙО

/Эр ₌ dv)f

/аух

0р)т

И Ср G_v —

2

Ар

ί-)

др)т д ό

При р=Const ~= αν, где а—коэф. кубич. рас-

от

0 Ί)

ширения от t°; так же при Т=Const —=—βν, где β—коэф. сжатия от давления; тогда

_ _Л ΑΤα²υ ^ср ^Cv ~ β

Из определений для а и β видно, что а—отвлеченное число на 1°:

* _ 1 Ου

^a~vdf’

а β измеряется м²1кг:

^r v Ор где р в килограммах/м². Таким образом общее измерение“ с_р и c_v будет

1 Cal·1° _# Ц _# ^. 1 _ Са!

кг · м 1°² кг м²!кг ~ кг · 1° ⁹

как и должно быть. Таким путем узнают c_v. там, где непосредственное определение очень трудно, например для воды или для твердых тел. Возьмем воду при 70° (= 343° абс.). Объем 1 %г-по Бриджмену равен 0,00102 м³; можно взять α= 6 · 10^-4/1°, β πό Бриджмену=4 · 1СГ⁹ 4²jm. Тогда

343.1,02 * 10-3. 36.10-3 427.4 * 10-9 ^:

0,07 Cal te 1°.

По Диетеричи (Dieterici) в этом случае с_р^ ^ 1,005 и следовательно c_v=0,935. Подобным вычислением убеждаемся, что c_v для воды между 0 и 100° непрерывно убывает.

Теорема Нернста для однородного тела. Мы видели, что теплоемкости c_v и с_р выражаются через характеристич. ф-ии F и Ф:

но

II	U τ*)υ	и	Ср=Т	/02ф ат2)
02F	(0S	и	Э2ф _ 1	(dS)
ОТ2 —	U τ)υ		ОТ2 1	U Т)р

Предположим, что Т убывает и стремится к 0, тогда обе теплоемкости будут стремиться к нулю, если только производные от энтропии па Т не стремятся к бесконечности. Они стремились бы к бесконечности, если бы энтропия в своем выражении содержала логарифмич. функцию Т, тогда в производных появилось бы количество вида ψ. Итак, если энтропия в своем выражении не содержит логарифмич. ф-ииТ, то теплоемкости c_v и с_Ршобращаются в нуль приТ= 0. Обратно, если бы опытным путем обнаружено было, что например c_v стремится к нулю при убывающих Т, то это служило бы указанием, что ~ не стремится к бесконечно сти и энтропия не содержит в границах, близких к Т= 0, логарифмич. ф-ии Т. Тогда можно было бы написать S=Const + аТ + ЬТ² + + сТ³ + ., где а, b, с .—ф-ии объёма, т. к. энтропия не м. б. ф-ией только t°, иначе адиабата S=Const совпала бы с изотермой. При Т=0 и разумеется конечных значениях а, Ь, с,. получаем S₀=(ff)₀⁼ Const=I. Ф-ия

F разностью своих значений дает работу изо-термин, процесса [из ур-ия d(TS—U)=dF== SdT + Ар · dv]. Но всегда можно иметь еще целый ряд ф-ий, которые удовлетворяют этому условию. Действительно возьмем F₁=F — Tk, где 7с—произвольное постоянное. Тогда имеем (F₁₂ — F^)=(F₂ — F_t) при T=Const, а так же

Ον

= Т

d²F_xОТ² *

и=Т²>

от

m

И т. д.

Но

0F i OF 7 m a (OF Λ 7 7

er “Sr^-* п_РиТ=0,

и, взяв k=l, имеем (~1=0, то есть всегда, можно найти такую ф-ию разностью своих значений дающую изотермическую работу, что

iw) ⁼ 0· Н° мы могли бы и прямо положить.

7=0. Тогда имели бы еще и следующее положение (М. Планк): для всякого тела, у к-рого> c_v стремится вместе с Т к нулю, можно положить S_T=0=0. Но, с другой стороны, мы имеем:

^с* ^{= Т}(И)»^=а:Г + 2ЬТ^а + ЗсТ*+ ···,

и, если α, δ, с,. являются ф-иями объёма, то можем положить 1=0, если же по. наблюдениям над теплоемкостью а, δ, с,. являются постоянными величинами, χο

£=p(_v) + aT+ δΤ² + οΤ³ +. и при Г=О S=φ (ν₀)=постоянной величине, к-рую мы произвольно положить равной 0 не можем. Тогда остается лишь первое положение о существовании ф-ии такой, что ( а^)₀^в 0.

Это и является в сущности теоремой Нернста для однородного тела, то есть если теплоемкость <c_v стремится вместе с Т к нулю, то всегда существует ф-ия F_l9 дающая разностью своих значений изотермич. работу, так что )_г_₀⁼

А в формулировке М. Планка: для всех тел, у которых c_v стремится вместе с Т к нулю, энтропию при Т =0 можно положить равной 0. Но, как мы видели, это можно принимать с известными ограничениями. При этом разумеется говорится о жидких или твердых телах, т. к. газы при малых Т перестают существовать. Здесь не лишним является поставить также вопрос: указывает ли Т. на возможность одновременного стремления к 0 теплоемкости и .Мы видели, что при независимых переменных V и S внутренняя энергия является харак-леристич. ф-ией по ур-ию dU =Т dS — Ap dv

и следовательно=Т. Представим себе систему координат: S—абсциссы, U—ординаты и нанесем в этой системе кривую Const. Тогда касательная к этой кривой при Т=0 будет параллельна оси абсцисс и вместе с тем будет геометрии, местом точек, где U=Const. Т. о. можем сказать, что кривая v= Const и прямая U=Const имеют две общие бесконечно близкие точки там,где Т=0. Перейдем теперь к системе координат Т, U и возьмем на оси ор-.динат точку, через к-рую проведем кривую v= Const. В этой точке Т=0 и следовательно здесь будут две общие бесконечно близкие точки между кривой v=Const и прямой U=Const,

то есть=0 или, другими словами, (1^=^

здесь р шно нулю. Таким образом Т. дает указание, что мы вправе ожидать стремление к нулю теплоемкости c_v одновременно с t°. То же самое можно сказать по с_р, если вместо U взять ф-ию г. Опыты над теплоемкостями >-c_v при очень низких t° немногочисленны в виду их большой трудности, но все они подтверждают, что теплоемкость стремится одновременно с Т к нулю. Графически ф-ия определяется по опытным данным относительно c_v или:

1) ИЗ ур-ИЯ G_V=T · οψ± или 2) из ур-ий дТ

№

dU

Вычерчивается сначала кривая c_v в координатах Т_г c_v, затем (во втором случае) определяется ее интегральная

U=f(T) + <p(v),

где φ (v)—произвольная ф-ия объёма, которая отбрасывается, т. к. здесь ищется зависимость

f(T)

U от £°; далее строится кривая и ее интегральная. Помножением ординат этой последней на Т получаем F_x в ее зависимости от t°.

В первом случае вычерчивается кривая γ,

ее интегральная S и затем интегральная этой .последней. Значения c_v идут только до опреде ленной t° и далее до абсолютного нуля продолжаются от руки. Здесь дана примерная табличка (фигура 11) нахождения по опытам относи-

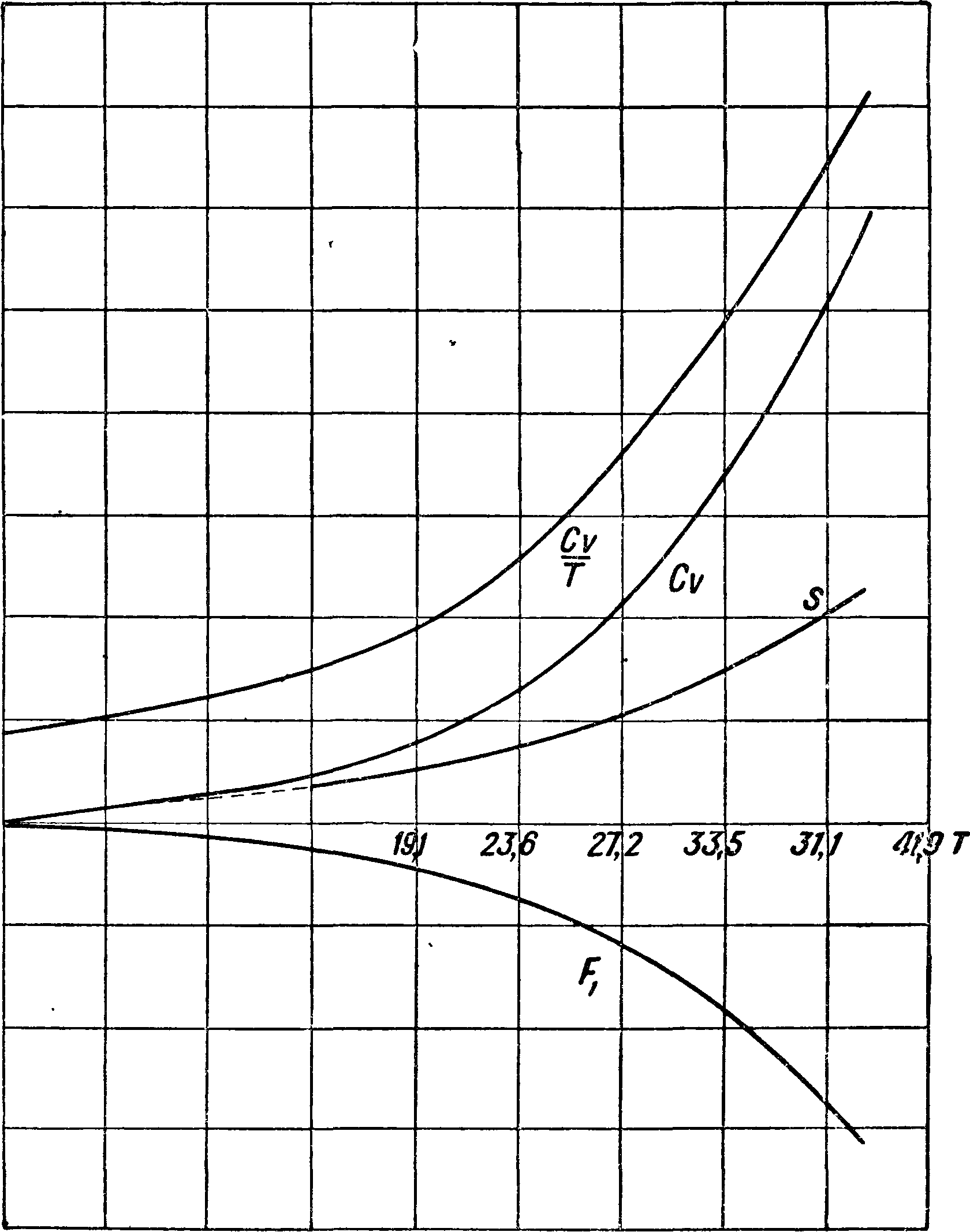
Фигура и. тельно c_v для алюминия. Кривая F₁ получается явно касающейся оси Т при Т=0, т.е. (ууг)₀⁼ 0, что и требовалось.

Относительно теплоемкости c_v существует теория Дебая (Debye), основанная на теории квант и лучистого тепла. Она приводит к тому, что при малых Т c_v=cT³, где с—постоян-наядля каждого тела. Это выражение c_v несовместимо, как было указано, с формулировкой М. Планка теоремы Нернста. Но на примере алюминия можно видеть, что формула Дебая является лишь первым приближением к опытам и можно подобрать более точную формулу для c_vвида аТ + δΤ² + сТ³ + ., где α, δ, с,. м. б. и ф-иями объёма. Из приложенной здесь таблички видно, что крйвая γ для алюминия не стремится к нулю, как следовало бы по Дебаю. Поэтому формулировку М. Планка нельзя заранее отвергать. Примем, что и для других тел c_v=аТ δΤ² + сТ³. Возьмем ур-ие адиабаты из общего ур-ия

6Q=с„ dT + AT ~ dv=с. (IT + Т dv=0.

Отсюда

dv _ c_v _ аТ+ЬТ2 + сТЗ _ а+ ЬТ + сТз

df ~ rW ~ _т j>²>_ ~ 9S

dTdv dTdv dv

но так как

С*=т (?§)_в=аТ + bТ² + сТ

ТО

8=аТ + I Т* + ^с- Т³ и ~=аТ + у Т⁷² + f- Т

где а δ, с—производные по v. Следовательно

dy___α + bТ + сГз __

^d^ аТ — Тз

2 3

и при Т=0 выражение обращается по абсолютной величине в со, т.е. адиабатич. расширением (dt < 0) не достигнем абсолютного нуля, т. к. для этого нужно бесконечно большое изменение объёма, а т. к. c_v и с_р стремятся к нулю, то и охлаждением мы не можем его достигнуть. Отсюда выводят положение о невозможности достижения абсолютного нуля. Но если мы возьмем формулу Дебая, то с_т-оТ S=9>(«) + 5-T», 秓9>(»)

и получаем

dv а

~dTJо ~ φ(ν₀)

Следовательно формула Дебая несовместима и с положением о недостижимости абсолютного нуля. Вопрос впрочем этот и вообще остается открытым, т. к. опытным путем он не проверялся. Все значение теоремы Нернста—не в области однородного тела, а в области химич. реакций, где она формулируется иначе, о чем речь будет дальше. Мы видим из всего сказанного, что теорема Нернста вытекает из обоих принципов Т. и следовательно не м. б. поставлена наряду с ними как нек-рый третий принцип.

Об измерении температуры. Термодинамически ί° должна определяться из соотношения

Карно ^. Поэтому если представим себе цикл Карно между двумя t°, из которых одна соответствует таянию льда при нормальном давлении (760 миллиметров рт. ст.), а другая—кипению воды при том же давлении, то, определивши количественно теплоты ζ)₀ и Q_u участвующие в этом цикле, имеем ^=·—. Представим, что разность между этими t° выражается числом 100° (это число с термодинамич. точки зрения

М. б. ВЗЯТО произвольно), получим Т₀=--

оГ¹

Это будет термодинамич. t° тающего льда при 760 миллиметров давления. Т. о. определяется начало счета термодинамич. шкалы, то есть расстояние в градусах от абсолютного нуля до t° тающего льда. Однако здесь возникают трудности с опытной стороны как в точном измерении количества калорий Qi и Qo, так и в точном воспроизведении адиабатных процессов. Также и внешнее давление должно строго оставаться постоянным, иначе t° таяния и кипения изменятся. Поэтому обращаются к газовым термометрам, причем наблюдают или изменение объёма вследствие изменения t° при постоянном давлении или изменение давления при постоянном объёме. Назовем через а коэф. расширения газа от t°, тогда имеем в первом случае где V—конечный объём при темп-ре t_p, v₀— •объём при 0°. Для второго случая соответственно где β—коэф. изменения давления. Если бы газы точно следовали ур-ию pv=RT, тогда мы имели бы

₌ Т-Тр )р Т₀

и так же

/Р-Ро _ Т-То Ро /V Т₀

то есть и тогда газовый термометр вполне соответство вал бы термодинамич. шкале. В действительности однако этого нет, газы следуют уравнению pv — RT точно только при большом разрежении или при высоких t°. Поэтому для небольших давлений можно выразить а и β ф-лами

α= у + δρ, β=γ + δ_λρ

и из опытных величин для а я β находят у, δ и 0_г. Henning для водорода находит между давлениями 510 миллиметров и 1 100 миллиметров а · 10⁷=36 604 — 12 р₀ и β · 10⁷=36 604 + 17 р_и,

где Ро в м рт. ст. Отсюда γ=0,0036604 и следовательно Т₀=273,2°. Таким образом по Хеннингу абсолютный нуль лежит на 273,2° ниже 0° С. Но Битти и Бриджмен (Beatty а. Bridgeman, 1930 г.) дают для Т₀ 273,10°, что соответствует коэфициенту расширения водорода при 760 миллиметров, найденному еще Реньо. Вертело дает 273,09°. Для технических целей удобно число 273°.

Применение термгдинамических соотношений к исследованию свойств жидкости (воды) и насыщенного пара. Технически наиболее важной из жидкостей являете^ вода. К сожалению опытный материал для воды не вполне достаточен для полного применения термодинамич. соотношений. В технике вода является рабочим телом калорич. машины и нагреванием обращается в пар. Процесс испарения здесь является процессом кипения, то есть образования пара внутри массы жидкости. Но при данном давлении нужна определенная t°, чтобы начался процесс кипения. При этой t°, соответствующей определенному давлению, вода единицей веса занимает определенный объём. Если“ в какой либо системе координат (Т, v или v, р) отметим последовательное состояние воды при самом начале кипения, то получим так называется нижнюю пограничную кривую, то есть кривую начала испарения (кипения). Здесь давление является ф-ией t° и обратно и, как известно, за весь последующий процесс перехода 1 килограмм жидкости в пар при-данном давлении t° остается постоян

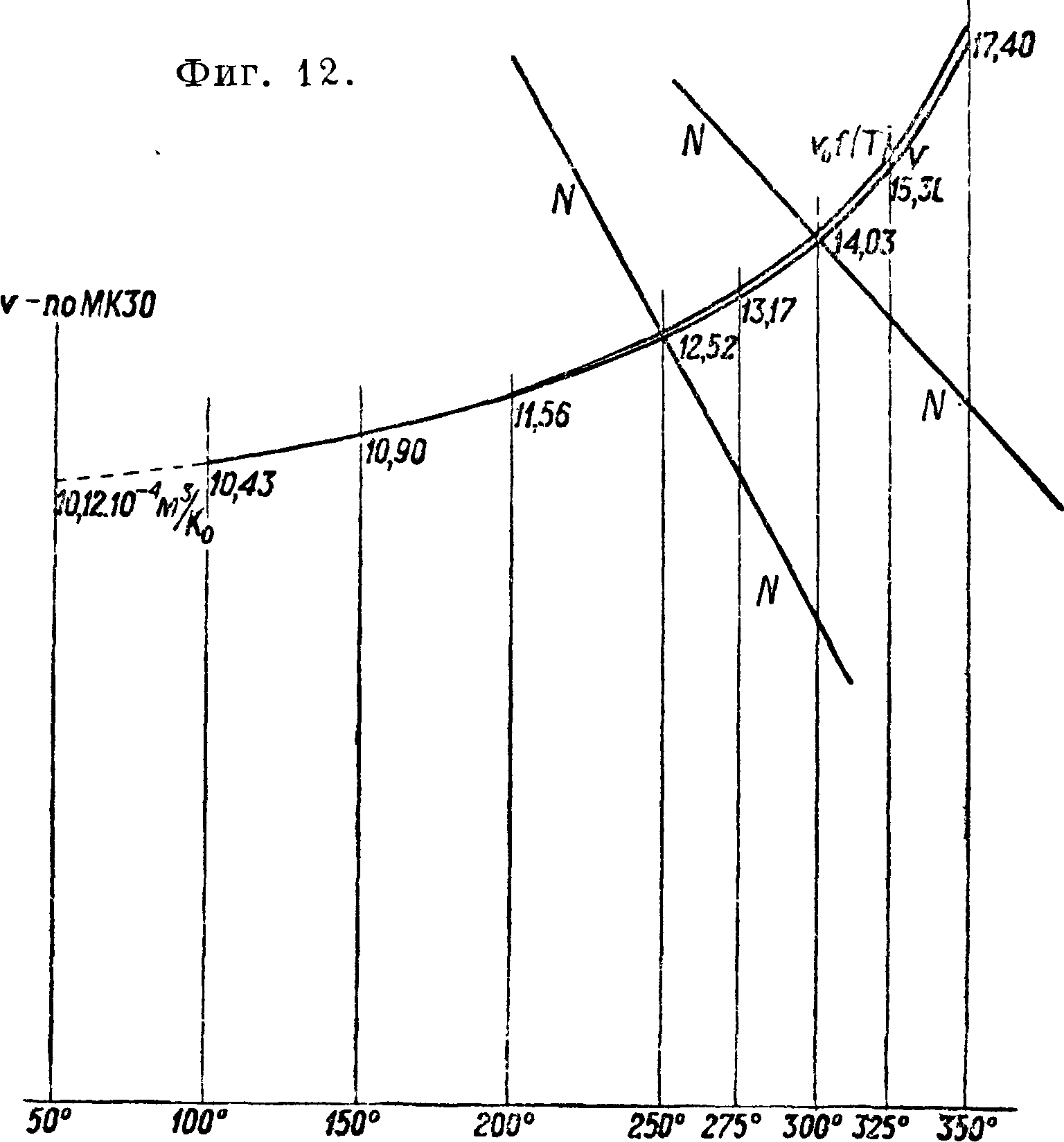
ной. На фигуре 12 даны объёмы в функции i° для нижней пограничной кривой. Но вода, как и всякая жидкость, сжимаема, хотя и очень мало. При давлениях, соответствующих нижней пограничной кривой, сжатие от давления невелико, и поэтому можно принять при этих а

Г. э. m. XXIII.

давлениях линейную зависимость объёма от давления, то есть написать

ν=ν₀[1-β(ρ-ρ₀ )]/(Т), где β—коэф. сжатия, даваемый опытом обычно на 1 atm. Этот коэф. зависит собственно от давления и от t°. Так, по опытам Амага между темп-рами 0 и 100° С и давлениями 0 и 400 atm β на 1 atm давления изменяется от .5,11 · 1СГ⁵ до 4,25 · 1СГ⁵. Richards и Stull дают для 20° С при давлениях 0—300 atm величину 4,4*10^-5. Но при 200° С и давлениях 100—200 atm β поднимается до 8,17 · 1СГ⁵ (Амага). При отсутствии систематизированного опытного материала о сжимаемости воды вблизи пограничного состояния, то есть между темп-рами 0 и 374° С и давлениями 0 и 225 atm, приходится ограничиться только приближенной величиной. В последнее время появилась работа Trautz и. Steyer [²¹], в которой приведены результаты опытов с водой при t° 0—370° и при давлениях до 300 atm. Нетрудно указанные здесь результаты соответственно изменить. Т. к. при слабых t° давления вблизи пограничного состояния невелики и поднимаются лишь после t° 200° С, то можно принять β=8 · 1СГ⁵ на 1 atm. Даже при 225 atm это дает уменьшение объёма в отношении 0,982 : 1, то есть незначительное. Что же касается (Т), то эта ф-ия выражает зависимость объёма от t° при постоянном давлении. Имея пограничную кривую и зная давления, соответственные ί°, мы могли бы построить ряд изобар в системе Т, ν, то есть дать графически зависимость этой ф-ии и от t° и от давлений. Напр. t° 300° соответствует на пограничной кривой давление 87,6 atm. Идя от соответственного объёма на пограничной кривой в сторону убывающих t° и изменяя ординаты ν в отношении

[1— β (87,6 — ро)] : [1 — β(ρ — Ро)], получим изобару 87,6 atm. При этом ν₀ можно положить равным 0,001 (при 4° С), а р₀== 0,0088 atm можно пренебречь. Наибольшее изменение ординаты будет в отношении — £- · Поэтому изменим ординаты пограничной кривой в отношении ^{и тог}да считаем,

что кривая представляет собой v₀f(T). Измененная кривая весьма мало разнится от пограничной. В параллель с этим имеем по Амага значение среднего коэф-та расширения между 0 и 50° для 1 aim, равное 0,000238. На пограничной кривой имеем между 0 и 50° значение, равное 0,00024, числа тождественные. Далее коэф. расширения, данный еще Гирном (до 200°), также подходит к объёмам, даваемым теперь, на пограничной кривой. Более поздние опыты Ватсона для 400 atm дают в пределах до 200° также сходственные значения. Для 1° высших получается расхождение, но 400 atm значительно выше давлений, встречающихся на пограничной кривой. Теперь обратимся к ф-ии Ф для воды. Имеем:

в!=- ^Av=- [1 - β (р - Ро)] КТ).

Интегрируя, имеем

Ф=- AV„ (Р - р_а) · b£i|TP!). ·ί{Τ) + φ (У), где φ (Т)—ф-ия от Т, подлежащая определению. Для этого воспользуемся соотношением

= -ATv_t(p-p_a) ·. f" (Т) + Τφ" (Т).

Имея график v₀f(T), определим v₀f"(T) и далее первое слагаемое в выражении С_р для давлений, соответствующих пограничной кривой. Если бы для этих давлений С_р было нам известно в функции f°, то мы могли бы составить график Τφ" (Т) и графич. интегрированием перейти к <р(Т). Не останавливаясь пока на этом, обозначим Τφ" (Т) через с_р и перейдем к выражению энтальпии и энтропии для воды. Имеем

^1=ΤΙτ~^{Φ =} ~ ^Αυο (Р — Ро)

• · [ТГ (У) - /(У)] + Τφ(Τ) - φ (У),

но т<р(Т) - ?> (У)=Jс_Ро ат и поэтому’

i=-4(p-p₀).^L<f^>.

- [У«о/(У)-«о/(У)] + с_Ро(1Т.

Далее для энтропии

^s=If=- Λ- (р - Ро) ·. f(T) v₀ +

+ φ(Τ)=- A (p - p₀) · *z£LP-zPsL. _{r(T) Ve +}

+ Яг ^dT

и внутренняя энергия и=г - Αρν=ί-Αρ[1-β(ρ- р₀)] v_Qf (Т). Можно считать, что v₀ и р₀ относятся к 0° С и т. к. количество, зависящее от давления, играет роль только при больших давлениях, то пренебрегаем р₀=0,0062 atm сравнительно с р. Величина v₀f(T) определяется по графику v₀f(T). Перейдем теперь к процессу испарения. В какой-либо момент имеем в 1 килограмм смеси жидкости и пара ж кг пара и (1 — ж) кг жидкости и, называя удельный объём пара через ν, имеем удельный объём смеси г>₂=ν₁χ + (1 — ж) ν, где ν—объём на нижней пограничной кривой. Здесь ν есть ф-ия t°, точно так же и v_u равное г>₂ при ж= 1, то есть когда вся жидкость обратилась в пар. Разность v₁ — v=u будет также ф-ией только t° (или давления) и можно написать ν₂=ν хи. Состояние одного кг смеси дается т. о. величинами ж и Т (или жир). Предположим процесс испарения происходящим при р=Const,тогда имеем 6Q=di —Αν dp=di и Q=г_х — г₀, где i_x—энтальпия смеси, когда в смеси имеем ж кг пара, а г₀—энтальпия жидкости на пограничной кривой при данном р. Но количество тепла для испарения ж кг жидкости есть гж, где г—скоростное тепло испарения 1 килограмм при данном давлении, и следовательно Q== rx=i_x — г₀, отсюда г_х=г₀Агж. Но, с другой стороны, SQ=TdS и при изотермич. процессе Q=T(S_X-S₀)=rx,

то есть Оя=уг + о₀; таково выражение энтропии смеси. Для внутренней энергии смеси получим ЦУ= г_х — Ар (ν + ж и)=% — Αρν + ж/г — Ара). Количество г — Ари называется внутренним скрытым теплом ρ, a i₀ — Apv. есть внутренняя энергия Uq жидкости на пограничной кривой при давлении р. Поэтому U_x=U₀Aqж. Если представим себе процесс в смеси при постоянном объёме, то

SQ=c_vxdT=dU_x= d (TJ₀ -f ρж),

v₂=v + xu=Const=a

но и следовательно

c„dT=d (и₀ + д^)·

Отсюда теплоемкость

^C«⁼dT (^ϋ° ^{+ ρ?}ίτ)’

она зависит от объёма а и от t° (или давления). Представим себе опять изотермич. процесс в смеси. Для всякого тела имеем

<5 Q-cJT + AT^dv

и при то есть

Т=Const

AT %dv=TdS,

Адр дТ

dv=TdS,

но здесь dS=ψ dx и при Т=Const dv=и dx,

др dp Adp г гл далее ^ и следовательно -^ψ- и=—. Это соотношение Клапейрона связывает величины

dp

£ψ, и, г и позволяет определять заранее какую-нибудь из трех величин, если две известны из опытов. Предположим, что мы процесс испарения доводим до конца, то есть до х=1, тогда для различных давлений получим ряд различных состояний жидкости, обращенной полностью в пар и имеющей теперь объём V ₂=V + и при давлении р (и соответственной этому темп-ре Т). Изобразив в каких-либо координатах, например V, р, это состояние, получим верхнюю пограничную кривую, или кривую сухого насыщенного пара. Дальнейшее нагревание при постоянном давлении поведет уже к повышению ί°, и пар теперь будет перегретым, то есть мы имеем полностью газообразное состояние тела. Но вблизи сухого насыщения газ не будет следовать закону Мариотта-Гей-Люссака и о нахождении его характеристич. ур-ия будет сказано дальше. Для сухого насыщения имеем соотношение:

Назовем ф-ию Ф для газообразного состояния тела через Ф_г и для жидкого через Ф₀. Для всякой точки верхней пограничной кривой, как для начала полного газообразного состояния, имеем и для нижней пограничной кривой дФ о дТ

поэтому ψ =

дФ_х дФ₀ ^

. Берем производную по

Т, помня, что на пограничных кривых р является ф-ией Т, получим

Г, i dr д“ф_х, д“Ф_л dp д“Ф₀ д“Ф₀ dp

“ dr ~ “

Г^{2 1} Г dT ОТ^{2 1} дрдТ dT дТ² и по общему свойству ф-ии Ф имеем

1 dr ^ср_х Ср дрдТ dT

-L· 4-

Г 2 ¹. Т

_ _ ^СР __ A ^dP

dT Т Т ^ άτ I

[Вг),-Щ]·

где с_р—теплоемкость газа (для р=Const) на пограничном состоянии, а с_р—то же для жидкости. Отсюда получим, принимая во внимание ур-ие Клапейрона:

) указывает на расширение газа при

/р дг __ дТ ~ °Р_г

Здесь (

р=Const от пограничного состояния при изменении Т и, то же для жидкости. Этой ф-лой пользуются иногда, применяя для перегретого пара ур-ие pv= RT и пренебрегая объёмом жидкости V. В этом случае получим dr _ dT ~ °Р_г ^GP

Для воды это упрощенное соотношение не годится, так как пар водяной вблизи насыщения не следует ур-ию pv — RT. Само соотношение дает возможность сопоставить значения, даваемые для с_р в жидкости и в перегретом паре, и оценить относительные величины с термодина-мич. стороны. Для этого нужно знать величины, относящиеся к перегретому пару, к чему мы и перейдем. Но прежде рассмотрим процесс с паром, когда он остается сухим насыщенным. Этот процесс м. б. характеризуем соотношением для энтропии:

+ S₀.

С тепловой стороны имеем:

6Q=TdS_t=Td (Г + S₀)=άν-^τψ- + TdS₀

и, называя теплоемкость этого процесса через h, получим

h dT=dr — γ 4- TcISq.

Отсюда

, ₌ dr __ ту

dr Г

т

dSp

«Г

Здесь S₀—энтропия на нижней пограничной кривой, и, пренебрегая при небольших давлениях зависимостью ее от давления, получим

dS₀-

^СР о

dr

Т. О.

₇ dr г,

^}l dT ~ Т ^{+ С}Р₀ *

Для водяного пара эта величина отрицательная, то есть процесс сухого насыщения (верхняя пограничная кривая) для паров воды требует отнятия тепла при повышении t°.

Перегретые пары. Мы не вполне еще выяснили термодинамич. величины для жидкости (воды) и для насыщенного пара. Но выяснение их, как мы видели, связано с параллельными сведениями о перегретом паре. В перегретом паре, то есть в газе, существует зависимость между р, V, Т—характеристическое ур-ие. Для действительных газов ур-ие ρ^Λν=RT является лишь предельным, к которому газ подходит по мере повышения t° при данном давлении или по мере понижения давления при данной Г. Вследствие этого заменяют ур-ие pv=RT более сложным, например типа Ван-дер-Ваальса: [p + f (Т, V)] (v — b)=RT

или

p(v — b)=RT — f_x (Т, v).

Все ур-ия этого типа Имеют однако существенное неудобство для своего приложения: и в технике и в физике состояние газа легче всего дать параметрами р и Т и затем уже определять V из характеристич. ур-ия. Между тем в ур-иях названного типа v имеется в какой-нибудь степени и определение становится весьма затрудненным. Притом же все такие ур-ия возникли и на почве механич. теорий, которые не могут обнять собою термодинамич. положения, а Т. дает возможность по опытным данным не

*3

только составить ур-ие, но и проконтролировать параллельные опытные определения основных физич. характеристик данного газа. Мы всегда можем положить, что характеристич. ур-ие имеет вид

pv=RT — f (ρ,Τ),

где, по сказанному, (р,Т) убывает с убыванием давления и возрастанием Р. Непосредственных опытов для параллельного определения р, V и Т имеется, например дл^ паров воды, очень немного. Проще определять вместо v другую физич. характеристику, например с_р, или же измерять разность энтальпий при постоянном давлении, т. к. она будет равна количеству тепла

Q — (^1 Ч)_Р — Const»

пошедшему на нагревание газа. Но имеем основное соотношение а

ί-Ί =

др)т

(?),·

-АТ*-_йт

} Т °Т w Jp

Поэтому, определив ряд значений энтальпий для ряда Р при р=Const и проделав это для ряда давлений, мы тем самым можем составить график: Его интегральная кривая дает значения ψ — ψ-, чем последовательно определяется значение объёмов для разных Р и давлений. После этого характеристич. ур-ие будет представ гено в виде графика дополнительных ф-ий (р, Т) для разных t° и давлений или таблицами р, v и Т или подходящей к таблицам интерполяционной ф-лой. Если определялись не г, а с_р, то необходимо сначала путем графич. интегрирования определить для соответственных давлений г в ф-ии Т. Затем в координатах риг построить изотермы для взятых нами при вычислении г темп-p, определить касательными дтя данного давления (di

-ΜΑΤ² а

(Ip)r’ ^затем построить ф-ии Т и найти ее

15

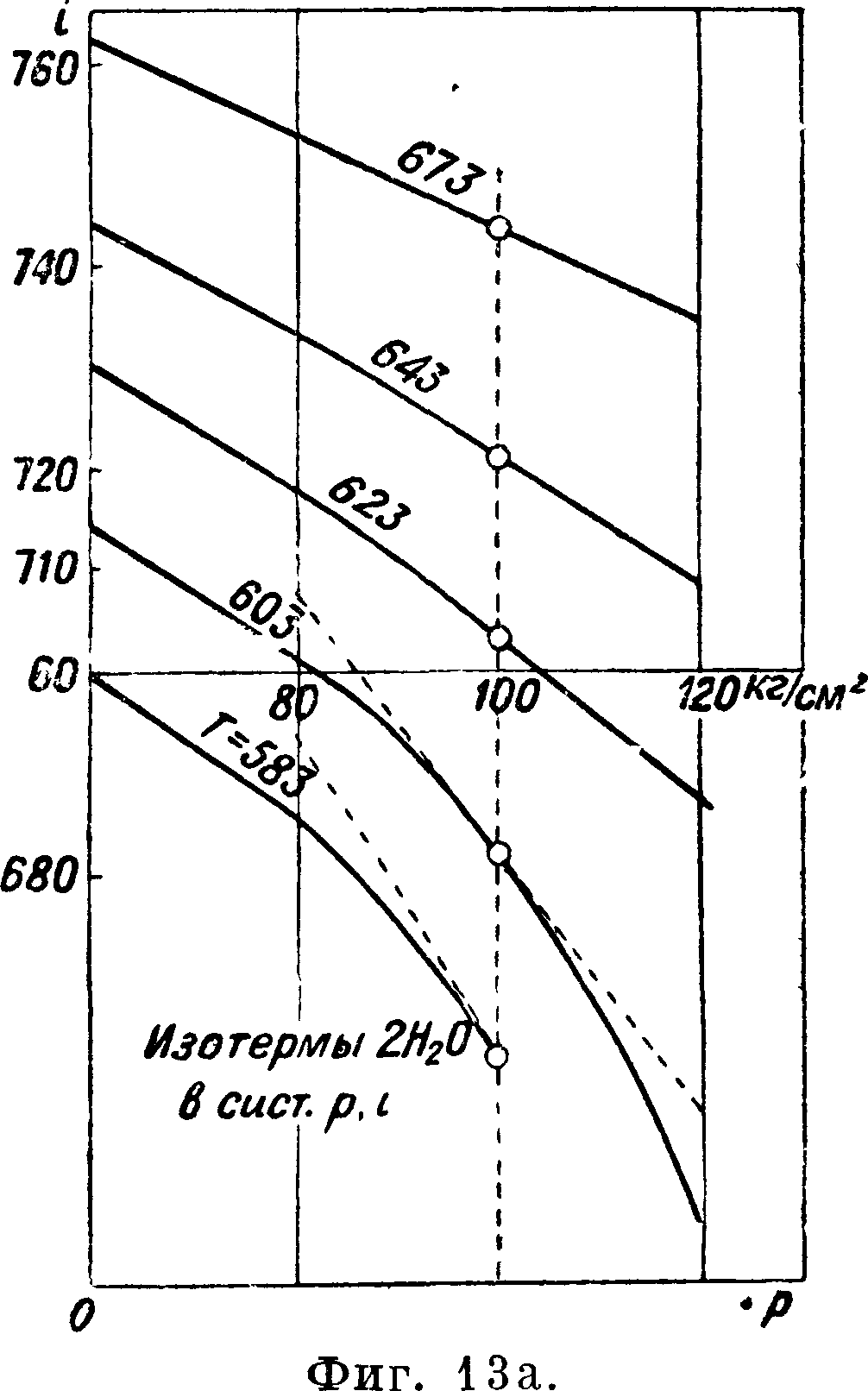
кривую _{АТ2 Кдр)т}тральную. Возьмем для вычисления табличку c_v (фигура 13), обнародованную Кноблаухом в 1929 г. и дающую результат его опытов с с_р для перегретого водяного пара до давления 120 atm. По этой табличке графическим интегрированием мы определим для давлений в 60, 80, 100 и 120 atm разность между энтальпией для какой-нибудь t° (например 623° Т) и энтальпией для Р насыщения. Предположим, что энтальпия насыщения,^ е. ее разность с энтальпией воды при 0°, нам известна из опытов над водой и насыщенным паром. Тогда определяются энтальпии для перегретого пара приР 623° и указанных давлениях. Теперь строим в координатах г и р изотерму 623° между давлением 60 и 120 atm. Подобным же образом построены на фигуре 13а изотермы для 583—673°. Табличка наглядно показывает, что пар по мере повышения t° все больше подходит по своим свойствам к совершенным газам: для совершенного газа энтальпия зависит только от t° (г=U + Αρν) и изотермы были бы прямыми, параллельными оси р. Мы и видим, что изотермы стремятся к прямолинейности и угол между ними и осью

0.5

I	1 юо ф0 ал
’К	*У Ч

200 250 300 350 400 450 Фигура 13.

р постепенно уменьшается. Проводим теперь для какого-нибудь давления, например 100 atm, касательные к изотермам и узнаем таким путем

Шг ^для Р^азлич-ных изотерм. Разделив эти величины соответственно на АТ², узнаем последовательно ве-

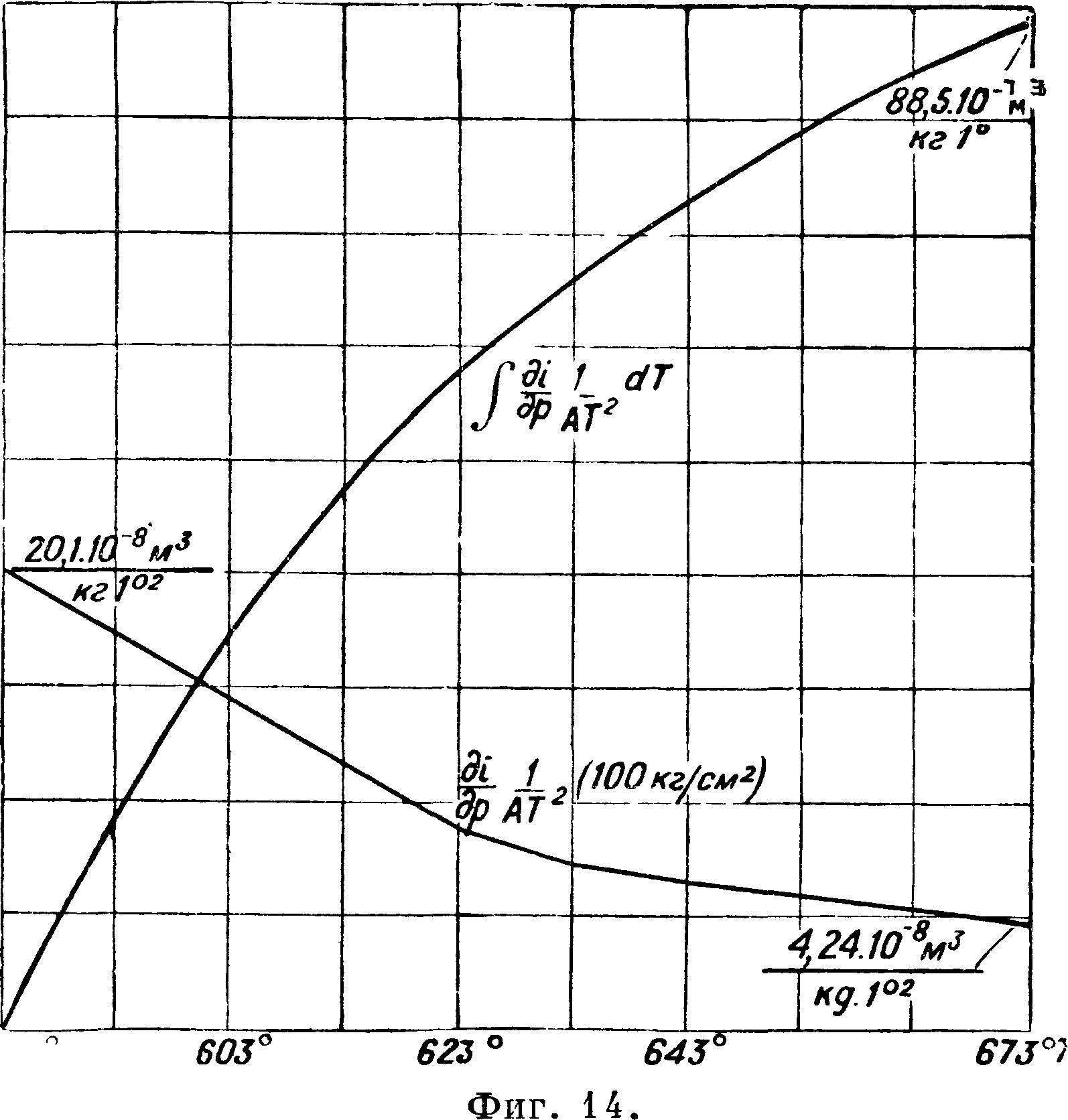
личины οψ и строим кривую этих величин (фигура

14) для 100 atm в функции Р. Интегральная кривая этой кривой и да-

ет нам, где г>₀ и То относятся к насыщению. Отсюда определим v для разных t°, зная v₀ и Т₀. Фиг.

14 дает например для Р=350° г>=0,0229; на Международной конференции

по водяному пару 1930 г. (МК 30) принято v=0,0231 с допуском в ± 0,0005, для t° 400° v== 0,0269 и по МК 30 v= 0,0270. Отсюда видим, что опыты Кноб-

лауха легли в основание определений объёмов на МК 30. Характеристич. ур-йе перегретого водяного пара можно написать в форме pv== RT — φ. Для R можно взять значение R — 47 (Календер) (47,1 Молье и Кноблаух) и следовательно pv=47 Т — φ. Величины удельных объёмов выразятся v=—-^ и на основании сказанного могут вычисляться по теплоемкости Ср, а следовательно можно вычислить величины

^ для различных давлений и Р. Представим теперь эти величины для различных Р в ф-ии давлений, то есть создадим по величинам v диаграмму значений ^ в ф-ии давлений для разных Р. Другими словами, нанесем изотермы в системе координат, .где на оси абсцисс откла-

дывается р, а на оси ординат Приложенная диаграмма (фигура 15) составлена по величинам v,

скаемых отклонений. Строго определяется прямая для изотермы 623° (°К) по допускам для насыщения (168,7 atm) и для 100 atm. Для

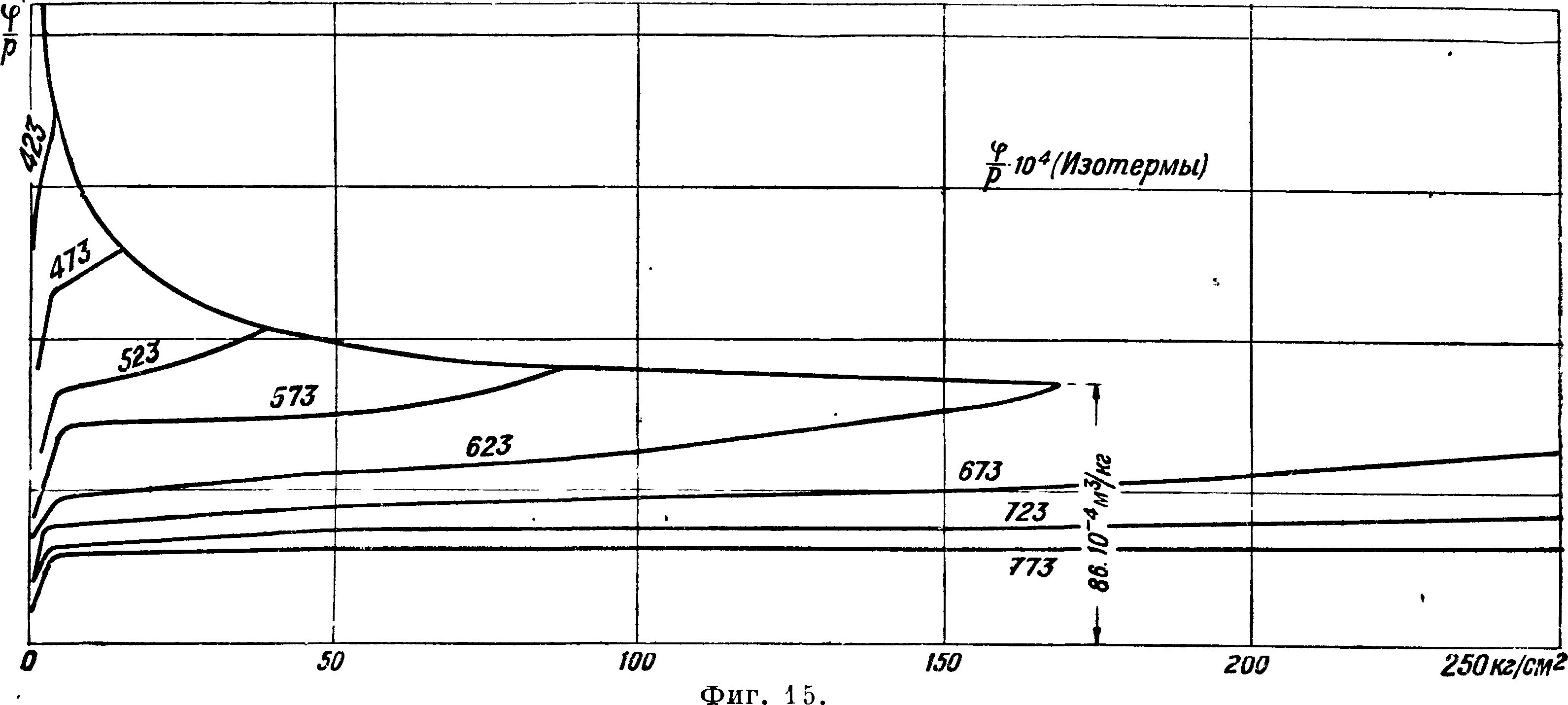
принятым МК 30. Все изотермы имеют вид I остальных изотерм заменяющие их прямые удлиненных кривых, и если принять во внима- | могут иметь небольшую амплитуду отклоне

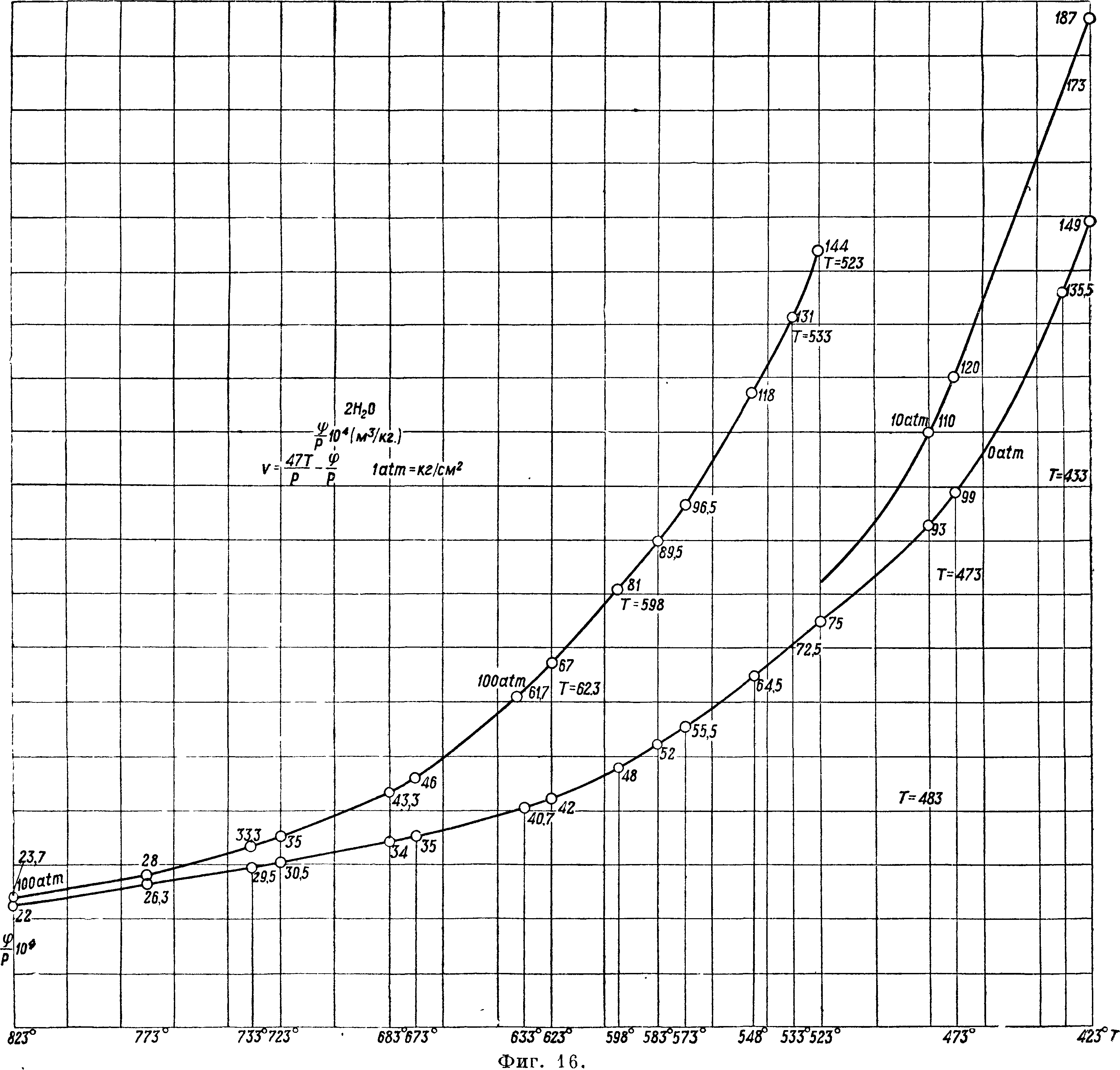
ние допуски, определенные МК 30, то эти кри- I ния в ту или другую сторону. Замена изотерм вые можно заменить прямыми в границах допу- | прямыми представляет существенные удобства для вычислений, как мы сейчас увидим, и даже, если мы несколько и теряем в точности результатов, соответствующее упрощение вычислений имеет значение. Прямые, как и следовало ожидать, постепенно уменьшают свой наклон к оси р, и уже для 823° прямая почти параллельна оси р. Для определения прямых нужно дать только две точки для каждой. Поэтому здесь на прилагаемом графике (фигура 1C) даются ординаты прямых для р=0 и для р=100 atm. Последняя дана только до t° 523°, для более низких t° ординаты при р=100 становятся очень велики, и поэтому даются ординаты дляр=10. По ним строятся кривые в системе, где на абсциссах откладываются t°, а на ординатах—соответственные значения ординат прямых для р=0 и для р=100 (или р=10) (фигура 16). По этим кривым легко найти значение поправочного члена ^ для любой t° и любого давления. Действительно для данного значения Т проводим ординату и ей пересекаем кривые для р=0 и для р= 100; отрезок ординаты между кривыми берем в отношении ^ (или

^, где п—данное число атмосфер, и прибавляем эту величину к ординате нижней кривой,— это и будет значение ^, после чего определяется объём пара. Здесь дается таблица объёмов,

тексте правило линейности м. б. принято как удобное приближение к результатам опытов Кноблауха. Далее по этим кривым можем определить разность ф-ий Ф по изотерме между какими-нибудь давлениями. Имеем

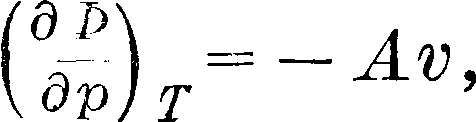
поэтому

(Φ«-*ύι=-Α f v dp=— ART ln^+AjUp

и вследствие линейной зависимости ^ от р

J+P= (ί>»-2± +

где ~ — среднее значение ~ между давлениями р_п и р_х для данной изотермы, читаемое по кривым для р=0 и для р=100. Т. о.

(Ф_й - Ф± - - ART In & + А(р_п - р,)

а разность энтр для тех же данных выразится

- ЛВ ш §5 + А(_Рп - Рд ± Of).

Величину ± (f) найдем, или построив f

для трех значеций Т— 10°, Т и Т+10° и прсн ведя касательную всредней точке полуденной таким путем кривой или просто отойдя на

Таблица объёмов.

Давле ние, кг{см2			T е м π i	3 ρ a τ у ρ а	в градус	ах Цельс	И Я
	150°	200° j	250° 300°	350°	400°	450° i	500°	550°
1		1	2 4508 12,6875	2,9239	3,1596	3,3946	3,6305	3,866
		ί __	2,452 ±3-10-3 2,689 ±4.10-3	2,925 ±4-10-3	3,161 ±5·10~3	3,306 ±5-10-3	3,632 ±5-10-3	3,868 ±5·10-3 0,15246
25		1 _	0,0891 ΙΟ,1011	0,1123	0,1227	0,1322	0,14265
	_		0 0890±3 ·10_1!θ, 1010±3·10~4	0,1120±3·10-4	0,1224 ±3-10~4	0,1325 ± ЗЛО4	0,1424 ±4-10-4 0,06994	0,1521 ±5·10~4 0,07509
50		1 __	— !ο,οΐ63	0,0531	0,0592	0,0646
	__	1 _	— !0,0465±4·ΐ0-4	0,0531 ±4* ΙΟ-4	0,0590 ±3-10-4	0,0644 ±3-10-4	0,0697 ±4-10-4	0,0747 ±5-10-4
100		__	_ —	0,0226	0,0270	0,0304	0,0335	0,03633
		_	_ 1 _	0,0231±5·10-4	0,0270 ±5·ΙΟ"4	0,0304 ±4-10-4	0,0333 ±5·10“4	0,0361 ±5-10-4
150			_ 1 _	0,0116	0,01595	0,0189	0,0213	0,0233
200	—	I _	—	0,0119±5·10-4	0,0160 ±5-10-4 0,01011	0,0189 ±4-10-4 0,01302	0,0212 ±4-10-4 0,01519	0,0233 ±5-10-4 0,0168 4
		1 _	_ _	_	0,01028±5·10-5	0,01305 ±3-10-4	0,01515±35·10-δ	0,01685±4·10-4
250 ;)		! —	_ _	_	0,00640	0,009415	0,01148 |θ,01140±25-10 5	0,01290
	—	г	— ί —	—	0,00636±5·10-3	0,00940 ±15·10-4		0,01290± 4·10~4

определенных для различных изотерм по кривым (и правилу линейности), и объёмов, принятых МК 30. Верхняя цифра дает первый объём, нижняя—второй с соответственным допуском.

Как видно из таблицы, значения, полученные по правилу линейности, лежат вообще в области допускаемых МК 30 значений за исключением величины объёма при 400° и 200 atm, которая дает погрешность в 1,68%. Однако нет надобности изменять основные кривые, т. к. ошибка невелика, да и значения для 200 и более atm могут измениться. Дальнейшие опыты Кноблауха (до 200 atm) дают для энтальпий величины, близкие к принятым на МК 30. Так, для 150 atm и 400° по Кноблауху 716,2, по МК 30 715+2,5; для 450 по Кноблауху 759, по МК 30 759+2,5; для 200 atm и 400° по Кноблауху 678, по МК 30 676+2,5; для 200 atm и 450° по Кноблауху 735,5, по МК 30 737+3. Отсюда следует, что нормы МК 30 подтверждаются опытами Кноблауха. Для объёма при 200 atm и 400° величина Кноблауха выходит несколько ниже нормы,а для 200 atm и 450°—в норме, если принять объёмы на линии сухого насыщения по экстраполяции норм МК 30. В общем данное в

10° от Гв сторону возрастающих темп-p и взяв для тех же давлений отношение

-{^1:10.

LA Р т+ ю V р J тл

Энтропии конечно нужно вычислять непосредственно по теплоемкостям с_р. Теплоемкости, как мы видели, даются изобарами в системе Т, с и мы можем последовательно вычислять, идя по изобаре, разности энтр между двумя близкими t° на основании соотношения откуда

(Si-SOp-J4^=c_ftnl+>

где cp_m—средняя из теплоемкостей для темп-р Г₂ и Т_1} если разность между Т₂ и Т_г не превышает 10°. Таким путем мы вычисляем Энтропии для различных давлений и t°. Этот путь дает более точные результаты. Но, с другой стороны, вычисляя энтропии на основании приближенно линейной зависимости —· от р. мы можем сравнивать их с более точными значениями и т. о. поверять основное соотношение линейности. Для разности энтальпий имеем опять по изотерме

(»» - Ч)_т= T(S_n - SO + ^ fv dp=- ln^+

+ + /> =

= Α(ρ_η-_Ρι)[τ^^)-^].

Отсюда можем определять энтальпии или, наоборот, вычислив энтальпии по теплоемкостям, как было выше указано, исправлять кривые для определения объёмов, переходя по изотермам от изобары в 1 atm, для которой имеются уже давно установившиеся данные, к изобарам высоких давлений. Ф-лу можно написать так же, если принять во внимание, что

ΐ™.= [(^φλ — 1 ^{711+ П}° д_ (ϋΛ

V Llp/ioo pJoJ 100*2 ¹ Vp/o

для давлений n и щ atm,

^-Ч={^о^П°[й(^Д/-^Д)-^Д] +

+ S^A"-(pU<ⁿi-ⁿ»>⁴·¹⁰*·

Здесь Δ=(—) — (—) для Т + 10°, Δ—то же для Г’ иД"=(|)_о(Г+1в)-(У_в(!Г).

Возьмем например изотерму 623° (одну из наиболее отклоняющихся в величинах ~ от закона линейности) и будем переходить от 1 atm к 50,

100 и 168,7 (насыщения) atm. По чертежу для ординаты Т+10 можно принять (на пробу)

(I.)=40 7 · 10”⁴; (—)=61,7 * 10“⁴.

Т. о. Δ=21 · 10“⁴, Δ дается в 25 · 10“⁴ и Δ"== (42 — 40,7) · 10“⁴=1,3· 10“⁴. Тогда получим, взяв для Т atm энтальпию в 759 Cal (759+2 МК 30), для 50 atm 736,9 (734+2,5), для 100 aim 698,4 (701,5+3) и для насыщения 619,3 (615+8), числа, вполне удовлетворительные, хотя два первых немного выходят из допусков МК 30. Для других изотерм имеем также вполне хорошее согласие. Т. о. и здесь мы видим, что правило линейности величин в своих следствиях не дает больших отклонений от опыта. Соответственно для энтропии получим

8,-S^-AR 1п^ +

+ ++++-^Δ)·

• ΐι+Ι!» + Δ"] · КГ·

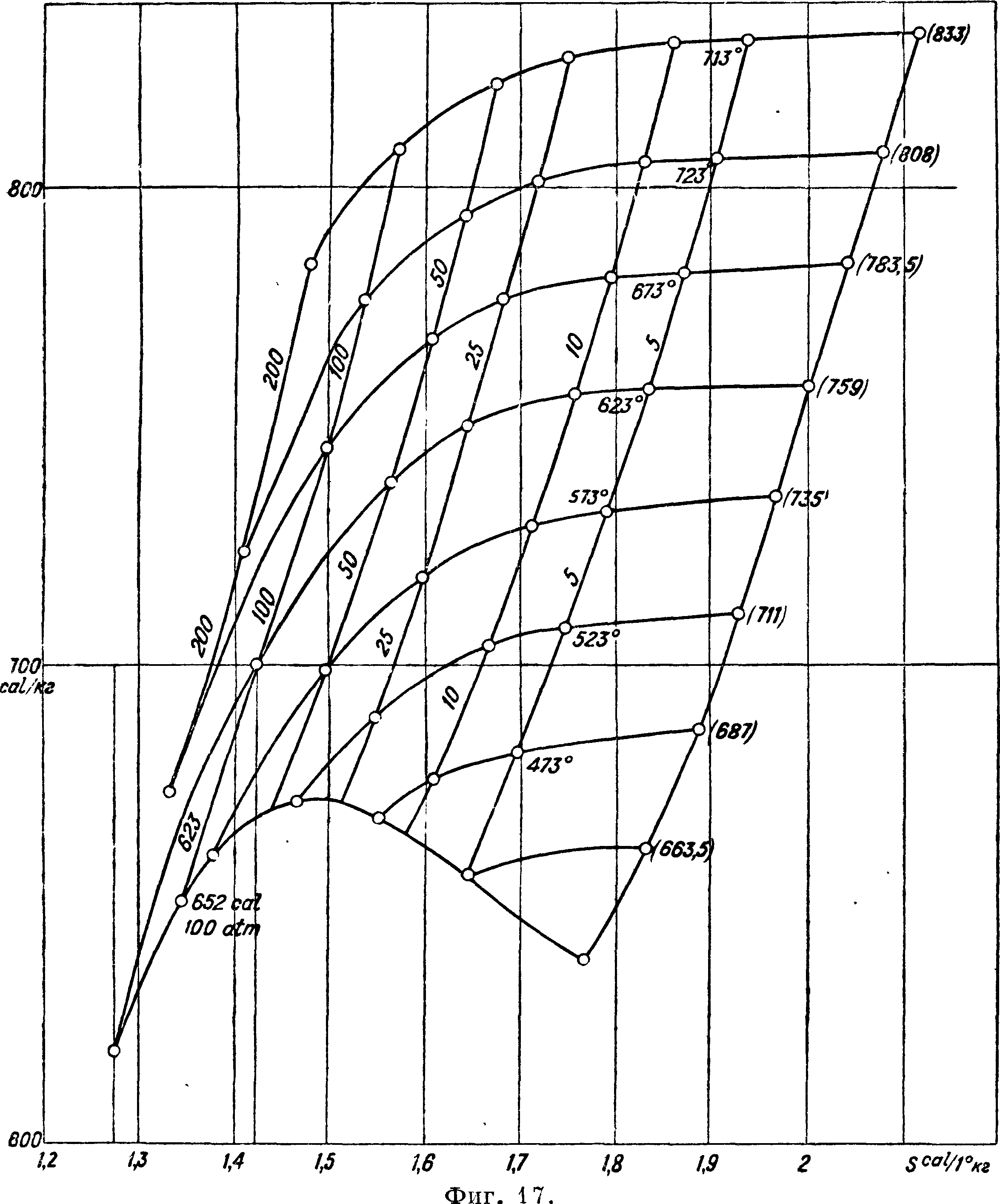
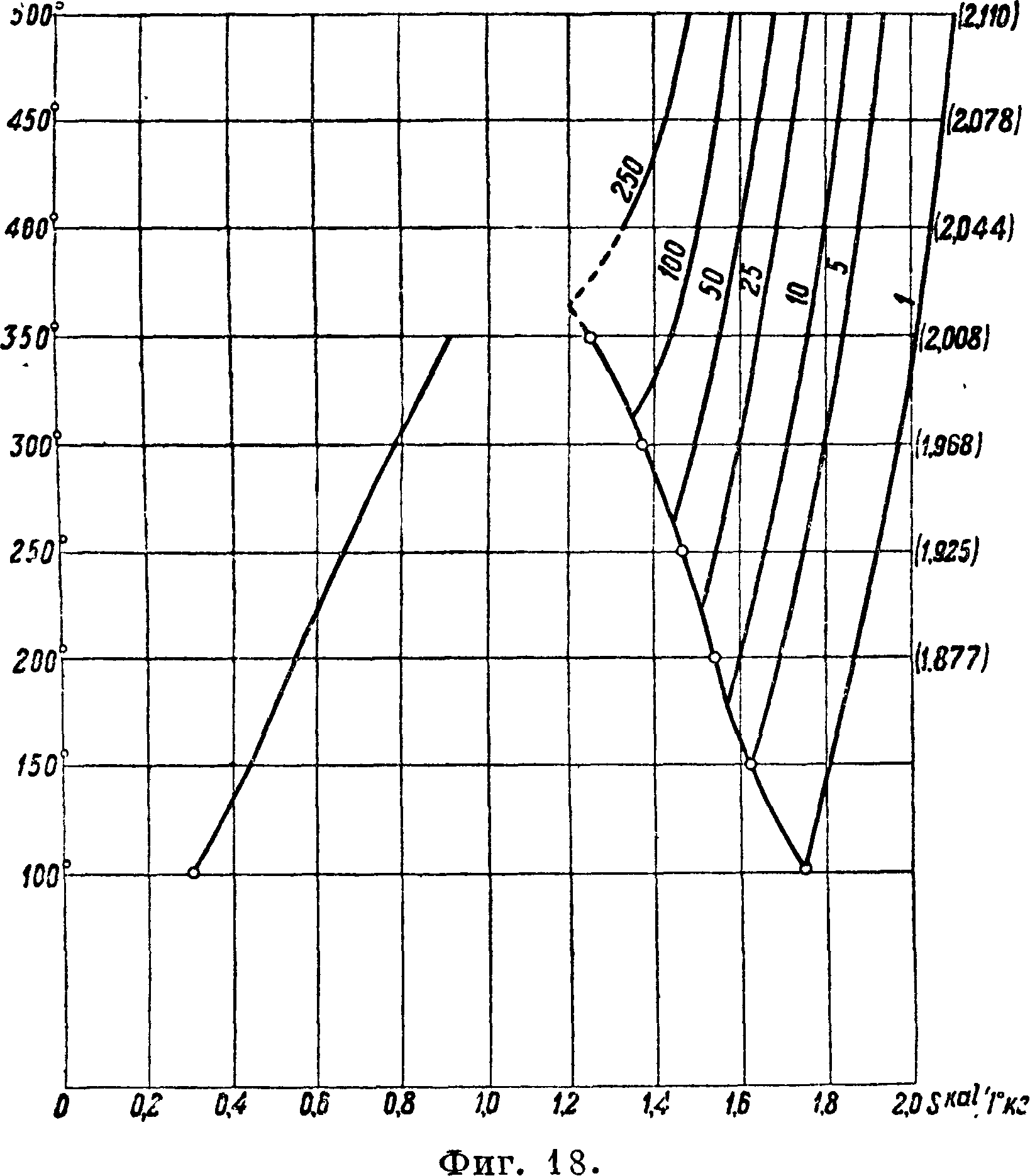
и, взяв значение S₀ для 625° и 1 atm, например по Молье (Molli ег), получаем энтропии для различных!давлений (то есть превышение энтропии над энтропией воды при 0°). Таким путем составлены неоол ыние прилагаемые таблички в системе координат ins (фигура 17), а также и в системе Т, Ф(фигура 18), могущие служить для приближенного ознакомления с величинами энтальпий и энтр. Нужно еще раз заметить, что составление величин энтальпий и энтр по кривым объёмов служит гл. обр. для поверки этих кривых. Точное же вычисление г и S, например для составления новых таблиц, должно разумеется быть произведено по данным о теплоемкости перегретого пара или по опытным данным о разности энтатьпий, как об этом было сказано. Составление ур-ия для перегретого водяного пара пока преждевременно; еще нет достаточных опытных данных даже для скрытого тепла парообразования при высоких давлениях (Якоб до 310°) и хотя имеются отдельные данные об энтальпиях перегретого пара (Гавличек до 225 atm), но определение скрытого тепла парообразования необходимо для сравнения и контроля различных опытных величин. Далее нужно заметить, что при определении объёмов по кривым мы пользуемся уравнением pv=47 Т — <р, причем T=t- -273. Если бы мы согласно Битти и Бриджмену положили Т=<-|-273 ДЗ, то нужно было бы вместо 47 положить 46,99,—результаты получились бы те же самые. Данные здесь кривые объёмов и представляют в сущности графически характеристическое (приблизительное) уравнение вместе с табличками г, S и Т, S. Кривая насыщения по нормам МК 30 удовлетворяется этими графиками как со стороны объёмов, так и со стороны энтальпий.

Дополнительные соотношения для жидкости и насыщенюго пара. Теперь мы можем опять вернуться к жидкости и коснуться неоконченных ранее вопросов. Опытное определение теплоемкости воды было сделано Диетеричи еще в 1904 г. Общая схема опыта была следующая:

в кварцевую трубку определенного объёма вводился водяной пар, к-рый там конденсировался, и излишняя вода удалялась при помощи воздушного насоса испарением, затем трубка запаивалась. В ней при общем известном объёме V находилась смесь жидкости и пара, общая масса коей была известна. Далее производилось нагревание трубки до определенной ί°, и затем трубка быстро падала в ледяной калориметр Бунзена, в к-ром и определялось количество тепла, выделившееся при охлаждении. Принимая, что общий объём, занятый смесью, не изменился за время опыта,мы имеем очевидно процесс охлаждения смеси при постоянном внешнем объёме, и следовательно количество выделившегося в калориметр тепла определится (на единицу веса смеси) по соотношению

t

dQ~du_x=d(u₀ + ex), т. e. ρ-ιJ₀ + e^~’

О

где U₀—превышение внутренней энергии на пограничной кривой при t° нагрева над энергией при 0°, а—удельный объём смеси. Для известного веса М это будет

_Ям=ми₀ + (>Цр,

О

где V—внутренний объём трубки. Далее по соотношению Клапейрона имеем г=АТ^и, то есть ρ=Α

и следовательно

t

Q_M=Μϋ₀ + A j -p)(F - Mv).

О

Второе слагаемое правой части равенства под-

dp

считывается по опытным определениям р, V для темп-p t и 0°, общее количество Q_Mопределяется по калориметру как разность тепл от, отданных калориметру всей трубкой и ее стенками, и т. о. определяется превышение внутренней энергии жидкости на пограничной кривой при температуре t над энергией жидкости на той же кривой при 0°. Следовательно в опытах Диетеричи определялось собственно изменение внутренней энергии жидкости на пограничной кривой по мере повышения t* (и давления). Но, зная объёмы и давления на пограничной кривой, мы можем определить и энтальпии по соотношению г=U + Apv. Та-кем обртзом мы получаем, принимая условно· энтальпию при 0° С равною 0, энтальпии на пограничной кривой. Определенные таким путем по опытам Диетеричи величины мало разнятся от величин, даваемых опытами Осборна [^б], и до 250° согласны с величинами, принятыми МК 30. При 300° (опыты Диетеричи шли только до 303°)

й?=316,5; %кзо ⁼ 322 + 2»

эта разница объясняется вероятно тем, что“ входящие в определение ϋ_ύ величины ν, а также -- для темп-p, больших 270°, определены Диетеричи экстраполяцией за отсутствием тогда опытных данных. Мы можем теперь принять во внимание общее выражение энтальпии для жидкости г - - Αν₀ (р - р₀) ^^Ро)^_ТГ(Т) _ _/(Т)] + + f с_Рд с1Т.

Отсюда, пренебрегая р₀, получим i + Ар (l — -|· р) [Tvо f (T) - ®₀ f (T)]=f c_po dT.

С помощью касательных к кривой v₀ f(T) определяем v₀ f(T) и далее все второе слагаемое левой части равенства. Капр, возьмем Т= 523^е* (250°С), р в этом случае на пограничной кривой=40,6 atm, ν₀ /(Τ) согласно кривой v₀ f(T) молено принять=27 · 10~⁷, так что Tv₀f₀(T)-==0,00141 м³, далее vJ(T)=0,001253 ж³ и следовательно второе слагаемое=~ · 40,6 · 10⁴ · •0,998*16· 10“⁵, то есть <0,2 cal, им можно пренебречь и написать г=§ с_Ро dT. Это равенство и дало повод говорить, что Диетеричи определял теплоемкость с_р для воды. Если мы возьмем 300°, то слагаемое дает ок. 2,2 cal, так что при г=332+2 (МК 30) оно опять не будет заметным, но при 350° вследствие быстрого подъема давления и значения v₀f(T) слагаемое дает ~ 19 cal и при общей величине г =

= 404+5 МК 30 даст f с_Рос1Т - 423. Т. о. при давлениях, близких к давлениям на пограничной кривой, соответственно до t° 250° мы можем пользоваться соотношениями

^ f%^dT

и С_Р0 брать по известной формуле Диетеричи. При более высоких давлениях ц соответственно t° мы по данным на пограничной кривой строим кривую j c_pQdT и касательными определяем с_Ро, а затем и с_р. Но разумеется полученные величины годны лишь в области давлений к темп-p, недалеко отстоящих от пограничных значений (ср. [²¹]). Вычисление же энтропии на самой пограничной кривой для получения ее изображения в системе Т, φ можем вести непосредственно, исходя из равенства

Avdp

Т

+ J Yi dT-Af^dp.

Строим кривую ~ в системе ~, Т согласно значениям г на пограничной кривой, далее кривую ~ в системе ~, р, определяем их ин тегральные и получаем значение энтр на пограничной кривой. Но, с другой стороны, если нам даются значения энтальпий на пограничной кривой жидкости и на кривой сухого насыщенного пара, то разность энтальпий для одной и той же t° есть скрытое тепло испарения, и если мы последнее разделим на Т, то получим разность энтр на кривой сухого насыщения и на пограничной кривой жидкости, как это следует из ур-ий, данных для насыщенного пара. Это соотношение дает возможность контроля над принятыми величинами. Вычисленные по данной формуле энтропии на кривой жидкости для 423°, 523° и 623° имеют значе ния 0,444, 0,673, 0,915; энтальпии для сухого насыщенного пара, определенные по правилу линейности (для перегретого пара) соответственно равны 656, 672, 619 (в круглых числах). Взяв энтальпии на нижней пограничной кривой по МК 30, имеем 151, 259, 404 (±5); по разделении разности на соответственные Т и прибавлении частного к величинам энтропии на нижней пограничной кривой получим энтропии сухого насыщения величинами 1,638, 1,461, 1,252 до 1,260, а по правилу линейности 1,637, 1,459, 1,252—согласие, вполне удовлетворительное. Вторым контрольным соотношением является, как уже было указано ранее, соотношение между теплоемкостями с_р для жидкости и перегретого пара вблизи насыщения, скрытым теплом испарения и коэф-том темпер гт-урного расширения жидкости и пара. В применении к водяному пару это соотношение дает возможность определить коэф. темпе-

dv₂

ратурного расширения от пара. Пусть наир. применяется это соотношение при Т= 523. Мы могли бы определить коэф-т расширения в точке сухого насыщения таким образом: _л, RT φ „ (dv₂ R ο

v

р и

/dn₂ й__д (<р дТ)_р р дТ[р)_р’

то есть строим кривую со значениями — для 523,

533 и скажем 548 при давлении р=Const== 40,6 atm. Касательная к конечной точке (523°) этой кривой и дала бы искомый коэф., но касательную в конечной точке трудно провести точно, и соотношение между теплоемкостями может служить именно для нахождения коэф-та расширения и поверки таким путем характеристич. ур-ия графического или алгебраического.

Критическая температура. В диаграмме Т, S (фигура 18) для паров воды мы видим, что нижняя пограничная кривая и кривая сухого насыщения сближаются постепенно с повышением t° и следовательно сливаются где-нибудь. Точка слияния на диаграмме не показана, т. к. табл. МК 30 идут лишь до 350Т Слияние это произойдет при t° приблизительно 374°, како вая и носит название критической t°. Основание для такого названия общеизвестно и наглядно поясняется диаграммой Т, S: если мы, имея перегретый пар в 1 aim давления и 300°, будем его изотермически сжимать, то есть на диаграмме пойдем в сторону убывающих энтр (отнятие тепла), то приведем пар при давлении 87,7 .atm к сухому насыщению, после чего дальнейшее изотермич. сжатие поведет к конденсации пара и обращению его в жидкость. Но если мы тот же процесс проделаем при Г 450°, то совсем не встретим кривой сухого насыщения, и пар будет оставаться газом. Отсюда известный закон Андрьюса: изотермич. сжатием с t° выше критической ни при каком давлении нельзя обратить газ в жидкое состоя-рие. Само слияние двух пограничных кривых (жидкости и сухого насыщения) представляют обычно так, что обе кривые касаются в слиянии критической изотермы, и для критической точки (точки слияния) высказываются следующие положения: 1) тепло испарения=0; 2) коэф. температурного расширения, то есть=оо;

3) с_р= оо; 4) (jfy_T=0. Первое положение неяс но с термодинамич. стороны: если обе кривые касаются критич. изотермы, то есть имеют общий малый элемент, то тепло испарения м. б. очень мало, но не будет в точности равно“ нулю, что непосредственно видно из диаграммы Т. S. Второе, третье и четвертое положения с>ть чисто математич. условности, т. к. говорить например о коэф-те ί°-ного расширения, когда изотерма и изобара совпадают, с точки зрения действительности не приходится. Но и вообще если в слиянии обе кривые имеют общий элемент с изотермой, то переход из жидкого состояния в газообразное при t° _Kpumt будет отличаться от обычного процесса испарения только своей относительной быстротой и для нас неуловимо малым количеством тепла испарения, по существу же это будет тот же самь и процесс с термодинамич. стороны. Точно так ж.) и положение Андрьюса о невозможности путем сжатия обратить газ в жидкость при t° выше критической можно было бы сформулиро-ватьтак: t°_Kpvm есть темп-рный предел возможности ожижения газа доступными для нас давлениями. С термодинамич. же, да и с мехакич. точки зрения ничто не препятствует предположить существование другой фазы, подходящей по своим свойствам к жидкости, при очень высоких давлениях и при относительно высоких температурах. Также неясен и вопрос об объёме в критической точке. Объем этот собственно определяется экстраполяцией по правилу Кайете и Матиа: если отложить на абсциссах темп-ры, а на ординатах—плотности жидкости и сухого насыщенного пара, то среднее арифметическое из этих ординат лежит приближенно на прямой, которая разумеется проходит через точку слияния кривых, представляющих плотности. Это правило имеет место и для воды. На фигуре 19 представлена прямая, ординатами подходящая к средним арифметическим из плотностей жидкости и пара. Если ее продолжить, то получим в пересечении с критич. изотермой (374°) плот-

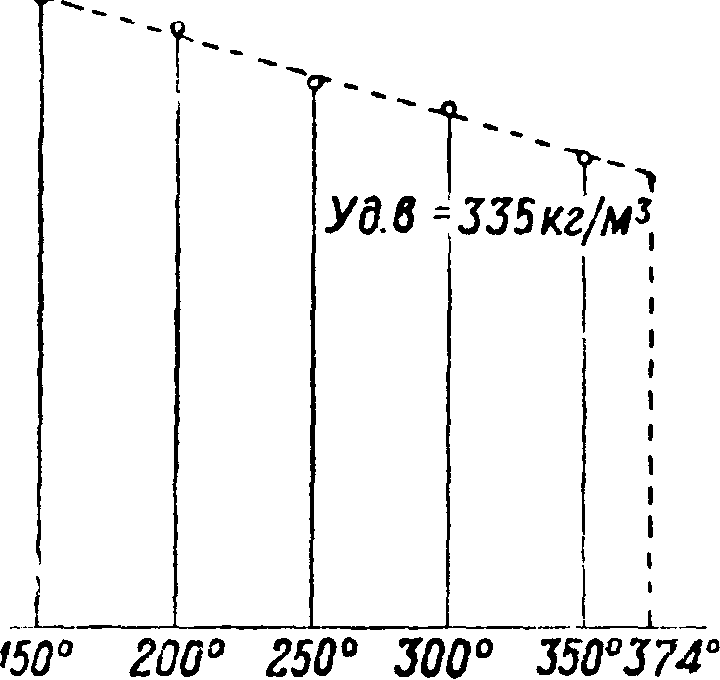
Фигура 19.

ность в критич. точке, то есть и уд. объём. Вероятный уд. в таким путем определяется в 335 килограмм/м³, то есть вероятный уд. рбъем в 0,003 м³/кг. Но опыты Гейна (Hein) с углекислым газом показали [⁶],. что т. н. критические явления м. б. наблюдаемы в довольно широких пределах плотностей, и т. о. уд. критич. объём является величиной неопределенной. Это дает основание Нернсту утверждать, что нижняя пограничная кривая жидкости и кривая сухого насыщения соединяются при V

крит. небольшим отрезком критич. изотермы, где имеется состояние неустойчивого равновесия между жидкостью и ее паром, благодаря чему и уд. объём вообще неопределенный. Но тогда, как уже было указано, переход жидкости в пар и в критич. состоянии с термодинамич. стороны по существу остается тем же, что и до этого.

Переход из твердого состояния в парообразное и жидкое. Общеизвестный факт испарения твердого тела дает основание применить уравнения Т. и к переходу из твердого состояния в парообразное и жидкое. В частности ур-ие Клапейрона г=АиТ м. б. также применено к испарению твердого тела, причем здесь г будет тепло испарения твердого тела, соответствующее данной t° (и давлению пара), и обозначается часто через s (Sublimation), величина и есть разность уд. объёмов пара и твердого тела v— При этом можно пренебречь то есть уд. объёмом твердого тела, сравнительно с объёмом пара, и тогда

dp

AvT

dT

€ другой стороны, переход твердого тела в жидкое связан с теплом плавления; обозначим его через I, тогда опять можно применить соотношение Клапейрона к этому процессу

»l).

где v₂—объём жидкости. Для воды v_±>v₂ при 0° и 760 миллиметров рт. ст. г>₂=0,001; гд=0,001091 (лг³/гсг).

• У1* 1U -

Следовательно=— ~

= — 73 · КГ⁸. Возьмем приближенно ~

dT

и ΔΡ=8,1 Atm, тогда ΔΤ=73 · 1(Г⁸ · 8,1 · • 10⁴ · 1,0332=0,0616. Другими словами, при повышении давления на 8,1 Atm температура таяния льда понижается на 0,0616°. В. Томсон нашел понижение опытным путем в 0,059°. Наоборот, для тех тел, у которых при плавлении объём увеличивается (^₂>гд), iпл. повышается с повышением давления [⁶]. При %_л. м. б. существование смеси из пара, жидкости и твердого тела. Если обозначить через г скрытое тепло испарения жидкости, то в этом случае s=r- -l и т. к.

r=AT(v-v₂),

^ дгп ( dp_

— ^J±-^Lv dT dT)

dP, dT) dP dT)

T. к. тепло плавления l всегда существует, то

dp dP

всегда имеется разность » ^τ· ^е· если мы построим в координатах Тир кривые σ и σ₁зависимости р от Т в процессе парообразования для жидкости и твердого тела, то при они пересекаются, имея разные касательные в точке В пересечения^

Фигура 20.

273

(фигура 20). В сторону возрастающих Т от обеих кривых будет область газообразного состояния·; в сторону убывающих Т в одном случае будет область жидкости, в другом—область твердого тела. Обе области в свою очередь разделяются кривой сг₂, указывающей на зависимость t^. от давления.

Г азы. В настоящее время все газы нужно рассматривать как перегретые пары, находящиеся б. или м. далеко от состояния насыщения. Мы видели уже, что закон Мариотта-Гей-Люссака является лишь пределом, к к-рому по своим свойствам пары стремятся по мере повышения t°. Поэтому если для какого-нибудь газа провести опыты над изменениями произве

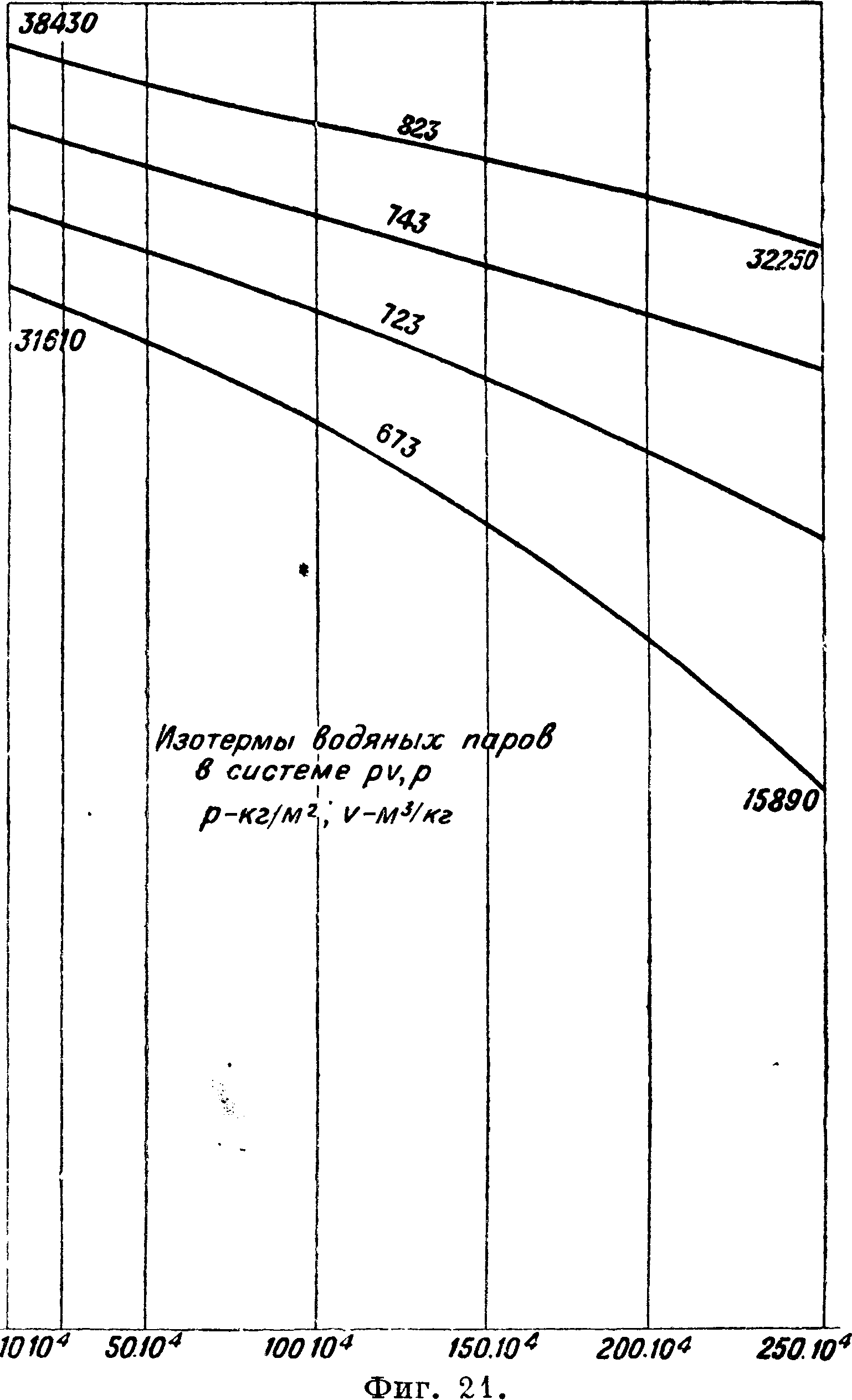
дения pv в зависимости от р при данном Т или в зависимости от Т при данном р, то мы не получим в первом случае прямых, параллельных от р, а во втором—прямых, наклонных к оси Т (возрастание ординат пропорционально Т). Если мы по нормам МК 30 построим в системе р, pv изотермы для перегретых водяных паров, то получим кривые (фигура 21) с ординатами, убывающими по мере возрастания р; кривые стремятся к спрямлению и параллельности оси р по мере возрастания Г. Течение их показывает, что характеристич. ур-ие должен быть всегда pv — RT — φ, где <р—положительная величина, т. к. произведение pv убывает с возрастанием р. Если бы мы изобразили какую-

нибудь изобару в системе Т, pv с давлением например в 50 atm и начали бы с Т=623°, то ординаты (pv) имели бы значения 26 5 5 0(623°)“, 29500(673°); 32200(723°); 34850(773°); 37350(823°);

разности между двумя последовательными ординатами с расстоянием между ними в 50° были бы 2950; 2700; 2650; 2500, то есть убывающими с возрастанием Т. Отсюда мы заключаем, что

—· при р=Const убывает, то есть < 0 и следовательно, по равенству

Шт=-^АТ («-£),· ё-^>0·

как на самом деле и имеется в опытах Кнобла-уха, то есть теплоемкость возрастает с давлением лри данной Т. Для углекислого газа изотермы p_v в системе р, pv име-

¹ ют другой вид (опыты

Амага) (фигура 22): произведение pv падает до 200 atm (приблизительно), а затем возрастает, но изотермы постепенно спрямляются по мере повышения Г.После-___ довательные разности

ФИГ. 22. (дт)p=Const Убывают и в той и другой части кривой (для давлений 100 и выше атмосфер) и «следовательно здесь c_v возрастает с давлением, но Люссана нашел, что и для меньших давлений также возрастает с давлением [⁷j. Подобная же зависимость найдена была и для аммиака NH₃. Прилагаемая диаграмма (фигура 28) (взята у Jellinek) показывает, что пары аммиака в отношении теплоемкости с_р очень сходны с парами воды. Для воздуха имеются исследования двоякого рода:.с одной стороны, определялось произведение pv, с другой,—теплоемкости с_р, при различных t° и давлениях. Первые исследования [⁸] представлены диаграммой в системе р, pv (фигура 23) и диаграммой Т, pv (фигура 24); вторые [⁹] представлены таблицами с_р в системе Т, с_р (изобары) (фигура 25) и в системе р, с_р (изотермы) (фигура 26). Изобары между б и 50° отчасти дополнены по Витковско-му, данные Ребук (Roebuck) взяты по статье О. Бриджмена [¹⁰]; затем имеется еще исследование (Холборн и Якоб) по теплоемкости с_рвоздуха для 60° между давлениями l-f-300 atm. Значения здесь близки к значениям по Ребуку. Таблица изобар с_р по Ребуку указывает, что и воздух имеет между темп-рами 50° и 280° свойства теплоемкости с_р, похожие на свойства с_р у паров воды, только разумеется зависимость от давления меньшая, нежели у паров, и при 280° теплоемкости для различных давлений очень сближаются, так что можно с большим основанием считать их при темп-ре высшей (например 400—500°) не зависящими от давления (в пределах 1-7-200 atm), а только от f, как это имеет место для газа, следующего соотношению pv=RT. То же самое мы видим и по изотермам с_р, т. к. изотермы по мере увеличения Т стремятся к прямым, параллельным оси р, то есть к независимости от давления. Сопоставим теперь данные относительно с_р с данными относительно pv. Изотермы pv сравнительно мало отклоняются от горизонтальных прямых, но не имеют той правильности в характере своего отклонения от горизонталей, какая замечалась на изотермах углекислого газа: например изотерма 200° более отклоняется от горизонтали, нежели изотерма 50°. Посмотрим, насколько отношение объёмов в том и другом случае отступает от закона Мариотта; возьмем объёмы (v_x) при 10 метров рт. ст. и (v₂) при 70 м, их отношение для изотермы 200°

Ρι^ι ϊ>2 _ 1,7406-7 _ β

ρ._Δν₂ * Pi 1,7927 ^Ь·’⁷

и для изотермы 50°=Vi§ii~⁼ 7,0194; по Мариотту и в том и другом случае должно быть 7. Т. о. отступлено от закона Мариотта в

1,7406 1,5555 1,3695 11825 0,9934 pv			2001. 1500			W	___1 )27	,8027 1,6052 1,4037 1,1932 0,9708
			100°				167
			50°			ffl	m
			0°			W	Ю4
		(Но (Но, pv	Изот возд, всист lborn& Iborn & =1 при f i	ермы уха iPKP SchultZi Otto 192 )=1мНд	? 1915) 2-25) U0° P	0,9	709

(0 20 30 40 50 во 70 80м.Нд

Фигура 23.

первом случае (200°) больше, чем во втором, а между тем, если судить по теплоемкостям, должно бы быть наоборот. Поэтому мы можем сказать, что значения pv, данные опытами Холборна, не вполне соответствуют данным с_р по Ребуку, и следовательно нужны новые более обширные опыты для полного термоди-намич. выяснения свойств воздуха при невысоких темп-pax и относительно высоких давлени-

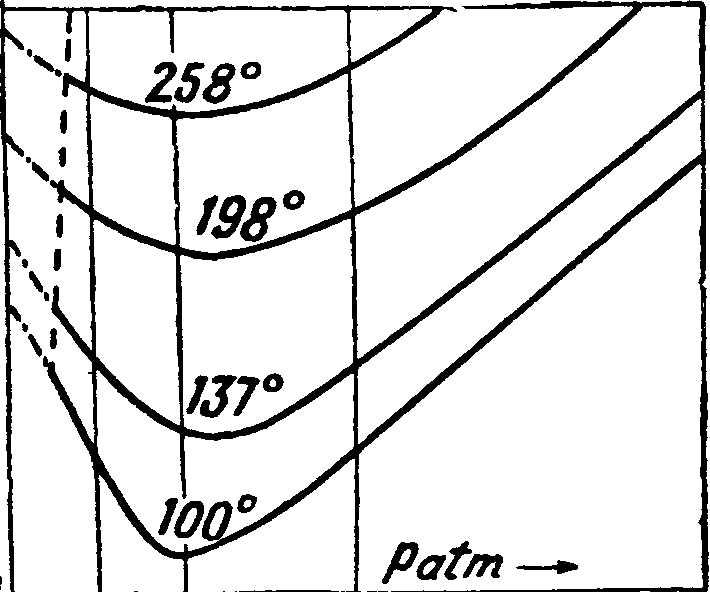
ях. Характеристич. ур-ие, данное для воздуха (и других газов) Битти и Бриджменом,·хорошо

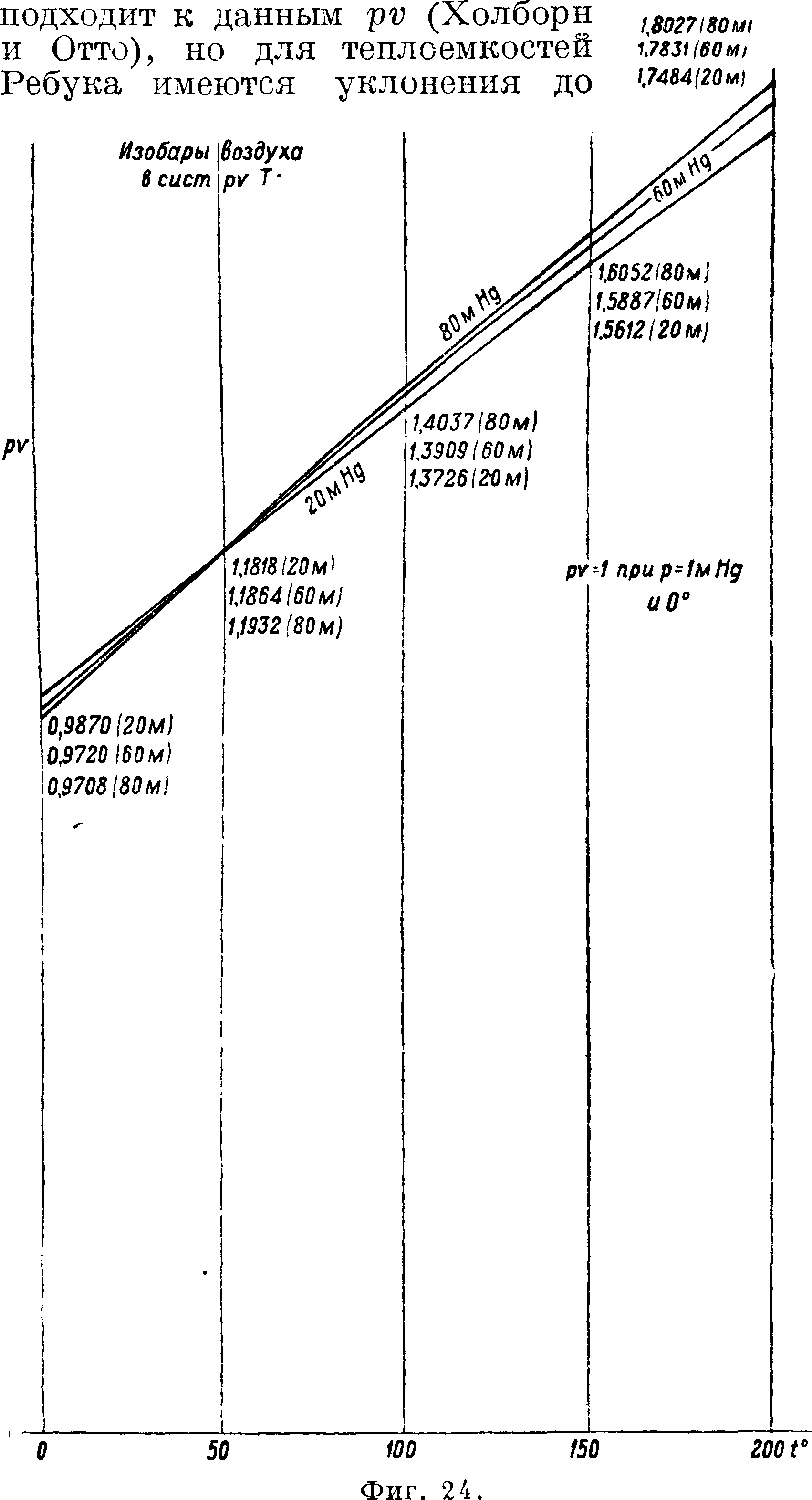
8%, что также подтверждает неполное соответствие между опытами относительно pv,

с одной стороны, И Ср,—с другой. При полном соответствии между обоего рода опытами мы могли бы по таблицам для с_р и ρυ построить в координатах S, Т линии р=Const и v=Const и т. о. рассмотреть разницу в изображениях в системе S, Т, когда мы принимаем воздух как совершенный газ и когда мы берем во внимание зависимость теплоемкости от давления. По изобарам для с_р высчитываем для какой-нибудь изобары последовательно причем здесь в виду небольшой зависимости с_р от р можно было бы интервалы для постепенного

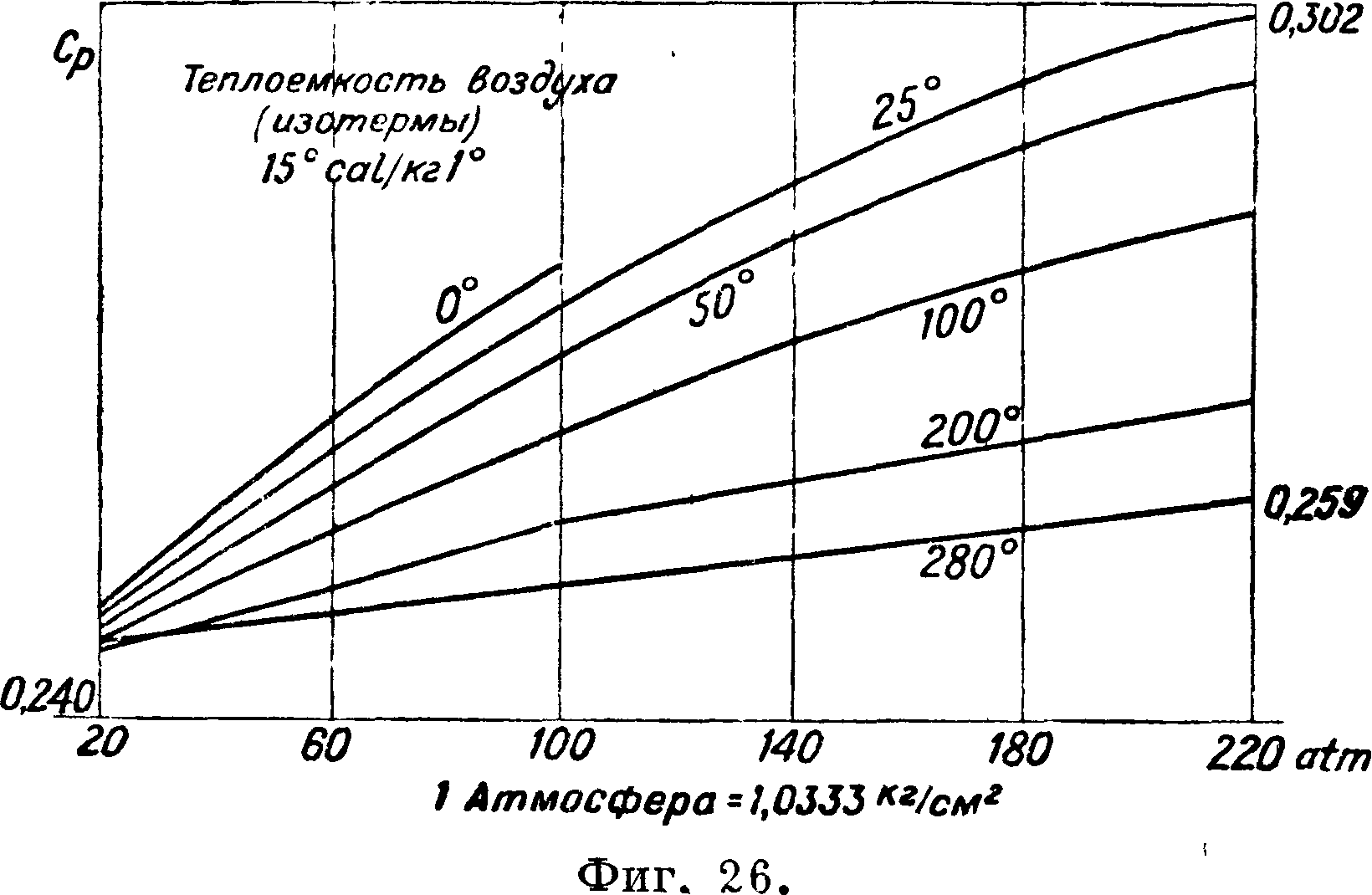
интегрирования взять в 50°, так что интеграл обратился бы в 2 o_Pm In —ψ·⁵⁰, где с_Рт—средняя теплоемкость интервала. Т. о. разность энтр для последовательных Т определилась бы, и мы взяли бы произвольную точку на изотерме 273°, провели бы из нее линию р=Const, например для 20 atm. Для отыскания начальной точки другой линии, например в 60 atm, мы можем воспользоваться ур-ием

<5Q=c_p dT — AT g® dp,

для какой-нибудь изотермы (здесь например 0° С) имеем

0Q-TdS — AT%’-dp,

отсюда

Строим изобары pv для различных давлений между 20 и 60 atm в системе Т, pv и для изотермы Т=273° проводим касательные к этим изобарам, получаем для различных давлений. Затем откладываем на абсциссах р (от 20 до 60), а

d(pv) 1

на ординатах ~_т~ · —, и интегральная кривая от полученной кривой даст значение S_β0 — S₂₃ по изотерме 0°. От полученной начальной точки для 60 atm строим кривую р=Const== 60 atm, как и для 20 atm,. Но ее можно построить также, если мы будем высчитывать S_6{)- S₂₎ для различных t°. При полном согласии между данными для pv и с_р оба способа должны привести к одному и тому же результату. В разбираемом случае этого у нас нет, и поэтому здесь можно только указать способ построения линии р=Const в системе S, Т;

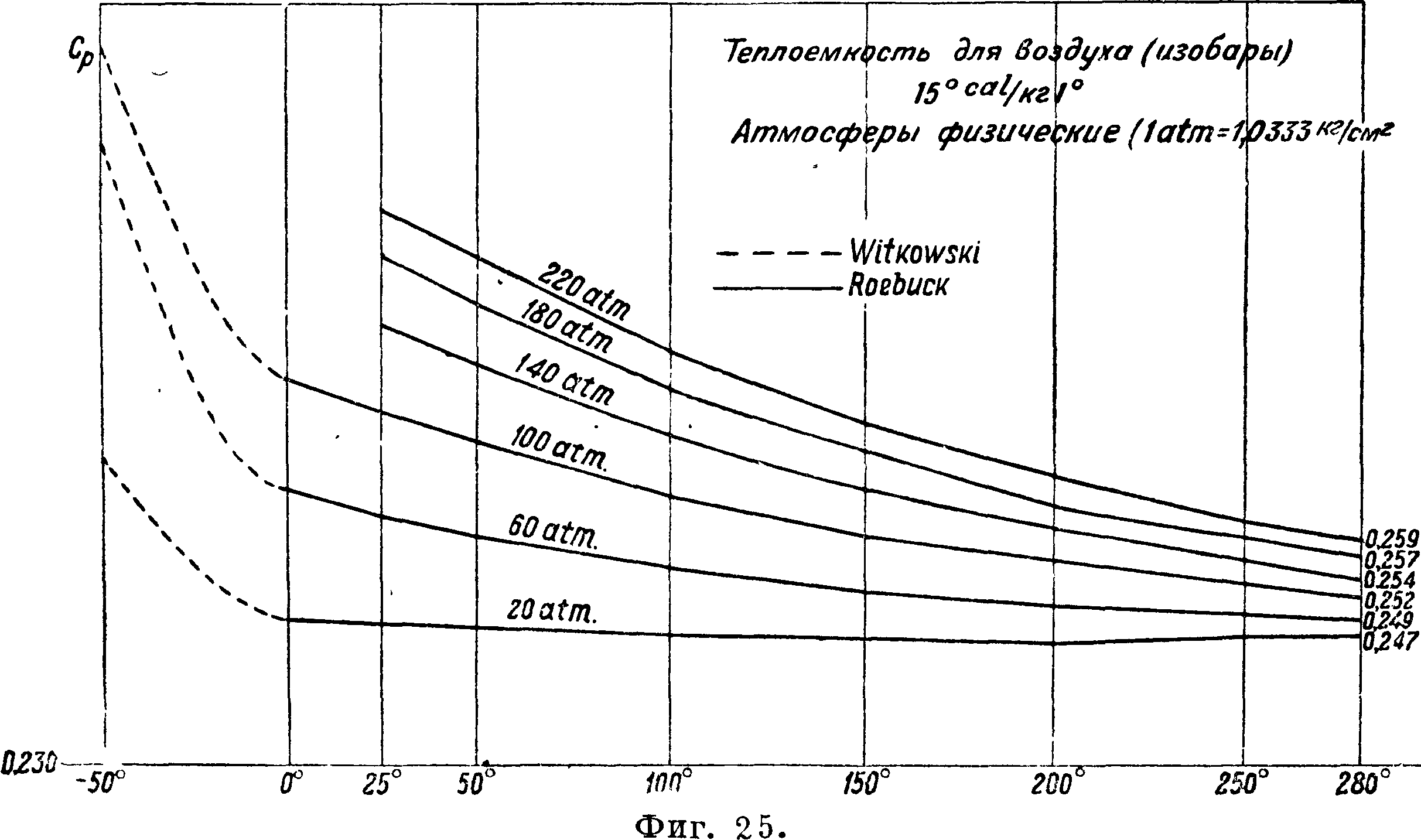
аналогично можно построить и v=Const. Заметим, что в пределах невысоких давлений (между 1-р60 atm) зависимость с_р от давлений для воздуха невелика, если основывается на опытах Ребука. Поэтому можно принимать теплоемкость с_р постоянной величиной в пределах Р до 280°, а далее считать ее зависящей лишь от Р. Что касается характеристич. ур-ия для воздуха, то, как уже сказано, для составлений в области невысоких t° и сравнительно высоких давлений пока нет достаточно согласованных данных. Всякое ур-ие, как мы видели, например для водяного пара, является лишь подходящей интерполяционной ф-лой, и единственным общим и закономерным во всех таких ф-лах является то, что в пределе всякий газ по своим свойствам приближается к характеристике pv=RT со всеми термодинамич. следствиями этой характеристики [⁶]. Что касается вида характеристич. ур-ия в общем случае для газов, то Камерлинг-Оннес предложил следующую интерполяционную ф-лу

В, С, D

pv=RT + — + т»+-^г+ ···.

ъ_гт где В, С, D суть ф-ии /° вида В=b₀ -

+ Τ + ΙΪ+-

Такие ур-ия отличаются большой сложностью и практйч. неудобствами при вычислениях, но зато могут более полно представлять опытный материал. К этому виду относится и ур-ие Битти-Бриджмена где

νΤа

Pv=RT( -e) (1+1)

ь В-Во (1-1·); ^=Λ(ι-^Τ

так что в раскрытом вице получим

pv=RT-± (4£-RTB₀ + А)--(RTBvb+^-aA,)

Ь cRb₀ 1 ^_‘ Уз и непосредственно усматриваем его родство с ф-лой Камерлинг-Оннеса. В этом уравнении р считается в физических атмосферах (1 Atm —=1,0333 килограмма/см², то есть 760 миллиметров рт. ст.), v—в л/моль, то есть на количество граммов, равное мол. в газа—т. н. граммолекула. Нетрудно убедиться (по уд. весам газов), что в этом случае при р=1 Atm и 0° объём однородного газα=22,412 л (в среднем), поэтому постоянное R в ур-ии Мариотта-Гей-Люссака определится в 22

, то есть в 0,0821 (округленное число Нерн-

ста) л · Atm/1° моль. При этом 1 л Atm== 103,33 килограммадм=10,333 килограммам=0,02419 Cal -= 21,19 cal и следовательно постоянное К== 1,985 cal/l° моль. Воздух есть смесь газов; мол. в смеси определяется, как известно, ф-лой

-=А~т^-, для.воздуха он принимается=28,96;

^ т_п

объём одного моля также=22,412 л и постоянное R—то же самое; Бдття и Бриджмен принимают R=0,08206, затем Т=273,13+ t и для воздуха следующие постоянные: А== 1,3012, В=0,04611, α= 0,01931, 5 =

= —0,01101 и с=4,34 · 10⁴. Ур-ие Битти-Бриджмена неудобно тем, что кроме значительной сложности оно дает дополнительную (к ур-ию pv=RT) величину в ф-ии v и Т, и при данных р и Т определение v становится весьма затруднительным. Поэтому например для сравне ния опытных определений теплоемкости с_р с теми значениями, которые термодинамически вытекают из характеристич. ур-ия, приходится прибегать к обходу: сначала определять c_v, вытекающее из ур-ия, на основании соотношения

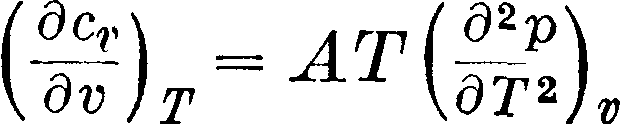
и далее пользоваться равенством

Gp AT

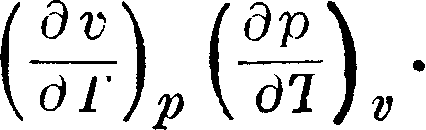
Удобнее поэтому обратиться к тем интерполяционным ф-лам, где дополнительная величина дается в ф-ии р, Т. Холборн и Отто дают для своих опытов с определением произведения pv (смотрите график, фигура 23) относительно воздуха формулу pv=Л+Бр+Ср², где В я С суть ф-ии Т, а А—величина, пропорциональная (или почти пропорциональная) Т. Как уже было указано (фигура 23), в опытах произведение pv считается равным 1 при 0° и 1 метров рт. сг. Эторав-ноценно 7 991 килограммм (если принять вес 1 м³ воздуха при 0° и 760 миллиметров рт. ст. в 1,293 килограмма). На этом основании можно по данным pv подсчитать удельные объёмы v. С другой стороны, можно ур-ие Битти-Бриджмена заменить другим приближенным, если подставить вместо v в правой части его ^. Тогда имеем

pv

— р²

= RT-p(£-b₀+ £)-

(^во^ь, Я?с _п УМ 4- Г)3 ^b»^bc

КНТ^НТ ^а R2T) А Р

Здесь правая часть является ф-ией р и Т, и потому вычисление объёмов по данным р, Т более удобно. Но все же ур-ие отличается большой сложностью и притом, как уже было сказано, если из него термодинамически определится с_р J^Ha основании соотношения =

= — АТ ], то в области темп-р 0—50° С

полеченные с_р при высоких давлениях довольно сольно разнятся с спышыми величинами Ре-бука. Битги указывает на возможность здесь ошибок в опытах. Но можно ограничиться как первым приближением более простым ур-ием, к-рэе до известной степени представляло бы как опыты Ребука, так и данные Холборна. Изотермы с_р по Ребуку представлены на фигуре 26. Как первое к ним приближение можно взять наклонные прямые и выяснить наклон этих прямых в ф-ии темп-ры, другими словами, поло-

жить просто -= (Т). Это будет конечно лишь приближение. Можно остановиться на следую-

дСп CL

щем выражении:=ψ^, где а—постоян ное, к-рое мы потом определим. Отсюда г=_^аУ-^ΌΡ у²’²⁷

+ φ(Τ).

Здесь φ (Т) определим, приняв во внимание данные Госуд. физич. ин-та Германии относительно с_р для одной физич. атмосферы t¹¹]: с_р=0,2353 + 19 · 10^_6 Т. Слздоватзльно с_р=+ <р(Т)=0,2353 + 19 · 10“° Т;

отсюда φ (Т)=0,2353 + 19 · 10"» Т - —и с_р=(р -1,0333 · 10*) + 0,2353 + 19 · 10"^β Т.

Здесь р в килограммах/м², и если введем физич. атмосферы, то с_р=а_г -|^27 + 0,2353 + 19 · 10^_6 (Г.Подбираем так, чтобы не было слишком больших уклонений от опытов Ребука. Можно остановиться на di=120, тогда получим табличку, где имеются значения с_рио формуле (Ф), по Ребуку (ίΐ) и по ур-ию Битти-Бриджмена (Вт).

Изотерма 273°				1 Изотерма 298°
Atm Ф		R	Вг	Atm	Ф	R Вг
20 60 100	0,249 0,269 0,285	0,249 0,266 0,280 1 j	0,250 j 20 0,271 1 60 0,298 j 140 220		0,247 0,259 0,281 0,305	0,249 0,263 0,287 0,302	0,249 0,266 0,299 0,327

Изотерма		, 373е		Изотерма		473°	Изотерма		553°
Atm	ф ! 1	R	Вг	Ф	R	Вг	Ф	R	Вг
20	0,246	0,247	0,246	0,248	0,246	0,247	0,247	0,247	0,247
100	0,260,	0,266	0,263	0,251	0,257	0,255	0,253	0,252	0,253
220	0,281	0,281	0,283	0,267	0,268	0,265	0,261	0,259	0,260 1

Табличка указывает, что значения по формуле при более высоких темп-pax точны в общем почти так же, как значения по ур-ию Бриджмена, при более низких—более точны, и потому формулу в общем можно признать первым приближением к опытам Ребука. А на этом основании можно составить и характеристич. ур-ие. Имеем а у 2,27

и следовательно

d²v

от²

откуда

V=шТ -г Шл

АТ³> 27 ⁷

1

2,27

ЯТЬ27 ’

где ш я ш₁ могут быть ф-иями р. Мы возьмем т= ^ и ш_х — Const, далее имеем р и тогда а —

120

101-1,0333 104-1,0333

RT

V

1,7201

Ш ДЩ 27 *

Выбираем здесь т_±=1,2· 10“³ и проверяем формулу по значениям ν, даваемым опытами Хол-борна. Тогда получим при R=29,28 следующие сопоставления:

Изотерма 0°			Изотерма 100°		Изотерма 200°
Давл. в м II g	Ф-ла	Хол- борн	Ф-ла	Хол- борн	Ф-ла	Хол- борн
10 80	0,05860 0,00716	0,05840 0,00713	0.08058 0,01031	0,08049 0,01034	0,1024 0,01324	0,1023 0,01324

Т. о. молено принять формулу как первое приближение к опытам Холборна. Выведем теперь выражение энтропии, энтальпии и внутренней энергии для воздуха по данному здесь ур-ию. Обращаемся к ф-ии Ф

дФ, л (RT, т₂

— _-Av~-A[— + m₁- у-_)V7).

отсюда

Ф=— ART Ы р~ А — р + {(Т).

Произвольную ф-ию (Т) определим, обратившись к выражению

А -1,27 - 2,27

Q -Т-^Ф-

^ср~ ¹ дт²~

J2,27

- + Tf"(T)=0,2353 +

+ 19 · ΙΟ"⁸ Т + ^ (р -1,0333 · 10⁴)

и принимая во внимание, что т₂=^т

находим

1,0333а · 104

Tf" (Т)=0,2353+ 19 · 10~⁶ Г

7-2,27

Отсюда, интегрируя один раз, находим. t T)=0,2353 In Т + 19 · 10"» Т + 44

1,0333 - 104« 2,2ТТ2>²⁷~

+

+ Const

и следовательно получаем энтропию:

о д^ф

-AR lnp-^£L*p + /(T) =

= 0,2353 In Т+19 · 10“« Т — AR In р-

- (р -1,0333 · Ю⁴) + Const,

и при α= 0 выражение обращается в обычное выражение энтропии для совершенного газа (^=0^. Далее получаем энтальпию“, приняв во внимание, что=с_р=0,2353 +

+ 19 - 1(Г⁶ Т + ^ (р - 1,0333.10⁴).

Отсюда, интегрируя, имеем г=0,2353 Т + “ · 10^_6 Т² -

- г_7ίΤτ·ττ, CP—1,0333 · 10⁴) + f(p).

Произвольную ф-ию f(p) определяем, пользуясь соотношением

(--Ϊ

др } Ί

др ) т здесь следовательно /дгл__ART 1,27 Ат₂

Т=А ^дъ

др ОТ др ^ дТ

Αν

др) р

J-1,27

ART Р ~. А-2,27т₂

= ^Ami--

Ат₂’ 7+27

Ат₁ --

и, с другой стороны,

{др)1у27Т~-²⁷ + ί (^) ·

Сопоставляя равенства и принимая во внимание, что а 1

получим

f(p)=4m_i} т. e. f(p)=Аш_хр + Const.

Т. о. г=0,2353 Т + “ 1СГ⁶ Т» + lm_lP -

• (р — 1,0333 · 10⁴) 4- Const. Затем получим и внутреннюю энергию по соотношению

17- г- Apv, U=0,2353 Т + γ · Ю^_6 Т² — ART—

а I 1,0333-1044 ,.

- ТМ7 (р —Чат^-) + ^{С onst}·

Из выражения энтропии видим, что в диаграмме Т, & кривая постоянного давления одной атмосферы пойдет приблизительно так же, как и при а= 0, т. к. выражение энтропии можно написать

S - 0,2353 In Т 19 · 1(Г⁶ T-ARlnn-

- “ ^{1 )+ C0nSt}’

где п—число физич. атмосфер; при числе атмосфер > 1 изобары более отлоги, т. к. раз-

ность энтр увеличивается на величину [~^27 ’ положительную при

Г > Т_х. Выражение энтальпии дает объяснение так называемым эффекта Джоуля-Томсона. Представим себе два пространства, занятых газом, из которых в одном давление положим 68 Atm, а в другом 1 Atm. Напр. достаточно длинный цилиндр разделен перегородкой, в которой имеется узкое отверстие с клапаном, на два таких пространства, и с внешних сторон в обоих пространствах вместо крышек имеются поршни. Перегоняем, открыв клапан, газ из одного пространства (68 Atm) в другое (1 Atm), медленно двигая поршень так, что давление в пространстве сжатия остается постоянным. Газ, расширяясь после Выхода из отверстия, гонит второй поршень, и можно урегулировать клапаном движение и этого поршня так, чтобы оно было достаточно медленным и давление было бы постоянным. Процесс этот необратим, и если внешних влияний тепла нет, то он будет адиабатным необратимым. Мы можем однако применить к нему ур-ие эквивалентности и, назвав внутреннюю энергию, уд. объём газа и давление в первом пространстве через U_x, v_l9Ри а во втором—через U₂, v₂, Ра> ^ПР^И достаточной медленности движения поршней можем написать:

ϋ_ι+Λρ₁υ₁=ϋ₂+Λρ₂ν₂,

то есть г_г=г₂. Процесс будет т. о. изоэнтальпи-ческим. Возьмем теперь систему координат i (абсцисса) и Т (ординаты) и, пользуясь выражением энтальпии для воздуха, данным выше, нанесем изобары на эту систему (фигура 27) с

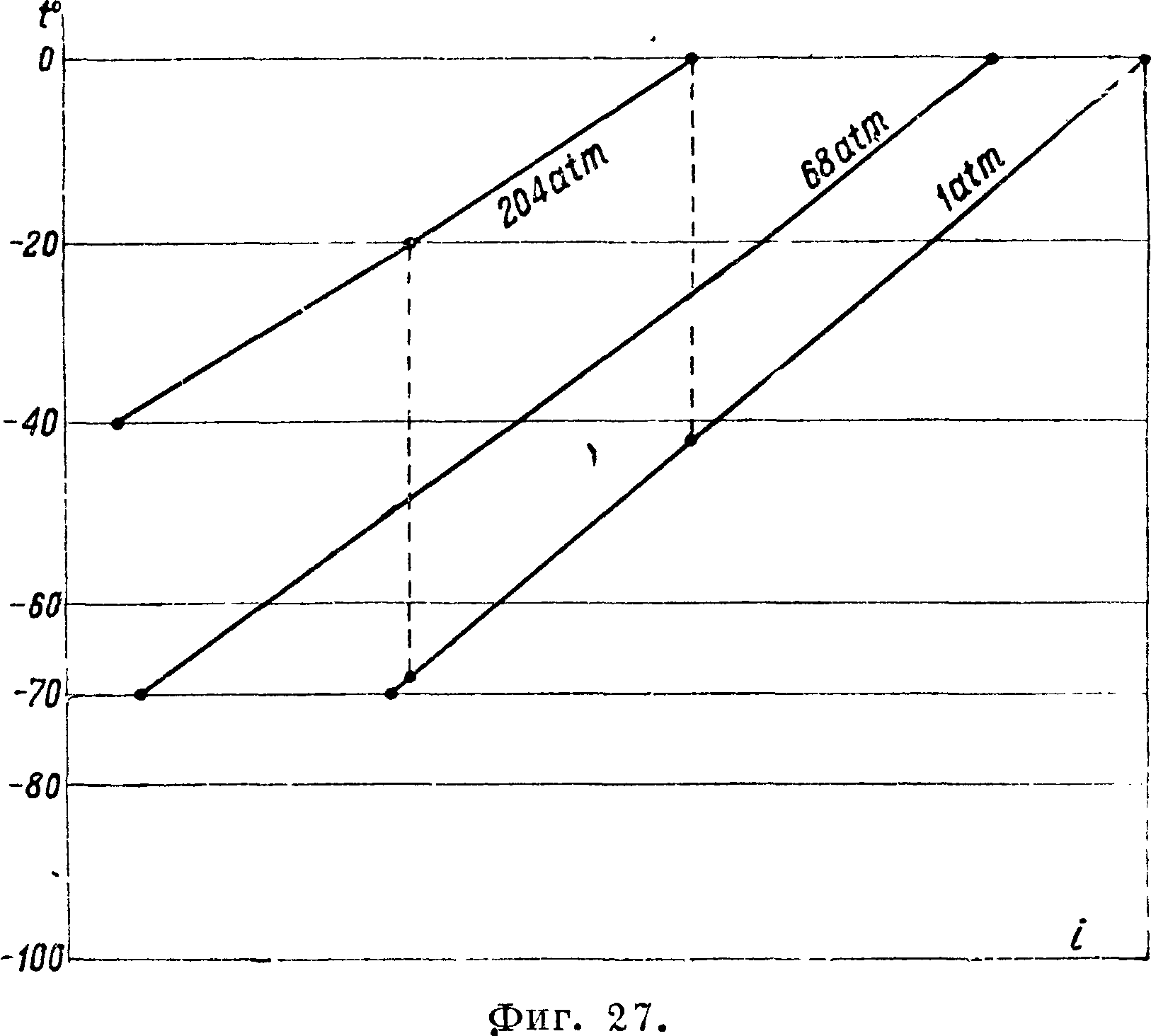
давлением в 1, 68 и 204 Atm. Начальную Г изобар возьмем в 0° С и ведем их для t° <0° С. Тогда по чертежу видим следующее: если воздух имел Г=0° С и р=68 Atm и описанным процессом давление его снизилось до 1 Atm, то f его понизится до —15°; если он имел начальное давление в 204 Atm и опять снижение до 1 Atm, то t° его понизится до —42,5°. При начальных Г—20° С и р=204 Atm, конечном р=1 Atm t° снизилась бы до —69°. Непосредственные наблюдения Брадлея-Галя (Bradley-Hale) дают числа —17°, —46°, —72°; согласие ур-ия с наблюдением в этой области можно признать удовлетворительным для первого приближения. Из выражения энтальпии для воздуха мы видим, что если бы воздух был со вершенным газом (т. e. т₁=0 и т₂= 0), то никакого снижения t° не было бы, т. к. тогда все изобары в системе ί, Т слились бы в одну кривую. Это понижение при внезапном падении давления и составляет эффект Джоуля-Томсона; но если бы Мы в характеристич. ур-ии имели ж₂=0, но т_х> 0, то, наоборот, по энтальпии увидели бы повышение Г с падением давления. То же самое было бы, если бы в характеристич. ур-ии (подобном выше данному) какого-нибудь газа соответственно имелось неравенство:.

.. а-1,0333*104 а

Атрр Τ “ пт^п пт^п

В этом случае однако неравенство, имеющее место для одних t° и давлений, могло бы изменить свой знак на обратный при других Г и давлениях. Это явление имеет место у водорода и например при падении давления с 76 Atm до 1 Atm и соответственно начальных t°: —47°, — 70°, —84,5° произошло бы нагревание на 1,2°, 0,5°, 0,07° и затем при начальных t°: —99°, —128° произошло бы охлаждение на 0,5°, 1,8° Как видим, в области этих t° эффект Джоуля-Томсона для водорода ничтожен, но меняет· свой знак при переходе с —84,5° на —99° (для давления в 76 Atm). На эффекте Джоуля-Томсона основана, как известно, идея машины Линде, а также Хемпсона для охлаждения воздуха. Она наглядно поясняется диаграммой г, Т (фигура 27).

Предположим, что воздух сжимается изотермически при 0° до 204 Atm и затем по трубе, заключенной в другую, отправляется в камеру с давлением в 1 Atm, проходя через регулируемый кран. Темп-pa его упадет при расширении скажем до —35° (по диаграмме До —42,5°); отсюда он всасывается опять в компрессор через внешнюю трубу и попутно охлаждает идущий из компрессора воздух, к-рый перед входом в камеру будет иметь уже t° скажем —20°; в камере он будет иметь t° —60° и т. д. пока постепенно не достигается t°, насыщенная при 1 Atm (—191°), после чего воздух будет ожижаться. Для ожижения водорода подобным же образом необходимо сначала его охладить до t° более низкой, чем та, при которой (соответственно давлению) меняется знак эффекта Джоуля-Томсона. У гелия имеется то же самое, что и у водорода, только t°, при которой меняется знак эффекта, значительно ниже (ниже —173°), и его приходится охлаждать кипящим при пониженном давлении водородом (Камерлинг-Оннес первый получил жидкий гелий). Здесь нужно опять вернуться к замечанию о знаке эффекта Джоуля-Томсона. Мы видим, что если характеристич. уравнение имеет вид p(v—тД== RT, то эффект Джоуля-Томсона будет состоять в нагревании, а не охлаждении. Между тем иногда дают подобные характеристич. ур-ия для той области t° и давлений, где подобного нагревания не имеется. Это будет термодинамически неправильно; также неправильно будет считать (по Бернулли), что мы здесь величиной т₁ вводим лишь поправку видимого объёма на действительно меняющийся объём, вычитая объём, занятый массой молекул. На самом деле, вводя эту поправку, мы термодинамически приписываем телу свойства, которых оно может и не иметь. Далее из выражения внутренней энергии для воздуха видим, что если бы α= 0, то внутренняя энергия была бы ф-ией только Г, но газ однако мог и не быть совершенным, т. к. мы можем иметь уравнение вида ρζν—τη^^Β,Τ. Следовательно мы можем ска-

зать, что совершенный газ всегда имеет внутреннюю энергию зависящей только от Г, но обратного заключения не имеем права делать. Затем относительно воздуха можно также указать, что и для него существует область инверсии эффекта Джоуля-Томсона, то есть когда

Арш_г +

а· 1,(Н ί3·10ΐ

1,27ГЬ27

>

1,27 ГМ?

Р·

То же самое видно и по диаграмме г, Т: кривые р=Const, будучи продолжены для t°>0°, пересекаются, и мы получим обратный эффект. Напр. по неравенству для 200 Atm давления зто будет при Г ок. 300°; непосредственные наблюдения дают ок. 250°,. что опять указывает на пригодность данного здесь ур-ия как первого приближения. Инверсия эта однако

И в том и другом случае между начальным и конечным состоянием газа при постоянных давлениях в начальном и конечном пространствах существует соотношение на основании первого принципа г₀=г₁ при отсутствии внешнего влияния тепла. Переведем теперь газ из конечного состояния в начальное обратимым процессом, например обратимым изоэнтальпическй. Тогда по ур-ию dQ=—Avdp найдем разность энтр между конечным и начальным состоя-1

нием=J* — ^^2₉ здесь dp > 0 (процесс сжа-2

тия), и следовательно разность S_x — S₂ будет <0, т. e. S₂—Sг > 0. Т. о. при этом адиабатном необратимом процессе энтропия увеличивается.

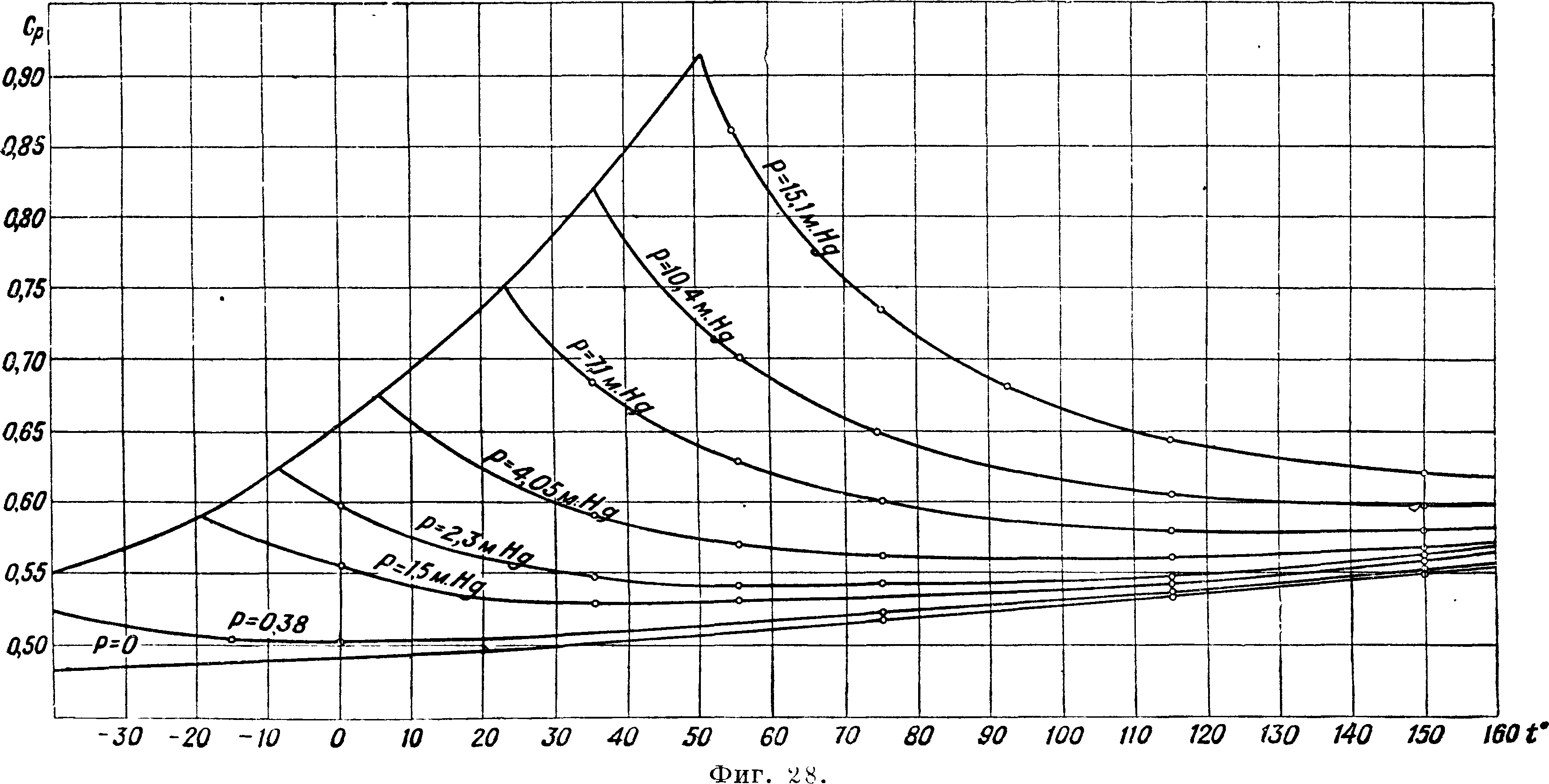
практич. значения не имеет ^в противоположность водороду и гелию. Самый эффект Джоуля-Томсона, как "мы видим, происходит при процессе необратимом адиабатном. При внезапном падении давления, соответственно быстром внешнем движении и значительной внешней кинетич. энергии мы не можем уже определить состояние тела параметрами р, v, Т, следовательно не можем говорить об энтропии или о какой-либо характеристич. ф-ии; не поможет нам здесь и прием разделения объёма на малые элементы, т. к. тогда пришлось бы еще выяснить тепловые взаимодействия элементов, нам неизвестные. Только после наступившего успокоения во внешнем движении мы опять можем йользоваться понятиями энтропии и характеристич. ф-ий и тогда можем говорить о том или ином изменении энтропии. Для определения его мы можем вести тело из конечного состояния в начальное любым обратимым процессом, если только это возможно. Отсюда следует, что в необратимом процессе мы можем говорить об изменении энтропии лишь в том случае, если из конечной стадии процесса, где можно уже определить состояние тела параметрами, мы можем провести тело в начальное каким-либо обратимым процессом. Но если и нет внезапного падения давления, а газ например протекает медленно из одного пространства в другое через сопротивляющуюся среду, то опять мы имеем необратимый процесс, т. к. работа трения необратима.

Здесь мы имеем частный случай т. н. принципа увеличения энтр: во всякой изолированной системе, совершающей необратимый процесс, энтропия увеличивается. Мы видим однако, что необходимы определенные предпосылки, чтобы обнаружить увеличение энтропии. Если эти предпосылки не соблюдаются, то нельзя говорить об увеличении энтропии, т. к. и само определение энтропии становится затруднительным или невозможным. Мы рассмотрим теперь перегретые пары аммиака NH₃, пользуясь данными о теплоемкости с_р, изображенными на фигуре 28 [¹²]. На фигуре 29 даны c_v в изотермах для t°: 0°, 50°, 100° и 150° по табличке Битти (из тех же опытов Осборна и др.). Изотермы имеют вид удлиненных кривых, но Замела на их прямыми, то есть зависимость ^=f (Τ), не дает хороших результатов, т. к. изотерма 50° довольно сильно разнится от прямой. Битти дает для с_р приближенную формулу типа с_р=c_Pq -f + {Т)_р, но по ней получаем для t° ниже 100° значения с_р, не подходящие к опытным. Весьма точную формулу дает Р. Планк типа

^ср ⁼ % + йт^й+1^ *

Ф-лы этого типа (как и прежняя формула Кноблау-ха для водяных паров) дают сложной формы характеристич. ур-ие и неудобны тем, что могут обращать значение с_р в бесконечность [¹³]. Найдем сначала путем графич. интегрирования превышение энтальпий для данных в опы-

тах изобар c_v над соответственными энталь-

vp

пиями на линии сухого насыщения по равенству ^ ^нас. ⁼ J* ^

С_р dT.

Получаем таблицы приращений, представлен

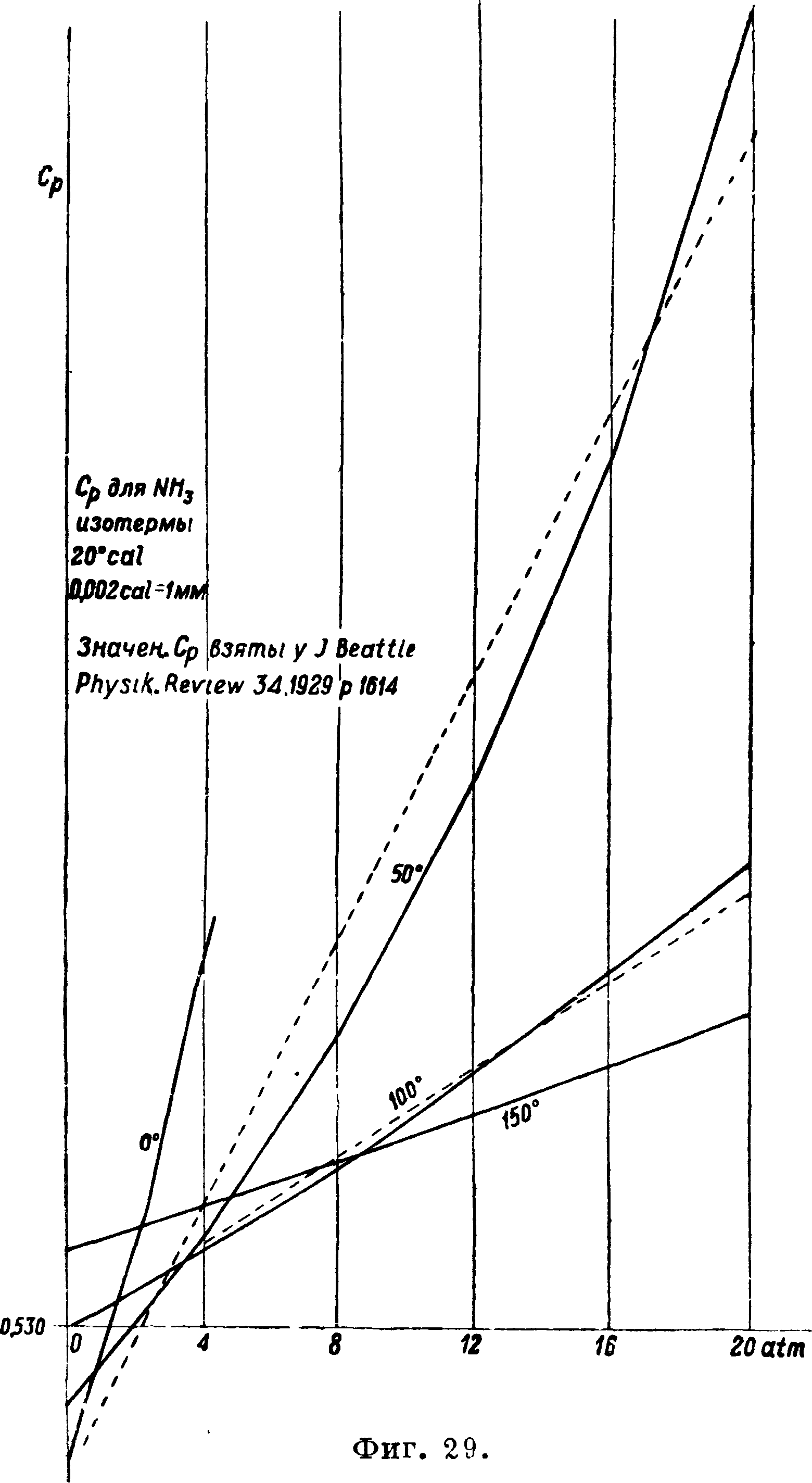
ные на фигуре 30 кривыми i_n — i_s. Далее находим соответственно приращение энтр по равенству S — S_HaC=J причем интеграл вычисляем, пользуясь последовательно равенст-вами S_T-S_T__w^c_Pm n, где с_Рт — средняя теплоемкость между Т и Т—10. Получаем таблицу приращений энтр по соответственным изобарам.

Далее может быть составлена небольшая диаграмма изобар в системе i и S для аммиака, но она может служить лишь для поверки какого-нибудь ха-рактеристич. ур-ия вследствие того, что теплоемкости определены опытом лишь для немногих давлений. Приближенное ур-ие можно получить, если основываться на том, что линейная зависимость с_р от давлений не дает, как сказано, подходящих к опытам значений с_рдля f ниже 100°. Поэтому можно положить зависимость от р в некоторой небольшой степе-

ни, например + /i(T). Основываясь, с од-

ной стороны, на изменении среднего наклона изотерм с_р (фигура 29) в зависимости от Г, а, с другой стороны, на изменении с_р в зависимости от давлений, можем положить =

1013

—, если давление выражено в физических атмосферах. Теперь далее /ДТ) есть зависимость с_р от темп-ры при очень слабых давлениях (собственно при р=0). Ее можно положить (по диаграмме изобар с_р) равной 0,49 +

+ 0,00039 t. Таким обр. с ¹⁰¹³

V ‘

т 6

η¹»²⁵ + 0,49 +

+ 0,00039 t, где п — число физич. атмосфер, и получим сравнительные таблички.

Изотерма 0°
2 Atm	4 Atm	Примечание
0,518 0,553 0,523	0,626 0,639 0,555	По формуле Опыт Битти и Бриджмен
Изотерма 50°
2 Atm	10 Atm	20 Atm	Примечание
0,531 0,531 0,526	0,667 0,651 0,592	0,882 0,917 0,675	По формуле Опыт Битти и Бриджмен
Изотерма 100°
0,538 0,541 0,511	0,595 · 0,591 0,589	0,686 0,667 0,627	По формуле Опыт Битти и Бриджмен
Изотерма 150°
0,554 0,560 0,559	0,581 0,586 0,589	0,624 0,622 0,613	По формуле Опыт Битти и Бриджмен

По табличкам видно, что формула в общем значительно ближе подходит к опытам, нежели упрощенная формула Битти и Бриджмена, но разумеется хуже, чем более сложная формула Р. Планка. Если от физич. атмосфер перейти, как обычно, к кг[м², то получим с.-^м10т^т;^?|’^,- + /₁(т)

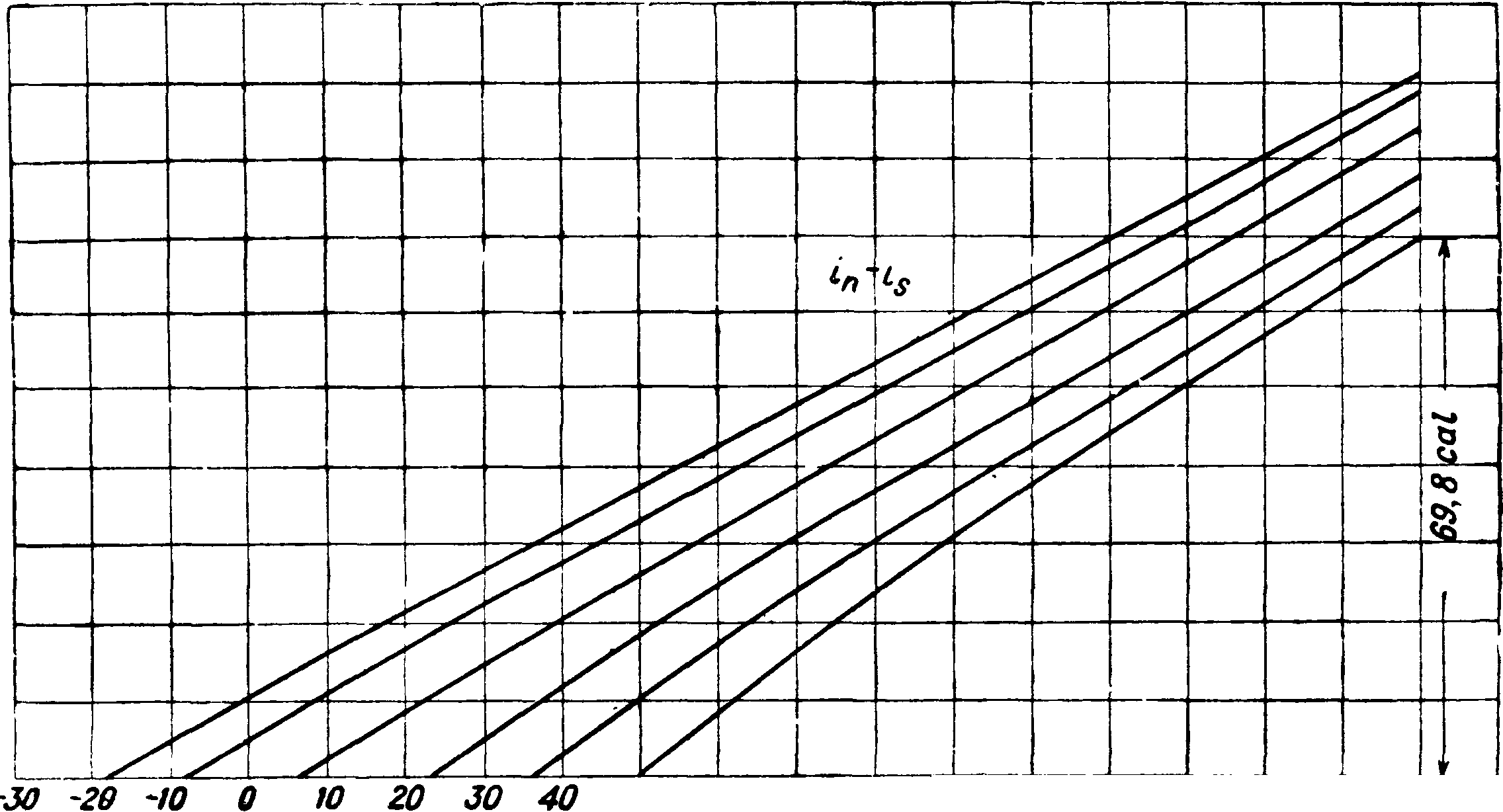
SO ВО 70 ВО

Фигура 30.

30 ЮО ПО /20 Ш /40 ISC /601 °

и отсюда указанными выше приемами получаем характеристич. ур-ие

V=- 0,004 ·

г» ⁷

109.1,708 _/

J

Т. Э. m. XXIII.

поверить его пригодность можно на линии сухого насыщения; прилагаемая таблица указывает удовлетворительную согласованность.

1°	р, кг/см2	V, мз jm	V по ф-ле
-50	0,417	2,617	2,6204
-30	1,219	0,963 0,290	0,9637
0	4,379		0,2893
10	6,271	0,206	0,20 19
40	15,85	0,083	0,0826
50	20,727	0,061 (0,0623 Dieterici)	0,06293

Данные взяты по Bureau of Standards [Осборн, Крагое (Cragoe), 1923]; они приводятся во всех справочниках. Для t° выше 0° они в общем согласуются с данными ойытов Диетеричи, для t° 50° имеется нек-рое расхождение, и формула дает значение объёма, лежащее между обоими опытными данными. Теперь указанными выше приемами получим выражение энтальпии:

i

0,384Т + 0,00039 ~—

1,92.107. pl,25 jis

— А 0,004 р + Const.

Постоянное определяем по энтальпиям на линии сухого насыщения. Возьмем для этого энтальпии при —50°, 0°, + 50°; в первом случае Const =190, во втором=190,4, в третьем=190,4; это согласие в значении Const также указывает на пригодность ф-лы. Берем Const== 190,3. Для перегретого пара получаем тоже удовлетворительное согласие с данными опыта, например при р=15,1 метров рт. ст. (20,577 килограмм/см²) разность энтальпий для 150° и на линии сухого насыщения по теплоемкостям=69,8 cal и по формуле 70,86 cal, что можно считать удовлетворительным; для изобары в 7,1 метров рт. ст. (9,653 килограмма/см²) по теплоемкостям имеем (между сухим насыщ. и 150°) 77,7 и по формуле 78,0; для изобары 62,3 метров рт. ст. (3,127) по теплоемкостям —88,2, по формуле — 87,6. Отсюда видно, что формула может быть употребляема в пределах темп-р —50° Ч—[-150° и давлений от 0,417 до 20.7 килограмм/см². Точно так же отсюда видно, что и объёмы для перегретого пара, вычисленные по характеристич. ур-ию, будут удовлетворительно сходиться с объёмами, определенными по теплоемкостям. Способ определения по теплоемкостям был уже указан в отделе о перегретых водяных парах. Для энтр имеем также по вышеуказанному способу (через ф-ию Ф)

S=0,384 1пТ +

+0,00039 Т—А -49,6 In р-А ⁶>⁸³^¹⁰⁹ р¹,²⁵ + Const,

или

S=0,384 In Т +

+ 0,00039 Т-А- 49,6 In р - —^_e— р¹.²⁵ + Const.

Постоянное опять определяем по линии сухого насыщения. Как для энтальпии, так и для энтропии условно принимается, что обе величины равны 0 для жидкости на нижней пограничной кривой при 0°. Возьмем опять t°: -50°, 0° и + 50°. Получаем значение Const в первом случае +0,108, во втором случае +0,110 и в третьем +0,107. Это опять указывает на пригодность формулы. Берем Const —0,108. Теперь можно составить как диаграмму г, S, так и диаграмму Т. S и решать относящиеся к аммиаку задачи. Однако на этом мы останавливаться цёбудем/Относительно углекислоты и ее паров существуют обширные опыты Амага, приводимые во всех справочниках, над произведениями ρυ в зависимости от Т и р, как уже об этом было сказано раньше. Эти опыты, к сожалению, велись только для t° выше 0°. На фигуре 31 они представлены изотермами в ко-

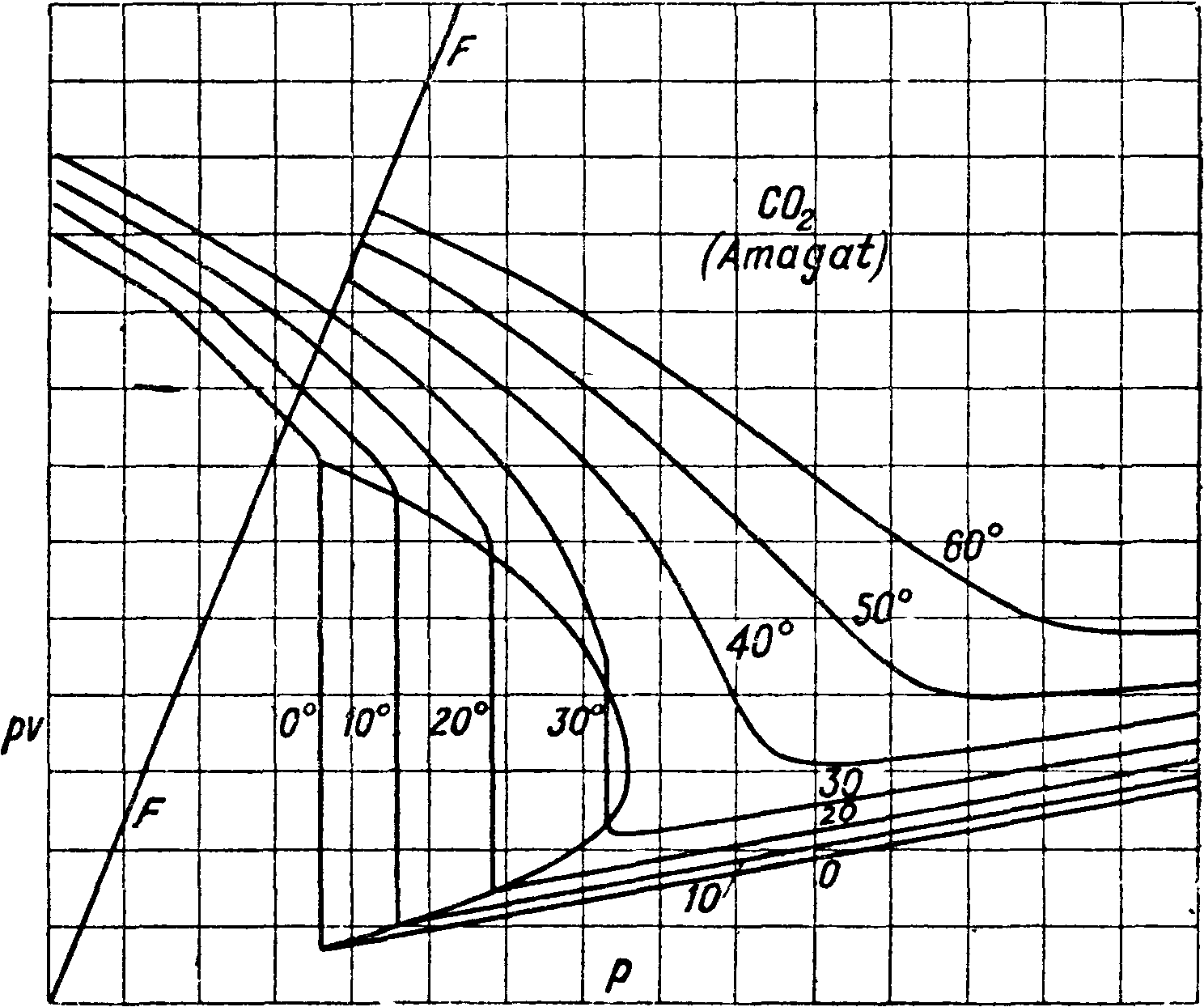
0 25 50 75 100 ί50«^ζ/α*

Фигура 31.

ординатах р, ρν для изотерм от 0 до 60° и давлений от 1 до 150 Atm. Здесь видны нижняя пограничная кривая и линия сухого насыщения, сливающиеся при t° =31,35° и давлении 75,3 килограмма [см² (смотрите замечания о критических темп-рах). Нижние изотермы от 0 до 31° представляют следовательно кривые жидкости. Прямой FF отделяются наблюденные величины (вправо) от экстраполяций (влево). На основе этих наблюдений и экстраполяций созданы таблицы Молье, также приводимые во всех справочниках. Здесь уместно сказать, что если бы мы имели подобные систематич. наблюдения например до Г=— 50° и давления 1 Atm и, с другой стороны, имели бы для с_р наблюдения для Atm также в широких пределах, то тогда составление термодинамич. таблиц, то есть практически важных диаграмм Т, S и г, S, могло бы Вестись сл. обр.: по изотермам для ρυ высчитываем объёмы для различных t° и давлений, зная объём при 1 Atm и 0° (1 л С0₂ при 0° и 760 миллиметров рт. ст. весит 1,9769г), далее по теплоемкостям с_рдля 1 Atm определяем постепенно изменение энтропии при р= 1,0333 килограмма/см² для различных t° по равенствам

Т + 10

s-s₀- f

CpdT

~Y~^:

^СРШ ^1η

Τ4-10

Τ

Затем отсюда переходим к линии сухого насыщения по равенству п

(fin ~ $l)r=Coibt ⁼ ~ A J (дт)р

«1 Р

( dv

при этом определяем I для различных дав-

^ Αν

лений (при данном Т=Const) как _дт, взяв из таблиц объёмов

Δν=(ν_τ+10 -ν_τ)ρ и ΔΤ=10°. Интегрирование ведем графически. Т. о. получаем изменение энтропии на линии сухого насыщения, то есть изображение этой линии в S, Т диаграмме. Далее по данным для Т и р на

dT

линии насыщения определяем ^ и по ур-ию Клапейрона скрытое Тепло и т. о. получаем нижнюю пограничную кривую в системе S, Т. В этой диаграмме определяем энтальпии на линии сухого насыщения, приняв условно энтальпию жидкости при 0°=0 и планимет-рируя по нижней пограничной кривой по ур-ию

i=f Т cIS +

(для JА V dp изображаем пограничную кривую в системе р, υ и там планиметрируем). Затем строим линии р=^Const для перегретого пара, пользуясь тем же ур-ием для энтропии, и по ним, ггланиметрируя, получаем энтальпии. Далее от нижней пограничной, кривой, имея зависимость υ от Т для жидкости (по тем же изотермам в системе р, pv), находим тем же прие-» мом изобары жидкости в диаграмме S, Т, а потом и в диаграмме S, г [¹⁴,¹⁵]. Для теплоемкости с_р имеются данные Холборна-Хенига, приводимые во всех справочниках, далее отрывочные наблюдения при различных t° и давлениях [Луссана, Дженкина (Jenkin) и др.].

Приложение принципов Так как теории лучистого тепла. В истории развития Т. было время, когда считали, что Т. бессильна объяснить явления лучистого тепла и выводы ее приводят к «парадоксам». Парадоксом считалась и схема, данная А. Бартоли [¹³J и приводящая к тому, что должно существовать лучистое давление на материальные тела, если принять постулат Клаузиуса. Величину этого давления не трудно определить по схеме Бартоли. Представим себе излучающее тело в виде сферы малого радиуса г, находящейся внутри сферы очень большого радиуса R с внутренней поверхностью, абсолютно отражающей падающие на нее лучи. Между сферами предполагается пустота, и падение лучей на большую сферу можно считать нормальным в виду малости радиуса внутренней сферы. Пусть энергия испускаемых малой сферой лучей будет I, они отражаются большой сферой и падают опять на малую, где отчасти вновь отражаются, отчасти поглощаются .Предположим, что их энергия в пространстве между сферами есть S, и часть ее AS поглощается малой сферой. Предположим, что существует t°-ное равновесие, и вся система не подлежит внешнему воздействию. Тогда £=J-f-(l—A) S, т. e. AS, так как, если бы этого не было, малая сфера нагревалась бы или охлаждалась, а между тем никакой внешней работы не имеется. Если бы малая сфера была абсолютно «черной», то А — 1 (абсолютное поглощение), и тогда I₁—S, где I —энергия испускаемых черной сферой лучей. Отсюда имеем известный закон Кирхгофа:

j=Ι_λ—отношение испускательной способности к поглощательной для какого-нибудь тела не зависит от его природы и равно испускательной способности черного тела, всегда I < 1_г, т. к. А < 1. Нетрудно видеть, что это соотношение применяется к лучам любой длины волны, т. к. все рассуждение велось независимо ст длины волны (как говорят «от окраски»).

Далее можно вывести положение: во всяком замкнутом пространстве, не пропускающем наружу лучистой энергии и находящемся в Г-ном равновесии,энергия излучения не зависит от природы находящегося в нем тела (или тел) и равна энергии излучения абсолютно черного тела. Предположим опять две сферы: внутреннюю, малую, «черную» и наружную, большую, отражающую и проведем мысленно сферу

Г А V dp

радиуса R — сШ, где ii—радиус большой сферьк Пусть количество энергии, падающей на сферу R, будет Q cal на единицу поверхности и в единицу времени. Пусть скорость распространения лушеи будет v. Т огда какой-нибудь луч, проходя через воображаемую сферу R — dR[

достигнет затем сферы R через время падая на нее нормально. За это время упадет· на сферу тепло в количестве, однако за

X X-------- ~ ^ Чу ^ XT -⁴-⁴·×CtXUJIbU —-

Слэдовательно в пространстве между сферами R — clR и К в объёме с основанием, равным единице поверхности, и высотой dR будет заключаться количество энергии. р£₀_

личество энергии (падающей и отраженной) в

^ т~ ---- г- 2Q

υ

единице объёма будет =f — это называется энергетич. плотностью стоячей (падающей и

^ ТОПТТХТТт Т> оттал __________

p.u.u а 14UJ4 задающей I

отраженной) волны в слое, граничащем с по· верхностыо, при нормальном падении. Количество же будет плотностью падающей волны. Сожмем теперь сферу R до радиуса R-dR, тогда количество энергии ψ от каждой единицы объёма сжатия должно будет погютиться малой сферой и быть отведено в наружную среду, если мы предполагаем неизменяемость t -ного равновесия. При этом сжатии была затрачена работа на единицу поверхности сферы R, равная р dR, где р— лучистое давление нормальное к поверхности, на единицу пс2 верхности. На единицу же объёма работа будет равна р. Предположим, что энергия единицы объёма зависит только от Г, тогда по первому принципу Т. для изотермич. в данном случае процесса имеем *

р-=Е

2 Q

где и,—плотность (в кгм/1 об.) энергии ноп-мально.падающей волны в пограничном c m’ верхностыо сферы R слое. Если поверхнота не вполне отражающая, а частью поглотаю щая, частью отражающая, тогда мы пассаж даем так: когда падающий луч проходит длину

dR за время —, поверхность получает за это время энергию Ш, но за то же время она

eQdR

отражает — —, где е— отражательная способ-

?°У^Ь ”Г^{РХН0СТИ}· Следовательно в объёме 1 х dR будет_дзаключаться количество эне^

гии (1 + е) _ю, и тогда нормальное давление получится р=E (1 + е) |=₍₁ + _{в) при нор}_ мальном падении и отражении Эта ф-ла, полученная А. Бартоли чисто тен-модинамич. путем, проверялась опытно П Н Лебедевым, к-рому принадлежит честь впервью опытно доказать существование лучистого давления, затем после него америк. учетами Ни кольсом и Халлем (Hull). Обнаружилось что соотношение оправдывается для лучей различ ных длин волн. Входящие в щ различ-

ределялись: 1) да.лЯГна’ Й^ТоГой стороны серебром стеклянную пл!станку Гоа стеклянную и серебряную стороны^ отделbLol при помощи крутильных весов с исключенирм влияния воздуха (весы находились в^простпан“ стве с давлением вб«р_т от) 9) L ^Р д. е. отражательная фотометра, 3) величина и_п=—, то есть собственно величина Q,—при помощи калориметра, причем заставляли исследуемые лучи падать на вычерненную серебряную стенку калориметра, и определялось его нагревание. Разница между наблюденным и вычисленным по формуле давлением у америк. ученых не превышала 1.1%. Если принять во внимание необычайную трудность наблюдений и чрезвычайно малые величины давлений, то можно сказать, что формула абсолютно точно подтверждается опытом. Но формула была выведена в предположении зависимости плотности энергии излучения только от t°. Поэтому мы можем принять как опытный факт, что плотность энергии черного излучения в пустоте является ф-ией только t°. А т. к. давление (нормальное) на абсолютно отражающую поверхность по формуле является ф-ией плотности энергии, то оно является также ф-ией t°. В формуле Бартоли давление выражено как ф-ия плотности слоя, граничащего с поверхностью. Можно выразить давление как ф-ию так называемой средней плотности энергии в пространстве с равномерным черным излучением в пустоте. Средней плотностью энергии в этом случае называется количество энергии, приходящееся на единицу объёма.

Представим себе опять сферу очень малого радиуса, абсолютно черную, внутри другой большого радиуса R с абсолютно отражающей поверхностью. Тогда, как и раньше, можно сказать, что какой-нибудь луч, выходя с поверхности малой сферы, пробудет в пространстве между сферами время ~, если радиусом малой сферы пренебречь. За это время с малой на большую сферу упадет энергии в количестве

— Q4=nR² и отразится столько же. Следовательно количество энергии в рассматриваемом пространстве будет равно

— Q · 4 лВ²=—^

V ^ V

и средняя плотность будет

8nR3Q _ 6Q

Но давление р=и следовательно р=|-Е-

Теперь мы можем применить ур-ия Так как явле-

ниям лучистой энергии. Принцип эквивалентности дает

dQ=dU + Ар dV=d (uV) +

+ Ар dV=d (uV) + | и dV.

При изотермич. процессе имеем dQ=dV, т. к. величина и есть ф-ия только t°. Для адиабатного процесса имеем

d{uV) + udV=О,

по разделении на uV получим d (uV) 1 dV л uV 3 V

4 4

и по интегрировании uV³ — Const или pV³== Const. Т.о.,если мы возьмем обычную систему координат V, р, мы видим, что изотерма в явлениях черного излучения изобразится прямой, параллельной оси абсцисс, как у насыщенного пара, адиабата же будет мало отличаться от адиабаты совершенного газа с постоянной теплоемкостью C_v. Представим себе теперь бес конечно малый процесс Карно для равномерного черного излучения в пустоте. Он изобразится в координатах V, р так же, как такой же процесс с насыщенным паром, то есть параллелограммом с двумя сторонами, параллельными оси абсцисс. Площадь цикла выразится величиной dp · dV, где dV—бесконечно малый объём изотермич. расширения, a dp—разность давлений для двух изотерм Т и Т — dT. Соотношение Карно дает

Qi-Qa _ Г1-Г2 Q1 Τι

В этом случае ^ - Q₂=AL=A dp dV=~du dV,

§₁=^мйГ,Т₁-Т₂=<?Т, Тг=Т,

следовательно

^du dV dV

dT

T

ИЛИ

di

и

4 dT T ’

откуда по интеграции и=аТ“, то есть средняя энергетич. плотность равномерного черного излучения в пустоте пропорциональна четвертой степени t°. Это соотношение называется законом Стефана и было открыто им чисто опытным путем. Затем Больцман вывел его из ур-ия электромагнитной теории света, почему часто называют его законом Стефан-Больцмана [¹⁶]. Так. обр. опытным путем доказана справедливость применения принципа Карно к явлениям лучистой энергии. Заметим, что соотношение

A dp dV dT

—clq—⁼ ~f~ Дает, как известно, соотношение Клапейрона для насыщенного пара. Поэтому можно сказать, что закон Стефана есть теорема Клапейрона для черного излучения.

Но в цикле Карно имеются адиабатные процессы. Адиабатный процесс происходит без участия внешнего тепла. Если мы представим себе какой-нибудь процесс с черным излучением, происходящим например в цилиндре, то мы можем .вообразить, что дно этого цилиндра абсолютно черное, а стенки абсолютно отражающие. Для адиабатного процесса мы должны будем на время заменить черное дно также абсолютно отражающим. Тогда однако является вопрос, остается ли при этом энергия, в цилиндре заключенная, с теми же свойствами равномерного черного излучения, как и прежде. Согласие теоретич. вывода с опытом дает утвердительный ответ, то есть мы можем производить адиабатич. процессы с черным излучением, не опасаясь изменения характера излучения.

До сих пор мы рассматривали равномерное черное излучение. Но это излучение состоит из ряда излучений с различными длинами волн. Поэтому среднюю плотность излучения мы должны себе представить как. суммарную из плотностей излучений различной длины волн. Назвав поэтому длину волны через Я, мы имеем по определению суммарных величин для какой-нибудь t°

00

и=J Щ dX,

о где и_х άλ—средняя плотность для излучения между λ и λ -f dX. Если мы на абсциссах будем откладывать Я, а на ординатах значения и_х для какой-нибудь t°, то площадь, ограниченная кривой и_х, двумя ординатами для Я и Х_г и осью абсцисс, даст энергетич. плотность черного излучения в пустоте с длиною волны от Я до λ_χ. Величина же и выразится всей площадью, заключенной между кривой, осью абсцисс и ординатами для 1=0 и для Л=оо. Но для Я — 0 ордината очевидно=0, а так как площадь должна давать конечную величину, то для Я=оо ордината должна также быть равна нулю. Кривая и_я должна асимптотически стремиться к оси абсцисс и будет иметь своими ординатами один или несколько максимумов. Т. о. и_л будет ф-ией и длины волны и t°. Но плотность излучения между длинами волн Я и Я + άλ равна η_λάλ, давление на повер-

ггдси хность по сказанному выше —— и для излучения между длинами λ_χ и λ_χ -f άλ_χ те же вели-чицы будут соответственно u_?LJll₁ и —^—. Применив к тому и другому излучению схему Карно, мы придем опять к соотношению Стефана и следовательно получим: их άλ : ux_ldk₁=Т⁴ : Т. В цикле Карно имеются адиабатные процессы. В схеме с двумя сферами (малой черной и большой отражающей) мы можем представить себе адиабатный процесс происходящим с расширяющейся внешней сферой и на время процесса окружаем малую сферу тоже малой сферой с отражающими поверхностями. При этом расширении сферы нужно принять во внимание соотношение между длинами волн, падающих и отраженных, т. н. принцип Допплера. Представим себе элемент расширяющей сферы, к-рый можно принять за плоский. В начале движения элемента нек-рая волна достигает его, к концу времени dt достигнет элемента та волна, которая вначале находится на расстоянии от начального положения плоскости, равном (v—v_x)dt, где V—скорость распространения волн, a v_x— скорость движения элемента. Следовательно все волны, находящиеся на отрезке АВ=(v— v_x)dt, попадут на элемент во время его движения. Пусть число их будет п, а длина волны Я, тогда пЯ=(v—v_x) dt. Но отраженная в начале движения волна к концу движения элемента будет находиться от него в расстоянии (v + v_x)dt и следовательно отраженные п волн займут пространство (v + v_x)dt и, называя длину отраженной волны через Я, имеем пЯ=(v +" v_x)dt; т. о. для однократного отражения получаем

Г^{= и П}Р^И малой ν_χ сравнительно с v

д 2

получим —=1 +. При ж-кратном падении и отражении имеем

Это и есть принцип Допплера. Для сферы R имеем полный путь луча за время падения и отражения, равный 2К, и за время dt получим vdt dR X(^m)., dR

m=, далее ν_χ=_ж и т. о. -j-= 1 + -_R.

Положим Я<^ш>= Я -f άλ, тогда получим ~.

То же самое имеем и для другой какой-нибудь волны Я при расширении сферы на dR. Отсюда

Const

получаем по интегрировании

А r ^:

для адиабатного процесса. Но адиабатный процесс для какой-нибудь плотности и характеризуется

4

соотношением иУ^ъ=Const, по закону Стефана

1_

и=аТ⁴, следовательно TV³=Const. Для сферы у=з_# отсюда TR=Const и по найденному выше равенству ТЯ= Const. Таково соотношение для адиабатного процесса между Т и Я. Теперь имеем по сказанному выше^ЙЯ: η_λ άλ_χ =

= Т⁴ : Tj, далее=-у=· Следовательно и_яЯ : η_λλ_χ=Т⁷⁴ : Tf и при ЯТ=λ_χΤ_χ получим и λ : и_л=Т⁵: Т⁵. Т. о. при адиабатном процессе, то есть когда ТЯ= Const, величина и_л для различных длин волн, деленная на соответствующее Т⁵, дает постоянную величину. Отсюда заключаем, “х *

что вообще ψζ=F (Τλ) или, помножив обе части равенства на Т⁵Я⁵, получим 4_λλ⁵=(Τλ), это соотношение называется соотношением Вина. Сама же, пока неизвестная, ф-ия (ТЯ) должна удовлетворять закону Стефана, то есть при каком-нибудь Т

оо оо и=аТ⁴=J* π_λάλ= J Я"⁵/(ТЯ) άλ_φ

о о

Было указано, что если вычертить для какой-нибудь t° кривую и_л в зависимости от Я, то кривая имеет по крайней мере один максимум. Теперь имеем

Мд=λ-η (Τλ), ~=- 5 λ-η(Τλ) + λ->ΤΓ(Τλ)

и для максимума

5 _Г(ТХ) хт пт λ)

Отсюда f_m (Τλ)=а (ЯТ)⁵, где f_m—значение ф-ии для и₇=шах, следовательно и,=а_лТ^ъ. то есть

Л А **· ⁷

если мы построим изотермы в системе Я, и_л, то максимальные значения ординат этих изотерм пропорциональны Т⁵ или, что то же, лежат на одной адиабате. Это соотношение также называется законом Вина. Теперь остается отыскать вид ф-ии /(ТЯ). Эта ф-ия не есть простой алгеб-раич. многочлен, т. к. обращается в 0 и при Я=0 и при Я=оо. Она м. б. какой-нибудь показательной ф-ией Τλ. Заранее видно, что удовлетворить соотношение Стефана можно разными ф-иями, и разумеется каждая из таких ф-ий должен быть проверена по опытным данным над зависимостью и_л от Τλ^:—так называемым распределением спектральной энергии. В отыскании какой-нибудь из этих неизвестных ф-ий мы можем пойти следующим путем. Возьмем неопределенный интеграл J Я"⁵ (Τλ) άλ и, интегрируя по частям, напишем:

f λ-η (Τλ) άλ=а-» f_x (Τλ) + 5 J λ-η_χ (Τλ) άλ,

где

fi (Τλ)=f ί(Τλ)άλ.

Чтобы освободиться постепенно от множителя под интегралом, попробуем наложить на /_Х(ТЯ) условие /х(ТЯ)=Я²/(ТЯ). Тогда получаем дифе-ренциальное ур-ие (рассматривая Т как постоянное)

Тх [Я² (Я)]=f(λ)=2λf (λ) + Λ*/(Я),

/(Λ) 1 — 2 Д

то есть ущ=“> ^интегР“РУ^я> имеем In (Я)=— * — 2 In Я,

то есть

1

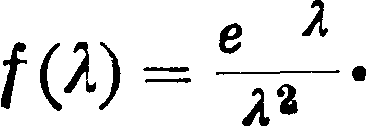
Следовательно в наших целях мы можем

_е Τλ

взять (ТА)=“ непосредственно убеждаемся, что а продиференцнровав обратно выражение — А²·

J

а

ТА

по А. Т. о., взяв (ТА) =

а е ТА

даЬаТ⁶ -._T2A2i

получаем постепенное уменьшение показателя а при А. Но мы можем взять ипросто /(ТА)=е ^τλ

и надисать А"⁵е та _

А~3 е а

"та

J Л~⁵ е тмя- J

Т²А

а

А~з _е ТА

Т2А2

Т². Тогда имеем Т²с?А =

., Тз _е ТА • ~сГ "т²А² + ^

/а

3-2 в"^

Т2А2

с?А

и, взяв определенный интеграл в пределах оо, 0, получим

/д-.-Й_<п_Д_!^ _{+ ф}

о о

ТА

Т²А²

с?А.

Но

/а

_е~Тл

АЗ

1 о _г о

^: — — у, [для определения - поло жим А=^, тогда —

та

АЗ

aq с³ е^с^

, но при А=О,

^=оо, и известными приемами убеждаемся, что неопределенность есть 0. Следовательно оо

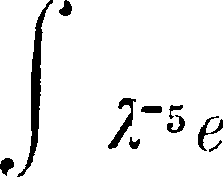
0

τλ J

a tJ

Τλ

Τ²Α 2

ίΖΑ.

Производя дальнейшее интегрирование по частям, мы последовательно будем иметь количества, стоящие вне интеграла, равными нулю, и останется лишь количество оо. г --

6 т⁵ е ^гя __ 6 Т*

’аз“ Л Т²!²" ^{С Л} ""

0

или просто αΤ⁴. Т. о. убеждаемся непосред-

а ственно, что е ^Ίλ есть ддна из ф-ий, удовлетво-

а ряющая соотношению Стефана. Но если е ^Τλ удовлетворяет этому уравнению, то и сумма

_ а_ 2 а д

Ь е ^тл t е ^тя +.=— тоже ему очевид-

_eTA_i

но удовлетворяет, и следовательно мол-сно поло-исить (Τλ) =, так. обр. щ =

е^тл -1 е^тл-1

Это и есть известная формула М. Планка для распределения спектральной энергии, выведенная им при помощи рассмотрения системы резонаторов и введения понятия о квантах.

Здесь однако, как видно, дело идет просто о нахождении ф-ии, удовлетворяющей соотношению Стефана, с одной стороны, и опытам по распределению спектральной энергии,—с другой. Проверка в последнем соотношении необходима, т. к. молено, как сказано, подобрать ряд ф-ий, удовлетворяющих соотношению Стефана. Напр.,· идя но указанному выше пути, мы можем наложить на искомую ф-ию условие /,(*)=А»/(А) и получаем ур-ие

(А) — 3 А³ (А) + А³ (А),

отсюда

fW =

Аз

ИЛИ

р Т²А²

Далее, как и в первом случае, берем

«1

f(TX)=e ^тч

а затем сумму таких ф-ий, то есть

/(ГА)=-^—.

_еТЧ*__±

что дает л° a i

_етФ _ i

Затем можно комбинировать оба выражения в сумму, то есть положить

1 ь, i

и_к -

Аб

>ТА

-1

_ΡΤ²λ 2

CL <1

Далее можно взять /(ТА)=Ье ^τλ + Ь_хе ^тя+. и тому подобное. Так же можно отыскать и иного вида ф-ии. Не нужно разумеется усложнять .дело, и с этой точки зрения формула М. Планка как наиболее простая заслуживает предпочтения.

Обратимся теперь к опытам. Прежде всего в опыте нужно воспроизвести «черное» излучение. Мы видели, что всякое замкнутое пространство, не пропускающее наружу лучистой энергии и находящееся в температурном равновесии, имеет «черное» излучение.

Поэтому лредставим себе сферич. или другой какой-либо формы пространство, окруженное непроницаемой оболочкой и поддерживаемое каким-либо источником тепла при постоянной Т. Если теперь мы устроим узкий канал в этой замкнутой системе, идущий изнутри в наружную среду, то при условии не-нарушениятемп-рного равновесия получим «черное» излучение данной ί°. На фигуре 32 показано одно из простейших «чер-^; ных» тел: железный ящик в шамотной печи с узким каналом наружу. Вместо мета л л ич. ящика для высоких t° берут пустой угольный цилиндр, также окруженный непроницаемой

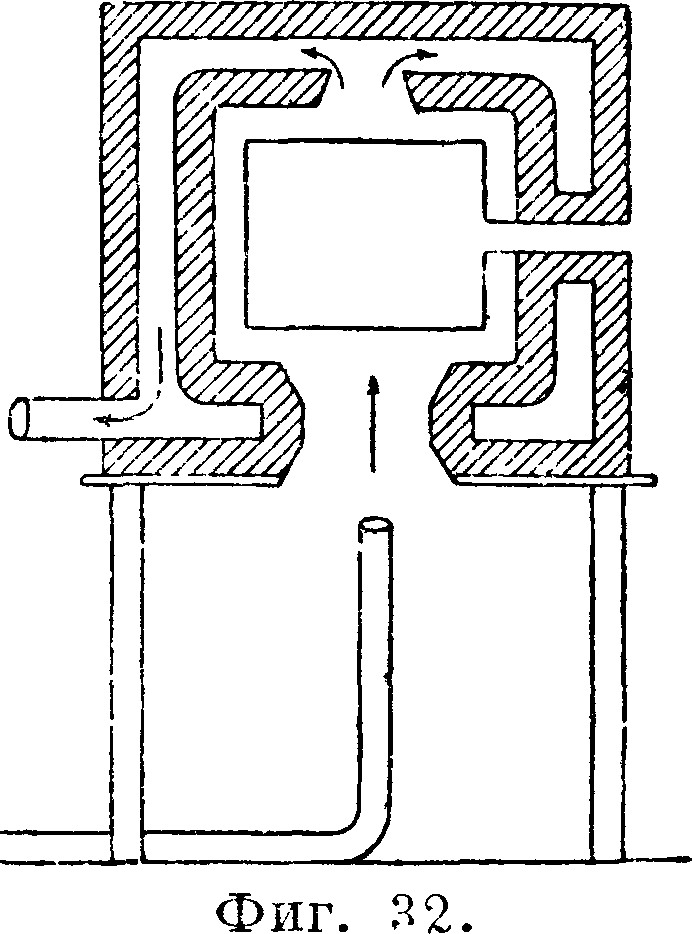
оболочкой и отапливаемый электрич. током [¹⁷]. Энергия излучения измеряется болометром. Инструмент этот, как известно, основан на принципе изменения сопротивления в элект-, рич. токе при изменении £°. Поэтому, если очень тонкую металлич. зачерненную полоску или ряд таких полосок, находящихся в электрич, цепи, подвергнуть действию лучистого тепла и тем изменить <°, сейчас же изменяется сопротивленце, а по нему можно судить и об относительной величине энергии, воспринятой болометром, если «освещать» его лучами различной t°. Если иметь в цепи две полоски (или два ряда полосок) и одну «освещать», а другую дополнительным током нагревать на столько же и т. о. восстанавливать электрич. равновесие, то можно получить и абсолютную величину энергии, воспринятой болометром (компенсационный болометр) [¹⁸]. На основании закона Стефана можно предварительно проверить «черноту» избранного устройства для черного тела. Если нагревать черное тело до различных t° и определять болометром-относительные энергии излучения, то энергии д.б. пропорциональны ТС При всех подобных опытах с хорошо кон струированными «черными» телами закон Стефана оправдывался. Тем самым получается подтверждение и закона Кирхгофа. Далее получается распределение спектральной энергии, если всю энергию разложить по длинам волн и определять относительные величины энергий при помощи спектроооло-метра [¹⁹].

Тем же путем Люммер (Lummer) и Прингсхейм (Pringsheim) получили целым рядом опытов распределение энергии в спектре «черного» тела

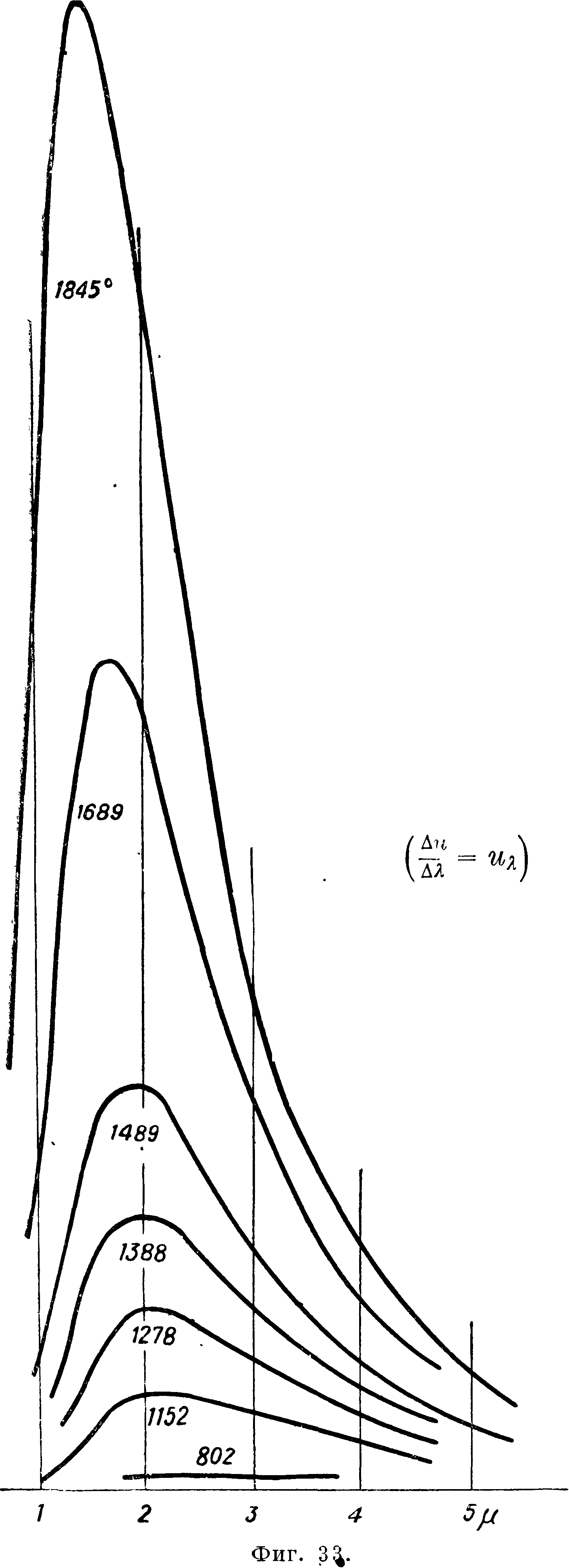
34). Для «черного» спектра получается полное подтверждение законов Вина,то есть A_WT=Const, где —длина волны для максимального значения и_я при данных Т и и_т ·

. Т"⁵=Const, где и_т — максимальное значение (сравнительное) ιι_λ. Можно было бы вычертить все изотермы, зная только одну опытную в достаточно обширной области. Мы можем провести из точек опытной изотермы ряд адиабат по и%

ур-иям λΤ=Λ^,ΙΙ jrj=—ι

и на них отметить точки с одинаковой Г. Т. о. можно получить сеть адиабат и изотерм, если опытная изотерма вычерчена в соответственно хорошем масштабе. Адиабата максимальных^ и соответственных λ_Μ получается по табличке из опытов Люммера и Прингсхейма.

Как видим, согласие опытных t° и вычисленных по формуле адиабаты не оставляет желать ничего лучшего. Тем самым дается способ измерения t° какого-нибудь излучающего тела, если считать его чер-

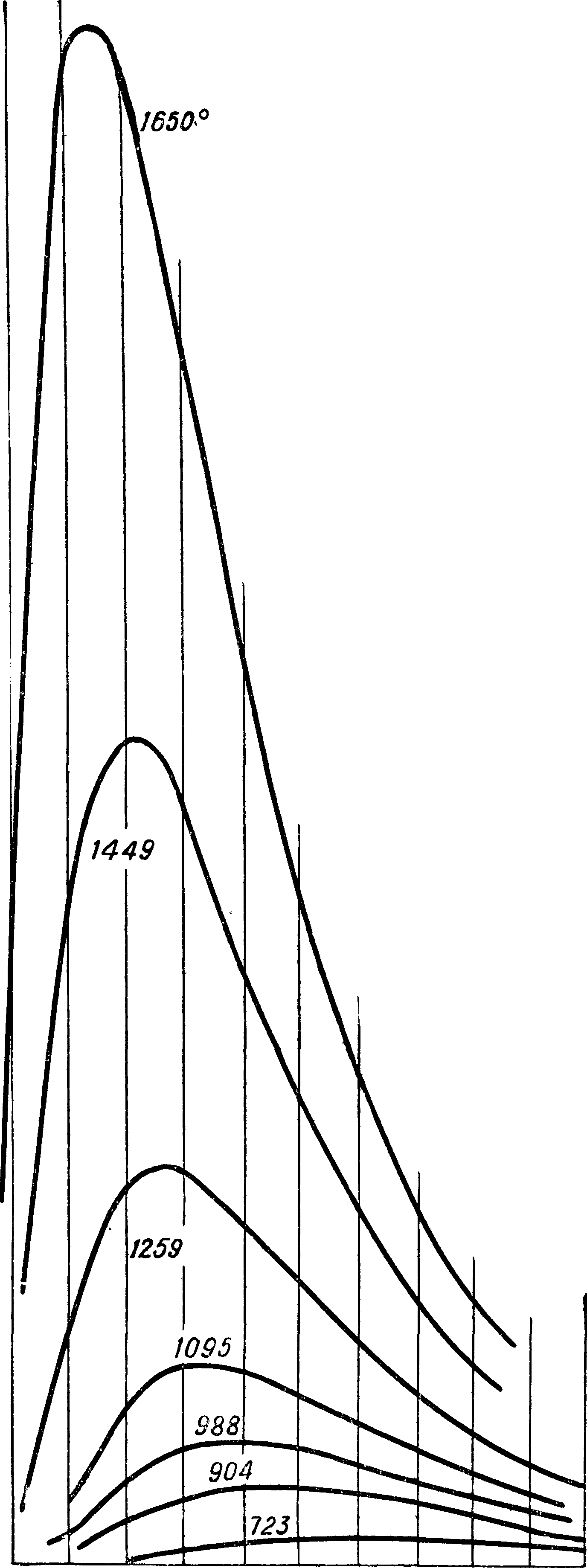
и для сравнения также в спектре полированной платины. Здесь даны изображения полученных изотерм в системе Я, ϊΐ_λ, гдедлягбд даются лишь сравнительные величины (фигура 33,

1 2 3 4 5 6JJ

Фигура 34.

ным. Определяется спектроболометром кривая значений и_к для испытуемого тела и по ней и_т. Для сравнения масштабов определяем

Значение величин А, В и Т.

т I	λτη	vm	Α=λγηΤ	B=umT-6 j	T — j/nm/Bm
1 646	1,73	270,6	2 928	2 246.10-17	1 653,5
1 460,4	2,04	145,0	2 979	2 181.10-17	1 460,0
1 259,0	2,35	68,8	2 959	2 176-10-17	1 257,5
1 091,5	2,71	34,0	2 936	2 134-10-17	1 092,3
988,5	2,96	21,5	2 956	2 168-10-17	998,5
908,5	3,28	1 13,66	2 983	2 208-10-17	910,1
723	4,08	1,28	2 950	2 166-10-17	721,5
621,2	4,53	2,026	2 814	2 хЭО-Ю-17	62.,3
			Am=2 940	Bm=2 188.
				•10-1’

параллельно показания инструмента для конструированного «черного» тела. при известной Т_г и по ним и_т. Далее по равенству

—=—4 определяется Т. Но так как тела в т^{5 τ}ϊ

природе вообще не могут быть названы абсолютно черными, то необходимо для сравнения иметь спектр заведомо нечерного тела, например сильно отражающего металла, каким является полированная платина (фигура 34). Здесь уже будут несколько иные законности. Максимальные значения удовлетворяют соотношению λ_ηιΤ=Const, но значения и_ш удовлетворяют скорее соотношению=Const. Пользуясь этим, теми же приемами определяют t° тела, если бы оно обладало свойствами платины. Таким путем получают пределы, между к-рыми лежит t° тела, например для свечи (т. н. нормальной) получены числа 1 960 и 1 750. Но кроме изотерм, к-рые, как было уже сказано, м. б. получены из одной только опытной изотермы, мы можем получить в системе Т, и_х изохроматы, то есть кривые и_л в ф-ии Т для черного излучения одной и той же длины волны. Взяв например опытную изотерму в 1 650°, мы получим изохромату для Я=3μ из соотношений Я · 1 650 =

и „ “Л

= 3μ· Т и -ψτ=Гб50^ * ^{По пе}Р^в0МУ равенству, взяв определенную Т, получим λ, то есть точку на изотерме 1650°, где адиабата из точки 3μ, Т пересекает эту изотерму. По этой длине Я узнаем на опытной изотерме в 1 650° соответственное и_к и по второму равенству узнаем ν_3μ искомой точки. Задаваясь различными Т и узнавая различные и_х, строим изохромату. На фигуре35 показана изохромата 3μ. Подобные

600 800 1000 1500 2000 2300 Г

15 2,1 2,7 3 4J5 6 ГК

Фигура 3 5.

изохроматы могут также служить для определения t° тела. Если исследовать спектроболо-метром небольшую область излучения данного тела между Я =2,5 μ и Я =3,5 (или более узкую), то можно определить u_S/x, далее для сравнения масштабов то же сделать для «черного» тела известной Т и затем по изохромате определить Т для тела.

По существу как изотермы, так и изохроматы“ представляют собой формулу распределения спектральной энергии только в виде графика, и всякая аналитич. формула должна с известной точностью передавать его. В частности формула Планка, как известно, довольно хорошо подходит к опытам Люммера и Прингсхейма [¹⁸]. Собственно каждая изохромата дает в известном масштабе графически вид ф-ий (ТЯ) в соотношении и_л=Я"⁵ (ТА). Действительно возьмем изохромату 3 μ и вместо абсцисс Т подставим абсциссы ТЯ, то есть 900° · 0,003=2,7;

1 000° · 0,003=3 и т. д. Тогда различные ординаты будут равны (ТЯ), то есть в известном масштабе представляют (ТЯ) в зависимости от ТЯ. Т. о. любая изохромата м. б. в этой системе получена простым изменением ординат для 3 μ в отношении

(ЗаО* _ /з 5

(ημ)ό п; ⁵

и каждая кривая дает одну и ту же ф-ию, только в разных масштабах; и как из одной опытной изотермы мы получим другие изотермы и изохроматы, так и из одной изохроматы получаем разные изохроматы и изотермы применением термодинамич. соотношений. Поэтому формулу М. Планка нужно проверить только для одной изохроматы. Мы возьмем согласно Люммеру и Прингсхейму в формуле М. Планка а= 14,6 миллиметров - °К и затем определим b, вставив и_л для 1 400° и для 1 460°, взятые по изохромате, в ф-лу. Среднее из полученных значений дает lg (5-QQ35)=3,1824. Затем вычисляем ил для 900°, 1 260°, 1 650°, 2 000°, 2 500° и сравниваем с данными изохроматы:

τ	Изохр.	Μ. Планка
900	6,78	6,85
1 250	32,6	32,7
1 550	83,6 ‘	81,13
2 000	149,9	116, 1
2 500	255,6	253,5

До 1 650° согласие не оставляет желать ничего лучшего, дальше идут расхождения, но небольшие. Легко видеть, что если бы мы взяли формулу в виде

CL €L CL 2

и_л=bе ^τλ- -bе ^Τλ + Ь₂е ^Τλ + .,

то, подбирая последовательно коэф-ты b и а, мы могли бы удовлетворить изохромате на любом протяжении, аналогично тому, как это делает Каммерлинг-Оннес для ур-ия газов. Но такие ф-лы, отличаясь сложностью, не могут иметь практич. значения, поэтому, как было уже сказано, нужно отдать предпочтение формуле М. Планка, по ее сравнительной простоте, пока не имеется непосредственных опытов при высоких t° (выше 2 500°) или при 1 650° для более длинных волн. Мы видели, что формула получается без каких-либо гипотез и совершенно не зависит от понятия о квантах. Поэтому с термодинамич. стороны все вопросы о квантитативном испускании и непрерывном поглощении лучистой энергии являются излишними.

Но с формулой М. Планка связана теория де-Бройля, объединяющая корпускульную и волновую теории свет. Она выходит из следующих элементарных соображений. Какое-либо колебание всегда состоит из простых гармонии. колебаний, и последнее характеризуется соотношением

S=A sin 2π (nt + ψ),

где & — отклонение от среднего положения колеблющейся частицы, п—число колебаний в ск., t—время, ψ—некоторое начальное постоянное. Выражение <р=2 π (nt + ψ) называется фазой волны. Если скорость распространения волны есть V, то для какого-нибудь расстояния х от начальной точки фаза очевидно будет

<Рх= 2π[η(ί- I) + ψ]·

Предположим, что имеем еще другую волну с числом колебаний п + dn и скоростью распространения

v+^dn,

и найдем точку х, где фазы обеих волн будут одинаковы. Тогда мы имеем соотношение

Ψχ=Ψχ + ⁹-§ξ dn, то есть ^=0 или d (-)

2π(-2πχ _у2 + 2я^=0.

an dn

Отсюда

*=_ί_(ί+

_d /гг V ^ dn) dn

Соотношение показывает, что точка х будет двигаться со скоростью

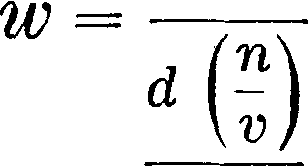
dn

и будет служить центром двух волн с колебаниями п и η + dn. Мы можем представить себе аналогично, что из точки х выходит целый ряд волн с колебаниями от п до п + Ап при Δη достаточно малом, и точка х двигается со скоростью w, к-рую можно принять:

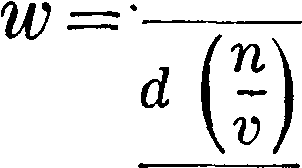
dn

Эта точка будет энергетич. центром этих волн, т. к. колебания различных волн с малыми разностями фаз в ней будут складываться. Это и будет по де-Бройлю корпускулой.

Теперь представим, что имеем излучение с длинами волн от А до А + ΔΑ. Мы можем положить, что в этом излучении имеется целый ряд подвижных энергетических центров. Пусть число их равно Ν₀, причем No^-большое число. Различные центры будут иметь различные энергии, которые можно принять различающимися .хотя и на малые, но конечные величины. Пусть^Уф центров имеют энергию,равную нулю. N₂ — N_г—энергию (каждый)ΕΑλ,Ν₃—Ν₂—2ΕΑλ, Νι-Νζ—3 ΕΑλ и τ. д. Энергия всего движения будет

" ΕΑλ (Ν₂-Ν,) + 2 ΕΑλ (Ν_ζ - Ν₂) +

+ 3 ΕΑλ(Ν,~Ν_ζ) +.

Но, с другой стороны, по формуле М. Планка энергию излучения в этом случае можно принять

«_;ΔΑ=Λ-*ΔΑ - ----- -

^Л а е™- 1

/а 2 а

= Г»-b е~™-е~ ^ + .)ДЯ =

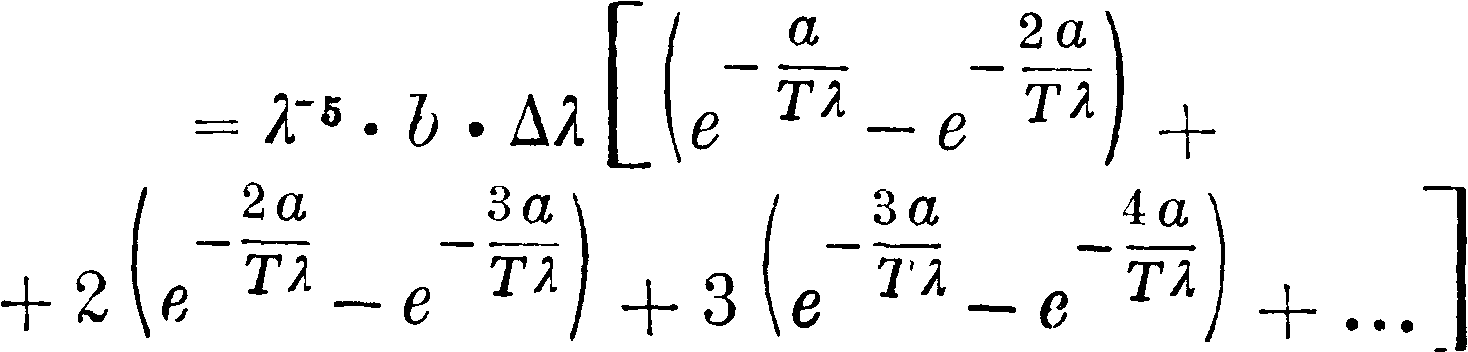
и мы можем при сравнении обоих выражений энергии излучения положить

_а_ 2 а

3 а

N,-N_t=Ν₀ β~^Τλ - i^Tx),

N_t-N_m=N₀

a (т-1) am

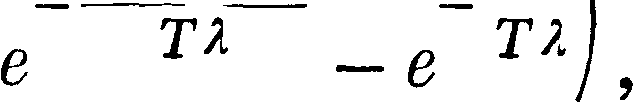
где ж—число групп (тоже большое) с одинаковыми энергиями. Теперь, помножив первое равенство на ΕΑλ, второе на 2 ΕΑλ и т. д., сложив и сравнив при ж=большому числу с ф-лой М. Планка, получим ΕΝ₀=ίλ~⁵. При-

мем теперь £/= —, где к—нек-рая величина _у

тогда N₀=я No м. б. большим числом при достаточно малом k, а Е будет малой величиной. Далее по равенству ηλ=ν получим Е =

=. Здесь ν—величина, зависящая от п, но<

мы можем подобрать к всегда таким, чтобы=Const и тогда E=hn. Величина Е_у

пропорциональными которой являются разности между энергиями различных энергетич. центров, и будет носить название основной световой кванты для числа η колебаний. Т. о. все излучения с колебаниями от η до η + Ап (или с длинами волн от λ до λ + ΔΑ) представятся исходящими от целого ряда подвижных энергетич. центров с энергиями, пропорциональными основной световой кванте, и символически можно говорить о движении световых волновых квант.

Но если мы применим к этому случаю обычное ур-ие механики для изменения энергии какой-нибудь движущейся точки с массою ш (в общем случае переменной), то имеем, назвав скорость точки через w,

w dt · d=dE=fh dn,

где /—фактор пропорциональности. Отсюда

d (mw)=f —^η=fh dn

dn ’

t. к. скорость энергетич. центра w =

dn

, сле довательно

mw=~ + Const,

fhn

m=— vw

a

w *

Но при w=0 масса ж не м. б.=оо, поэтому α= 0 и на том же основании vw=Const, т. e.

hn

m —, где с—нек-рая постоянная величина.

Далее т.

©

d -

1_

w

1 ν dv κ> п dw

ν ν² dn~~ с² с² dn ⁹

dn

η

wdn

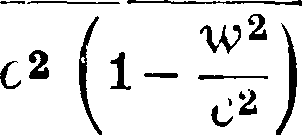
dn

я но интеграции

Const

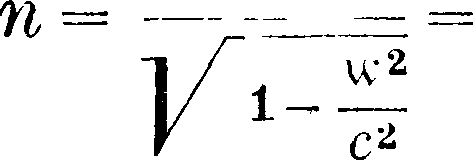
F

r-r— ?

W>2

&

при атом v₁G₁=v₂G₂ =.=V, и следовательно по сложению равенств (р_х + 24 + ···) И=T£GR и по закону Дальтона pi 4- р₂ +.=Р, т, е. PF=TZGR=Pr£G,

далее ж -

Ьп

~с“

hF

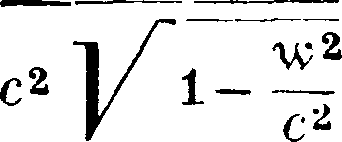
Обозначим массу покоя через т₀, тогда т₀ =

h F

F =

т₀с²

и следовательно m =

У >-s

Таково выражение массы.в механике де-Бройля, таково же оно и в теории относительности. Скорость w только тогда может равняться с когда ж₀=0, ибо ж не может равняться оо. Но wv=с², следовательно скорость корпускулы только тогда равняется скорости распространения волн, когда ее масса покоя равна 0. При некоторой малой массе покоя скорость движения корпускулы будет меньше скорости распространения волн. Отсюда мы заключаем, что постоянная с в соотношении wv=с² есть скорость света, и корпускулы движутся со скоростью, меньшей, а волны идут со скоростью, большей с. Дальнейшие подробности и применение к теории атомного строения нужно искать в специальной литературе.

Приложение принципов Так как химическим процессам. Предварительно предположим химич. процесс происходящим внутри газовых масс, следовательно в некоторой газовой смеси. Для простоты берется .ур-ие Мариотта-Гей-Люс-сака. Пусть γ—уд. в газа, тогда ур-ие будет

<т. к. γν=1) ~=RT, для другого газа при тех же р и Т y=R_xT отсюда yR=y_xR_x=.,

следовательно вообще R=если у₀ и R₀

у

•отнести к водороду. Но, назвав мол. вес газа

m у через ж, а водорода через ж₀, имеем — — — и следовательно R_m=R₀m₀=R_lm_l=. Количество R₀m₀ можно принять равным 847. Т. о. если мы возьмем количество кг равным ж, то получим

pvm=mRT=pV=847,

где V—объём т. н. моля (кг/мол.). Число 847 в •кгм/1°, а в калориях это будет ~1,985, т. ч. АрУ=1,985 Т. Если два газа взяты в количествах G_X и 6г₂ кг при одинаковых Тир, то, ру_гО_г=G_XR_LT, pv₂G₂=G₂R₂T η

v_lG_{l =} GiR±₌V1 v₂G₂ G.R₂ v

Если молекулярные веса будут ш₁ и ж₂, а число молекул п_х и п₂, то G_l=n_lm₁, G₂^n₂m₂ и следовательно

n_lm₁R₁ _ _ ύ _λ

n>m₂ R₂ ν_Δ ~~ ⁹

и при V_x=V₂ получаем, что в равных объёмах при одинаковых р и Т число молекул однородного газа одно и то же для всех газов (закон Авогадро)—само по себе очевидное следствие принятого соотношения между молекулярными и уд. весами.

Для смеси однородных газов пользуемся законом парциальных давлений Дальтона, т. ч. если газы занимают один и тот же объём при некоторой Т, то

ViV_xG_x=G_XR_XT, p₂v₂G₂=G₂R₂T,

отсюда

TWR

zg~

Ρυ,

^v G R

T. e. R смеси=· Представим по Цейнеру два газа в пространствах, разделенных перегородкой, с темп-рами Т_х и Т₂, давлениями 24 и р₂, объёмами F₁hF₂h весами G_x и G₂, затем перегородка уничтожается, и процессом диффузии (необратимым) оба газа занимают объём V _х- - F₂. Процесс шел без участия внешнего тепла и без внешней работы, следовательно для изменения общей внутренней энергии имеем dU=0 или (G_x + G₂) U=G_xU_i0 +

Н-еДс/Г, + Jt?) + G₂U₂₀ + G₂(r₂T₂ + j T₂)== (Gi + G₂) U₃₀ + (Gi + G₂) + γ,

и отсюда по сравнении постоянных количеств тт _*GUo “ ЗУ IG ’

то есть постоянное внутренней энергии вычисляется тем же способом, как и R, далее вычисляется по сравнении переменных членов общая t° смешения, но для этого нужно знать с₃ и а₃.

Предположим, что Т_х=Т₂, тогда для совершенных газов и Т₃=Т_Ь а отсюда 4 ^{= и}

а₃= ^, то есть вообще c_v =, точно так же

^ср =* · Процесс смешения газов, то есть диф фузии, есть процесс необратимый, и потому относительно энтропии смеси можно только тогда что-либо сказать, когда или каким-либо обратимым процессом мы вновь разделим газы или введем предположение б. или м. вероятное. Первый путь—М. Планка—предполагает, что мы можем иметь перегородки: одну—проницаемую для одного газа и непроницаемую для другого и другую—с теми же свойствами относительно другого газа. Тогда легко видеть, что можно устроить разделение газа путем обратимого процесса и в результате получить, что энтропия двух газов, имеющих одну и ту же t° при смешении, равняется сумме энтр отдельных газов. По поводу этого способа рассуждения можно только сказать, что если бы такие перегородки и существовали для всех газов, то процесс разделения наверно сопровождался бы явлением трения и поэтому был бы необратим, то есть мы пришли бы к начальному затруднению. Второй путь, Пуанкаре, есть путь гипотезы, полагающий, что при смешении каждый газ диффундирует независимо от другого, и потому увеличение его энтропии происходит независимо от другого^ Тогда до смешения мы имеем сумму энтр, равную G₁S_l+ G₂S₂, при диффузии первый увеличивает энтропию на Gi (S12 — Si)j где S₁₂ — энтропия первого газа, занявшего объём смешения при Т, для второго имеем увеличение, равное G₁(S₂₂ — S_z), и энтропия смеси равна

G_XS_X + G₁(S₁₂ — S₁) + G₂S₂^Jr G₂(&_s

= GiSi*

₂-S₂l·

G₂S₂

t. e. энтропия газов, смешивающихся при T, равна сумме энтр отдельных газов, вы-

численных в предположении, что каждый газ диффундирует независимо от другого. Гипотеза о независимости диффузии аналогична закону Дальтона относительно парциальных давлений.

Рассмотрим теперь явления химич. реакций в газообразной среде. Химическая реакция м. б. обратима, и наряду с процессом соединения может идти и процесс распада. Это обозначается по Вант-Гоффу стрелками—знак химического равновесия, например

2Н,+0₂ ^ 2Н₂0, 2С1₂+2Н₂0 ^ 4С1Н+0₂и в общем

7ί[ · М + ri₂M₂ +. ϊtn]M] + п"₂М"> +.

Вследствие обратимости мы можем применить основные термодинамич. соотношения к химич. реакциям. Возьмем ф-ию F, имеем dF== d (TS — U)=S dT + AP dV. Реакция может идти изотермически, т. к. в случае образования или поглощения тепла можем внешней средой воздействовать соответствующим образом. В этом случае dF=АР dV. Рассмотрим сначала простейшую реакцию—сгорание водорода в кислороде. Пусть β_χ—мол. вес водорода, β₂— кислорода, β₃—паров воды, n_l9 п₂, п₃—числа молекул, х—доля кг_ч относящаяся к гремучему газу, ϊι (1 —ж)—то же для паров воды. Тогда имеем:

χη_ιβ_ι кг Н.»=у_1?χη₂β₂ кг 0₂=γ₂,

(1-χ)η₃β₃Κ2 Н₂0-ж и по формуле соединения + η₂β₂=η₃β_ζ.

Кроме того имеем η_χβ_χ х ρ_χν_χ=ΡΤη_χβ_χχ или η_χβ_χχρ_χν_χ=R_mTn_xx и далее

η₂β₂χρ₂ν₂ — R_mTn₂x, η₃β₃ (1 - х) ρ_ζν₃=R_mTn_z (1 - χ) и~так как

η_χβ_χχν_χ=V=η₂β₂χν₂=η₃β3 (1 - χ) ν_Ζ9то по сложении и по закону Дальтона получим PV=R_mT [п_хх + щх + щ (1 - х)]₉откуда видим, что можем иметь Т=Const и V=Const или Т=Const и Р — Const, так как вместо трех параметров имеем 4, то есть Р, V, Т, х. Тогда

F=TS- U=F (S_xy_x + S₂y₂· + S_zy_z) -- {iu_tl + п (Г)]У1 + [U₀₂ + U (T)]Yz +

+ Жз + /з(0]Уз} >

где соответственно буквой S названа энтропия, U₀ —постоянное внутренней энергии и (Т)— зависимость ее от Т. При Т=Const,

dF=TL (у % dv + 8 dy) -ϊ,Ό dy.

Каждое шз

8= In (y^cOj>^AJV^(T>) + Const =

‘ In (т^с‘о (1)^Ай_в/(Т))₊const

и следовательно os

, dv AR dV · AR dy

Т. 0.

_я dv=AR ---------

ου ν V у

2 (у ^dv+S dy)=£ (S - AR) dy + ~ £ARy

И

dF=T(S - AR) dy-£Udy + тЦ ZARy,

при этом

dy_x=η_χβ_χ dx₉ dy₂=η₂β₂ dx и dy₃=- η₃β_ζ dx.

Тогда

Σ (S — AR) dy=(S_xn^_x -f 8₂η₂β₂ — β₃η₃β₃) dx —

— AR_m (n_x + Щ — n₃) dx,

так как

AR_xd_x — ΑΡ₂β₂ — ΑΡ₃β 3 — AR_m9далее по правилу смешения и следовательно

- dF=Т [S₁n$₁ -f 8₂η₂β₂- 8₃η_ζβ_ζ— AR_m (η_χ -f п₂ — п₃)] dx -f АР dV — £U dy =

= ΣΑργ dV=AP dV.

Отсюда

Т [Β_χΎΙ_χβ_χ 8₂η₂β₂ — Ь_zn₃β.₃ —

- ARn. (% + Щ + и₃)]=^ZUdy =

= [ϋ_β1 + fi (Τ)] η,β, + [U„₂ + f₂ (Τ)] η₂β₂ +

+ [Uo₃ + /з (Ρ)] Пфз-

Правая часть равенства даст разность внутренних энергий гремучего газа и паров воды, если бы произошел полный переход гремучего газа в пары воды. Примем V=Const, тогда это будет по первому принципу полным теплом реакции. Обозначим его через (дпф₃₉ тогда:

~ 8_όη₃β₃ — AR_m (n_L -f- и₂ — n₃) =

__ Qn 3^3

ψ— ·

В каждом из S имеем количество v^AR =

Назовем концентрацией вес какого-нибудь компонента на единицу объёма и обозначим ее С, тогда а в 8₁η₁β₁ под знаком In будет С_г =

= С_х. ^АЯ^^п1 и следовательно в общем выражении под знаком In будет

(с Г⁹¹¹ с₂~^пЛАП_т с₃~^п3

Остальные члены в равенстве между Q и энтропиями будут ф-иями t° или постоянными, и следовательно мы получим, что ер⁰¹ СГ^П*

С₃~^пг

ИЛИ

с?¹ с^

Сз³

в изотермич. реакции, являясь ф-ией t°, будет величиной постоянной.

Нетрудно видеть, что мы будем иметь то же самое при скольких угодно компонентах реакций. Это есть закон концентраций Гульдберга и Вааге, т. ч. если п_х молекул одного газа А_г с п₂ молекул другого А₂₉ с п₃—третьего А₃ и т. д. дают соединение в п[ молекул А, Щ мол. А2 ит. д., то при изотермической реакции [⁶]

с-А

= К=Const.

Зависимость К от £° м. б. разумеется выведена из основного соотношения, но удобно выразить эту зависимость в диференциальной ф°Р^мш Возьмем производную по Т от обеих частей равенства, приняв во внимание, что вообще

^cv — ^cv_Q +

dS =

ip(T),dU

c_r dt

c_v dt -f- ψ (T) dt,

+ ψ·Μ·

ARdv

T

получим по правилу смешения

d In К

^»з/?₃ + ^1У,(Т)У^з(Г)Ч/?₃

гр ^,1/ЗКЗ ¹ J¹ ^ЗГ

, Qn₃ /Г _ П3/З3 dQ Т2 Т dT ’

где знак 4 относится к гремучему газу, а 3-к водяным парам. Но dQ=d (U₄ — Ug),

1 dQ т т Отсюда

^CV_ni~^CV_n

V4(T)-V₃(T)

j

d In×_ Qno/Зз _ Q_xdi T² Та’

тепло при .полном соединении Это соотношение принадлеяшт где ζ?!—все и F= Const.

Вант-Гоффу и в этой форме удобно“ Применимо для скольких угодно компонентов реакций.

В применении к реакции гремучий газ водяные пары оба соотношения дают возможность вычислять степень диссоциации. Здесь К=с² с

= - ¹ -₂ -, и можно выразить концентрации че-^сз рез величину х. Действительно в этом случае имеем

Г(2 + ж)

чем распад паров воды. Повышение давления уменьшает распад, также уменьшает и избыток кислорода по соотношению Гульдберга и Ваа-ге. Но по тому же соотношению всегда совместно с парами воды имеется и гремучий газ, только при t° невысоких он имеется в ничтожных количествах, например при 1 000° и 1 Atm 100ж=0,000026. Нужно заметить, что приведенные соотношения относятся, как уже сказано, к т. н. химич. равновесию, то есть мы можем их наблюдать при процессах медленных. Поэтому например для наблюдения зависимости диссоциации водяных паров от Т и Р нужны особые методы, дающие уверенность, что мы имеем дело с установившимся равновесием при данных ТиР.

Одним из таких методов в известной области Т служит метод полупроницаемых стенок. Платина, иридий и палладий обладают при высоких Т свойством пропускать водород и не пропускать других газов. Схему использования ч

Λ.

У

Фигура 36.

и следовательно

^ _ ’ 2 Ρβ_χχ „ _ Ρβ·ίΧ_

°¹ K_WT(2 + х) > ² Д«Т(2 +я),

Г ^2ρβ 3⁽¹-^χ)

³ R_mT{2+x),

_к Рх³ β β% _ κ₁β^β₂

^Ά Р_шТ(2 + х) (i-x)² β* β-j -

Взяв 1η и откидывая 1η -^-_г- как постоянна ное, имеем

d 1 у _ d, Рх³__ _Qi_^

df ^{m Ά}1 ~ dt R_mT (2 +я) (1-х²) ~ AR_mT²*

По Нернсту (здесь на 2 моля Н₂0)

Q=ИЗ 820 + 2,65 Т-4,41.10“⁴ Т² +

+ 1,252.10“⁶ Т³—9,12 · 10"¹⁰ Т⁴ + 4,36 · 10“¹⁷ ТК После подстановки и соответственной интеграции, перехода на десятичные логарифмы и подстановки постоянного интеграции J=— 1,08 (Нернст) получаем

lg Κ_λ=- + 1,335 lg Т - 0,965 · КГ¹ Т +

+ 0,137 · КГ⁴ Т-~0,665 · ΙΟ^-10 · Т³ +

+ 0,191 · 1(Г¹⁷ Т⁵ + J

и отсюда узнаем х, то есть степень диссоциации в зависимости от Т и Р. Соответственно приводим из Нернста:

	100х
т	1 Atm	1		100 Atm
2 500 В 500	4,21 30,9		0,927 7,79

Также для углекислого газа по формуле 2С0₂г2С0+0_а:_

	100х
Т	1 Atm	100 Atm
2 500	17,6	4,09
3 500	83,2	39,8

Таблички показывают, что распад углекислоты значительно больше при тех же условиях,

этого свойства дает фигура 36. Здесь в электрич. печи при известной t° текут медленно пары воды и встречают сосуд А (например из иридия), из которого предварительно удален воздух и на конце которого имеется манометр М. Водород, находящийся в смеси паров воды и гремучего газа, проникает в сосуд и по манометру узнают его парциальное давление и далее определяют процентное отношение. Разумеется в этом способе определяется диссоциация лишь при р=1 Atm. О других способах см. у Нернста [⁶]. Можно рассмотреть процесс сгорания водорода в кислороде при постоянном внешнем объёме и при отсутствии влияния внешнего тепла.

В этом случае по первому прин-^х ципу Т. U=Const за все время

Ч. процесса соединения. Это дает

^Ч. соотношение между х и Т и да-

X лее по теореме Вант-Гоффа, а также по характе-ристич. уравнению определяем х, Т и Р по достижении равновесия. Удобнее

Фигура 37.

В

3000 “ 3500 4000 Т

решать вопрос при помощи двух графиков. Один (М) представляет зависимость между ж и Т из условия U=Const, другой (В)—ту же зависимость из соотношения Вант-Гоффа совместно с характеристич. ур-ием (фигура 37) и показывает схему решения. Рассмотрим теперь процесс Р= Const, Т= Const. Возьмем ф-ию Ф, тогда άΦ=S dT — AV dP=0 и следовательно άΦ=0=Т dS — Но это равенство может

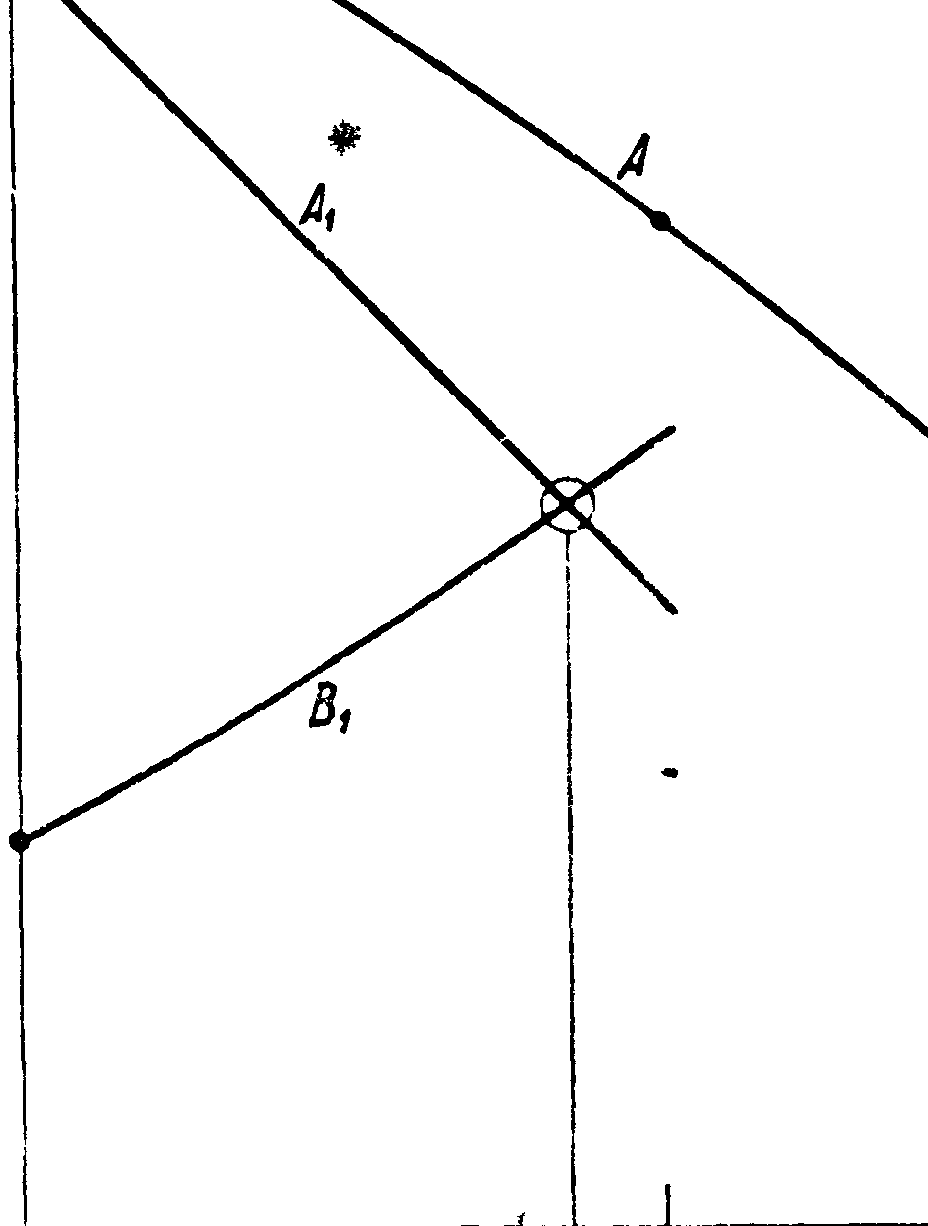
быть написано в с те дующем виде:

TdS-di^T dS - dU - Ad(PV) =

-= T dS — dU — AP dV=0,

T. K. P=Const. T. о. мы приходим опять к тому же равенству, что и прежде, то есть

dF=АР dV при Т=Const.

В результате мы опять получим соотношение T£(S - AR) dy — £U dy=О, из которого можно вывести соотношение Гульд-берга-Вааге, если применить понятие концентрации к меняющемуся объёму. Но разность внутренних энергий здесь уже не будет полным теплом реакции. По первому принципу полным теплом будет разность энтальпий (dQ=di-AV dP). Мы имеем однако прежнее соотношение (взяв для примера опять реакцию 2H_aO«t2H_a + O_a)

Τ(8ιΐΐ₁β_ί -f- $2^2/^2 ~ S₃n₃fi₃)=(Z7₄ — υ~)η₃β₃ -f-+ AR_mT(ni + n₂ — n₃).

Здесь в предположении P=Const AR_mT(n_x n₂)=APV_X

тогда, когда x=1, и AR_mTn_z=APV₃, когда ж= 0. Отсюда видно, что правая часть написанного равенства есть разность энтальпий между смесью с очень малым содержанием Н₂0 и парами воды с очень малым содержанием гремучего таза, а это и будет равняться теп-лу Q при полном (в идеале) соединении для Р=Const. Тогда равенство можно написать

T(S₄-S_a)=Q[· S₄-S₃=f

и, взяв производную по Т и приняв во внимание, что

_4_ Qi__дС Οι

dt T ~~ dt T

(т.к. jr Ή.γ разнятся на постоянное), имеем опять соотношение Вант-Гоффа, только во второй части будет не все тепло реакции, а разность внутренних энергий смеси с х=0 и х= 1 (в пределе). Т. о., если мы имеем задачу о равновесии при Р=Const и Т=Const гремучего газа и паров воды с условием отсутствия влияния внешнего тепла, то по первому принципу имеем г=Const и далее опять соотношение Вант-Гоффа вместе с характеристич. ур-ием.

Способ решения указан на той же фигура 37 кривыми А_х и В_л. Первая дает зависимость между х и Т при г=Const, то есть

U_i^JrAR_mT - 3=xU + (l-x)U₃AAR_mT_x(2 + x). Но

U,=σ,₄ + U(T), и₃=ио_з + UT),

поэтому

^0₄ + UT) + AR_mT. 3=x[U_0i + и(Тг) - 1 --Ш⁷!) + AR_mT_x] + U_H + f_z{T_x) + AR_mT_x. 2 или

^Ό4 - “о3 +=x[U₄ - и_ч +

+ Ш ) - U (Т_х) + AR_mT J + f_z (Тг) + 2AR_mT_x.

Разность постоянных внутренних энергий есть постоянная в выражении тепла реакции (при F= Const) в зависимости от Т; /₃(Т)и/₄(Т) определяются по теплоемкостям; Т—начальная температура, Т_х—произвольная. Отсюда определится зависимость между х и Тдля г= Const. Она предоставлена схематически кривой А₁₉ а кривую В_х находим указанными выше соотношениями (Вант-Гоффа и характеристич. ур-ия), дающи ми зависимость х от Р и Т (здесь Р=1 Atm)· Пересечение дает Т равновесия. Она ниже, чем для V=Const, и соответственно диссоциация больше.

От газов непосредственно можно перейти к теории слабых растворов при помощи введения понятия об осмотич. давлении. Из элементарного факта диффузии растворимого в растворителе можно по Вант-Гоффу вывести следующее заключение [⁶]. Предположим, что над раствором имеется поршень, пропускающий растворитель и не пропускающий растворимое, и нальем над этим поршнем растворитель (например воду). Если мы будем давить на поршень,опуская его вниз, то часть воды перейдет вверх и раствор сгустится, если, наоборот, мы будем поднимать поршень, то вода перейдет вниз и раствор будет слабее, т. к. растворимое частью перейдет в вошедший растворитель. Мы можем следовательно принять, что на поршень производится давление растворимым, стремящимся занять соответствующее пространство во всем растворителе. Это давление называется осмотическим давлением и аналогично давлению, оказываемому газом на поршень цилиндра, в котором газ работает. Давление это фактически измерялось (о способах см. у Нернста [⁶]) и например для 4%-ного раствора сахара в воде при 13,7° оно равняется

2,74 Atm. Дальнейшими опытами обнаружено, что осмотическое давление пропорционально при данном Т концентрации С,.а при данном С

пропорционально Т. Так как С=γ, то первое соотношение есть pv=Const, то есть закон Ма-риотта, а второе—закон Гей-Люссака, и все вместе, если отнести к кг-мол., дает PV=R_mT, то есть осмотическое давление равно тому, которое получилось бы, если бы после удаления растворителя кг-мол. данного вещества в газообразной форме (или фазе) при данной t° занимала объём V. Но так же, как для газов, закон Мариотта-Гей-Люсдака тем точнее, чем при данной t° меньше Р, и для осмотич. давления данные соотношения точны для слабых растворов. Растворимое может находиться не только в жидкой, но и парообразной форме, а к насыщенному пару закон Мариотта-Гей-Люссака применим лишь при слабых давлениях. Поэтому и возникла теория слабых растворов. Но что касается растворения газов в жидкостях, то известно опытное соотношение Генри, гласящее, что газы растворяются пропорционально их давлению. Отсюда непосредственно следует, что осмотич. давление в этом случае равно давлению газа. Далее имеем также, что осмотич. давление следует закону парциальных давлений Дальтона. Мы можем на основании сказанного применить соотношения для газовых реакций к теории растворов.

Для примера рассмотрим нек-рые элементарные случаи. Всякий насыщенный пар можно считать находящимся в равновесии с своей жидкостью. Для р небольших можно положить для 1 (тсз-мол.) пара pV=R_mT и концентра-

1 р

ЦИЮ - С - у - γ—ψ.

Соотношение Вант-Гоффа дает

~1п~= ^d In —=__g__

dt 1 dT R_mT AR_mT²

и отсюда

A i_{n v =} Q±Apy ₌_L_,

dT V AR_mT² AR_mT* где r—все тепло парообразования 1 моля.

Этой ф-лой пользуются иногда для определения тепла парообразования при небольших давлениях. Когда жидкость представляет слабый раствор, то давление насыщенного пара может измениться и стать р₁. Предположим, что г (все скрытое тепло) мало изменилось, тогда можно написать а отсюда

d ·,

тЛ^пр-

АЛ_тТ*

In — =

Pi Ali

Xh-iY

All_mTi

Это соотношение дает изменение t°_Kun, раствора в зависимости от изменения давления насыщенного пара. Подобным же образом определяется и изменение давления при замерзании [⁶]. Соотношение между р и Т для насыщенного пара м. б. написано

± In — =__^Q—

dt Т AR_mT²

и также для небольшой разницы 1° можно написать или

In Т — in

ш ^ ш _{Γι ARn}

InC-lnC^^y-

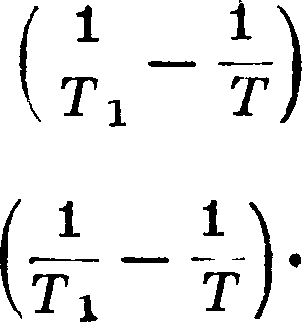
Соотношение м. б. непоерэдственно применено к растворам и дает возможность определить тепло растворения по различным концентрациям насыщенного раствора в зависимости от Т.

Так как твердые тела также испаряются, то распад твердого тела подлежит тем же соотношениям. Пусть при испарении твердое тело распадается на ряд тел с числом молекул п₁₉ п₂,. и парциальные давления будут р₁₉ р₂, ··· Соотношение Вапт-Гоффа напишется:

d, Ρ*·^χ Р₂^Л. Q,

dt (R_mT)ⁿ i + ⁿ*.+ Ati_mT²’

где Q₁—тепло испарения. Если общее давление— Р, то имеем

Рп_л

1ь _:Vb

и т. д., следовательно

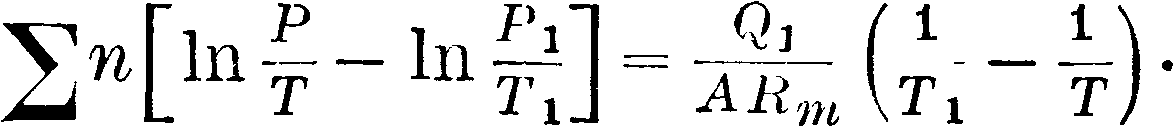
Растворение газов также характеризуется соотношением Вант-Гоффа

Q _d nK AR_mT 2 dT 5

по Бунзену можно взять

К-

аТ ^: ‘Δ16 ’

где а—коэф. поглощения. Диссоциация в растворе исследуется при помощи того же соотношения. Само соотношение Вант-Гоффа, как мы видели, вышло из применения ф-ии F к химич. процессам. По по известному свойству ф-ии F имеем и_₌ a (F

Та bт тонн)

или же и-и, ₌ д F — F г т2 ат т² )’

Назовем разность F_t — F через

U-U^Q,

Q_ ₌ _ ^д т± от т I

51, тогда и, сравнивая с ф-лой Вант-Гоффа

Гт-ЬХ-АЖ

2’

получим

AR_m In К - — ~ + а, то есть AR_mT In К= - Та. Величиной

5ί из меряется химич. сродство, т. ч. реакция идет в сторону наибольшей 5Е Поэтому в частности представим себе газ, находящийся в двух фазах: 1) в жидком или твердом растворе и

2) в газообразном виде над этим раствором. Концентрации пусть будут С и С_л. Тогда, как уже имели выше, получим (принимая во внимание, что К=— и Iii =

AR_mT In C =k- Та и

AR_mT In C_±=5l_x - Tap,

при равновесии имеем 5ί=51 _г по сказанному (иначе было бы или испарение или поглощение). Поэтому

AR_mT In С + В=AR_mT In С_х + В₁

или

Г_ _ В_х-В СД AR_mT

Применение этого соотношения—см. Окклюзия.

Мы видели, что теорема Нернста связана с ф-иейЕ⁷. Но разностью ф-ий F для соединения и реагентов, как мы видели, измеряется химич. сродство. Теорема Нернста в этом случае м. б. формулирована

i(Fi-20^0=0.

Тогда определение величины 5ί м. б. произведено до определению тепла реакции при V=Const. Пусть имеется

Q^U₀-U_Oi + aT + βΤ* + γΤ*+.

тогда

_ о (т дТ Т )

В_

Т*

+ ψ + βΤγΤ^. .,

где В=U₀- U₀₁.

Отсюда %=В-аТ In Τ-βΤ^ζ- £ Т³ +. + Та;

но ^ПР^И Т-0 по теореме Нернста, к следовательно а=0, т. к. иначе имели бы —а- оо=— ос и α= 0,то есть 51=В - £Е² - | Т³ +.

Если β,γ и т. д.—незначительные величины, то 5ί=U₀— U₀₁ и мы получаем положение Вертело, что каждая химическая реакция идет в ту сторону, где имеется наибольшее развитие тепла. Это положение справедливо лишь при независимости U от £°. Наоборот, если например величиной β пренебрегать нельзя, то можно найти такую Т, при которой 5Ϊ=0, из равенства

51=В -βΤ²

и от этой Т в одну сторону будет один вид химич. равновесия, в другую—другой; t°_nj[, по одну сторону которой тело в жидком состоянии находится в равновесии с парами его, а по другую сторону—в твердом состоянии, будет одним из примеров такой Т. Так как вообще то, приняв с„=уТ, имеем U=U₀ +

Т 2

-f у — и следовательно

Ггр _Тг ₌ _ и_0з + βΤ²=Q.

Для Г,

имеем

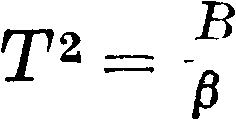
U_0l-U о. β

Q __гр2

β ’

τ. e.

_Q___-

^CV₁~^CV₂

где Q—тепло при переходе из жидкого в твердое состояние (или наоборот). Разумеется это соотношение справедливо лишь там, где можно принять c_v= γΤ. Мы видим теперь, что главное значение теоремы Нернста лежит в области химии, т. к. при ее помощи можно по тепловым данным вычислить величину %—меру химич. сродства и, наоборот, если эту величину можно найти непосредственно из наблюдений над химическим равновесием, можно судить о тепле реакции в том случае гл. обр., где тепло это мало зависит от Т [⁶, ^а0].

Этим кратким эскизом можно закончить статью. Мы вышли из положения о невместительности Т. в рамках механики Ньютона и можно в заключение привести один из принципиальных вопросов, решение которого также не дает механика. Это вопрос о perpetuum mobile. С технич. стороны его можно заменить вопросом: можно ли создать машину, в которой кпд с механич. стороны был бы равен 1? Он решается указанием на вредные сопротивления (трения) в механизмах. Работа вредных сопротивлений обращается в тепло, к-рое и рассеивается. Отсюда мы видим, что объяснение невозможности т. н. perpetuum mobile 1-го рода может дать только Т. Вопрос о perpetuum mobile 2-го рода следует за первым: но возможно ли это тепло, уходящее вследствие вредных сопротивлений ц машине, вновь обратить в работу [⁶]? Он решается отрицательно уже тем, что процесс этот по постулату Клаузиуса необратим. Можно также поставить аналогичный вопрос о тепловой машине с кпд, равным 1. Вопрос решается принципом Карно, дающим кпд идеальной машины—машины Карно—в зависимости от £°. При этом здесь невозможность получить кпд, равный 1, зависит вовсе не от вредных потерь тепла, а от самой сущности работы калорич. машины между двумя данными t Т. о. на оба вопроса отвечает только Т. и они м. б. объединены в одно положение: ни с механической ни с термин, стороны мы не можем создать машину с полезностью, равной 1.

Лит.:¹) Lagrange J., M6canique analitique, t. 1— 2,8 6d., P., 1853—55; ²).K i r c h h о f G., Meclianik in gesammelte Abhandlung, Lpz., 1882; 3) Haas A., Ma-leriewellen u. Quantenmeclianik, B., 1928; «) MayerR., Die Mechanik d. Warme, 2 Aufl., Stg., 1874; 5)Osborn, «Mechanical Engineering», 1930; β) N e r n s t W., Theo-ret. Chemie, 15 Aufl., Stg., 1926; ⁷) J e 1 1 i n e k K., Lehr-iuichd. physikal. Chemie, В. 1, 1928; β) Η о 1 1 b о r n u. S c h u ] t z e, «Ann. d. Phys. u. Chemie», Lpz., 1915, 9. 47; Hollborn u. Otto L., ibid., 1925, p. 33; 9) Roebuck, «Proc. Am. Acad.», 1925, p. 60, 537; !0)Bridgemann O., «Physical. Review», 1929, v. 34, p. 527—533; n) «Annalen d. Phys. u. Chemie», 1919, p. 59; ¹²) B e a 11 i e J., «Physical Review», 1929, v. 34, p. 1615, 1930, v. 35, p. 643; Щ Мерцалов H., Краткий курс по термодинамике, отдел основной, М.—Л., 1927; «Exners Repertorium der Physik», В. 21, W.; ^u) Мерцалов H., О внутренней энергии жидкости, «ВИ», 1927, 1; ¹⁵) Heck К., «Mechanical Engineering», 1930, p. 133; !б) В oltzman.n, «Ann. d. Phys. u. Chemie», Lpz., 1884, B. 22, p. 291 u. f.; ¹⁷) L u m m e r u. Pringsheim, «Berichte d. deutschen Physik Ge-sellschaft», Lpz., 1903, p. 56; Щ «Ann. d. Phys. u. Chemie», Lpz., 1899, p. 417, 1900, p. 159; *») «Yerhandl. d. Deutsch. Phys. Gesellschaft», Lpz., 1899, p. 91, 1900,

p. 215, 1901, p. 36.; ^)Nernst W., Die theor. u. expe-rim. Grundlagen des neuen Warmesatzes, 1924; 21) T r a-utzu. Steyer, «Forschung», B. 2, B., 1931, 2.—Б лох Э., Кинетическая теория газов, пер. с франц., М.—Л., 1925; Бр андт А., Основания термодинамики, 4 изд., ч. 1—2, М.—П., 1923; Младзеевский А., Термодинамика и теория фаз, М., 1922; Тимирязев А., Кинетическая теория материи, М.—П., 1927;×в о л ь-с о н О., Курс физики, т. 3, Берлин, 1923; Я ш н о в А., Основа термодинамики в применении к тепловым двигателям, ч. 1—2, М.—Л., 1926; Ястржембский А., Технич. термодинамика, М., 1926; Мерцалов Н., О теореме Нернста, «ВИ», 1930; Carnot S., Reflexions sur la puissance motrice du feu, P., 1924 (2 p., 1878); Mayer R., Bemerkung uber. die Krafte der unbelebten Natur, Liebigs Annalen, Heidelberg, 1842, v. 42, p. 1; Joule, Proceedings of Royal Societv, L., 1837—43; Clausius, «Pogg. Annalens», Lpz., 1850, B. 81, p. 168, 1851, В. 83,

p. 118, 1854, B. 93, p. 481, 1857, B. 100, p. 353, 1858, B. 105, p. 239; Thomson W. (Lord Kelvin), Transactions of the Royal Society of Edinburgh, 1851, v. 20, p„. 281, 289; Kirchhof G., Vorlesungen uber d. Theorie d. Warme, Lpz., 1894; Helmholtz H., Vorlesungen hber d. Theorie d. Warme, Lpz., 1903; Winkelmann, Handb. d. Physik, B. 3, Die Warme, 2 Aufl., Lpz., 1906; Plank M., Vorlesungen hber Thermodvnamik, 6 Aufl.„ Lpz., 1921 ;BoltzmannL„ Vorlesungen uber Gastheorie, T. 1—2, 2 Aufl., Lpz.,1908; Knoblauch, «Forschung^, В., 1932, 1—2; Hausen, ibid., 1931, 9; Plank M., Die Warmestrahlung, 5 Aufl., Lpz., 1923; P о i n c a r έΗ., Thermodynamique, 2 6d., P., 1923; Haas A., Atom, theorie, 2 Aufl., B., 1929; d e Broglie L., Untersuchun-gen uber Quantentheorie, Lpz., 1927; Batschinsky

A., Ein thermodynamischer Trugschluss, Ztschr. f. Ph.,

B., 1929; Lenner G., Techmsche Thermodvnamiaue,

B. 1—2, Lpz., 1906. H. Мерцалов.