Траектория

Траектория, линия, представляющая собой совокупность всех последовательных положений точки, движущейся относительно некоторой системы отсчета или системы координат. Так как эти последовательные положения непрерывно следуют в пространстве друг за другом, то Т. представляет собой линию не-

прерывную. Если точка движется, оставаясь в одной и той же плоскости, то и Т. представляет собой плоскую кривую; в противном же случае Т. есть кривая неплоская или кривая двойной кривизны. Последний случай представляется например при движении точки по винтовой линии. В частности Т. может представлять собой прямую линию. Необходимо иметь в виду, что вид траектории точки зависит от кинематич. состояния системы отсчета, по отношению к которой происходит, данное движение, т. ч. одно и то же движение точки в одно и то же время может происходить относительно наблюдателей, связанных с различными системами отсчета, по различным Т. Так, если наблюдатель, стоящий неподвижно на палубе движущегося парохода, бросает предмет вертикально вверх, то последний будет двигаться по отношению к этому наблюдателю по вертикальной прямой. Для наблюдателя же, стоящего неподвижно на берегу, Т. этого же движущегося предмета будет казаться в виде параболы. Допустим, что движение точки отнесено к декартовой системе координат (смотрите), и пусть даны функциональные зависимости текущих координат точки х, у, z от времени 1, то есть пусть даны ур-ия движения точки

®=fl(f) Ί

2/=м.о }· е>

£=/₃(ί) J

Эти ур-ия представляют собой в то же время и ур-ия Т. в параметрич. форме, т. е‘ ур-ия, определяющие вид Т. в зависимости от параметра t. Если исключить из ур-ий (1) параметр t, то можно получить ур-ия кривой в обычной форме, а именно в виде:

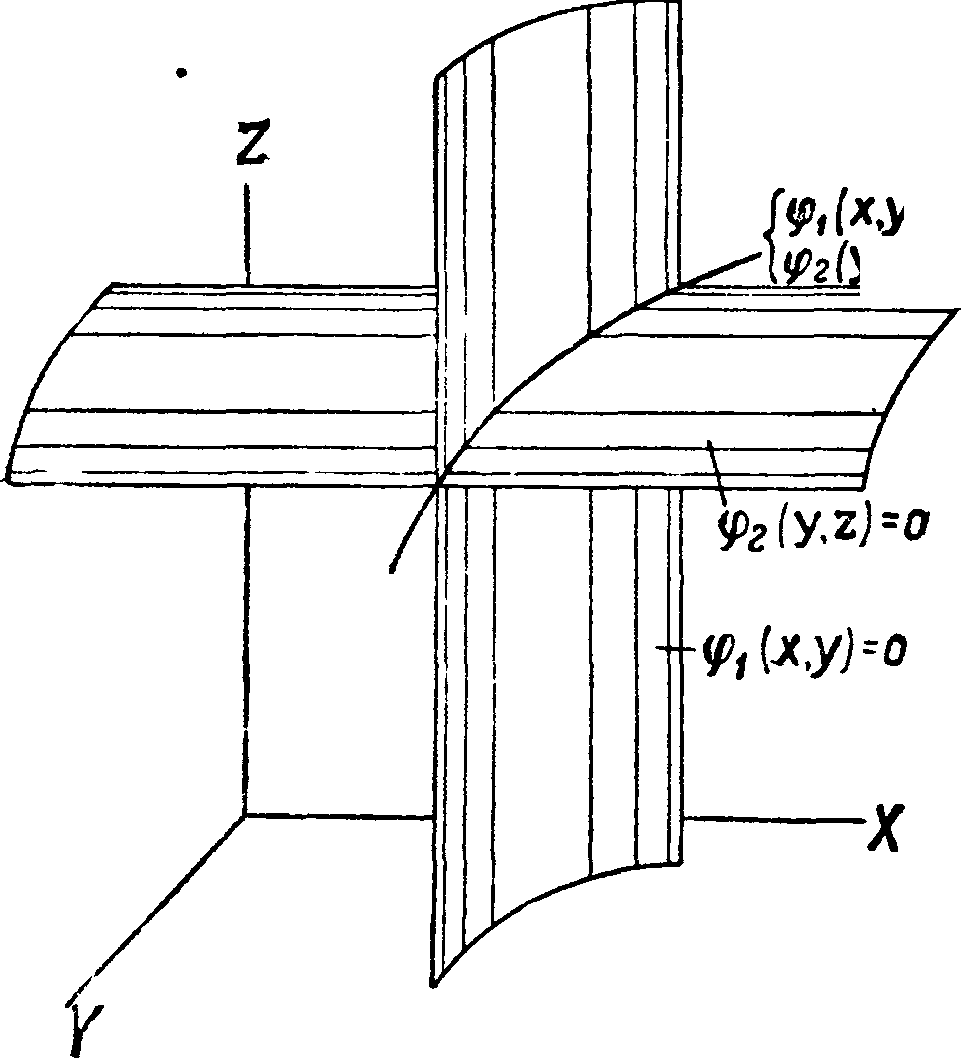
9>ι (Ж, У)=0 1 9>2 (У, г)=0 )

Первое из ур-ий (2) представляет собой нек-рую цилиндрич. поверхность, параллельную оси Z

(фигура), а второе из ур-ий (2)—цилиндрич. поверхность, Ί=σ параллельную оси X. Т. будет представлять собой кривую, по которой эти две поверхности взаимно пересекаются. Т. к. в один и тот же момент движущаяся точка не может находиться в различных точках пространства, то параметрические ур-ия T. (1) должен быть однозначными ф-иями от t. Вследствие же непрерывного характера Т. бесконечно малому приращению времени dt должно соответствовать бесконечно малое изменение положения точки, то есть бесконечно малые изменения координат dx, dy, dz, поэтому ф-ии (1) должен быть непрерывными относительно t. Помимо этого точка в каждый момент имеет определенные, и притом конечные, скорости и ускорения; следовательно ур-ия (1) должны допускать для любого значения t первую и вторую производную по t.

В случае плоского движения точки можно, взяв в плоскости движения две ортогональные

оси координат X, Y, представить Т. только при помощи двух ур-ий:

Ж=МО I /оч у-июг ⁽³⁾

Исключив из (3) параметр t, получим ур-ие Т. в виде

У=Ψ (ж)· (4)

Если точка движется по прямой, то, взяв эту прямую в качестве оси X, получим ур-ие движения точки в виде

(5)

Вместо декартовой системы координат м. б. взята и любая другая система координат q_ltg₂, например цилиндрич. координаты г, <р, h, сферич. координаты г, ψ, *0. В этом случае будем иметь параметрич. ур-ия Т., аналогичные (1), а именно вида

<ii=fi( 0. (⁶)

где i=1, 2, 3.

Исключая из трех ур-ий (6) параметр t, мы можем получить ур-ия Т. в виде:

Ψι Οι, За) =0 Ί /₇₎

Ψ2 Оа» За)=0

Аналитич. свойства ф-ий (6) должен быть те же, что и вышеупомянутые свойства ф-ий (1).

Если имеется система, состоящая из п точек, то в нек-рых случаях вводят понятие Т. системы точек, причем под этим понятием подразумевают нижеследующее. Пусть п точек системы имеют относительно некоторой декартовой системы 3 п координат

(®1? У и ^l)> (®2> 2/2? ^2*)’ (®3> 2/з ? ^з)> · · · > ,(Я?П5 Уп·) так что движение системы определяется 3 п ур-иями вида

= и_г (0. Уг=fi_t (О, Zi=fi₃ (i), (8)

(г=1, 2, ., η)

соответствующими трем ур-иям (1) для одной движущейся точки. Мы можем однако абстрактно считать все 3п координат координатами одной единственной точки, перемещающейся по некоторой кривой Зп-мерного пространства. Эту кривую, имеющую Зп—2 измерения, называют условно Т. системы. В нек-рых случаях такое обобщение понятия Т. оказывается полезным при теоретич. выводах. О Т. материальной точки, брошенной под углом к горизонту в пустоте и в сопротивляющейся среде, см. Баллистика. м. серебренников.

Лит.: см. Механика теоретическая и Баллистика.