Трансфигурация

Трансфигурация, метод, применяемый при исследовании электрических цепей для превращения одной конфигурации сочетания проводов в виде определенной фигуры проводов в эквивалентную другую, которая м. б. введена вместо первой при всякого рода расчетах в схему замещения. Особенно часто применяется при исследовании несимметричных трехфазных систем, а также при расчете электрич. сетей. Впервые была предложена Кеннелли [⁹] для вычислительных нужд электроизмерительных лабораторий применительно к трехфазным схемам и схеме мостика Уитстона; в дальнейшем разработана и обобщена Герцогом и Фельдманом [⁶,⁸]. Т. позволяет заменить образуемый проводами замкнутый контур в виде мн-ка эквивалентной звездой, то есть пучком сходящихся в одной точке фиктивных проводов, общее сопротивление которых удовлетворяет условиям эквивалентности. Реже Т. применяется для обратного процесса: превращения звезды в замкнутый контур. Требования эквивалентности: 1) распределение токов в остальной системе проводов (вне преобразуемой части) должно сохраниться неизменным; 2) разности потенциалов между точками, в которых преоб разуемая часть присоединена к остальной системе проводов (наир, между углами мн-ка), должны оставаться прежними. При расчете сложных сетей (смотрите Сети электрические) Т. позволяет избавиться от замкнутого контура, чтобы иметь возможность затем применить к сети способ постепенного упрощения ее по методу Фрика, неприменимому при наличии замкнутых контуров; при расчете сети по методу узловых напряжений Кольтри уменьшение с помощью Т. числа замкнутых контуров в сети облегчает расчет, уменьшая число узловых ур-ий |⁴,⁸]. На практике чаще всего‘при этом Т. применяют для преобразования тр-ка в звезду; с этим же случаем приходится иметь дело и при исследовании несимметричных трехфазных систем (смотрите Трехфазный ток) [⁵,⁷].

Если число сторон замкнутого контура превышает 3 (четырехугольник и т. д.), то Т. возможна только при наличии дополнительных условий и становится настолько сложной, что практич. ценность ее значительно понижается Г⁶].

Применение Т. для преобразования треугольника в звезду. Чтобы тр-к из проводов, обладающих сопротивлениями а, b и с и соединяющих в какой-нибудь системе проводов узловые точки А, В ж С (фигура), превратить в эквивалентную звезду, вычисляют сопротивление α, β и у, которые должны иметь фиктивные провода (лучи звезды) для выполнения требований эквивалентности, пользуясь ф-лами:

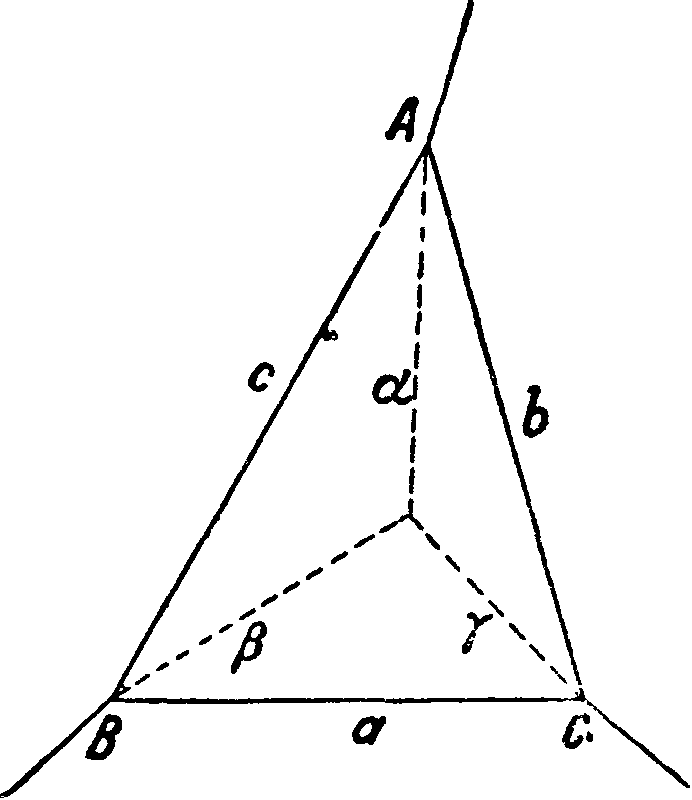
_ Ьс_. η __ ас__.

^α__α^-b-fc^, ^ а+Ь +с ’

У =

аЬ

Т. о. сопротивление одного луча звезды, эквивалентной тр-ку, равняется произведению сопротивлений двух прилегающих к вычисляемому лучу сторон тр-ка, деленному ыа сумму сопротивлений всех сторон тр-ка. При этом для постоянного тока под сопротивлениями надлежит понимать омич, сопротивления, а при переменном токе—полные (кажущиеся) сопротивления (смотрите Переменные токи). Практич. применение преобразования треугольника по методу Т. при исследовании несимметричных трехфазных систем: при нагрузке, включенной тр-ком, приходится при расчетах линейные токи вводить в виде разностей фазных токов (что удлиняет расчет, делая его не наглядным); Т. позволяет нагрузку, включенную тр-ком, заме нить нагрузкой, включенной звездой, причем все токи и напряжения остаются теми же, которые были при тр-ке [ ^а,⁴,⁵].

Преобразование звезды в треугольник осуществляется путем вычисления проводимостей сторон тр-ка λ_α, X_h и А_с по заданным проводимостям лучей звезды λ_α, λβ и λ_γ с помощью ф-л:

^λβ^λγ. * ^λα^λγ. _§ ^λα^λβ

^{λα =} ’·α+Ζβ + ^ ’ ^Аb ~ ^λα + ^λβ + ^λγ ’ ^Г° “ *a + ‘/i + V_,

причем λ_α, λβ, λ_γ и λ_α, Α_δ, λ_ύ обозначают проводимости (при переменном токе полные), то есть величины, обратные сопротивлениям (при переменном токе полным):

,1-1

^А«=5‘> *«.=ϊ и т. д.

Для Т. можно кроме описанного выше анали-тич. способа определения сопротивлений (или проводимостей) искомой эквивалентной фигу-ры пользоваться также разработанным для этой цели графическим методом [⁶]. На практике более распространен аналитический метод, сопряженный обычно с меньшей затратой времени.

Лит.: ^А) Г е ф н е р Ф., Системы распределения тока и расчет электр. сетей, пер·, с нем., СПБ, 1909; ^а) СЭТ, Справочная книга для электротехников, т. 1, 2 изд., Л., 1930; ^ь) Ф а у л ь Ф., Справочник по электротехнике, пер. с англ., т. 1, М.—Л., 1928; ⁴)×а щ и н с к и п В., Канализация электр. энергии (сети), ч. 1, 3 изд., Л., 1931; ⁵) Ч е р д а н ц е в И., Теория переменных токов, 3 изд., М.—Л., 1932; &) Herzog u. F e 1 d m a η n, DieBerech-nung elektr. Eeitungsnetze in Theorie и. Praxis, 4 Aufl., B., 1927; ⁷) Fraenkel A., Theorie d. Wechseistrome, 3 Aufl., B., 1931; »)Herzog J. u. Feldmann C., Ueber widerstandstreue Umgestaitung elektrischer Netze (Transfigurierung), «ETZ», B., 1900, p. 167; ⁹) К e η n e-1 1 у A. E., On the Determination of Current Strength in Threepointed Star Resistance Systems, «Е1. World», N. Y., 1899, y. 34, p. 268, 413. В. Хащинский.