Трехфазный ток

Трехфазный ток, наиболее распространенный в технике вид многофазных электрич. токов (смотрите Переменные шоки и Системы переменного тока); представляет собой совокупность трех переменных («однофазных») токон одной и той же частоты, сдвинутых друг относительно друга на 120°, то есть на 7з периода (фигура 1).

Общие сведения. Для получения Т. т„ статор электрич. машины снабжают тремя симметрично расположенными одинаковыми обмотками («фазами»), в которых индуктируются 3 одинаковые, но сдвинутые по фазе (смотрите Сдвиг фаз) друг относительно друга на 120° эдс. Изображенные на фигуре 1 три синусоиды и векторная диаграмма могут—в другом масштабе— изображать также и эдс. Проведя к потребителям от каждой фазной обмотки по два провода, мы получили бы несопряженную (несвязанную) трехфазную систему с шестью проводами, состоящую из трех независимых электрич. цепей, в которых действуют 3 эдс с равными амплитудами U_m и одинаковой круговой частотой (электрич. угловощскоростью) со; их мгновенные значения:

u₁=U_msin((ot),

u_z=U_mein (ωί -γ),

u₃=U_m sin ("i-Д ·

При одинаковой («симметричной») нагрузке трех фаз (одинаковых амплитудах силы тока 1_ти одинаковом угле сдвига фаз φ между током и эдс во всех трех фазах) мгновенные значения сил токов:

11=I_m sin(cot~<p),

1₂=I_m sin 1

Ч=1т sin (ωί-⁴3^π_-^). )

Несопряженная трехфазная система на практике не применяется из-за неудобства большого числа проводов. С л ожив_ последние три ур-ия (2), получим:

Н Т~ 7 Т~ Ц⁼®· (3)

Отсюда следует основное достоинство Т. т.: сумма мгновенных значений токов двух фаз всегда равна взятому с обратным знаком мгновенному значению тока третьей фазы, т. ч. две фазы в любой момент как бы несут обратный ток третьей фазы; это позволяет, связывая между собой три фазные обмотки (для получения сопряженных трехфазных систем), обойтись тремя (или четырьмя) проводами вместо шести. Ток в четвертом, т. н. нулевом, или нейтральном, проводе (фигура 5) при равномерной нагрузке трех фаз и синусоидальном токе равен нулю. При наличии высших гармонических по нулевому проводу, даже при равномерной нагрузке всех фаз, протекает сумма всех то-

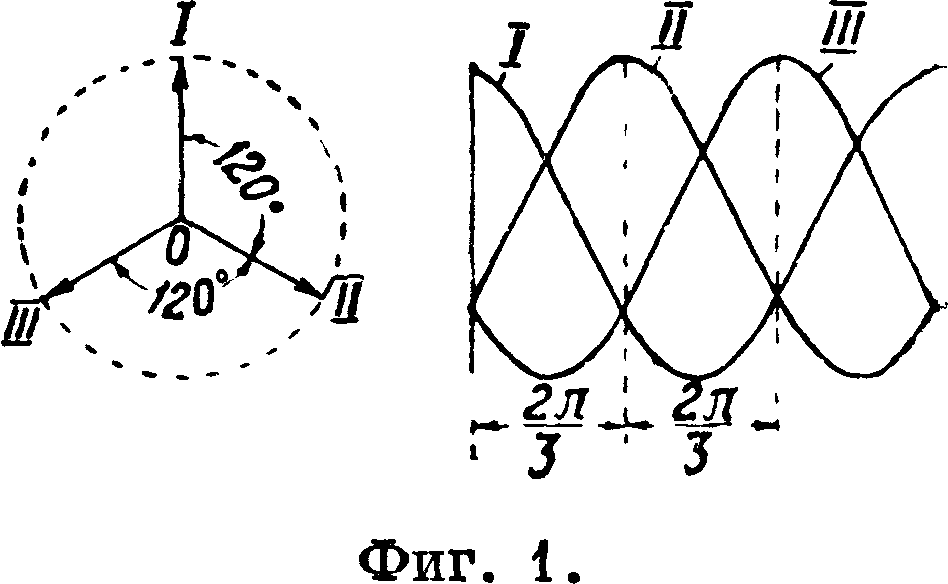
ков тройной частоты. Отдельные фазные обмотки соединяют последовательно, то есть конец каждой обмотки с началом другой,—т. н. соединение треугольником (фигура 2), или же соединяют 3 одноименные точки обмоток (3 «начала») в одну общую («нулевую») точку, к которой присоединяют нулевой провод, а от трех других концов обмоток ведут 3 («фазных») провода к потребителям—т. н. соединение звездой (фигура 3). Эти способы соединения принято схематически изображать, как показано на фигуре 4 и 5. При соединении звездой система

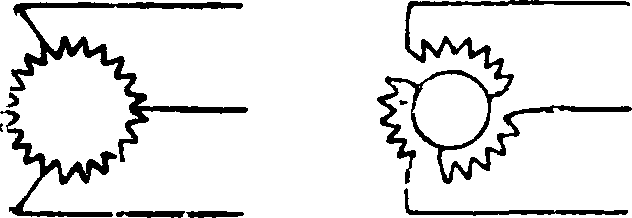
Линейный провод _ъЛин провод

Линейный провод Нулевой провод

.Лин провод

Лин, провод

Фигура 2. Фигура 3.

Фигура 4. Фигура 5.

м. б. четырехпроводной или трехпроводной, при симметричной нагрузке трех фаз ток в нулевом проводе согласно ур-ию (3) равен нулю и он становится ненужным. Независимо от способа соединения генератора приемники м. б. соединены также и тр-ком и звездой. На практике применяются также комбинации этих двух основных способов соединения. Для исследования соотношений между эдс и токами в трехфазных цепях с помощью векторных диаграмм пользуются топографическим методом, сопрягая какую-либо точку цепи с определенной точкой плоскости соответственно величине и фазе напряжения, к-рое существует между ней и некоторой произвольной точкой цепи; тогда вектор напряжения между двумя точками цепи можно определить, соединив на диаграмме две точки, соответствующие этим точкам цепи, прямой. Особенно удобен для ана-литическэго исследования трехфазных цепей символический метод, которым в этом случае пользуются аналогично применению его для однофазных цепей (смотрите Переменные токи). Напряжения и токи в обмотках *фаз называют фазными; напряжения же между проводами двух соседних фаз, ведущими от генератора к приемникам, носят название линейных (а также междуфазных, главных или сопряженных) напряжений, а токи в этих проводах—линейных токов.

Основные свойства и практическое применение. Т. т.—род тока, наиболее распространенный в технике сильных токов; чаще всего применяется в силовых и осветительных установках (для электрич. тяги на ж. д. в виде исключения, гл. обр. в Италии). В СССР, как и во всех других странах, в основу электрификации положены районные станции и сети Т. т., на питание от которых должны постепенно переходить и потребители всех других существующих пока отдельно установок. Только при передаче энергии на очень большие расстояния, с к-рыми приходится например иметь дело при проектировании единой высоковольтной сети Союза, намечается возврат от Т. т. к постоянному току; при этом Т. т. вероятно останется главным средством для распределения энергии в городских, промышленных (заводских) и районных сетях.

Достоинства Т. т.: значительная экономия металла на провода (смотрите Распределение электрической энергии) и одинаковая пригодность для •осветительных и силовых целей благодаря наличию весьма совершенных двигателей Т. т., асинхронных и коллекторных.

Симметрия систем Т.т. и ее нарушения. Нормально трехфазная система симметрична. Трехфазные генераторы и трансформаторы дают во всех трех фазах эдс, которые с достаточной для целей практики точностью можно считать равными и сдвинутыми друг относительно друга на равные углы. При проектировании и эксплуатации трехфазных установок стремятся распределить все приемники поровну между тремя фазами не только количественно, но и качественно (то есть не только по мощности, но и по характеру приемников). Поэтому на практике в нормальных условиях рабочего режима приблизительно одинаковы и нагрузки всех трех фаз. Т. о. при расчетах обычно приходится иметь дело с симметричными системами Т.т. Несимметричные системы, например случай неодинаковой нагрузки фаз, при нормальных условиях встречаются редко; однако они в ,е же представляют практический интерес, так как с ними приходится иметь дело при нарушениях правильного рабочего режима (при коротком замыкании, случайном замывании на землю, при разгрузке одной из фаз вследствие повреждения приемника и прочие). Для суждения о симметрии (например в отношении изоляции) служат особые приборы—асимметры.

Соединение звездой. При симметричности системы для соединения звездой топография. диаграмма имеет вид правильной звезды из трех лучей (фигура 1), изображающих фазные напряжения Пф_г Линейные напряжения являются геометрия, разностью напряжений соседних фаз и равны П_л=ϋφΥ 3. Токи линейный и фазный равны: 1_Л=1ф. Мощность всей системы (во всех трех фазах вместе) при том лее условии симметричности

Р=3 ϋφΐφ COS ψ=Υ3 и_л1_л COS φ.

Преимущество включения звездой (по сравнению с тр-ком) — более высокое напряжение в линии, сокращающее расход металла на провода. 1) Четырехпроводная система (фигура 6). Здесь можно использовать два различ-

Фигура 6. Фигура 7.

ных напряжения—фазное и линейное, поэтому возможно присоединение к одной и той же сети осветительных приборов (включаются между одним из фазных проводов и нулевым) и двигателей (присоединяются к трем фазным проводам); кроме того четырехпроводная система применяется там, где можно ожидать неравномерного распределения нагрузки между тремя частями (фазами) системы, нулевой провод при этом выравнивает несимметричность, неся разность токов:

b()~ ll ΐ₂ ^3*

Сечение фазных проводов рассчитывают в соответствии с нагрузкой (смотрите Провода), а сечение нулевого провода берут от V₃ до V₂ или Vi от сечения каждого из фазных проводов (для ну-. левого провода м. б. взято тем меньшее сечение, чем равномернее распределена нагрузка между тремя фазами и чем меньше вероятность значительных колебаний нагрузки, нарушающих симметричное ее распределение). 2) Т р е х-проводная система (фигура 7) применяется в тех случаях, где уверенность в том, что нагрузка всех трех фаз всегда будет одинакова, делает нулевой провод ненужным. В случае нарушения симметричности нагрузки силы токов в трех проводах автоматически устанавливаются такими, чтобы сумма их была равна нулю; вследствие этого нагрузка в разных фазах окажется под различными напряжениями: трехпроводная система весьма чувствительна к колебаниям нагрузки.

Соединение треугольником (фигура8). При симметричности системы для соединения треугольником топографии.диаграмма имеет вид равностороннего тр-ка (фигура 9); стороны его изображают линейные напряжения, которые в этом случае равны фазным: υ_Λ=ϋφ. Линейные токи являются геометрии, разностью токов соседних фаз и равны 1_х=1_фУb. Мощность всей системы (во всех трех (фазах вместе) при том же условии симметричности

Р=3 υ,βΐ,β cos ?>=]/3 (7_Л7,.

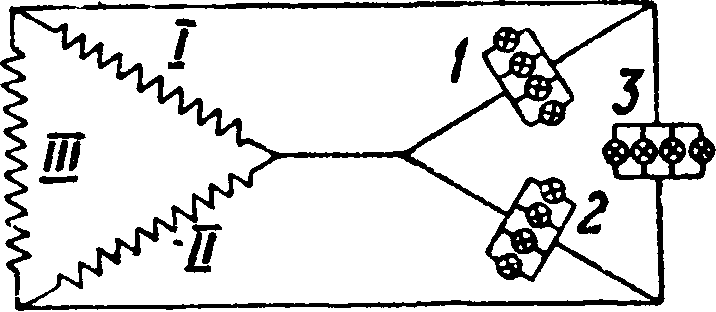
Фигура 8-

Преимущество включения тр-ком — меньшая чувствительность к колебаниям нагрузки (при включении фаз генератора и нагрузки тр-ком приемники в каждой фазе нагрузки находятся под фазным напряжением, независимо от соотношений между сопротивлениями отдельных фаз).

Недостаток включения трехфазным током (по сравнению со звездой) — меньшее напряжение в линии, вызывающее больший расход металла на провода.

Изображение эдсв симметричной системе Т. т. с помощью символического метода. С помощью комплексных величин 3 эдс Т. т. изображаются сл. обр:

и^и,

~^l~J— и - (- 0,5 - ) 0,866) и =

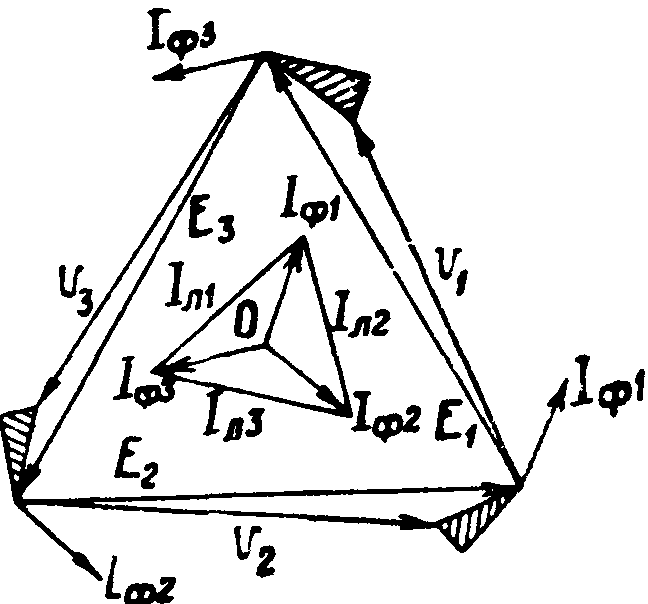
Фигура 9.

,2л ₍. 4 π

-Ue~^J Т =,

Г,

-ι-i-jY з

U=(— 0,5 + j 0,886) U =

Л π ,2 л

— Λ 4- 7

lie ^{J 3} =Ue *.

(4)

T. о. вектор U₂ получается из и_г умножением последнего на поворачивающий множитель

. 2 л

~ 3 Л^- « 2 π

е ³, к-рыи выражает поворот на j в отрицательном направлении (то есть по часовой стрел-

, Лл

-[-j —

ке), или умножением нас ³, к-рое выражает

4 л поворот на — в положительном направлении

(против часовой стрелки).

Расчет цепей Т. т. 1) При расчете симметричных трехфазных цепей исходят из приведенных выше основных соотношений между напряжениями и токами в фазах и в линии.Иногда применяют для расчетов эквивалентную однофазную цепь, напряжение которой равно фазному напряжению трехфазной системы, а мощность равна мощности одной фазы трехфазиой системы. Можно также пользоваться однофаз ной эквивалентной цеиыо, напряжение которой равно линейному напряжению трехфазиой системы, а мощность равна общей мощности (всех трех фаз) трехфазной системы. Обе эти разновидности расчета по способу эквивалентной цепи дают одинаковые результаты. 2) Для несимметричных систем (неравномерно нагруженных или с несимметричными приложенными напряжениями) решение вопроса о распределении токов п напряжений возможно только для всей системы вместе, а не для каждой фазы порознь, т. к. токи и напряжения отдельных фаз находятся во взаимной зависимости. Токи и напряжения в несимметричных системах м. б. вычислены путем приложения законов Кирхгофа к точкам разветвления и замкнутым контурам, образуемым частями системы. Можно также при расчетах трехфазную систему разлагать на отдельные однофазные цепи, -к-рые соединяют затем водно целое, определяя результирующие токи по методу наложения (смотрите Трехпроводные системы). Общая мощность трехфазной системы определяется посредством сложения мощностей в отдельных фазах. При соединении приемников тр-ком и неодинаковой нагрузке фаз расчеты сложны; их упрощают, заменяя тр-к из проводов с полными сопротивлениями z₁₂, z₂₃ и z₃₁ (фигура 10) эквивалентной звездой, сопротивления лучей которой z_lf z₂ и £₃ вычисляют по ф-лам:

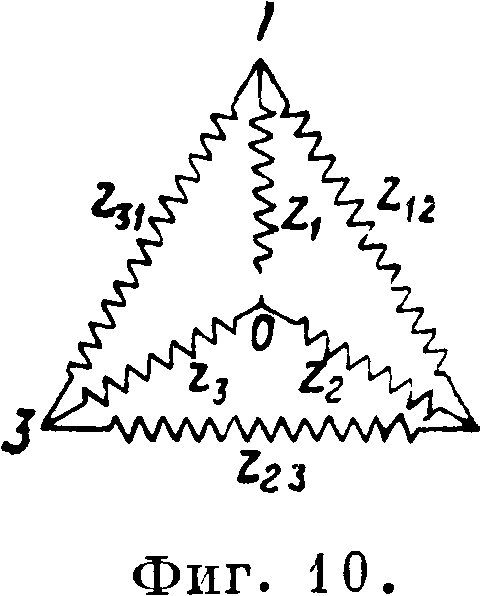
2 + Z-2 3 4" ²

(3)

___

-12T-23I-31 )

Обратное преобразование звезды в тр-к осуществляется путем вычисления проводимостей сторон тр-ка у₁₂, у₂₃ и у₃₁ по заданным проводимостям лучей звезды у_г, у₂ и у₃ с помощью. формул:

У 1*1/2

Уг + У г -Уг1

Уг · 1/з_

У г + Уз 5

(6)

-Уз У i ~

__Уз · Ух__

" Ух + Уз + Уз

При соединении звездой удобен метод расчета,

при к-ром в качестве вспомогательного неизвестного вводят напряжение U₃ между нулевыми точками генератора и нагрузки (фигура 11). Генератор дает фазные эдс E_ltE₂ и Е₃. В трех фазах нагрузки расходуются напряжения:

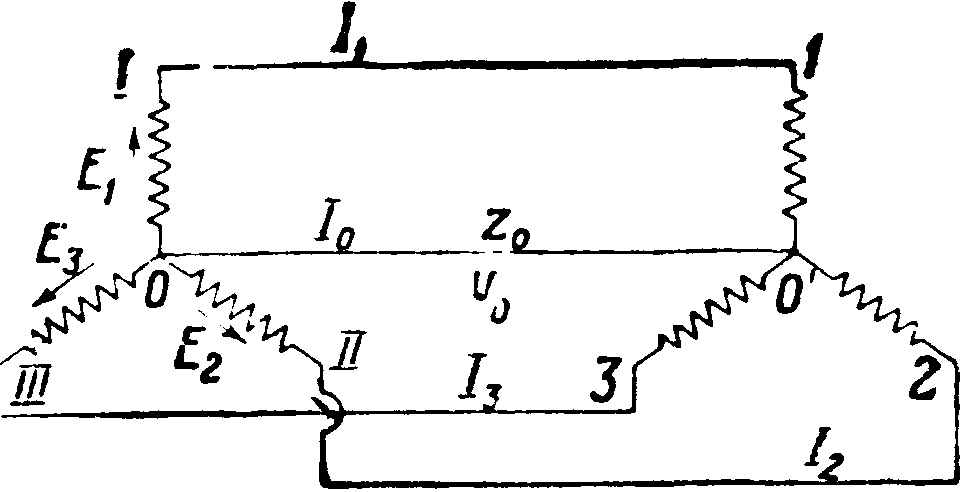
Фигура 11.

Um—Ei U₀; U_h2~E₂-U₀; U_H3-E₃—U₀. (<)

Применяя законы Кирхгофа для замкнутого контура каждой’ фазы, состоящего из фазной обмотки генератора, линии, фазного сопротивления приемника и нулевого провода, получим :

Е_L^-I_iz₁^Jr U_Q] E₂~I₂z₂ -J- Uq,

Ез=ϊ₃ζ₃U₀ 0=1_ьЯо~ ~и₀, )

где z_l4 ζ₂ и £₃—полное сопротивление одной фазы (фазной обмотки) генератора, линии и фазы приемника, a ζ₀—полное сопротивление нулевого провода. Вводим в эти ур-ия проводимости отдельных фаз

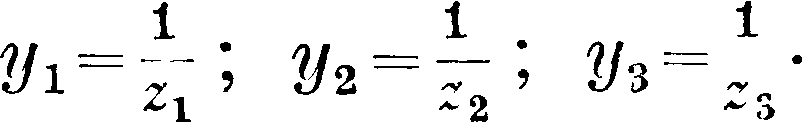
Решая уравнения (7) относительно сил токов, полупим:

Τι=—Ua)yi, j

Г,== (В* -и₉)у_л,} (9)

b=—Т~-=(Ё₉-и₀)у,. )

Согласно первому закону Кирхгофа 1_Х + 1₂ +

+ Is +=подставив сюда значения токов из ур-ий (8), найдем

⁰ Ух + У2 + Уз 4" Уо

(10)

Подставляя найденное U₀ в ур-ия (7) и (9), найдем напряжения в фазах приемников, а затем и .токи. Если нейтрального провода нет, то £₀=оо и у₀=0; тогда -

jj _Е_ху₁- - Е^Уг 4~ -Е’зУз ⁰ У1 + У2 + У3

(И)

Метод симметричных составляющих. За последнее время для вычисления токов короткого замыкания и для решения других аналогичных практических задач при исследовании несимметричных трехфазных систем широкое распространение получил предложенный Фортескью метод разложения несимметричной трехфазной системы на две симметричные, позволяющий свести исследование несимметричной системы к исследованию двух симметричных. Для получения окончательного решения налагают затем друг на друга результаты, полученные для каждой из составляюсь их симметричных систем в отдельности. Амплитуды напряжений этих двух систем неодинаковы; порядок следования (нумерации) фаз во времени системы с большей амплитудой U_А такой лее, как и у исходной разлагаемой (несимметричной) системы; у системы с меньшей амплитудой U_в порядок следования фаз обратный (фигура 12). В общем случае системы сдвинуты одна относительно другой на нек-рый угол а. Если напряжения несимметричной системы и_г, U.у и Р₃, то:

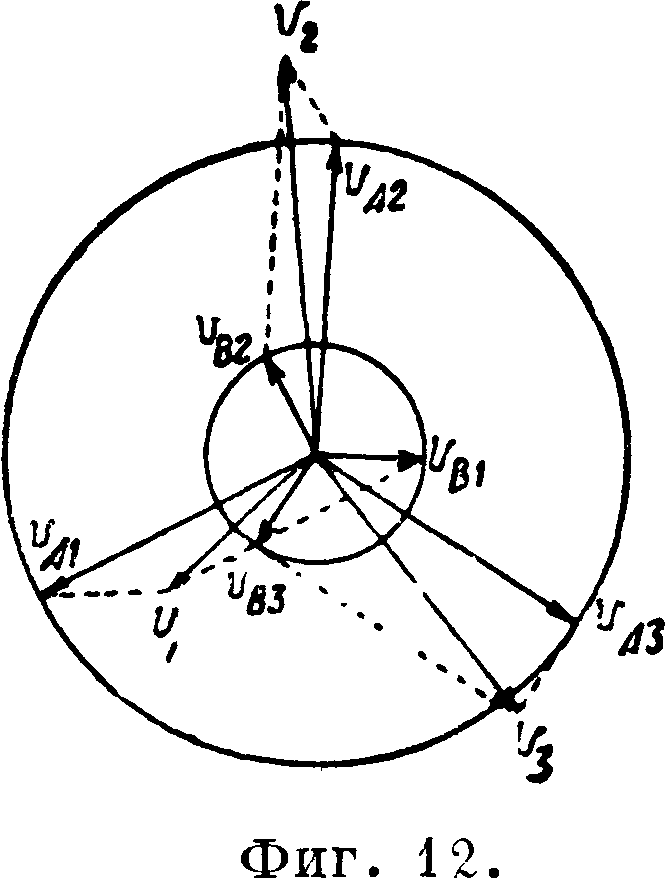
U_X=U_A i + U_Bl;

_ .2π

Uo=U_Az + U_B,=U _Alc

. In

и_з=и_Лз+и_Лз=и_А1е~³Т

+ Г_В1е⁺³1Г;

. in

+ &В1^{е 6} i

(12)

с.·. + 3 ~гг отсюда, множа второе из этих ур-ии на е ^ό,

. 2 π

а трете е на е ^{3 3} и складывая с первым, получим U_Al и U_Bl, которые определяют вполне обе искомые симметричные системы:

Αι=-“

. 2 π

+ J-

4- Он e

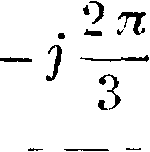
.2 η

U -i~TJ 2 β + С7зе тич. операции, то есть умножение на

“Вх

Существует несколько графич. способов нахождения U_Al и U_Bl, основанных на построениях, которые воспроизводят приведенные выше анали-

. 2 π

е ~ з (соот-

2 п

ΊΓ

положительном или отрицательном направлении). Аналогичный способ разложения на симметричные составляющие применим и к звезде токов несимметричной системы.

Измерение мощности в цепи Т. т. Симметричная нагрузка. У асинхронных двигателей и трансформаторов нулевая точка доступна (часто И в распредели- Ваттметр тельных устройствах). Тогда мощ-

Ваттметр

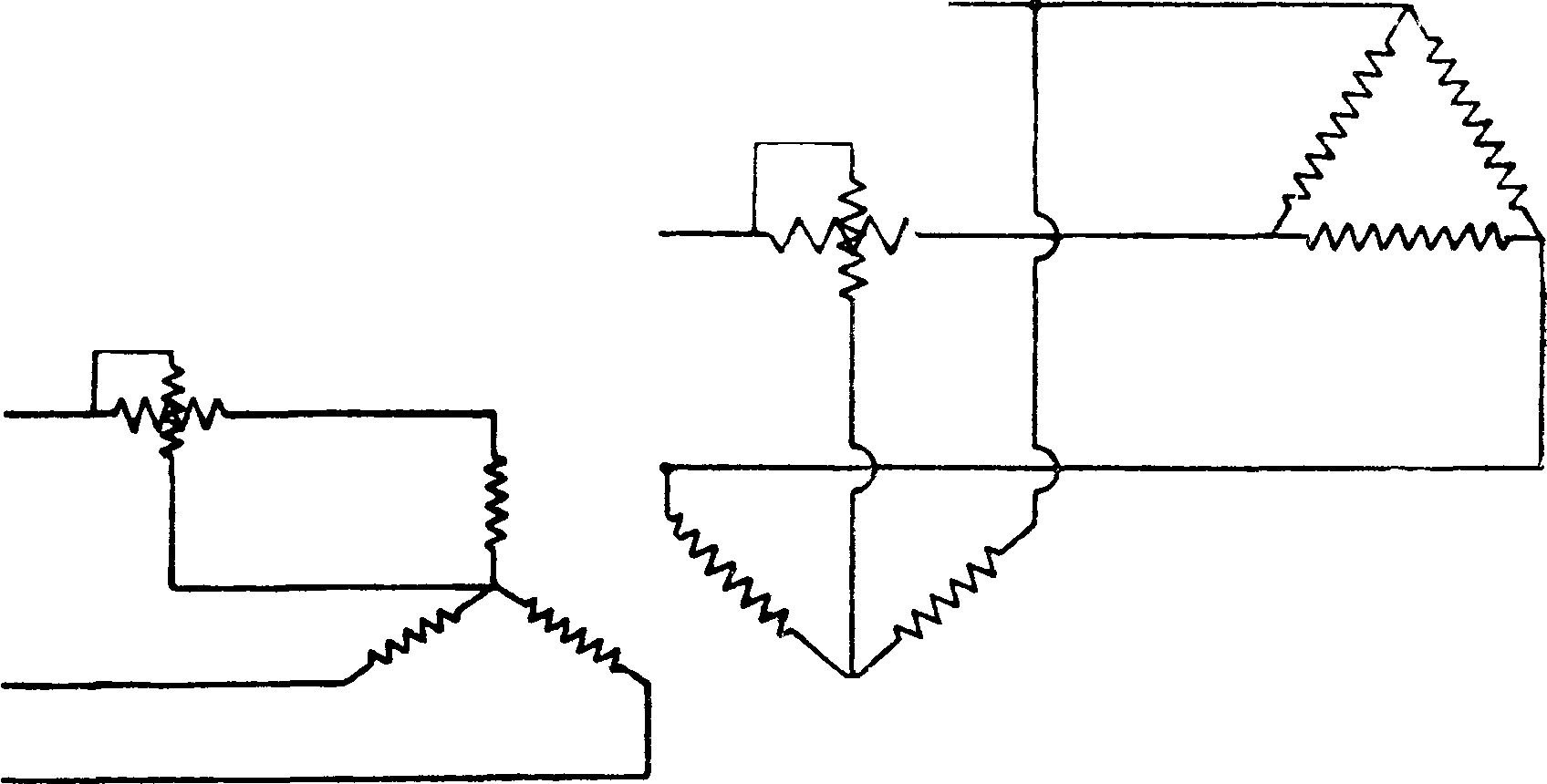
Искусственная нужв. точка

Фигура 13.

Фиг- 14.

ность измеряют одним ваттметром по схеме фигура 13. Множа показания ваттметра на три, получают полную мощность всей системы (во всех трех фазах). Если нулевая точка недоступна, например при соединении тр-ком, то создаюτ искусственную ну- Bam/iwiempl

левую точку, включая звездой три одинаковых сопротивления, одним из которых служит топкая обмотка ваттметра (фигура 14).

Для получения полной мощности показания ваттметра ^фиг* ¹⁵·

множат на 3. И е с и м м е т р и ч н а я нагрузка. В трехпроводных системах мощность измеряют по схеме Арона (фигура 15). Мгновенная мощность, измеряемая двумя ваттметрами I и III:

Р=Pi + Рз=Ч (“1 - ^?з) + Ч (.щ - Щ) =

= bЛ1-1 3*2^2 + УоЗЬо,

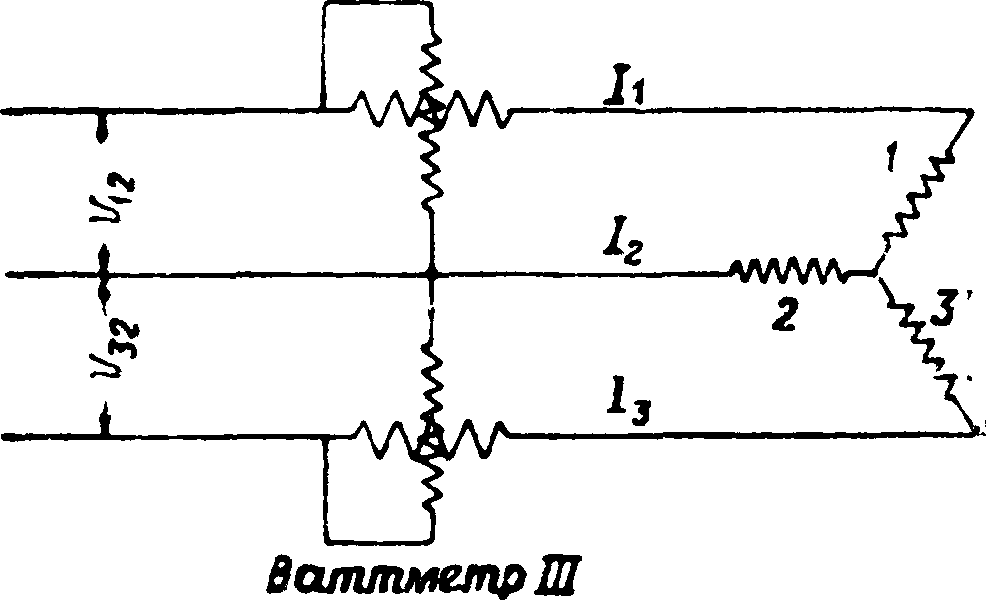
где г с соответствующими индексами—мгновенные значения токов в линии, а и с индексами—· фазных напряжений. Т. к. г_х + /₂ + ?₃=0 или Ч=-(Ч + Ч), то р — i₁u₁ — (ii 4- г₂) и₂ + 1₃щ — г₁и₁ + i₂u₂ + з₃?ц, а это есть мгновенная мощность системы. Т. о. мощность цепи Т. т. (во всех трех фазах) равна алгебраич. сумме показаний обоих ваттметров. Если звезда напряжений симметрична, то ваттметр I покажет Р_х=U₁₂I₁ ccs (3(Г + <р_г), а ваттметр III покажет P₃=U₃₂I₃cos (30° — <р₃), где Р_ги Р₃—средние за период значения мощности, U и 1с соответствующими индексами—Действующие линейные напряжения и токи, <74и <р₃—углы сдвига между соответствующими фазными токами и напряжениями. Для индуктивной нагрузки при <р_х < 00°, Р_г > 0 и Р=Р_г + Р_ч (оба слагаемых положительны); при φ > 00°, Р_х< 0

з и Ρ=·Ρ₃ —Ρχ: у ваттметра, показывающего отрицательную мощность, переключают концы тонкой обмотки (чтобы можно было производить отсчет). Схема Арона применима и для нагрузки τρ-ком (доказательство аналогично). В эксплуатонных условиях применяют вместо двух ваттметров один трехфазный (два однофазных ваттметра, совмещенных в одном приборе, к-рый имеет одну шкалу и стрелку, укрепленную на одной оси с подвижными элементами обоих ваттметров). Четырехпроводные системы. Мощность измеряют тремя ваттметрами, толстые катушки которых включены каждая в один из линейных проводов последовательно, а тонкие—к нулевому проводу и соответствующему линейному проводу. Полная мощность равна сумме показаний трех ваттметров.

Измерение энергии в цепи Т. т. Симметричная нагрузка. При доступной нулевой точке энергию можно измерять (без особой точности) одним однофазным счетчиком, к-рый включают как ваттметр на схеме <фигура 13. Для получения энергии всей цепи показания счетчика множат на 3. Счетчик можно также сразу проградуировать так, чтобы он показывал энергию всей цепи, то есть утроенную. При недоступной нулевой точке можно применить один счетчик со сдвигом в 60° между напряжением и потоком, к-рый создает ответвленная обмотка, включая ее между двумя проводами линии (т. ч. она находится под действием линейного напряжения); толстую обмотку счет-ника включают последовательно в один из линейных проводов. Для получения энергии всей цепи показания счетчика умножают на 3. Уже при небольших нарушениях симметрии (напряжений или нагрузок) оба способа дают значительные ошибки; поэтому и при симметричной нагрузке предпочитают применять трехфазный двухэлементный счетчик (смотрите ниже). Несимметричная нагрузка. Энергию трехпроводных систем измеряют двухэлементным трехфазным счетчиком, включаемым по схеме Арона (фигура 15); ]В таком счетчике один элемент расположен над другим, а диски укреплены на общем валу (иногда оба элемента воздействуют на один единственный диск). Энергию четырех-проводных систем измеряют обыкновенным трехфазным двухэлементным счетчиком с тремя трансформаторами тока, двухэлементным счетчиком с тремя последовательными обмотками или трехэлементным счетчиком.

Порядок следования фаз во времени. Для правильного соединения между собой генераторов, трансформаторов (о соединении обмоток трансформаторов Т. т. см. ОСТ 4815) и двигателей Т. т., а также для включения приборов необходимо знать порядок следования фаз во времени. Для определения последовательности фаз применяются специальные указатели, основанные на различных принципах: 1) миниатюрный асинхронный двигатель с тонким металлич. диском в качестве ротора (если ротор вращается по направлению, указанному на приборе стрелкой, то последовательность фаз правильная-*^ соответствии с порядком цифр или букв у зажимов прибора, например 1, 2, 3; если ротор"вращается против стрелки на приборе, то порядок фаз 1, 3, 2); 2) две лампы накаливания и конденсатор, включенные звездой в цепь Т. т., для которой надо определить по следовательность фаз (сильный накал лампы, напряжение на зажимах которой отстает на 120° от напряжения на конденсаторе; накал другой лампы очень слабый). Применяются и другие видоизменения этих двух устройств. Последовательность фаз можно также (при симметричной индуктивной или емкостной нагрузке) определить по величине показаний двух ваттметров, включенных по схеме Арона.

Влияние составляющих выс-ших порядков в цепиТ. т. Если эдс генератора отклоняется по форме от чистой синусоиды (смотрите Переменные токи), то составляющие эдс порядка 3 к (к—целое нечетное число), то есть 3-я, 9-я, 15-я,. гармоники, во всех трех обмотках генератора совпадают по фазе т

(так как разность фаз в у трех эдс этих обмоток для составляющих порядка 3 к равна их собственному периоду или целому числу периодов); поэтому при соединении генератора звездой эти гармоники дают результирующую, равную нулю: линейные напряжения будут свободны от составляющих порядка 3 к, между тем как фазные напряжения их содержат; в линейных напряжениях останутся гармоники 5-го, 7-го, 11-го, .порядков, т. ч. в результате форма кривой линейного напряжения будет отличаться от формы фазного напряжения. При наличии нулевого провода сила тока в нем, даже для вполне симметричной нагрузки, при этом уже равна не нулю, а сумме всех токов составляющих порядка 3 к: составляющие каждого такого порядка суммируются арифметически. При соединении генератора τρ-ком эдс каждого порядка 3 к (3-го, 9-го и т. д.) совпадают по фазе и суммируются арифметически: сумма эдс внутри тр-ка не будет равна нулю, как при чисто синусоидальной эдс, и в обмотках генератора будет течь ток даже при разомкнутой внешней цепи.

Преобразование Т. т. вдругие виды тока. На практике чаще всего приходится иметь дело с преобразованием Т. т. в постоянный, к-рое осуществляется с помощью вращающихся преобразователей (смотрите). Преобразование Т. т. в двухфазный с помощью статич. трансформаторов, для чего было предложено несколько схем (смотрите Системы переменного тока), в настоящее время большого практического распространения не имеет, встречаясь в лабораторной практике и в некоторых специальных случаях.

Лит.: Аснин И. и Луценко Н., Задачник по курсу теории переменных токов, М.—Л., 1932; Воронов А., Переменные электрические токи в применении к распределению энергии, П., 1915; В и дм ар М., Научные основы электротехники, пер. с нем., М.—Л., 1932; Генсель Г., Электротехника в задачах и примерах, выл. 2, Переменные токи, М.—Л., 1930; Жане П., Общий курс электротехники, пер. с фраиц., т. 2, М., 1929; Круг К., Общий курс электротехники, т. 2, Теория переменных токов, 3 изд., М.—Л., 1932; Л у-ценкоН., Теория переменных токов, 2 изд., Л., 1931 (литогр.); Миткевич В., Теория переменных токов, конспект курса, Л., 1931 (литогр.); СЭТ, Справочная книга для электротехников, т. 1, отд. 2 и 3, Л., 1928; Угримов Б.иГенсель Г., Основы техники сильных токов, т. 2, Переменные токи, 5 изд., М.—Л., 1930; Фауль Ф., Справочник по электротехнике, вып. 1, отд. 2 и 3, М. — Л., 1928; Френкель А., Теория переменных токов, пер. с нем., М.—Л., 1928;×а щ и н-ский В., Канализация электрической энергии, ч. 1, Электрический расчет, 3 изд., Л., 1931; Черданцев И., Теория переменных токов, 4 изд., М.—Л., 1932; Черданцева 3., Электрические измерения, 2 изд., М.—Л., 1931; Шателен М. и Пономарев Н., Пособие к лабораторным занятиям по электрическим и магнитным измерениям, М.—Л., 1931;Щ уркевичП., Переменные электрические токи и теория круговых диаграмм, ч. 2, Многофазные токи, Л., 1932 (литогр.);

В enischke G., Die wissenschaftlichen Grundlagen d. Elektrotechnik, 6 Aufl., B., 1922; Cohen L., Formulae a. Tables for the Calculation of Alternating Current Problems, N. Y., 1913; Deutscher Kalender fiir Elektro-techniker, hrsg. von G. Dettmar, Mch.—B., 1932; D o-nati L. eSartori G., Elettrotecnica, Milano, 1930; D о v e r A., Theory a. Practice of Alternating Currents,

L., 1926; Fraenckel A., Theorie d. Wechselstrome, 3 Aufl., B., 1930; Karapetoff Y., The Electric Circuit, N. Y., 1912; Kittler E., Allgemeine Elektrotechnik, B. 2, Einfuhrung in die Wechselstromtechnik, unter Mitwirkung von W. Petersen, Stg., 1909; L а С о u r J. L. u. B r a g s t a d t O. S., Theorie d. Wechselstrome, B., 1923; M a 1 t i M., Electric Circuit Analysis, N. Y., 1930; Steinmetz C., Theory a. Calculation of Alternating Current Phenomena, N. Ϋ., 1916. В. Хащинский.