> Техника, страница 86 > Триангуляция

Триангуляция

Триангуляция, сеть точек, отмеченных на поверхности земли особыми постоянными знаками и расположенных т. о., что они составляют между собой треугольники. В такой сети одна из сторон, именуемая базисом, измеряется непосредственно, далее измеряются все углы в тр-ках, благодаря чему затем можно по правилам тригонометрии вычислить стороны всех тр-ков и наконец координаты вершин их в какой-нибудь системе. В таком виде эти вершины тр-ков называются тригонометрическими пунктами, которые на земле отмечаются подземными либо надземными постройками, именуемыми центрами^ координаты их вносятся в особые каталоги, печатаемые для всеобщего пользования.

1. Сети Т. (тригонометрические сети) разделяются на несколько классов в зависимости от их цели и назначения. Т. первого класса прокладываются в виде цепей из простых тр-ков (фигура 1). Такие первоклассные ряды идут по направлению меридианов и па-

50

раллелей, образуя четырехугольники со сторонами 200—400 км. На основе рядов первого класса прокладываются несколько упрощенными приемами ряды второго класса, следующие на расстоянии 80—100 км один от другого и пересекаемые такими же поперечными рядами. Наконец оставшиеся незапол- ненные пространства покрываются гу-У~Л стыми сетями Т., состоящих из мелких тр-ков, опирающихся на ряды первого У "Ч и второго классов. Они служат опорою для сплошных съемок, которые имеют b целью дать точные топографии, карты *4 страны. Длина сторон тр-ков в рядах первого класса достигает 25—50 и даже более км. В рядах второго класса сто-Фигура i. роны доходят до 30 км) в заполняющих же сетях длина сторон зависит от назначения сети и в соответствии с масштабом будущей съемки устанавливается от 3 до 15 км. В этом отношении заполняющие сети проектируются с таким расчетом, чтобы на каждый планшет съемки пришлось бы 3—5 опорных пунктов. При выполнении цепей Т. первого класса преследуется очень большая точность, т. к. они простираются на большие расстояния и имеют не только практическое, но и научное значение. По ним можно вычислить элементы земного сфероида, то есть размеры большой и малой полуосей его. Практическое значение этих данных весьма важно, так как все геодезич. измерения, производимые на земле, вычисляются на их основе. Т. о. общей целью работ на Т. является покрытие больших пространств поверхности земли опорными пунктами на основе точных геодезич. измерений с наименьшими затратами времени и средств. Поэтому всегда желательно насколько возможно больше увеличить длину сторон тр-ков. Это обстоятельство помимо того способствует и сохранению точности результатов работ, которая постепенно падает в цепи тр-ков по мере удаления их от исходной—непосредственно измеренной—стороны. Относительная ошибка стороны какого-либо η-го тр-ка цепи подсчитывается по следующей ф-ле:

t=±V (т У + 2 <^{ctg3 А} +^{ctg3 B}>’ ⁽¹>

где а—исследуемая сторона, b—исходная или измеренная сторона, ε—средняя ошибка измерения угла в цепи тр-ков, выраженная относительной величиной, А и В—углы в тр-ках, противолежащие вычисляемым сторонам. Обычно в виду большой точности линейных измерений первый член приведенной формулы очень мал и принимается равным нулю; углы 4,Бит.д. принимаются равными 60°, т. к. в Т. стремятся придать тр-кам форму, близкую к равностороннему, каковая форма и является наиболее выгодною. При таких условиях, заметив еще, что ctg60°=^=, приведенное выражение принимает следующий простой вид:

~=±°VTⁿ- (2)

По этой формуле обычно производится предварительный подсчет относительной ошибки конечной стороны цепи из п тр-ков, если по качеству инструмента можно заранее знать, какова будет примерная величина ε. Весьма часто по проекту работ, наоборот, заранее

Δα

ставят условием предельную величину — и,

определив число тр-ков п, находят величину ε, соответственно чему подбирают инструмент и метод работ:

*=±^г- (3)

^аУ ^п

При ошибке измерения угла г=-{-0,5" или=4qq~qqo получаются следующие значения ~:

При п= 6 9 16 25

1111

•VI—

лС-Т

200 000 160 000 120 000 98 000

Из этой таблички видно, как быстро падает точность определения длины сторо ы цепи по мере увеличения числа а треугольников.

2. Н а и в ы г о д н е fi-шее построение Т. Таким образом всегда желательно удлинить стороны тр-ков, чтобы уменьшить число последних.

Однако удлинение сторон влечет за собою необходимость поднять инструмент на нек-рую высоту, т. к. вслед-, ствие кривизны земли с одной вершины тр-ка не будут видны другие (фигура 2). Необходимая высота поднятия подсчитывается по следующей формуле:

I2

/R

Фигура 2.

¥

0

h =

2 R’

(4)

где I—половина длины стороны тр-ка, R—средний приближенный радиус земли, принимаемый равным 6 370 км. Вычисления по этой формуле дают следующую табличку для h в м при I в км:

I. 1 2 3 5 10 15 20 25

h.. 0,08 0,3 0,7 2,0 7,8 17,7 31,5 50,0

Отсюда видно, что при стороне тр-ка в 30 км нужно подняться на двух противоположных вершинах почти на 18 м, чтобы установить взаимную видимость. Кроме того добавляется еще 4—6 метров для того, чтобы отдалить луч зрения от поверхности земли. Т. о. возникает вопрос о подъеме на нек-рую высоту геодезич. инструмента, служащего для измерения углов в τρ-ке; этот вопрос разрешается постройкою тригонометрических знаков, которая производится после соответствующей рекогносцировки сети на местности.

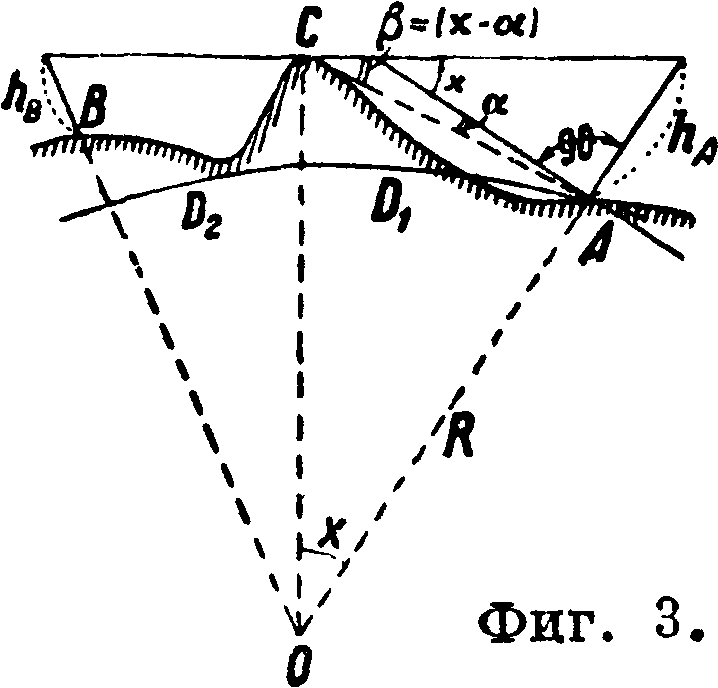
3. Рекогносцировка Т. При возникновении необходимости проложения Т. прежде всего собираются картографические материалы и сведения о характере местности намечаемого района. По этим данным в зависимости от назначения Т. составляется проект сети на карте наиболее крупного масштаба, имеющегося для данного района. Затем этот проект рекогносцируется, для чего намеченные на карте места знаков объезжаются и посещаются триангулятором последовательна вдоль всей цепи или сети, начиная от базиса, если Т. самостоятельная, или от исходной стороны Т., ранее проложенной в данном районе, причем новая сеть служит ее развитием. Наиболее трудная задача рекогносцировки заключается в опредении высоты знаков, необходимой для взаимной их видимости. Если местность гористая или сильно всхолмленная и открытая, указанный вопрос разрешается сравнительно легко, т. к. небольшого подъема над поверхностью земли бывает достаточно, чтобы можно было в бинокль или трубу различать местные предметы на значительном расстоянии. Если же местность покрыта лесами, то разрешение задачи весьма затрудняется. Существуют два метода для определения необходимой высоты знака при рекогносцировке. Первый способ непосредственного определения искомой высоты достигается подъемом наблюдателя на месте постройки будущего знака на требуемую высоту с помощью мачты с блоком вверху, через который продет канат. Один конец его завязывается петлей, куда и садится наблюдатель, вооруженный бинокулярною трубою. Рабочие, подтягивая канат, поднимают наблюдателя на должную высоту, которая затем и замеряется. Для той же цели весьма удобно применить легкие раздвижные лес τη и ц ы до 20 метров высотой. Несмотря на простоту и ясность такого метода рекогносцировки в широкой практике этого дела он не встречается, так как для своего применения он требует хороших транспортных средств, что является наиболее слабым местом полевых геодезии. работ. Вторым средством для определения высоты построек знаков является тахеометрическое или барометрич.^ нивелирование. В случае невозможности проследить на местности непосредственно направление намечаемой стороны треугольника определяют последовательно от одной до другой вершины его наивысшие характерные изломы поверхности земли или верхушек деревьев леса и строят продольный профиль, по которому затем уже рассчитывают высоту знаков, принимая во внимание кривизну поверхности земли. Если наблюдателю из точки А нужно увидеть точку В (фигура 3) через препятствие С в виде например гребня лесов, покрывающих возвышенность, он прежде всего по имеющейся карте определяет расстояние до препятствия С, пользуясь для этого буссольными засечками. Азимуты, измеренные при рекогносцировке в направлении на препятствие с различных пунктов, прокладываются на карте, и таким путем расстояние получается с точностью до 0,1 км. Далее задача сводится к определению отрезка h_A путем измерения тахеометром (или кипрегелем) вертикального угла а в направлении на точку С, к-рый м. б. как углом повышения, так и понижения (+или-). Затем вычисляется величина угла х в минутах дуги по ф-ле где В_г—расстояние от i до С в 1,85 км—

средняя длина дуги в одну минуту на поверхности земли. После этого отрезок h_A вычисляется по ф-ле

h_A=(x-a) х 0,3D_u (6)

причем, как указано, углы х и а выражены в минутах, а расстояние —в км. Таким же путем наблюдатель, проехав на точку В, определяет величину отрезка h_B. Было бы невыгодным воспользоваться полученными величинами h_A и h_B непосредственно. Целесообразнее знаки построить примерно равной высоты, для чего высоту знака на точке В увеличивают, а на точке А уменьшают, пользуясь пропорцией Ah_B : Ah_A=JD₂: JD_l9

где Ah_B и Мг_А — поправки к вычисленным отрезкам h_B и h_A.

Результаты, получаемые тахеометрически, дают достаточную точность, если работа производится тщательно и расстояния определены без грубых ошибок. При барометрич. определениях следует рассчитывать на возможность ошибки в высоте до ^4 м, что однако удовлетворяет решению задачи. Данный вопрос представляется особо трудным собственно только при очень длинных сторонах в 25—50 км, что встречается в Т. I класса. В мелких сетях с короткими сторонами при известном навыке средняя высота знака устанавливается более просто, причем здесь применяются оба способа одновременно: и подъем на невысокие мачты, деревья или подходящие здания и метод инструментального определения высоты перегибов местности, служащих препятствием для видимости. В зависимости от данных рекогносцировки проект сети видоизменяется, уточняется и устанавливается окончательно. При этом собираются также сведения о наличии лесного материала, средств и направления его доставки.

4. Тригонометрические знаки и центры. Как уже указано, вершины тр-ков тригонометрических сетей отмечаются на местности знаками. Было бы желательно во всех случаях обойтись для этого местными предметами, как tq: башнями, трубами заводов, высокими зданиями и тому подобное. Однако этих предметов обычно нехватает, и помимо того они хороши б. ч. лишь как объекты наблюдений, т. к. они хорошо видимы издали. Пользование же ими как местом для измерения углов в большинстве случаев совершенно невозможно, а если и возможно, то с большими осложнениями будущих вычислений. Вследствие этого на пунктах наблюдений обычно воздвигаются специальные постройки, местные же предметы определяются попутно засечками. Простейшим тригонометрическим знаком является веха (фигура 4). Для ее постройки нужно 5—б жердей., а Из них собирается небольшая пирамидка высотою 3—4 м, под к-рою и ставится инструмент. Ноги пирамиды углубляются на 1—1V₂ м в землю и плотно ут-рамбовываются. В вершине пирамиды /^ίΛΑ укрепляется отвесно собственно веха также 3—4 метров высоты, с решеткою _ф, из планочек наверху. Таким путем получается знак до б—8 метров высотою, весьма простой в постройке и удобный для работы на нем в поле. Если нужно достигнуть большей высоты, то строят простую пирамиду (фигура 5). Для этого заготовляют 5 бревен толщиною до 15^:—20 сантиметров в нижнем отрубе длиною, какую только можно добыть в местном лесу (8—12 ж). Из такого материала и сооружается четырехногая пирамида с толстою болванкою при вершине. Болванка м. б. удлинена прибивкою вехи, благодаря чему пирамида может достигнуть высоты 15— 16 метров В обоих описанных Фигура 5. Фигура 6· случаях инструмент для наблюдения ставится со штативом на земле под знаком. Однако возникают случаи, когда, как уже было указано, для преодоления кривизны земли или же пре-1 пятствия между знаками приходится поднять

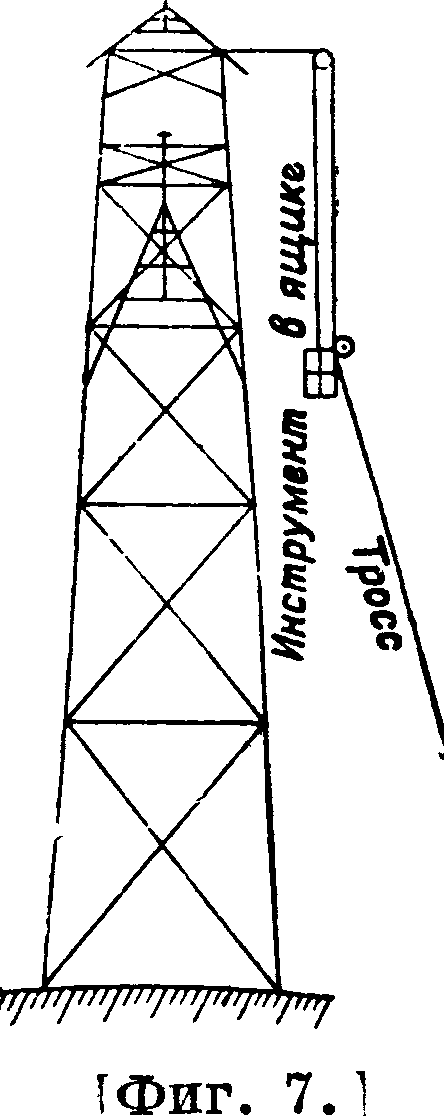
инструмент на некоторую высоту. Тогда подобную же пирамиду строят повыше, длящего в случае нужды сращивают бревна. Затем внутри возведенной постройки устанавливают вторую пирамиду (фигура 6), болванка которой служит столиком для установки инструмента. Пол для наблюдателя изолируется от этого столика и опирается на ноги внешней пирамиды. Для подъема на пло-_ί? щадку к ногам прибиваются ле стницы; площадка обносится перилами. В таком виде знак получает название двойной пирамиды. Во всех случаях пирамиды строят четырехножными, т. к. они имеют симметричный вид и более устойчивы. Только внутренние пирамиды возводятся иногда трехножные. В лесных местностях для достижения видимо-, сти приходится возводить еще более высокие постройки (до 25 и болееж),к-рые называются сложными сигналами (фигура 7). Эти знаки отличаются от предыдущих тем, что ноги их поставлены с наклоном всего от 1 : 12 до 1:16. Бревна для ног сложных сигналов срощены (сбиты внакладку одно на другое не менее!чем на 2 м).

hi По высоте постройка разделена на я р у с ы поясами—в е н ц а м и—и скреплена крестовинами. Ноги сигнала в отличие от пирамиды вверху не сходятся вместе, а венчаются легкою решетчатою четырехскатною крышею, в вершине которой вертикально укреплена болванка. Внутренняя пирамида со столиком для инструмента поднята до верхнего яруса и ноги ее длиною около 6 метров упираются и прибиты к ногам наружной постройки. Пол для наблюдателя не касается столика, обнесен перилами; размер площадки 2x2 метров Благодаря такому устройству достигается устойчивое положение инструмента на столике несмотря на то, что внутренняя пирамида стоит не на земле, а своими ногами опирается на ноги сигнала. Для подъема наблюдателя делаются лестницы из ступенек, врезанных в ноги наружной постройки, а иногда ставятся от этажа к этажу внутренние стремянки.

Инструмент поднимается на тросе, перекинутом через блок, к-рый прикрепляется для этой цели к перекладине, прибиваемой к ногам под крышей (фигура 7). Некоторые триангуляторы к сложным сигналам большой высоты добавляют еще подпоры по углам от земли до */з высоты знака. Однако опыт показал, что тщательно сбитые знаки стоят достаточно прочно и без подпор. Считается более целесообразным при высоте знака свыше 30—35 метров ставить добавочные ноги по каждой стороне знака посредине между основными ψη^^,ρ/⁴ ногами (фигура 8). Промежуточные ноги делят пополам венцы и крестовины, которые с ними скрепляются, и тем самым облегчают поперечное сечение этих частей постройки. Во избежание деформации знака в горизонтальном направлении ноги расшиваются через один-два яруса горизонталь

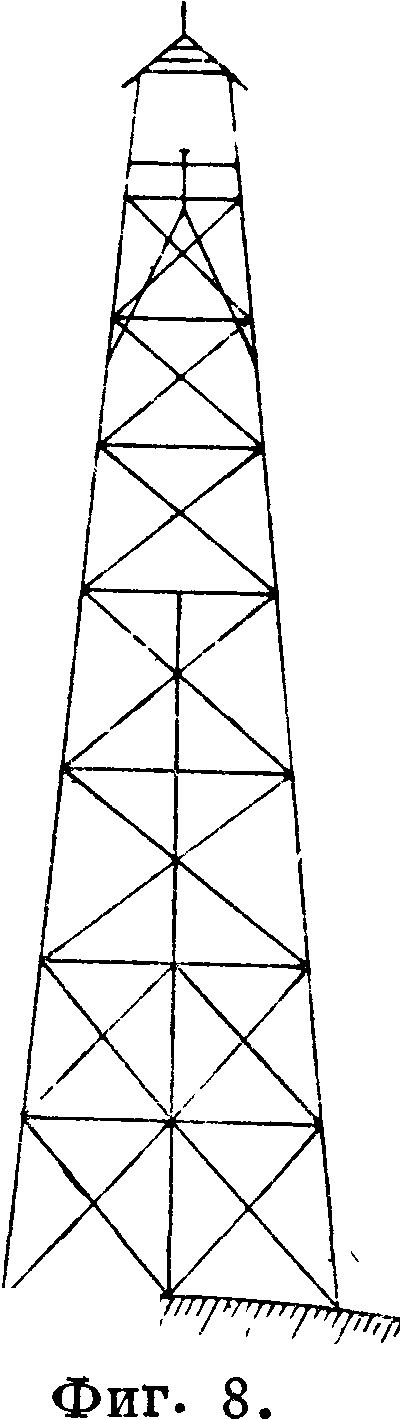
ными крестовинами, на что необходимо обращать внимание. Существует еще промежуточная конструкция знака — простой сигнал, отличающийся от двойной пирамиды большей высотою и меньшим наклоном ног, которые поэтому не сходятся вместе вверху, а венчаются такой же крышей, как и в сложных сигналах. Простые сигналы весьма устойчивы и хороши для наблюдений, но требуют много материала и потому в последнее время выходят из применения. Так как все перечисленные постройки имеют характер временный (стоят 3—4 года), то они возводятся по типу строительных лесов, то есть в соединениях здесь обходятся простыми врубками или совсем без них; бревна в ногах, а также сопряжения крестовин и поясов с ногами скрепляются не болтами, а коваными (барочными) гвоздями длиною 15—50 см. Особое внимание уделяется закреплению ног в земле на глубину 1¹/₂—2 метров в зависимости от высоты знака и грунта. Чтобы противостоять опрокидыванию всей постройки ветром, к ногам в ямах прибивают поперечные перекладины, называемые якорями. Самая постройка знаков производится без каких-либо вспомогательных лесов и небольшим (числом плотников (4—5) и рабочих. Для подъема частей сигналов применяются блоки одно- и двухшкив-ные и стальные тросы 5—12-мм сечения, кроме того—легкие канаты, веревки. Для подъема ног (наиболее тяжелые части постройки) Пользуются 7г—Ι-m лебедкой. Существуют специальные инструкции и наставления (Главное геодезич. упр.) для постройки тригонометрических знаков.

Тригонометрии. знаки имеют характер временных построек, между тем как их геометрии, место на земле, весьма точно определенное, должно сохраняться возможно долгий срок, чтобы намеченные т. о. пункты м. б. легко возобновить для последующих работ. С этой целью в земле закладываются особые центры. Тип их различен и находится в зависимости от назначения Т. На Т. I и II классов закладывают двойные центры (фигура 9)

Фигура 9.

Фигура 10.

бине до 2 метров В кладке утапливаются чугунные м а р к и тт. о., чтобы центры их, отмеченные крестиками, находились бы на одной отвесной линии, которая и является геометрическим местом центра знака. На мелких сетях, служащих для целей опоры съемок, центры закладываются более облегченные, в риде бетонных столбиков (фигура 10), больших валунов, бутылок и прочие На конструкцию и тщательную закладку центров необходимо всегда обращать серьезное внимание, т. к. утрата такого вещественного знака сводит нанет всю работу по определению тригонометрич. пункта.

5. Переносные тригонометрические знаки. При работах в местностях степных и открытых для рабочих сетей весьма выгодно применяются переносные деревянные или металлические знаки, конструкции к-рых разработаны с таким расчетом, чтобы при наибольшей высоте они имели бы небольшой вес и легко перевозились бы на грузовике или даже на одной парной повозке. В настоящее время в СССР применяются для основных рядов Т. II класса переносные сигналы, построенные по типу американских (Бильби), собранные из стальных труб (строительная сталь № 3). Вес их 1 500 килограмм при высоте столика до 20 метров Для более мелких Т. весьма выгодны железные переносные знаки весом до 300 килограмм при высоте до 6—8 метров и железные пирамиды еще меньшего· веса при высоте до 4—5 метров При такой организации работы триангуляционная партия снабжается 5—7 переносными знаками, которые перемещаются постепенно вперед по мере продвижения работы. На-месте бывшего знака в этом случае остается центр той или другой конструкции, и над ним насыпается земляной курган высотою 1—П/г м, земля для которого берется из канавки сомкнутого очертания, вырытой вокруг заложенного центра. В горах земляные курганы заменяются сухою кладкою из подручного камня в форме конусов. Основной центр выбивается в виде креста на скале.

6, Базисные сети. Непосредственному измерению на Т. подвергаются только особо для того намеченные линии, называемые базисами. Проще всего было бы избрать базисом непосредственно какую-либо сторону одного из треугольников сети. Однако при длинных сторонах тр-ков и пересеченной местности такая работа в большинстве случаев является невыполнимою. Поэтому обычно прибегают к особому добавочному построению— базисной сети. Простейший и наиболее удобный вид базисной сети—р о м б и ч е-с к и й—симметричный (фигура 11) или с диа-

D

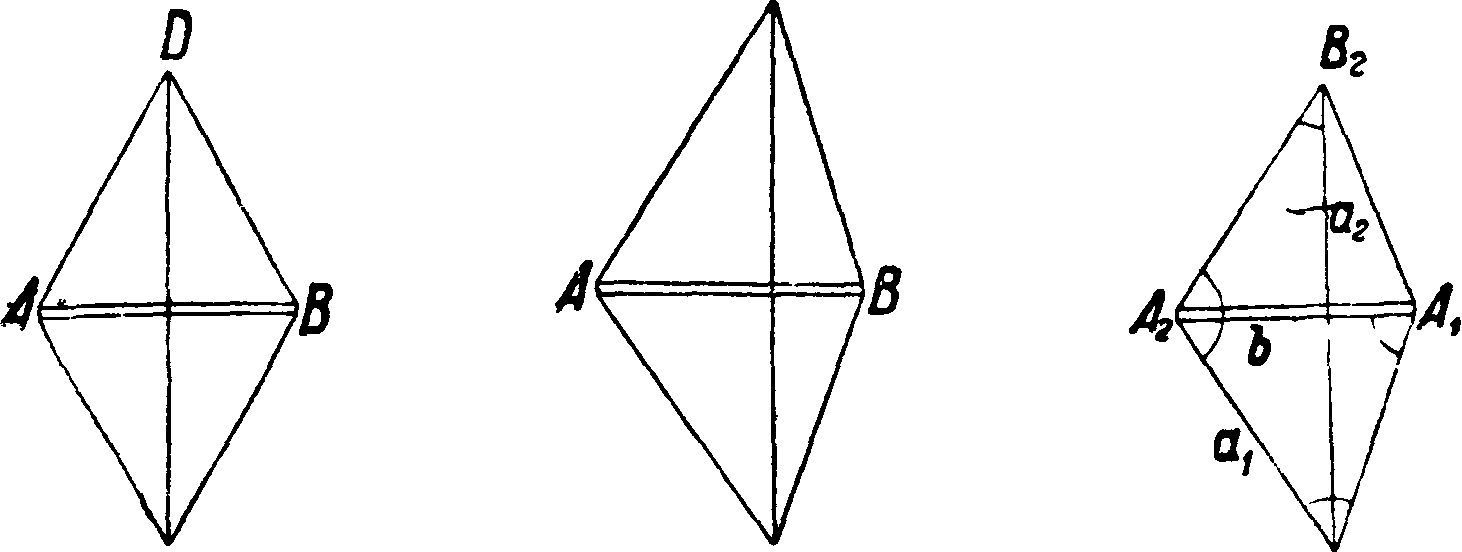
сев,

Фигура 11. Фигура 12. Фигура 13.

гональю, прижатой к одной из вершин ромба (фигура 12). Короткая диагональ АВ является собственно базисом и измеряется, а длинная DC получается вычислением и служит затем исходною, или выходною, стороною для всей Т. При рекогносцировке построение ромба рассчитывают т. о., чтобы острые углы при точках D и С не оказались бы менее 35°, и при таком условии выходная сторона будет в 2,8—3,0 раз больше базиса. Т. о., обратно, если из задания известна длина выходной стороны, к-рую нужно достигнуть, то можно подсчитать необходимую длину базиса; например если требуется получить выходную сторону CD (фигура 12) длиною в 25 км, то нужно рекогносцировкой отыскать базис, соответственно расположенный и длиною 8 — 9 км. Далее при рекогносцировке базисной сети измеряют минутным теодолитом или буссолью все углы с точностью хотя бы до 1° и подыскивают синусы и котангенсы тех из них, которые войдут в вычисление выходной стороны. Так например (фигура 13), в базисной сети базис

А₁А₂=b, выходная сторона В_гВ₂=а₂. По формуле синусов

		п sinA2. л		sin А2
		U _, (to sinfip 2	= ах	sin В1 *
Измеренные		углы	sin	ctg	Ctg2
			1,00	0,09	0,0081
В i.		40°	0,61	1,19	1,4161
А .в.			0,94	0,36	0,1296
б2.			0,57	1,43	2,0449

Подставив величину синусов в ф-лы (7), получим, что

Qj₂

= Ь

1,00-0,91 0,61-0757

= Ь- 2,6,

то есть выходная сторона получается в 2,6 раза длиннее измеренного базиса. Далее, положив, что относительная ошибка измерения базиса равна например 1 : 100 000, а такая же ошибка

Δαо выходной стороны по заданию не должна превосходить 1 : 50 000, можно по формуле (1) подсчитать предельную допускаемую среднюю ошибку измерения угла ε, а именно: сумма квадратов котангенсов углов А_1у В_1} А₂ и В₂составляет 3,60; следовательно

_τ4γ=±1/(τ^Γ + ^£2·³-⁶·

Имея в виду, что первый член подкоренного количества—весьма малая величина, его можно отбросить, и тогда получается следующее соотношение:

,-ж-±«КР.

ИЛИ

£ <- _¹ ·

^ 1,9 - 50000’

по округлении

ε < 1 : 95 000,

что соответствует примерно синусу угла в 2", Другими словами, при измерении углов базисной сети в данном случае наибольшая средняя ошибка измерения угла не должна превзойти ±2", соответственно чему подбирается инструмент и соображается метод работы. Из приведенного примера видно, каким образом можно, задавшись определенною точностью результатов измерений на триангуляцию, найти ту точность, с которою необходимо производить измерения. Должно оговориться, что приведенные ф-лы являются приближенными, но вполне достаточными для практич. их применения. Не всегда удается на местности базисную сеть построить в виде ромба. Иногда строят на большой его диагонали второй ромб; иногда получается довольно сложная сеть из тр-ков весьма различного вида. К этому приходится прибегать, когда по местным условиям не удается выбрать базис достаточной длины.

7. Измерение базисов. Ранее высказанные соображения показывают, что базисы для обоснования Т. должны быть измерены с большою точностью и притом приборами, которые в результате дадут длину линии базиса, выраженную в действительных метрах. Для этой цели у нас применялись (в Германии и до сих пор применяются жезловые базисные приборы) особые жезлы (базисный прибор Струве); в настоящее же время в СССР базисы измеряются исключительно базисным прибором шведского ученого Едерина, усовершенствованным французами. Существенную часть этого прибора составляют проволоки длиною 24 м, диам. 1,65 миллиметров, изготовленные из инвара (смотрите). Коэфициент расширения его редко превышает 1 : 5 000 000. Благодаря этому влияние перемены t° на длину проволоки во время измерения ничтожно и легко учитывается с достаточною точностью. Проволоки на своих концах снабжены шкалами, занумерованными слева направо от 0 до 80 миллиметров. При измерении базиса проволоки поддерживаются на высоте ок.1м особыми станками с блоками и гирями, дающими натяжение в 10 килограмм. Т. о. проволоки находятся в подвешенном состоянии, причем шкалы их помещаются над целиками специальных штативов, устанавливаемых в линии базиса через 24 метров Для той же цели часто применяются колья, прочно забитые в землю. В последнее время стали применять проволоки длиною 48 м, что способствует еще большему успеху работ. Полный комплект прибора Еде-рина состоит из 4 инварных проволок по 24 метров или 48 м_у служащих собственно для измерения базиса; к ним прилагаются: проволока в 8 метров и лента в 4 м, которыми измеряют остаток базиса. Затем 2 станка с блоками и гирями, 2 лотаппарата для проектирования центров на концах базиса и в перерывах работы •и некоторое число штативов с целиками. Нивелир с П/а—2-м рейкой служит для определения разностей высот между соседними целиками, что необходимо для вычисления «приведений к горизонту» длины проволоки, расположенной наклонно. Таким прибором можно пройти двумя проволоками в одну сторону

2—3 км в день.

Эталониро-вание проволок (определение их длины сравнением с нормальными мерами) производится на особых компараторах с микроскопами, которые имеются в Москве и Ленинграде. Точность измерения прибором Едерина при тщательной работе достигает 1 : 1 000 000 длины. Окончательная длина базиса вычисляется по следующей формуле:

L=nl₀+ 2 (A-R)-^^ + lcHt-t₀) + r, (8)

где п—число пролетов, 1₀—длина проволоки из эталонирования, А и R — отсчеты по шкалам передней и задней, h — разность высот между соседними целиками, к— коэфициент линейного расширения проволоки на 1°, t—темп-ра измерения, £₀—темп-ра эталонирования, г—остаток базиса, измеренный инварною лентою. Длина базиса приводится к уровенной поверх ности океана, для чего поправка вычисляется по формуле

ДЬ=-

(9)

где L—вычисленная длина базиса, Н—абсолютная высота одного из концов базиса, h— средняя из превышений всех целиков над центром того же конца базиса, R—длина среднего радиуса земного сфероида для данной широты места.

8. Измерение горизонтальных углов. Для измерения углов на Т. применяются теодолиты и универсальные инструменты. Различие их заключается в конструкции трубы: у теодолитов труба, прямая и скреплена с осью вращения по середине ее. Универсальный инструмент служит не только для измерения горизонтальных углов между земными предметами, но и для астрономия, наблюдений, почему труба у него или ломаная или прямая внецентренная, то есть прикрепленная к концу своей оси вращения вне лагер. Кроме того универсальный инструмент обязательно имеет вертикальный, круг. У нас в СССР применяются 1-, 2- и 5-секундные инструменты с микроскопами; 10-секундные с верньерами. В настоящее время входят в употребление теодолиты со стеклянными кругами и оптическими микрометрами Цейсса и Вильда, а также инструменты со шкаловыми микроскопами. Все эти инструменты должны иметь сетку нитей, в которой были бы 2 вертикальные и 2 горизонтальные нити (фигура 14). Это необходимо потому, что при достаточно больших расстояниях изображение наблюдаемого предмета не должно покрываться вертикальной нитью, как это делается при работе с малыми теодолитами, так как в этом случае оно исчезает. Если же имеются две нити, то изображение сигнала вводится микрометрия, движением в промежуток между нитями и располагается там симметрично относительно этих нитей. Для контроля устойчивости инструмента в продолжение измерения угла или нескольких направлений иногда применяется поверительная труба, которая помещается под лимбом и скрепляется наглухо или со втулкою его или с трегером инструмента с помощью одного или нескольких зажимных винтов. Вертикальные круги обязательно снабжаются точными уровнями, которые скрепляются с алидадою. Они дают возможность измерять вертикальные углы по-

Фигура 14.

Таблица 1. —Журнал измерения горизонтальных направлений.

Пирамида Иванцево Высота инструмента над центром 2,1 м

5/VI—1932 16 ч. 35 метров Высота болванки над центром 8,8 м

Десятисекундный теодолит № 1532

Название предметов	Круг L			Круг К		L+R 2	! Направ- | ление
	Отсчеты по верньерам	Среднее	2С —L — R	Отсчеты по верньерам	Среднее
					Ср. 0°10,6" ИЗ (1) И (2)
Васильково.	ло .,20" 0 1 30	0° 125"	+45"	180*0^	180° 040"	0° 1 2,5" (1)	о о о
Володино.	43 28 1	13 28 17,5	42,5"	223 27 То	223 27 35	43 27 56,2	43 26 55,6
Мамино.	-S	68 42 37,5	42,5"	218 41 52 60	218 41 55	68 42 16,2	68 41 15,6 I
Васильково.	•‘S	0 1 22,5	47,5"	40 180 0 — 30	180 0 35	0 0 58,7 (2)	j

добно тахеометрич. теодолиту, но с большей точностью. Условия, которым должны удовлетворять эти инструменты, совершенно те же, что и в малых теодолитах, но конечно вся регулировка их совершается более точно и требует опытной руки. Инструменты тщательно оберегаются, во время работы обязательно защищаются от солнца и ветра зонтом или палаткой, для перевозки внимательно укладываются в ящик.

9. Способы измерения углов. При измерении горизонтальных углов на Т. применяются следующие способы, а) Способ круговых приемов (Струве) заключается в том, что измеряются собственно не углы, а н а п-равления на все знаки и предметы, которые должен быть засечены с данной станции на сигнале. Для этой цели труба наводится при вертикальном круге слева поочередно на все предметы, начиная с первого, избранного начальным; при этом алидадный круг вращается вправо, по часовой стрелке. После наведения на каждый предмет делаются отсчеты по двум микроскопам или верньерам, которые и записываются в журнал. Обойдя все предметы, труба снова для контроля положения лимба наводится на начальный предмет, и второй отсчет также записывается. Этим заканчивается подуприем; затем труба переводится через зенит, и работа повторяется, но в обратном порядке, то есть алидадный круг вращаемся от начального предмета влево, против часовой стрелки. Таким порядком во в т о-ром полуприеме повторяются наведения на все предметы, и весь круговой прием заканчивается четвертым наведением на начальный предмет. Обработка журнала наблюдений одного приема видна из прилагаемого образца (табл. 1). В результате получаются т. н. направления. На каждом пункте выполняют от 3 до 12 таких приемов в зависимости от требуемой точности, и за окончательный результат берут среднее арифметическое из всех приемов по каждому направлению. В табл. 2 приведен пример записи наблюдений в журнале при измерении направлений универсальным инструментом с микроскоп-микрометрами.

При измерении направлений круговыми при-смами горизонтальный круг переставляется перед началом каждого приема, чтобы отсчеты во всех случаях приходились бы на различных делениях. Эти перестановки лимба для исключения влияния систематических ошибок делений самого лимба делаются через равные промежутки, а именно: круг переставляют так, чтобы например при 6 приемах на начальный предмет отсчет был бы близким к следующим цифрам (в градусах):

Другими словами, при 6 приемах круг переставляется на 30° или вообще от приема к приему круг переставляется на где п —

число приемов. Исключение влияния систематических ошибок делений лимба основано на свойстве коэф-тов ряда, которым м. б. представлена систематич. ошибка Σ каждой черточки ϋ, а именно:

Ά-ι si*¹ (Р ~l· ^ai) ~l· А₂ sin (2 Θ + а₂) +

+ А₃ sin (3 θ + a₃) -f-.

в I приеме.	0	в IV приеме.	90	ей
» II »	30	» V »	120	со
» III ».	60	» VI »	150	а

В

В

H л

a d 2 wa §

о© Я ьои о со a

ЯЯш

в

« i

cO f

s g

g §

s о

I s

* 3

a ^s

N о

И «

со

ш

а к к к _Λ и в

О оз щ в а« g 2 а К δ

s^sg

О ^И

WR tr В со α> о V И 03 сО о

ЯЯЯ

Ρί +

а о

+ <м e I

и	а
в и ft в	в^
В1 эВ й	Я
as
и ft сО оз	Микр. А

а·*

ft «

Я

I

II

о и

g ^и ft в

Ц

аВ ^Я

|в й ft

rt £

а к

ВО)

я в^

Я

3 £

|и

Ii

ftB

ⓧ

и и со со оз «

Я

+

ЙОО

Н

в а

Н

Здесь коэф-тыД_г, Л₂, А₃,. и углыа₁₅а₂,а₃,. нек-рые постоянные, которые можно определить из исследования лимба. Однако если делать перестановку лимба через равные угловые промежутки, то отсчитанные черточки расположатся симметрично по всему кругу, сумма ошибок Σ q всех приемов выразится суммою членов, в которой каждая из постоянных Л₁₉ А₂, А₃,. будет умножаться на сумму синусов кратных дуг, каковая равна нулю. Благодаря этому и Σ_θ обратится в нуль. Одновременно с этим ослабляется влияние и случайных ошибок делений лимба вследствие увеличения числа всех отсчетов. На начальный предмет всегда делают наведение при отсчете, близком к 0°.

После обработки журнала составляется список направлений для данного пункта (табл. 3), полученных из всех приемов, а за-

Таблица 3. —Список направлений на пирамиде Иванцево (5/VI—1932 г.).

I i I в		Н а з в	а н и	е п ·	у н К Т О в
Ά В и	Ва
21	силь- ново	Володино	V	V2	Мамино	V	V2
I	0°00"	43°2655,6"	+1,9	3,6	68°4115,6"	+1,2	1,4
II	0	50,3	— 3,4	11,6	10,1	-4,3	18,5
III	0	48,2	-5,5	30,3	8,3	-6,1	37,2
IV	0	59,4	+5,7	32,5	16,7	+2,3	5,3
V	0	51,8	— 1,9	3,6	21,2	+6,8	46,2
VI	0	57,0	+3,3	10,9	14,3	-0,1	0,0
Ср.	=0°00"	43°2653,7" ± 1,7"	Σ v2.	= 92,5	68°4Г 14,4" ± 1,9"	Σ г?2=Ю8,6

тем вычисляется средняя ошибка одного приема по ф-ле

⁶ι ⁼ ±ΐΛ»Π+ 0°)

где V²—квадраты уклонения отдельных приемов от среднего, п—число приемов. Средняя ошибка результата измерений из всех п приемов равна

*„-±КдЙ <“>

В данном примере для пункта Володино ε_η== zfc 1,7", для пункта Мамино £„=±1,9".

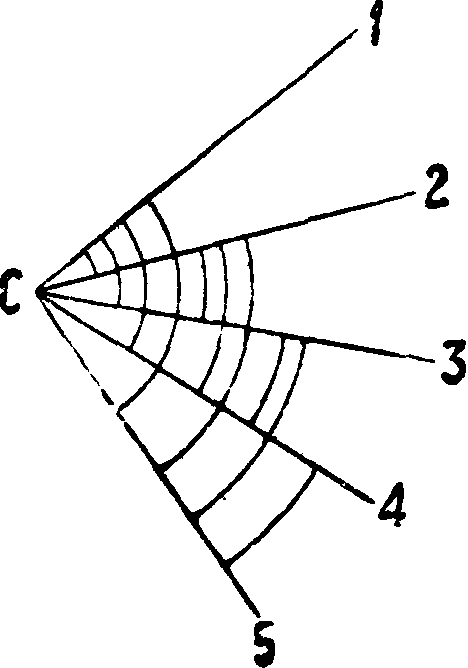
б) По существующим в СССР инструкциям способ круговых приемов применяется при измерении направлений на всех Т., за исключением Т. I кл., где установлен способ Шрейбера. Сущность этого метода заключается в том, что в отличие от способа Струве здесь измеряются не направления, а именно углы между отдельными знаками и предметами. Порядок расстановки этих углов соображен т. о., что в результате, в среднем, из ’всех измерений и на все предметы получаются те же направления, что и круговыми приемами, причем вес всех направлений строго одинаковый; систематические ошибки делений лимба также исключаются. В способе Шрейбера измеряются на станции углы между предметами 1, 2, 3, 4, 5 во всех комбинациях (фигура 15), а именно: 1—2, 1—3, 1—4, 1—5, 2—3, 2—4, 2—5, 3—4, 3—5, 4—5, причем каждый угол измеряется несколькими приемами, а прием состоит из двух полуприемов: при круге «лево» и при круге «право». Кроме того ставится еще необходимое условие,

чтобы всякое направление измерялось бы при одном и том же положении горизонтального лимба один раз, то есть отсчет по кругу был бы всегда разный, и наконец чтобы все отсчеты расположились бы по кругу симметрично (так же, как и в способе круговых приемов). Для этой цели Шрейберов даны формулы, по которым составляются таблички установок лимба для различного числа приемов и различного числа направлений на станции. Если обозначить через п число направлений на станции, т—число приемов, которым должен быть измерен каждый угол, а—угол поворота лимба между приемами при измерении одного и того же угла, <5—угол поворота лимба при переходе от измерения углов одной группы к другой, не примыкающих друг к другу (например от 1—5 к 2—3), тогда число всех перестановок лимба р:

р=т (п — 1) при четном п, р=тп при нечетном п₉

180°

σ =-,

т ’

δ=при четном п,

δ=^ при нечетном п.

Таблица 4. — При п—2и т~ 12.

Угол

Приемы

I

II

IIlJ IV 1 V VI

VII

VIII

IX

X

XI

XII

1—2

0°

15°

30°

45°

60°

75°

90°

105°

120°

135°

150°

16ο·°

Таблица 5. — При п=3и 8.

Угол	Приемы
	I 1 II III		IV V VI		VII	VIII
1—2 1— 3 2— 3 ·	0° 7,5 15	22,5° 45° 30 52,5 37,5 60	67,5° 75 82,5	90° 112,5° 97,5 120 105 127,5	135° 142,5 150	157,5? 165 172,5

Таблица 6. — При n=4u m=6.

Угол	Приемы j
	I	II	III	IV	V	VI
1—2	0°	30°	60°	90°	100°	150°
1—3	10	40	70	100	530	160
1—4	20	50	80	110	110	170
2—3	20	50	80	по	140	170
2—4	10	40	70	100	130	160
3—4	0	30	60	90	120	150 !

Таблица 7. — При n=bu m=5.

! Угол	Приемы
	I	II	III	IV	V
1—2	0°	36°	72°	108°	144° i
1—3	7,2	43,2	79,2	115,2	151,2 i
1—4	11,4	50,4	86,4	122,4	158,4 1
1—5	21,6	57,6	93,6	129,6	165,6 !
2—3	14,4	50,4	86,4	122,4	158,4
2—4	21,6	57,6	93,6	129,6	165,6
2—5	28,8	64,8	100,8	136,8	172,8
3-4	28,8	64,8	100,8	136,8	172,8
3—5	0	36	72	108	144
4—5	7,2	43,2	79,2	115,2	151,2

Таблица 4, 5, 6 и 7 составлены по этим ф-лам применительно к Т. I кл. при тп=24; установки лимба показаны в градусах. Обращается внимание на то, что цифры в таблицах не

Фигура 15.

означают отсчета по лимбу для установки его на левый предмет при измерении данного угла. Для этой цели нужно или прикрепить к тре-геру инструмента постоянный указатель, по которому и делать установку лимба по цифрам таблицы, или на каждой станции избрать какой-либо постоянный предмет, хорошо видимый и легко находимый, наводить на него трубу перед каждым приемом, затем поворачивать лимб и подводить под первый микроскоп отсчет, указанный в таблице 4—7. Далее по закреплении лимба начинать собственно измерение угла. Обработку результатов измерений углов на станции по способу Шрейбера см. табл. 8. Преимущество способа Шрейбера перед способом круговых приемов заключается затем на предмет В, и отсчет тоже не записывается. Если предположено делать например три повторения, то записывается отсчет b₃ (фигура 16, II), и окончательная величина угла будет равна

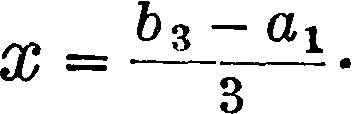
То же самое повторяется при другом положении вертикального круга, и затем берут среднее как окончательный результат. Таким путем измеряются все углы между пунктами, каждый угол отдельно. Если на данном знаке случится иметь 4—5 направлений, то работа становится утомительной, однако при слабых по качествам инструментах способ повторений может выручить. Во избежание грубых просчетов рекомендуется записывать отсчет Ь_1% чтобы ужо

Таблица 8. —Обработка результатов измерений углов на станции по способу

Шрейбера.

На станции 8 направления Измерены углы 1—2,1—8,2—3; каждый 8 приемами, большим теодолитом с микроскопами

	(1-2)	(1-3)	(2—3)
	55° 54	109° 26	53° 32
I	49,15"	6,10"	17,38"
II	49,52	6,94	17,61
III	47,25	4,54	17,75
IV	48,28	8,49	18,06
V	48,22	6,48	20,91
VI	49,60	5,33	20,23
VII	49,70	5,41	20,43
VIII	49,01	6,76	18,39
	48,82"	6,26"	18,85"

Наблюденные уравненные направления

1.		0	0"
2.	55	54	48,35
3.		26	6,73

Уравнение измеренных углов (1—2). 48,82" (1—3). 6,26"

(1—2). 48,82 (1—3). 6,26

-3) —(2—3). .47,41 (1—2) + (2—3). .7,67

(1-

Л =48,35" Н=6,73"

Средняя ошибка угла по согласию результатов отдельных приемов

Σ г?2 т—п

Средняя ошибка угла из 8 приемов т₂=±

j/e

Σ <52

1) (п-2)

= ± 0,81".

Средняя ошибка уравненного угла т₃=±

т₂

= ± 0,66"

_где: у —уклонения от среднего из всех приемов, <5 —уклонения этих средних от уравненных, т—число приемов (24), η —число направлений (3).

в том, что, во-первых, измерение одного угла протекает весьма быстро, и потому больше гарантии в том, что лимб остается неподвижным; во-вторых, именно в Т. I кл. при больших расстояниях (до 50 и более км) не всегда удается одновременно видеть все предметы, что совершенно необходимо для измерения круговыми приемами. Количество же наведений трубою и отсчетов по микроскопам при способе Шрейбера возрастает, и работа становится громоздкою тем более, чем больше направлений на станции. в) В нек-рых случаях для измерения горизонтальных углов применяется способ повторений, главным образом тогда, когда инструмент не обладает достаточной точностью отсчетов или вообще потрепанный. При этом методе работы также измеряются отдельные углы между направлениями на два сэседних пункта сл. обр. (фигура 16,1): алидадный круг скрепляют с лимбом, наводят трубу на левый предмет А и делают отсчет а_г; затем, как обычно, оставляя лимб неподвижным, наводят трубу на предмет В. Далее, вместо того, чтобы сделать отсчет b_х и получить искомый угол х=b₁ — a_lf открепляют лимб и, вращая его вместе с алидадным кругом и трубою, наводят последнюю вновь на предмет А, закрепляя лимб и действуя нужным микрометрия, винтом. Т. о. искомый угол х как бы откладывается на лимбе. Отсчет а₂ (равный. b_г) не делается, а труба, как обычно при измерении углов, наводится после двух первых наведений получить приближенную величину угла. Далее, из всех повторений измеряемый угол должен получиться близ

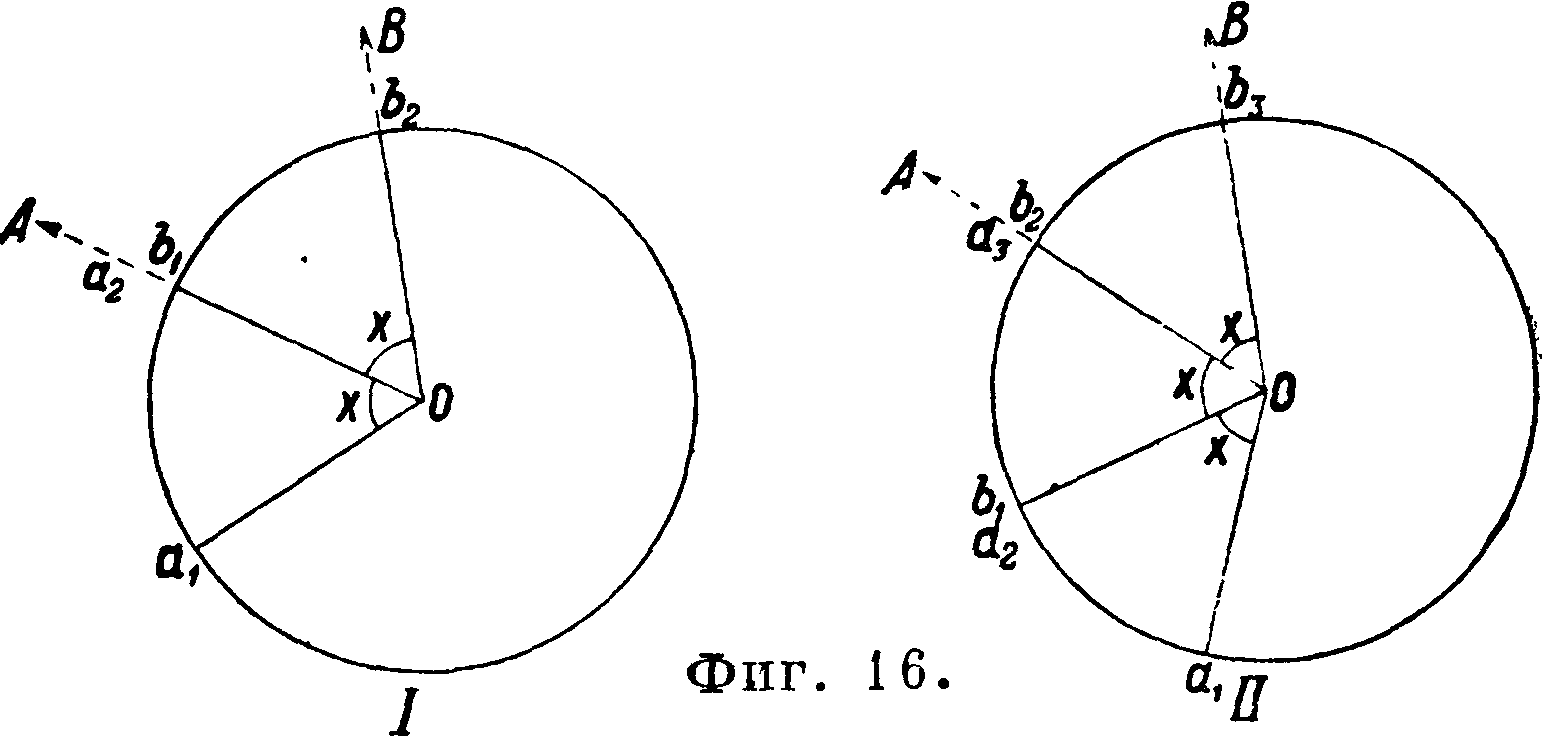
ким к вычисленному из первого измерения, что и служит контролем измерений и вычислений.

10. Общие замечания к измерению углов на Т. При измерении углов на Т. необходимо с полным вниманием отнестись к каждому своему движению, чтобы^ выработать совершенную четкость этих действий и не делать ничего лишнего. Во всех геодезия, измерениях все приемы располагаются симметрично как в пространстве, так и во времени относительно какого-либо предмета или момента; обычно именно при соблюдении таких условий работа оказывается наиболее рационально налаженною. Этим же путем ослабляется или даже совершенно исключается влияние разного рода погрешностей в работе (отсчеты по лимбу делаются по двум верньерам, удаленным друг от друга на 180°, вертикальные·

углы измеряются при круге «право» и «лево», нивелир ставится посредине между рейками и т. д.)· При измерении углов на Т. встречаются еще с влиянием атмосферы. Видимость построенных знаков в трубу инструмента оказывается возможною только утром через час-два после восхода солнца до 8—9 ч. утра, если нет тумана. Затем в солнечные дни работа становится невозможною, т. к. изображения предметов в трубе расплываются и кажется, что воздух струится. Успокоение и наи-.лучшая видимость наступают после полудня, часов с 16 дня, и продолжаются почти до заката солнца. Эти явления особенно дают себя •чувствовать в степях, где в полдневные часы работа совсем невозможна. В горах, наоборот, премя плохой видимости сокращается. В пасмурную погоду и при легком ветре можно работать почти целый день, если нет тумана. На Т. 1кл. и вообще в случаях, ответственных при измерении углов, не делают наведений трубою непосредственно на изображение знака, а применяют искусственную сигнализацию: дне^ на знаках устанавливают гелиотроп ы—визирные приборы с зеркальцем, которое направляет пучок отраженных лучей солнца в сторону наблюдателя (зайчик); ночью устанавливают фонари, ацетиленовые или электрические, -с рефлекторами, также обращенными в сторону наблюдателя. В настоящее время на Т. I кл. почти исключительно применяются именно ночные наблюдения с фонарями, так как в это время суток состояние атмосферы наиболее ^спокойное и изображения наблюдаемых светящихся точек резко очерчены.

11. Центрировки и редукции. Общие формулы. При измерении горизонтальных углов на Т. инструмент с помощью отвеса устанавливается над центром знака. В таком случае, как бы аккуратно ни была поставлена пирамида, все-таки болванка ее не будет находиться в одной отвесной линии с центром знака и осью инструмента. Между тем «со следующего знака мы будем наводить на болванку, а не на центр сигнала или на инструмент. Наоборот, если ось инструмента совместить с отвесной линией болванки, то центр знака окажется в стороне. В том случае, когда инструмент ставится не на штативе, а поднимается на столик внутренней пирамиды,— несовмещение центра знака, оси инструмента и оси болванки еще более заметно. На этом основании необходимо до или после измерения углов, а если таковые протекали не один день, то и до и после наблюдений, определить

Фигура 17.

Фигура 18.

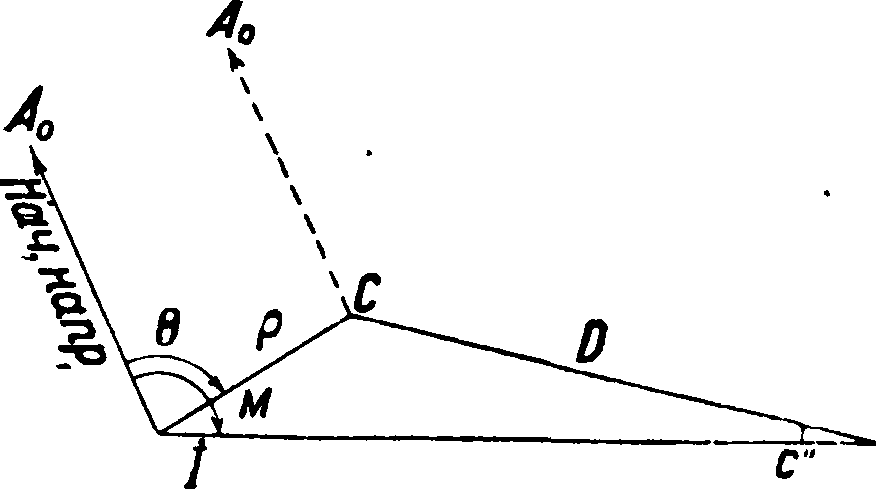
^элементы центрировки и редукции, чтобы затем можно было ввести соответствующие поправки в измеренные углы, а) Поправка на центрировку инструмента, или приведение к центру знака. Положим, ’что (фигура 17) центр знака—С; инструмент стоял ша точке I) начальное направление—А₀ М—

угол, измеряемый от начального направления на какой-либо пункт М, расстояние до которого равно В. Тогда расстояние ρ от оси инструмента до центра знака и угол Θ от начального направления и будут элементами центрировки, которые дадут возможность вычислить поправку с" (в ск.). Из фигура 17 видно, что

^c"=№^siii(^M-^e)· <¹²>

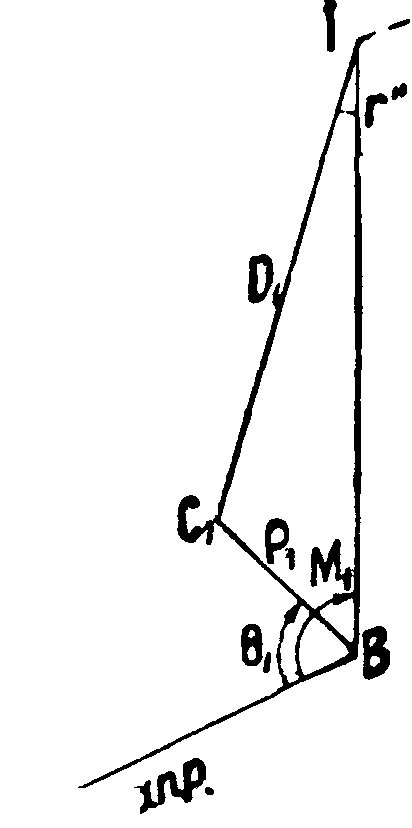
По этой формуле и вычисляются приведения к центру знака, б) Редукция, или п р и в е д е-ние, болванки к центру знака. Положим, что .из точки 1, где стоит инструмент (фигура 18), мы визируем на болванку В соседнего знака, центр которого находится в точке С_г. Редукция в этом случае выразится углом г", для вычисления которого нужно определить элементы ρ_χ и 0_Х. Тогда

»·-5Γβί (13)

По этой формуле вычисляются редукции; конечно, если с" и г" настолько малы·, что не превышают ошибок измерений углов, ими можно пренебречь,

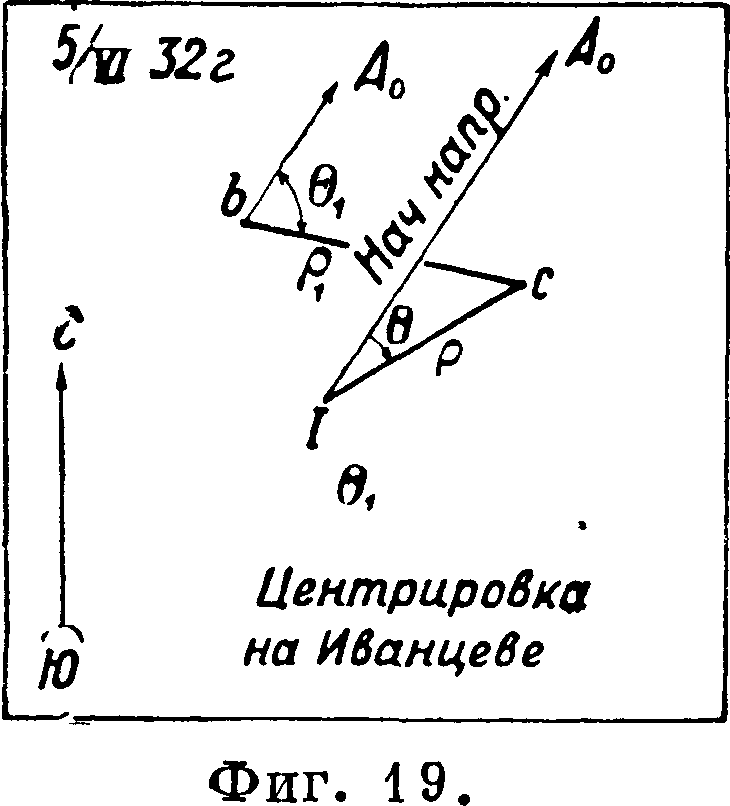
12. Определение элементов цен-трировок графически. Если ρ центрировки и ρ_χ редукции не превышают 1—2 дм, то их определяют графически. Для этой цели триангулятор делает себе столик на трех ножках с гладкой верхней доской. Этот столик устанавливается над центром знака, и на поверхности доски кнопками накалывается лист плотной бумаги. Небольшой теодолит, хорошо проверенный и снабженный уровнем на горизонтальной оси трубы, устанавливается по трем направлениям под углами примерно в 120° вблизи столика на расстоянии 10 — 15 метров в зависимости от размеров площадки и высоты знака. С каждой установки на столик проектируются трубою как расположение центра знака, так и место оси инструмента и оси болванки (фигура 19).

Тут же с помощью линейки прочерчивается приближенное до нескольких минут направление на начальный предмет А₀и по буссоли—направление меридиана. Длины ρ и ρ_χ определяются по масштабной линейке, а углы Θ и 0_Х, всегда считаемые от начального направления по направлению движения часовой стрелки, измеряются транспортиром. Необходимо заметить, что три одноименных направления, спроектированные теодолитом, вместо того чтобы пересечься в одной точке, обычно образуют треугольник погрешностей. Существующие инструкции позволяют брать искомую точку внутри такого тр-ка, если стороны его не превышают 1 см. В противном случае работу нужно переделывать. Заметим еще, что в случае высоких знаков и заметной коллимационной ошибки трубы, а также наклонности горизонтальной оси трубы проектировать нужно с каждой точки стояния при круге «право» и при круге «лево». Практика работ последнего времени установила такой порядок: если инструмент для измерения углов ставится на штативе на земле, то его с помощью тяжелого отвеса (чтобы ветер

не выгибал шнура) достаточно точно устанавливают над центром знака. Если инструмент поднимается на столик внутренней пирамиды, то предварительно туда с помощью центриро-вочного теодолита, как описано, с трех точек проектируют центр знака, а затем инструмент в продолжение всего периода работы на знаке ставят аккуратно над этой точкой. Т. обр. центрировку в обоих случаях обращают в нуль. Редукцию же определяют, как было описано, или со специальным столиком или же болванку проектируют на столик внутренней пирамиды, для чего там накалывают бумагу. Если строителю удалось ось болванки точно пригнать над центром знака, то и редукция обращается в нуль [для этого триангулятор обыкновенно сначала строит знак, затем с помощью тяжелого (1—2 килограмма) отвеса на струне ось болванки йереносит на землю, и там закладывает центр].

13. Определение элементов центрировки непосредственно и аналитически. Бывают однако случаи, когда одна из ног знака закроет предмет наблюдения, и тогда инструмент приходится нарочно выносить в сторону и настолько далеко * что q уже не поместится на столике. Чаще всего это происходит на знаках, к-рыми служат избранные для того здания, например колокольни. Здесь удаление оси инструмента от оси здания доходит иногда до нескольких м. В таких случаях элементы центрировок и редукций определяются более сложными приемами, а) Непосредственное измерение элементов центрировки делается обычно на колокольнях(фигура 20). Для увеличения кругозора в таких случаях инструмент приходится ставить на подоконниках окон, нацр. в точке I; эту станцию затем и нужно привязать к центру С, измеривши ρ непосредственно рулеткой, а угол Θ теодолитом. Положение точки С в случае полной сим-

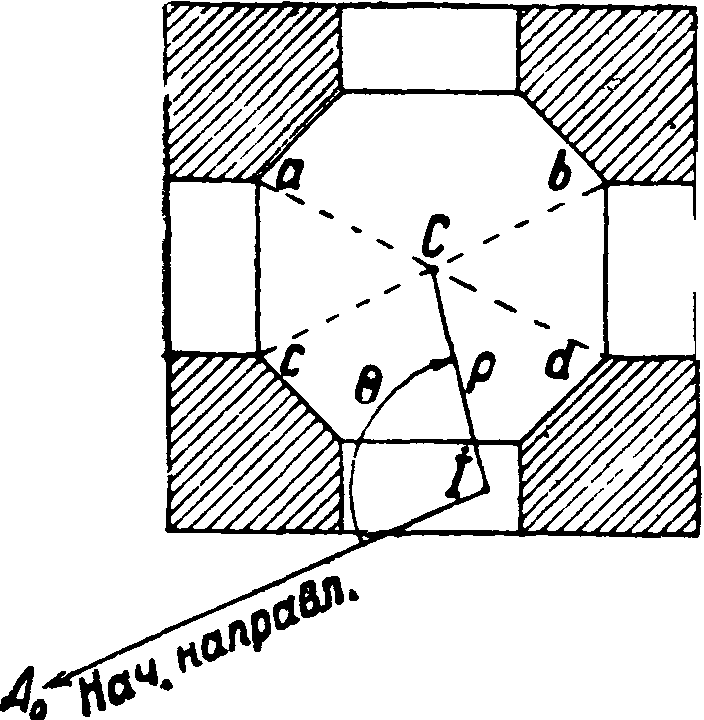
Фигура 20.

метрии здания находится замерами рулеткой диагоналей ad и bс. Если пересечение их будет равно отстоять от точек а, Ь, с и d, то эту

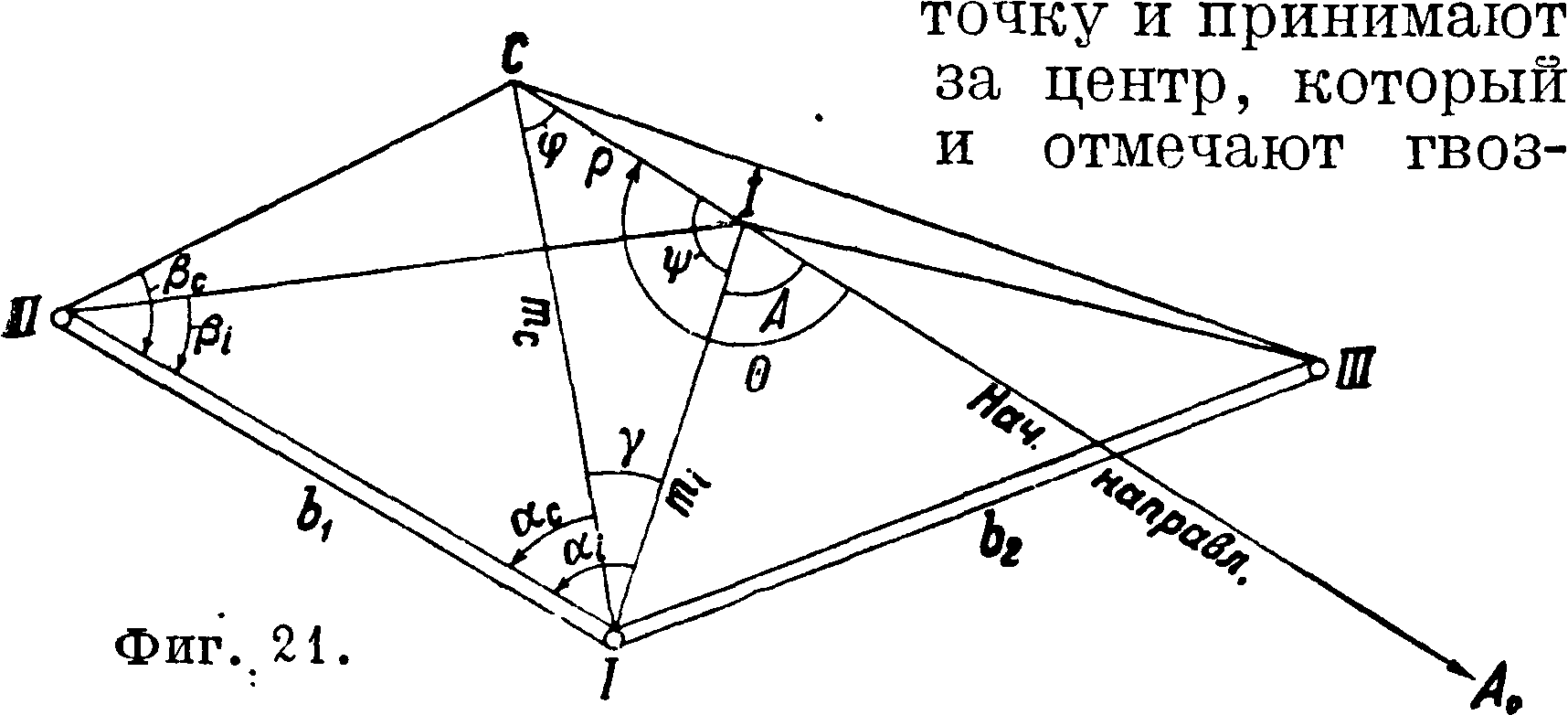
дем или чугунной маркой. Если же фигура плана здания окажется неправильной и появится сомнение в соответствии оси здания с венчающим его куполом, шпилем и тому подобное., то на пол проектируют купол, подобно болванке знака, с помощью теодолита с трех точек стояния. Такое проектирование обычно встречает много трудностей, если здание высокое и у подошвы его нет достаточной площадки для установок инструмента. В этих случаях триангулятор должен сам проявить изобретательность, прибегая иногда к сооружению небольших надстроек в виде подмостков, бал кончиков и тому подобное. б) Если центрировка велика и самый центр невозможно спроектировать на пол (часто мешают перила, колокола и прочие), то положение инструмента привязывают непосредственно к куполу, а если работа шла на знаке, то к его центру. Для этого у подножия здания (или знака) выбирают и измеряют лентой один, а еще лучше два базиса (фигура 21) и с концов их теодолитом измеряют углы а_г- и β_ί на ось инструмента I; затем углы а_си β₍.—на купол С (что и будет центром) или, если на знаке,—на нить отвеса, подвешенного над центром. Кроме того во время измерения углов на знаке с точки I измеряют угол А от начального направления на один из концов базиса. Из фигура 21 видно, что

	ί sin /5^ С~ 1 Sill(ac+ ββ) ’
точно так	же ш -b 8ίηβι 1 1 Sin (ai + βι)
Далее
	У=аг — ас>

зная ш_с, т_г· и угол у, можно из I τρ-ка CI получить ρ и угол гр, а затем и угол Θ, равный А + гр. Для решения такого τρ-ка по двум сторонам и углу между ними рекомендуется прием из тригонометрии, к-рый приводит к следующим формулам:

φ + гр=180 — у,

Ш_с=m_t tg μ,

tg 7а О - Ψ)=ctg I Ctg (μ + 45°);

зная φ + гр и φ — гр, вычисляют оба угла, а затем

sinV _л smy

Точно таким же образом получается ρ по данным измерений со второго базиса b₂. Величина угла Θ, как уже упомянуто, получается по углам А.и ψ, сообразуясь с чертежом построенной вспомогательной сети, схему которой во избежание грубых промахов обязательно нужно предварительно составить.

Общим и весьма важным примечанием к определению и вычислению центрировок и редукций необходимо отметить следующее: в виду того что поправки на центрировки и редукции меняют знаки в зависимости от расположения окружающих пунктов, по своей же величине эти поправки в большинстве случаев малы,— необходимо с полным вниманием производить самое определение элементов центрировок и аккуратно помечать все нужные данные на цен-трировочных листах. Затем при вычислениях внимательно следить и расставлять знаки при получаемых значениях элементов, т. к. введенные не с тем знаком и малые по своей величине поправки только исказят полевые измерения, а не улучшат их, и такие промахи трудно будет обнаружить. Необходимо отметить, что длина сторон D, необходимая для вычисления центрировок и редукций, получается из предварительных вычислений сети. Для этой цели берут измеренные углы тр-ков, округляют их до минуты, исходную сторону округляют до 10 мин., и с этими данными по ф-лам плоской тригонометрии вычисляют длины всех сторон тр-ков сети, пользуясь 4- или 5-значными логарифмами. Пример вычисления центрировок и редукций приведен в таблице 9. (смотрите стб. 951—952).

		Дв. пир. Плотникова
ρ=0,11 М.	lg ρ=9,04139		ρΐ=0,08 М	lg 0ι =	: 8,90309
0=124°ЗО"	lg. ρ=4,35582 Sin 1 *		01=134°О	lg -Д-=в Sin 1"	: 4,21752
Центрировки
Наблюден, пункты	Протопопова	Портягана	Кор чу гаи	Ячунова	Таловка
м-ь lg sin (Μ-θ)	-124°30 9,91599	—44°19 9,84424	+14°57 9,14158	+80°32 9,99404	+121°15 9,93192
lgsinl"sin(M 0)	4,27181	4,20008	3,76740	4,34986	4,28774
lg D lg c" c"	4,21959 0,05222 -1,13" 4-1,13	4,03301 0,16705 -1,47" +1,13	4,15236 9,61501 +0,41, + 1,13	4,35559 9,99427 +0,99" + 1,13	4,12997 0,15777 +1,44" + 1,13
	0,00"	-0,34"	+1,54"	+ 2,12"	+2,57"
Редукции
M—0i lg sin (M-0!)	-134°0 9,85693	—53°49 9,90694	+ 5°27 8,97762	+ 71°2 9,97576	+111°45 9,96793
lg -7-^77, sin (M-0!) sin 1	4,07115	4,12446	3,19514	4,19328	4,18545
lg D lg r"	4,21959 9,85486 1 -0,72"	4,03301 0,09145 -1,23"	4,15236 9,04378 + 0,11"	4,35559 9,83769 +0,69"	4,12997 0,05548 + 1,14"

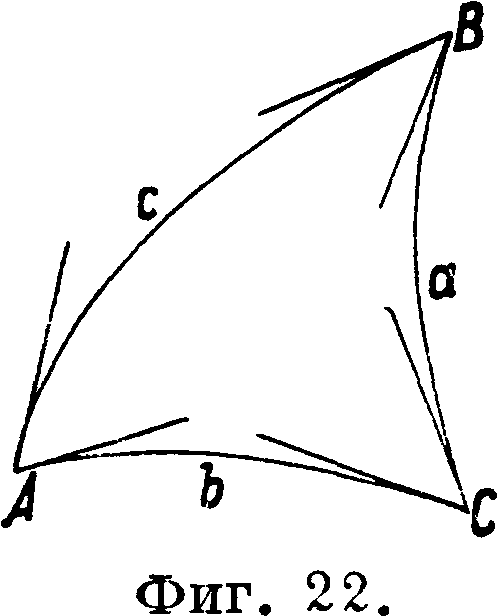
14. О сферическом избытке и теореме Лежандра. Прежде чем перейти к вопросу об, обработке Т. необходимо отметить, что тр-ки на земле образуются не прямыми линиями, а дугами а, bи с (фигура 22) и называются сферическими тр-ками, а углы их h, В и С— сферическими углами. Сумма их не равна 180°, как это имеет место в плоском тр-ке, а при сложении получается еще нек-рый излишек, "называемый ким избытком и обозначаемый о. в сферич. тр-ке сумма внутренних углов равна

А + В + С=180° + е.

Плоскость лимба теодолита или универсального инструмента при измерении углов на сигнале приводится в горизонтальное положение, а потому на Т. этими инструментами измеряются собственно углы, составленные касательными к дугам а, b и с сферич. тр-ка, проведенными через точки стояния инструмента А, В и С (фигура 23). Между тем из сферич. тригонометрии известно, что эти углы и являютСчЧ как-раз мерою сферич. углов тр-ка. Отсюда следует, что на Т. из измерений теодолитом получаются именно сферич. углы тр-ка.

Это обстоятельство как-будто обязывает при всех дальнейших вычислениях Т. применять ф-лы сферич. тригонометрии, что однако привело бы к значительным усложнениям. Их можно избежать, если иметь в виду, что стороны треугольников малы по сравнению с радиусом земного сфероида и составляют в большинстве случаев едва 1 : 200 длины этого радиуса. В геодезии обработка и вычисления Т. производятся на основе теоремы Лежандра, которая доказывает, что такие тр-ки можно с совершенно достаточною точностью вычислять как плоские; необходимо только углы сферич. тр-ка уменьшить на одну треть его сферического избытка. Т. о. если обозначить сферич. углы тр-ка через h, В и С, а углы преобразованного плоского тр-ка через А_1} В_г и Си то по теореме Лежандра получают:

I

В,-В-Л. (14)

Длины сторон а, b и с остаются без изменения. Полные ф-лы Лежандра для шара следующие:

*⁴i=^-| + 60T(°²-^m>>

Сг=С-{+^-_Лс“-т),

3

Последний поправочный член этих ф-л весьма мал и практич. значения для сторон тр-ков до 80—100 км не имеет. Таково же значение поправочных членов к формуле Лежандра для сферо идич. тр-ков. Для вычисления сферич. избытка существует несколько выражений, из которых на Т. обычно применяется следующая ф-ла:

^e=s4lT-«^&sinC’ (¹⁵>

где В—средний радиус земного сфероида для данной широты, а и b—две какие-либо стороны тр-ка и С—угол между ними. Для логарифма множителя _R2g-_Dl//=f приводится табл. 10 применительно к широтам φ от 36 до 72°.

Таблица 10. —Значения 1 g применительно к широте φ.

<Р	lg	Ψ	lg
36 38	1,1050—10 48	56	30
40	46	58	28
42	44	60	27
44	42	62	25 1
46	40	61	23 j
48	38	66	22
50	36	68	20 1
52	34	70	19 j
51	1,4032—10	72	1,4018—10 1 i

сферичес буквою ε. Т.

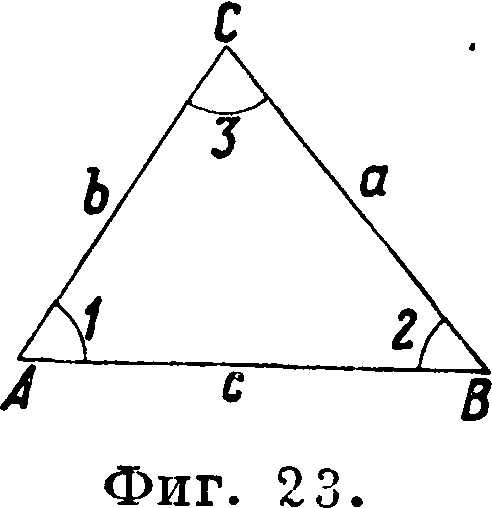
Широта φ для этих вычислений берется приближенная по существующей карте, на которой нанесена схема Т., если конечно не было специальных определений широты, долготы и -азимута для ориентирования всей сети.

Примеры вычисления сферич. избытка:

9>=45°, тр-к равносторонний с углами по 60°:

а=b=30 км α= b =20 км а=Ь=10км

I ga. 4,4771 4,3010 4,0000

1 gb. 4,477ί 4,3010 4,0000

lg Sin 60°.. 9,9375—10 9,9375—10 9,9375—10

1 gf. 1,4041—10 1,1011—10 1,4041—10

lg 6. 0,2958 9,9436—10 9,3416—10

ε=1,97" ε=0,88" ε=0,22"

Из этих примеров видно, что ε в условиях наших Т., где стороны редко превосходят 30 км, вообще величина небольшая и исчисляется секундами и их долями. Однако при точных работах пренебречь сферич. избытком нельзя. В малых Т. со сторонами тр-ков менее 10 тглг-и при условии, что ошибки измерений углов превосходят величину сферического избытка, наоборот, тр-ки можно считать плоскими.Существует еще один способ вычисления сферич. тр-ков заменою их плоскими, а именно способ аддитаментов. Он заключается в том, что отыскиваются поправки к сторонам сферич. тр-ка, углы же остаются без изменения. Для вычисления логарифмов сторон а_и b_г и с₁ даются следующие выражения:

lga^lga-^a²

lg^-ΐβ

lge^lgc-^c²

и обратно

lga-lgOi+^fa* lgb =lgb₁+~bⁱ ·, lgc=lgc!+

где а, b и с—стороны сферич. тр-ка, М—модуль, R—средний радиус кривизны для данной широты. Таблицы аддитаментов даются в специальных курсах геодезии, но вообще этот способ редко применяется на производстве.

15. Уравнивание сетей. Как уже упоминалось, на Т. всегда измеряются все три угла каждого тр-ка несмотря на то, что собственно для решения его достаточно иметь одну сторону и два угла. Делается это для того, чтобы получить контроль полевой работы. Вследствие ошибок измерений сумма измеренных углов i, В и С не получается равной тео-ретич., то есть 180°+ε, а выходит несколько большей или меньшею:

A+B + C=(180°+£)+v, ? где V называется ошибкою, или невязкою, треугольника. Пользуясь ей для различных тр-ков сети, можно вычислить т—о шибку измерения одногоугла по формуле итальянского геодезиста Ферреро, а именно

|г» (18)

где Σν²—сумма квадратов найденных ошибок тр-ков, а п—число их. Предельная допускаемая невязка ν тр-ка устанавливается ин

(16)

(17)

струкциями соответственно назначению Т. и инструментов, которые применялись для измерения углов. По существующим инструкциям в СССР для Т. I кл. невязка ν не должна превосходить 3"; для Т. II кл.—не более 5" при работе инструментом с 2-ск. микроскопами; не более 7" при 5-ск. микроскопах и не более 12" при 10-ск. верньерах. После подсчета указанным путем сумм углов в тр-ках и их невязок ν (после введения поправок на центрировки и редукции) еще нельзя по этим сырым материалам вычислять длины сторон тр-ков, т. к. будут получаться различные данные в зависимости от того, какая сторона будет взята за исходную и какие углы будут вставлены для вычислений. Эти с ы р ы.е "материалы нужно предварительно обработать и представить в таком виде, чтобы в простом тр-ке или в сети из простых тр-ков сумма углов в каждом тр-ке в точности равнялась бы теоретической, то есть для сферич. тр-ка

A -f- В -f- С=180° -}- ε, для плоского тр-ка

А + В А С — 180°.

Такая обработка Т. называется уравниванием Т., что имеет целью привести материалы по измерению углов к такому виду, чтобы вычисления, от какой бы стороны Т. они ни прошли, давали бы одно и то же значение для искомой стороны (в пределах точности вычислений). Эта задача разрешена Лежандром и Гауссом, к-рыми создан прием уравнивания, дающий возможность найти необходимые п о-правки к измеренным углам или направлениям сети. Они приводятся к такому виду, чтобы были удовлетворены все геометрические условия сети и кроме того чтобы сумма квадратов поправок была бы наименьшею; отсюда и самый прием называется способом наименьших квадратов. Он дает строгое решение поставленной задачи.

16. Условные уравнения. Если бы в тр-ке были измерены одна сторона с и два угла А и Б, то положение третьей точки С (фигура 23) легко получилось бы после вычисления длины сторон а и b; угол С определился бы как дополнение суммы углов i и В до 180°, чем и заканчивалась бы задача по решению треугольника. Однако в геодезии такое определение всех элементов тр-ка или сети обязательно сопровождается контролем, для чего измеряются все три угла тр-ка. Вследствие этого например для угла С получаются два значения: одно из непосредственных измерений, другое из последующих вычислений. Если бы исходною стороною служила сторона а, такое же разногласие получилось бы в угле А, и т. д. Происходит это потому, что в данном тр-ке вследствие неизбежных ошибок наблюдений не соблюдено необходимое геометрии. условие: сумма измеренных углов не равна сумме теоретической, и это разногласие нужно устранить. Поэтому и говорят, что простой тр-к имеет одно условие ф и г у р ы, а именно должно существовать равенство:

1 + 2 + 3 - (180° + ε)=0, где 1, 2 и 3—углы тр-ка (фигура 23). На самом деле обычно получается, что

1 + 2 + 3 — (180° + ε)=-у, (а)

где ν—невязка тр-ка. Задача уравнительных вычислений заключается в отыскании таких поправок (1), (2) и (3) к углам тр-ка, после введения которых сумма

1 + (1) + 2 + (2) + 3 + (3)-(180 + в)«0. (Ь) Если вычесть равенство (а) из (Ь), получим, что (1) + (2) + (3) + !>-0. (с)

Для всякой другой сомкнутой геометрич. фигуры это равенство будет следующего вида:

(1) + (2) + (3) + (4) +1.+V - 0, (19)

что и составляет общий вид условного ур-ия фигуры. Решением ур-ия (с) в тр-ке уравнивание заканчивается, и все разногласия устраняются (смотрите дальше). Если взять более сложную сеть (фигура 24), состоящую из двух тр-ков, но связанных еще диагональю, то здесь возникают, во-первых, три необходимых условных ур-ия фигур:

(1) + (2) + (3) + (4) + v_x=0 i

(1) + (2) + (7) + (8) + ν_β-0>. (^d>

(5) + (6) + (7) + (8) + ί;₃=Oj Такое же условное ур-ие для четвертого тр-ка BCD составлять и решать не требуется, т. к. оно будет удовлетворено само собою решением приведенных ур-ий, которые возникли вследствие избыточного измерения углов 4, 7 и 5. Одновременно с этим излишнее измерение угла 6 на точке С влечет за собою при построении точки Ώ возможность получения тр-ка погрешностей pqr (фигура 25) и т. о. вносит неопре

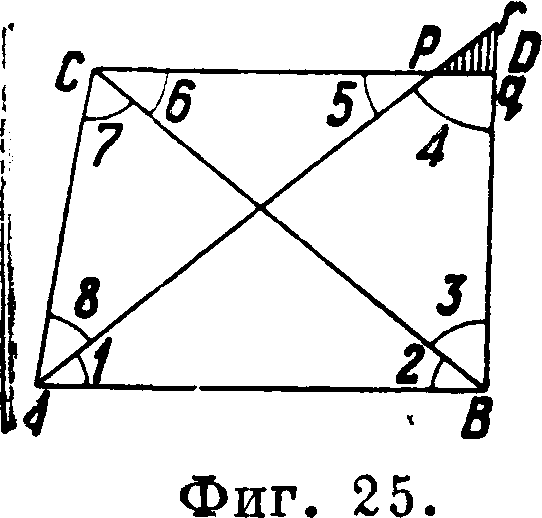
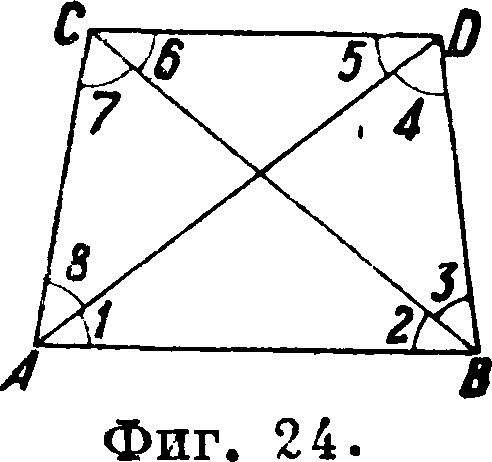
деленность в решение расположения вершины Ώ четырехугольника. Для устранения такого разногласия необходимо выполнить еще одно геометрич. условие, называемое условием полюса (или боковое). Оно следовательно вытекает из необходимости пересечения лучей CD, AD и BD в одной точке D, без всякого тр-ка погрешностей. Это требование выполняется лишь в том случае, если будут удовлетворены следующие соотношения:

CD _ sin8. AD sin(2+ 3). BD ₌ sin6 ,. AD ~ sin(6+7) ’ BD ~ sinl ⁹ CD sin3*

Перемножив эти равенства, получим следующее ур-ие

sin8 sin(2 + 3) sin6 _ ^

sin(6 + 7)·sini·sin3 “ ’

составляющее условие полюса. Если это выражение логарифмировать, то получится, что сумма логарифмов множителей в числителе без суммы логарифмов множителей в знаменателе равна нулю. В действительности же однако вследствие ошибок измерений в итоге логарифмирования этой ф-лы получится не нуль, а нек-рая величина ί;₄, выраженная единицами последних знаков логарифма. Таким путем получается, что

lg sin 8 + lg sin (2 + 3) + lg sin 6 - lgsin (6 + 7)— lg sin 1 — lgsin 3=v₄. (f)

Задача уравнивания и в этом случае сводится к тому," чтобы найти такие поправки к измеренным углам числителя и знаменателя, вве дением которых выражение (f) обратилось бы в нуль, то есть чтобы

lg sin [8 + (8)] + lg sin [2 + 3 + (2) + (3)] +

+ lg sin [6 + (6)] - lg sin [6 Ц- 7 + _v6) + (7)] -

- lg sin [1 + (1)] - lg sin [3 + (3)]=0. (g>

Поправки к углам обыкновенно выражаются секундами, а перемены соответствующих логарифмов синусов углов на одну секунду символами а — для углов нечетных или для углов, находящихся в числителе, и 0—для углов четных или для углов, находящихся в знаменателе. Тогда можно написать следующие равенства:

lg sin [8 + (8)]=lg sin 8 - β (8), lg sin [2 + 3 + (2) + (3)]=lg sin (2 + 3) + β (2) + + «(3),

lg sin [6 + (6)]=lg sin 6 + β (6), lg sin [6 + 7 + (6) + (7)]=lg sin (6 + 7) +

+ 0(6) +a (7),

lg sin [1 + (1)]=lg sin 1 + a (1), lg sin [3 + (3)]=lg sin 3 + a (3).

В соответствии с этим формула (g) примет следующий вид:

lg sin 8 + 0 (8) + lg sin (2 + 3) + 0 (2) + a (3) + .— - lg sin (6 + 7) - 0 (6) - a (7) - lg sin 1 -

~ ^a (1) —.=0. (h>

Если теперь из выражения (h) вычесть (f), получим условное уравнение полюса - a (1) + 0 (2) - a (7) + 0 (8) -. + t>₄=0, (k> где a и 0 — перемены логарифмов синусов углов на 1 ск., υ₄—разность между суммою логарифмов синусов углов числителя и такою же суммою синусов углов знаменателя полюсного условия, составленного для данной сети. Т. о. для рассмотренных фигура 24 и 25, называемых геодезическими четырехугольниками, вследствие избыточных измерений углов возникают следующие 4 условных ур-ия для поправок к измеренным углам: 3 для фигур

(1) + (2) + (3) + (4) + г?₄=0|

(1) + (2) + (7) + (8) + 1’₂=(+ (20>

(5) + (6) + (7) + (8) + v₃=oj 1 для полюса

- a (1) + 0 (2) - a (7) + 0(8) +=0.

В этих ур-иях величины v_lf v₂, v_s и г?₄ известны и называются постоянными членами, поправки же являются неизвестными, которые и нужно найти. Коэф. при неизвестных в трех первых ур-иях (фигур) равны 1, в ур-ии же полюса выражаются несколькими единицами с дробью последнего знака логарифма. Приведенную систему условных ур-ий и нужно решить для нахождения поправок. При уравнивании сетей чаще оперируют не с углами, а с направлениями, т. к. в поле измеряются именно направления (смотрите раньше способ круговых приемов и способ Шрейбера). На фигуре 26 дан случай, когда в геодезич. четырехугольнике не измерено одно направление с точки D на С, что и выражено на фигуре пунктирной линией. Применительно к этому случаю проставлены номера направлений от 1 до 11 на каждом пункте по движению часо-

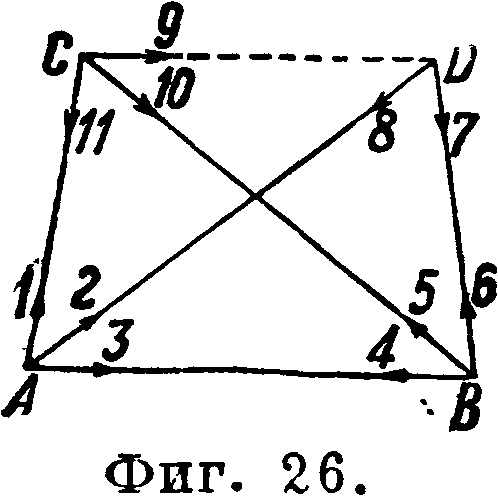
вой стрелки—слева направо. В соответствии с этим в данном примере отпадает одно ур-ие фигур, и условные ур-ия представятся в следующем виде:

2 для фигур

- (1) + (3) - (4) + (5) - (10) + (11) + υ_χ=о,

- (2) + (3) - (4) + (6) - (7) + (8) +=0;·

1 для полюса

- α (1) + β (2) - а (3) - β (4) + а (5) + β (10) -

-a(ll) + t?_a-0. (21)

Во избежание пропусков при составлении условных ур-ий руководствуются следующими ф-лами:

число N всех условных ур-ий в сети равно JV=D — ЗР + 4; число А ур-ий фигур равно

‘4-J-P + 1, (22)

число В ур-ий полюсов равно В-L-2P + 3,

где В—число всех направлений сети, Р—число всех точек, I—число сплошных линий в сети, то есть наблюденных прямо и обратно, L—число всех линий в сети сплошных и односторонних. В применении к фигура 26 по этим формулам получится

JV^ll-12 + 4=3;=5~4+1=2;

£=6-84-3=1.

Бессель дал правило для графического подсчета числа условных ур-ий: нужно все точки сети соединить между собою сплошными линиями, как бы полигоном, и отметить их толстой ломаной линией. Число оставшихся излишних сплошных же линий даст число условных ур-ий фигур (на фигура 26 осталось 2). Далее нужно получить как бы засечками последовательно одну за другой все точки сети от исходной стороны и утолстить пройденные линии. Число оставшихся сплошных и односторонних линий даст число условных ур-ий полюсов (на фигура 27 осталось 1).

.17. Общий вид условных уравнений и их решение по способу наименьших квадратов. Условные ур-ия, числом г, в общем виде можно написать:

Фигура 27.

*ι(1) +ва(2) + 0*(3) +*.

*ι(1) + ^г(2) + &з(3) +.

ч(1)+ с₂(2)+с.(3)+.

+ а_п (η) + V + b_п (п) 4*

+ Сп (^п) +

01=0) 02=0 03=0 »

Vi=oj

(23)

i (1) + Η (2) + % (3) +. ·. + in (ⁿ) + фичем η—число поправок. Коэф-ты а_х, а₂?ι, Ь₂, ., с_х, с₂, ., г_х, г₂,. в условных ур-иях эигур равны +1 или—1, а в условиях полю-ов являются переменами логарифмов сину-ов соответствующих углов на 1"; v_x, ν₂—по-тоянные, или известные, члены, представляющие или невязки фигур, и тогда они выражена в ск., или ошибки полюсных условий, ко-орые выражаются несколькими единицами оследних знаков логарифмов. Число неиз-естных поправок в этой системе ур-ий всегда олыне числа самих ур-ий, почему в таком виде ешение их является неопределенным. Поэто-:у добавляется еще условие минимума суммы вадратов поправок, то есть

(I)² + (2)² + (З)² +. + (п)²=min. (24)

Ур-ия (23) и (24) решаются совместно, причем путем преобразований и введением неопределенных множителей, называемых к о р р е-л а т а м и, к_г, к₃, .к_п получается следующая система ур-ий искомых поправок:

(1)=к_ха_х 4- к₂b_х -j- к₃с_х 4-

(2)=к_ха₂ + Tc₂b₂ + к₃с₂ +

(3)=к_ха₃ + к₂b₃ + к₃о₃ 4~

(ή) — к_ха_п- - к₂Ь_п+ к₃с_п 4-

. + kii_x. + к{ь₂

. + ki%₃

> > (25>

· 4“ ki%_n

по к-рым^их и можно вычислить, предварительно найдя корреляты из нормальных: ур-ий:

[(id] к_х+[аb] к₂4-[ас] к₃-{-*_г-4- ν_χ=0 [а&] к_х- - bb~ к₂- - bс к₃ 4-. .- ~ bi] к i 4- v₂=0 [dc] к_х- - bс] к₂~ ~[сс] &₃4-.4-[сг] 4-03=0

М26>

[аг] к_х+[Ы]к₂- -[сг] &₃4-.4-[гг] **4-0*=0,

Коэф-ты нормальных ур-ий, обозначенные символами [aa], ., [Ьс], ., [се, ., [гг], составляются по коэф-там условных ур-ий следующим: образом:

[aa]=a_xa_x 4- ^2^2 4“ ^з^з 4- ·· · 4- (^_п^ап ^

[ab]=а_хЬ_х 4- α₂δ₂ 4- %^з + ··· 4- ^Фп [bb] — Ь_Хb_Х 4- Ь₂Ь₂ 4" δ₃δ₃ 4~ ··· + ^п^п (

Число нормальных ур-ий соответствует числу коррелят, а потому решение их возможно. Затем с вычисленными значениями коррелят по“ формулам (25) находят поправки углов. Поверкою вычислений служит равенство

(I)² + (2)² + (З)² +. + (я)²=- (k_xv_x +

*202 4“ *303 4" ··· 4“ *г0г)· (28)»

Средняя ошибка угла или направления получается по ф-ле

W=± Ш+Ш, (29 >

где г—число условных ур-ий.

18. Примеры составления нормальных уравнений. В тр-ке очевидно будет только одно условное ур-ие фигур следующего вида (фигура 23):

(1) + (2) + (3) + 0ι=Ο.

Поэтому коэф-том также одного нормального- ур-ия будет [aa]=3 и нормальное ур-ие

3*₁4-0ι=Ο, откудα=

Поправки .к углам вычисляются по ф-лам (25)>

(1)=(2)=(3)=— -у·

Отсюда следует, что для уравнивания тр-ка. по способу наименьших квадратов нужно невязку тр-ка разделить на 3 и придать с обратным знаком к углам его. В геодезия. четырехугольнике (фигура

28) с одним односторонним направлением CD даны:

*Фигура 28.

Приведенные к центрам знаков направления

И з	пункта А н	а:	И 3	пункта	В н а:
С.		0,0"	А.	0	° 0 0,00
D.	72 44	33,44	С.,	21	5 27,45
В.		5,06	D.	. 12	10 39,83.

Углы

Из пункта С на: Из пункта D на:

D. 0° 0 0,(Г В. 0° 0 0,0"

В. 18 23 7,54 А. 70 56 54,29

А. 37 40 39,94

lg АВ. 4,4313638

Вычисление приближенных размеров сети АС=АВ ЁБ_?_{; ЛС}=ЛВ BD=AB ^s,n2

ЯШ fi’ SUI 6

AD =AB .-ⁿ.ff±i2

sin 5

Δ ABC Углы

1+2 139°37,0 € 19 17,5

3 21 5,5

Δ ABD

2 66°52,5^;

5 70 56,9

3+4 42 10,8

lg sin углов

9,8115

9,5190

9,5561

9,9636

9,9755

9,8270

1 g

sin (1+2)

sin 6 · 0,2925 4,4314=AB 0,0371, sin 3

^lgiIFe. sin 2 ^g sin 5 9,9881 4,4314 9,8515

sin 5’

lg сторон 4,7239=ВС 4,4685=AC

4,4195=BD

4,2829=AD

Вычисление сферич. избытков, например φ=51°0

Δ ABC

Δ ABD

lg АС. 4,4685, lg АВ. 4,4311 + lg Sin (1+2) 9,8115—10 lg /. 1,1035—10		lg BD. 4,4195, lg AB. 4,4314 "Hg sin (3+4) 9,8270—10 lg /. 1,4035—10
lg *1 ·	,. 0,1149	lg ε2. 0,0814
lg AC .lg AD Mg sin lg ·	£!=1,30" Δ ACD. 4,4685. 4,2829 1. 9,9800—10. 1,4035—10	ε2=1,21" Δ BCD 1 g BD. 4,4195, lg ВС. 4,7239 "Hg Sin 4. 9,5560—10 lg f. 1,4035—10
lg «3 ·	0,1349	lg ε4. 0,1029
	ез=1,36"	ε4=1,27"
	Контроль «i+e4=	=ε2+ε3=2,57"

Составление условных ур-ий фигур, подсчет невязок тр-ков

Δ АВС Δ ABD

1+2=139°37 5,06" 3+4= 42°Ю 39,83

+ 3= 21 5 27,45 2= 66 52 31,62

6= 19 17 32,40 5= 70 56 54,29

(.180+£ι)

180 О=180 О

4,91

1,30

180 О (180+в₂)=180 О

5,74

1,21

г? != +3,61" υ₂=+4,53"

Условные ур-ия фигур

(1) + (2) + (3) + (6) + 3,61=О,

(2) + (3) + (4) + (5) + 4,53=0.

-Составление условного ур-ия полюса (при точке D) CD AD BD _ sinl-sin(3 + 4) -sin7^

AD * BD * CD ~ sin (6+ 7) · sin 2·sin 4*

1

3 + 4 7

72°4433,44 42 10 39,83 18 23 7,54

te^sin на“ 1" 9,9799950.7 + 6,6 9,8270024.1 +23,2 9,4988723.5 * +63,4

		ε4 =9,3058698
	Углы	lg sin	β на 1"
6 + 7. 2. 4.		9.7861974.4 9.9636236.5 9,5560387.0	+ 27,2 + Μ + 54,6

ε₂=9,3058598

εΐ-ε₂=100=Τ₃

+ 6,6 (1) + 23,2 (3) + 23,2 (4) + 63,4 (7) -- 27,2 (6) - 27,2 (7) - 9,0(2) - 54,6 (4) + 100=О или после приведения подобных членов.

+ В,6 (1) - 9,0 (2) + 23,2 (3) - 31,4 (4) -

- 27,2 (6) + 36,2 (7) + 100=0.

Чтобы в дальнейшем вести вычисления с меньшими чи, козф-ты условного ур-ия полюса и известный член делят на 10 (или на 100); тогда окончательно:

+ 0,66 (1) - 0,90 (2) + 2,32 (3) - 3,14(4) -

- 2,72(6) + 3,62(7) + 10,0=0.

Обращается внимание на знаки в столбцах а и β. Перемены логарифмов и синусов острых углов всегда со знаком +, тупых углов со знаком —. Кроме того нужно принять в расчет знаки числителя и знаменателя. Далее составляется список коэфициентов условных уравнений в виде табл. 11.

Суммы [as], [bs] и [cs] составляются для получения контроля при подсчетах не только козф-тов нормальных ур-ий, но и дальнейшего их решения, как будет видно из табл. 12.

Нормальные ур-ия для данного примера представятся в следующем виде:

+ 4,00 к_х + 2,00 к₂ - 0,64 к₃ + 3,61=0;

+ 2,00 к_х + 4,00 к₂ - 1,72 к₃ + 4,53=0;

- 0,64 к_х - 1,72 к₂ + 36,99 к₃ + 10,00=0;

[as]=+ 8,97; [bs]=+ 8,81; [cs]=+ 44,63.

19. Решение нормальных ур-ий по· схеме Гаусса. В системе нормальных ур-ий

[бкх] к_х + [(Z&] к₂ + [<хс] к₃ + v_x=0,1

[ab] к_х + [bb] к₂ + [Ьс] к₃ + ν₂=оЛ (а)

[ac] к_х + [Ьс] к₂ + [сс] к₃ + ν₃=0, j

число неизвестных коррелат равно числу ур-ий, а потому имеется возможность решить эти ур-ия любым из способов, которые даются алгеброю. В геодезической практике применяется

Таблица И. — Список коэфициентов условных уравнений.

i ! № поправок	Коэф-ты при них	Вычисление поправок *	Поправки *
			m 1 m2
(1) (2) (3) (4) (5) (6) (7)	+1 0 +0,66 +1 +1 -0,S0 +1 +1 +2,32 0 +1 -3,14 0+1 0 +1 0 -2,72 0 0 +3,62	-0,424 -0,216 -0,424 -1,062 +0,294 -0,424 -1,062 -0,759 -1,062 +1,027 -1,062 -0,424 +0,889 -1,184	-0,640 -1,192 -2,245 -0,035 -1,062 +0,465 -1,184	0,410 1,416 5,051 0,002 1,124 0,217 1,392
V +3,61 +4,53 +10,0			Σ2=+ 9,612
fei Ьз * -0,424 -1,062 -0,327		Средняя ошибка угла по формуле (29) Σ1= -9,612 т=±/~+Г=±1 >7Г
hv -1,531 -4,811 -3,270
* Эти графы заполняются после нахождения коррелат кх, ^з·

Таблица 12. — Составление коэфициентов нормальных уравнений.

[αα]		[ab]	[ac]	[as]	[bb]	[be]	[bs]	[cc]	[cs]
(1)	4-1	0	4-0,S6	41,66	0	0	0	+ 0,436	0, 133
(2)	+1	+1	-0,Ю	4-1,10	+ 1	-0,90	4-0,10	+ 0,810	0,810
(3)	+1	+1	4-2,32	+4,32	+1	4-2,32	+ 3,32	+ 5,382	5,382
(4)	0	0	0	0	+1	-3,14	-2,14	+ 9,830	9,830
(5)	0	0	0	0	+1	-0	4-l,oo	+ 0	0
(6)	+1	0	-2,72	-1,72	0	-0	0	+ 7,398	I 7,393
(7)	0	0	0	0	0	0	0	+ 13,101	1 13,101
	+4,00	4-2,00	-0,64	4-5,36	4-4,00	-1,72	4-2,28	4-36,990	4-36,99
			Όχ	= 4-3,61		tab]	= 4-2,00	[ac]	= - 0,64
						У 2	= + 4,53	[be]	= - 1,72
			[as]	= 48,97					=4-10,00
						[bs]	=4-8,81
								[cs]	=+44,63

наиболее совершенная и изящная схема, предложенная Гауссом и заключающаяся в методе последовательной подстановки и выключки неизвестных, начиная с первого. к_1: и обратно. Из первого ур-ия

1_Н

[аЬ]. ₇ _ [[ас]., _ Ух [аа] ’ ² [аа] ’ ³ [аа]

(Ь)

Найденная Jc₁ подставляется в последующие ур-ия, и делается приведение подобных членов: _ [аЬ] [аЬ] -, _ [оЬр[ос], _ [abyoi,

[αα] ² [αα] ³ [αα]

+ bb] к₂ + [6с] k_z + V₂=О (с)

ИЛИ

[_[И]_мв«]“, ₊ [_м_М1йа]»,₊

⁺ [ ⁼ °· ^,с,)

Точно так же для 3-го ур-ия

(С")

Т. о. получается новая система из 2 ур-ий с 2 неизвестными. В них вводятся новые символические обозначения, благодаря чему ур-ия представляются в таком виде:

[bЬ 1] к₂ + [bс 1] к₃ + [v₂1]=0; (d)

[be 1] Тс₂ + [сс 1] k_z + [v_z 1]=0. (d")

Из первого ур-ия находится Jc₂

ко —

[bell

~1bb1

ко —

[Pal]

1ЬЫ]^}

(е)

а затем, после подстановки во второе, получается

[[eel]-

[bell ГссЦ [bbl]

]*₃ + [гм]-

ГРаП rbcin _ _Λ

[bbij J~^u

Или после введения ских обозначений

[сс 2] к₃

последующих символиче-

+ [^₃2]=0;

(f)

откуда

k_z

[Ра21

[CC2J

(g)

Все показанные действия проделываются и со столбцом контрольных сумм [as], [bs] и [cs], благодаря чему получается поверка каждой строчки вычислений. Далее идет обратная подстановка найденных значений коррелат, последовательно начиная с k_z, и т. о. получаются к₂ и к_г. Когда корреляты будут вычислены, то по ур-иям (25) отыскиваются поправки к измеренным углам и проводятся все контроля, как это показано в таблице коэф-тов условных ур-ий. С помощью найденных поправок подсчитываются окончательно значения уравненных углов или направлений, а затем вычис ляют длины сторон тр-ка данной Т., применяя теорему Лежандра, то есть уменьшая подсчитанные углы на */₃ сферического избытка. Вычисления по схеме Гаусса (смотрите пример) делаются с 4- или 5-значными таблицами логарифмов (еще лучше на арифмометре). Ход вычислений можно проследить, внимательно сопоставляя расположение цифр примера с предыдущими формулами (а), (b), (с), (d) и +). Необходимо отметить, что благодаря симметрии в расположении коэфициентов нормальных уравнений повторяющиеся коэф-ты левой половины этих уравнений не выписываются. Вычисления по схеме ведутся последовательно строка за строкой в каждом ур-ии, и после каждой выключки просматривается согласие сумм по контрольному столбцу [ss]: эти суммы должны сходиться в пределах точности вычислений. Необходимо весьма внимательно соблюдать знаки. Вычислительный труд по решению нормальных ур-ий чрезвычайно возрастает по мере увеличения числа неизвестных коррелат, или, другими словами, при большом числе условных ур-ий. Арифмометр сокращает работу и упрощает самую схему, но тем не менее в дальнейшем приведен пример решения нормальных ур-ий с помощью логарифмич. таблиц, т. к. этот способ доступен каждому (табл. 13). Объяснение к схеме Гаусса в порядке ее решения: (1), (2),(3)—коэф-ты нормальных уравнений и цифры контрольного столбца; (4)— логарифмы коэф-тов первого ур-ия; (5)—логарифм дроби ^[^j; (6)—логарифмы выражений

№ I5SI^; ит. д.; (7)—числа, найденные по этим логарифмам; (8)—коэф-ты первого преобразованного ур-ия (с) или (d) [контроль: + 3,00 - 1,40 + 2,73=+ 4,33]; (9)—лога-

рифм дроби (10)-

[ас]

[ас]. _v [ас]

[SS]

Гас].

-логарифмы выражений

¹ [аа] ’ " ,оа|> -"“ЧЩ’ UD—числа, найден-

ные по этим логарифмам; (12) — коэфициенты преобразованного уравнения (с") или (d") [контроль: - 1,40 + 36,89 + 10,57=+ 46,06]; (13)—логарифмы коэф-тов ур-ия (с); (14)—логарифм дроби ; (15)—логарифмы выраже-

^ГЬС1]- - ”^[Ьс11· —^Лч16)-чис-

ний [belli

[bЬ .]

[Ьэ +

ла, найденные по этим логарифмам; (17)—коэфициенты уравнения (f) [контроль* + 36,24 + + 11,84=+ 48,08]. Из этого уравнения получается непосредственно 7г₃= —^β ~~ 0,327,

что выполняется в порядке (18), (19) и (20). Далее отыскивается к₂ по ур-ию (е), для чего выписываются логарифмы (21) и (22), сум-

57.

Т. Э. m. XXIII.

	[аа]	[ob]		[ac]		V		[ss]	1 1
	+4,000	+2,00		- 0,64		+ 3,61		+ 8,97
	0,6021	0,3010		9,8062ft		0,5575		0,9528	(*)
		9,6989	(5)	9,2041ft	(9)	9,3554			i
(29)	9,6989	0,0000		9,5051ft		0,2564		0,6517	(6) !
(30)	0,0261^			9,0103		9,7616/г		0,1569ft	(10),
(31)	9,7250/г	+4,00		-1,72		+4,53		+ 8,81	(2) 1
		+1,00		-0,32		+ 1,80		+ 4,48	(7),
(32)	9 9,041ft	+3,00		- 1,40		+ 2,73		+ 4,33	(8)
(33)	9’ 5142н	0,4771		0,1461ft		0,4332		0,6365	(13)
(34)	8,7183			9,6690«	(14)	9,3591
		9,6690ft	(21)	9,8151		0,1052ft		0,3055д	(15)
(35) i 1	9,9551	9,5142ft	(22)	+ 36,99		+ 10,00		+44,63	(3)
		9,1832	(23)	+ 0,10		- 0,57		- 1,43	(H)
(36)	-0,530	9,9591	(24)	+ 36,89		+ 10,57		+46,06	(12)
(37)	+0,052			+ 0,65		- 1,27		- 2,02	(18)
(38)	+0,902	+ 0,152	(25)	+ 36,24		+ 11,84		+48,08	(17)
(39)	+ 0,121	+0,910	(26)	1,5532		1,0734		(18)
		+ 1,062	(27)			lgk3= 9,5142ft		(19)
		&!=— 0,424;		k2=— 1,032;		k3=—0,327"	(20)	I
				0	,0261,		(28)	1 1

ма их (23) и логарифм дроби ^(24). По ним находятся числа (25), (26) и (27), откуда к₂== —1,062, и выписывается логарифм (28). Затем отыскивается к₁₉ для чего выписываются из схемы логарифмы от (29) до (35) и по ним отыскиваются числа от (36) до (39). Отсюда к~ 0,424. Найденные значения коррелят к₁₉ к2 и к₃ вписываются в таблицу коэф-тов условных ур-ий (смотрите выше) и там же вычисляются неизвестные поправки к углам. Контроль:=im²; i_L=— 9,612 и i_a =

= + 9,612; средняя ошибка измеренного угла получилась ±1,79". Дальнейший контроль

Δ ABD

(3 + 4) 42°1039,83" —2,245" — 0,35" 42°1037,55"

2 63 52 31,82 -1,192 66 52 30,43

5 70 53 54,19 -1,032 70 53 53,23

180°+ е₂=180°01,21"

После этого вычисляются окончательные длины сторон тр-ков по 7- или 6-значным логарифмам; обычно длина сторон в м отыскивается лишь по мере действительной необходимости, оставляя остальные стороны выраженными в логарифмах. Окончательные вычисления длины сторон сети по логарифму данной стороны АВ=4,4313638.

Δ ABC Углы	Уравненные	Углы плоские“	lg sin углов	sin (1+2) ё sin 6	lg сторон
1+2	139°37 3,23"	139°37 2,79"	9,8115000	0,2924753	4,7238391.	BC
6	19 17 32,87	19 17 32,44	9,5190247	4,4313638= lg AB
3	21 5 25,20	21 5 24,77	9,5561033	0,0370816	4,4681454.	AC
				Sin 3
	180° 0 1,30"	180° 0 0,00"		lg —г sm 8
				sin 2
Δ ABD				ig -г — ‘ sm 5
2	66э5230,43"	66“5230,03"	9,9636227	9,9880885	4,4194523.	BD
5	70 58 53,23	70 56 52,81 42 10 37,14	9,9755342	4,4313638=lg AB
3 + 4	42 10 37,55		9,8269961	9,8514639 sin 3+1 ° Sin 5	4,2828277.	AD
	<м о о 00	о о о о о 00
Вычисление стороны CD делается дважды (контроль):
1	72°4432,80"	72°4432,34"	9,97999 14	0,1038003	4,1766280.	CD
6+7	37 40 39,22	37 40 38,76	9,7831941	4,2828277=lg AD	4,4763281.	CD
4	21 5 12,34	21 5 1,91	9,5560376	9,7527890
5 + доп.	140 31 42,98	140 31 42,55	9,8032486	4,7*38391=lg BC

* По теореме Лежандра—^х/з «·

вычислений достигается подстановкою поправок углов в условные ур-ия; они должен быть удовлетворены. Затем измеренные углы исправляются этими поправками, что дает новую поверку из сравнения вычисленной суммы углов и теоретической Д80°Н-е).

Δ АВС

(1+2) 139°37 5,06" —0,640" —1,192" 139°37 3,23"

6 19 17 32,40 +0,465 19 17 32,87

3 21 5 27,45 -2,245 21 5 25,20

180°-|-е₁=180^о 0 1,30"

При известном навыке в работе схему Гаусса можно заметно сократить и уменьшить число строк, применяя для всех промежуточных суммирований логарифмов вспомогательные листки бумаги. Помимо того рекомендуется весьма удобная и краткая схема Дулитля (Америка), которая приводится в специальных курсах по геодезии и математике.

20. Различные виды построений Т. В геодезич. практике наиболее часто встречаются определенные схемы построений Т., для уравнивания которых можно дать еле-

дующие указания, а) Цепь простых треугольников, проложенная от одной исходной стороны b или от одного измеренного базиса (фигура 29). Так как в каждом тр-ке измерены все три угла, то прежде всего подсчитывают невязки

-^-V-V тр-ков v_l9 v₂, v_z, ., прини-

Фигура 29. ^{мая или не} принимая во внимание сферич. избытки в зависимости от размеров сторон цепи. Далее работа сводится к приданию поправок к измеренным углам каждого тр-ка в размере

7з V этого тр-ка (30)

(смотрите выше об уравнении тр-ка в примерах составления нормальных ур-ий). Знак поправки дается обратный знаку невязки ν. Контролем вычислений служит вторичное суммирование углов в каждом ^ тр-ке цепи: везде должно получиться 180° ε (или 180°). На этом и кончается уравнивание такой цепи, после чего вычисляются длины всех сторон тр-ков. б) Цепь между двумя базисами. Выше было разобрано и подсчитано, насколько падает точность определения стороны Т. по мере увеличения числа треугольников [ф-ла (!>]. Наилучшим средством к повышению точности определения как последней стороны, так и протяжения всей цепи тр-ков является измерение второго базиса в конце цепи, •с длиною которого сравнивается вычисленная сторона (фигура 30). В этом случае уравнивание цепи несколько усложняется, т. к. к первому геометрии. условию — сумма измеренных углов должен быть равна сумме теоретической [(180° + ε) или 180°]—прибавляется новое: цепь должен быть уравнена так, чтобы, вычисляя ее от стороны b_имэжнэ было бы в точности получить длину стороны b2 (или обратно). Геометрически это условие выражается следующим соотношением: sin дсх singes sin .sinx_w — 1 siny₁siny₂siny₃.siny_n b₂ ~ *

Фигура 3 0.

(31)

к-рое называется условием базисов цепи тр-ков. Если это выражение логарифмировать и преобразовать, то получится, что сумма логарифмов множителей в числителе без суммы логарифмов множителей в знаменателе равна 0. В действительности же однако вследствие ошибок измерений в итоге логарифмирования этой формулы получится не нуль, а некоторая величина ν, выраженная в единицах последних знаков логарифма, а именно:

lg sin x_L + lg sin x₂ + lg sin x_s +. — lg sin y_x — - lg sin y₂ - lg sin 2/3-. -(lg b₂ - lg b_x)=v. (31)

Задача уравнивания сводится к тому, чтобы найти такие поправки к измеренным углам х и ?/, введением которых выражение (ЗГ) обратилось бы в нуль. Логарифмы длин опорных сторон не получают поправок, т. к. эти данные считаются хорошо известными и не подлежащими изменению. Рассуждая далее подобно тому, как это указывалось при составлении ур-ия полюса, и вводя символы а и β, означающие перемены логарифмов синусов углов х и у на I ск., получим условное ур-ие базисов в следующем виде:

а (х_±) + а (ж₂) + а (Х₃) +. - β (2/ι) - β (j/₂) -

-Р(Уз) ~. + v =0, (32)

где (ж) и у)—поправки связующих углов в тр-ках цепи (фигура 30), ν—разность между логарифмами числителя и знаменателя ф-лы (31), или другими словами, разность между логарифмами вычисленной второй стороны иизмеренной в натуре. Т. о. для уравнивания цепи из п тр-ков между двумя известными сторонами или базисами должен быть составлены условные уравнения фигур вида

(®ι) + (г/ι) + («,) + («!>=0, (33)

числом пик ним добавлено одно условное ур-ие базисов (32). Далее, все эти ур-ия должен быть решены совместно при условии минимума суммы квадратов искомых поправок. Однако в виду простоты ур-ий (33), с одной стороны, и их большого числа, с другой,—для упрощения вычислительной работы уравнивание цепи производят раздельно, а именно: сначала решают все условные ур-ия фигур, то есть невязки тр-ков поровну распределяют на все три угла в каждом из них; затем решают отдельно условное ур-ие базисов, вводя новые условия

*--[(®) + (у)]“,

Σ [(ж)² + (2/)² + (Ж) + (?/)²]=min,

где х, у и z—поправки к углам. После соответствующих преобразований получаются следующие ф-лы для последовательного вычисления поправок к углам тр-ков цепи:

(*)-- ик^ + РУ’ (у)=+ кг_а(^а + ²РУ ·

(34)

где ν—постоянный член условного ур-ия базисов (32); α= j [α² + β² + (а +,β)²], cl и β—перемены логарифмов синусов связующих углов х и у при изменении их на 1 ск. Поверкою вычисления служит равенство

ΣΚ*)· +(у)²+ (*)·]-£·. (35)

При уравнивании звеньев триангуляционных рядов I класса между двумя базисами вводят еще условие азимутов, которые определяются астрономически на обоих базисах или исходных сторонах. в) Центральная система. Под этим названием разумеется построение сети, показанное на фигуре 31, к-рое в настоящее время весьма широко применяется в городских геодезии. работах. В этом случае точно так же, как и в цепи, сначала подсчитывают и исправляют суммы углов в тр-ках; затем отнимают от углов по ¹/_? сферич. избытка (теорема“ Лежандра); далее вычисляют по ф-лам синусов от одной какой- ^Фиг* ³¹ *

либо связующей стороны а все остальные и снова приходят к стороне а, получая второе значение ее а_х. Таким путем составляется базисное условнее ур-ие обычного вида (32), в к-ром Σ* (х) - Ζβ (у) + ν_χ=0, ( 36)

где v_x=lg а_х — lg а, (х) и (у)—поправки связующих углов, а и β—перемены логарифмов

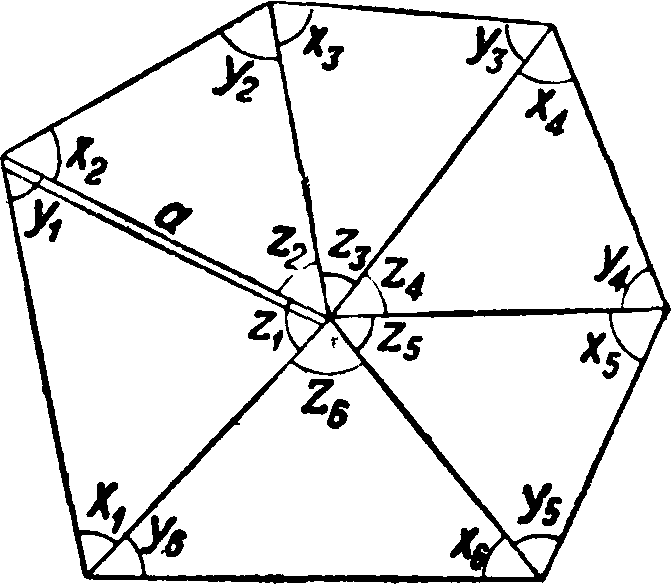
* Чтобы не расстроить сумм углов в тр-ках, уже исправленных. синусов этих углов при изменении их на 1". Далее вводятся новые условия:

(Z)=- [(ж) + (у)],

~ [СО + 0г₂) + (2₃) +. + (*_и)1=Σβ- 360°=е₂, Σ {(ж)² + (2/)² + [(ж) + (у)]² } =

первое для того, чтобы не расстроить уже исправленных сумм тр-ков; второе,—чтобы удовлетворить условие горизонта, которое требует, чтобы сумма сферич. углов С, измеренных вокруг какой-либо точки, равнялась бы 360°; третье—общее условие уравните тьных вычислений. Посте соответствующих прообразов лнид получаются следующие ф-лы дтя вычисления поправок к углам:

где

(χ)=[Α{2α + β) +В], (У)=- Д (α+2β) ~В], (*)-||/1 (β-α)-Β],

_л - 2ηνι + ν₂Σ(β - а).

^— Г Г 12 »

2ηΣσ — - |^Σ (jS-α)J

_Ώ 3υ₂^Σσ - ^υι^Σ (β-°). “ - ff W ’

2ηΣσ — - |^Σ (β — α)J

<Τ=1[α2+^_{(α + /?)2}];

= ig «i - ig о; Vz=£C- 360°;

(37)

η—число тр-ков в системе. Для контроля вычислений служит ф-ла:

Σ [(Ж)² + (3/)² + (Я)²]=- Αν, + Βν₂.

г) Точно так же можно раздельно уравнять и геодезический четырехугольник (фигура 24), для которого сначала составляют условное ур-ие фигур:

(1) + (2) + (3) 4- (4) 4- (5) 4- (6) + (1) + (8) + v i — 0, а) + (2) - (5) - (6) +v₂=0,

+ (3) + (4) -(7)-(8) + о₃=0.

Решение их приводит к следующим значениям коррелат:

*ι=-

»2.

Поправки равны

(1)=(2)=hi + fc₂=- д

(3)=(4)=lc₁ + fc₃=- i - J v₃,

(5)=(6)=1;_л(7)=(8)=hi

^2--8 4

^=-5%+N₃.

(38)

По этим простым равенствам и подсчитываются поправки к углам, после введения которых условия фигур будут удовлетворены. Далее сос^тав-ляется условное ур-ие полюса, причем за таковой принимают точку пересечения диагоналей, то есть пишут, что

sini-fsin3 f sin5-fsin7 ^ sin2 + sin i-fsino + sins “ *

После соответствующих преобразований ур-ие полюса приводится к общему виду: •Σα(χ)-Σ4υ) + ν ₄=0,

где (х)—поправки к нечетным углам, (у)—поправки к четным углам. К нему вводятся те же условия, как и в предыдущих случаях, а затем получаются следующие равенства для вычисления поправок к углам:

(Да)=+ t 4- 1ι, (у )=4- t — t_l9

(Ж₂)=ί + ^2> (Vi)=— t — t₂, I /gg

0*0=+ t + /₃; (t/д)=+ t — t_z, J

(ж₄)=— t 4- tf₄; (2/4)=-- t — /₄, J

где

A (a_x + pj); t_z=A (a₃ + β₃); t₂= A (a₂ + βζ) U=A (a₄ -f /?₄);

*=a [(“1 - A) - («. - A> + K- A) - («4- A)];

Λ ₌_________ -”4_________.

^Ά 1 Г -12

₄[(ai-/3i)-(«2-/3J4-(a₃-^)- (a₄-/5jj +Σ(α + 0)2

д) Весьма часто требуется уравнять у е д и-ненную точку Р (фигура 32), на к-рую измерены углы 1, 2 и 3 Ь

с трех точек А, В и С тр-ка Т., уже уравненного и вычисленного (прямая засечка). Этот случай весьма выгоден и в практике Т. широко применяется. Уравнивание сводится к вычислению вспомогательной величины по формуле Фигура 32.

^ ⁼ (0+<5)² + (0-у)2+(а-<5)2 ’ ^

где перемены логарифмов синусов для углов“ 5, А — 1 + 2 2 vl 1 + 3 обозначены последовательно буквами α, β, γ и <5;

V=lg b + Ig sin (3 - I ε₂) + lg sin (^-2 +

+ 2 - I ε₂) - lg C - lg sin (2 - | ε₂) - Ig sin (2 +

+ ³ - t ®i)«

причем —сферич. избыток Δ ЛСР, ε₂—то же для АЛВР. Затем находятся поправки к углам

(1)=-(£4-*)7с, л

02)- + (/?-у) Λ, (41)

(3)-+(а)

При малых сторонах введение сферического избытка отпадает, и уравнивание. производят даже графически.

21. Упрощенный способ уравнивания. Только что описанные методы уравнивания типичных случаев построений “т.— цепи между двумя сторонами, центральной системы и геодезич. четырехугольника,—хотя уже и носят нек-рые признаки упрощения, но все же отыскание вторичных поправок к углам из ур-ия полюса или базисного представляет еще довольно сложную работу. Происходит это потому, -что вновь вводится условие минимума суммы квадратов вторичных поправок. *На этом основании в практике геодезии издавна известен и сейчас широко применяется еще более упрощенный способ уравнивания трех перечисленных типичных построений Т. Этот способ заключается в том, что, как и при строгом уравнршании, сначала исправляются гуммы углов тр-ков, а затем составляется уже описанным порядком полюсное или базисное условие общего вида (36). Однако это выражение еще не дает возможности вычислить вторичные поправки к углам, т. к. ур-ие одно, а неизвестных много, и получается неопределенное решение. Кроме того если бы и вычислить по-

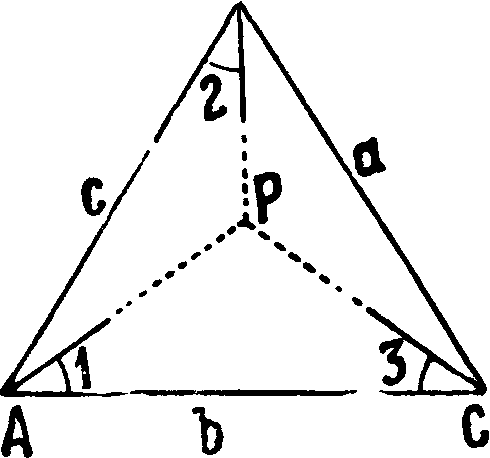
правки и ввести их в углы, то расстроилось бы первое условие равенства измеренных углов в тр-ке (теоретич. сумме 180° + ε). Вследствие этого, считая, что все углы измеряются с одинаковою точностью, полагают, во-первых, что и поправки для них можно взять равными между собою; во-вторых, чтобы введением новых поправок в углы не изменить уже исправленные суммы углов в тр-ках, берут эти поправки для одного и того же тр-ка с разными знаками, то есть полагают, что

(®i)=-(y)=(я₂)=- (Vi)=(ж₃)=(Уз) =. И т. д. Тогда ур-ие (36) примет следующий вид:

Σ« (х) + Δβ (У) + V=0.

Но т. к.

(х)=- (.У),

то можно написать, что

(ж) (ia + Ζβ)=- У

или окончательно

(х)=— (у)=— _{I(a + i8)} ·

Т. о. работа по отысканию вторичных по-

/ур-ру. правок сводится к про-

, /zSk ^стьш арифметич. дейст-

У V Л^я ^ виям. Пример. Цепь из 3 тр-ков (фигура 33) опи-_{фиг 33} рается на две известные из предыдущих измерений стороны Ь_г и b ₂, причем

lg b_г=3,355857; lg b₂=4,011780.

Т. к. длина сторон невелика, то сферич. избытки в расчет не принимаются. Для уравнивания цепи прежде всего удовлетворяются условия фигур введением в углы поправок, равных j ε для каждого тр-ка. Затем с исправленными углами составляется базисное условие, причем попутно с подысканием логарифмов синусов углов выписываются и их изменения a и β на 1"

1-й тр-к 2-й тр-к

Углы измеренные *!=* 65°5855,4" УА=41 03>,1 Zj=70 0 5 ,0	Углы 1 3 ϋι исправленные 65°58{3,9# 44 0 36,6 70 0 49,5	Углы измеренные Х2=98°5212,9 У2=35 16 52,4 z2=45 50 48,7	Углы + 4»2 исправленные " 98>5214,9" 35 16 54,4 45 50 50,7
180° 0 4,5"	ο о о 00	180 5954,0	00 о о о
ϋ1 = +4,5"		υ2=-	-6,0"
	3-й τρ-κ - *-гз
	Х3=86° 6ЗО.Г	85° 628,6"
	Уз= 29 41 51,1	29 41 49,6
	23= 64 11 43,3	64 11 41,8
	180э 04,5"	о о о о 00
	Г3="Ь 1,5"
Исправл.	lg sin	Исправл.	lg sin
углы	угюв а	углы	углов β
Я1==65°5833,9"	9,930650+0,9	уА =443 036,6"	9,84 85 4-2,1
х2=98 Ы 14,9	9,994774-0,4	у ,=35 16 54,4	9,761626+2,9
Χ3=8ϊ 6 28,6	9,9989 i7+0,2	у3= 29 41 49,6	9,694969+3,7
lg ЬА.	3,355857	lg ь*.	4,011780
Σι*	= 3,310278	ς2-	=3,310226

Σι - Σ₂=ν=+ 52;

Σ«=+ 0,7; £β=+ 8,7;

(X)=- (У)=0=- 5,5".

Контроль

Оконча		Оконча
тельно ис	in	тельно ис	lg sin
правленные углы	углов	правленные углы	углов
Χι =65 5828,5"	9,960644	Ух=44° 042,0"	9,841862
х^=98 52 9,5	9,994776	1/2=35 16 59,8	9,761642
Х3=86 6 23,2	9,998996	у3=29 41 55,0	9,694989
lg -.	3,355857	ig ь2,	4,011780
V "1	= 3,310273	— ς2=ο	Σ2=3,310273

Далее с исправленными углами вычисляются все сто-

	роны цепи
		1-й тр-к
XA=65c5828,5" Ух= 44 0 12,0 Ζχ= 70 0 49,5	9,960644 9,841862 9,973024	0,118782 3,355857. bх 0,131162	3,474639. 3,487019	b
о о о 00		2-й тр-к
Х2= 98с52 9,5" У&= 35 16 59,8 ζ2= 45 50 50,7	9,994776 9,7f+S42 9,855814	0,233134 3,474639. b 0,094172	3,707773. 3,568811	b"
о о о 00		3-й тр-к
Х3= 86° 623,2" Уз= 29 41 55,0 ζ3= 64 11 41,8	9,998996 9,694989 9,954378	0,301007 3,707773. b" 0,259389	4,011780. 3,967162	b2
о о о 00
Приме	ч а н и	е. Т. I кл., прелагаемые в

виде цепей простых тр-ков на большом протяжении, образуют сомкнутые фигуры, называемые полигонами. Вследствие этого здесь возникает необходимость вторичного переуравнива-ния цепей, чтобы в местах стыков их не было бы разногласий не только в длинах сторон тр-ков, но и в азимутах и координатах общих точек. Такое уравнивание носит название п о-лигонального и представляет довольно сложную задачу. Для ее разрешения разработан и хорошо описан В. В. Витковским т. н. британский способ, применявшийся англичанами в Индии.

22. Особые случаи уравнивания сетей. Точность измерений. Различные углы на базисных сетях для достижения большей точности в выходной стороне иногда измеряют различным числом приемов, а именно для более острых углов берут и большее число приемов. Вследствие этого результаты измерений получают различные веса, которые приходится принимать во внимание при уравнивании. Для этого случая Бесселем разработана общая теория, по которой углы сначала уравниваются на станциях, вычисляются для них весовые коэф-ты, после· чего и общее уравнивание производится с весами. Вопрос о правильном и целесообразном распределении количества приемов по станциям в зависимости от величины углов и их значения при вычислении выходной стороны также теоретически разработан. При необходимости уравнивания весьма сложных и больших сетей по способу наименьших квадратов перед вычислителен встает весьма сложная и неблагодарная работа по решению большого числа нормальных ур-ий. Поэтому в таких случаях стремятся сеть разделить на группы и уравнивать их последовательно. Этот прием однако приводит к большим искажениям углов сети в последних группах уравнивания. Для таких случаев рекомендуется способ Вольца, который дает возможность подыскания приближенных значений коррелат по особым таблицам. Особый способ уравнивания сетей по группам, который разработан Хаттом, значительно облегчает вычисления.

23. Подсчет точности измерений на Т. По окончании уравнивания сети обыкновенно вычисляется средняя ошибка угла [см. ф-лы (18) и (29)] или вычисляется средняя ошибка «единицы веса», о чем см. в специальных курсах о способе наименьших квадратов. В настоящее время входит в практику способ уравнивания сложных сетей в прямоугольных координатах. Помимо того в практике геодезии при уравнивании базисных сетей и цепей между базисами вычисляется относительная о ш и б)к а выходной или второй контрольной сторону (базиса) цепи. Для этого пользуются величиною постоянного члена v условного уравнения базиса, к-рый является диференциалом логарифма контрольной или выходной стороны. Следовательно

V_b=Δ lg b_г. (42)

Из диференциального исчисления известно, что

Alg b_г=^М или ^ =

где М—модуль Неперовых логарифмов и равен 0,434. Т. о. относительная ошибка вычисленной конечной стороны цепи b₂ равна

^__Ξ_. (43)

ь₂ 0,131 ^ν ’

В предыдущем примере v=52 единицам 6-го знака логарифмов.

Отсюда

ΔЬ₂ _ 52 _ 1

ТГ ~ "оДзТПов “ 5ί ооо“

24. Вычисление диагоналей в цепи или сети треугольников. Весьма часто в уравненной уже цепи тр-ков требуется вычислить длины диагоналей, а затем и все расстояние между конечными точками Р_х Р₂ (фигура 34). В этом случае вычисления ведут последо-

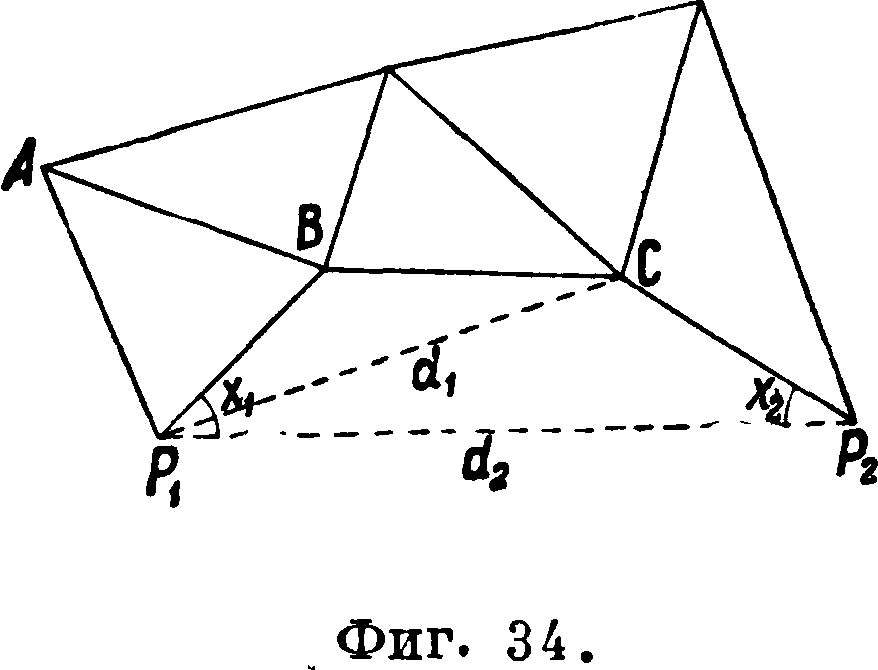
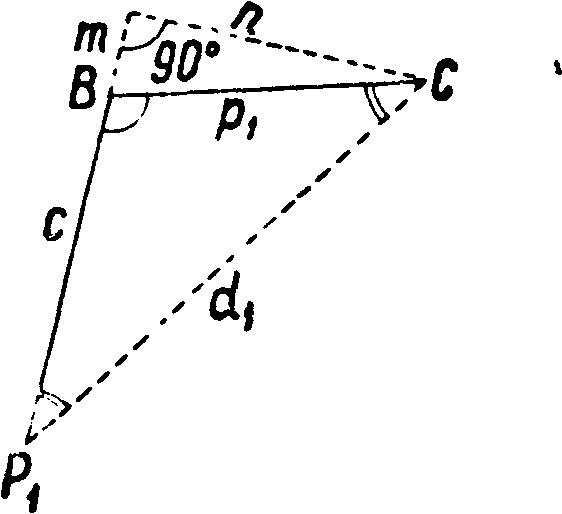
Фигура 35.

вательно от вершины к вершине, причем здесь всегда встречается случай вычисления тр-ка по двум сторонам и углу между ними, наир.: в Δ Р_ХВС известны, стороны Р_ХВ и ВС и угол Р_ХВС; дальше в ДР_гСР₂ вычислены стороны Р_ХС и СР₂ и угол Р_ХСР₂. В данном случае при вычислении используется прием, рекомендуемый в тригонометрии, а именно введение вспомогательных величин тип (фигура 35):

т=Р_х cos (180° — В); п=Р_х sin (180° — В),

tgP_x =

*х-

COS Р_:

; C=180*-(B+Pi).

(44)

Далее таким же порядком вычисляется диагональ d₂ и углы х_х и х₂ (фигура 34).

25. Вычисление координат пунктов сети. Пункты уравненных Т. служат опорными точками для последующих геодезич. работ или съемок, поэтому для них вычисляются координаты в какой-либо системе, а именно: для пунктов рядов I кл. и основных II кл. вычисляются географии, координаты (широта и долгота), для сетей следующих порядков или прямоугольные сфероидические (Гаусс-Крюгера) или тоже географические в зависимости от назначения сети. Более мелкие рабочие Т. вычисляются на шаре и даже на плоскости в прямоугольных координатах. а) Географические координаты. Вычисление географии, координат известно в геодезии под названием решения прямой и обратной геодезических задач (смотрите).

б) Прямоугольные сферические координаты Зольднера. Для пунктов сетей, служащих опорными для съемок, в настоящее время вычисляются прямоугольные сфероидич. координаты Гаусс-Крюгера. Сущность этого метода определения расположения точек на поверхности сфероида легче уясняется, если предварительно ознакомиться с более простою системою координат Зольднера — тоже прямоуголь-ных, но вычисленных для^а поверхности шара. Радиусом такой сферы берут средний радиус для широты точки О, служащей началом координат избранной системы (фигура 36) и лежащей на осевом меридиане NS. Координатами точки Р служат дуги больших кругов х по меридиану и у под углом к нему в 90°. Через точку Р проведена дуга малого круга параллельно меридиану NS и от нее дан угол а для стороны Т. S; этот угол в отличие от азимута называется дирекционным. Требуется вычислить координаты х_х и у_х точки Р, а также обратный дирекционный угол а_г. Для этого случая Зольднером дана следующая система ф-л:

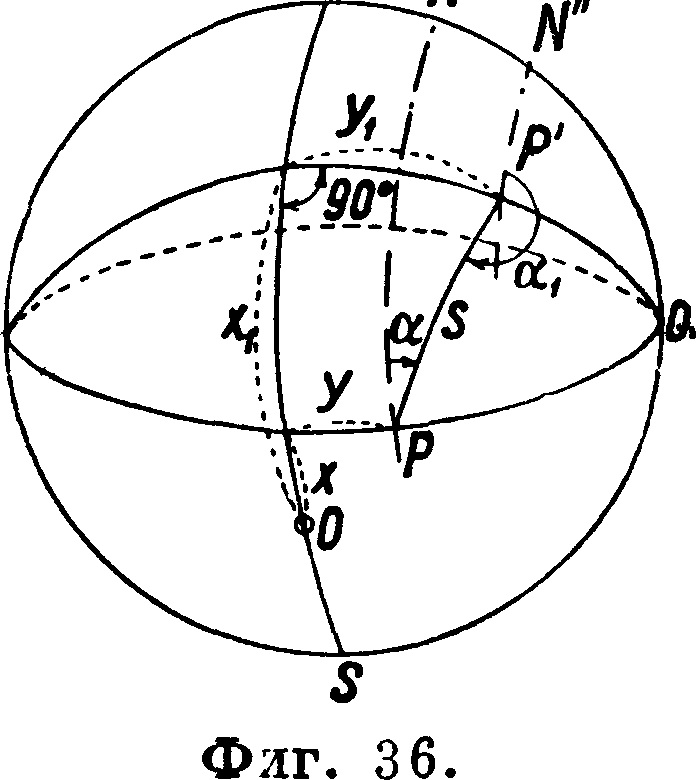
Vi=У + v-

т²у m²v ~2R² "" 6#*’

,. “У i

Χ_χ—×U t~rI —

uv²

2R² 6R²’

(45)

α_χ=а + 180° - иу -

2R2

uv,

причем

v=s sin α,

и=s cos α,

_ 1 ^ ^— siru" *

R—средний радиус кривизны для широты начала координат.

Обратная задача решается по следующим ф-лам: даны ж, у и х_и у_х, а также а_х, найти s и а. В первом приближении

u^Xi-x; tgα= -_и-

Затем с этими данными вычисляются и²у, v²v

у=Vi - У

2R 6 #2’

г/?/? UV 2

U=Х_х —×— -2Д2 ” ~QR2 ’

S=-

та cosa

(46)

α=α_χ + 180° + иу + ^2^uv-

В ф-лах (45) и (46) обращается внимание на члены v и и, которые являются обычными приращениями координат, вычисленными точно так же, как и на плоскости. Следующие члены являются поправочными к первым, потому что вычисления ведутся на поверхности шара. Первые поправочные члены всегда вычисляются, вторые же—только тогда, когда стороны

Т. велики, и эти члены оказываются значащими чи; в противном случае они опускаются. Коэф-ты jh ^{меняются}

в зависимости- от широты, поэтому для них даются готовые таблицы. Прежде чем вычислять координаты Зольднера для пунктов какой-либо сети, необходимо один из них, география, координаты которого известны, перенести на проекцию Зольднера, то есть вычислить его ординату ж и абсциссу у от оси проекции, для чего служит следующая система ф-л. Дано: для начала координат широта 9?₀, долгота L₀; для искомой точки—геодезии, или астрономии, пункта широта φ и долгота L; требуется вычислить х, у, а также дирекционный угол а, если дан астрономии. азимут а.

λ=L — L₀ (переводится в ск.),

<Рл -= φ ΊΓ № sin φ COS φ,

Δρ

где

ν²=Υ 1 4- e² cos² φ

_χ __ <Ρι-Ψο Nm

(готовые таблицы)

по 5-значным логарифмам,

г/= cos φ_χ +

[2j! 3ρ2

cos ψι sin² <p_l9

контроль

У ⁼ Wi ^{C0S φ} ~ Wi бЬ ^{C0S Ψ Sin2 V}’

причем первые члены этих формул берутся по

7-значным таблицам, а вторые—поправочные по 4-значным Коэф-ты [l]_w, [2]_х берутся из таблиц Шарнгорста.

Сближение меридианов

δ=λ sin φ_χ - ~ Sin φ_χ COS² <p_lt

контроль

δ=λ sin φ + sin φ COS² φ.

Первые члены точно так же вычисляются по 7-значным, а поправочные по 4-значным таблицам логарифмов. Окончательное значение берется как среднее из двух; ж и у вычисляются до см. Дирекционный угол равен α= а — δ.

Получив ж,ра для одной из точек сети, вычисляют координаты для всех остальных по ф-лам (45). Иногда требуется решение обратной задачи: по прямоугольным сферич. координатам х и у какой-либо точки найти географии, координаты ее φ и Z/, причем начало координат системы Зольднера имеет широту φ₀ и долготу L₀.

<Pi-<Po+ [l]_m®.

(bhy)²

Ψ=<Ρι---2~₆-^²tg φ_ΐ9

2}ιυ_ у i

- _β Ш У _

COS<p 1

cos^j 3ρ2

sin⁴ φ_±,

контроль

_λ"_ϊ*ϊϋί + №) __t

COS<p V COS?) 6ρ²

В=L₀ + A,

δ=[2]_xytg φ_χ

(47)

контроль

<5=[2]i2/tg<p-

([2]ιί/)³

6ρ2*

tg φ (2 +tg³9?),

a=a + <5.

В предыдущих ф-лах первые члены вычисляются по 7-значным, а вторые по 4-значным таблицам логарифмов. в) Прямоугольные сфероидичес-кие координаты Гаусс-Крюгера. Из фигура 36 видно, что в системе координат Зольднера абсциссы х суть выпрямленные дуги меридиана, служащего осью проекции; ординаты у—дуги больших кругов, проведенных перпендикулярно к осевому меридиану и потому для всех точек, пересекающихся в полюсах Q и Q (фигура

36). При развертывании на плоскость и построении самих координат ординаты и абсциссы представляются в виде прямых, перпендикулярных между собою (фигура 37). Т. о. две точки А и В, расположенные друг от друга на расстоянии ж, в координатах Зольднера и на его проекции окажутся в точках а и b на расстоянии ж; фигура ABCD на шаре не будет подобна фигуре abed на проекции (фигура 38). Эти искажения тем более увеличиваются, чем дальше от осевого меридиана отходят пункты Т. Следовательно координаты Зольднера не дают ни конформных (подобие в бесконечно малых частях) ни эквивалентных (равновеликих) построений. Тем не менее эта система координат имела и имеет еще распространение, т. к. сравнительно проста в обработке и пользовании. Помимо того и самые искажения для расстояний от осевого меридиана до 70 км не ощутительны для малых Т., а именно:

г г - ^ху2

^{Х Х} “2K2’

что на 100 км от осевого меридиана составит ок. 1 : 7 000. Гаусс, как и в его известной конич. проекции, для сохранения конформности увеличил ординату у в соответствии с увеличением абсциссы ж на проекции. Это соотношение ординаты η на проекции к ординате у на шаре представляется следующей ф-лой:

ч-»(1 + пЭ· ⁽⁴⁸⁾

У		___с А
) $ X			¥Й*
	Фи	г. 38.	i tor

Благодаря такому построению система координат Гаусса, разработанная затем Крюгером, дает конформные изображения, то есть например фигура на шаре с 4 прямыми углами будет построена на проекции в виде квадрата или прямоугольника. Если же стороны будут малы (строго говоря, бесконечно малы), то они на проекции будут пропорциональны.

Система координат Гаусс-Крюгера—сферои-дическая и как более совершенная допускает увеличить ширину зоны влево и вправо от осевого меридиана до 3° и для съемок даже и до 6°. Пункт какой-либо сети сначала переносится по географии, координатам на проекцию, то есть для него вычисляются координаты Гаусс-Крюгера от начального меридиана, причем абсциссы здесь считаются от экватора. Затем от этого пункта и дирекционного угла какой-

либо стороны вычисляются координаты всей сети. Осевые меридианы совпадают со средними меридианами листов 1:1000 000 международной карты, а именно долготы от Гринича: 30°,33°, 36°, 39° и т. д. к востоку. Формулы и примеры на вычисления прямоугольныхсфероидических координат не приводятся, т. к. в специальных д ш тиго таблицах Красовского и Матусевича, без которых вычисления невозможны, приведены не только списки ф-л, но и подробные примеры вычислений.

26. Организация партий по работе на Т. На больших Т. I кл. и ведущих рядах II кл. обычно для каждого вида работ организуется специальная партия, а именно: по возможности за год вперед идет рекогносцировщик, к-рый по проекту работ окончательно устанавливает направление рядов и места знаков. Затем зимою производится заготовка лесного материала и вывозка его по ж.-д. путям или простым дорогам к местам построек сигналов. Весною начинается постройка знаков специальными строительными партиями. Вслед за ними уже идут наблюдатели, измеряющие углы на пунктах ряда, а также базисные партии, измеряющие базисы. Рекогносцировщик работает обыкновенно один в сопровождении 3—4 рабочих с подводами. Заготовки леса производятся порайонно, перевозка совершается под наблюдением старших рабочих. Строитель работает на знаке также один с 4 плотниками и рабочими по мере необходимости (4—12). Общее руководство постройками на определенном участке ряда возлагается на опытного инже-нера-геодезиста, ответственного как за качество построек, так и за «достижение взаимной видимости» между соответствующими по проекту соседними знаками. Наблюдатель из наиболее опытных инженеров-геодезистов работает с помощником (ведет записи и наводит по-верительную трубу) и техником для связи, к-рый устанавливает гелиотропы и фонари и следит за работою рабочих-гелиотропистов, разбросанных по окружающим знакам. Он же делает предварительные центрировки. Т.о. общий состав партии наблюдателей—три лица инже-нерно-технич. состава, 8—10 гелиотропистов (по 2 на знак) и 2 сторожа при наблюдателе. В строительной и наблюдательской партиях набирается груза строительных снарядов, палаток и инструментов 1—2 т₉ а поэтому транспорт играет весьма чауто решающую роль в успехе работ. На эту сторону снаряжения триангуляционных партий следует обращать серьезное внимание. В более мелких Т. рекогносцировка соединяется с постройками. Затем идут наблюдения. В случае переносных знаков организуются комплексные партии: обычно начальник партии ведет рекогносцировку; техники по его указанию закладывают центры, и под их наблюдением собираются переносные знаки. Далее идут наблюдатели попарно: один по знакам левой, другой по знакам правой стороны ряда; при каждом из них помощник для поверитель-ной трубы. Техник в тылу партии разбирает законченные наблюдением знаки и отправляет их вперед. Т. о. общий состав партии выливается в следующем виде: 7—8 лиц инженерно-технич. состава и рабочие в числе до 20 чел. Транспорт, по возможности автомашинный, имеет в данном случае первенствующее значение. Успех работы по измерению углов на больших Т. зависит от разных причин, а гл. обр. от погоды и состояния сигнализации. Собст венно на измерение углов на одном знаке Т. I кл. нужно не более 3 вечеров. В мелких Т эта работа выполняется в 1 вечер. Ветер, мгла, дождь весьма задерживают наблюдения; переезды на слабых лошадях и в плохих тележках отнимают часто больше времени, нежели самые наблюдения.

27. Определение высот тригонометрическим нивелированием. В мелких сетях для целей топографических съемок весьма выгодно определять разности высот пунктов из ‘тригонометрического нивелирования. Для этого измеряются вертикальные углы тем же самым инструментом, к-рый служит и для измерения горизонтальных углов,если только при нем есть вертикальный круг.

Обычно в этих инструментахпо вертикальному кругу отсчитываются не" углы возвышения или понижения, как в малых теодолитах или кипрегелях, а зенитное расстояние, то есть угол, составленный отвесной линией данной точки с направлением на избранный предмет (фигура 39). Нормальное положение круга обыкновенно влево от трубы, почему при круге «лево»

Z=Jl-M_z,

z

при круге «право»

Ζ=Μ₃-Π.

Отсюда место зенита зенитное расстояние л+п 2 *

Л-П

(49)

где Л—отсчет при круге «лево», П—отсчет при круге «право». Таким путем зенитные расстояния измеряются обыкновенно тремя приемами с перестановкою круга на 60°. Кроме того измеряется высота инструмента г от центра знака, на к-ром стоит этот инструмент, и высота над центром того знака, на к-рый наводится труба инструмента. Разность высот между центрами двух знаков как правило вычисляется из двух наблюдений—прямого и обратного—для исключения влияния рефракции. В сущности такое исключение возможно только при одновременных наблюдениях, или, как их называют, взаимных, с обоих соседних знаков, что на практике однако редко бывает. Следует избегать расстояний более 20 км не брать таких направлений, в которых луч зрения,проходит близко над землей (предел 6 м). Измерение вертикальных углов производйтся около полудня во время" самых беспокойных изображений, т. к. именно в эти часы перемены рефракции наименьшие и коэф. ее наиболее устойчив. Разности высот вычисляются по следующим ф-лам:

для односторонних наблюдений

h =sctg^ + s² - ^ - (l₂ - ii), (50)

для взаимных наблюдений

Здесь s—расстояние между пунктами, z_x и z₂— измеренные зенитные расстояния, к—коэф. ре-

фракции (около 0,16, R — радиус земли,

г_г и г2—высоты инструмента над центром соответствующего знака, 1_х и i₂—высоты знаков. Пример:

ст. А	ст. В
ίχ=15,00 Μ	i2=18,55 m
Ιχ=16,00 Μ	1.Δ=20,(5 M
Ζχ=90°116,3"	89r5033,3
90-24=0 11 6,3	+ 0 9 26,7
lg s. 4,08733	4,08736
Igtg (90-24). 7,61310	7,43893
lg [s tg(90-24)]. 1,70016	1,52629
Jgs2. 8,17172	8,17472
lg (tw) · · · 2’81796	2,81796
lg[s2 ^2R ] * ‘ * °’99268	0,99268
s tg (90-24)=- 50,18 M	+ 33,60
saO=+8·83	+ 9,83
-(12-ΐχ)=- 5,65	— (ii—1*2)+ 2,55
h=— 46,00 m	h = + 45,98 M
прямое	обратное

Обыкновенно разности высот определяют по цепи тр-ков, причем наблюдают по возможности все направления, чтобы иметь контроль. В необходимых случаях высоты центров Т. получают из геометрии, нивелирования, однако в горных районах такой метод работы не выполним, почему в этих случаях тригонометрии, нивелирование применяется как обязательное правило.

Лит.: Витковский В., Практич. геодезия, 2 изд., СПБ, 1911; Красовский Ф., Руководство по высшей геодезии, ч. 1, М., 1926; его ш е, Высшая геодезия, ч. 2, Л., 1932; Иордан В., Руководство по высшей геодезии, пер. с нем., М., 1881; Матусевич и Ющенко, Таблицы, формулы и краткое руководство для вычисления плоских прямоугольных координат Гаусс-Крюгера, М.—Щ, 1933; Iordan W-, Handb d. Vermesmngskunde, 7 Aufl., B. 3, Stg., 1933. О. Дитц.