Тригонометрия

Тригонометрия, отдел математики, основной задачей которого является вычисление элементов тр-ка по числовым данным. В зависимости от того, рассматривается ли тр-к на плоскости, на поверхности шара или на поверхности сфероида, применяются методы соответственно плоской (прямолинейной), сферической или сфероидич. Т. Связь между сторонами и углами тр-ка Т. устанавливает при помощи т. н. тригонометрии. ф-ий углов.

Радиальное измерение углов. Длина s дуги окружности, как известно, пропорциональна радиусу R окружности и (при данном R) величине а центрального угла, то есть

5=JcRa, (А)

где к—коэф. пропорциональности, значение которого находится в зависимости от того, какой единицей измеряется угол а. Если за единицу угловой меры взят 1°, то то есть к=^=0,0174533.

Чтобы формула (А) имела наиболее простой вид 5=Ra (А)

(то есть при к=1), необходимо принять за единицу угловой меры такой угол, центральная дуга которого s равна единице длины при R=1. Эта единица носит название радиана. Следовательно радиан—центральный угол, дуга которого 5=1 при R =* 1 или дуга которого имеет длину, равную радиусу. Если за единицу измерения длины принять·R,то формула (А) примет вид:

5=а, (А")

где 5—длина дуги, измеренная в радиусах, и а—величина центрального угла в радианах. Т. к. центральная дуга прямого угла равна то по формуле (А) радиальная мера прямого угла α= отсюда угод в 1 радиан содержит 90° : | == ^ 57° 17 45". Обратно: угол в Г содержит ^ : 90 ξξ —=0,0174533. радианов.

Прямой угол также носит название г р а д и а-н а; т. о. например 0,5 градианов соответствуют углу в 45°. Существует деление прямого угла на 100 частей; Vino часть прямого угла называется градом, последний в свою очередь делят на десятые, сотые,. части (смотрите Градус). Т. к. угол измеряется отношением дуги к радиусу, то его единица не зависит от выбора основных единиц, следовательно угол имеет нулевую размерность по отношению к основным "единицам массы, длины и времени: [а]=[т° Г t°.

ТригономсТ!и есиие функции—элементарные трансцендентные периодич. фун сции, то есть такие, которые при определенном наращении аргумента вновь получают прежнее значение:

(х + со)=(аз),

где со—значение периода. Смысл тригонометрии. ф-ий острого. угла выясняется язк[ фигура 1, где R=1, х— радиальная мера угла, причем угол отсчитывается от неподвижной стороны ОА обратно движению часовой стрелки (положительное направление). Всего различных три-

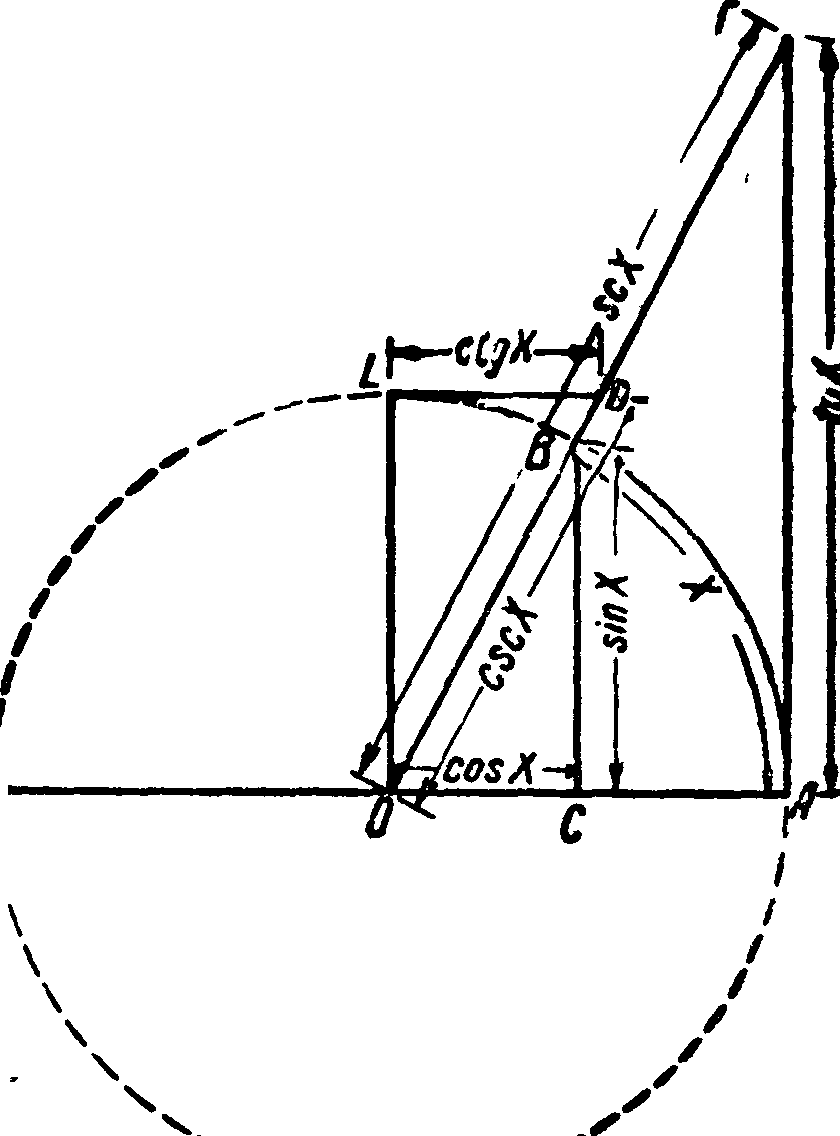
Фигура 1.

Всего различных гонометрических (прямых) ф-ий шесть:

вс

^sina?=~jp; LD

^: и

cosx =

ос

ctgx

SC×=

ОТ. R ⁵

tgx =

CSC x

AT,

R OD ‘jK ’

T. обр. тригонометрии, ф-ии, представляя собою величины отношений между линиями, являются отвлеченными чи. Приведенные ф-ии выражаются через аргумент х при помощи действия, к-рое нельзя произвести непосредственно над числовой величиной независимого переменного х. Это недоступное прямо трансцендентное действие бывает возможно заменить нек-рым конечным числом элементарных действий (сложений, умножений) путем разложения функций в бесконечные степенные ряды, так:

sina?=а? - ™ + ~

·· - Σ (- ¹>^п

_Х2П+1

(2η + 1)!⁹

w м

cos х=1 — ₂₁

4ί

= S (-1)"·

71=0

_х2 П

(2П)Г

Примером других процессов подобного рода является бесконечное произведение (как предел последовательности частичных произведений). Общеизвестным примером является разложение в бесконечное произведение функции sin π ж:

Sinлх=πχ (l - ζ) (l - g (l - g). =

= πχ Π (l-£)·

n=1

Если в степенном ряду для cos х заменить переменную х чисто мнимой величиной гх, то непосредственно получается ряд для chx. Это соотношение выразится трансцендентным ур-ием: cos ?ж=ch х.

Аналогично получается соотношение sin гх=г sh х.

Соответствующие формальные соотношения существуют для ф-ий tg х и thx, ctgx и ctha?,"a

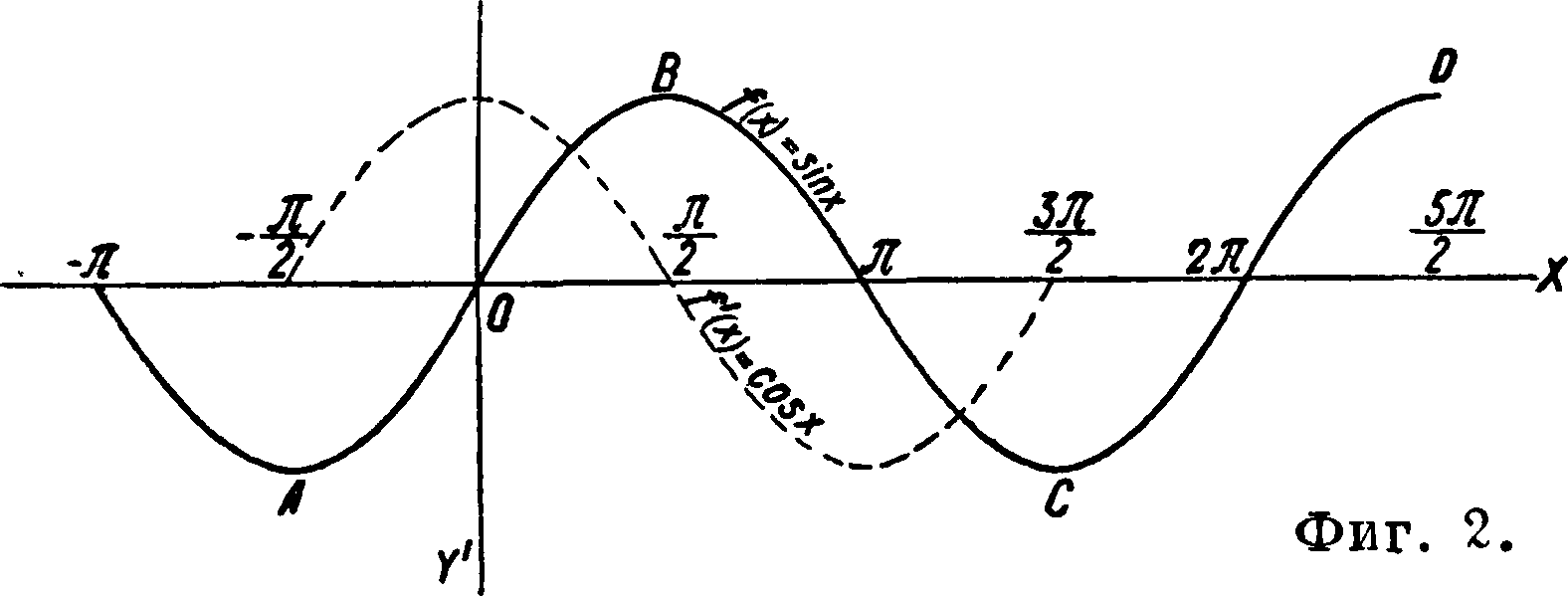
также для ф-ий, обратных тригонометрическим и гиперболическим (смотрите Гиперболические функции). Необходимо отметить, что sin х=cos х и ^ cos х=— зтж/Г.о.диференциалыюй кривой для синусоиды у — sin х является косинусоида Y y=cosx (фигура 2), а диференци-

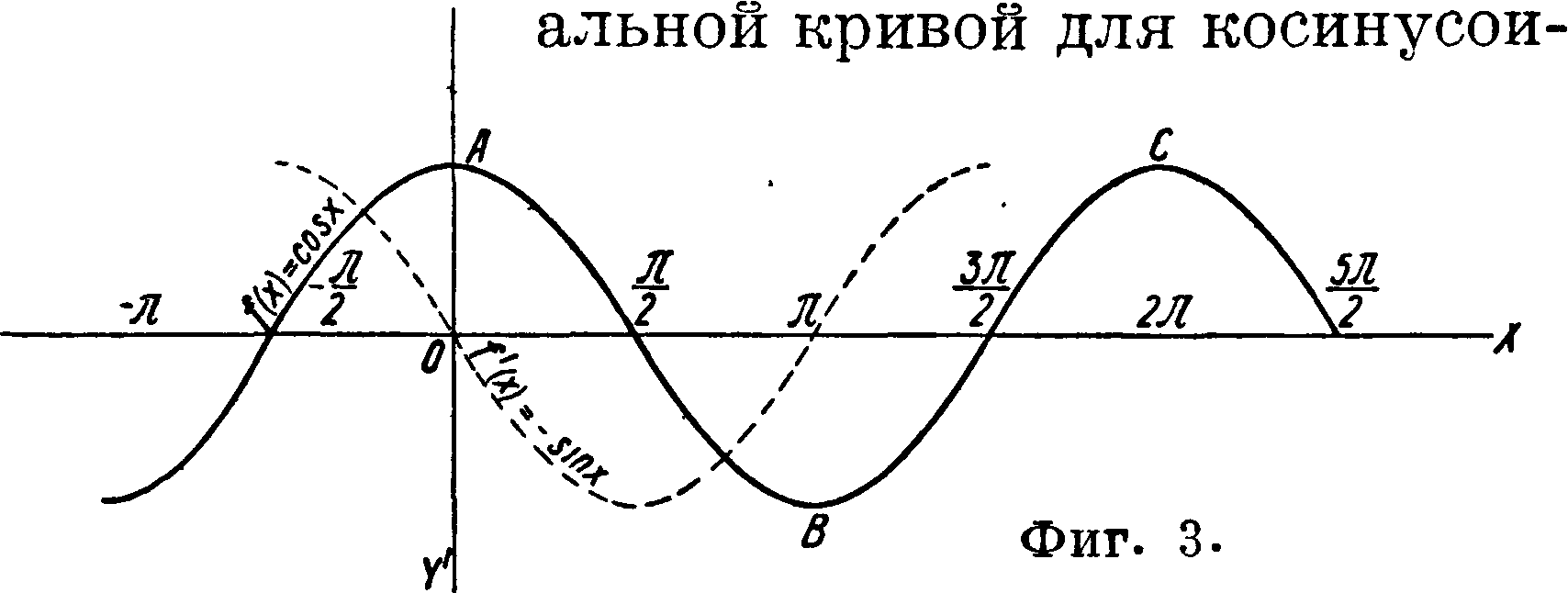
ды у=cos ж служит кривая у=— sina? (фигура 3). Периодичность тригонометрич. ф-ий выясняется при движении (например в положительном направлении) точки В (фигура 1): дуга АВ все

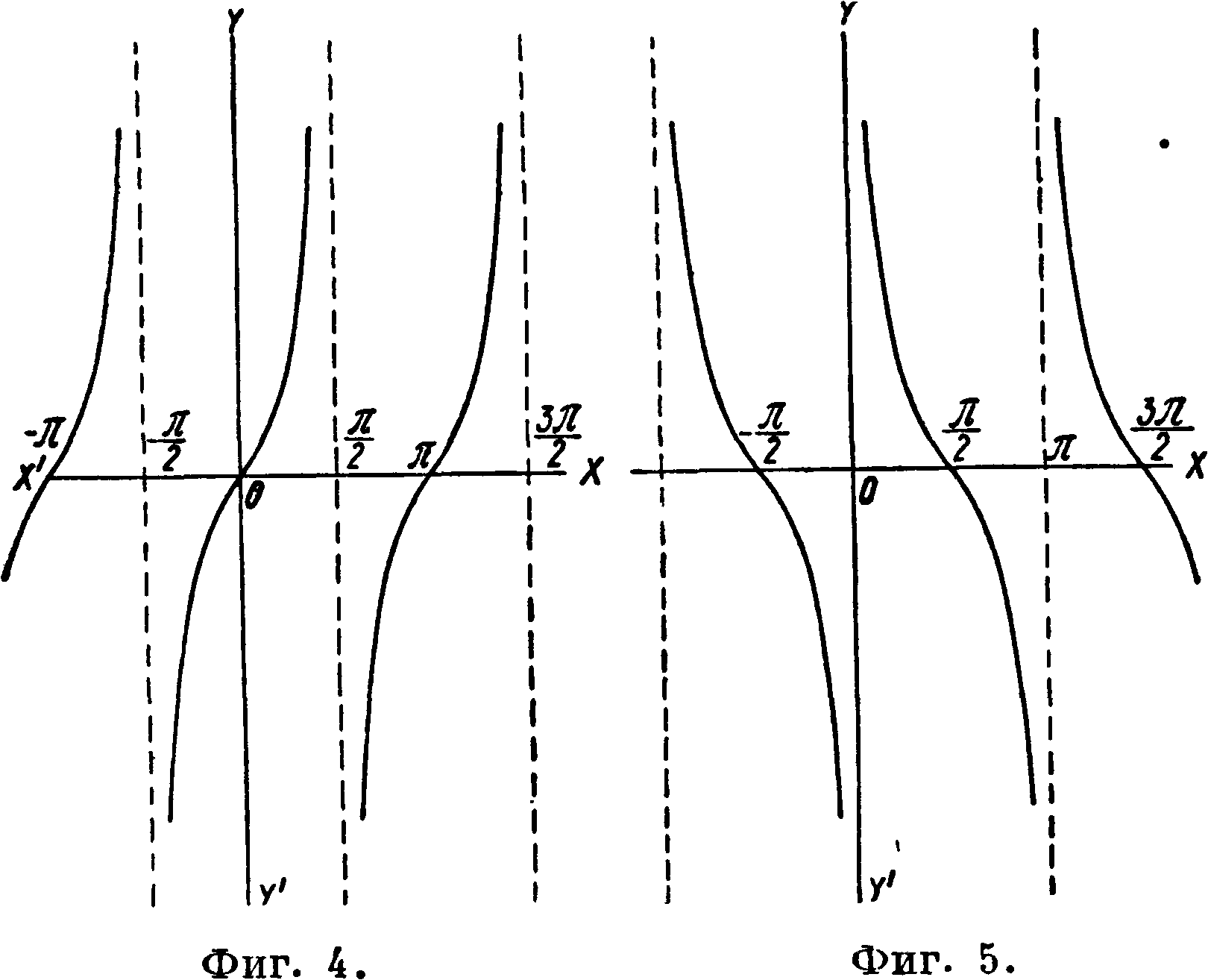
время растет, причем когда точка В передвинется на 1,2, 3,. окружности,то есть вернется в исходное положение, то все тригонометрич. ф-ии вернутся к прежним величинам. Полную характеристику тригонометрич. ф-ий (прямых круговых) дают их графики: синусоида (фигура 2),

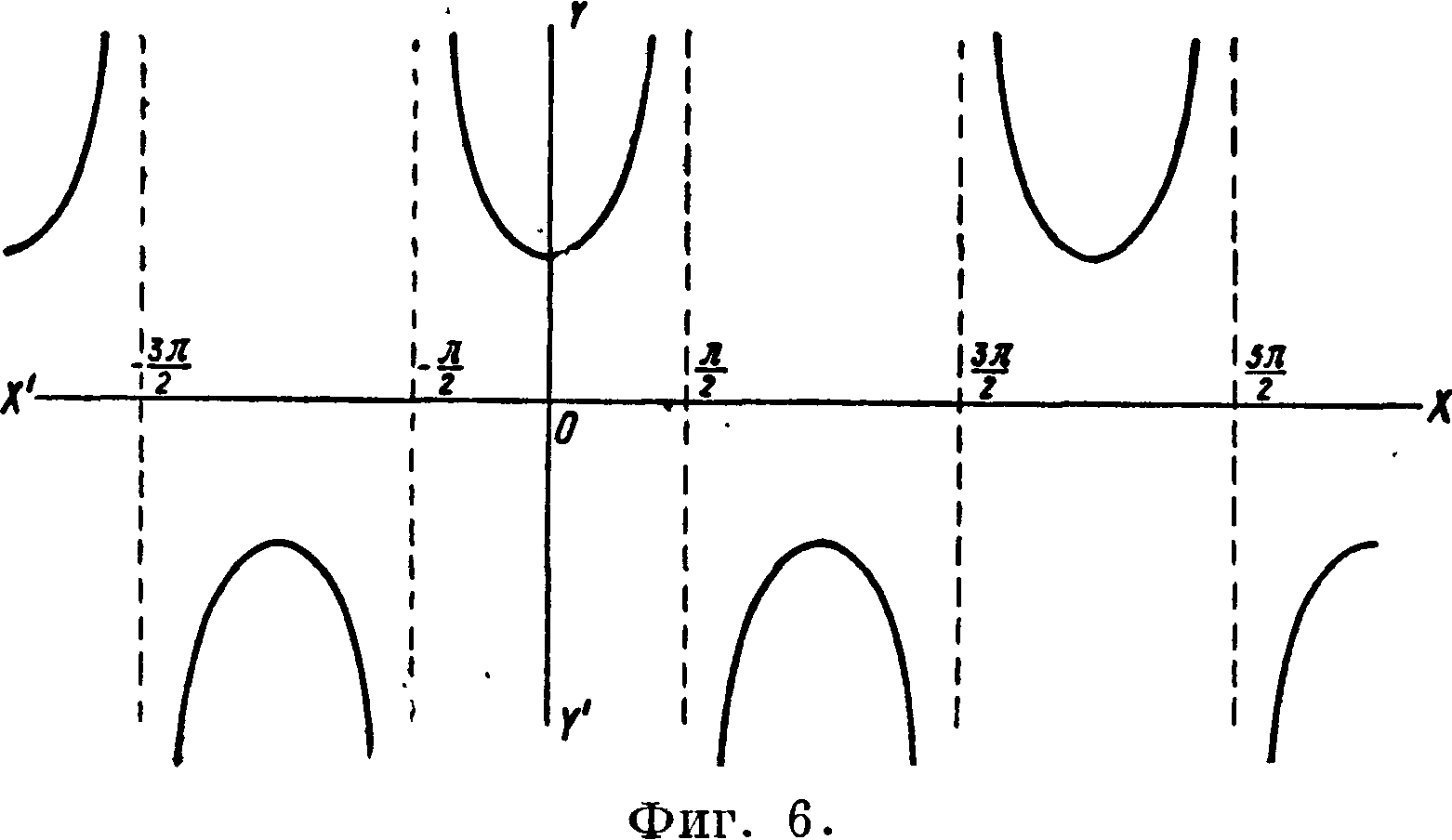
кривая cos ж (фигура 3), тангенсоида (фигура 4), кривые ctgx, sex, esc ж (фигура 5, 6, 7), где прямая XX—окружность, развернутая несколько раз. Из рассмотрения графиков видно, что период sin ж, cos ж, sc ж и esc ж равен 2 я, период

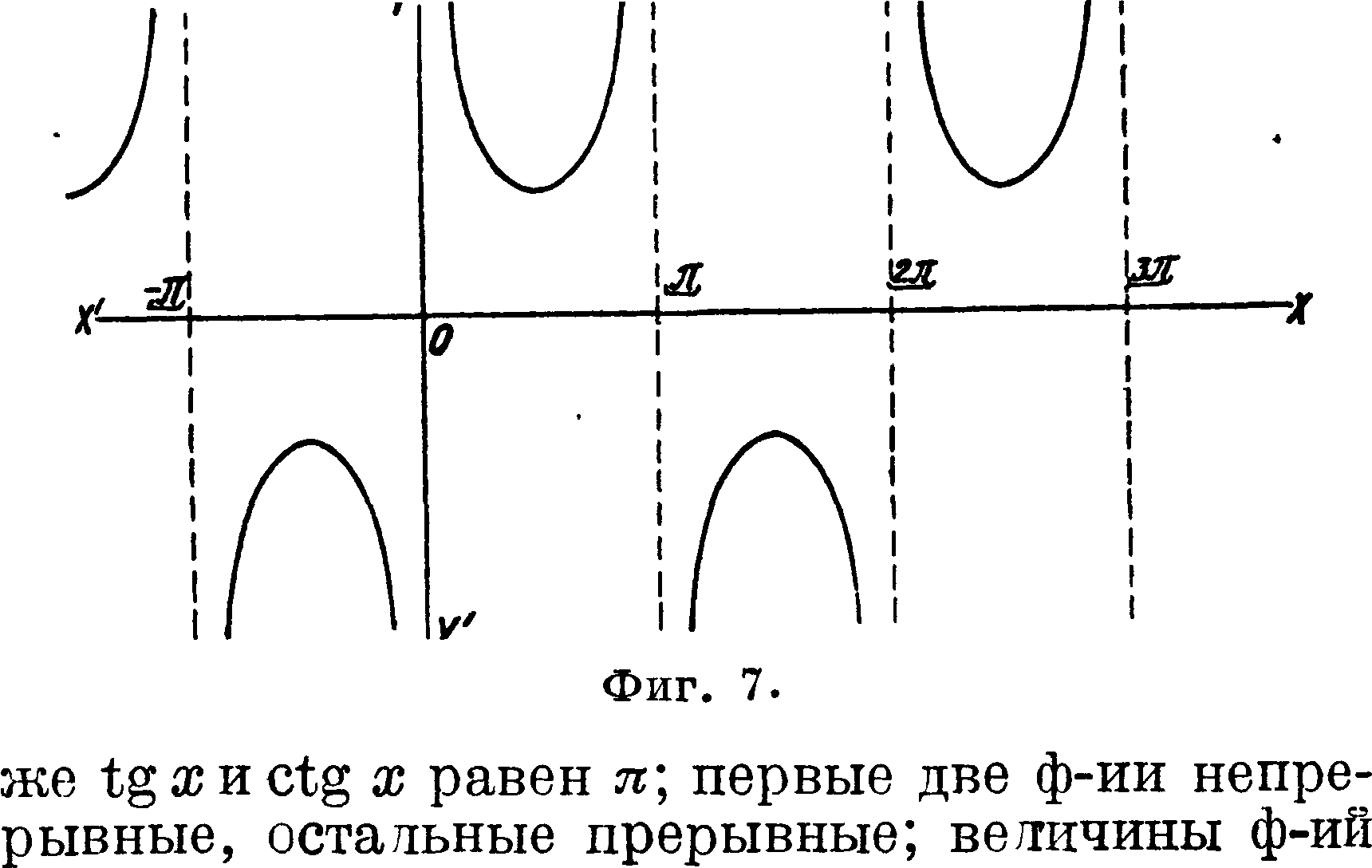
изменяются в следующих пределах:

— 1<зтж<1; — 1<созж<1;

— оо < tg ж < + — оо < ctg ж < + оо;

1 < sc ж < + оо; — оо < sc ж < — 1;

1 < esc ж < + оо; — оо < esc ж < — 1. Зависимость между тригонометрическими функциями ОДНОГО и того же угла:

sin² а + cos² α= 1; tg α=

¹ ° COS а¹

j I

Ctg α= ;

sc а · cos α= 1; esc a-sin α= 1;

из этих основных ф-л вытекают следующие: tg а · ctg α= 1; 1 + tg² α= sc² a;

1 + ctg² a=esc² a.

На основании этих ф-л легко получить величины тригонометрич. ф-ий для нек-рых частных случаев (фигура 1):

1. Υβ. J_

Yl^!

sin^; cosj=Y; tgg= —;

ctg=Уз; csc~=2; sc£ =

точно так же

. π Υβ ^sm3=ΊΓ^:

Sin-г =

Формулы приведения (тригонометрич. ф-ий тупого угла к ф-иям острого угла) сводятся к следующему правилу: 1) если при-водимая ф-ия имеет отрицательное значение, то ф-ию острого угла умножают на —1; 2) название приводимой ф-ии сохраняется, если острый угол взят при горизонтальном диаметре, и меняется на сходное, если острый угол взят при вертикальном диаметре. Пример. Привести sc 310° к ф-ии острого угла, не превышающего 45°. — Т. к. 310°=360°-50°=270°+ 40°, то sc 310°=SC (270° + 40°) - esc 40°.

Тригонометрические функцииот-рицательных углов: в случае cos ж и sea? минус в аргументе можно опустить, а в остальных ф-иях минус у аргумента можно вынести за знак ф-ии, например cos (— 60°)=cos 60°, sin (- 60°)=— sin 60°.

Общий вид углов, соответствующих данному значению тригонометрической функции. Если а—наименьший положительный угол, удовлетворяющий данной тригонометрии, ф-ии, то общий вид углов выразится сл. обр.: 1) sin ж — sin а; х — — пк 4- а (— 1/, где к—произвольное детое число; 2) cos ж=cos а; х=2 пк ± а; 3) tga?=tga; х=лк- -а 4) ctg ж=ctg а; х=лк- -а.

Тригонометрические функции суммы и разности двух углов, двойного угла и половины угла: sin (а + β) == sin а cos β -{- cos a sin β sin (a — β) s= sin a cos β — cos a sin β; cos (α - -β)=cos a cos β — sin a sin β; cos (a — β)=cos a cos β + sin a sin β;

S ( ¥ /0 1 ± tga tg/3 »

sin 2 a -= 2 sin a cos a; cos 2 a=cos² a — sin² a;

, ₀ 2 tga.

tg2a —

1 —tg² a ^!

cos

Sin a

’ 1 + COS a ‘

1 + COS a _e2 ’

1-COS a

14-COS a

Пользуясь ф-лами двойного угла и половины угла, можно показать, что sina? и cos а? выражаются рационально через tg ~. Действительно, если tg~=g, то

1 + tg²1=1 + г²=sc²1 =

ИЛИ

2 х

COS² -

^cos2f=iT^ ^{и sia2}f⁼r^;

1 —z²

отсюда:

cos ж (= cos²1 - sin² f)=sin x (= 2 sin I cos f=2 tg f cos² f)=jJ^·· Из равенства £^=tg| следует

2 cos² *

_ l + z²

Тил л doc

. o.=₁₊-_z>-, T. e. и производная выражается рационально через #. Точно так же sin² a?, cos² а? и sin ж· cos а? выражаются рационально через #=tgx, а именно:

cos² ж =

sin² ж =

Z²

1 _{+ Ζ}2 > οχιά ^-_1+za,

1 + ζ²

sin ж · cos ж (= i sin 2 ж^ =

Рассмотренные соотношения имеют применение при интегрировании нек-рых общих классов ф-ий. Так, подстановка tg приводит к рациональному виду подинтегральную ф-ию в интеграле J R (ccs ж, sin ж) dx. Применяя ту же или вторую подстановку, приводят к рациональному виду ф-ию под знаком интеграла

a² sin² b² cos² х Приведение суммы и разности функций к логарифмич. виду:

sin а + sin β --

₀. о 4- β α — β

- 2 sin — cos —;

о α+ β · <

sin а — sin β=2 cos —p¹ sin

COS а + cos β -

- 2 cos cos

α-β

COS а ·

n c а 4- β. β —

COS P=2 Sin —p- Sin

Точно так же на основании предыдущих соотношений:

1 + COS α= 2 COS² I,

1 - cos α= 2 sin² |,

tg α 4- tg β - ·

° ^{1 G r} cos a · cusp

Решение треугольников:

2 (закон

iiiJ “Пгв=й£с^=2Л (закон синусов), где R—радиус круга, описанного около тр-ка; а

²=b² с² — 2 bс cos А (закон косинуса); sin А + sin В 4- sin С=4 cos

tg А 4- tg В 4- tg С=tg А

ctg у 4- ctg у 4- ctg ~ -

: ctg

L В С.

-· COS—. COS у,

tgB · tg С;

• ctg·⁵-, · ctg

sin

COS

(p — b) (P-C).

-V-__

— l/"p (P-a).

V be ⁹

_ ]/(p^v07p-c). r p(p-a) “. A P· sm —

C ¹

• COS--

r sin

2 S» sin A sin В *sin C *

где p—полупериметр тр-ка, S—площадь тр-ка.

Обратные тригонометрические функции (обратные круговые). Если в ф-ии у — sin ж значение аргумента определяется дугой, измеренной в радиусах, а значение ф-ии при установленной единице определяется соответствующей линией в круге, то, принимая во внимание только одну связь такой ф-ии с кругом (вне отношения к тр-ку), ее называют круговой ф-ией. А т. к. всякая монотонная и непрерывная в нек-ром интервале ф-ия всегда в этом интервале обратима при помощи однозначно определенной непрерывной же ф-ии, то ф-ии у=sin ж; у=cos ж; y=tg ж; у=ctg ж имеют однозначные обратные ф-ии. Последние имеют вид:

ж=arc sin у] х=arc cos у ж=arc tg у х — arc ctg у.

Из рассмотрения графиков прямых круговых функций (фигура 2—7) видно, что ф-ии у=sin ж и y=tg х непрерывно возрастают в интервале

- I < ж < j, ф-ии у ^=r cos ж и у=ctg ж убывают непрерывно в интервале 0 < ж < π.

График ф-ии х — arc sin у (фигура 8) показывает, что эта ф-ия возрастает от — | до + |, когда у возрастает от — 1 до + 1. В этом интервале имеем главное значение (основную ветвь) ф-ии арксинуса; в других интервалах получаются другие ветви ф-ии. Без указания интервала arc sin у представляет многозначную функцию от у. Многозначность эта м. б. выражена так:

х=/ся + (— 1)^к [arc sin у]₉где к—положительное или отрицательное целое число. Все эти значения ф-ии дают бесчис

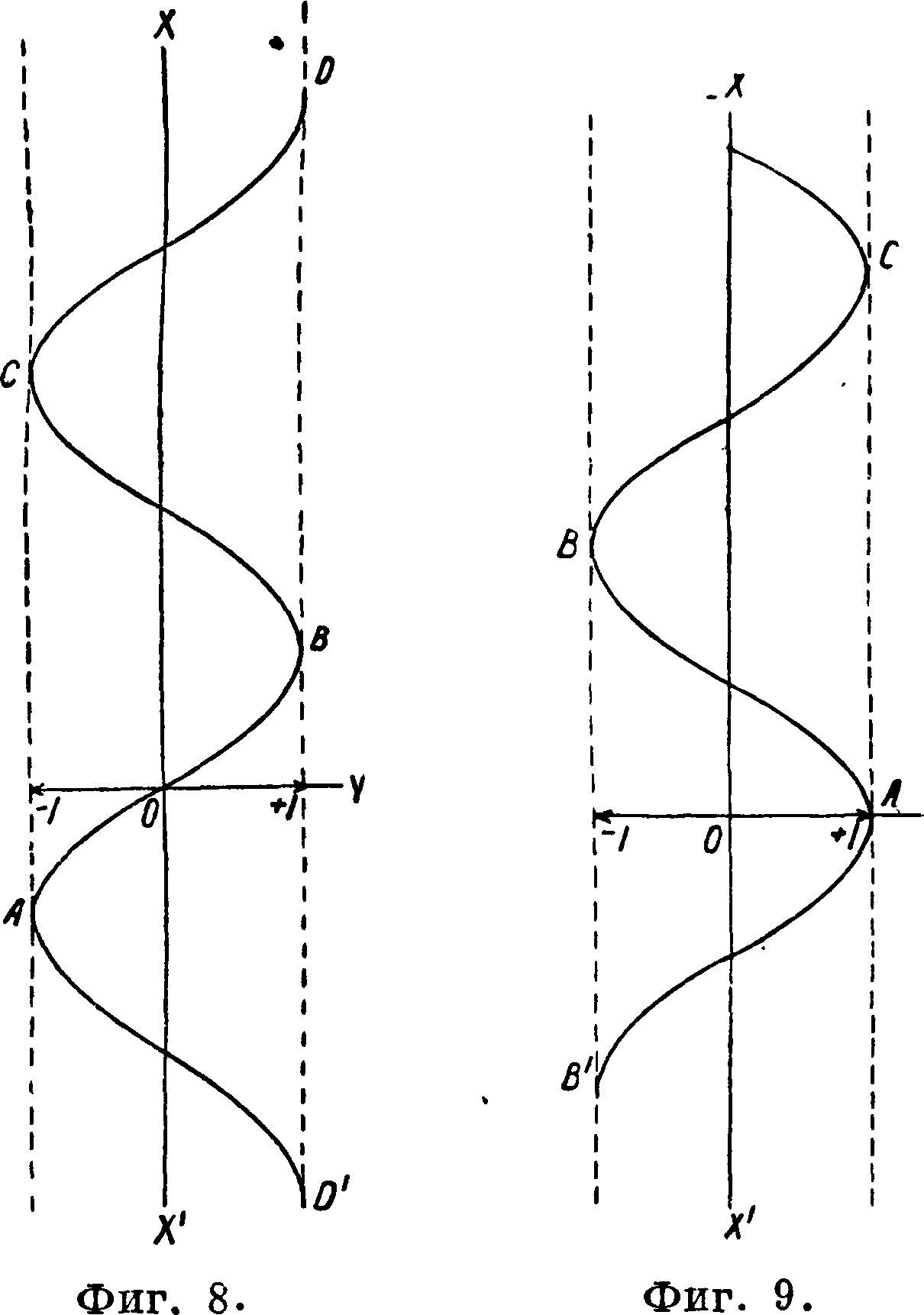
ленное количество непрерывных дуг, из которых одни (АВ, CD, .) соответствуют непрерывным возрастающим однозначным ф-иям, служащим ветвями многозначных ф-ий; другие (CD, AD,.) соответствуют убывающим непрерывным ф-иям. Все возрастающие ветви получаются простым сдвигом основной ветви

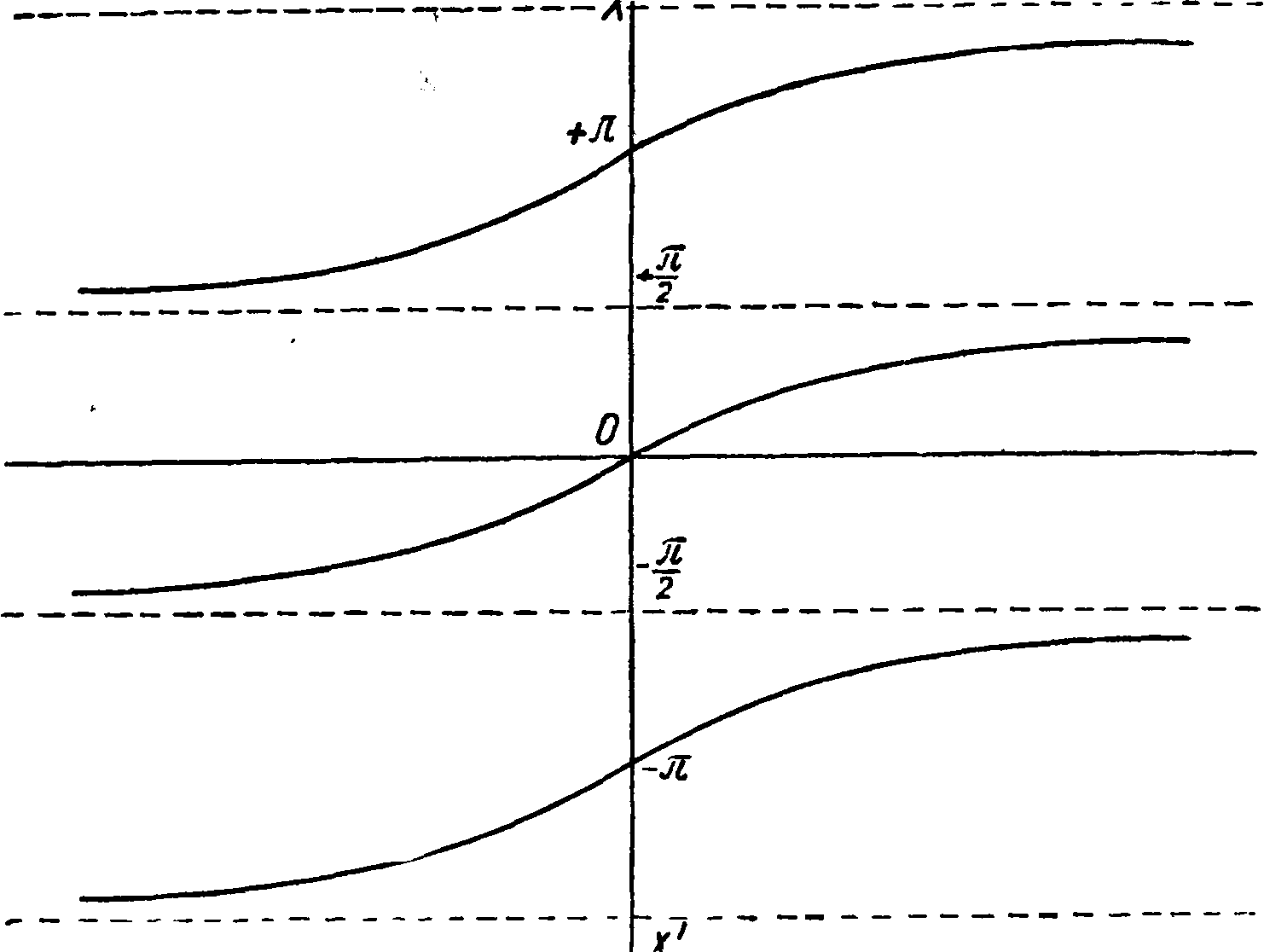
Фигура 10.

А В вверх и вниз на расстояния + 2 π, ^ 4 п,. Обычно основную восходящую ветвь АВ обозначают символом [arc sin у].

График ф-ии х=arc tg у (фигура 10) показывает, что ф-ия определена теперь уже на всем промежутке — оо < i < + оо и представляет ряд подобных друг другу восходящих ветвей. За основную ветвь выбирают ту, которая проходит через начало координат. Ее ординаты образуют непрерывную ф-ию, возрастающую от — - до

-Ь ~. Остальные ветви получаются сдвигом вверх и вниз основной ветви на расстояния, кратные π, следовательно все значения многозначной ф-ии arc tg у будут заключаться вф-ле х=[arc tg у] +

Аналогично соответственные заключения относительно arc cos у и arc ctg у можно сделать

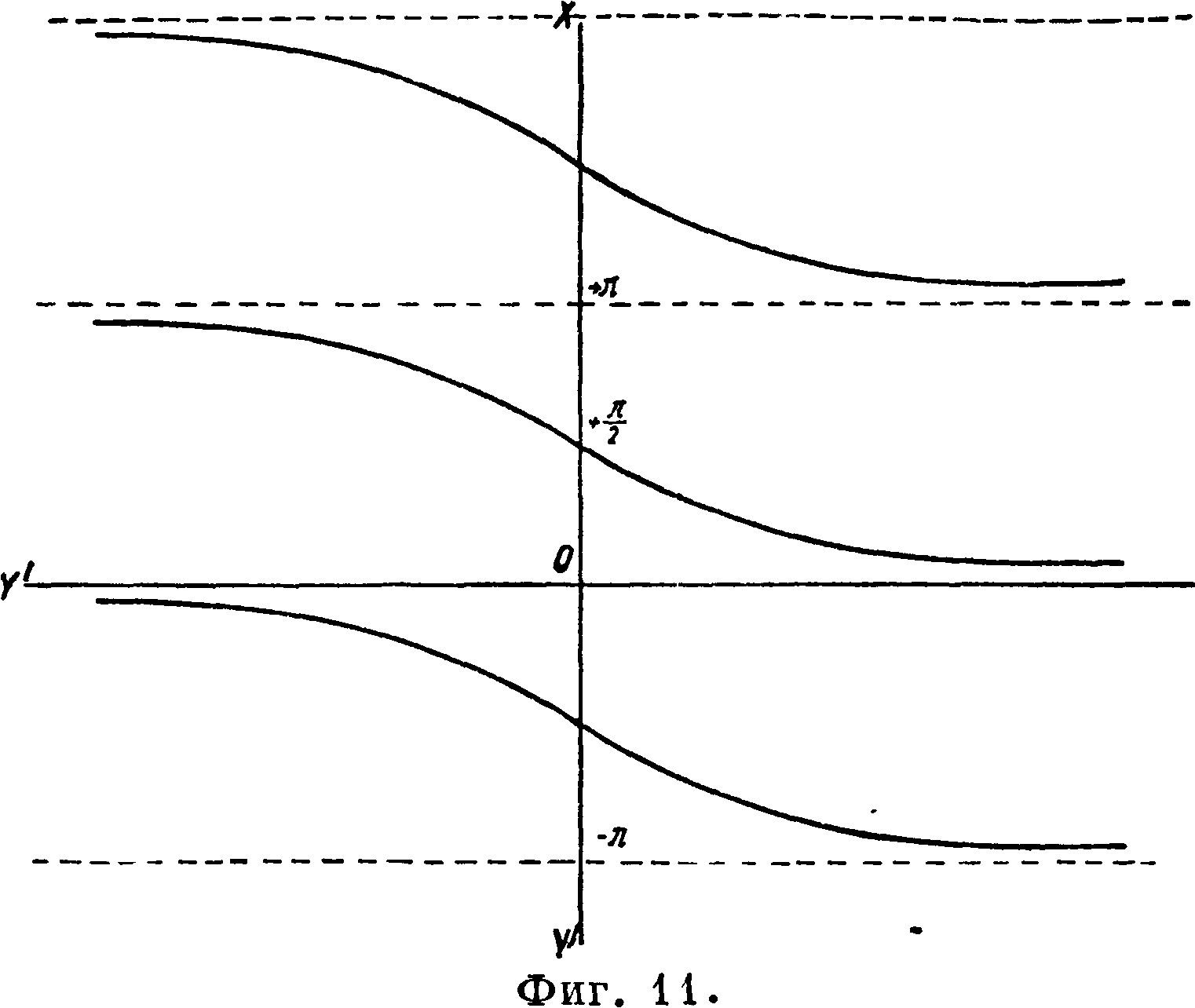
на основании их графиков (фигура 9 и 11). Ф-ии arc sc у и arc e sc у неупотребительны.

В заключение приведем несколько вспомогательных ф-л, применяемых при изображении периодических ф-ий (ряды Фурье) посредством тригонометрич. сумм. Очевидными являются:

2л 2л

I cos пх dx -= 0 и J sin пх dx=0. о о

На основании ф-л

cos а · cos β=~ cos (α + β) + | cos (α — β), sin a · sin β— cos (α — β) — cos (a -f β),

sin a. cos β=sin (a + β) -f sin (a - β)

легко показать справедливость соотношений, выражающих свойства ортогональности тригонометрич. ф-ий:

²η^π 7 Г 0 при шфп

cos тх · cos пх dx=< ^ _m

J I π при т^=п(тф0),

2л

j sin тх · sin пх о

2 л

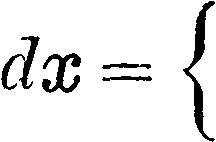
0 при тфп π при т=п(мф 0),

J sin тх · cos пх dx=0. о

Необходимо также отметить графически очевидные соотношения:

2 я, 1 л

cos - + cos

6π., 2πρ

cos — +. Ί^- cos -ρ— =

2 nq Ρ

= 0;

VI · 2nq r,

Σ ^sinT⁼⁰·

q=i

Далее, если η—целое число, то

VI 2 nnq. Чп

2J cos + 2J si

sin²"⁷¹-0 Р

q=l " <7=1

при условии, что п не является кратным р, в противном случае сумма рядов равна р. Если т и п—целые? числа, каждое не более у, то

2 cos^cos²-^=0 Q=i И

S2nmq. 2япд _Л

sm - — sm —^=О v v

<z=l

при условии, ЧТО Ш=фп но обе с^ммы будут равны каждая |, если т — п, за исключением того частного случая, когда ж=п=|, и первая сумма равна р, а вторая—нулю. Аналогично выводится, что

§sin^cos²-^=0 β-ι ^{р р}

во всех случаях. Наконец рассмотрим интеграл

S**^d *(=?)·

Положив с — — а- -1b, имеем с» оо

j _е-ах+гbх „ f _е~ах (_cos j_)X ^ _g|_n ^ _

О ό

I _е(-о + гb)х I⁰⁰ _ -1 _ а + гb _ а + гb

~ I _а+ ib |о ~~ -a + ib~ (α + ib) (a-ib) ~ а²+ Ь2* Интегралы действительной и мнимой частей предыдущей подинтегральной ф-ии выразятся сл. обр.:

со

J e-** cos bх dx=;

^;sin bxdx=_w+—_%·

См. Дифференциальное исчисление, Бесконечное произведение и Ряды.

Сферически я Т. Определения и основные формулы. Сферическим тр-ком, как известно, называют фигуру, лежащую на сфере и ограниченную дугами трех больших кругов (фигура 12). Углы сферич. тр-ка— линейные углы двугранных углов, образованных плоскостями, дающими в пересечении со сферой сферич. тр-к. Центральный угол между двумя радиусами, идущими к вершинам сфе

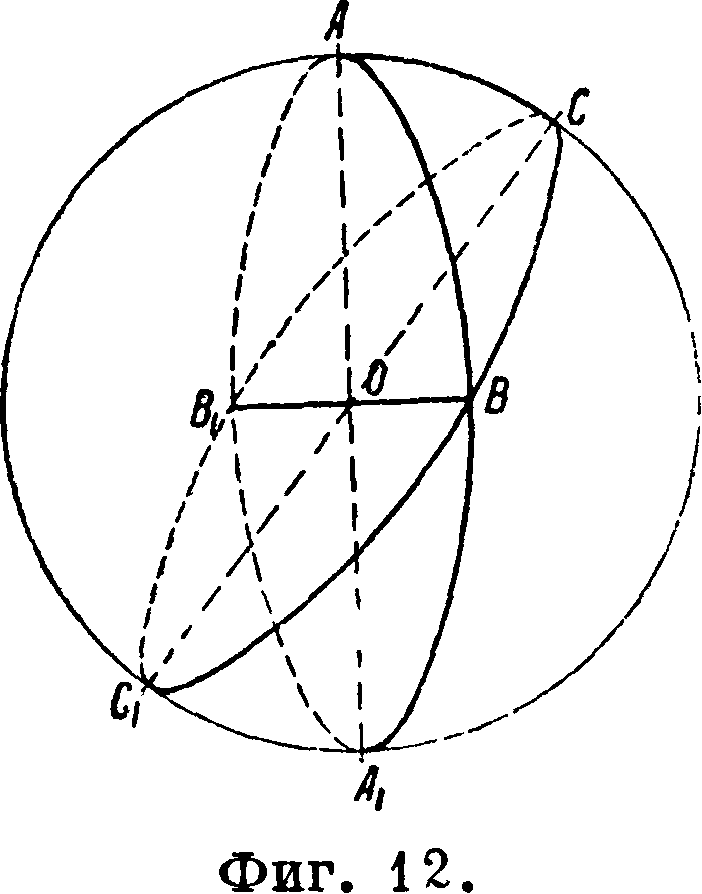
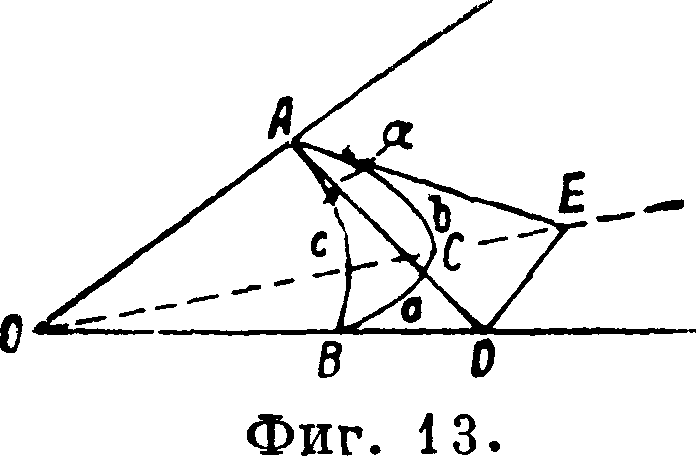
рич. тр-ка, носит название стороны тр-ка. На фигуре 13: А, В и С—вершины сферич. тр-ка; стороны его в соответствии с противоположными вершинами: a — Z ВОС, Ь — z АОС и c — Z АОВ соответственно вершинам углы имеют обозначения: α, β и у, например AD и АЕ—перпендикуляры к О А, лежащие в плоскостях, образующих двугранный угол с ребром О А, следовательно ΏΑΕ=а. Площадь сферического тр-ка определяется по ф-ле:

= г² (α + β + γ-η)>

где а, β и у—углы тр-ка в дуговых единицах, г—радиус сферы. Из этой ф-лы следует, что а + ^ + у=тг + ^·

В сферич. Т. рассматривают 6 основных задач (против 4 задач Т. на плоскости). Эти 6 случаев относятся к решению тр-ка по данным: 1) а, b, у; 2) а, β, у; 3) а, а, β; 4) а, b, с;. 5) а, b, а β) а, β, γ. В первом и четвертом случаях применяется ф-ла:

cos α= cos b cos с + sin Ь sin с cos а,

или

cos α= —

а-cos Ь cos с sin b sin с известная под именем теоремы косинусов сферич. тр-ка. Во втором и шестом случаях применяется теорема косинусов для углов сферич. тр-ка, выражаемая ф-лой:

cos α= — cos β cos у + sin β · sin у · cos а,

или

_ COSa + COS β COSy

^cosa~ ШрШу

По аналогии с плоским тр-ком теорема синусов для сферич. тр-ка выражается ф-лой sin а _ sin b _ sin с sin a ^— sin β ~ sin у“

Формулы, приведенные к логарифмическому виду:

1) S-φ ормулы:

sin (S-b) sin (S-c). sin b· sine *

COS

1=K 1=1 tg|=1

, i /"sin (S-a) sin (S-b) sin (S-IgQ - у “sin S

— ^s*ⁿ S · sin (S-a).

^— V sin b .sin c ’

sin (S-b) sin (S-c). sin S *sin (S-a) ’

причем a+b + e — 2S и ρ—радиус круга, вписанного в сферич. тр-к.

2) σ-φ ормулы:__

. а _ | COSa cos (<r-a)

^Sm 2 “ V

COS

i-V

sin β siny COS (О-β) COS (σ —y)

sin£ siny

причем α- -β + γ= 2σ.

3) Гауссовы формулы: a - b

я cos-^— a+ β 2

sin —=

cos £;

a- β

cos

α+β

cos -

a — b

cos -. a +1

^mJJT

. c

COS

sin £;

sin

(1)

(2)

(3)

(4)

4) Неперовы аналогии. Разделив (2) на (4) и (1) на (3), получают первую пару яепе-ровых аналогий:

a — b

. α-β ^8Ш —

tg-Z-

sin

a 4- b 2

a - b

ctg|;

a + /5

a + b

^CtSj

Разделив (2) на (1) и (4) на (3), получают вторую пару неперовых аналогий:

. а — β

. а-b ^Sm 2, с.

.*8 — ·--„—я-tB*’

sin -

-β

Применение сферической Т. в г е о д е з и и—см. Географические координаты, Геодезическая задача, Геодезические координаты.

Применение сферической Т. в астрономии. Для определения положения светила на небесной сфере служат: а) система горизонта—высота и азимут светила, б) система экватора — склонение и прямое восхождение светила, в) система эклиптики — астрономическая широта и астрономическая долгота светила. От соединения систем экватора и горизонта получают параллактический тр-к, от соединения же систем экватора и эклиптики—а строномический тр-к.

Сферо идический треугольник — см. Геодезические треугольники и Геодезия.

Лит.: Филипс Г., Диферендиальное исчисление, пер. с англ., 3 изд., М., 1932; «Курант Р., Курс дифе-рендиального и интегрального исчислений, пер. с нем., ч. 1, М.—Л. 1931: Рыбкин Н., Учебник прямолинейной тригонометрии и собрание задач, 11 изд., М., 1931; Пржевальский Е., Пятизначные таблицы логарифмов чисел и тригонометрии. величин, 6 изд., М.—Л., 1926; Привалов И., Ряды Ф^рье, 2 изд., М.—Л., 1931; К р а н и Н., Сферическая тригонометрия, пер. с нем., М.—Л., 1932; Eagle A., A Practical Treatise on Fourier’s Theorem a. Harmonic Analysis, L., 1925; В a I-ser L., Spharische Trigonometrie, Lpz., 1927; см. также Параллакс. В. Никаноров.