> Техника, страница 87 > Трубопроводы

Трубопроводы

Трубопроводы. T. состоит из ряда отдельных звеньев труб, фасонных частей и арматуры, соединенных в определенном последовательном порядке так, чтобы образовалась одна непрерывная линия, работающая так же, как работала бы и изготовленная из одного цельного куска материала. По роду подаваемого вещества, газообразного, жидкого, Т. носят названия: паропроводы (смотрите), газопроводы (смотрите), воздухопроводы (смотрите), нефтепроводы (смотрите), водо-

* Фигура i.

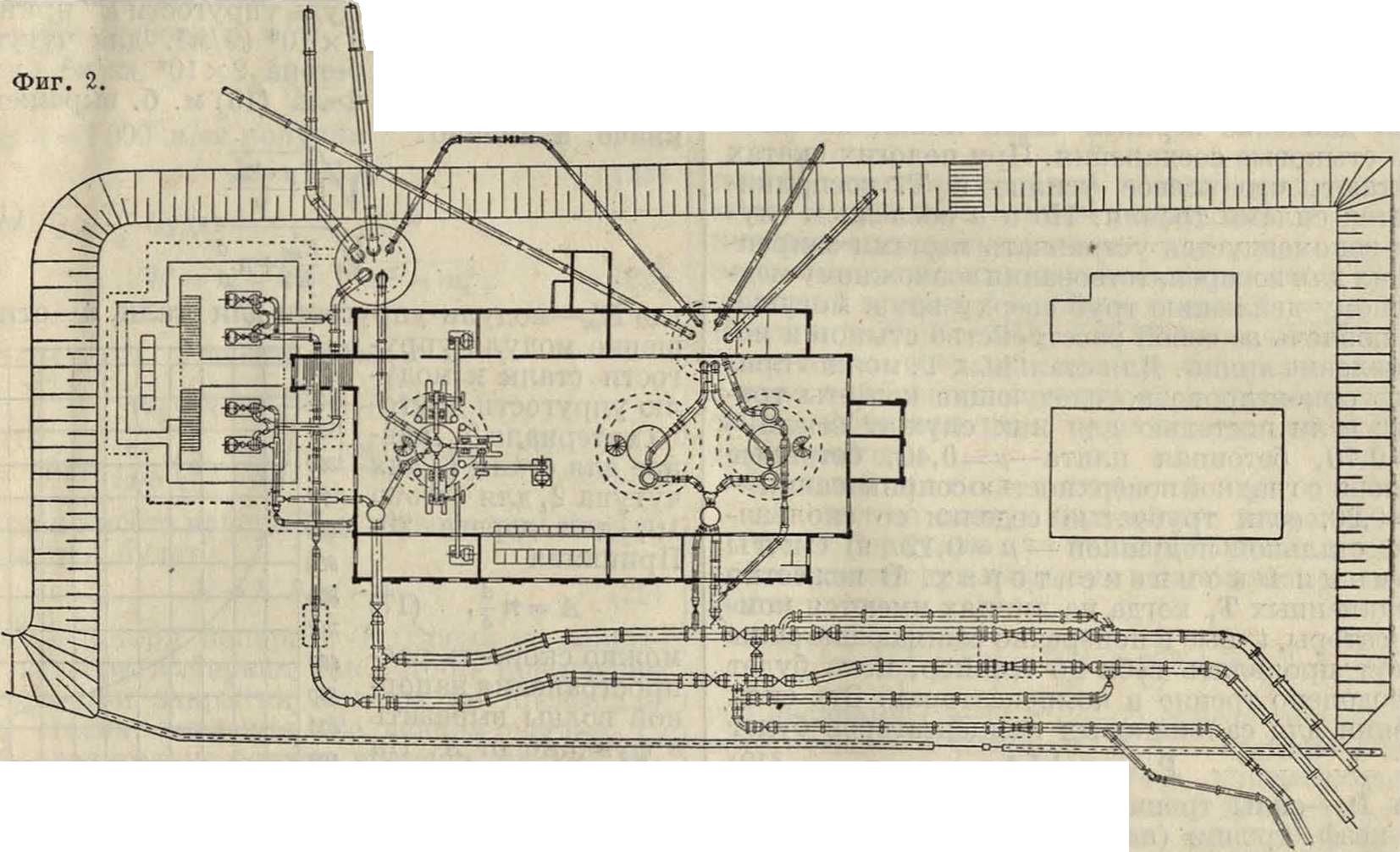
проводы и прочие На фигуре 1 показаны отдельные трубопроводы: самотечные а, всасывающие b, нагнетательные с напорные d. На фигуре 2 представлен участок водопроводной сети.

Силы, действующие на Т. При расчете Т. необходимо принять во внимание в соответствующих случаях следующие основные силы, а) Внутреннее давление в килограммах[см², выражаемое высотою напора Н в м, с учетом давления атмосферы. Наибольшее напряжение на растяжение у внутренней поверхности Т. в тангенциальном направлении определяется по ф-ле:

0,4r? + l,Sr|

I - Vi -2, 2 ’

Га+П

(1)

где р_г—внутреннее давление в килограммах!см², к-рое не должно превышать величины су : 1,3; ту—внутренний радиус Т. в сантиметров г_а—наружный радиус Т. в см. Наибольшее напряжение на сдвиг

2

(?)

Га-Т{

При малой толщине стенок Т. среднее напряжение в направлении окружности м. б. определено по ф-ле

= (3)

где d_t—внутренний диам. Т. в см, δ—толщина стенки Т. в см. В осевом направлении среднее напряжение будет равно

c_z=^d-§. (4)

Т. к. Pi=H γ (полное давление воды), то, выражая йийвж, apHdjB m/м², можно формулу (3) написать так:

_ djHy _ djH ,сч

² 2д 20 ’ ^t>

где Н—полная высота напора, выраженная в м вод. ст., γ—уд. в воды, равный 1 m/м³. Для стального Т. формула (5) примет вид

„ _^ιΗν

2ηβ

(5а)

где η есть коэф. надежности шва (0,70—0,90). По ф-лам (3) и (5) м. б. произведен расчет лишь

в том случае, если толщина стенок мала сравнительно с внутренним диам. трубы, то есть когда <5 <^, и если рабочее давление не превышает одной трети напряжения материала (<т.: 3). В данном случае допускается не учитывать упругих свойств материала (обусловливающих различие напряжений в материале), т. к. получаются приближенно верные результаты для толщины стенок труб. В тех же случаях, когда отношение толщины стенок трубы к внутреннему диам. ее равно или более 0, 2, то есть % > 0,2,

или когда рабочее давление превышает 50 atm, расчет ведется по теории упругости, причем принимается во внимание осевое напряжение в трубе [ф-лы (1), (2) и (4)]. См. также Трубы железобетонные, деревянные и прочие б) Внешнее давление (давление грунта, временная нагрузка, давление _фиг 2 1 щ атмосферы) н а п о-

^ верхностьТ.

где P_t — сжимающая (растягивающая) сила при понижении (повышении) температуры в т, а—коэфициент удлинения, равный: для стали 0,000012, для бетона и железобетона 0,000010, для дерева 0,000004, Е—модуль упругости в т/м³, равный: для стали 20 000 000 т/м², для бетона и железобетона 2 000 000 m/м², для дерева 1 000 00.0 т/м³, значения величины (аЕ) приведены ниже:

(аЕ)=240 т/м2—для стали

(аЕ)= 20 т/м“—для бетона и железобетона

(αβ)= 4 т/м²—для дерева

ω—площадь поперечного сечения стенки трубы в .и², t—температурное понижение (повышение) в градусах С. При Т., жестко закрепленных в своих концах и состоящих из труб разного диам. и разной длины, Г-ная сила будет равна

Рi=(аЕ) -

г) Усадочные напряжения. В бетонных трубах (при отсутствии <°-ных швов) учи-

Давление от грунта в вертикальном направлении увеличивается с увеличением глубины, но не пропорционально, достигая своего максимума на глубине около 5 м, после чего давление для больших глубин остается постоянным. Вес увлажненного грунта берется равным 2 000 килограмм/м³. Давление от подвижной нагрузки не оказывает никакого влияния на слои грунта, расположенные на глубине, большей чем 5 метров Нормальная временная нагрузка принимается равной 5 000 килограмм/м³. Давление от грунта р_е, давление от подвижной нагрузки и полное внешнее давление р„ в зависимости от глубины h залегания трубопровода выразятся следующими чи:

при h в м:	1	2	3	4	5 и более
Ре в килограммах/м2.	1627	2 613	3 120	3 307	3 333
Pv » ».	3 200	1 800	800	200 —
Ра » ».	4 827	4 413	3 920	3 507	3 333

При хорошем грунте (глине, гравии, каменистом и тому подобных грунтах) давление р_ем. б. взято равным ²/₃ давления, указанного в таблице, в) Температурные силы. Т. длиною I изменяет свою длину под влиянием изменения t° на величину

ΔΙ=atl. (6)

Если Т. не может изменять свою длину, то в нем возникают (°-ные силы, выражаемые ф-дой

Р,=(аЕ)оЛ, (7)

тываются усадочные напряжения, принимаемые эквивалентными пониже-нию <° на 10°. д) Силы, вызывающи!» поперечное сжатие стенок Т. Вследствие давления на стенки Т. происходит поперечное сжатие стенки на величину

ΔΓ =

dm.

2 SmE’

когда такое сжатие невозможно, то в стенках Т. появляется растягивающее усилие

^=^я^г· т

Если Т., жестко закрепленный в своих концах, состоит из участков труб разной длины, разного диам. и с различными высотами напора, то

Р=— 1 2 т

2(К)

2 а

(11)

В ф-лах (9), (10) и (11): d—внутренний диам. Т. вм,Н—полная высота напора в м вод. ст.,

I—длина рассматриваемого участка Т. в м, δ—толщина стенки трубы в м, т—коэф. Пуассона, равный: для стали 3,3, для бетона 7,0, для дерева не принимается во внимание, Е— модуль упругости материала стенки Т. вт/м³, P_q — растягивающее усилие вследствие поперечного сжатия Т. в т, ω—площадь попереч-

ного сечения Т. в м². Для практич. целей в большинстве случаев достаточно взамен расчета по формуле (11) определить P_q по формуле (10), принимая в последней за d диам. труб наибольшей длины, а за Н среднюю высоту напора. Не следует упускать из виду учета силы P_qпри конструировании компенсационных частей, е) Влияние со бственного.веса Т. На горизонтальных и пологих участках составляющая от собственного веса Т., действующая в направлении оси трубы, воспринимается полностью силами трения. На крутых участках приходится однако считаться с этой осевой силой, в особенности учитывая силы трения от сотрясений, увлажнения соприкасающихся с трубами плоскостей и других причин, ж) Трение между трубой и ее опорами. Силы трения различны для пустого и заполненного жидкостью Т. При крутых скатах сила трения приравнивается нулю, вследствие чего в этом случае необходимы неподвижные трубозакрепительные опоры, имеющие целью разгрузить давление верхней части линии на нижние стыковые соединения. При пологих скатах считают, что осевое усилие в Т. воспринимается силами трения." Но и в последнем случае рекомендуется устраивать местами закрепления для воспрепятствованиявозможному медленному движению труб сверху вниз, могущему повлечь за собой расстройство стыков и искривление линии. Для стальных Т. можно принять ориентировочно следующие коэф-ты трения: если постелью для них служит земля— /<=0,70, бетонная плита—/<=0,40, бетонные желоба с гладкой поверхностью соприкасания— /<=0,20, если трубчатые седелки со скользящей стальной подушкой—/<=0,12. з) Силы трения в компенсаторах. В нежестко соединенных Т., когда на линиях имеются ком-, пенсаторы, Г-ные и поперечно сжимающие силы могут проявлять себя до тех пор, пока будет преодолено трение в компенсаторах. Эта сила, трения для сальниковых компенсаторов будет Ρ_Λ=πμά_Λ1_Λη, (12)

где P_d—силы трения в компенсаторах в т, μ—коэф. трения ( по стали: /<=0,25), d_d—внешний диаметр набивки в м, l_d—длина набивки в м, h—статич. высота напора в м (динамическая высота напора в данном случае не учитывается). Приближенно для раструбных Т. можно принять P_d=P₍ при ί°=3 -Э 5°. и) Разные силы. Кроме перечисленных выше сил на Т. действуют усилия, происходящие от неправильной укладки и плохого соединения труб, и такие, которые по их малости обыкновенно не учитываются. К первым например можно отнести усилия, возникающие в стыковых зазорах вследствие неплотной и косой пригонки труб одна к другой и могущие быть выражены величиной

P_s=?(d²-d²)H; (13)

ко: вторым—силы, растягивающие Т. в продольном направлении, равные

Ρ_Ζ^Κ. (Ή)

центробежные силы в закруглениях и др. В практике все второстепенные силы учитываются обыкновенно введением в расчет практического коэф-та. При определении толщины стенки Т. таким коэф-том является практич. прибавка С, равная для стали 1,59, для чугуна 3,17, для меди, свинца, олова и цинка 2,54, для сосны и дуба (вдоль волокон) и для. бетона 12,7.

Влияние закрытия и открытия затворов на величину напора в напорном Т. а) Скорость распространения напорной волны в Т. может быть определена по формуле проф. Н. Жуковского или итальянского инж. Альеви (L. Allievi), причем обе ф-лы дают одинаковое выражение:

* ·/

Е"

D

(15)

где а—скорость распространения напорной волны в Т. в м/ск, д—ускорение силы тяжести в м/ск², равное 9,81 μΙοκ², γ—вес единицы объёма жидкости в килограммах1м³, Е—модуль упругости жидкости в килограммах/м², Е—модуль упругости материала Т. в килограммах/м², d—внутренний диам. Т. в м, δ—толщина стенки Т. в м. При различных диаметрах и различных толщинах стенок труб берут средние значения d и б. Модуль упругости Е" принимается: для стали 20 x10^е к г/м², для чугуна 10x10® кг/м², для бетона 2x10® кг/м², для дерева 1x10® кг]м². Ф-ла (15) м. б. выражена иначе, а именно:

α=

V

w+*i

(16)

где Еж—модуль упругости для стали, п—отношение модуля упру- аи/ск гости стали к моду- ¹⁵⁰⁰ лю упругости другого материала Т., равное для стали 1, для чугуна 2, для бетона 10, для дерева 20.

Принимая

(17)

Α=ηί,

то то то то юоо

soo

800

700

600

500

т

300

200

100

можно скорость распространения напорной волны выразить в функции от А. На фигуре 3 дана диаграмма скорости распространения напорной волны в ф-ии от А по Леви. Для железобетонных Т. получим по Мюльхоферу (Muhlhofer) приведенный модуль упругости железобетона равным

ПО 200300 Ш500600700800300

*--"Т Фигура 3.

Е}=Еж · 4- + Е1

-d г».

-=

+ (<5-<5)]; (18)

δ ¹ <5 δ δ

отсюда А для диаграммы выразится ф-лой:

A=^.i₌ f^ (19)

_E’ δ ίη+(ί-ί)

где Е"_г—приведенный модуль упругости железобетона, δ—толщина стального Т., мысленно заменяющего собою арматуру, δ—толщина стенки железобетонного Т., Еж—модуль упругости стали, Е"₆ —модуль упругости

Е_ж

= 10.

бетона, d—внутренний диам. Тп —

Для жесткого трубопровода, когда Е"=со, получим по формуле (15)

Е=207 000 000 килограмм/м²

9 900

а-

при γ=1 000 килограмм/м? и

К*

,3-Ь

1010

Для стальных,

d

E" ’ a бетонных,

= 1 425 м)ск.

(20)

железобетонных и деревянных Т. достаточно в практике принять в среднем

α= 1 000 м/ск.

Время, необходимое для прохождения напорной волной Т. длиною L м в обоих направлениях (вперед и назад), равно

= (21)

б) Высота напора у затвора при его закрытии. При закрытии затвора происходит в Т. повышение напора, высота которого определяется следующим образом. Если обозначить через L длину Т., измеренную по оси, в м, h—гидростатич. высоту напора у затвора в м, h—добавочную высоту напора у затвора в момент его закрытия в м вод. ст., T_s—время, потраченное на закрытие затвора, в ск., V—скорость течения жидкости в Т. перед закрытием затвора в м/ск, то при Т₈ будет li=у · (22)

Для α= 1 000 м/ск получим

h=102 V. (23)

о г

При T_s> — будет

h=m—h — У то² — т, (24)

где т=т₁-7. αν

m₁=h + — =

- ^V2 i ^{2L 2 1 -} 2S²h ^α tJ ⁼

: h + 102 v,

0,021^2(500 T_s-L)·

hr!

Полпая высота напора Я у затвора при его з а-крытяи будет

H=h + h-h₁, (25)

где h!—потеря напора в Т. Время на закрытие затвора выбирают так, чтобы повышение напора при закрытии затвора не превзошло 20% статич. давления. Во всяком случае T_sдолжен быть значительно больше времени пробега на

2 L

порнои волны —.

в) Высота напора у затвора при его открытии. Открытие затвора влечет за собой падение напора в Т., к-рое м. б. выявлено сл. обр. Примем, по аналогии с пред-идущим, следующие обозначения: L — длина Т., измеренная по оси, в м, h — гидростатич. высота напора у затвора в м, h— высота падения напора у затвора в момент его открытия в м вод. ст., Т„—время, потраченное на открытие затвора, в ск.,«— скорость течения воды в Т. перед открытием затвора в м/с к. Высота падения напора у затвора выразится равенством:

h"=+ Yn(2h + п)-п,

причем при Т„<^ будет а²«^г 2g^zh ’

при т₀>~ будет п-

(26)

(27)

п =

2v4J g*T$h ’

(28)

Высота напора Ну затвора при его открытии будет равна

H=h — h"+ h, t.29)

где h,"—величина, определяемая по формуле (26)

на основании формул (27) и (28). Если дана высота падения напора h", то при Т₀>Ц^ будет гп _ 2vL 1 Гh-h"

h-" V ~h

(30)

Время на открытие затвора должен быть не менее вре-

от мени пробега напорной волны — и по возможности не менее 8 ск. При скоростях «<0,02h происходит вслед за падением напора большее или меньшее повышение его, причем в наиболее неблагоприятных случаях это повышение достигает четверти статической высоты напора. При скорости «>0,02h такого повышения напора не бывает. г) Величина напора в Т. с разными диаметрами труб. Если Т. состоит из нескольких участков с разными диаметрами, а следовательно и с разными скоростями течения жидкости в Т., то высота напора рассчитывается по средней скорости течения жидкости

41«)

L

(31)

где v_m—средняя скорость течения жидкости в м/ск, I—длина отдельных участков Т. с одинаковыми внутренними диам. труб в м, v—соответственно скорость течения жидкости в этих участках в м/М, L—общая длина Т. в м. По Креснигсу (Р. Kresnik) повышение напора учитывается на всем протяжении напорной линии в виде прибавки величины h к гидростатической высоте напора в рассматриваемой точке трубопровода.

Общий метод расчета напорных Т. основан на следующих ур-иях гидравлики: а) ур-ие Бернулли для цельного потока реальной жидкости при медленно изменяющемся движении

w + ( г¹ + Μ =1ΪΓ + [у + ь₂) + К, (32)

где значками (1—1) и (2—2) отмечаются соответствующие сечения, «_г и «₂ — средние скорости в них, а_х и а₂— коэф-ты, учитывающие неравномерности распределения скоростей по поперечному сечению потока (^ 1,1), Ь_г и /г₂—

отметки над горизонтальной плоскостью, —¹ и «2. г

~—приведенные высоты давления, h_w—совокупность потерь напора на гидравлич. сопротивления при движении жидкости в трубе, д—ускорение силы тяжести (9,81 м/ск)·, б) гидравлич. ур-ие неразрывности

Q=F · «, (33)

где F—живое сечение трубы, «—средняя скорость, Q—расход жидкости (объём жидкости, протекающей в единицу времени через данное живое сечение). В практике водопроводного дела приходится определять количество воды, подаваемое трубой, и напор, затрачиваемый на подачу воды. При подаче воды из резервуара е отметкою земли по Т. диам. d в конечную точку с отметкою Z₂ можем написать на основании ур-ия Бернулли

_Ζι + Η + Ζ=Ζ, + £+ F + h, (34)

где Я—уровень воды над землей в м, F—давление жидкости, в данном случае равное давлению атмосферы, «—средняя скорость истечения воды из трубы, h—потери напора на гидравлич. сопротивления при движении жидкости в

2

Ί. Э. т. XXIV.

трубе, д—ускорение силы тяжести. Для свободного напора -

Н=Z₂ — Z₁+ h + ^=Н_г + h + 2^· (35)

На основании этой ф-лы свободный напор расходуется: 1) на подъем воды на высоту Я, равную разности отметок земли у резервуара и центра выходного отверстия трубы, 2) на преодоление гидравлич. сопротивлений в Т. вследствие вихреобразования, а также и местных потерь, 3) на образование скорости истечения воды из трубы при затрачиваемом напоре, что имеет особое значение в практике тушения пожаров посредством водяной струи, а также при устройстве фонтанов и прочие Потеря напора на гидравлич. сопротивления при длине Т. I с учетом местных потерь напора м. б. представлена следующей ф-лой:

(36)

Если Т. имеет значительное число фасонных частей (задвижек), то составляет 5—10%

потери напора на трение в Т. Т. о. для определения общего напора м. б. представлена следующая ф-ла:

(37)

П=Н_г + ef_bl+f_g×+

V²

В том случае если Т. не постоянного сечения, при расходах в отдельных пунктах по пути, состоит из отдельных участков l_lt l₂, с со ответствующим сечением труб d_lt й₂, ., d_m, то приведенное ур-ие м. б. представлено в следующем виде:

п=т 2 2

Н=н₁+ 2 (*Α·1,+ %Χ)+ψ_β· (38)

η=ι ““

Потерей напора на сопротивление при кходе воды в трубу пренебрегают. Для определения потери напора на трение в трубах пользуются ф-лой Шези

«=с|/Я-г, (39)

где R—гидравлический радиус для круглых труб диам. d, причем Д=^, г—потеря напора на единицу длинь!, v—скорость, с—коэф., зависящий от формы трубы, состояния стенок и условий протекания воды. Если в формулу (33) подставить значение и, то получим

Q=F с УвГ~г (40)

ИЛИ

-4=К-с R=K; Vi

(41)

К будем называть модулем расхода, коэф. с ф-лы Шези. м. б. определен по различным эмпирич. ф-лам. Наибольшее распространение получили ф-лы: 1) формула Куттера для коэф-та в, имеющая вид

_{С =} ш-^Я. _т

Коэф. т—для чугунных и железных труб, бывших в употреблении, равен 0,25; для деревянных 0,20 и для цементных 0,25—0,35; 2) формула Манинга для коэф-та с имеющая вид е=-· - Д°-¹⁶⁷. (43)

η η 0 ⁴

Коэф. и принимают=0,012. Величины модуля расхода K=FcYR для труб разных диам. даны в табл. 1 при коэф-те с по Куттеру (для т= =0,25) и в таблице 2 по Манингу (для и=0,012).

Т а б л. 1. — В е л и ч и и а модуля расхода по Куттеру.

d, миллиметров К, л/ск	40 3,59	50 6,78	75 21,43	100 48,10	125 89,84
d, миллиметров	150	175	200	225	250
К,л/ск	149,37	2-9,20	331,70	459,02	613,59
d, миллиметров	300	350	400	450	500
К, л/ск	1,012-103	1,540-103	2,220-103	3,057-103	4,067-103
d,MM К, л/ск	600	750	800	9 00	1 000
	6,655*103	12,13-103	14,42-103	19,76-103	26,18-103
Таблица 2. —Величина модуля расхода по М а н и н г у.
d, миллиметров	40	50	75	100	125
К, л/ск	4,87	8,81	26,1	56,3	101,5
d, миллиметров	150	200	250	300	350
К, л/ск	165,0	355,0	644	1,047-103	1,580-103
d, миллиметров	400	450	500	600	700
К, л/ск	2,256-103	3,089*103	4,041-103	6,652*103	10,03-103

d, миллиметров К, л/ск

800

11,3.103

900

19,6-103

1 000 26,0-103

1 209 42,0-103

Кроме приведенных выше ф-л для определения коэф-та с в 1923 году была предложена Форхгей-мером следующая показательная ф-ла:

с=- R*=-.

η η

R⁰,².

(44)

Для предварительных расчетов Т. могут быть применены логарифмо-графич. таблицы.

10000-

5000-

mth

зооо-

2000-

1500-

1000-

500н 400-

300-

200-

гоо-

50-

40

зо-

W

Фигура 4.

4-

Но

-5

-4

-3

-г

-1

--0,5

Z 0,5-|> 0,4-

0Q

0,3-

0,2-

0.1-

(21131

0,006

0,01-

0,01-

I 0,02-

. « 0,03. I 0,05:

0,01

- 0,02,.

С I

0,05^

3=0,

0,2

-0,1

-0,05 - 0,04 i -0,03

-0,02

0,0

0,1

0,2-

0,3--

-0,4

0,5·

0,1-

0,2 4

--0,3 1

„ * „ i g °*

I 1. 2 ’

и Й

5~

10=:-

20-

30

(41

0,3

-0,4

-0,5

0,02-0,03-0,04-005-

05

0,7

-0,8

-0,9

1

I

i i.

20

J—327 S £ АО ^ О SO

„1⁵³ -

I g 0,4-

II «4 §. §

£ &

1—

(5)

3

4- f

5-(6)

r-o 5 §

5

H* -

7

8 -9

R)

На фигуре 4 представлена номограмма для о пре-

деления потери напора h_w и скоростной высоты h_v, составленная по сл. формуле (на 100 метров Т.):

К=0,08264 Q² ( ²⁴;_^п±-- ·<**)% (45)

n/d + 49,ln2

при тг=0,012 и и=0,016.

Прямая, соединяющая величину Q (шкала 1) с величиной d (шкала 2) или F (шкала 3), пересекает по продолжению величины h_w (шкалы 4 и о), /)„ (шкала 6)и» (шкала 7).

По Форхгеймеру (Ph. Forchheimer)

К =6,9644 и² (46)

где коэф. η равен: для стального Т. 0,013— 0,015, для деревянного 0,011—0,012, для бетонного (пементонго)—0,0135. На фигуре 5 пред-

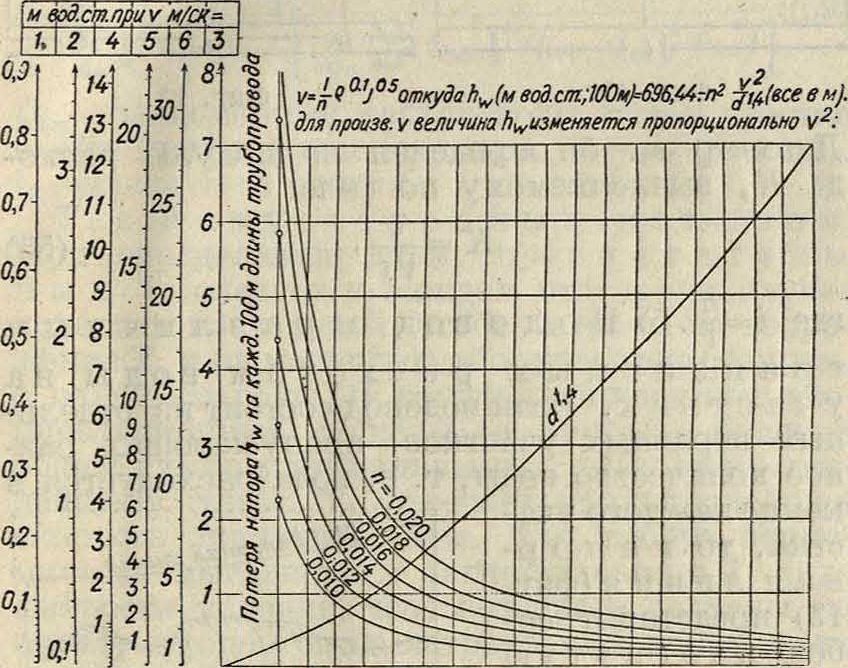
0 Of 0,60,81 (2 Iff 16 2 2ρ2,42β2,85 ί23,43,63 4и

Bfiym диаметр d Фигура 6.

ставлен график, составленный по формуле (46) для определения величины h_w на каждые 100 метров Т. Потери на местные сопротивления оцениваются величиной

(4?)

где коэф. сопротивления ζ имеет следующие значения, а) При входе жидкости в Т. коэф. сопротивления ?_в=0,5-у0,1 · б) При поворотах коэф. сопротивления по Вейсбаху

£»=ϊδ[θ·13 + 0,16 (£)·>*], (48)

где а—угол отклонения потока, а ρ—радиус кривизны, в) При расположении в Т. дроссель

	1	1,
1.	^-!	ί
	1г :	—г---ψ—
! f Фигура 6.		:- Фигура 7.

ных дисков (фигура 6 и 7) происходит потеря напора вследствие последовательного сужения и расширения струи воды, причем коэф. сопротивления:

(49)

где

^ UiFi J ’

«i=0,63 + 0,37 (fi)³.

(50)

г) Если вход в трубу закрыт сетчатой коробкой, то коэф. сопротивления будет равен 1, причем скорость в формуле (47) м. б. взята равной (по Эшеру)

2 г ’

(51)

где Q—расход воды, F_s—сумма площадей всех отверстий сетки, д) При ответвлениях происходит потеря напора, которая по Мелье и Же-нийсу (Miillet et Genieys) м. б. приближенно оценена коэф-том сопротивления ζ₀=2, причем скорость в формуле (47) представляет собою в данном случае скорость течения воды в ответвленном- Т. е) При расположении на Т. арматуры в виде разной системы задвижек, клапанов, кранов, вентилей коэфициент сопротивления ζ_α варьирует в широких пределах в зависимости от конструкции затворов и от большего или меньшего закрытия, например при открытом затворе £_α=0,05 и более, ж) При выходе воды из Т. в широкий сосуд (резервуар) ζ₀ м. б. взят равным 0,1.

Расчет параллельных водоподающих Т., заменяющих один. Если по расчету размеры одного водовода превысят нормальные размеры, то м. б. по конструктивным и транспортным причинам более выгодным заменить один водовод несколькими параллельными для пропуска по ним того же количества воды. Бауерсфельд (W. Bauersfeld) доказал, что при замене одного Т. на п параллельных вес и потеря напора от трения увеличиваются в j/w раз, например при п=2—в у^2=1,104 раза. Поэтому проложение нескольких Т. вместо одного может оказаться выгодным лишь в том случае, если убыточность от большего веса Т. и большей потери напора от трения компенсируется меньшими расходами по изготовлению и транспорту труб. При этом следует иметь в виду, что расположение нескольких параллельных магистралей взамен одной обеспечивает непрерывность подачи воды в сеть на случай порчи одной магистрали. Располагая п водопроводных линий вместо одной с пропуском воды по каждой в — часть всего расхода, получим внутренний диаметр каждой водопроводной линии равным

d_n=dy^ (s)²’ (52)

где d — диаметр одного водовода, пропускающего то же количество воды, что и п водоводов. Следовательно для п=2 диам. d„=0,75d, для п=3 диам. d„=0,64d. Прокладывая несколько параллельных водопроводных линий взамен одной, следует таковые располагать в достаточном расстоянии друг от друга во избежание подмыва соседнего трубопровода при разрыве одной линии.

Определение напорной линии. Если на закрытом, находящемся под давлением Т. предположить установленным ряд вертикальных (пьезометрических) трубок, то вода в таковых в зависимости от существующего в данном месте гидравлич. давления займет положение, по которому (соединением отдельных положений воды в пьезометрических трубках) можно определить напорную линию. Последняя будет относиться к определенным (в каждом отдельном случае) значениям Q, d, г, V, причем падение лйнии давления или относительная (на единицу длины) потеря напора выразится ур-ием (фигура 8):

г=~=1

dz dy

(53)

Если вместо открытых (пьезометрических) трубок взять закрытые сверху трубки (как у барометра), то при построении (по положению

*2

воды в них) напорной линии АВ получим таковую расположенной параллельно первой аb (фигура 9) и выше ее соответственно

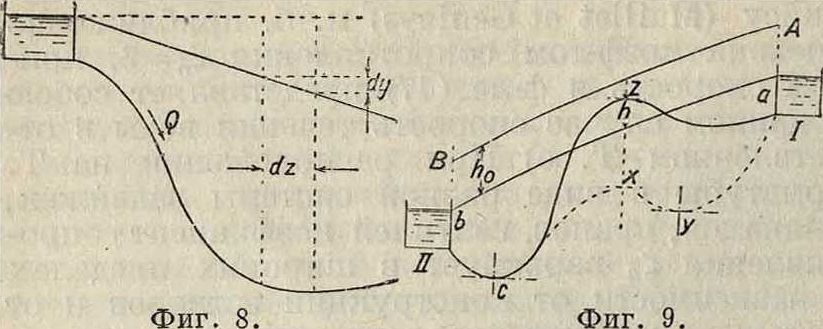
атмосферному давлению р₀ на величину высоты напора воды:

^feo=V=TШ=¹⁰>³³³ М’ (⁵⁴)

где у—уд. в воды. По расположению обеих параллельных напорных линий можно судить о том положении, к-рое нужно придать Т. в¹ продольном профиле. Если р есть давление (напор) в определенном месте водовода, то отдельные ветви его, расположенные .между напорными линиями аb и АВ, находятся под давлением, меньшим атмосферного (р<ро. но Р>Ро—всасывающий или сифонный водовод); водопроводные ветви, расположенные ниже напорной линии аb, находятся под давлением, большим атмосферного (р>р₀)‘> для водовода, расположенного по линии аb (между резервуарами I и II), давление равно атмосферному (р=Ро — открытые водоводы-каналы). В Т. azcb на участке, лежащем выше напорной линии аb и имеющем в высшей точке ^воздушный клапан (вантуз) для выпуска накопляющегося там воздуха, вода (рассматривая вопрос теоретически) будет течь до тех пор, пока h < 10,33 метров Практически вследствие потери напора от трения величина h не превышает 8,04-8,5 м, при проектировании же ограничиваются выбором этой величины от 5,5 до 6,0 л». Т. аухсb (фигура 9), расположенный ниже напорной линии ab, может занимать с тео-ретич. точки зрения произвольное положение в продольном профиле, с практической же точки зрения необходимо учитывать все изгибы, устанавливая во всех высших точках (ж) перегиба трубопровода воздушные вантузы (фигура 10),

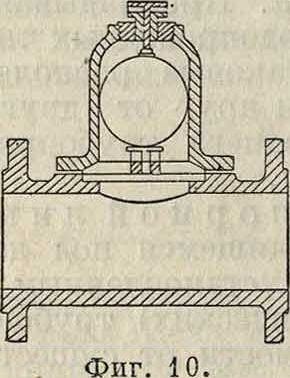
Фигура 11.

а во всех низших точках (у, е) перегиба Т. (фигура 9)—спускные приспособления или осадочные вантузы (фигура 11).

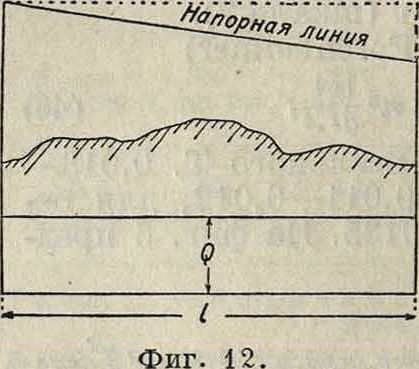
Т. с естественным напором (гравитационные водоводы) должен быть так рассчитан, чтобы была вполне обеспечена подача воды на определенное число лет во все пункты потребления при наименьших капитальных затратах. При водопроводах с естественным напором учитывается обыкновенно лишь минимум расходов в отношении самих водоводов. Для определения наивыгоднейших размеров водовода необходимо знать по ложение экономичной напорной лини и, имея в виду, что последняя, как выяснил Маннес (Marines) в своих исследованиях, отвечает наименьшей стоимости водовода, а) В о-довод с одним транзитным расходом воды. Если водовод должен пропускать определенное количество воды Q без того, чтобы расходовалось что-либо в пути, то напорная линия будет прямая (фигура 12).

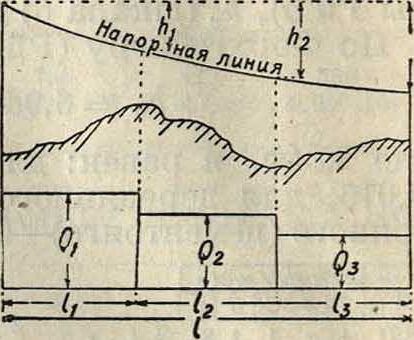
Фигура 13.

Диаметр м. б. определен по модулю расхода К, вычисляемому по ф-ле:

К--

Yi

(55)

h

где ί=γ. б) Водовод с различным транзитным расходом воды на участках. Если водовод состоит из отдельных неравных участков, пропускающих разное количество воды, то есть вода расходуется в конце каждого участка, то напорная линия (фигура

13) представит собою и з о г н ут ую вниз кривую.

Дляопределения ее положения необходимо вычислить потери напора h_lt h₂,

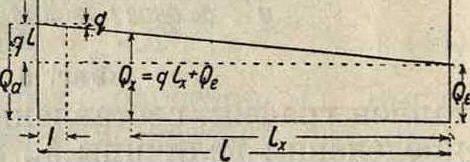
h.

К

характе-

Фигура 14.

ризующие эту кривую, в) Водовод с транзитным и путевым расходами воды. Если водовод расходует воду равномерно по пути с отдачей воды в конце, то напорная линия будет, как и в предыдущем случае, изогнутая вниз кривая (фигура 14).

Для определения потери напора в Т. можно воспользоваться также ф-лой:

h ~‘^l WY /грч

"ю— _Кл · —(об)

или более упрощенной ф-лой:

}{ — ¹ (Qa + Qc ² с-m,

где q—расход воды, приходящейся на единицу пути, Q_a — количество воды, поступающее в начале рассматриваемого водовода (общий расходводы), Q_e—транзитный расход воды, г) Для водоводов с различным транзитным и путевым расходами воды на участках напорная линия рассматривается для каждого участка отдельно, причем в каждом участке она изобразится изогнутой вниз кривой (фигура 15). По отношению к крайним пунктам

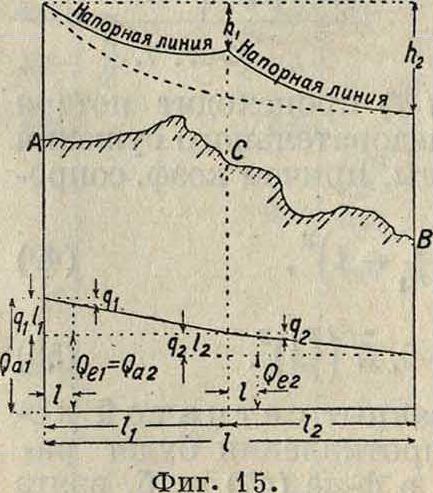
А и В экономичная напорная линия изобразилась бы пунктирной линией, но, рассчитывая водовод по этой наивыгоднейшей напорной линии, мы не получили бы достаточного напора в точке С. Потерю напора определяют поэтому последовательно для каждого участка по формуле:

^п ⁼ (Qan] Qan ~ Qen Qen ) + ^п-1> (°8)

где Q_an—количество воды, протекающее в начале и-го участка, в л/ск (общий расход воды и-го участка), Q_m—количество воды, протекающее в конце п-то участка, в л/ск (транзитный расход η-го участка), q_n—расход воды на единицу длины (1 п. м) п-то участка в л/ск, С— коэф., равный

__^ .,-QN

2 V ^1,1 + 2 (я«^п V ®^ап~ Qe«) J

Qkn—равномерный расход воды на п-м участке в л/ск (путевой расход воды на п-м участке), 1_п—длина и-го участка.

Т. с искусственным напором. При определении диам. нагнетатель-н ы х Т. следует в каждом отдельном случае исходить из условий, чтобы затраты на сооружение Т. и на машинное оборудование станции, с одной стороны, и капитализированные эксплуатонные расходы, с другой,—были в общей сумме минимальными. Этому наивыгод-нейшему диам. Т. отвечает наивыгоднейшая скорость движения воды. Для выбора экономически выгодного 0 нагнетательного Т. надо соблюсти условие, чтобы годовые расходы на оплату процентов на затраченный капитал, на по^гашение его и эксплуатонные расходы (обслуживание и содержание Т. и части машин, необходимых для преодоления сопротивления движению воды в трубах) были наименьшие. На оснозании этих данных наивыгоднейший диам. Т. определится из ф-лы, выведенной автором статьи в 1929 г.

V-

320 Q*h_m>а_г(р_т+±°^ t-kt,)

лЗс2р_г. k_r ·γ· р

(60)

где Q—средний годовой расход воды в м³/ск, к_т—стоимость машин за 1 секундо-метротон-ну произведенной работы, Тс_г—стоимость, 1 то труб, включая и все расходы по их прокладке, к_ь—стоимость одного сило-часа работы машин, Vm—проценты на затраченный капитал, на погашение его и на содержание части машин, необходимых для преодоления сопротивления движению воды в трубах, р_г—то же касательно самого Т., η—кпд насосов, t—число часов работы машин и насосов в течение года, у— вес 1 м? труб в то, р—избыточное давление воды в Т. в atm, с—коэф. Шези, а_г—допускаемое напряжение материала стенки Т“. в килограммах/см². Подставляя в формулу (60) известные величины, мы можем зависимость между d и Q выразить упрощенной ф-лой:

da= 1,2 Q⁰-¹³;

(61)

ф-ла эта применима для предварительных приближенных расчетов. В 1931 г. Ля.льгя.уз (Dahlhaus) дал приближенную по результату к формуле (61). Ф-ла_/1ет вид:

d=1,26 Yq(

Последняя ф-ла, но с коэф-τί» дана раныце Вейраухом (К. ^т“"

по ней по мнению Дальгауза для Т. больших размеров получались излишне большие диаметры. Наивыгоднейшая скорость движения воды в нагнетательном Т. может быть определена по формуле Форхгеймера:

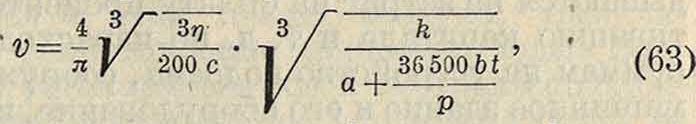
где η—кпд насосов, с—коэф. трения, к—стоимость 1 п. м Т. диаметром d=1 м, а—стоимость 1 1Р двигателя, b—эксплуатонные расходы на 1 И? в час, t—число часов работы насосов в течение суток, р—размер процентов. По другой формуле Форхгеймера

(64)

_ 0,5 0,6

^ν~ψ~β ψβ’

где β—частное от деления числа годовых часов действительной работы машин на число часов в году 365x24.

Напорные Т. силовых установок. Для определения наивыгоднейшего диаметра d стального напорного Т. Бауерсфельд (W. Bauersfeld) и Лудин (A. Ludin) дали следующие ф-лы:

^Й-|У

(¹⁺TFu)

(65)

для верхнего участка напорного Т. с наименьшей толщиной <5₀ его стенок

V

+ t-iQj 4~ ··)

(¹⁺i!)) ^y/t2tf°^w2

(66)

Принимая η_χ=0,82, ??₂=0,92, %=0,85, р=10, у=7,8 и (t_xQ + tiQl + .)= tQ^z, можно ф-лы (65) и (66) представить в более упрощенном виде для приближенных расчетов по ним. Наивыгоднейший диам. d стального Т. будет тогда равен

d =

V¹

,57 aw₁tQ3 _ф

(67)

для верхнего участка Т. с наименьшей толщиной <5₀ его стенок для промежуточных частей Т. (для определения увеличения диам. труб водопроводной линии снизу вверх)

^d*=Vw_x-^d· (⁶⁹>

В ф-лах (65—69) означает: d—внутренний диам. в м г _х—кпд турбины, обыкновенно равный 0,82; »?₂ — ^КПД генератора, обычно равный 0,92;

коэф. надежности шва (0,70—0,90); σ—допускаемое напряжение материала Т. в т/м²; <ι, f₂—число часов работы машин при расхо-Д^е QnQi,···, t—число часов работы всех машин в течение года; р—процентная прибавка к весу труб для учета веса фланцев, муфт, компенсационных частей и прочие (обыкновенно p^lQ%); у—уд. в материала Т. (обыкновенно у=7,8); Q_x, Qа, .—расход воды в м³/ск; Q—средний расход воды в м³/ск, к-рый берется несколько бблыпим среднего годового расхода воды; с—ткоэф. Шези; Н—общая высота напора в м вод. ст. у нижнего конца T.; w±—средняя стоимость 1 kWh у зажимов генератора; w₂—годовая стоимость 1 то стали в деле, включая расходы по отрывке рвов, монтажу, доставке и прочие; <5₀—наименьшая толщина стенок труб в м d_x—

внутренний диам. труб в произвольном месте Т. в м Н_х—общая высота напора в м вод. ст. в произвольном месте Т. Величина w_x получается от деления годовых расходов на число годовых kWh, причем годовые расходы складываются из затрат на оплату процентов, амортизацию капитала и т. д. по израсходованным суммам на устройство водоема, сооружение Т., машинное здание и его оборудование, исключая трансформаторы и устройства по распределению тока. Величина w₂ определится, если годовые расходы по Т. разделить на полный вес последнего; годовые расходы в данном случае состоят из затрат на оплату процентов, амортизацию капитала и т. д. по израсходованным суммам на сооружение Т., включая все расходы, связанные с постройкой его. Т. к. коэф. Шези с зависит от диам. d, то принимают с для определенного d, и в случае несовпадения d с расчетным повторяют расчет с новым принятым с и т. д. То же относится и к высоте напора Я, имея в виду, что динамич. повышение напора также зависит от d. Диам. напорного Т. силовых установок имеет вверху линии наибольшие размеры, книзу линии диам. Т. уменьшается, наоборот,—толщина стенок труб сверху вниз увеличивается (обыкновенно при стальных Т. последовательно на 1 миллиметров). Бетонные опоры напорных Т. силовых установок должен быть рассчитаны на растяжение, сжатие, сдвиг по общим правилам строительной механики, учитывая при этом все действующие силы. Для лучшей передачи давления на опоры к трубам прикрепляют кольца из уголковой стали (не менее двух колец). По Бундшу (F. Bund-schu) наивыгоднейший диам. стального Т. может быть определен по упрощенным ф-лам:

а) турбинная силовая установка:

, ⁷ А60 570-w_xtQ

^а=У ^Н«Г”’

б) насосная установка:

Я=л/~ 111

У c-Hw₂ > *

в) турбинно-насосная установка:

d _ 60510(v>_xtQa+t,8lvj_zt_pQp)

У C*Hv>₂ ’

где w₃—стоимость 1 kWh на зажимах мотора (насосный ток), Q_p—среднее количество воды, подаваемое насосами, в м³/ск, t—число часов работы турбин в течение года, t_P—число часов работы насосов в течение года, остальные величины,·—как выше.

Расчет кольцевой водопроводной сети труб. В кольцевой сети приток воды ко всякому пункту потребления может быть с двух сторон, что обеспечивает снабжение водою потре--1 бителей. Пусть ма-_L гистраль, идущая __f от напорного резервуара (фигура 16) до кольцевого узла 1, имеет длину 1₃ + 1_Хи диам. d_x; на участке 0—1 этой магистрали расходуется вода в количестве Q!, в то время как другая часть воды в количестве Р_х протекает по всей длине 1_Х и распределяется по разветвляющимся от узла 1 кольцевым линиям соот

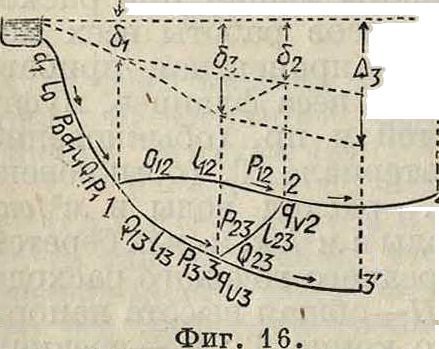
ветственно их диам. d и относительным потерям напора г=^. Обозначим для кольцевой линии 1—2: расход воды Q₁₂, протекающее количество воды Р₁₂, длину ϊ₁₂, диам. d₁₂, потерю напора h_X2 и т. д.; соответственно этому должен быть обозначены величины других кольцевых линий; от узлов 2 и 3 идут ответвления 2—2 и 3—3 с расходом воды q„ и q_vz полная потеря напора на концах этих ответвлений равна Л₂ и Δ₃. Для наивыгоднейшей с экономической точки зрения комбинации размеров рассматриваемой кольцевой сети потери напора 01, <5₂, <5₃₎. в кольцевых узлах 1, 2, 3,. должен быть так подобраны, чтобы стоимость устройства А этой сети была наименьшей. Если, как выше, стоимость 1 ж проложенных труб равна к,., то величина А будет равна:)

А=щк_г [d_x (l₃ + l_x) s_x + d_X2l_l2s_L2 + d_X3l₁₃s₁₃ + + d₂₃l_2Ss₂₃] (магистраль и кольцевая сеть) +

+ myk_r (i d_2nl_2ns_2n + Σ d_3nl_3ns_3n) (ответвления).

Если в ур-ии h=el(p + aQ)²d~^b взять для краткости р + <*Q=q, то получим соответственно:

δ_χ=ed_x³ [l₀ (р_х + Q_L)² + l_xq_x], h_x2=δ₃=εά_Χ3

^13 ⁼ ^з ^—=εί*03⁵ ^1з2?з>

h₂3 ⁼ ^3 ^2 ^{= ε}^23 ^2з31з“

(71)

Для ответвления 2 с расходом воды q_v2 наивыгоднейший диам. будет равен

„‘/а

Чгп

--ГГ· (⁷²)

(μ·₂μ₃ .-.μη) ^,6

В ур-ии для А величины в_х, <3₂, <5₃,. будут дА д А

переменные, поэтому при=0,=0 ит. д. получится наиболее экономичное решение. Ур-ие напора в узле 1 будет

Л_И=Л₁₂ +Л₁₃, (73)

где

1>Ы=«5Γ^δ/5(ϊο + ϊι) [ϊχ (Pi + Qi)² + hull¹⁵ (74) (напор в магистрали),

D i2=(δ₂ - д_х)-*1чг₂* qlL* (74а)

(напор в кольцевой линии 1—2). Также напишется ур-ие напора для кольцевой линии 1—3. Ур-ие напора в узле 2 будет

Л₁₂=Л₂₃+Л_Я2, (75)

где

D_m=(J, - <5₂Г⁶^ М1!*Ы_т, (75а)

M_v2 — ϊ₂ιί₂ί³ 4“ Т ^23*?₂з³ (/^гг^гз) “Ь

+. + (μ₂₂μ₂₃. ftj_s)^5/e, (756)

N_v2=l_2lp₂[^a + h₂qli^zMM^U+ ··· +

+ hzqli* (,«22^23 · · /^{2зГ^1/б· (^75в)

Ур-ие напора в узле 3 будет

Л₂₃=D_a + Аз. (76)

Решая эти ур-ия узлового напора и прибегая к приближенному способу нахождения искомых величин δ_χ, δ₂, δ₃, получим три ур-ия (77):

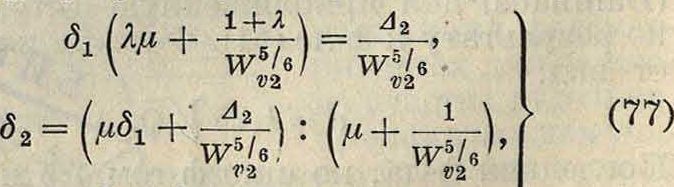
^з — <5χ + Ψα (δ₂ — <?ι).

В этих ур-иях означает:

[С

ι*»+$)·«

ju=’l:[W_la—

w_bl=(l₀

4β

(9>8ΐ-1)^β/5-*i)[I.(Pi + 0ι)· + ϊιίϊ1

W_u=№q]L·, W_lz=№qU°,

Чъ_аЧь

23 Ϊ23 >

= м‘₃^/5я_г.₂, : Л#»#“,

w₂₃=№ W, 2

(77a)

φ₃₁—йюэфициент, определяемый приближенно по напорным линиям. Найденные величины (5_Х, δ₃, б₃ подставляют в ур-ие узлового напора, составленное для узла 3, причем должно получиться тождество, в противном случае решение повторяют с новым φ₃₁ до получения удовлетворительного результата. Зная величины δ, определяют по ур-ию напора в отдельных водопроводных линиях наивыгоднейший диаметр труб. Ур-ия узлового расхода воды напишутся для рассматриваемого случая сл. обр.:

для узла 1

Pi=Pl2 + Qn + Ри + Qis> для узла 2

Pi2=in + Раз + *?2з>

для узла 3

Ρ23 + Ρΐ3=2*3· J

При распределении наивыгоднейшим образом определенных количеств воды (величин р) по линиям кольцевой сети следует направлять (при расчете) транзитное количество воды только по одной линии, останавливаясь в конечном результате на той, которая окажется наикратчайшей и большего диаметра.

Принципы начертания сети. В общем следует придерживаться следующих принципов начертания сети труб: а) высота подъема воды из источников в бак (резервуар) должен быть возможно меньшей, т. к. всякое увеличение ее вызывает постоянные излишние затраты на топливо и требует более сильных машин;

б) распределение давлений в сети должен быть по возможности равномерным; в) начертание всей сети должно отвечать наименьшей стоимости ее устройства и эксплуатации; г) в случаях повреждения одной из главных линий в каком-либо пункте ее водоснабжение сети не должно расстраиваться сколько-нибудь заметным образом. Условия первое и второе определяют место водонапорной башни, располагаемой обыкновенно возможно ближе к центру потребления воды. Второе, третье и четвертое из перечисленных условий влияют вместе на начертание самой сети труб, делаемой возможно более сомкнутой во всех своих частях для обеспечения питания каждого отдельного пункта водоснабжения. Условия наименьшей стоимости и равномерности давлений в сети приводят к следующим требованиям: 1) магистрали следует проводить по участкам наибольшего потребления воды и по наиболее возвышенным частям населенного места; 2) магистрали, а за ними и линии первого порядка следует вести по возможности по уклону вниз.

Арматура трубопроводов. Арматурой служат: задвиэюки (смотрите), вентили (смотрите), клапаны (смотрите), вантузы, компенсаторы (см.

Трубы специальные), гидранты (смотрите), водоразборные краны (смотрите), водомеры (смотрите) и прочие Воздушные вантузы (фигура 10) устанавливаются в повышенных точках Т. для обеспечения правильного удаления из них скапливающегося в этих точках воздуха, увеличивающего сопротивление движению воды. Вантузы эти устанавливаются в смотровых колодцах. Воздушные клапаны устанавливаются не только в повышенных точках водопровода для удаления скапливающегося здесь воздуха, но и для впуска воздуха в трубы водопроводов больших диаметров, притом длинных, особенно если они уложены с крутыми подъемами

и спусками, чтобы скорым впуском необходимого количества воздуха предупреждать опасности образования вакуумов и гидравлических ударов при опорожнениях труб, влекущих за собой сплющивание тонкостенных стальных Т. или разрыв чугунных и железобетонных Т. Если на сети Т. нет вантузов или их имеется мало, то всякие опорожнения магистралей следует производить очень медленно, соблюдая большую осторожность. Ту же осторожность необходимо соблюдать также при наполнении водопроводных линий. Если в какой-либо части сети необходимо уменьшить давление, не прерывая сеть, то вставляется предохранительный клапан (смотрите Клапан), в котором часть давления воды поглощается упругостью пружины, действующей на клапан; давление пружины м. б. регулировано действием винта. На Т. в пониженных

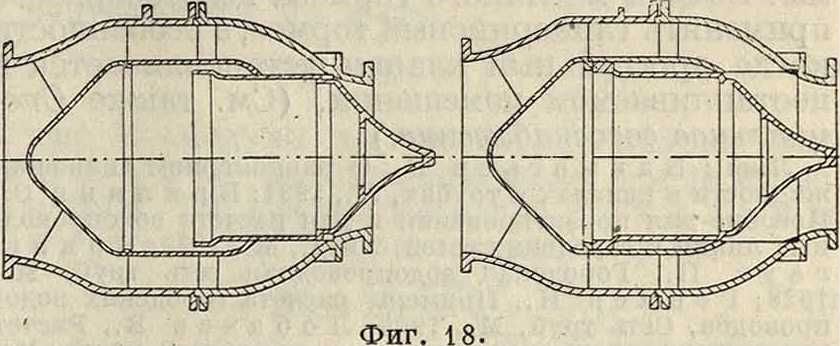
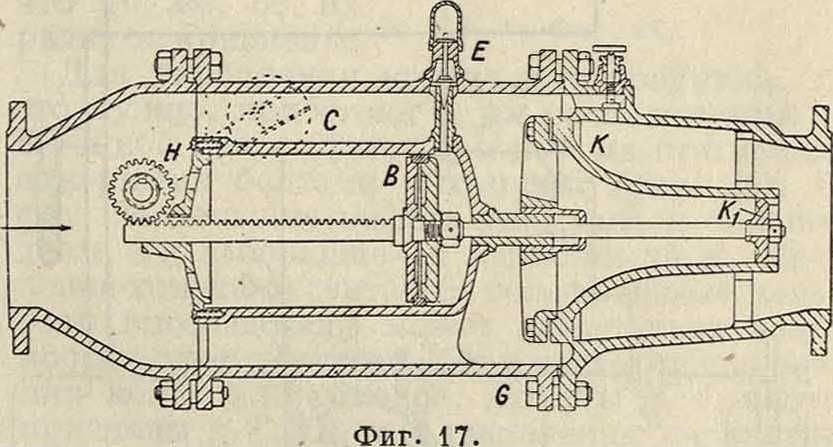
точках должен быть установлены выпуски для опорожнения участка водопровода от воды на случай ремонта, переустройства водопроводных линий и прочие Такие выпуски необходимы также при промывках и очистках труб. Особенное значение имеют клапаны, запирающие Т. в случае его разрыва. На фигуре 17 показана схема такого клапана конструкции Бопп и Рейтер, состоящего из кожуха G с большим запорным конусом К и с тормозным цилиндром С, к-рый имеет поршень В и штанги, соединенные с нагруженным рычагом Я. Кроме того тормозной цилиндр имеет регулирующий вентиль Е. В запорном конусе К имеется маленький клапан К_х, предупреждающий появление больших гидравлич. ударов при остановке движения воды. Скорость закрытия Т. регулируется вентилем Е. На фигуре 18 представлен запорный клапан сист. Джонсона, получивший широкое распространение за границей, особенно для Т. гидросиловых установок. На фигуре 19 дана схема комбинированного

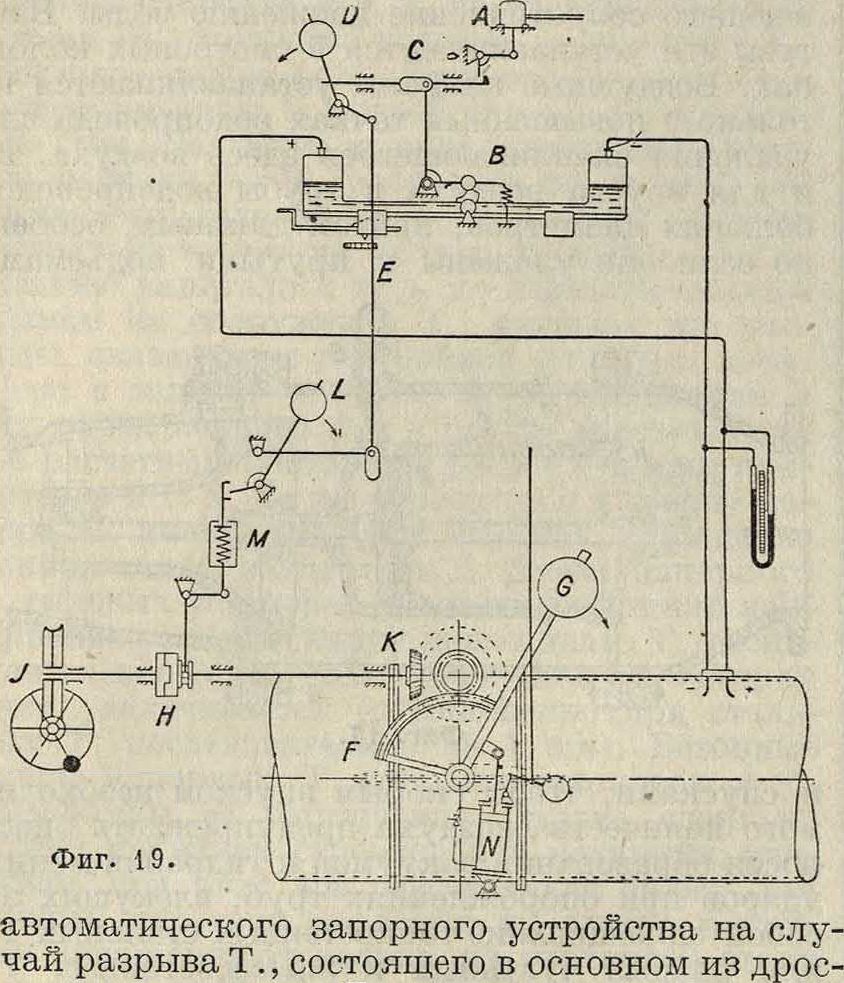
сельного клапана F- с противовесом G, соединенным с масляным тормозом N и с зубчатой передачей К (передачи на расстояние), для произвольного выключения или включения устройства и сигнального приспособления, причем: А—подъемный магнит, В—ртутные рычажные весы, С—запорное устройство, D—противовес, Е—тяга, L—противовес, М—пружинный контакт, Н—сцепление, J—червячная передача. Дроссельный клапан закрывается, как только скорость течения воды в Т. превзойдет определенную безопасно-максимальную скорость. Взаимодействие частей устройства ясно из схемы. Взамен масляного тормоза целесообразнее применять глицериновый тормоз, в особенности когда дроссельный клапан устанавливается в неотапливаемом помещении. (См. также Специальное водоснабжение.)

Лит.: Бахметьев Б., О равномерном движении жидкости в каналах и трубах, Л., 1931; Брилинг С., Пособие для цроектирования и для расчета водопроводных линий и городских сетей, 2 изд., М., 1930; Бринк-гауз П., Городская водопроводная сеть труб, М., 1928; Гениев Н., Примеры расчета городских водопроводов, Сеть труб, М., 1929; Лобачев В., Расчет противопожарных водопроводов и пожарных струй, М., 1929; Максименко Ф., Курс гидравлики, М., 1921; Павловский Н., Гидравлический справочник, Л., 1930; Саткевич А., Руководство к проектированию систем водоснабжения, ч. 1, СПБ, 1900; Справочник для инженеров строительной специальности, М., 1928;

Bauersfeld W., Die Wirtschaftliche Berechnung der Hochdruckturbinenleitungen, «Z. 1. d. gesamte Turbinen-wes.en», 1907, 28; Biegelelsen B., Berechnung des wirtschaftlichen Rohrdurchmessers d. Wasserleitungen, Lpz., 1918; Biegelelsen B. u. Buko w ski, Grundlagen der Wasserrohrleitungen, Miinchen, 1914; ВгавбеК., Rohrnetzberechnung in der Heiz- u. Liiftung-techmk, 2 Auli., B., 1918; Bundschu F., Druckrohr-ieilungen, 2 Aufl., B., 1929; Durand W., Hydraulics of Pipe Lines, N. Y., 1921; Gibson A., Hydraulics a. Its Applications, 2 ed., L., 1920; H r u s c li k a A., Die Berechnung yon Druckrohrleitungen, «Ztschr. d. Elektr. Verems», W., 1922., 46; Hruschka A., Die Druck-rohrleitungen der Wasserkraftwerke, W., 1929; к г i s c h-mer 0., Untersuchungen liber den Gefallsverlust an Reclien, «Mitt. d. Hydr. Inst. d. techn. Hochschule»,

Mch., 1926, H. 1; К 1 e i η 1 о g e 1, Rohrleitungen f. hohen Innendruck, «Der Bauingenieur», B., 1920, H. 10; Kreitner H., Druckschwankungen in Turbinenleitun-gen, «Die Wasserwirtschaft»,Wien, 1926, H. 10; L 6 vv у R., Druckschwankungen in Rohrleitungen, Wien, 1928; L u d i n A., Die wirtschaftliche Bemessung von Triebwas-serleitungen, «Ztschr. f. d. ges. Turbinenwesen», 1914, 13; Lummert R., Neue Methodend.BestimmungderDurch-lassigkeit, Braunschweig, 1917; M annes H., Die Berechnung yon Rohrnetzen stadtischer Wasserleitungen, Mch., 1912; Mis es R., Elemente d. technischen Hyd-romechanik, Lpz., 1914; Mlses R., Berechnung yon Ausfluss- u. Ueberflusszahlen, «Z. d. YDI», 1917, B. 61; Poschl Th., Lehrbuch d. Hydraulik, Berlin, 1924; В 1 e i c h Fr. u. lelan J, Taschenbuch f. Ingenieure u. Architekten, Wien, 1926; Forster M., Taschenbuch ftir Bauingenieure, B., 1928; Schwedler F-, Handb. d. Rohrleitungen, Berlin, 1 932; «Das Gas- u. Wasserfach», Mch., B.; «Proc. Inst. Civ. Eng.», N. Y.; «Transact. Amer. Soc. Ciy.Eng.», N. Y.;«Der Bauingenieur», B.; «Eng.Rec.», N. Y.; «Die Wasserkraft», В. С. Брилинг.

Фасонные части T.—тройники, крестовины, колена, отводы, переходы, муфты, патрубки, заглушки .а) Тройники и крестовины

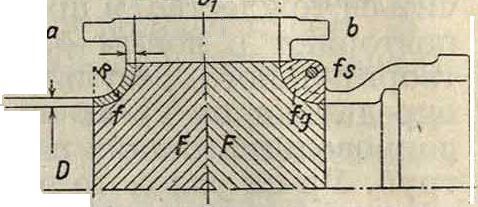
применяют для присоединения к трубопроводу всякого рода ответвлений, для установки задвижек, пожарного _ крана, вантуза и прочие Наиболее опасное сечение у тройников и крестовин—горловина (фигура 20,а),к-рая воспринимает давление, изображенное площадью F, и испытывает на

Фпг. 20.

пряжение

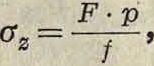
(79)

где р—давление воды в трубе в килограммах [см², f—площадь сечения горловины в см². Чем меньше радиус закругления горловины, тем меньше сечение (при равной толщине стенок фасонной части) и тем больше следовательно напряжение, испытываемое горловиной. Указанный выше расчет является приближенным, т. к. в действительности давление, начиная от цилин-дрич. частей и кончая горловиной, возрастает последовательно. Если нельзя придать горловинам чугунных тройников и крестовин более плавных закруглений, компенсирующих избыточное давление, то утолщают горловины ребристыми выступами или увеличивают толщину их стенки или усиляют горловины с помощью стальных болтов, закрепленных (в нагретом состоянии) в проушинах утолщенных частей горловин. Усиление при помощи ребер трудно поддается расчету вследствие неопределенности распределения сил; кроме того могут получиться нежелательные напряжения чугуна. Если в этих ребрах сделать отверстия для скрепления ребер между собой болтами, то является возможным увеличить прочность горловины в 3—5 раз. Если обозначить через f_g и а_д соответственно площадь поперечного сечения и допускаемое напряжение чугуна, а через f_s и a_s соответственно площадь поперечного сечения и допускаемое напряжение стали, то мы можем написать (фигура 20,& и 21):

fg^ag + f_s°s=F-P· (80)

Так как

F=[(0,5 Ό + R) (0,5 Ώ₁- - R) — цр]> (81)

то по формуле (80) получим и=[(°>^5Ό+ Я)(0,5Di (82)

L -I у у

Поперечное сечение состоит из площади сечения горловины и площади ребра, что м. б. выражено ур-ием:

⁽⁸³⁾

откуда

При расчете рассматриваемых фасонных частей сначала определяют размеры усиливающих ребра болтов и радиус закругления R. Радиус г определяют по ф-ле

r=d+ 5 -f-10 миллиметров.

Толщина стенки горловины м. б. определена по формуле:

«=+ (85)

где σ_ζ—допускаемое напряжение на растяжение в килограммах/см²; С=7-(-10 миллиметров—практическая прибавка для чугуна.

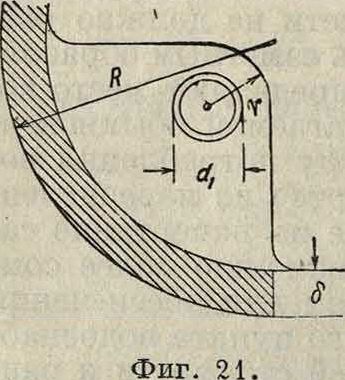
Применяются тройники сферической формы, в пользу которой приводятся следующие соображения: при отливке исключается возможность образования пустот, получается более плавный переход по сравнению с тройником цилиндрической формы, нижняя часть шара удобна для присоединения трубки к конденсационному горшку при устройстве паропроводов (фигура 22). Такой тройник м. б. рассчитан по сл. ф-лам:

1) при малой толщине стенок сравнительно с диаметром (когда напряжения в стенках можно принимать равномерно распределенными)

5=4^ +С; (86)

2) при сравнительно большой толщине стенок тройника

a=o,5i>(^±Mf-i) + c. ⁽⁸⁷⁾

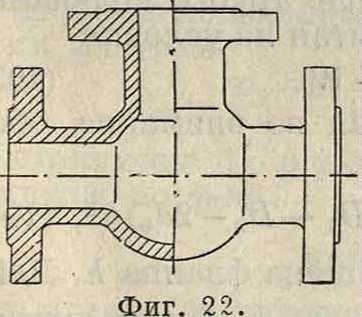
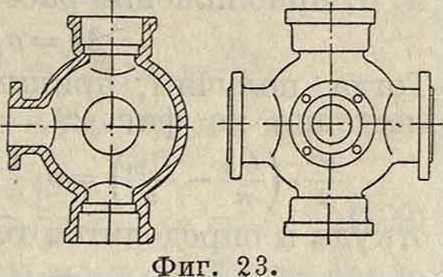
Для лучшего распределения воды по всем направлениям применяется шарообразная крестовина, представленная на фигуре 23.

б) К о л е н а (при центральном угле в 90°) и о т в о д ы (при центральных углах в 45°, 30°, 15°) служат для плавного перехода от одного направления к другому (для перемены направления). При движении жидкости через колено или отвод со средней скоростью v и при давлении р в трубопроводе необходимо считаться с силою, стремящейся переместить колено по направлению биссектрисы угла между направлениями соединяемых линий труб. Сила, которая при этом развивается, определится из формулы

Р=1,57 JD*(p+- S?) sin |, (88)

где Ώ—внутренний диам. колена или отвода, у—вес единицы объёма жидкости, д—ускорение силы тяжести (д=9,81 м/ск²), а—цен-

тральный угол колена или отвода. Когда ста-тич. давление p_s внутри трубопровода больше давления р при движении жидкости, то силу Р следует определять по ф-ле:

Р=1,57 D²p_s sin “· (89)

Из этого равенства видно, что сила, стремящаяся сдвинуть колено или отвод в сторону, противоположную углу поворота трубопровода, зависит от давления в последнем, от диам .колена или отвода и от их центрального угла или, что то же, от их радиуса кривизны.

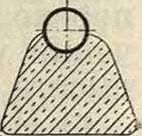
Для укрепления колена или тройника, где это нужно, прибегают к их расположению на бетонной опоре (фигура 24) или к их стягиванию анкерными болтами в хомутах (фигура 25). На. фигура 24 меньшие цифры относятся к большим диам. Т., а большие—к меньшим диам. Крепление хомутами считается более рациональным, если впоследствии может встретиться надобность в производстве работ в местах расположе-,ния колен или отводов. Хомуты должен быть плотно пригнаны к Т. Против ржавления соединение обматывают джутом и осмаливают. Для сборных колодцев, напорных резервуаров, часто-для постановки пожарных кранов и в тому подобных случаях пользуются коленами с

Фигура 24.

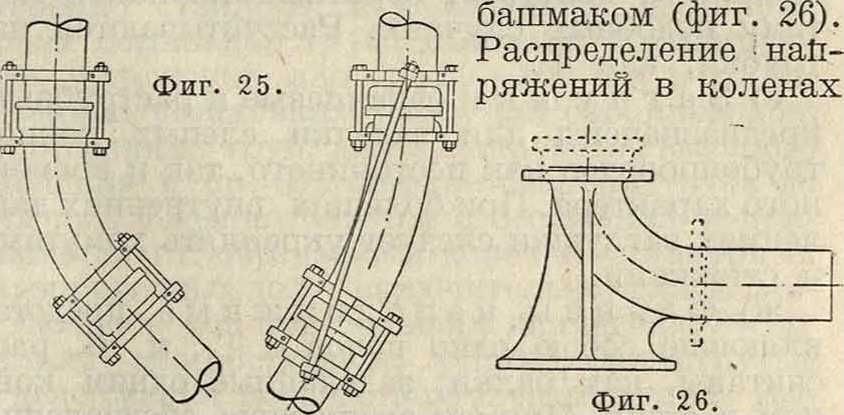
и отводах не прямолинейное, а криволинейное и различное для каждого отдельного случая.

Чугунные и толстостенные стальные колена, подверженные изгибу, рассчитываются по ф-ле:

М_ь=Е I

tH)·

(90}

где Е—модуль упругости, I—момент инерции, r_k и г“—радиусы кривизны оси до и после изгиба. Тонкостенные стальные коленадолжен быть рассчитаны по ф-ле:

(91}

" Vrv r_kJ

где в первом приближении величина κ по Карману (Karman) берется равной

1 9 * 1 10+ 12 Я2 ’	(92}
А =^>0,3.	(93}

где

Напряжение σ на расстоянии у от нейтрального волокна в первом приблиясении приравнивается:

"-.«•ЧНИ^ЫЯ <*>

По итальянским нормам колена рассчитываются на допускаемые напряжения на 10% меньше, чем принятые для прямых Т. из. того·

же материала, причем стенки колен должен быть по крайней мерена 2 миллиметров толще стенок прямыхТ.

в) Переходы применяются для плавного перехода чаще от большего диам. к меньшему и реже наоборот. Переходы надлежит рассчитывать по ф-ле

P_W=(F₀-F_U)H, (95)

где P_w—давление воды на переход в т, F₀— площадь поперечного сечения широкой части перехода в м², F_u—площадь поперечного сечения узкой части перехода в м², Н—полная высота напора в середине перехода в м вод. ст. г) М у ф т ы употребляются: при ремонте, в случае устройства ответвления от магистрали, там, где надо поставить более длинные патрубки или удалить стык от слишком близкого соседства с другими фасонными частями. При подвижных Т. между ними оставляют зазор примерно в 5 сантиметров и ставят муфту, чем устраняется опасность появления в металле вредных напряжений. Разъемные муфты применяются для перекрытия дефектного места. Расчет муфт ничем не отличается от расчета прямых Т. (неразъемные цельные муфты) и свертных фасонных частей (разъемные муфты).

д) Патрубки представляют собою короткие Т. с фланцем на одном конце и раструбом на другом или с фланцем на одном конце и буртом на другом; служат для перехода с фланцев на раструбы и, наоборот, при установке задвижек, вантузов, обратных клапанов и в дому подобных случаях. Рассчитываются патрубки, как Т.

е) Заглушки (фланцевые и раструбные) предназначены для заделки слепых концов трубопроводов как постоянного, так и временного характера. При больших внутренних давлениях заглушки следует укреплять хомутами и_х стяжками.

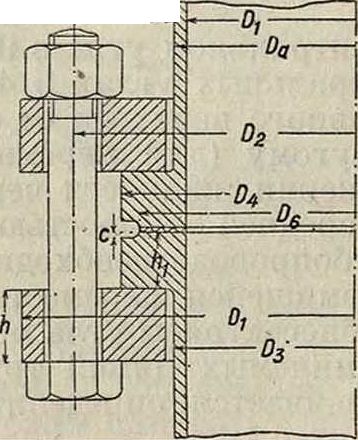
*ж) Фланцы неподвижные, представляющие собою одно целое с Т., м. б. рассчитаны, как балки, заделанные одним концомв стену. Примем следующие обозначения

(фигура27а, 276): ft-толщина фланцав см, р — давление воды в трубе в килограммах/см², D—внутренний диам. Т. в см, D_l—внешний диаметр Т. в см, b—ширина куска фланца, приходящаяся на один болт, в см, чх—плечо (расстояние от наружной поверхности Т. до центра болта) в см, п—число болтов, а_ь—допускаемое напряжение на изгиб в килограммах/см², Р—нагрузка, приходящаяся на один болт. Изгибающий момент в данном случае выразится следующими двумя равенствами:

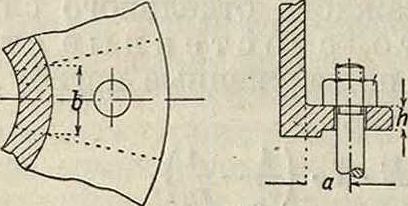
Фигура 27а.

Фигура 276.

М=-

4 гг

(96)

M=W-a_h=^^=—¹^· (97)

⁰ 6 6 71 ⁴

Приравнивая последние выражения в обоих равенствах и определяя ft, получим с прибавкой практич. величины С ур-ие:

-⁼¹’²³¹⁾УШь^+с·. ⁽⁹⁸⁾

Болты рассчитываются по ф-ле:

где f—площадь поперечного сечения стержня,

ft =

σ_ζ—допускаемое напряжение на растяжение. Напряжение фланца от изгиба получится равным (фигура 28)

Ρ·α

W

где

πΏ mV.

Dz — D,

W:

πϋχ (/l + C)².

; (loo)

4 ’ 2

D_m—средний диам., считая по прокладке. Толщина фланца должен быть не менее ⁵Д толщины болта, дабы не под- г~ i----

вергать стенку Т. i

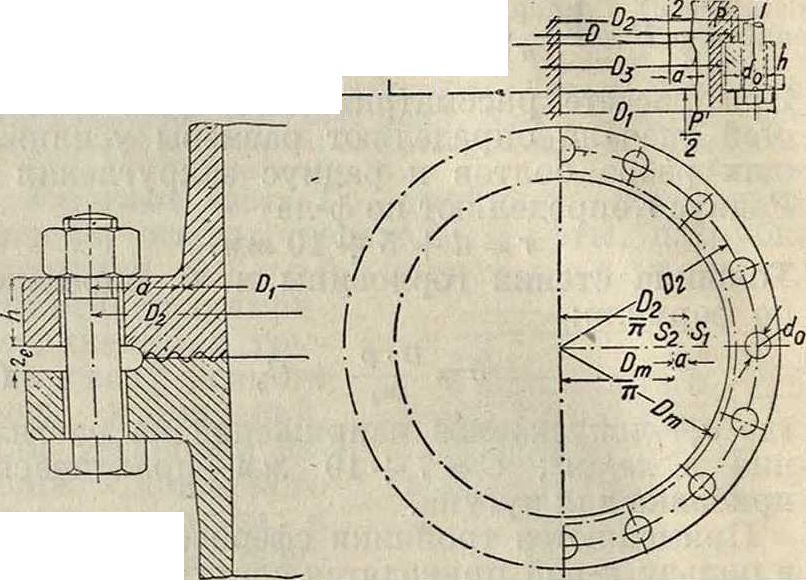
Фигура 28.

Фигура 29.

чрезмерно высоким добавочным напряжениям. По Баху толщина неподвижного флан-ц а определится из ф-лы:

ft=]/"

К·*·¹

8 (П_г-П-2е)а⁷ (¹⁰¹>

где D_d—диам., считая между крайними точками прокладочного шва, Of—внешний диам. фланца, е—диаметр отверстия для болта, I— расстояние от середины ширины прокладочной площади до окружности,^ проходящей через крайнюю точку отверстий для болтов, за вычетом толщины стенки Т., а—напряжение во фланце. Для воспринятия произвольной осевой силы S толщина фланца по Баху должен быть

^{h =} MJ)_a-D-bе)о (¹⁰²)

Подвижной фланец, удерживаемый на Т. наваренными на конце трубы кольцами, м. б. приближенно рассчитан из условия

М=о_ь· W. (ЮЗ)

Тогда получим, принимая во внимание обозначения на фигуре 29,

т (тг-пг)=^ап ^ ^{2do) ha}’ ⁽¹⁰⁴⁾

откуда и определится толщина фланца ft. Дей-L·

	Т	-ЗД Ί !	0, ! оа-
‘Л	тТ	Щ ч
	1	ШФ	“2
	1	,1ш!
	I	ш
Щ		рг ^
		г	_

Фигура 31.

Фигура 30.

ствующее в болтах усилие Рм. б. взято равным (фигура 29, 30 и 31)

P=l>²mp= V p. (105)

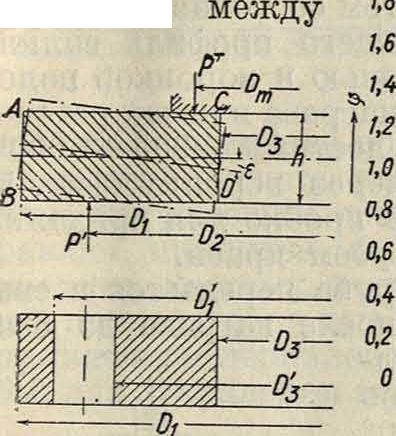
Более точный расчет, учитывая и поворот фланца на угол ε (фигура 32), получается по ф-лам Вестфаля (WestpHal·:

„, 3 P(D₂-D_m)

^σ1 — It *

л=±

πΠ₃/ΐ² · In 3P(Di

Ξι’

Dz

Dm)

лДзМ-Ιη^ϊ

Di D3

(106)

(107)

Ф-ла (106) не учитывает ослабления сечения отверстиями для болтов и определяет наибольшие напряжения вдоль внутренних ребер С и D фланца (смотрите верхний рисунок фигура 32). Ф-ла (107) учитывает влияние отверстий для болтов при числе их п=со. Для ограниченного числа отверстий действительное напряжение во фланцах будет находиться

		Λ

0,2 о,·i

Фигура 32.

0,6 г, 0,8 1,0

~~ ь

Фигура 33.

предельными напряжениями σ_χ и σ₂, определенными по ф-лам (106) и (107). Напряжение в подвижном фланце м. б. проверено по формуле Энсли-на (Ensslin), дающей однако преувеличенное значение этого напряжения. Формула Энслина имеет вид:

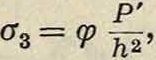
(108)

где значение коэф-та φ может быть взято из графика (фигура 33) по соотношению радиусов ^гг ^{и г}а· На фигуре 30 изображены плоские подвижные фланцы, а на фигуре 31 рекомендуемые Вестфалем подвижные скошенные фланцы. По этим фигурам

D4 + D3

. γ _

2 » 2

Напряжение бортового кольца определится по ф-ле

— ^бРа °^Ь ~

(109)

где плечо а изгибающего момента будет равно

α=

Рт~Рд

2

Работа на срез выразится напряжением

P

nD_ah

(ПО)

По немецким индустриальным нормам каждый ф ланец должен иметь число отверстий для болтов, кратное четырем (например 4, 8, 12, 16, 20 и т. д.), причем эти отверстия должен быть расположены симметрично по отношению двух главных осей и так, чтобы они (отверстия) не размещались ПО ЭТИМ ОСЯМ. С. Брилинг.