> Техника, страница 87 > Турбулентное движение

Турбулентное движение

Турбулентное движение, движение жидкости, характеризуемое наличием переноса ее частиц в направлениях, поперечных к основ-ному (осредненному) потоку, определяемому руслом. Следя по Лагранжу за и н д и в и д у-альным движением жидкого элемента, убедимся, что он двигается по сложной траектории, переходя из одного слоя в другой. Определяли по Эйлеру скорость приходящих в данное место частиц, заметим, что составляющие скорости в рассматриваемом пункте потока колеблются около нек-рого среднего значения, измеряемого прибором. Поперечные движения частиц имеют следствием усиленное перемешивание струй в Т. д., а вместе с тем и перемешивание нагретых слоев с холодными, окрашенных или загрязненных (заиленных, несущих угольную пыль и т. д.) слоев с чистыми и другие явления. В этом практич. преимущество Т. д. перед ламинарным, где церенос субстанции происходит только в порщцге молекулярного обмена, ничтожного по сравнению с молярным, турбулентным обменом. При малых Рейнольдсовых числах ламинарное движение, устойчиво и не переходит в турбулентное; создаваемые возмущения потока гаснут, и движение быстро принимает вновь ламинарный характер. Наоборот, при Re>Re_Kpum. ламинарное движение становится неустойчивым и при наличии возмущения переходит в турбулентное. При улучшении условий входа в трубу и качества стенок удается сохранять ламинарное движение до очень высоких Re, но при этом получается очень неустойчивый поток. В аэродина-мич. трубах искусственная турбулентность создается спрямляющей решеткой, с планок которой срываются «дорожки» вихрей.

О. Рейнольдс дал основные ур-ия Т. д., положив в основу их расчленение действительной (актуальной) скорости на с р е д-н ю ю во времени и пространстве ипульса-ц и о н н у ю около средней. Если обозначить проекцию скорости на г-ю ось координат через

* В ст. Турбулентное движение рассматриваются исключительно вопросы, связанные с приложением теории турбулентности к техническим задачам.

V,;, то ν ; здесь черта наверху обозна чает осреднение скорости. Осредняя левую и правую части ур-ий Навье-Стокса, составленных для несжимаемой вязкой жидкости, Рейнольдс получил следующие ур-ия осредненного Т. д. жидкости:

k=1

dp. о

3

Σ

/i=l

дх/i

>

k =1

I djufc dx/c

= 0

(i)

где величины τ_Λ=— ρ ν₍ν_}ι играют роль компонентов тензора (симметричного) турбулентных напряжений, отражающего молярный обмен количеств движения, переносимого частицами жидкости. Для интегрирования уравнений Рейнольдса необходимы дополнительные законы зависимости величин τ_ίΛ от элементов среднего движения. Таким дополнительным предположением является в настоя-* щее время идея «пути смешения» (Mischungs-weg по Прандтлю). Предполагается, что частица, выйдя из слоя, имеющего нек-рую среднюю скорость, пробирается сквозь смежные слои, все более и более теряя свою индивидуальную скорость, пока наконец не придет в слой, где окончательно смешается с окружающей жидкостью. Если обозначить через I расстояние от слоя, из которого частица вышла, до слоя, в к-ром закончилось выравнивание скорости, и через U среднюю скорость второго слоя, то потерянная частицей скорость будет равна I ^ (слои предполагаются прямолинейными и параллельными между собою, ось у-ов направлена поперек слоев). Прандтль считает возможным заменить постепенное выравнивание скорости единовременным ее изменением и полагает пуль-сцционные составляющие скорости по оси ж-ов и у-ов (в этом плоском случае движения) пропорциональными разности средней скорости слоя и скорости пришедшей сюда частицы. На этом основании касательное турбулентное напряжение (сила трения между слоями, отнесенная к единице площади) будет равно (по Прандтлю)

I dU dy I dy

72 ! dU

^τ=?¹Ί^

(2)

Здесь в величину I включен коэф. пропорциональности (2), а абсолютное значение j ^ | выделено для правильности знака г. Ф-луПрандт-ля можно сравнить с ф-лой Бусинека, являющейся аналогом обычного закона вязкости,

т=А тогда коэфицйент А, называемый коэ-

фициентом обмена (Austauschgrosse), будет по Прандтлю равен

А =ρΙ*

dU

dy

(3)

В отличие от коэф-та молекулярной вязкости μ коэф. турбулентного обмена "А зависит от структуры потока и в разных местах одного и того яда потока, а также и при разных Рейнольдсовых числах I Re | имеет разное значение. На фигуре 1 показаны кривые Никурадзе для изменения коэф-та обмена в круглой трубе в зависимости от расстояния до стенки. На оси ординат отложена величина -j_, гдее=-^ (кинематйч. коэф. турбулентного обмена), v*=у -- и г — радиус трубы, причем под т₀ подразумевается трение на стенке, легко определяемое экспериментально

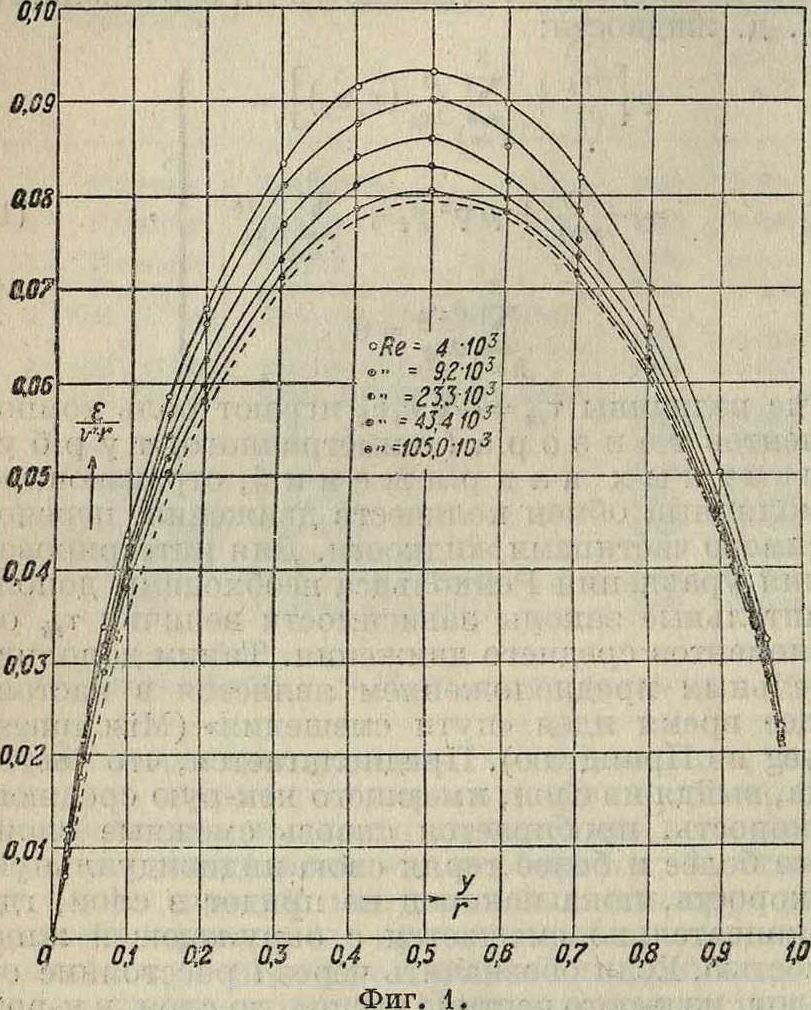
через перепад давлений. Наоси абсцисс отложено отношение расстояния до стенки к радиусу трубы. Величина А принимает максимальное значение приблизительно на четверти диаметра от стенки; значение коэф-та А на оси трубы не поддается экспериментальному определению. На фигуре 2 приведены экспериментальные кри. вые Никурадзе для пути смешения I при раз

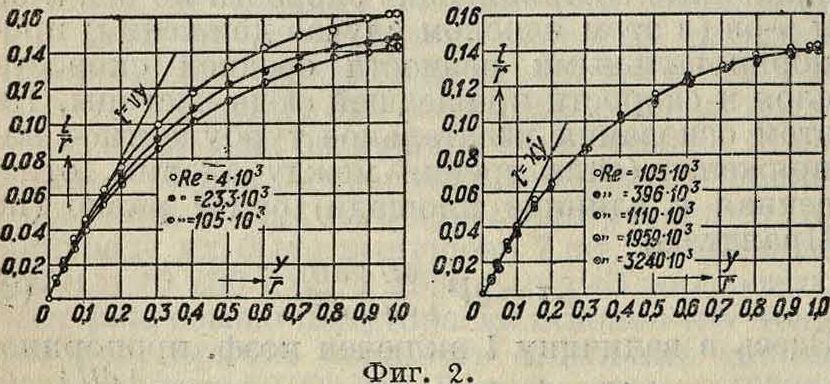
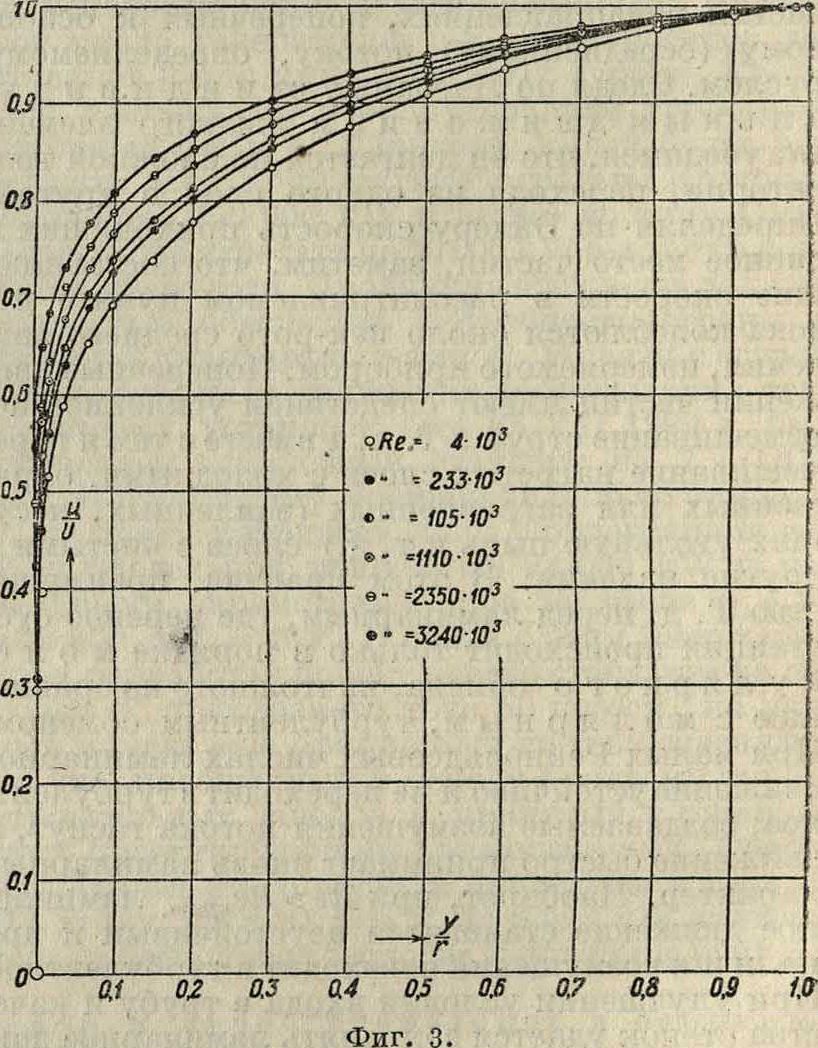
ных Рейнольдсовых числах. Угловой коэф. κ на стенке имеет значение ок. 0,4. Распределение скор остей в Т. д. резко отличается от параболич. распределения в ламинарном режиме. На фигуре 3 приводим кривые скоростей, по Никурадзе при различных Рейнольдсовых числах Re; на оси ординат отложено отношение средней скорости и в данном месте круглой цилиндрич. трубы к максимальной скорости U на оси трубы.

Карман, пренебрегая силами обычной вязкости, из соображений подобия дал закон изменения пути смешения I в зависимости от кинематических характеристик осредненных скоростей потока:

1=(4)

дающий при теоретич. расчете закон распределения скоростей, хорошо совпадающий с фигура 3

повсюду, кроме областей, где имеют значение силы вязкости (около стенки). Из теории Кармана может быть выведен закон изменения коэ-фициента сопротивления λ в известной формуле сопротивления:

(5)

Ар _χaUm

2d

Как известно, при ламинарном режиме в круглой трубе

λ=64 Re-¹. (6)

Для Т. д. при Re < 10⁵ пользуются экспериментальной фглой Блазиуса:

Л=0,3164 Де-о,²³, (7)

а при Re > 10⁵ также экспериментальной ф-лой Якоб-Эрка.:

λ=0,00714 + 0,6104 .Re Λ³⁵. (8)

Теория Кармана для гладкой трубы при Re, доходящих до 3,4-10^е, дает следующую ф-лу:

у“_;-=2,0 lg (Re ]/Д)— 0,8. (9)

Никурадзе взамен ф-л Блазиуса и Якоб-Эрка дает новую формулу сопротивления:

λ=0,0032 + 0,221 Re°>^2s7, (10)

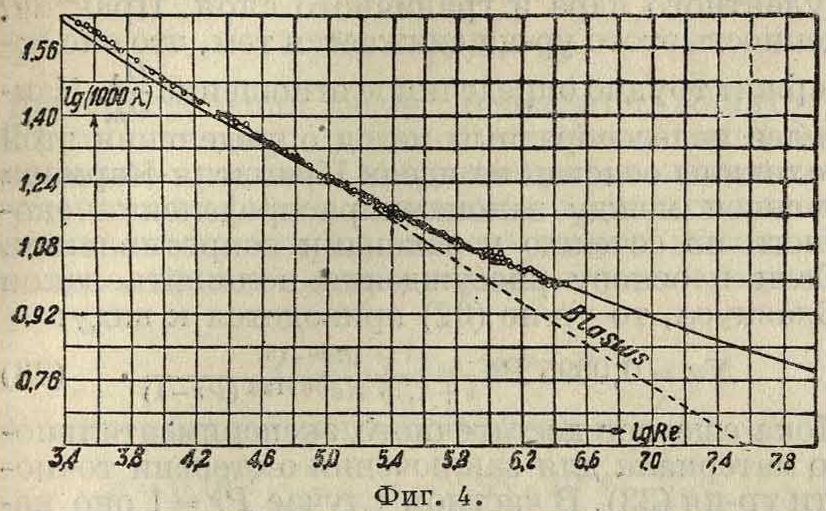
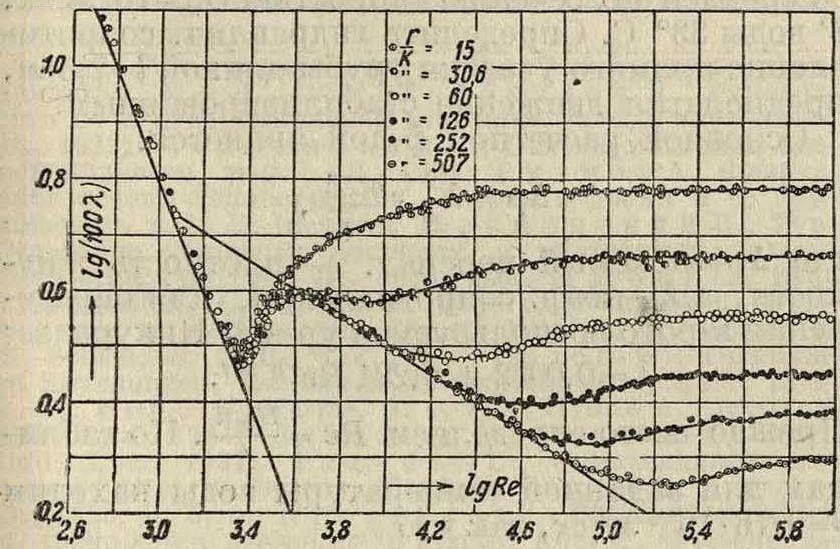
к-рая совпадает с опытной кривой, (фигура 4) до значений Ле=3 240-10³ и которая по мнению Никурадзе м. б. экстраполирована до Де=10^а.

Шероховатость стенок значительно· отражается на законе сопротивления при турбулентном режиме. Опыты Никурадзе показали, что: 1) при ламинарном режиме шероховатость не имеет значения; 2) чем больше относительная шероховатость ~ (отношение средней высоты к бугорков или выступов к радиусу трубы г), тем скорее происходит переход к квадратичному закону сопротивления; 3) закон Блазиуса справедлив в тем меньшем интервале, чем больше относительная шероховатость; при ?* > 0,02 закон Блазиуса не применим; 4) коэфициент сопротивления λ при больших

Рейнольдсовых числах (квадратичный закон) существенно зависит от относительной шероховатости. Все эти положения отчетливо видны на кривых Никурадзе (фигура 5).

В учении о Т. д. жидкости большое внимание уделяется исследованию процессов теплооб

мена. Процессы перераспределения механич. и тепловой энергии представляют собой различные стороны одних и тех же по существу явлений. Как установлено выше, следует различать две формы перераспределения энергии в потоке жидкости. Первая из них всецело обусловлена процессами молекулярной природы. Интенсивность молекулярного движения зависит только от термодинамического состояния среды. Поэтому величины, характеризующие те физич. свойства среды, к-рыми определяется интенсивность молекулярного обмена, м. б. ф-иями одних только термодинамич. параметров (давления, 1°). В противоположность этому вторая форма переноса—молярный обмен—зависит от состояния движения жидкости. Поэтому величины, с помощью которых определяют-

Фигура 5.

ся свойства потока, специфичные для молярного обмена, должен быть ф-иями параметров, характеризующих гидродинамич. обстановку процесса. Молекулярный обмен проявляется в процессах внутреннего трения (перераспределение механич.энергии) и теплопроводности (перераспределение тепловой энергии) и количественно определяется ур-иями:

(11)

где дополнительно к ранее введенным приняты обозначения: q—уд. количество теплоты (количество теплоты, проходящей в единицу времени сквозь единицу площади в направлении оси »/-ов), к—коэф. теплопроводности и &—температура. Из (ii) следует:

НФ <¹²>

Удельная сила трения, характеризующая интенсивность молярного переноса механич. энергии, определяется через коэф. турбулентного обмена в виде

(¹³>

Носителями тепловой и механич. энергии являются одни и те же элементы жидкости. Поэтому удельное количество теплоты м. б. представлено в виде

d»

q=B

dy

(14)

Коэф-ты турбулентного обмена А и В отличаются только тем, что в состав второго входит не масса единицы объёма ρ, а ее теплоемкость С=СрУ (где Ср—теплоемкость при постоянном давлении и γ—уд. в жидкости). Т. о.

(15)

т. е и ^ν

Из сопоставления ур-ий (12) и (15) следует, что соотношение между величинами q и τ в условиях молекулярного обмена зависит от одних физич. свойств среды, а в условиях молярного— от других. Только в том частном случае, когда удовлетворяется соотношение

i=-f; (ίο

оба ур-ия определяют отношение ® тождественным образом. Это означает, что в рассматриваемом специальном случае переход от молекулярной формы обмена к молярнойсопровождается одинаковым изменением интенсивности процессов переноса тепловой и механич. энергии.

Весьма важные выводы получаются при исследовании этого вопроса методами теории подобия (смотрите). Ур-ие (16) м. б. переписано в виде:

μ k Q ~ CpV	(17)
II	ОС
^=1.

откуда следует:

Но отношение ~ есть критерий Рг (Прандтль).

Следовательно условие (16) эквивалентно требованию

Рг=1. (19)

Если принять во внимание, что критерий Рг представляет собой отношение критерия Ре к критерию Ре, то ур-ие (19) сведется к условию:

Ре=Ре. (20)

Равенство между собой двух этих критериев, из которых один является определяющим для процесса движения жидкости, а другой—для распространения тепла в ней, свидетельствует о глубокой аналогии между тепловыми и гидродинамич. условиями процесса. Действительно, как это Прандтль установил еще в 1910 г., при выполнении условия (16) в основных ур-иях движения и распространения тепла обнаруживается весьма далеко идущее сходство. Более подробное сравнительное исследование обоих ур-ий приводит к заключению, что в этих условиях Р-ные и скоростные поля потоков жидкости должен быть между собой подобны. Требование Рг=1 с достаточным приближением удовлетворяется для газов и вовсе не удовлетворяется для капельных жидкостей. Поэтому соотноше-

над между величинами, характеризующими тепловые и гидродинамйч. условия процесса, отливаются особой простотой в случае потока газов.· Так, для движения газа по трубе можно установить связь между коэф-том теплоотдачи а и коэф-том сопротивления Я из следующих простых соображений (по Шиллеру и Бурбаху). Для коэф-та теплоотдачи имеем:

/d»)

или а _ 1

k ·0_0_η

d£ dy) о ^!

(21)

(22)

где индексом «О» отмечены значения величины непосредственно у стенки, а чертой наверху— соответствующие средние значения (изменением физич. констант с 1° для простоты пренебрегаем, хотя такое упрощение не является необходимым для выполнения вывода). Соответственно для коэф-та сопротивления имеем:

,βϋ,Ι /«дач=^Ыо	(23)
или
яецт_ 1 IdU) μ 8 Um dy)o’	(24)
Но вследствие подобия f-ного и полей должен быть:	скоростного
1 /d9 _ 1 /du »-ϋ0 Idyjo ~ Um dyl0	(25)
Следовательно:
а _ еитk. μ 8	(26)
ИЛИ
λ k gUm8 μ	(27)
Приводя это выражение к форме ур-ия связи
между критериями, получаем:
ad Я Ufjjd ~к = 8 V	(28)
или
Nu=1 Re.	(29)

В свою очередь Я есть ф-ия Re. Если для определения вида этой ф-ии принять закон Блази-уса, то ур-ие (29) приведется к зависимости: Nu=0,0395 .Re⁰.⁷⁵, (30)

к-рая весьма удовлетворительно согласуется с данными опыта. Применительно к капельным жидкостям этот вывод теряет силу, т. к. непра^ вильным является основное положение о подобии полей скорости и ί°. При соответствующей переработке (Шиллер-Бурбах) все представления значительно усложняются, теряют отчетливость, и самый вывод делается менее строгим. Поэтому при рассмотрении теплообмена в капельных жидкостях целесообразнее следовать системе рассуждения, предложенной впервые в 1910 году Прандтлем и независимо от него в 1916 году Тейлором. Сущность этой системы заключается в расчленении процесса теплообмена между жидкостью и стенкой на два составных явления—молярный перенос тепловой энергии в турбулентном ядре течения и теплопроводность в граничном слое—и определении удельного потока тепла для каждого из них. Сопоставление обоих выражений приводит к следующему ур-ию для коэф-та теплоотдачи:

У о_Ри_п

“ т

(31)

или

Nu=Ре -

i + (Рг-1) “ т

(32)

где U₁—скорость на поверхности раздела турбулентного ядра и граничного слоя. Практич. ценность этого ур-ия снижается тем, что оно содержит трудно определимое отношение ~. Наи-

U т оолее целесообразный метод определения этой величины основан на идеях Прандтля-Кармана о связи между законами распределения скорости по сечению и законами сопротивления. Если в основу рассуждения положить закон Блазиуса, то ур-ие (32) приводится к виду:

Nu - 0,0395 Рг — _ir-~₍р7Ш) · (33)

Пока еще нет достаточного экспериментального материала для заключения о степени точности ур-ия (33). В частном случае Рг=1 оно непосредственно приводится к виду (30). При весьма больших Рг (очень вязкая, мало теплопроводная жидкость) правая часть ур-ия стремит^ ся к выражению 0,0274 Ре⁰,⁸⁷⁵. Т. о. для реальных жидкостей (1 < Рг < со) показатель при Re должен лежать в пределах 0,750—0,875. Следует отметить, что все предыдущие рассуждения основаны на предпосылках, что наличие теплообмена не отзывается на законах гидро-динамич. сопротивления. Нек-рые исследования новейшего времени возбуждают известные сомнения в законности такого допущения.

Примеры расчета сопротивле^ ния и теплопередачи при больших значениях критерия Рейнольдса. 1. Вода течет по гладкой (латунной цельнотянутой) трубе диаметром d=10 ел?, со средней по сечению скоростью U_m= 10 м/ск, t° воды 33° С. Определить гидравлич. сопротивление прямого участка трубы длиной 1=2,5 м, предполагая движение с4абилизированным.

Основной расчетной ф-лой является:

Δρ=Я ^ _j

где Δρ—искомый перепад, ρ—плотность жидкости, а Я—коэф. сопротивления, для определения которого воспользуемся ур-ием Никурадзе:

Я=0,0032 + 0,221 i?e^_0>²³⁷.

Прежде всего определяем Re=^τ·^~. По таблицам для заданной температуры воды находим »"=0,76 · 10~⁶ м²/ск, так что

^Λβ“δ^4^=¹.³²·¹0^β·

Отсюда по ур-ию Никурадзе находим Я= 0,011.

Подставляя это значение в формулу для перепада давления, находим:

Δρ=0,011

= 1-390 M3/jn²s0,14 килограмма/см².

Следует отметить весьма значительную величину перепада давления (свыше 0,1 atm), обусловленную тем, что рассматривается движение воды. при. очень больших скоростях. В случаешероховатой трубы перепад давления весьма заметно возрос бы. Напр., как это видно из кривых Никурадзе (фигура 5), при ^=0,016 в тех же условиях Я=0,0355, то есть сопротивление оказалось бы примерно в 37г раза большим.

2. Определить коэф. теплоотдачи от потока дымовых газов средней t=440 °С стенкам дымогарной трубкис диаметром d= 5 см. Скорость движения i7_m=250 м/с к (котел типа Велокс); t° стенки трубы ^=200°. Основной расчетной ф-лой является

Nu=5 Re.

При определении физич. констант с достаточной для технич. расчетов степенью точности возможно принять следующее упрощающее допущение: 1) физич. константы дымовых газов равны значениям соответствующих констант воздуха; 2) все значения относятся к средней темп-ре

t_m=^t-~=339°.

В этих предположениях находим ρ=0,06 —, μ=2,96 · 10-6 Jc= 0,038 Cal/м ч. °С.

Вычисляем

Re =

0,06-250-6.10-2

= 127 · 10³.

2,96-10-6

Соответственно по формуле Никурадзе находим Я=0,017.

Подставляя эти значения в основную ф-лу, получаем

Nu=^ 127 · ΙΟ³=270,

откуда

Cal

α=? Nu=- 270=206.

d 0,0o Λΐ² 4.

И здесь надлежит отметить необычайно значительную интенсивность теплообмена, обусловленную чрезвычайно высокой скоростью движения газов.

Лит.: Александров В., Техническая гидродинамика, М.—Л., 1932; Лейбензон Л., Руководство по нефтепромысловой механике, ч. 1, Гидравлика, М., 1931; Лойцянский Л., Основы механики вязкой жидкости, въш. 2, Л., 1933; Г у х м а н А., Физические оснрвы теплопередачи, Теория подобия и ее приложения, т. 1, Л. (печат.); Лойцянский Л., Турбулентное движение жидкости и внутренняя задача, «Известия ГНИГИ», Л., 1933, вып. 9; HoplL., Zithe Flussigkeiten, Handbuch d. Physik, Mechanik d. Fliis-sigkeiten u. gasformigen Korper, hrsg. v. H. Geiger u. K. Scheel, B. 7, B., 1927; Tollmlen W., Turbulente Stromungen, Handbuch d. Experimentalphysik, hrsg. y. W. Wien u. F. Harms, B. 4, T. 4, Hydro- u. Aerodyna-mlk, Lpz., 1931; Schiller L., Stromung in Rohren, ibid., Lpz., 1931; Prandtl L., Untersuchungen zur ausgebildeten Turbulenz, «Ztschr. f. ang. Math. u. Mech.», B., 1925. B. 5, ff; Nikuradse J, Gesetzmassigkeiten d. turbulenten Stromung in glatten Rohren, «Forschungs-heft», B., 1932, 3S6; Prandtl L., Bemerkung liber den Warmeiibergang im Rohr, «Physikalische Ztschr.», B., 1928, B. 29, H. 14; Prandtl L., Neuere Ergebnisse d. Turbulenziorschung, «Ζ. d. VDI», 1933, B. 77, H. 5; Sehille H. u. Burbach Тй., Warmeiibergang strOmender Fliissigkeit in Rohren, «Physikalische Ztschr.», B., 1928, B. 29, H. 11; Selleri о A., Beziehungen zwischen Warmeiibergang u. Reibung, ibid., B., 1928, B. 29, H. 2; к a r m a n Th., Mechanlsche Ahnlichkeit u. Turbulenz, «Nachr. d. konigl. Ges. Wissenschaften», Gottingen, 1930. А. Гухман и Л. Лойцянский.