 > Техника, страница 87 > Угловая скорость
> Техника, страница 87 > Угловая скорость
Угловая скорость
Угловая скорость, со, предел отношения углового перемещения вращающегося вокруг оси твердого тела к соответствующему промежутку времени, когда последний стремится к нулю:
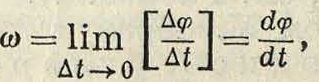
где φ есть угловое перемещение, являющееся функцией времени. В частном случае, если
ω=Const, вращение называется равномерным. При этом условии интегрирование дает φ=ωί + С.
Если в момент ί=0 начальный угол поворота Ψ=<р0, то С=<р0 и ур-ие равномерного вращения будет
φ=Ψο- - “ί·
За единицу У. с. принимают У. с. равномерного вращения, при к-ром угол поворота изменяется в единицу времени (секунду) на угловую единицу (радиан). Это—абсолютная единица
У. с., обозначаемая так:. В технике У. с. машин обычно измеряют числом оборотов в минуту, следовательно за единицу угла принимают полный оборот (2π радианов); в этом случае единицу У. с. обозначают: —j- · Т. о., если У. с. машины п об~, то
МИН. ’
_ Об. _ 2 π · η 1 _π·71 1
ω ~ П МИН. ~ 60 СК. ~ 30 СК.
Единицы У. с. показывают, что размерность ее такова:
[», г°. г»].
В табл. 1 приведены примеры У. с.
Таблица 1.—Угловые скорости.
| Вид ротора | Об. | 1 |
| мин. | СК. | |
| Земля (вокруг оси). | 7,0-10-4 | 7,8-10—6 |
| Минутная часовая стрелка. | 1,7-х 0-2 | 1,8-хО-З |
| Секундная » » | 1,0-.00 | 1,0-л.О—i |
| Паровая машина. | 3,0-хО2 | 3,1-iOi |
| Пропеллер аэроплана. | 1,2·хО3 | 1,3-хО2 |
| Электромотор .. | 3,0- -хО3 | 3,х-хО2 |
| Паров 1Я турбина многоступенч. Снаряд (12") вокруг оси. | 5,0-103 | 5,2-хО2 |
| 6,0-103 | 6,3-хО2 | |
| Турбина Лаваля. | 3,0-10- | 3,1-103 |
| вокруг оси. | 1,5-χΟδ | 1,6-101 |
| Конус в лабораторных условиях [‘J.. | 6,6-ΙΟδ | 6,9-101 |
Обычно в технике при установившемся движении У. с. изменяется периодически, принимая через известный промежуток, времени первоначальную величину, например для двухтактного одноцилиндрового двигателя период равен времени оборота главного вала. Величина перчодич. неравномерности хода характеризуется коэфициентом неравномерности δ:
причем
^ _ (°тах ~ ттгп юср.
м _ штах 4- ωτηζη шср. - 2
В табл. 2 приведены коэфициенты неравномерности хода некоторых двигателей.
Таблица 2. — Коэфициенты неравномерности хода двигателей.
| Область применения двигателей | в, % |
| Прокатные станы крупные.
» » мелкие .. Лесопильные рамы .. Динамо постоянного тока (осветит.). Генератор переменного тока (осветит.). |
8—10 4—6 3—5 1,5—2,5 0,3—1,5 |
Если точка вращающегося твердого тела находится на расстоянии г от оси вращения, то пройденный точкой за время t путь, соответ ствующий угловому перемещению φ, выразится так:
s=φ · г,
откуда
V
ds d<p di -Г dt
r · (O.
В отличие от У. с., которая одинакова для всех точек данного вращающегося тела, v называют линейной (или вращательной) скоростью, а также окружной скоростью (для точек на ободе вращающегося диска, маховика и др.). Вектор v какой-либо точки вращающегося тела направлен перпендикулярно к плоскости, проведенной через эту точку и ось вращения, в сторону вращения (смотрите фигуру).
Графически У. с. изображается вектором, численно равным со (в определенном масштабе); вектор откладывается вдоль оси, по отношению к которой вращение происходит по часовой стрелке (левая система координат). Этот вектор, как и всякий другой, можно разлагать по правилу параллелограма, проектировать на координатные оси, складывать геометрически с другими (У. с.) и т. д.
Пример 1. Радиусы трех шестерен, сцепленных между собою: г,=20 см, г2=10 см. г3=15 см. Найти У. с. третьей шестерни, если
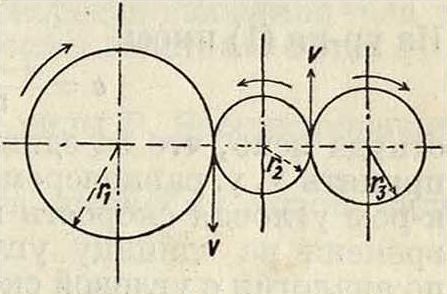
первая вращается по часовой стрелке с У. с. со!=60 об/мин. (смотрите фигуру).—В точках касания окружные скорости шестерен должен быть одинаковы, кроме того окружные скорости на okj уж-ности каждой шестерчи также одинаковы, следовательно г1со1=г.со3, откуда
Г, 20 Об. ол Об. со,=— со,=— · οϋ -3 г3 1 15
= 80-
Направление скоростей в точках касания определяет направление вращения 3-й шестерни.
Пример 2. Определить скорость точек на ободе маховика диам. 1,6 м, совершающего 270 об/мин.
V= 9π 0,8=22,62 м/ск.
Лит.: ‘)Henriot et Huguenard, Les grandes vitesses angulaires obtenues par les rotors sans axe solides «Journal dePhysique», P., 1927, t. 8, 11, p. 433. См. также Механика теоретическая. В. Никаноров.