> Техника, страница 87 > Удар

Удар

Удар, явление, имеющее место при внезапном изменении режима движения тела или системы материальных точек вследствие столкновения с другим телом или системой материальных точек. У. характеризуется действием относительно значительной силы в течение малого промежутка времени. Сила, возникающая при У., обычно очень велика, время же действия ее ничтожно мало, вследствие чего затрудняется измерение как самой силы, так и времени, в течение которого она действует. Поэтому при У. измеряют импульс силы, к-рый имеет нек-рое определенное конечное значение. Импульс силы при У. часто называют силой У. или же просто. У. Импульс силы при У. обычно настолько значителен, что при рассмотрении, явления У. возможно пренебрегать импульсами других сил, действующих на тело, как силы тяжести, силы притяжения или отталкивания и т. д., рассматривая только импульс силы, вызванный У.,— ударный импульс. Перемещение тела или точек системы во время У. является величиной того же порядка малости, что и время, в течение которого действует сила У.,

вследствие чего координаты тела или точек системы можно считать постоянными в течение времени действия силы У.

Действие мгновенной силы на материальную точку. Если на материальную точку, масса которой т, будет действовать мгновенная сила Р в течение малого промежутка времени τ=t - t₀, то изменение количества движения тела выразится так;

i

mv — mv₀=J Pdt—J,

ίο

где г“₀ и V—векторы скорости движения тела до действия силы и после действия силы Р, а

t -}- т

1=J Р dt—импульс силы Р. Рассматриваемое

ίο

изменение количества движения можно написать и так:

t

где тг — тг₀

J Pdt — I,

t₀

dr

^: Ж

* dr₀

= v, а ν₀=-^°=ν₍

dt

Закон количества движения наряду с законом движения центра инерции и законом моментов количества движения кладется в основу изучения явления У. Изменение живой силы до действия мгновенной силы Р и после ее действия для материальной точки находится по теореме В. Томсона: «если на материальную точку действует мгновенная сила с импульсом I, то изменение живой силы за малый промежуток времени ее действия равняется полусумме двух скалярных произведений из вектора импульса и скоростей в начале и конце рассматриваемого промежутка времени». Имея равенство mv — — mv₀=I и умножая его скалярно сначала на V, а затем на v₀, получаем:

mv² — m(v₀v)=(Iv) и m(w₀) — mv=(Iv₀);

складывая почленно, имеем теорему Томсона:

mv² _ mv& _ (J») + (J«o)

2 ~ΊΓ ~ 2

Действие мгновенных сил на систему точек. На систему п материальных точек, подчиненную Тс связям, действуют мгновенные. силы. Точки: т_х, т₂, ., т,·, ., т_п; связи заданы в виде ур-ий поверхностей, с которых не может сойти г-я точка,

/i=0, /α= 0, .··,/;=0, ·.·,/*=0.

Проекции скоростей точек должны удовлетворять ур-иям:

fdfi	dx{ dh	dm, Э/ι	dzi
дх(	dt дУг	dt ^ dii	dt
(Sfl:	dXi dfu	dVi. d/u	dip
dxi	dt dy{	dt dii	dt)

)=°

пли в векторной форме:

2 Gfv) fx=0, ., 2(tv)/*=0-

Диференциальные уравнения движения системы будут:

d%X{ -y. i dfi i	· +аЦ
,уу. d2Vi_ у i j d/1
d%Zi π, л d]x. midt* ~Zi + Λ1β7,+ ·

или в векторной форме:

^mi JF‘=^р* + ^;‘i 8^rad /1 +·.·· + ^я/.- grad fk-В последних ф-лах ж,·, у,·, z_t—координаты г-й точки системы, r=i ж_г· + jy₍ + 1м_г—радиус-вектор точки системы, _Р_г=гХ_{ + j Y_{ + JeZ_t—мгновенная сила, действующая на г-ю точку;

есть проекция реакции идеальной связи. Если %, г>_г·, ге_г—проекции скорости г-й точки до У. в момент времени <₀, а Г/_г·, F,·, TF,—проекции скорости г-й точки в момент ί₀ + т после У., то, интегрируя вышенаписанные ур-ия, имеем:

^тг (Ui — Wj·)=I_ix -!· т ··· + ·

^w« (F,· - Vi)=l_iy + μ_χ +. +,

vi i)=l(_z + /“l + · ·. + gj

или в векторной форме:

(г» - v_ai)=li + μ_χ gradfi +. + ц_к grad f_k, где

Vi=Wi + jV₍ + JeWj,=iu_{ + jv_t + ku>_h

t

^li=Hi* + ·> I in + ^li!iz=f F dt — ударный им-

«.

пульс,

ί (

μ_χ λ dt, ., /-Ц- ⁼ ^ Я_/( ί/£.

ίο ίο

Множители д_г, ., μ,. можно найти, подставляя значения скоростей из последних ур-ий в условия для скоростей при наличии связей; получим к ур-ий с к неизвестными, решая которые найдем все множители μ_χ, ., у_к. Для случая одной связи f_x=0 имеем:

*=*<* ++^S^radfi·

Подставляя в ур-ие

Σ (!*)$»

и имея в виду, что ~=v_{, получаем:

2 (^voiV)fi +2 (^/iV)f₁ + 2^/ti^;.(v/i-v)ii=0· Отсюда, имея в виду также, что iV)fi=О,

получаем:

2 тонны + Vi 2 4^{(grad =} °

И

Σ^^(ίν)/*

i«i=- ,--·

2 ^^C8rad/,)2

Если импульсы мгновенных сил и скорости точек в момент времени ί₀ будут даны, то можно найти скорости точек в момент f=(₀ + г. Следует иметь в виду, что при действии внутренних мгновенных сил количество движения системы не изменяется.

Теорема Карно позволяет найти потерю живой силы при мгновенном появлении новой связи или же при уничтожении одной из существо-вавших^ связей. Если движущаяся система в нек-рый момент времени подчиняется новой связи:

/(яι2Μι> —. ХпУп^п)=О,

причем старые связи сохраняются, то скорости изменяются согласно только что приведенным рассуждениям. К 1с ур-иям для скоростей при наличии связей присоединится еще одно:

9 _e dZi I df dyj дХг dt dy* dt

2 (а

-iL. ίϋΛ ₌ о

dZi dl I

а основные ур-ия, выражающие закон количества движения, примут вид:

^mi - ^Vi> +

I „ ^aJk + ax, ’

_i_ ^ah

i „ Ш + /** aTi

Если эти ур-ия умножить соответственно на Ui, Vi и Wi и почленно их сложить, то, принимая во внимание условия для скоростей при наличии связей, получим:

Эп_г(Щ + F² + W?) - щи_{- ViVi - WiW₍=О или

2 f (Щ + VI + W}) -2fW+ vj+w>i)+ + 2 тонны к«* - “*·)² + - ^F*·)² +(^wi - ^·)²^=°·

Последнее выражение позволяет найти потерю живой силы при внезапном появлении новой связи:

Г-Го=2у К“<- Ч)² + (e,-F,·)² +

+ (Wi - TF,·)²].

Это ур-ие и выражает теорему Карно: «если система подчиняется новой связи, то происходит потеря яшвой силы, равная той живой силе, к-рую система имела бы, если бы скорости ее точек равнялись потерянным скоростям».

У. твердых тел. Процесс соударения двух тел м. б. разбит на две фазы. В первой фазе происходит сближение тел, причем тела деформируются, а живая сила тел уменьшается, трансформируясь в потенциальную энергию, если деформация не выходит за пределы упругости. Во второй фазе тела удаляются друг от друга, восстанавливая полностью или частично свою первоначальную форму, и живая сила тел возрастает за счет потенциальной энергии, образованной в первой фазе. Принимают согласно Ньютону, что отношение абсолютной величины нормальной проекции относительной скорости тел после У. к ее величине до У. есть нек-рая физич. константа, зависящая от природы сталкивающихся тел. Эта постоянная называется коэф-том восстановления. Для тел, абсолютно неупругих, этот коэф. s=0; для тел, абсолютно упругих, е=1; для большинства практич. случаев 0<е<1. Величинами, которые требуется найти при рассмотрении явления У., являются следующие: момент столкновения, положение тел при У., скорости тел непосредственно по окончании У. и потеря живой силы или энергии при У. Если ур-ия поверхностей каждого тела в координатах, начала которых совпадают с ц. т. тел, а оси направлены по главным осям инерции, будут:

= 0 и f₂(x₂y_ze₃)=0,

а в основных неподвижных координатах ур-ия тех же поверхностей:

F^x, y,z,t)=0 и F_t(x, у, Z, <)=О,

то, имея в виду выражения косинусов углов между нормалью к поверхности и осями коорди-

нат для точки соприкосновения тел во время У., будем иметь:

1	dFi _	1	δ Fi
А,	дх ~~	δ2	дх
1	dFx _	1	dFi
Δί	ду ~	Δ2	ду
1	dFi_	1	dFi
Δΐ	дг	δ2	dz

где

dF Л дх )

+ρϊ

ду )

+ №)

+

т.·

Решая совместно 4 ур-ия

Fi(x, У, я, 0=0,

F₂(x, y,z, t)=0,

£ a^i _ _ 1 dF

Δ! дх Д₂ Зх ’

J. 3Fa _ _ £ SFs Д, ду ~ Δг ду найдем момент столкновения t₀, а также и положения тел при У. Скорости тел после У. можно найти, решая следующие ур-ия, которые легко получить, применяя закон движения центра инерции и закон моментов количеств движения, пользуясь ур-иями Эйлера для твердого тела:

M₁(TJ₁-u_l)=l_lI

M₁(V₁ — v₁)=m₁I M₁(W₁—w₁)=n₁I Α₁(Ρ₁-ρ_ί)=λ₁Ι BiiQi ~ Si)=Mil Ci(R1 - n) - vj

M₂(JJ2 “ ^2) — 1 M₂(V₂- v₂)=m₂I M₂(W₂-w₂)=n₂I A₂{P₂ — p₂)=Ri(.Qi ~ Si)=Mil Ci(Ri - r₂)=V

^ε(ν_2η-ν_1η).

В этих 13 ур-иях обозначают: и М₂—массы соударяемых тел, и С_х—главные цен тральные моменты инерции первого тела, А₂, В₂ и С₂—главные центральные моменты инерции второго тела, и_х, ν_χ и w_lt щ, v₂ и w₂—соответственно проекции скорое тей первого и второго тел до У., L, V_x и W_x, U₂, V₂ и W₂— проекции скорг стей первого и второго тел после У., р_1г q_lf r_L, p_t, q₂, r₂—проекции векторов вращения первого и второго тел относительно осей, связанных с телами, как указано выше, Pi, Qi, Ri, Р₂, Q i и R₂—те же величины после

⁸о+^т

У.; ударный импульс: I=J P,dt 1_Х, т₁, п_и

to

ί₂, т₂, п.₂—косинусы углов, образованных внутренней нормалью с подвижными осями координат, связанными с телами, например

• dh θχι

Ιχ.“

/(а+йа+еэ

1·ι=2/ι«ι - «Λ, Μι=ΖχΙχ - зд; ν_χ=х_хт_х - y_Ll_L; К=У-1^п1 - ЯгЩ, μ₂=.ζ₂1₂-χ.₁η₂, v₂=x₂m₂-y₂l₂; ε—коэф. восстановления; v_ln и ν_2η—проекции скоростей первого и второго тел до У. на направление нормали п в точке соприкосновения тел; V_ln н_7_2и—то же после У. Для решения из 13 ур-ий иметь

Vi„ и V_2п—то задач удобнее последнее в следующем виде:

J __ (^lW~^u2?t)(r-f-g)

Я

где постоянная величина для данных тел ч 2 2 2

_L b- _L ?»_ 4.

-2 ^ В₂ ^Т С₂ ’

и I V I Ю__, »1, Г

Л?! "Г "Г" В, f ci М₂

Пптрпю живой силы при У. можно найти по формуле:

(Г — ^е2)(вщ~в2п)² 2Я ’

где Т — Т₀—приращение живой силы за время У. Последнее ур-ие есть выражение теоремы Карно для твердых тел.

У. шаров есть частный случай У. твердых тел. Шары считаем идеально гладкими. Имеем в этом случае:

ж? + 2/? f z ^R, xt + yl + z!=Щ,

m

^m*~ к. коэф-ты: λ).== v_x=λ₂=μ₂=v₂=0, а следо вательно:

Ri — Pi, Qi-Su Ri — П, Pi=p₂, Qi=<z₂, K₂=r₂,

T. e. У. идеально гладких шаров не оказывает влияния на вращение шаров.Коэф. Н получает следующее значение:

ГУ ₌ J_, J_ ₌ M. + Mj.

Μι ⁺ М₂ M,M₂ ’

где М_хиМ₂—массы шаров. Скорости шаров при прямом У. (элем°нты путей ц. т. тел в момент У. имеют общую касательную) определяются сл. обр.:

т г ., Mztl + eK»·!-!)!)

^у 1 — ^υ1 +

V₂ — v₂ ~h

Μι + Μ₂Mi< i + e)(Vi-Vz)

^{2 1,8} >

Когда шары абсолютно неупруги (ε=0), то

ТГ _ у _ M iVi + MjVl

Μι + М_г

Когда шары абсолютно упруги (е=1), то

7ι=υι -

2Мо

М1 + М-2

(Vy-Vi),

^F2=^V2+

Если в последнем случае массы шаров одинаковы, то есть М_Х=М₂, то

Vi=v₂ и 7_a=«i.

то есть шары обмениваются своими скоростями.

Импульс при прямом ударе шаров выражается так:

I=M₁(V₁-v₁)=M₂(Vi-v₂) =

м_гм₂

(1 + ε)(ν_χ - υ₂).

Mi + Mi

Если известна продолжительность У., то отсюда можно найти среднюю величину реакции шаров. Потеря живой силы выразится так:

откуда видно, что для абсолютно неупругих шаров потеря живой силы равна:

^T~^T°=h

а для абсолютно упругих нет потери живой силы, то есть сумма живых сил до У. равна сумме живых сил после У.:

Т-Т₀=0.

В случае косого У. следует разлагать скорости на составляющие, из которых одна направлена по линии центров, а другая перпендикулярна к ней.Составляющие по линии центров изменяются, как указано выше, для скоростей при прямом У., т. к. в этом направлении действует ударный импульс, а перпендикулярные к линии центров составляющие останутся без изменения. Складывая геометрически измененные составляющие скоростей по линии центров и оставшиеся без изменения по перпендикулярам к линии центров, получаем как величины скоростей, так и направление движений шаров после У.

Теория У. шаров по Герцу. Если радиусы шаров R_x и Р₂, модули упругости материала шаров Е_х и Е₂, коэф-ты Пуассона μ_χи μ₂, то по теории упругости сближение центров шаров х связано с силой Р взаимодействия шаров друг на друга следующим соотношением:

где

У=1

Р=yx³h,

т/Ж ,У к и

4(1 —μί)

После начала У. и до конца его относительная скорость шаров м. б. выражена через расстояние между их центрами так:

dx

^ IX ⁼×— *

Обозначая через с_х скорость движения общего ц. т., скорость одного шара можем выразить так: М_г(у_1х-у_ы), м_г dx Мг + М-i ^х Мг+М _Ldt

^v lx — °х +

Ур-ие количества движения для одного шара, например первого:

Ж (М_х v_lr)

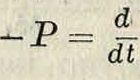
( М_хм₂

Iм₁+м₂) ^х’

но Р — у х³ 2, следовательно

= — ух ³/г, илиж=— yHx^aU.

Интегрирование этого диференциального ур-ия первый раз в ппеделах от ж₀=v_w — v₂₀=v₀ до ж приводит к виду:

Щ0²-чК-5^^ж5/2;

полагая в этом ур-ии ~=0, получаем конец первой фазы при У. (остановку перед восстановлением деформаций) и находим максималь-

2 s

ное сближение шаров ж_т=ляя значение у я Н, имеем:

UyH)

Подстав-

ν».⁴/*·

Отсюда максимальная сила давления между шарами при У. получает вид:

³/_а =

Г15(в1+д2)М1М2-|2/с	ГЙ1 + Й21
L 64 (МН-М2) J	L J

Ртах —

г у/у ( д,д₂ 1

sLenMi+M^J Ki-fWJ

%

3

Наконец из диференциального ур-ия можно найти продолжительность У. Подставляя в ур-ие х_тах, получаем знак + имеет значение в первой фазе У. при сближении центров тел, знак —во второй—при удалении центров тел друг от друга. Представляя последнее ур-ие в виде:

v₀dt=± ——

dx

г

и“ вводя новую переменную а — —— и интег-

^хшах рируя, получим для первой фазы:

^го ^Хтах

v₀ J dt=+ I -

dx

для второй фазы:

v₀f dt=~ г ^dx —

^т0 Хтах ~ f

г ^хтах и для всего процесса У.:

то

⁼ +^о j dt

та

ν₀τ =2 J

dx

откуда

2x_n.

V ч—г·

w d (—) ₀ l

ί ^χηιαχ %^χηιαχ J

^xmax

Последний интеграл можно вычислить приближенно посредством Г-функции гП

следовательно

= 1,4716,

τ=2,9432=2,9432 ^х™^ах.

^V0 Vio—Ozo

Теория Герца дает хорошие совпадения с экспериментальными исследованиями.

Действие У. на тело, имеющее неподвижную ось. Если ось ^совпадает с осью вращения, то закон моментов количества движения напишется так:

Μρ²(ϋ)₂ - ω_χ)=Х₀1_у;

здесь М—масса тела, q—плечо инерции тела относительно оси вращения, ω_χ и ω₂—угловые скорости вращения тела до У. и после У., I — проекция ударного импульса на ось У; ж₀— плечо ударного импульса. Условия, необходимые и достаточные для того, чтобы точки закрепления не испытывали У., когда само тело У. получает, заключаются в следующем: 1) У. должен быть направлен перпендикулярно к плоскости, проходящей через ось вращения и ц. т. тела:

Ус= 0;

2) У. должен быть расположен в плоскости, перпендикулярной к оси вращения и пересекающей эту ось в такой точке, для которой ось вращения есть главная ось инерции тела:

1₂=0; Ώ=0; ε=0;

3) Расстояние У. от оси вращения должен быть равно расстоянию от этой оси, как оси привеса, до соответствующей оси качаний:

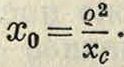
В последних ф-лахжс, у_с, z_c—координаты центра тяжести тела, I_z—проекция ударного импульса на ось 7, I)—центробежный момент инер-

циитела Ώ =^m_iz_iy_i, ε—центробежный момент инерции тела ε=^т_г(г_г- - г₀) (ж_г — х₀).

Потеря энергии притечении жидкости из узкого сечения трубы в широкое. Течение жидкости при внезапном расширении трубопровода может рассматриваться как явление У. абсолютно неупругих тел, т. к. быстро движущиеся в узкой трубе частицы жидкости должны при переходе в широкое сечение трубы значительно уменьшить свою скорость. Согласно Борда и на основании теоремы Карно потеря живой силы для единицы веса жидкости выразится так:

, _ (Ci-c_a)2 Гкгм]

^п 2 д L кг J ’

здесь h—потеря в кем энергии при перемещении 1 килограмм жидкости из узкого сечения в широкое, с₁ и с₂ — средние скорости течения жидкости в узком и широком сечениях, д—ускорение силы тяжести (<7=9,81 м/с к²).

У. струи о твердую преграду сильно отличается от У. твердых тел, т. к. при соударении двух твердых тел по окончании явления У. происходит разгрузка, при течении же жидкости частицы жидкости непрерывно действуют на преграду, создавая нек-рое постоянное давление на последнюю. Т. к. масса струи жидкости, притекающей в единицу времени к преграде, является величиной постоянной, то теорема о количестве движения м. б. написана для одной секунды и дать не только импульс силы, но, наоборот, самую силу, вызванную постоянным У. частиц жидкости о твердую преграду. Если М означает секундную массу жидкости, притекающей перпендикулярно к преграде и стекающей с нее, т. н. массовый расход, Q—объёмный расход жидкости, с—среднюю скорость притекающей жидкости, у— уд. в жидкости (вес единицы объёма) и β—угол, образуемый потоками струй, стекающих с пластинки или преграды с первоначальным направлением движения струи, то сила Р, действующая на пластинку или преграду, получит на основании закона количества движения вид:

Р=Мс( 1 — cos β) — I Qc (1 — cos β).

Если струи, стекая, движутся в направлении, обратном первоначальному движению, то β== 180° и cos^=-l, а

Р=2^с.

При отекании в направлении, перпендикулярном к основной струе, β=90° и

Р=- Qc=- Fc², в^v а ’

где F—сечение струи. Если ось струи не перпендикулярна к пластинке, а составляет с плоскостью преграды угол а, то нормальная сила, действующая на пластинку,-равна:

N=P sin a=- Qc sin a. g ^v

Сила, стремящаяся сдвинуть пластинку в направлении оси струи,

P_t — N sin a~~ Qc sin²a.

Если пластинка перемещается со скоростью и под углом <5 к плоскости пластинки, то вместо абсолютной скорости струи с надо в формулу количества движений подставить выражение: с sin a — и sin δ,

тогда Р — ^ Q(c sin a — и sin δ).

Гидравлический У. представляет собою явление внезапного повышения давления в трубах при резком изменении режима движения жидкости в трубопроводе, например при внезапном закрытии затвора. Если жидкость, двигавшаяся по трубопроводу постоянного сечения со скоростью с была внезапно остановлена путем закрытия задвижки, то кинетич. энергия, которой обладала жидкость до закрытия, не сразу рассеивается, а предварительно трансформируется в потенциальную энергию давления согласно следующим соображениям. Повышенное давление вызывает, с одной стороны, усадку продольного жидкого столба в трубе, которая м. б. вычислена по закону Гука, с другой стороны,— удлинение в материале стенок, к-рое м. б. определено на основании того же закона Гука, пользуясь ф-лой Мариотта. В результате этих деформаций получается общее укорочение продольного жидкого столба, выражающееся следующей ф-лой:

Δ=У(У — У о) + у El ’

где Δ—общее относительное укорочение продольного столба жидкости как вследствие усадки самой жидкости, так и вследствие растяжения материала стенок; у—вес единицы объёма жидкости; у—у о—повышение давления в м столба жидкости вследствие гидравлического У. (неизвестная величина); Е_г—модуль упругости жидкости (для воды Εχ=29 700 килограмм/см²; для нефти и масел Е_г=13 500 килограмм/см²); Е₂—модуль упругости материала стенок трубопровода (для чугунных водопроводных труб £7₂=1 000 000 килограмм/см²);И—диаметр трубы; <5—толщина стенок трубопровода. Т. к. жидкость получает усадку, то расход жидкости в первую секунду распределяется на некоторой длине а, носящей название •скорости распространения ударной волны. Т. к. kaF-=Q, то с=Да, где F—сечение трубопровода. Импульс силы, появляющейся вследствие гидравлич. У., равный у(у — y₀)Fdt, должен погасить количество движения ^γ- Qdt-a, которым обладает жидкость.

Исходя опять из закона количества движения, имеем выражение как для скорости распространения ударной волны, так и для повышения давления при гидравлическом У.

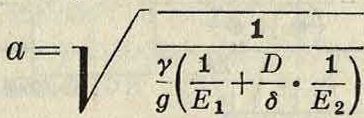
и у—у₀=— в м столба жидкости или Р~Ро=дЧ-о в единицах давления, где р — р₀—повышение давления при У. Изложенная теория гидравлич. У. принадлежит Альеви и проф. Η. Е. Жуковскому. Две приведенные ф-лы позволяют определить давление, к-рое получается внутри трубы в момент гидравлич. У. Как видно из выражения для скорости распространения ударной волны, она зависит исключительно от рода жидкости, от рода материала трубопровода и от геометрич. размеров последнего, вследствие чего для данной жидкости и данного трубопровода является величиной постоянной. При предположении абсолютно жесткого трубопровода приходим к ф-ле:

-лПБ:

У у У в ’

где ρ—плотность жидкости. Эта формула есть выражение скорости звука в среде с плотностью ρ

и с модулем упругости Е_г. Следовательно, если бы мы имели дело с абсолютно жестким трубопроводом, скорость распространения ударной волны равнялась бы скорости звука в данной жидкой среде. Упругость трубопровода уменьшает несколько эту скорость. Если бы трубы были абсолютно жесткими, а жидкость в свою очередь абсолютно несжимаема, то α= оо и трубы разрывались бы при малейших изменениях скорости течения жидкости. Зная величину а, легко вычислить и повышение давления в трубах от гидравлич. У. О расчете трубопроводов на ударное давление и мерах предотвращения явлений гидравлич. У. см. TvvPowpieodu.

Лит.: Мещерский И., Курс теоретической механики, ч. 2, М.—Л., 1930; Тимошенко С., Курс сопротивления материалов, изд. 11, М.—Л., 1931; Л о й-цянский Л.и Лурье А.,Теоретическая механика, ч. 2, Динамика, М.—Л., 1933; Лейбензон Л. и др., Гидравлика, М.—Л., 1932; Жуковский Н., О гидравлич. ударе, «Записки Академии наук по физико-матем. отделению», СПБ, 1900, т. 9, 5. В. Брилинг.

Напряжения в твердом теле при ударной натру зне. Внезапное приложение или снятие нагрузки, внезапное изменение скорости движущейся массы и сообщение скорости покоящейся массе вызывают явление удара. В сопротивлении материалов и теории упругости У. относится к одному из двух способов действия нагрузок и представляет крайний вид динамической нагрузки. Статич. и дина-мич. нагрузка—способы приложения грузов, действующих на сооружения и машины. Медленное введение груза со скоростью, близкой к нулю, столь же медленное снятие его характеризуют статич. нагрузку. Если скорость введения или снятия груза значительно отлична от нуля, нагрузка относится к динамическим. Среди динамических нагрузок особо выделяется ударная нагрузка, которая прилагается с большой скоростью, причем ускорение не м. б., измерено с достаточной точностью, но всегда очень велико. Названия «статическая и дина

мическая нагрузка» употребляются также в качестве характеристики внутреннего напряженного состояния сооружений и машин. Постоянный знак и постоянная величина напряжения определяют статич. нагрузку внутри сооружения и машины; перемена знака и величины напряжения в известный промежуток времени указывают динамич. нагрузку. Если знак и величина напряжения изменяются за весьма короткий промежуток времени, длительность которого м. б. измерена с большими затруднениями или совсем не поддается измерению,— напряжение должен быть отнесено к ударным.

В технич. практике действие собственного веса сооружений и машин чаще всего м. б. рассматриваемо как приложение статич. нагрузки; полезные нагрузки сооружения и машины б. ч. относятся к динамич. нагрузкам. В лабораторных условиях с большей определенностью м. б. проведено разделение между статической и динамической нагрузками.

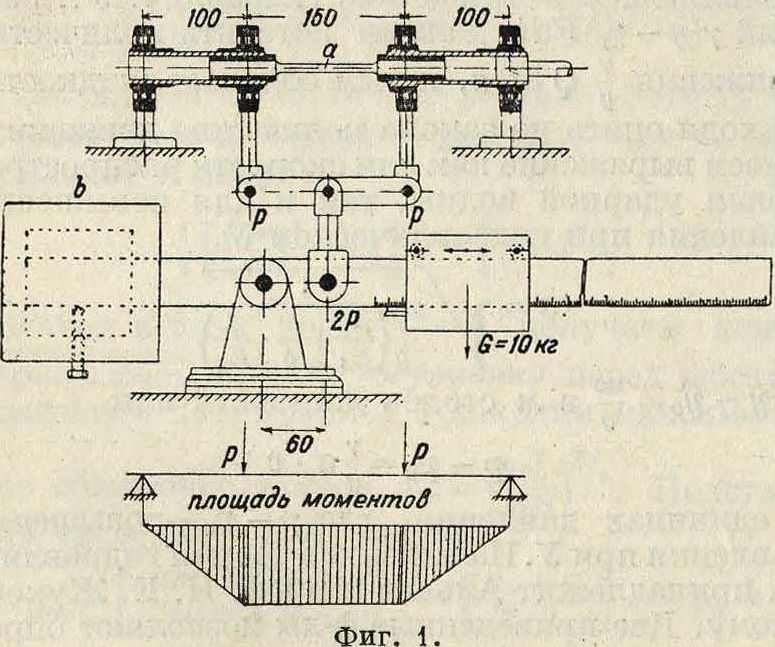
Машина для статич. испытаний вводит нагрузку на образец величиною 50—100 килограмм/см² в мин. На фигуре 1 представлена схема машины Шенка для динамич. испытаний (на усталость); а—пробный стержень, Ь — уравновешивающий груз.

Машина делает 2500—

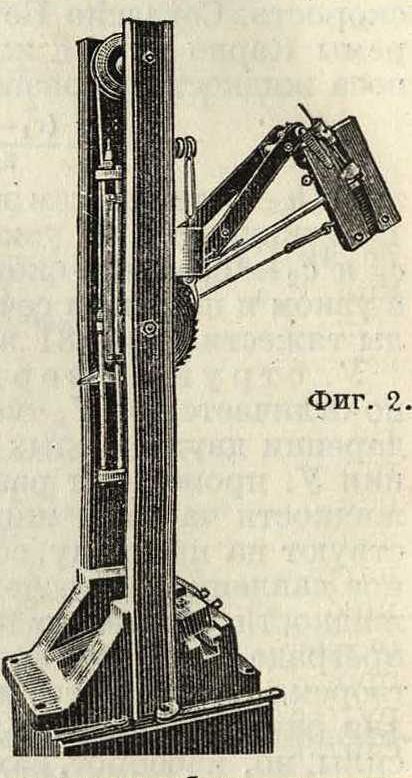
6000 об/м. и столько же раз в минуту изменяет знак постоянного по величине напряжения на изгиб в испытываемом образце. Типичной машиной ударного действия нагрузки и ударного напряжения является копер Шар пи (фигура 2).

Скорость приложения нагрузки здесь значительна; ускорение при современных условиях не может быть измерено с достаточной точностью, но очень велико. Опыт на изгиб, например в машине Краузе с меха-нич. приводом, может быть выполнен и выполняется в нормальных условиях в течение получаса, то есть при величине деформации в 3,0% от пролета скорость деформации равна 0,0016%

в ск. и быстрота роста напряжения

= 32 килограмма/см“ в ск. В опыте на усталость изгибом напряжение изменяется в зависимости от времени по закону:

а — σ₀ sin ωί,

где σ_α—наибольшее напряжение за оборот; поэтому быстрота нарастания и убывания напряжения равна;

и для ί=0

da,

^=σ₀ω cos ш

(Э,

Если машина Шенка делает один оборот в д-р-

мин., то (^)=10 000 килограмм/см² в ск., то есть при близительно в 300 раз больше против статич. действия машины. То же напряжение на копре Шарли вырастает за 0,0001 ск., и скорость напряжения следовательно равна 320 000 килограмм/см² в ск., то есть в 10 000 больше скорости статич. или в 300 раз скорости колебательной нагрузки.

Прочность и деформация материалов, а стало быть также прочность и деформация машин и сооружений, находятся в большой зависимости от величины и знака действующих напряжений. В соответствии с исследованиями Вёлера, Баушингера идр. прочность металлов при динамич. нагрузке всегда ниже прочности при статич. нагрузке. Соотношение временных сопротивлений при статич. и динамич. нагрузках выражается чи 3:2:1, где число 3 относится к статич. нагрузке, 2—к динамич.

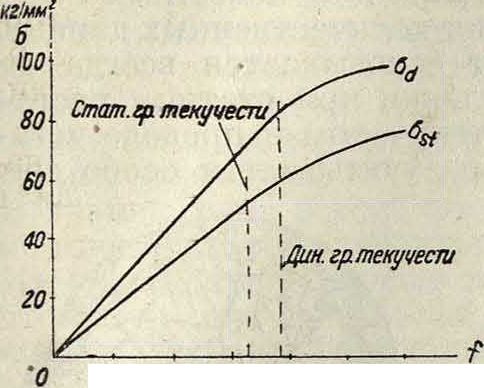
« а? о.з о,·* o.s of миллиметров

Фигура з. переменной от нуля до известного значения силы, 1—к динамической колебательной между отрицательным и положительным (и наоборот) значениями нагрузки. Временное сопротивление при ударной нагрузке не поддается надежному измерению, но результаты испытаний для железа и стали указывают на более высокое значение его по сравнению со ста-тич. нагрузкой (для случая ударной нагрузки одного знака). Временное сопротивление для ударной нагрузки оказывается в 1,5 (Планк)—2 (Дипник) раза больше против соответствующего статич. напряжения и во всех случаях известных испытаний не ниже его. На фигуре 3 приведена диаграмма Берга, из которой видно общее повышение напряжений при динамич. нагрузке по сравнению со статической (а—напряжение, f— прогиб). Модули упругости и удлинение считают одинаковыми. Повышение напряжения наблюдается также при испытаниях с большей скоростью, и ударная нагрузка таким образом не находится вне этого общего положения. Ударная прочность определяется более часто опытом над надрезанным образцом (фигура 4). Большое различие между металлами в этом отношении в зависимости от термической обработки видно из табл. 1.

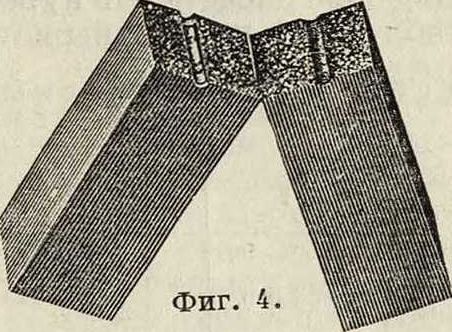
Таблица 1.—3 ависимост величины ударной прочности от термической обработки.

Никелевая сталь 0,36% С, 2,95% Ni, 0,48% Μη	Отжиг 1 ч. при 900°	Закалка с 900° и отпуск при 650°	Закалка с 90з° и отпуск при 350°
Удлинение в, % (при разрыве).	25,1	19,0	7,0
Поперечное сжатие ψ, %.	48,5	67,0	50,0
Предел текучести σ8, кг/мм2.	48,3	62,2	132,0
Временное сопротивление ОД, кг/мм2.	61,0	70,9	141,0
Истинное сопротивление разрыву σ^, кг/лш2.	101,5	140,0	202,0
Вязкость надрезанного образца а, кг/см2.	8,2	18,6	7,0

Испытание повторными У. (при числе У. < 5001 даст те же результаты, что и испытание одним У., то есть можно считать правильным утверждение, что ударная прочность—особое качество металлов, которое невозможно предусмотреть иным путем, кроме специального исследования. В машиностроении в качестве материала для изготовления деталей, которые подвергаются У. в работе, выбирают материалы с большой вязкостью надрезанного образца и кроме того принимают для расчета этих деталей пониженное допустимое напряжение против соответст

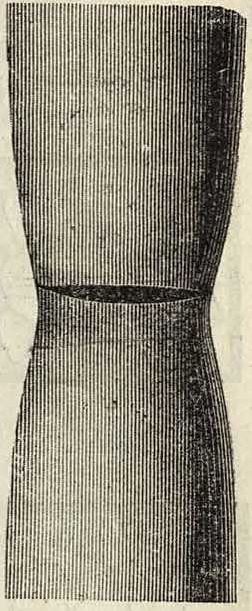
вующего случаю нагрузки. Употребительные коэф-ты понижения 1,5—2 и редко более, но не свыше 10. Все виды нагрузок отличаются друг от друга состоянием поверхности разрушения, поэтому возможно немедленно после разрушения установить характер действующей нагрузки внешним осмотром поверхности и особенно уверенно изучением ее под микроскопом. На фигуре 5—10 показаны виды поверхностей разрушения при статич. испытании на разрыв металлов различной вязкости. Фигура 5—ста- ^фиг· ⁵· Фигура 6. тич. разрыв круглого стержня из мягкой стали: (Хв=3 800 килограмм/сж²; б =28%; у=5 %; фигура 6— то же плоского стержня из более твердой стали:

Фигура 7.

Фигура 8.

<тд=4 000 килограмм/сж²; 6=25%; гр=5~%. Фигура 7 и 8— разрыв литой стали: σ_Β=4 10) кг/ом²; δ =22,%; ψ=50%. Фигура 9 и 10—разрыв специальной ста-

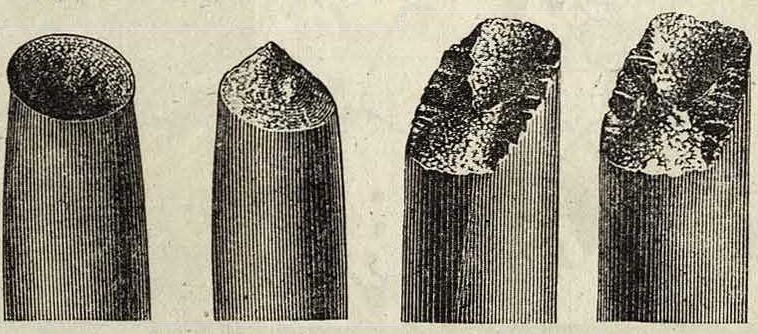
Фигура 9. Фигура ю. ли: ч_л=8 815 килограммам²; 6=75%; у=48%. Фигура 11 изображает поверхность разрушения при действии колебательной нагрузки (поверхность

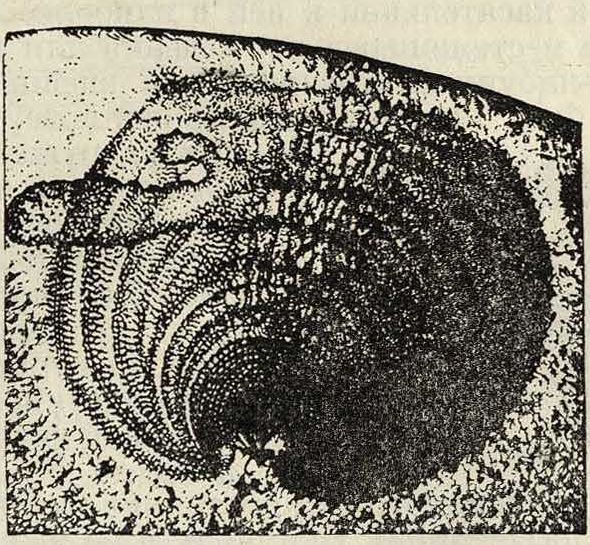
Фигура 11.

усталости). На фигуре 12, А и Б показаны микроскопии. картины поверхности исходного материала и разрушенного при статич. испытании: фигура 12,А—долевые деформации (а—естествен-

ное состояние, b—пластич. деформация при малых нагрузках, в—деформация перед разрушением), фигура 12, Б—поперечные деформации, (d—естественное состояние, е—при малых нагрузках, f—перед разрушением). На фигуре 13—то же при испытании на усталость (а—структура

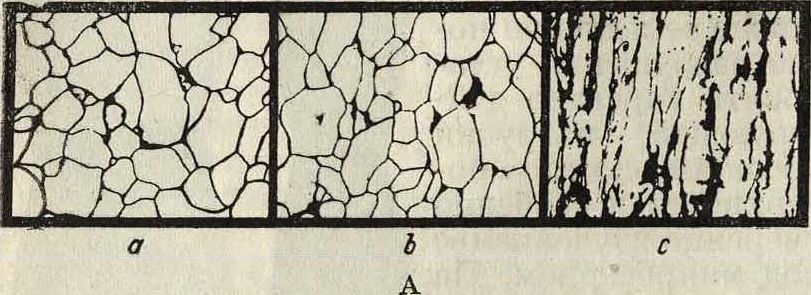
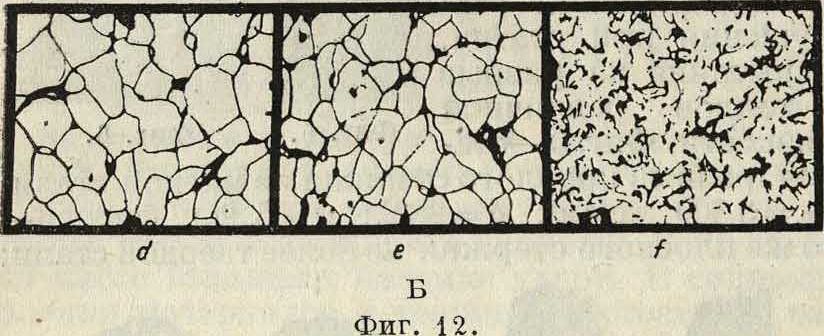
усталости, Ь—то же после отжига и с—структура с волосными трещинами разрушения). Можно усмотреть, что статич. испытание резко нарушает расположение кристаллич. зерен и их конфигурацию. Поверхность усталости (фигура 11) разделяется на две зоны—кристаллическую и

а b с

Фигура 13.

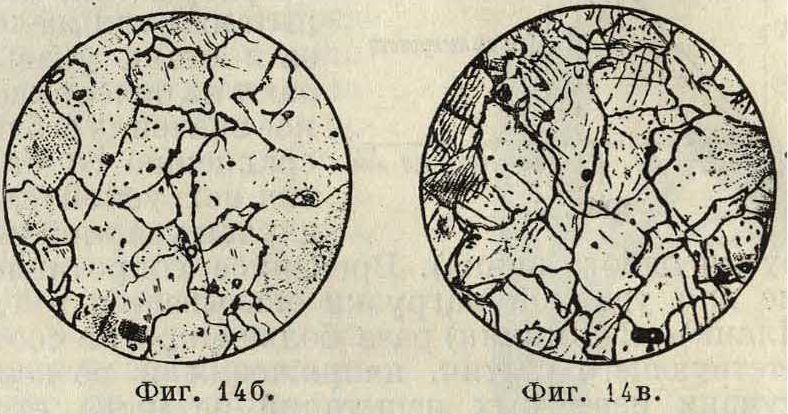
аморфную, причем аморфная образуется путем последовательного роста радиуса окружности с крайней касательной к ней в наиболее напряженном месте поперечного сечения или в месте какого-нибудь внутреннего или внешнего дефекта. Фигура 14а дает вид внешней поверхности при разрушении У. На фигуре 146 показаны микроструктура материала до У. и на фигуре 14в—после У. Здесь ясно выражена концентрация напряжений и деформированной зоны вблизи места У. Разрушение проходит через кристаллич. зерна (черные полосы—линии Неймана), а не между зернами, как при статич. испытании или на усталость (фигура 12 и 13). Концентрация деформированной зоны позволяет различать самые тонкие качественные черты металла и дает основание для надлежащей оценки нескольких способов термообработки данной стали (табл. 1).

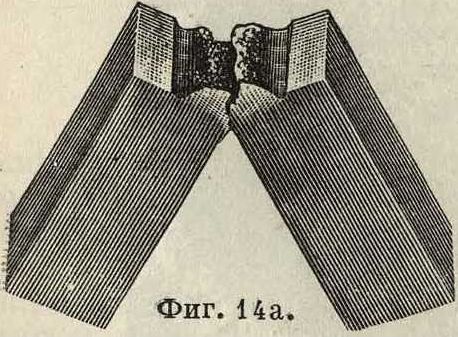
Изучение металла опытом на У. создает ясное представление о качественном состоянии и поведении металла и является прочным основанием для отбора металла для известных изделий, но не доставляет количественных данных для расчета. Расчет основывается всегда на временном сопротивлении при статич. растяжении (или начале текучести) и пределе уст з,-лости. Влияние удара учитывается особо для

каждой детали и должен быть указано при изложении способов расчета ее в курсах машиностроения. В табл. 2 [^х] приведены допустимые напряжения

Табл· 2. — Допускаемые напряжения для крановых конструкций (кг/см²).

Марка стали *1		*2	A	В	С
	σ8=1 930		1916 910	1 930 1 210	1 980 1 295
СО •4		II III I II III I II III I	2,16 ° 1 750 780	1,62 1210 1,60-ιοοο	1,51 1 29° 1757 1255
а н О	asch — i ^50		2,25 1 310 „„	1,75 1 000 1 310 _	1,45 1 256 1 310 975
	os=2 120		2,38 2 120	1,82 2 120 1 280	1,34 975 2 12». „ 1755““1370 1 850 1 280
Сталь 37			2,02 1 860 910	1,66 1280 1883 1010
	asch — I		2,3 1 380 575	1,75 1010 1380	1,45 1 280 а?— ши- ΪΓ-1-. 3 820 2 120
) Сталь 50	os — 2 715 °sch ~ 2 360 ow=1 690		2,4 2 ™ 1190 2,28 2-^=980 2,41 1690 «ЙК —6o5 2,52 3 620 1 510	1,75 745 т=1Ш 1 590 1Ж=87° 3 620
1>	asch — 8 100 aw=2 120	II III	2.4 3 100 1 250	1,8 3^=1 675‘ 1,85 2 120 1 060	1,71 31“ 1980
d Ε υ			2,48 2 120 820		1,59 2120 1510
			2,59	2	1,4 1
*! Марка стали обозначает временное сопротивле-
ние	разрыву в	mLwM2. Критич.		напряжение для по-
стоянной нагрузки			as равно пределу текучести, —
критич. напряжение при пеоемеинои нагрузке (от о
;ιο максимальной величины), σ				w—критич.	напряже-
ние	при колеблющейся нагрузке (от +ow до -ow).
Допускаемое напряжение получается как					частное от
деления критического напряжения на коэфициент безопасности. *2 Категория нагрузки.

при конструировании кранов и других подъемных устройств, причем возможное появление У. оценивается здесь в зависимости от скоростей подъема и передвижения, а также умеренной или напряженной работы привода. В основание таблицы положены три механические константы стали: предел текучести, временное сопротивление для переменной нагрузки и предел усталости. Напряжения даны для трех случаев нагрузки: спокойной (I), переменной (II) и колебательной (III). Напряжение в графе А относится к высоким скоростям и напряженной работе привода, в графе В—к незначительным скоростям и спокойной работе привода, почти одинаковой с ручным, и в графе С—только к железным конструкциям крана (не к машинным частям) и при достаточно тяжелой тележке. Предполагается совершенно справедливо, что сила инерции тяжелой тележки защищает конструктивные детали крана от внезапных ударов и прекращает колебания. В знаменателе всюду показаны достаточные, по мнению автора таблицы, запасы прочности. Из сравнения их можно вывести заключение, что автор дает У. и сотрясениям тем большую оценку, чем меньше удлинение материала; ко-эфициентам понижения напряжения он дает значения 1,44—1.8.

В элементарной теории У. предполагают, что: 1) смятия в месте У. не происходит, 2) влияние У. распространяется от места У. мгновенно (скорость передачи весьма велика), 3) длительность У. достаточна ^ для развития со ответствующей деформации, 4) скорость от места У. передается различным точкам упру-_I того тела по закону, к-рому подчиняется со.ответству-5) упругое тело восприни-

U—h —*·*--Δία

Фигура 15.

тощая деформация мает энергию от У. в одном только виде—потенциальной энергии, 6) закон сохранения энергии приложим к явлению У. и 7) упругое тело в своих изменениях подчиняется закону Гука.

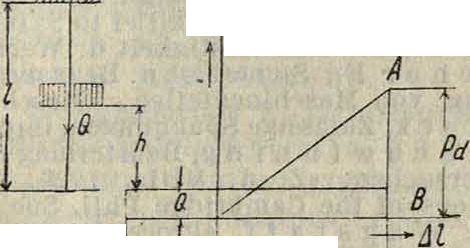
У. при растяжении и сжатии. Пусть груз Q падает с высоты h на подставку, присоединенную к стержню длиной I, поперечного сечения F из материала с модулем 1-го рода Е. До конца первого периода У., когда скорость груза и стержня будет равной нулю, закон сохранения энергии д. б,

QQb ₊ M_d)=l£^,

тде Al_d—абсолютное удлинение стержня, P_d— равнодействующая внутренних сил. На фигуре 15 представлено изображение ур-ия внутренней энергии стержня. Прилагая закон Гука в форме

P_d~EF^,

напряжение получим:

<*А

= в_st +]/"°ЬЛ-2о^Е 7,

удлинение

М

— &l_st + γΔϊ|ί + 2M_sfh.

Нели включить в рассмотрение массу стержня» придем к выражению

Δϊа~ Al_s< + Al_s* + 2Al_si/<^1

тде

rr —— Λ 7 _ °^s^ GSt~ p > St ~ p

(1)

(2)

^ad=o,t + ] ^{1 a}»t + ^2astE i (l — I yf-) > (3)

Г). *>

и G_e—собственный вес.

Выражения (3) и (4) показывают, что напряжение и деформация в имеющем массу упругом теле уменьшаются по сравнению с таковыми для невесомого стержня. Наименьшее напряжение от У. будет при h=0 и равно о>_г=2a_st. Если a_st—малая величина, можно принять вместо (3) и (4)

(У(1 — У ZcstE J	(l-l- 4 0 Osi·	j » (5)
А 1Л=У 2Meh[	, I «Λ 3	(6)

Высоту падающего груза можно заменить скоростью на основании того же закона сохранения энергии, а именно:

gft-f

Эта замена дает возможность распространения ф-л (1), (2), (3), (4) на те случаи, в которых вырота падения не входит непосредственно, например внезапная остановка при подъеме с известной скоростью, пуск в ход с большой скоростью или слишком быстрое торможение и прочие.

У. при кручении. Аналогично получим

St У •’SI I ι

^: Vst + Vrtt + 2φ>;ΐΨο,

(7)

<Pd=<Pst + V 9 t + 2φ_αφ₀, (8)

где G—модуль сдвига, l—длина вала, ?>₀г—произведение угла кручения на внешний радиус

j а>2

цилиндра, причем <р₀ =, I—момент инер ции масс относительно оси вращения цилиндра, ω — угловая скорость вращения, M_s—крутящий У. (внезапно приложенный момент кручения). Если начальная скорость масс до У. равна нулю, то

^rd=2т,„ (9)

в остальных случаях τ_ά будет еще выше.

Таблица 3. — Значения а и β.

Вид балки и нагрузка

β

А1,

i_	_ _ 2	a
h
t	ι Δ

Та

1/3

1/48

1 а‘ Ь* 3 12 /а

1/192

7/768

_1__С_

9ΫΊΓ ¹

1/4

ab

~W

1/8

3/16

Т. 9. m. XXIV.

15

У. при изгибе. Напряжение при У. равно

^ал=°st + V°lt + · ; · 7 · (Ю)

и деформация

h => fit + Vfh + (11)

где e—расстояние наиболее удаленного волокна опасного сечения от оси изгиба, I—длина балки, β — ксэф. пропорциональности между длиной балки и плечом силы, момент которой эквивалентен моменту maximum, а—коэф., зависящий от устройства опор .балки, /„ и f_st—стрелы прогиба в месте У. при динамич. и статич. нагрузке. В табл. 3 даны значения а νι β для различных видов/балок и расположения нагрузки.

Таблица 4. — Величины сил и напряжений для некоторых случаев удара.

Схема случая удара		Наиб, напряжение при У. °тох	Место °тах	Условия пользования ф-лой
ыт А 4	ιΑ h V l ϊ	Е —( Ym+1) а	Точка О	m > 24
И А 1	ТТ 1 1	E A (Fm+l,l)	о	24 > т > 5
ай А-	А т 1 Щ	2£ΐχ(ΐ+3_“)	О	5 > т
0 A v U Стержень свободен		еА. а	О	При всех значениях т
<АА г" i ши	t πτη h	V 1) 0,9Е — а 2) 1,5 Е — а 3) 2.0Е а	О	1) т=1 2) т=2 3) т=4
α= У~, т =^7=7 ’ »=Yigh, γ— уд. в.

В случае h=0 и a_d=Zc_s/; такое же соотношение, как и при других деформациях.

Принимая во внимание собственный вес балки, получим следующие ур-ия:

fa=fst + I fit + -jyq~ (12)

V

^{И а}*^=а*Ы ⁽¹³⁾

для балки, свободно лежащей на двух опорах;

для консольной балки множитель у второго члена (2f_sth) под корнем будет равен:

1

1 4- ^

U0 "Q

Если f_st— малая величина, то можно принять

°d=V^‘^ET-Ι-i·

Выводы теории У. используются в расчетах как указание для выбора допустимых напряжений. Допустимые напряжения для вероятной ударной нагрузки (быстроходные двигатели) и тем более для постоянной (молот) выбираются в 1/г—2 раза и более ниже тех, которые соответствуют случаю нагрузки рассчитываемой конструкции. В табл. 4 приведены величины сил и напряжений для других случаев удара.

Лит.: i) G а г 1 е р р, Zuhissige Spannungen u. Dauer-festigkeit im Kranu. Verladebriickenban, «Mascbinenbau», 1930, В. 10; Давиденков H., Динамич. испытание металлов, М., 1929; Todhunterl. a. Pearson К., A History oi the Theory oi Elasticity, v. 1, Galilei to Saint-Venant, L., 1886; Oral 0., Die Dauerfestigkeit d. Werk-stoffe, B., 1929; Rotscher F., Sicherheit u. Beanspru-chung bei d. Berechnung von Maschinenteilen, «Maschi-nenbau», B., 1930, B. 9; В о c k, Zulassige Spannungen, ibid., 1930, B. 9 u. 1931, B. 10; S ct w i ruling, Beurteilung d. Werkstoffe nach Kerbversuchen, «Ζ. d. VDI», 1929, p. 390; Sears, «Transactions ol the Cambridge Phil. Soc.», Cambridge, 1908, v. 20; W a g s t a 1f, «Proceed, of the Royal Society of London», L. 1924, p. 544. С. Лебедев.