> Техника, страница 88 > Ультрацентрифугирование

Ультрацентрифугирование

Ультрацентрифугирование, метод ускоренной седиментации (осаждения) высокодисперсных коллоидных частиц, введенный Сведбергом (1923) как новый метод коллоиднохимического исследования для определения размеров оседающих частиц, то есть для целей дисперсионного анализа (смотрите Седименто-метрия). Прибор, построенный Сведбергом для измерений по этому методу,—у льтрацен-

о т р и ф у г а (смотрите фигуру)—представляет собою обычную центрифугу (смотрите), в которой вращение сосудика АВ с коллоидным раствором происходит вокруг оси ОК в горизонтальной плоскости и с весьма значительной скоростью, создающей поле центробежной силы, иногда в 100 000 раз превышающее нормальное поле тяжести (10^s<?). Сосудик снабжен плоскопа-

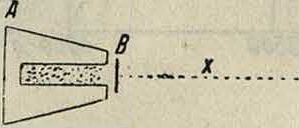
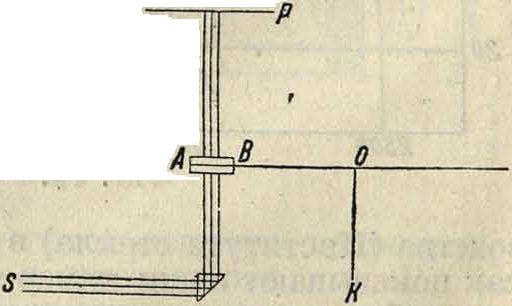
раллельными стенками и при прохождении через определенную точку окружности вращения автоматически фотографируется (S—источник света. Р—движущаяся фотопленка). Полученная кинематограмма позволяет посредством микрофотометрирования определить для каждого момента границу оседающих частиц в достаточно монодисперсной системе. Таким образом удается определить скорость оседания dx

дисперсных частип v=-^, а следовательно,

пользуясь законом Стокса (смотрите Седиментоме-трия), и их радиус и мол. вес, то есть мицеллярную массу (относительную массу мицеллы, или частицы, по отношению к массе атома кислорода равной 16)

^=6 щг% (1)

где F=V (I)₁— Р._г)а>^гх— центробежная сила, действующая на дисперсную частицу объёмом

F=| да⁸, плотностью 1)₁ в дисперсионной среде, плотность которой И₂, η—вязкость, со— угловая скорость центрифуги и х—расстояние до оси вращения. Интегрируя (1) и принимая во внимание наблюдения двух положений границы оседания χ_λ и ж₂, соответствующих на кинематограмме двум моментам т_х и т₂, находим выражение для среднего радиуса г частицы

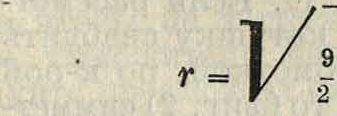
_о__

(jDi^— -0₂)^ω2

In

х₂

Xl

(2)

Так, для одного из Au-золей Сведберг находит по (2), что г=2,4 тц; ультрамикроскопически же получается г=2,5 тц. Кроме того удается количественно наблюдать Перреновское равновесие распределения дисперсных частиц в центробежном поле, вполне аналогичное тому, которое наблюдалось с грубо-дисперсными частицами в обычном поле тяжести. Эти последние измерения позволяют, пользуясь общепринятым значением числа Авогадро (JV==6,06х 10²⁸), вычислить массу дисперсных частиц (мицелл). Действительно, для седимента-ционного равновесия из условия равенства «потоков» растворенного вещества (от центра под влиянием «осаждающего» действия центробежной силы и обратно к центру под влиянием диффузии) имеем

RT 1п I - ^^V^-D₂)N _(ж1 _ _ж?))

(3)

где с₂, с_х—концентрации дисперсной фазы в точках х_г и x_lt определяемые микрофотоме-трированием снимков по сравнению со стандартами определенной концентрации. Т. к. вес частицы М=NVI>₁, из (3) легко найти М:

М=RT In—

^с2 <

2 Di

(xi-χϊ)

(смотрите Молекулярный вес). У. было применено Сведбергом и его последователями в Упсале (Швеция) и в США не только для исследования типичных лиофобных золей, например золей золота, но и значительного числа гидрозолей биоколлоидов (протеинов, гемоглобина крови и т. д.) с целью определения мол. веса растворенных веществ в этих золях, оказавшегося порядка 10 000—100 000. Т. о. вопросы, разрешаемые методом У., представляют не только большой дисперсоидологический, но и значительный биохимич. интерес. В случае по-лидисперсных систем (золей) У. может служить для снятия кривых распределения массы дисперсной фазы по размерам частиц.

Лит.: Freundllch Н., Kapillarchemie, 4 Aufl., В. 2, Lpz., 1932; Svedberg Th. u. Nichols, «Am. Soc.», 1923, y. 45, p. 2910; 1926, v. 48, p. 3081; 1927, y. 49, p. 2920; Syedberg u. Rinde, ibid., 1924, y. 46, p. 2677; Svedberg, «Ztschr. f. phys. Cbemie», Lpz., 1926, v. 121, p. 65; «Kolloid-Ztschr.», Dresden, 1930, B. 51, p. 10; T i s e 1 i n s, «Ztschr. f. phys. Chemie», Lpz., 1926, B. 124, p. 449; Lamm, ibid., 1929, A, B. 143, p. 177. П. Ребиндер.