> Техника, страница 88 > Упругая кривая

Упругая кривая

Упругая кривая, упругая линия, изогнутая ось, осевая линия деформированного сооружения. В сопротивлении материалов при расчете отдельного элемента сооружения определяют не только величины максимальных напряжений, но и величины прогибов и углов наклона. Для оценки жесткости спооектированной балки находят линию прогибов и сравнивают максимальный прогиб с допускаемым, к-рый обыкновенно назначают определенной частью от пролета. Под У. к. в сопротивлении материалов понимают упругую линию балки. Статика же сооружений занимается деформацией целого сооружения. Помимо оценки жесткости сооружения определение элементов У. к. имеет громадное значение при расчете статически неопределимых систем. Так, дополнительные уравнения деформаций при расчете на неподвижную нагрузку пишут, приравнивая нулю или заданной величине перемещений по направлению лишних неизвестных. Расчет же статически неопределимых систем на подвижную нагрузку, то есть построение линий влияния, проводится при предварительном построении упругой линии деформированного сооружения. Замечателен по своей простоте способ построения линии влияния усилий в любой сложной статически неопределимой системе; отбрасывают ту связь, усилие в которой ищут, и строят упругую линию сооружения, подверженного действию единичной силы, заменяющей действие отброшенной связи. Полученная упругая линия и есть модель линии влияния искомого усилия. Вопросами У. к. приходится заниматься и при разрешении проблемы устойчивости сооружений и их отдельных частей. Исходя из диференциаль-ного ур-ия У. к., находят критич. нагрузки.

Блестяще разрешающий ряд задач устойчивости стержней и пластинок метод вариации упругой энергии требует предварительного задания возможной формы отклонения стержня. Таково в главнейшем значение вопроса об определении У. к. Поэтому как сопротивление материалов, так и статика сооружений уделяют большое внимание У. к. и теории перемещений. Галилей, Бернулли, Эйлер, Навье, Коши, Клапейрон, Винклер, Мор, Тимошенко много работали над проблемой теории перемещений.

Задача определения элементов У. к. состоит в нахождении ординаты У. к. в произвольной точке бруса. Нередко интересуются и углом наклона касательной к У. к.в дан- !

ной точке к пер- р f ^р

воначальной оси.

Назовем ординату У. к. через у и угол наклона касательной к оси через а (фигура 1).

Для получения диференциального ур-ия УГк. воспользуемся известным соотношением между кривизной изогнутой оси и изгибающим моментом

1 М е Ы’

где ρ—радиус кривизны. М—изгибающий момент, Е1—жесткость. Подставляя сюда известное выражение кривизны, получаем следующее соотношение:

d²y

doc² _ Μ

И1ГГ^=Ш

Ограничиваясь случаем малых деформаций, пренебрегаем весьма малым сравнительно с единицей, и получаем общеизвестное диферен-циальное ур-ие упругой линии

d2y _ _м__ doc² ~~ Ы

Еще Ренкин подчеркнул диференциальную зависимость между следующими пятью элементами изгиба: если у—ордината У. к., то первая производная от у есть тангенс угла наклона касательной к У. к., вторая производная от у есть изгибающий момент, деленный на жесткость, третья производная от у есть поперечная сила, деленная на жесткость, четвертая производная есть интенсивность сплошной нагрузки, деленная на жесткость.

Среди многочисленных приемов нахождения прогибов балок следующие являются важнейшими: 1) метод непосредственного интегрирования диференциального ур-ия, 2) универсальная формула прогибов, 3) графоаналитич. способ Мора, 4) графич. способ. Первый способ состоит в непосредственном последовательном

ί м,

интегрировании выражения -=-gj в форме d²i м

- gj. Интегрируя это соотношение один раз, получаем

= tg α= J dx + G.

Интегрируя второй раз, имеем

У=Jtga · dx + JD=+ Cx + D.

Такой процесс интегрирования производится для каждой ветви У. к. Если У. к. имеет п

(ГоризонтI

(Горизонт)

фигура 1.

ветвей, то общее число произвольных постоянных интегрирования будет 2 п; отыскание их производится из условий непрерывности У. к. и опорных закреплений. Однако, представляя закон изменения нагрузки по длине одной и той же ф-ией от х для всех участков балки, Клебшу удалось дать прием быстрого сведения 2 п произвольных постоянных к двум.

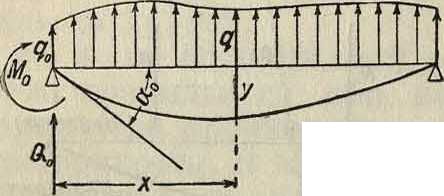
Второй способ отыскания ур-ия У. к. дает общую универсальную формулу для У. к. при любой нагрузке. Для случая непрерывной сплошной нагрузки, интенсивность которой меняется по определенному закону, получается особенно простое решение. Пусть (фигура 2) в начале координат, помещенном на левой опоре, приложен начальныймо-мент М₀, начальная поперечная сила Q₀ и начальная интенсивность сплошной нагрузки q₀. Пользуясь теперь диференциальной зависимостью между пятью элементами изгиба и применяя разложение ф-ии у в ряд по строке Маклорена, имеем следующую универсальную ф-лу:

Фигура 2.

У=У о + “о® +

Мо *2. Qo X³, gp я⁴. EI 2! EI 3! ⁺ El 4! ^

Здесь у₀—прогиб и а„—угол наклона в начале координат. Для случая балки, опертой на жесткую не оседающую левую опору, первый член разложения равен нулю, для балки, жестко заделанной левым концом, первые два члена равны нулю. Ур-ие же У. к. в случае любой прерывной нагрузки получают последовательным прибавлением к вышенаписан-

ному выражению добавочных членов —^——

на основании теоремы: «если п-я производная от ординаты У. к. имеет разрыв в виде конечного скачка величиной в Р (сосредоточенная сила—в эпюре Q, сосредоточенный момент—в эпюре Мит. д.), то есть

fp (с)=/‘^И)(с) + Р,

тде /1 (с) и f ₂ (с)—ур-ия У. к., первое при х ^ с и второе при х:з=е, то ур-ие У. к. на втором лластке /₂(ж) можно представить в виде ур-ия У. к. на первом участке /у (ж), прибавляя член р (ж-с)” п! ’

Аналитически это представляется так:

Если начало координат поместить на левой опоре для случая, изображенного на фигуре 3, м

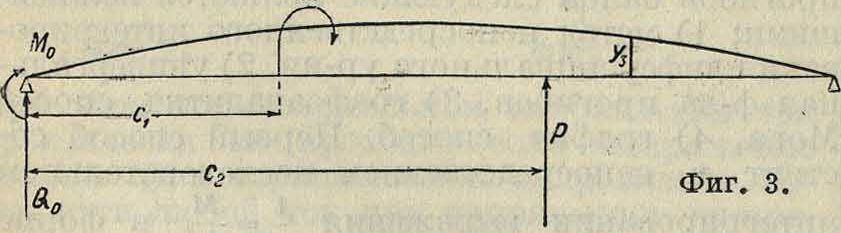
то ур-ие У. к. на третьем участке при условии приложения в пролете на расстояниях с_г и с₂момента М и силы Р примет вид:

-_ах, Μο.Ξΐ + Q» ΐ1 ₊

Уз - ^a0^J/ Л PI 2! Т- _{Е1 3}| Т

, м (Ж-С0>. Р (ac-Ci)·

^ EI 2! EI 3!

Обобщенное ур-ие У. к. было предложено Н. Снитко в 1926 году (Москва).

Графоаналитич. метод Мора использует прежде всего указанную диференциальнуЮ зави симость между элементами изгиба. Можно при этом подметить следующую аналогию. Если задана сплошная нагрузка интенсивностью q, то для поперечной силы и изгибающего момента получаются следующие зависимости:

Q=j qdx + C,

М=JJ qdx + Сх + Ю.

Совершенно аналогично, если в любом сечении м балки известно значение кривизны, к-рую примем за интенсивность фиктивной сплошной нагрузки q, для тангенса угла наклона и ординаты линии прогиба получим выражения:

tga=J* qdx + С,

У=JJ qdx + Сх + D.

Отсюда следует, что тангенс угла наклона касательной к У. к. можно подсчитать как поперечную силу от сплошной нагрузки, интенсивность которой в любом месте есть q, а ординату У. к. можно определить как момент левых сил от нагрузки q. Т. к. при построении эпюр поперечных сил и изгибающих моментов мы получаем большие навыки в нахождении поперечной силы и момента, то перенесение методов построения этих эпюр на отыскание элементов У. к. сильно упрощает решение.

Четвертый способ построения изогнутой кривой как веревочной кривой вытекает из графоаналитического метода Мора. Если требуется графически определить эпюру изгибающих моментов от заданной нагрузки, то для этого строят при произвольно выбранном полюсном расстоянии Н веревочно-стержневой мн-к. Произведение ординаты веревочного мн-ка, отсчитываемой от замыкающей, на полюсное расстояние дает величину изгибающего момента. По Мору ордината У. к. есть изгибающий момент от кривизненной нагрузки, и следовательно достаточно построить веревочный мн-к, соответствующий нагрузке q=^, и произведение ординаты веревочной кривой на полюсное расстояние дает ординату У. к.

Кроме перечисленных существует ряд других несущественных упрощений. Однако следует отметить замечательное по своей простоте

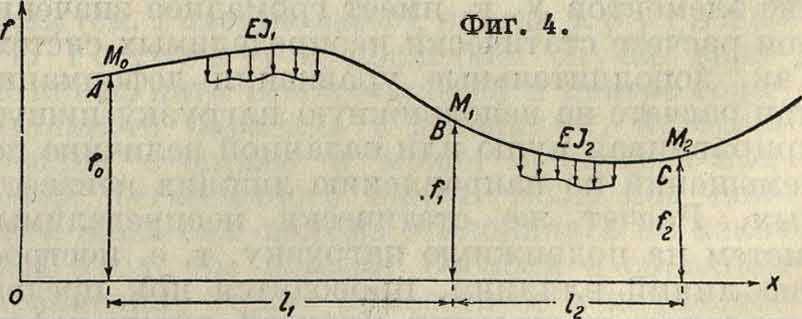
определение прогибов, используя ур-ие трех моментов для бруса с переменным моментом инерции. Инж. А. Попов (1933 г.) предложил находить прогибы из ур-ия трех моментов для балки на упругих опорах. Ф-ла, предложенная им, носит название уравнения трех перемещений и имеет следующий вид:

[foh ~ fi (h + h) + fzhl -

~¹Ψ[Μ₀1₁ + ΖΜ₂(1₁ + Μ₂) +

+ Μφ1₃ - - ^ϊ]·

Здесь согласно фигура 4 АВС—любая ветвь У. к. с воображаемыми в А, В и С оседающими опорами; /₀, /j и /₂—прогибы в точках А, В и С; М₀, М_х и М₂—изгибающие моменты в этих же точках; Е1_Х и Е1₂—жесткости для участков 1_Х и 1₂; Ω_χ и й₂—площади эпюр моментов от нагрузки для балок АВ и ВС, считаемых разрезными; а_х и Ь₂—расстояния д. т. эпюр моментов fij ий₂ соответственно до точки А и до точки С по горизонтали.

Лит.: Тимошенко С., Курс сопротивления материалов, 12 изд., М.—Л., 1931; КирпичевВ., Сопротивление материалов, ч. 1—2, М.—П., 1923; Попов А., Метод трех перемещений, М.—Л., 1933. Н. Снитко.