> Техника, страница 88 > Упругий гистерезис

Упругий гистерезис

Упругий гистерезис, явление отставания величины напряжения от величины деформации в упругой области, которое указывает отклонение свойств металла от закона прямой пропорциональности (Гук) и замедление роста (убывания) деформации по сравнению с ростом (убыванием) напряжений.

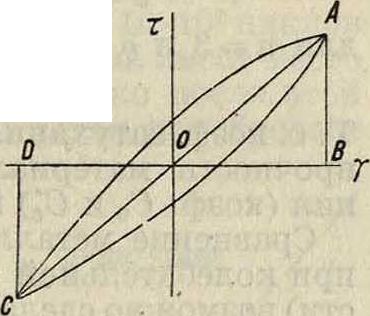
Соотношение между напряжением σ и деформацией ε, к-рое в теории сопротивления материалов должен быть признано основным, графически выражается в упругой области прямой АС в координатах σ и е для случая нагрузки и разгруз-

(V«
- о

-ε(Τ)

Фигура 1.

Фигура 2.

ки(фигура 1). Между тем опыт дает соотношение между σ и ε при большой точности измерения (в опытах Фёппля 10^-5) в виде некоторой кривой (фигура 2). На фигуре 3 представлена машина Шенка, которая позволяет видеть простым глазом эту кривую за цикл напряжений (от +т до —т) на матовом стекле. Машина состоит из оптич. индикатора и электромотора с механизмом для повторного скручивания образца а. В е ά закреплен один конец образца, а другой соединен с крутильным динамометром, правый конец с которого закреплен зиса (или петлю гистерезиса) можно наблюдать также в неупругдй области, притом очень легко при обычных средствах измерения, т. к. наибольшее и наименьшее измерения этой кривой, т. н. полуоси петли гистерезиса, велики по сравнению с теми же величинами упругой об

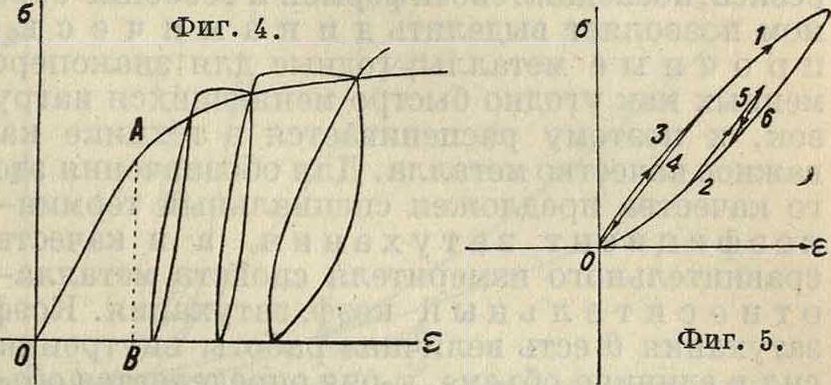
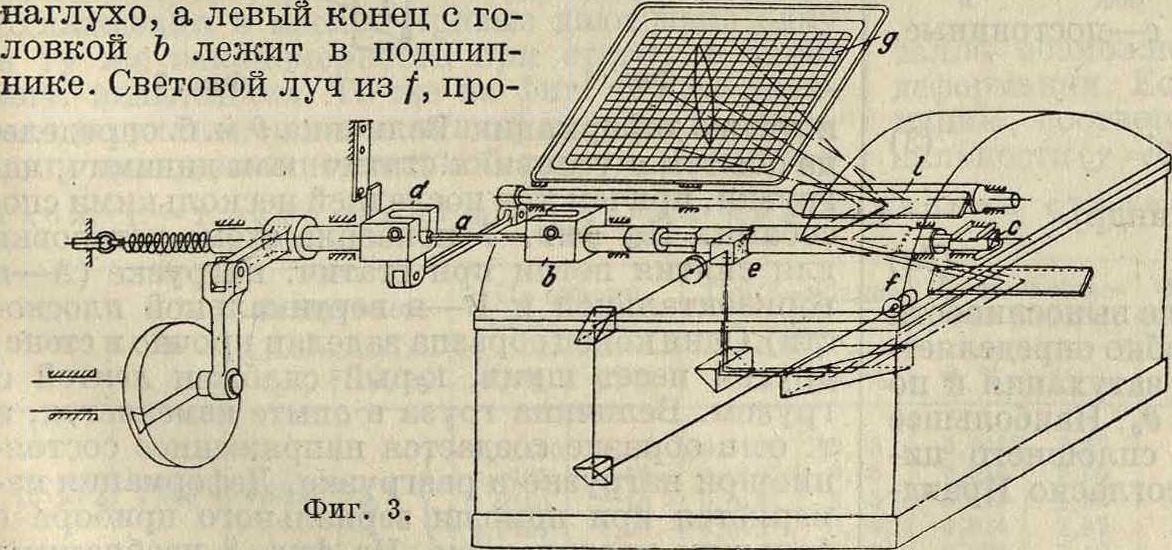
ходя через две призмы, падает на призму е, свободно насаженную на стержень динамометра, но связанную с головкой b и вибрирующую вместе с последней. От призмы е световой луч попадает через систему призм на матовый экран д и проходит на нем путь, составляющий диаграмму напряжение—деформация в течение каждой смены нагрузки образца, то есть при каждом обороте машины. Кривую гистере ласти (фигура 4). Петля гистерезиса обнаружена при переменной нагрузке (от 0 до σ) и знакопеременной нагрузке (от —σ до +σ) и в условиях как статического,так и динамич. действия нагрузки. Полуоси петли гистерезиса и объём ее (площадь) имеют различную величину для разных металлов и изменяются для одного и того же металла под действием особых факторов—истории металла (числа циклов предварительной нагрузки), высоты наибольшего напряжения в цикле, ί°, формы и размеров образца, вида деформации, а также термич. и холодной обработки. Фигура 5 изображает изменение петли от высоты напряжения. От скорости деформации появление петли и размеры ее повидимому не зависят; также и от продолжительности действия нагрузки. Нек-рые хрупкие металлы обладают гистерезисом (например чугун); вязкие металлы с удлинением при статич. разрыве не менее 5,5% всегда показывают петлю того или иного размера.

Электронная теория строения материи рассматривает закон пропорциональности между напряжением и деформацией в качестве первого и грубого приближения к действительным соотношениям, которые подчинены более сложному закону вида:

σ=Εε+±Εε*+±Ε"ε

где а — напряжение, ε — деформация, Ε, Е, Е", .—постоянные. Т. о. криволинейная зависимость между напряжением и деформацией соответствуетэле-ктрич. природе металла и ей вполне объясняется. Расхождение между кривой нагрузки и разгрузки (необратимый процесс) находит свое объяснение в явлениях внутреннего трения металлов (Warburg), или в явлениях упругого последействия (Bennewitz) или в совместном действии обоих факторов, или в явлении начальных напряжений (Sachs). В чистом одиночном кристалле явления упругого последействия и упругого гистерезиса не имеют места(идеально упругоетело),почему появление петли гистерезиса связано с дефектами внутри металла и остаточной деформацией в дефектных местах (Иоффе). Kuntze, снимая петлю гистерезиса при различных нагрузках и за разные периоды времени в условиях статич.испытания, приходит к выводу, что петля имеет один и тот же вид и объём в пределах нагрузок до 2/3 a_s(a_s—начало текучести). Если принять для рас-

пределения дефектов внутри сечения металла нормальную кривую Gauss’a, то возможно доказать совпадение результатов эксперимента (объёма петли гистерезиса) с вероятным значением их в пределах ошибок наблюдения.

Но какова бы ни была природа петли гистерезиса, последняя своей формой и особенно объёмом позволяет выделить динамически прочные металлы, годные для знакопеременных как угодно быстро меняющихся нагрузок, и поэтому расценивается в технике как важное качество металла. Для обозначения этого качества предложен специальный термин— коэфициент затухания, а в качестве сравнительного измерителя свойств металла— относительный коэф. затухания. Коэф. затухания & есть величина работы внутренних сил в единице объёма, которая определяется объёмом петли гистерезиса и усваивается металлом в необратимой форме (нагревание) за один цикл изменений. Размерность &— Относительный коэф. затухания·—частное от деления коэф-та затухания на величину энергии, соответствующей высоте напряжения петли гистерезиса при условии подчинения свойств металла закону Гука, то есть

£

Не

(1)

где U_e =гд для кручения. Объем петли гистерезиса и следовательно коэф. затухания зависят от высоты напряжения в цикле, поэтому различают средний коэф. затухания (#) для единицы объёма данного образца, наибольший (#„), соответствующий крайнему напряжению волокна, и предельный (#f), соответствующий пределу выносливости или усталости. По Rowett’y зависимость между # и #₀, также между #, #₀ и размерами полого скручиваемого цилиндра с наружным радиусом г_г и внутренним г₂ может быть дана в форме

$„= #

П + 2

2

НЕ

НГ^а

(2)

если считать действительным соотношение между #о и углом сдвига у₀ при кручении:

#о=^а7о “ 7о=сг, (2а)

где г—радиус цилиндра,

При П=27а а и с—постоянные.

И —=ρ:

#₀=2,16 9 ; (3)

при п=3 И ρ=0 (сплошной цилиндр)

#₀=2,5#. (За)

По опытам Фёппля п при пределе выносливости поднимается до 8. Из опыта удобно определяется величина среднего коэф-та затухания и по у-риям (2) и (3) отыскивается #„. Наибольшее напряжение τ₀ при кручении сплошного цилиндра с диам. d и длиной I, согласно Пранд-тлю, м. б. найдено из ур-ия:

^τ°⁼^ΓΛ^{3Μ +} ^·^γ°*)’ ⁽⁴⁾

dM,

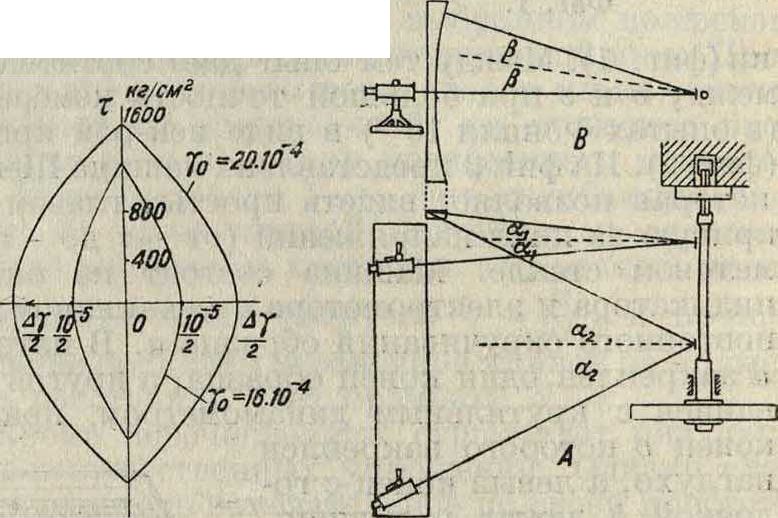
причем берем из кривой статич. испытании (диаграмма М и Αφ—крутящий момент и угол кручения) и строим новую кривую т₀ и у„. Петли гистерезиса изображают также в координатах т₀ и ~, откладывая по оси ординат т₀и по оси абсцисс полуразности углов сдвига крайнего волокна при нагрузке и разгрузке (фигура 6). На фигуре 6 изображены две петли для стали при угле сдвига γ₀=20· КГ⁴ и γ₀=16· 1СГ⁴. Очевидна разница между петлями по объёму. Если принять между действующим моментом и деформацией закон пропорциональности, что соответствует опытным данным, то

“=А=Const и М=ку₀

и ур-ие (4) преобразуется сл. обр.:

^r"⁼ L· (^{3 1} + ^А тонн) У»= ^Су«’ (^4а>

где С—константа. Поэтому наибольший коэф. затухания по ур-ию (2а) равен

#0=-QH > (5)

и средний коэф. затухания по ур-ию (2) будет равен:

#=(5а)

причем

Со

Для п=27₃

2 а

^: С^п (п + 2) *

‘ C₀T^21/s (1 - ρ^41/8)

ДЛЯ п=3 И ρ=О

1

ι-e²

(6)

#=С0тз. (7)

Т. о. коэф. затухания, и следовательно динамич. прочность материала, зависит от формы сечения (коэф. С₀ и С0) и высоты напряжения.

Сравнение металлов в отношении прочности при колебательной нагрузке (динамич. прочности) возможно сделать по величине &, найденной для одной и той же формы сечения и для одной

Фигура 6.

Фигура 7.

и той же деформации. Величина & м. б. определена опытом в условиях статич. или динамич. нагрузки, причем для последней несколькими способами. На фигуре 7 показана схема установки для снятия петли при статич. нагрузке (А—в горизонтальной и В—в вертикальной плоскости). Один конец образца заделан прочно в стене, другой несет шкив, к-рый снабжен лентой с грузом. Величина груза в опыте изменяется, и т. о. в образце создается напряженное состояние при нагрузке и разгрузке. Деформация измеряется при помощи зеркального прибора с большим увеличением. На фигуре 8 изображена машина для динамических испытаний кручением. Стержень а имеет один конец, жестко закрепленный в тяге b и подвижный вместе с ней, другой конец присоединен к маховику с. При вращении мотора стержень периодически скручивается; мотор подвергается регулировке до тех пор, пока система маховик— образец не оказывается в резонансе с системой мотора. Т. о. создается устойчивый режим колебаний, в котором образец воспринимает в необратимой форме известное количество энергии и нагревается. Амплитуда колебаний изме

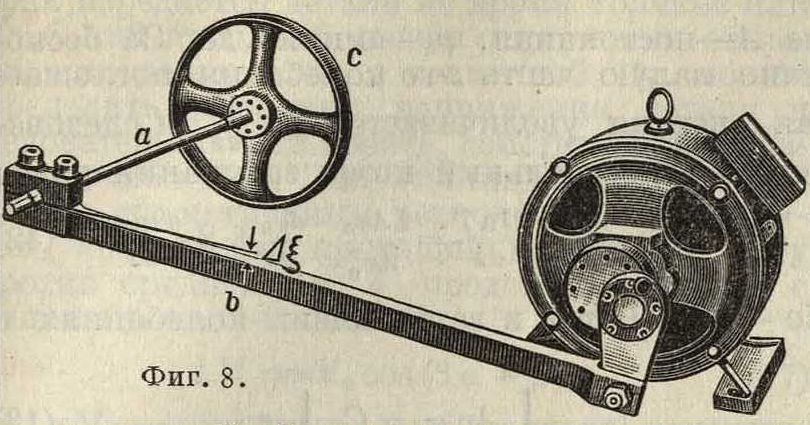
ряется путемШаблюдения за отметками на маховике (в виде тр-ков), которые отчетливо видны во время поворота маховика в начале размаха или м. б. сфотографированы. Повышение t° отмечается термоэлементом с точностью до 0,05°. Для определения площади петли гистерезиса измеряют: 1) отводимое образцом тепло в установившемся состоянии, или 2) изменение t° при пуске, или 3) непосредственно подводимую работу к системе маховик—образец. Во всех случаях образец д,б. подготовлен предварительно: он должен испытать не менее 10-10⁶ циклов при угле сдвига, большем того, к-рый имеет место в динамич. условиях, т. к. только после этой предварительной обработки петля приобретает

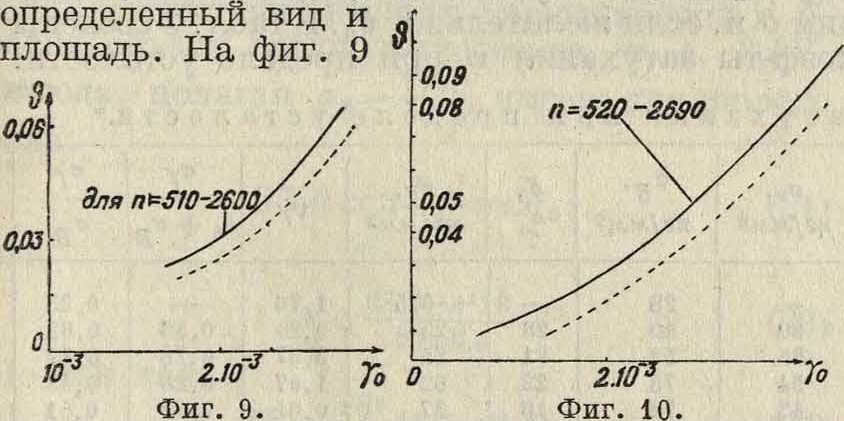
изображены кривые &, полученные измерением Г-ного градиента (полной линией) и статич. путем (пунктиром) для стали со следующими характеристиками: сг_в=7 380 килограмм/см“, δ=15,8%, τ_η =2 450 килограмм/см² при числе циклов ρ=2 · 10^е, после отпуска при t°=620° в течение 20 мин. и охлаждения в масле. Кривые дают явно одну и ту же закономерность при статич. и динамич. испытаниях. То же на фигуре 10, где динамич. затухание (полная линия) найдено по принципу измерения подводимой работы. В табл. 1

измерения при деформации кручения. На фигуре 11 сопоставлены кривые затухания, полученные из опытов на кручение: 1—железо Круппа, 2—сталь отожженная, 3—медь, 4—латунь и 5—электрон; пунктирные кривые относятся к изгибу, сплошные—к кручению. Расхождение замечается, но не существенное в отношении

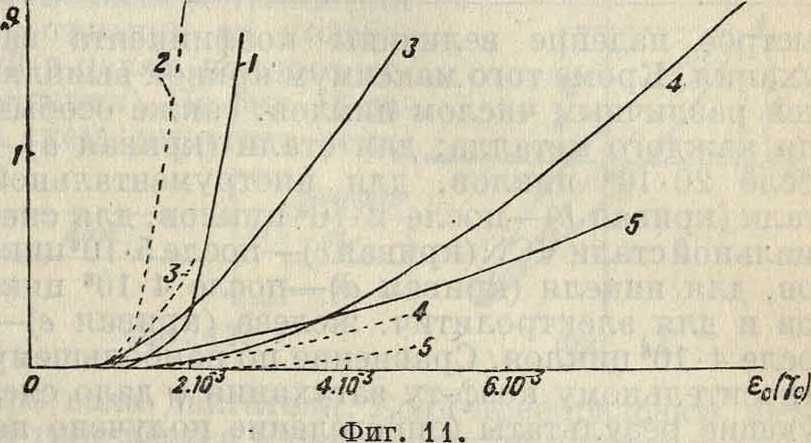
опытов на изгиб и кручение. Большая разница наблюдается между значениями коэф-та затухания для различной величины деформации и напряжения (фигура 9 и 10), поэтому принять коэф. затухания в качестве характеристики ме

талла возможно только при одной величине деформации. Если взять для сравнения деформацию, соответствующую пределу пропорциональности (у=0,002), получим средние коэф-ты затухания, приведенные в таблице 2 (стр. 571).

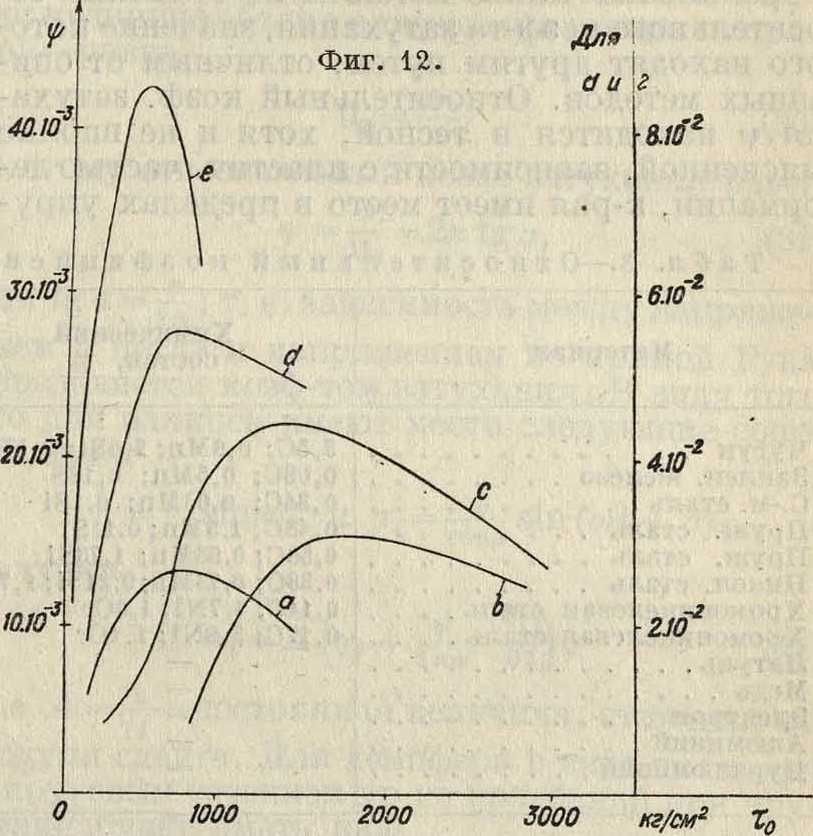
В основание суждения о динамич. прочности металла возможно положить наибольшее значение относительно го коэф-та затухания ψ, которое находится указанным путем измерения &. На фигуре 12 представлены кривые изменения относительного коэф-та затухания в зависимости от высоты напряжения при различном числе циклов для нек-рых металлов. Все кривые обнаруживают максимум при особом для каждого металла напряжении, после которого начинается

Таблица 1. — Коэфициент затухания при кручении стального образца.

У о

т0	Статическое			По отводимому теплу		По 4°=гради-енту		По поглощаемой работе		Число оборо тов п
	о, %	V, %		», %	V, %	д, %	V. %	», %	ψ, %
				0,01150	2,19	0,016	3,05	0,0135	2,57	150
				0,0135	2,57	0,016	3,05	0,016	3,05	600
				0,0110	2,10	0,016	3,05	0,015	2,86	1 200
				0,0105	2,00	0,016	3,05	0,014	2,67	2 400
				0,024	2,93	0,0235	3,23	0,026	3,17	150
	- - г,			0,025	3,14	0,0265	3,23	0,029	3,54	600
				0,02: 5	2,87	0,027	3,29	0,0285	3.48	1 200
				0,0225	2,79	0,028	3,42	0,0270	3,30	2 400
				0,044	3,73	0,055	4,66	0,050	4,23	150
				0,015	3,85	0,055	4,66	0,060	5,08	600
				0,040	3,39	0,0555	4,70	0,087	4,83	1 200
			1	0,046	3,90	0,0555	4,70	0,053	4,50	2 400

13 *ю-4

20*10-4

21*10-4

сопоставлены коэф-ты затухания для той же стали, что и на фигуре 9, из различных способов

Таблица 2. —Средние коэфициенты затухания.

Деформации	Железо Крупна	Сталь отожж.	Медь	Ла тунь	Элек трон	Же лезо
Изгиб.	0,5	0,5	0,3	0	0	0,125
Кручение.	0,1	0,1	0,06	0	0	0,025

быстрое падение величины коэфициента затухания. Кроме того максимум кривой выявляется различным числом циклов, также особым для каждого металла: для стали (кривая а)— после 20-10^е циклов, для инструментальной стали (кривая Ь)—после 2-10⁶ циклов, для специальной стали V CN (кривая с)—после 5 · 10⁶цик-лов, для никеля (кривая d)—после 4 - 10^е циклов и для электролитич. железа (кривая е)— после 4-10⁶ циклов. Сравнение по наибольшему относительному коэф-ту затухания ψ дало следующие результаты (определение получено на машине Шенка для динамического растяжения—сжатия) (в %):

Сталь № 14, 12. 1,3 Никель. 5,5

Инстр. сталь. 1,5 Электрол. железо. 4,25

VCN сталь. 2,2

Сравнивают также металлы по величине относительного ксэф-та затухания, значение которого находят другим путем, отличным от описанных методов. Относительный коэф. затухания ψ находится в тесной, хотя и не вполне выясненной, зависимости с пластич. частью деформации, которая имеет место в пределах упру-

Т а б л. 3.—О т н о с и т е л ь н ы и коэфициент гости. Если предел упругости найден с точностью до 0,003% (что соответствует международным нормам), то остаточная деформация равна ^ερΐ=0,003%. Для мягкой стали упругое удлинение в пределах упругости не превышает

^ел ~ 12-106 i ооо ’ ОД/о· (8)

Отсюда доля пластич. деформации в пределах упругости составляет или 3% общей деформации. По опытам Фёппля, Беккера и др. отношение λκψ колеблется очень значительно, среднее его значение м. б. взято между 0,16 и 0,23 для железа и стали, приблизительно 0,2, то есть

Ψ=5 λ. (10)

Величина ψ м. б. найдена также по кривой колебаний (в координатах <р и ί). Пусть колеба ние подчинено гармонии. закону, тогда поглощаемая в данный момент энергия равна:

Τ=ΑφΙ, (И)

где А—постоянная, ςρ₀·—амплитуда. За бесконечно малую часть 2-го колебания поглощае-

dT

мая энергия увеличивается на и следовательно относительный коэф. затухания равен

_ dT 1 _ dlnT _ 2А<Р₀ df₀__odln<p_{0 /10}Ч ^ψ dz Τ dz Αφ% di ^Λ dz

Но ^d_d°^y°=Const в затухающих колебаниях и

	Z=n Z—П
	1 lny„=C 1 z	(13)
	0 0
ИЛИ	In 9>„-1п <р0=Сп,	(14)
и далее	In —
	С=—δ, п ’	(15)

где δ—логарифмич. декремент колебаний. Наблюдая Ю последовательных колебаний или ме нее для любого случая, определяем — и затем

<Ро

In —= δ. По ур-ию (12) находим »/>=2<5. Поэтому,

<Ρθ

определив ψ по отношению (12) или (10), находим & и, если желательно, &₀. В табл. 3 сведены коэф-ты затухания ψ при пределе усталости. затухания при пределе усталости.»

Выбор материала на основании объёма петли гистерезиса представляет верный ход при конструировании машинных деталей, но не решает окончательно вопроса об их обязательной прочности в работе, т. к. петля гистерезиса находится в большой зависимости и от формы сечения детали [ур-ия (6) и (7)]. Коэф. С₀ Д. б. найден опытом для данной конструкции. Принимают для полого вала из отожженной углеродистой стали С₀=1675-КГ^П, для целого вала С0=500· Ю “, если величина деформации (у₀) находится в пределах ок. 0,0015—0,0020. Очевидно полная работа, к-рую воспринимает упругое тело с средним коэф-том затухания $ за один цикл и превращает в теплоту без изменения внутренней структуры и притом в течение какого угодно продолжительного времени, будет равна:

И„=7 (16);

где 7—объём детали в см³, & — средний коэф.

Материал	Химический состав, %		°s, кг/мм2	V кг/мм“	<5, о /о	Of, кг/мм“	xpf		Of
								а$ + °в	°Б
Чугун..	3,5С;	0,6Мп; 2,0Si; 0,5Р		28		6,5	1,76		0,23
Заклеп. железо.	0,08С	0,5Mn; 0,12S	29	40	26	25	0,26	0,36	0,62
С.-м. сталь ..	0,34С	0,6JMn; O.lSi	35	53	21	25	3,37	0,28	0,47
Пруж. сталь..	0.43С	Ι,δΜη; 0,12Si	54	75	22	32	1,07	0,25	0,43
Пруж. сталь..	о,53С;	0,53Mn; i,73Si	43	72	16	37	0,01	0,32	0,51
Нике л, сталь..	0,38С	0,73Mn;0,21Sl;l,7Ni	85	93	18	50	0	0,28	0,52
Хромоникелевая сталь.	о,14С;	4,7Ni; l,0Cr	85	91	19	60	0	0,34	0,66
Хромоникелевая сталь.	0,17 С	3,8Ni; l,lCr	47	78	26	45	0,65	0,36	0,58
Латунь..		—	33	47	13	15	0	0,20	0,34
Медь..		—	29	31,5	17	9	0	0,15	0,29
Электрон ..		--	—	23	18	9	0	—	0,39
Алюминий..		--	11	13,5	10	5,5	0	0,22	0,41
Дуралюминий..		---	22	38	13	14,5	0,15	0,24	0,38

* Sachs, Handbuch fur Physik, В. 5.

затухания по формуле (6) или (7) для полого и целого цилиндра с круглым сечением, или по табл. 2 или 3. Сравнивая внешнюю работу, которая передается детали во время толчков или колебаний при наибольшем отклонении от положения равновесия, с величиной 11₀, можем определить величину напряжения детали и следовательно установить действительный запас прочности ее. Для 6-цилиндрового мотора, например с симметричным расположением цилиндров, избыточный крутящий момент на валу (против среднего) м. б. представлен рядом с точностью до 3-го члена:

AM=εΜ₀ cos (3 α + β), (17)

где εΜ₀ — амплитуда избыточного момента, М„—средний момент, а—угол поворота вала, β — фазовый угол. Угол кручения во время резонанса выражается рядом:

φ=<Ро cos (з a i- β + · (18)

Поэтому величина избыточной работы будет:

2π

А =J AM άφ =3 Μ₀φ₀επ. (19)

О

Работа внутренних сил должна возрасти на величину

η_ο=Α=3πεΜ_οΨο (20)

и при отсутствии внешних сопротивлений должен быть равна объёму петли гистерезиса, то есть 3 &V. Отсюда, полагая <p₀=^j-, имеем для полого

Бс1Л£1!

3V& > 3 πεΜ„ (21)

ИЛИ

^ (*3(1 —ρ2)£ ^£< 8γοΜ~₀

(22)

Но так как

M₀=(l-g*)R_s, (23)

где R_s—расчетное напряжение, то 2&

ε

πγο (l+e²) R_s

Полагая— si (7, имеем: Уо

2Gв

ИЛИ

ε<

π(1 + q^z)tR_s2 GC₀r^lU

лНе

(24)

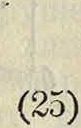
для’полого вала. Пусть во время колебаний напряжение не должно превышать допустимого в 2 раза, то есть тогда

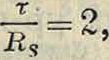
ε <

2 GCp л

2 ^7/зж!^/з

(26)

R_s>

(27)

•2 ⁷C?G³

Для С_е=1675 -10^-11 и G=0,8-10⁶ кг/см² имеем: R_s > 10^εε³. (28)

Если ε=0,17, то R_s> 17³-10 ⁶ -10⁵=500 килограмм/см²: допустимое напряжение должен быть не менее определенной величины для заданной амплитуды из быточного момента; чем выше наибольший момент по сравнению со средним, тем лучший материал должен быть выбран.

Относительный коэф. затухания у> имеет большое значение в теории упругого демпфера (так называется упругое тело различной формы, которое присоединяется ^

к основным деталям для амортизации их колеба- |

ний в целях полного ус- ^

покоения). На фигуре 13 дана схема упругого демп-

i		демпфер
1 Вал	m	md
*		— ι —i

Т Го

Фигура 13.

Фигура 14.

фера вала двигателя. Если преобразовать петлю гистерезиса в равновеликий эллипс, то объём ее будет равен:

#=jiy₀T₀tga, (29)

где Уо—наибольший угол сдвига, т₀—наибольшее напряжение в эквивалентном эллипсе (фигура 14). Площадь тр-ка ОАВ—величина энергии в единице объёма в случае изменения по прямой—равна

Uo=ir· (30)

Поэтому относительный коэф. затухания равен V’=^=2jrtg а, (31)

или tg α= —, то есть зависимость между напряжением в петле и напряжением по прямой Гука определяется коэф-том затухания. В виду того· что для эллипса имеют место следующие соотношения:

yi=y₀sin(ot и ^T=j5§5Sin(a)i + а),

получим

(32)

где А =^—постоянная величина, отличная от модуля сдвига. Для демпфера в виде цилиндра с круговым сечением ур-ие колебаний при кручении будет иметь вид:

-М_х + М_х+(fa -μΙ₀άχ^=0.

(33)

Здесь μ—удельная масса цилиндра, 1₀—полярный момент инерции сечения цилиндра, (М_х — ~Μχ+Λχ)—момент от гистерезиса, амплитуда.

Отсюда очевидно можно положить:

л д“Р ^ ^{= i?}«aE

M,=^_r*=—⁰ (у₍ + ^~

^ro ^ro V¹ 2 πω

-м_х

. _ ΛΙο (_r, уг-о

Г₀ ⁰ дхЬ 2 πω

Тогда придем к ур-ию:

Эуд Si ) *

д^г<Р πω dx^dt)

ч

+ — · дх² 2 πω dx^zdt

)

δ²φ _Λ

А* Д75=0;

(34)

Ψ и А находятся в зависимости от высоты напряжения для одного и того же материала. Если считать их постоянными, то интеграл ур-ия (34) м. б. представлен в виде:

φ =^φβ (a sin cot + β COS ωΐ),

(35)

причем

α= е

/j>qx

(A sin ωρχ -f В COS ωρχ) +

_!_ _е-“8^ж (Η _si_{n ω}ρχ -)- C cos ωρχ); β=е^ш9Х (В sin ωρχ — A cos ωρχ) +

J_r e~^mqx (A cos ωρχ — C sin ωρχ);

H=sin ωρί;

В=е~^2<“^зе + cos 2 cupi;

C=e^2<u?e + cos 2 ωρί;

В=В + C;

*-hVb P=Vl’

φ₀—амплитуда места закрепления демпфера. Пограничные условия:

ψχ-0=<Ро sin ^ωί; Ш Iχ~Γ^{ϋ при любш 1} (свободный конец цилиндра без напряжений). Для ψ —0 имеем свободное колебание самого демпфера, частота которого в резонансе с местом закрепления равна по ур-ию (35)

«<.=271/4· (36)

2п

Из ур-ия U₀=f М_х άφ найдем величину рабо-

0

ты, поглощаемой демпфером за цикл:

1 _α=πψΙΟ_Λν. (37)

Здесь обозначены:

Zip zn — siHZTC

1 — __.

η ΑΙ о.

4 cos²

ψ+{^)

-τ, ζ=—=* ^ωα

действительная угловая скорость демпфера круговая частота свободных колебаний цилиндра демпфера (без гистерезиса)

В случае резонанса «0 =

8π2 φξθα

Ψ

(38)

Включение демпфера на вал, свободная частота которого равна £, где с

G(вала _{и т}—_Пр_Иве.

т ’ ’ 1_В____

денная масса на конце вала вблизи демпфера, приводит амплитуду колебаний вала к величине

φ=-, -^М*---- _(39)

V (c-mmZ-Cd-u)· + (km + CdV)²

где М_е—амплитуда избыточного момента на валу,

jrzsin zn

U=-

4 COS² — +

(т)²

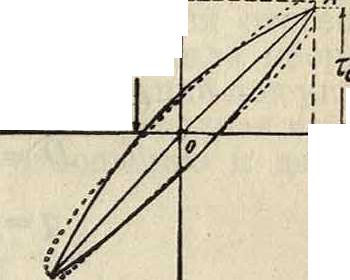
к—коэф. внешнего сопротивления вала, остальные величины известны. На фигуре 15 представлено изменение φ в зависимости от числа оборотов вала и относительной величины массы демпфера. Легко усмотреть, что резонанс наступает для каждого значения дважды; абсолютная величина амплитуды при известном резонансе дает указание относительно решения вопроса: включить демпфер или нет. Размеры демпфера в случае настройки его работы в резонанс с ва лом для определенного числа оборотов последнего можно найти сл. обр.:

i i k/πιω вала

¹ ψ/2π ’

_ тл2 c’_d _ ту,а ^т<г 1 ‘ с 8х ’

су² 2 π²κ⁹

m_d=pl₀l.

(401

Если при т_л демпфер нагревается очень быстро и выше нормы, работа его в консонансе с ва

лом невозможна, и размеры демпфера должен быть установлены по ур-ию (37), причем амплитуда колебаний определяется по ур-ию (39) для известного пульсирующего момента М_е. Послед

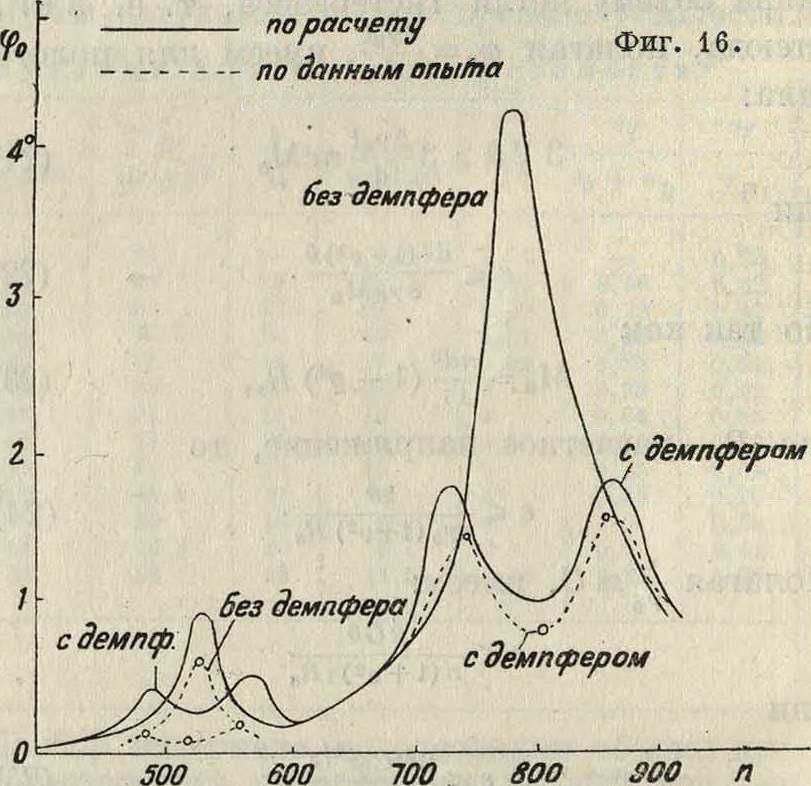
ний отыскивается гармонии, анализом кривой моментов двигателя. На фигуре 16 сделано сравнение кривых амплитуд двигателя — одной, полученной из опыта, другой—расчетом на основании приведенных ур-ий.

Лит.: Иоффе А., Физика кристаллов, М.—Л., 1932; Кузнецов В., Физика твердого тела, Томск, 1933; М о о г е A. and Kommers J., The Fatigue of Metalls, L., 1927; Gough H., The Fatigue of Metalls, L., 1924; Lehr E., Die Abkiirzungverfahren zur Er-mittelung d. Schwingungsfestigkeit von Materialen, Stg., 1925; Lehr E., Schwingungstechnik, B., 1930; Sachs G., Handbuch d.experim. Phys., hrsg. von W. Wien u. F. Harms, Band 5, B., 1932; Graf 0., Die Dauerfestig-keit der Werkstoffe u. d. Konstruktionselemente, B., 1929; Warburg E. u. Heuse W., «Verh. d. deut-schen Phys. Ges.», Brschw., 1915, B. 17, p. 212; Popple-well W., «Engineer», 1916, 121, p. 339; Wart en-b e r g H., «Verh. d. deutschen Phys. Ges.», Brschw., 1918, B. 20, p. ИЗ; К u n d s e η M., «Ann. d. Phys.», Lpz., 1915, B. 47, p. 697; Bennewitz K., ibid., 1919, B. 59, p. 193; Bennewitz K., «Phys. Ztschr.», Lpz. 1920, B. 21, p. 703; Mark K. H„PoIanyi M. u. Schmidt E., «Ζ. f. Phys.», Lpz., 1922; V о 1 m e r M.,

«Phys. Ztschr.», Lpz., 1921, B. 22, p. 646; Tolmer M., «Ztschr. f. Physik», Lpz., 1921;Yolmer 11., ibid., 1921, 7, p. 1 u. 13; P о 1 a n у i M., «Ztschr. f. Elektro-chemie», Lpz., 1922, B. 28, p. 16; M a s i n g &., «Wiss. Veroff. aus d. Siemens-Konz.», B., 1922, H. 3; А I t e rt-h u ш Η., «Z. f. Elektrochemie», Lpz., 1922, B. 28, p. 347; B e η n e w i t z, «Phys. Ztschr.», Lpz., 1924, B. 25, 17, p. 417; M a u к s c h W., «Ilitt. d. Kais. Wilh. Inst. f. Yletallkunde», B., 1922, 1, p. 41;Feussner 0. u. R a m b, «Ztschr. f. Metallkunde», B., 1927, 19, p. 115; Pert! E., Die Bestimmung d. Baustcffdampfung nach d. Verdrehungsausschwingverfahren, Sammlung Vieweg, Brschw., 1928, H. 91; F δ p p I Ο., «Z. d. VDI», 1928, B. 72, p. 1293; В e с к e r E. u.Fippl 0., «Forsch. Arb.», B., 1928, H. 304; S p a t h W., «Ztschr. i. ang. Mathem. u. Mechanik», B., 1927, p. 360; Voigt E., «Z. t. techn. Phys.», Lpz., 1928, 9, p. 321;Geller, «Arch. f. Eisenhiittemvesen», 1928, p. 257; J e n к i n C., «Engineering», 1922, Ili, p. 603; ibid., 13i, 612; M a i-

1 a n d er R., «Forsch. Arb.», B., 1922. H. 295; «St. u. E.», 1924, H. 21—25; A d e r s, «Mitt. Forsch. Inst. d. Vereinig. Stahlwerke», 1929; Boudouard M., «Bulletin de Ia Societd d’encouragement», P., 1910; F δ p p 1 O., Becker E., v. Heydekampf, Metallwirtschaft, 1929; Houdremont E. u. Ilailander R., «Kruppsche llonatshefte», Essen, 1929; Ros, Verh. des

2 int. Kongresses t. techn. Mechanik, Delft, 1926; R o-

wett F., «Proceed, ot the Royal Society of London», 1924, Ser. A., v. 89; S t г о in e у e r C., «Engin.», L., 1915;Lud vik P., Schwingungsfestigkeit, «Ztschr. d. osterreich Ingen. u. Arehit.-Vereins», W., 1929, B. 81, p. 403; Kuntze W., «Mitt. d. deutschen Material-priifungsanstalten», B., 1930, Sonderheft 14; F б p p 1 O., «Z. d. VDI», 1932, B. 76, p. 1129; T h u n A., ibid., 1931, B. 75, p. 324; «Ztschr. f. angew. Mathem. u. Mechanik», B. 1928 — 1933. C- Лебедев.