Упругость

Упругость, свойство тел, подвергнутых деформации (смотрите), после прекращения действия напряжений, вызвавших эту деформацию, возвращаться в первоначальное (недеформирован-ное)состояние, то есть восстанавливать свою форму и объём. Иначе У. есть способность тела испытывать обратимые деформации. В этом смысле У. противопоставляетсятглае»гмчмостм(смотрите)—свойству твердых тел, нек-рых высоковязких жидкостей и дисперсных систем испытывать остаточные деформации, сохраняющиеся в теле и после прекращения действия напряжений.Обыч-ные жидкости и газы явЛяются практически вполне упругими телами, обладая однако У. лишь по отношению к деформации всестороннего сжатия. Твердые тела, вообще говоря, всегда упруги по отношению к достаточно малым деформациям, до предела упруго-р с т и (фигура). Когдг, предел У. превзой-( ден, тело деформируется пластично (течет). Тело называется хрупким, если предел прочности его (соответствующий разрушению тела при данной критич. деформации) лежит до предела У. и при том обычно в области малыхдеформа-ций (кварц, стекло). Хрупкиетеламогут испытывать т. о. только упругие деформации вплоть до своего разрушения. В противоположность этому пластичными телами называются такие, в которых предел прочности лежит значительно дальше предела упругости, причем последний наступает обычно уже при весьма малых деформациях (свинец, воск). Такие тела обладают лишь очень малой областью упругих деформаций, уже при небольших деформациях начиная течь, давая картину пластического потока.

Характерным признаком упругих (обратимых) деформаций является применимость закона Гука независимо от рода деформаций. На

пряжение р_х пропорционально вызванной им деформации:

р_х=К^=Щ. (1)

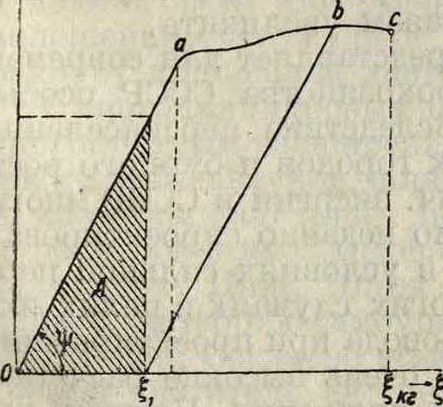
Здесь £—относительная деформация. Диаграммой У. называется график, связывающий для данного тела напряжение с вызываемой им деформацией (смотрите фигуру). Согласно закону Гука упругая часть диаграммы является отрезком прямой линии, исходящим из начала координат и наклоненным к оси деформаций под углом Ψ, тангенс которого графически определяет модуль упругости (смотрите) по отношению к данной деформации:

tg w=^d-V?=K. di

Величины, обратные модулям, называются к о-эфициентами У.:

A=7fc=ctg φ; £=k -2V (2)

3 основных модуля (всестороннего сжатия К, линейного растяжения Е и сдвига Ν) для каждого изотропного тела связаны друг с другом основным соотношением теории У.:

(3 К+ Ν)Ε=9 ΚΝ. (3)

Важную роль при расчетах играет также вспомогательная величина—к оэфициент П у а с_с она

4=V (4)

при помощи которого основные модули связаны следующим соотношением:

E=3K(l-2y)=2N(l+y); (5)

у представляет собой отношение поперечного сжатия I к продольному удлинению ε при одностороннем растяжении. При этом 0 ^ η 0,5. Т. к. по ур-ию (5)

13K-2N “ 2 SK+N

(6)

то при N=0 для жидкостей η приобретает крайнее значение ι;=0,5; у существенно положитель-

з но и потому gΚ>Ν.

Изучение упругих свойств тел или вообще их механич. свойств (и за пределом У.) составляет одну из основных задач молекулярной физики. Математич.часть этого отдела физики развилась в особую науку—теорию У., являющуюся вместе с гидродинамикой частью механики деформируемых систем и служащую основанием всех областей механич. технологии, строительной механики и учения о сопротивлении материалов. Теория У. является также основой акустики, т. к. звуковые волны представляют собой упругие колебания, распространяющиеся в данном теле, то есть упругие деформации, периодически изменяющиеся во времени. Теория У. анизотропных тел—кристаллов—представляет большое значение для кристаллофизики.

После приложения к деформируемому телу заданного постоянного напряжения деформация принимает равновесное значение во времени не сразу, а лишь асимптотически, практически через довольно продолжительное время (несколько месяцев). Это явление называется упругим последействием. Если же задать определенную деформацию, то напряжение, необходимое для ее поддержания, падает со временем, асимптотически приближаясь к нек-рому наименьшему значению—явление релаксации (смотрите). Максвелл указал на то, что причиной явлений после-

Т. Э. m. XXIV.

действия (релаксации) надо считать неоднородность материала. Особенно сильны эти явления в дисперсно-гетерогенных телах—гелях, поли-кристаллич. агрегатах, каковы все металлы, и т. д. В физически совершенно однородных телах, например однородных крист (кварце, метал-лич. монокрист) последействие практичес-. ки отсутствует (Иоффе). Работа, потребная для обратимой изотермич .упругой деформации тела, запасается в нем в форме свободной энергии:

— А=ΔΡ=J ρ_χάξ; о

№ выражается площадью упругой диаграммы (смотрите фигуру) от 0 до ординаты, соответствующей заданному напряжению р_х (или данной деформации ξ). По закону Гука:

-A=bF=|l²=fpi,

при этом вообще упругая энергия является однородной квадратичной ф-ией от деформаций или напряжений. Наличие упругого последействия вызывает появление петли гистерезиса даже в упругой области диаграммы (смотрите фигуру), хотя эта петля и не имеет практич. значения из-за сравнительной малости последействия. При переходе же деформации за предел У. в пластич. область гистерезис приобретает огромное значение. Упругие и пластич. деформации тела могут рассматриваться как обратимые и необратимые процессы методами общей термодинамики (смотрите). При этом можно например найти связь между изотермич. К,- и адиабатич. К_амодулями (или коэф-тами) У.

Лит.: Хвольсон О., Курс физики, т. 1, Берлин, 1923; Иоффе А., Молекулярная физика, П., 1923; его же, Физика кристаллов, М.—Л., 1929; Кузне ц о в В., Физика твердого тела, Томск, 1932; Брандт А., Основания термодинамики, ч. 1, М., 1923; Сборн. Ын-таинж. путей сообщ., П., 1915, выП. 90; Тимошенко С.и Лессельс Дж., Прикладная теория упругости, пер. с англ., 3 изд., Л., 1931; Ши л л ер Н., «Ж», часть физич., СПБ, 1879, т. 55; Handb. d. Phys. u. techn. Mechanik, hrsg. v. F. Auerbach u. W. Hort, Б. 1—4, Lpz., 1926—32; Mathematical a. Physical Papers oi Lord Kelvin, v. 1, Cambridge, 1884; V о i g t W., Lehrbueh d. Kristallphysik, Lpz., 1928. П. Ребинпер.