> Техника, страница 88 > Устойчивость

Устойчивость

Устойчивость. Равновесие тел можетбыть устойчивым, неустойчивым и безразличным. Устойчивым называется такое положение равновесия, когда при малом отклонении от этого положения тело опять к нему возвращается; неустойчивым,—когда тело при малом отклонении уже не возвращается в прежнее положение, а отклоняется далее; безразличным,—когда тело, будучи отклонено, остается в равновесии и в новом положении. Примером устойчивого равновесия может служить тяжелый шарик В, находящийся внутри чашеобразной поверхности АС (фигура 1,а);неустойчивого—шарик, расположенный в верхней точке выпуклой поверхности (фигура 1,δ),безразличного—тот же шарик, лежащий на горизонтальной плоскости (фигура 1, с).

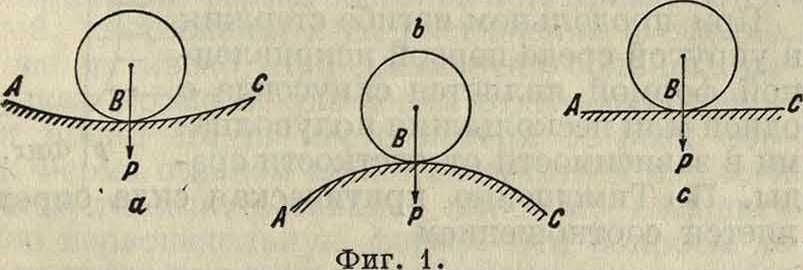
Характер равновесия м. б. различен для различных направлений отклонения от положения равновесия. Например если вместо сферической чаши возьмем цилиндрическую с горизонтальной образующей и сечением вертикальной плоскостью по линии АВС, то для случая по фигура 1,а при отклонении шарика из положения равновесия по направлению образующей равновесие будет безразличным, при всяком другом отклонении—устойчивым, а для случая по фигура 1, δ при отклонении вдоль образующей равновесие тоже будет безразличным, при всяком другом—неустойчивым. Возьмем седлообразную поверхность (гиперболический параболоид) и поместим шарик в срединной точке поверхности (фигура 2). В этом случае характер равновесия тоже будет различен для различных направлений отклонения. При одних направлениях равновесие будет устойчиво, при других—неустойчиво.

Аналитический признак У. таков: в положении равновесия работа δ А всех приложенных к телу сил на бесконечно малых отклонениях от положения равновесия равна нулю (начало возможных перемещений). Работа ΔА на малых, но конечных отклонениях от положения равновесия будет отрицательной при устойчивом равновесии и положительной при неустойчивом; если ΔΑ =0, то равновесие будет безразличное. Другой признак: в положении равновесия потенциальная энергия имеет либо минимум либо максимум. Если минимум—равновесие устойчиво, если максимум—неустойчиво (теорема Дирихле).

У. равновесия может зависеть также от величины действующей силы: при малой силе равновесие м. б. устойчиво, при большой — неустойчиво. То значение силы, при к-ром равновесие из устойчивого переходит в неустойчивое, называется критическим (Р_кр.) (смотрите Сила критическая). Если при возрастании силы Р работа Δ А приложенных к телу сил при малом его отклонении от положения равновесия меняет свой знак, то Р_кр, существует, если же работа сохраняет свой знак, то Р_кр. не существует. Для нахождения Р_кр надо приравнять эту работу нулю и решить соответственное ур-ие относительно Р. Можно воспользоваться теоремой Дирихле. Если с изменением силы Р минимум потенциальной энергии переходит в максимум или наоборот, то соответствующее этому переходу значение Р и будет критической силой Р_кр.

Для упругих систем тоже возможно несколько положений равновесия, которые могут быть как устойчивыми, так и неустойчивыми. Работами Брайана, Саутвелла, Мизеса и др. были выяснено, что теоремы Кирхгофа об однозначности решений ур-ий теории упругости неприменимы к таким телам, как тонкие стержни, пластины и оболочки, и что для них может иметь место несколько положений равновесия. Так, по Мизесу, если нагрузки, приложенные к упругому телу, заданы с точностью до некоторого числового множителя А, то существует такое значение этого множителя А₀, что для всех значений λ < λ₀ имеется только одно положение равновесия и притом устойчивое. Если λ стремится к 0, то это положение переходит в естественное, ненапряженное состояние тела. Если же λ > λ„, то возможно несколько положений равновесия. Нагрузку, соответствующую значению А=А„, называют критической. В отдельных случаях А₀ может равняться со; для такой системы существует только одно устойчивое положение равновесия и для нее критической нагрузки не существует. Практически существование нескольких форм равновесия имеет значение лишь в тех случаях, если при λ=λ„ не превзойден предел упругости. Это будут тела, у которых один или два размера малы сравнительно с третьим (пластины, тонкие стержни). Одни из этих форм равновесия устойчивы, другие неустойчивы. Для технич. целей чрезвычайно важно знать, какие из них являются устойчивыми, какие неустойчивыми, т. к. безусловно необхо-

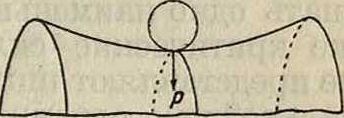
Фигура 2.

димо, чтобы те формы равновесия, которые кладутся в основание расчетов на прочность, были устойчивы. Неустойчивое или безразличное равновесие в таких вопросах не может даже считаться равновесием. Во всех подобных задачах для инженера не так важно знать самую форму равновесия, как величину критич. силы, то есть то значение ее, при котором равновесие из устойчивого переходит в неустойчивое. Для упругих систем существует вообще несколько критич. сил, из них для технич. целей важно знать одно наименьшее значение Р_кр, высшие же критические силы в большинстве случаев не представляют никакого интереса. Поэтому в дальнейшем ограничимся нахождением лишь наименьшей критич. силы.

Переходя к результатам определения критической силы, прежде всего отметим, что все они получены в предположении, что деформации происходят в пределах упругости и что материал следует закону Гука. Для тех случаев, когда форма равновесия становится неустойчивой при напряжениях, превосходящих предел упругости, имеется лишь очень небольшое число решений и то лишь для простейших случаев. Так, по Карману для основного случая продольного изгиба надо в формуле Эйлера модуль Юнга Е заменить через

F ^ίΕΕι

² (Уе + УЖ)²’

где=—отношение приращения напря жения к приращению деформации—должен быть найдено из предварительных опытов на сжатие за пределом упругости. Теория Кармана хорошо согласуется с опытами. Действительные значения критич. силы при деформациях за пределами упругости являются меньшими, чем вычисленные в предположении упругой деформации.

Устойчивость стер ж ней. Наиболее важным и вместе с тем простым случаем является задача об У. сжатых прямолинейных стержней; о ней см. Изгиб продольный, здесь приводим лишь нек-рые дополнения. Если сжатый стержень ослаблен заклепочными отверстиями диам. b, лежащими на равных расстояниях друг от друга, то по Диннику критич. сила

P_KJ,.=P_e[l-(JV-S)],

где Р_е—Эйлерова критич. сила для стержня без учета ослабления заклепками, М—уменьшение момента инерции I заклепочными отверстиями, N—число всех заклепочных отверстий, S—вспомогательная величина. Вычисления показывают, что заклепочные отверстия мало влияют на величину Р_кр. Если например они уменьшают сечение и момент инерции на ~ 10%, то Ркр. уменьшается на 1—2%; т. о. при расчете на продольный изгиб надо брать сечение брутто и не вычитать заклепочных отверстий. В инженерных сооружениях часто применяют составные стержни, склепанные из 2 или 4 стоек, соединенных решеткой. Их сопротивление продольному изгибу значительно меньше, чем сплошной стойки с тем же моментом инерции, и зависит от конструкции решетки. Для стержней (фигура 3, А) Р_кр.=<рР_е, где Р_е—Эйлерова критич. сила, φ—коэф. уменьшения, определяемый из ур-ия

1 _ 1 I р ί_1__ i Ь

<р ^е EFi sin a cos² a ‘ EF^a) ’

где J¹] и F₂—площади сечения диагонали и распорки, а b—длина распорки (ширина стерж ня). Для случая фигура 3, В член

EF₂o.

отбрасы вается; если решетка имеет перекрещивающиеся диагонали, то вместо F_x надо поставить 2 F_x.

Фигура з.

J

1=1 4- Р [-

φ ^Т « (l2£i₂

1^Р р

L J L J

Га ~1 Г в П

Если пояса соединены между собой рядом поперечных планок (фигура 3, С), то

ab а²

+ 24 Ei л ) ’

где 1_Х—момент инерции каждого пояса, 1₂—момент инерции сечения планки при изгибе ее в плоскости изгиба всего стержня. Опыты в общем подтверждают эти ф-лы. При слабой решетке или слабых планках Р_кр, для стойки м. б. значительно меньше, чем Р_е. Так, для сжатых стержней моста через реку св. Лаврентия в Квебеке, рухнувшего вследствие недостаточной устойчивости сжатых элементов, Р_е=88 000 м, критич. же сила, вычисленная по приводимым ф-лам, оказалась всего 31000 т.

При продольном изгибе стержня в упругой среде первой искривленной формой является синусоида с одной или несколькими полуволнами в зависимости от жесткости среды. По Тимошенко критическая сила определяется соотношением

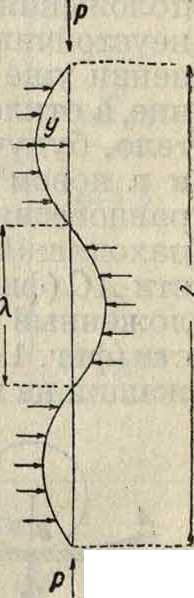
Фигура 4*

Ркр.=Ре (

m^t

, 16 £2

где т—число полуволн (на фигура 4 тонн=3) и

hi4

В²=jjrgy, где к—коэф. жесткости среды, то есть то число, на к-рое надо множить прогиб стержня у, чтобы получить реакцию среды на единицу длины стержня. Величина В², соответствующая моменту перехода от т полуволн к т + 1, определяется из ур-ия

^w2 + ^=(^wl + ¹)³+ ^18В2

откуда

π* ( m + 1)²

_B2 ₌ i__ma (_{TO +} l-)2.

Подставляя вместо m последовательно 1, 2,

3, 4ит. д., получим ряд соответствующих значений В², приведенных ниже:,

т. 1 2 3 4 5

£2. 2 1 219 877 2 430 5 480

Пока В² < 24,первая искривленная форма имеет одну полуволну; если 24 < В² < 219, то—две полуволны и т. д. При большом числе полуволн т длина их приближается к

^λ=πΫ Τ’

а критическая сила к

В случае нагрузки Q, распределенной вдоль длины стержня (фигура 5, а), ее критич. значение

Круглое кольцо радиуса R под действием внешнего равномерно распределенного давления р начинает искривляться в своей плоскости и принимает эллиптическую форму, если давление на единицу длины кольца достигает величины з ΕΙ

Ркр. — 2i3 ’

где I—момент инерции сечения кольца. Эта формула хорошо согласуется с опытами. Для круговой арки с углом а при центре при опертых; концах (фигура 6)

4 π² —α² ΕΙ

Р>‘Р- ⁼ Si ‘ W

При α= π эта формула переходит в предыдущую. В случае зажатых концов

_ кΕΙ.

Рхр. ~ R3 ’

значения Тс для нек-рых углов а даны ниже:

Для 3 простейших случаев (фигура 5,6, в и з)коэф. к таков: 5,12, 7,87 и 16,1. Если стержень сжимается силами, распределенными симметрично

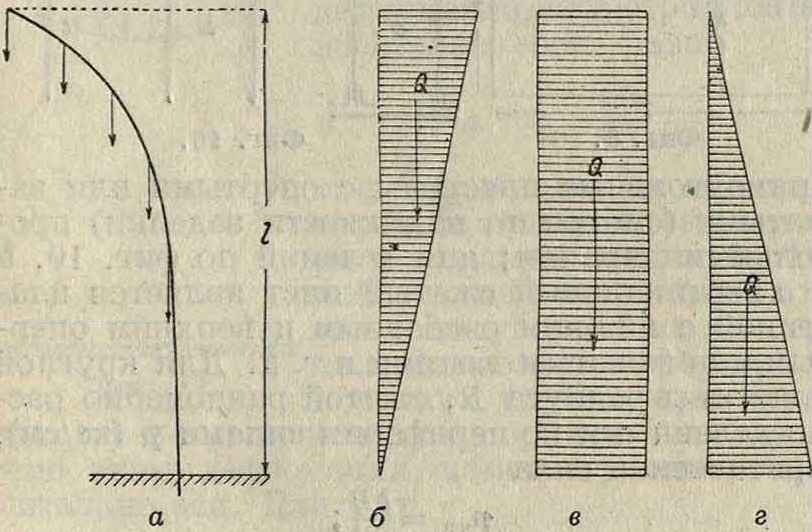
Фигура 5.

относительно его середины и направленными к середине (случай сжатых поясов открытых мостов), то каждая половина стержня находится в условиях, изображенных на фигуре 5. В случае обоих опертых концов к имеет указанные выше значения; при обоих зажатых концах Тс соответственно равно 13,77, 18,92 и 30,94. Для статики сооружений очень важным является вопрос об У. стержневых систем. Напр. в шарнирной ферме, состоящей из прямых стержней, напряженных на растяжение и сжатие, но не на изгиб, при достаточно больших нагрузках кроме искривления отдельных стержней может иметь место потеря У. всей фермы. Ферма в целом может выпучиться из своей плоскости или, оставаясь плоской, изменить свою первоначальную форму. Эти вопросы до настоящего времени разработаны очень слабо. Для работающего на кручение тонкого круг-його вала с опертыми концами прямолинейная форма перестает быть устойчивой и вал искривляется, если крутящий момент М достигает своего критич. значения

Если кроме М действует продольная сжимающая сила Р, то М_Кр₄ определяется из ур-ия:

(jTLzpA“. Л - 21

zEI ) "Г Е1 - й

В случае растягивающей силы надо изменить знак "при Р. Сжимающая сила уменьшает У. вала, растягивающая же увеличивает. а. 120°

к. 18,18

180°

8,00

210°

4,57

300°

3,28

360°

3,00

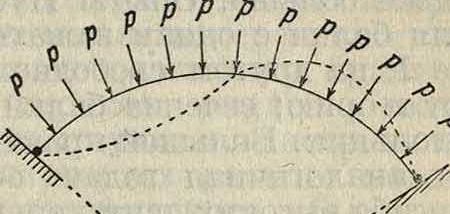
Кроме плоской деформации сжатое кольцо может потерять свою У., превратившись в пространственную кривую, то есть дать «восьмерку». При этом если сжимающие силы р при деформации кольца остаются направленными к его центру, то

Ркр, — 4+1 кз > ^гД^е λ— С ·

Если силы р при деформации остаются параллельными первоначальной плоскости кольца, то

9_ Е£.

Ρ^χν· ~ 3+ λ R3 ’

в обеих ф-лах ΕΙ— жесткость при изгибе в плоскости кольца, Е1_Х — жесткость в плоскости^ ней перпендикулярной, С—жесткость кручения. Для круговой арки (фигура 6) при пространственной деформации и силах, направленных к центру арки_г

(4 π²—α²)² ΕΙ ‘ΡκΡι α*(4π² + λα²) R³

Эти ф-лы указывают на сильное падение У. сжатого кольца или арки, если λ велико, то есть если жесткость кручения мала сравнительно с жесткостью изгиба.

Винтовая пружина теряет У. и начинает-искривляться на сторону, если сжимающая сила достигает величины

-η fil

Фигура 6.

И₀

где 1₀—начальная высота пружины, I-пружины, сжатой силой Р_кр,

аНо eg, 4лг³

-высота

А-

2 лг E + 2G

Ίι =

ЕаН₀

причем 2а—диам. проволоки, из которой свита, пружина, 2г—средний диам. витков пружины,. G—модуль сдвига.

Устойчивость плоской формы изгиба. Если одна из главных жесткостей балки мала сравнительно с другой, то, изгибая балку в плоскости ее наибольшей жесткости, можно, постепенно увеличивая силу, достигнуть предела, когда плоская форма изгиба перестанет быть устойчивой. Ось балки ис-

кривится в направлении меньшей жесткости, причем отдельные поперечные сечения балки поворачиваются. Вместо плоского изгиба по

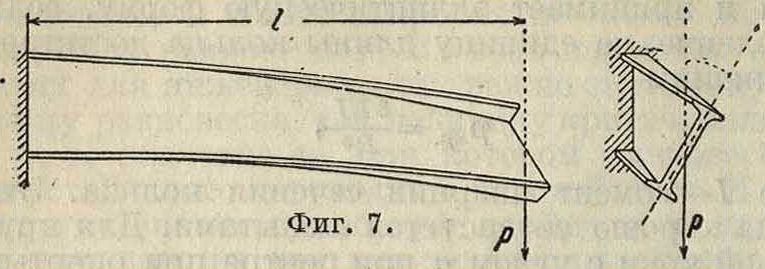
лучается изгиб оси по линии двоякой кривизны, сопровождаемый кручением (фигура 7). Критическая сила

Р

кр.

kY вс Iа ’

где В=EI—наименьшая жесткость балки при изгибе, С—жесткость при кручении и к— коэф., зависящий от рода нагрузки и способа закрепления концов балки. Для балки с одним зажатым и другим свободным концом {фигура 7) при силе Р на свободном конце к=4,01; при равномерно распределенной нагрузке к== 12,81. Для балки с обоими опертыми концами, изгибаемой сосредоточенной силой по середине пролета, к= 16,94; при равномерно распределенной нагрузке к=28,3; для тех же нагрузок при зажатых концах балки к=26,6 и 102,8. Если балка изгибается моментами М, приложенными на обоих концах ее, то при опертых концах М_кр.=^л ; при обоих зажатых—

вдвое больше. Опыты Нуссбаума и Прандтля для балки с одним зажатым концом при силе Р на другом свободном конце подтверждают теорию; сечение балки—вытянутый прямоугольник. Большой практический интерес имеет аналогичная задача об У. плоской формы изгиба высоких двутавровых полок. Она разрешена С. Тимошенко, давшим подробные таблицы для расчета таких балок. Его опыты дали хорошее совпадение с теорией.

Устойчивость пластин. Вопрос об У. пластин гораздо более сложен, чем вопрос об У. стержней. В настоящее время имеют-

а —(--.—, ся удовлетворитель-

ные решения лишь " для прямоугольных : и круглых пластин. - Для прямоугольной _фиг_ ₈_ пластины, сжимае мой силами, равномерно распределенными по двум противоположным сторонам (фигура 8), критическое сжимающее напряжение в килограммахп. см.

_ Λ*»β Рхр- - bh ’

где D=Ϊ2(i-да)—жесткость пластины, h—ее толщина, δ—постоянная Пуассона, коэф. к по Тимошенко дан в первой строке табл. 1. Для длинных пластин при а > 3 b можно считать к=4. При а < b |/2 первой искривленной •формой является синусоида с одной полуволной; начиная с α= 6|/2 до α= b ]/б,—тоже « двумя полуволнами; далее с тремя и т. д. Длинная пластина при выпучивании стремится подразделиться на отдельные квадраты. Вторая строка табл. 1 дает коэфициенты к для пластины, три стороны которой оперты, четвертая же AD свободна; третья строка дает к, если стороны АВ и CD оперты, ВС зажата и ΛΏ свободна; четвертая строка, -если и АВ и

Таблица 1.—Значения коэфициентов k в за-висимости от отношения а : b.

Значения отношения а : b

0,5	1	1,2	1,4	1,6	1,8	2	3
6,25	4,10	4,13	4,47	4,20	4,04	4,00	4,00
4,40	1,44	1,13	0,95	0,33	0,76	0,70	0,56
—	1,70	1,ί7	1,36	1,33	1,34	1,38	1,34
7,69	7,69	7,05	7,00	7,29	7,05	_	_
—	9,42	8,0	7,3	7,0	6,8	6,6	6,1

CD оперты, а обе продольные стороны зажаты. Наконец в последней строке дано к для пластины с опертыми краями при действии касательных сил т, равномерно распределенных вдоль сторон пластины (фигура 9). С У. прямоугольных пластин приходится считаться при расчете стенок клепаных балок, стоек и сжатых мостовых поясов коробчатого или таврового сечений. Например боковые листы пояса (фигура 10, а) надо рассматривать как длинные

			1	Г “I	Г Ί	Г L	Г 1
				а		i	с
			J	Г L	L

Фигура 9.

Фигура 10.

прямоугольные пластины с опертыми или зажатыми (смотря по надежности заделки) продольными краями; для сечений по фигура 10, b и с вертикальный сжатый лист является пластиной с нижним свободным и веохним опертым или зажатым краями и т. д. Для круглой пластины радиуса R, сжатой равномерно распределенными по периферии силами р (кг/см), критическая сила

_ kD.

Укр. — _Д2»

при опертых краях к=4,19, при зажатых к== 14,68; D—как было дано выше.

Устойчивость оболочек. Оболочками называются тонкие пластины, имеющие в своем естественном ненапряженном состоянии криволинейную поверхность. Несмотря на значительное число исследований вопрос об У. оболочек надо считать слабо разработанным. Причина заключается в сложности задачи благодаря многочисленности различных типов деформации оболочек. Наиболее важной для техники и вместе с тем простой является задача об У. цилиндрической оболочки. Для весьма длинной круговой трубы при толщине стенки h, сжатой гидростатич. давлением q (например жаровая труба парового котла),

_ ЕЬ*(п2-1)

Ц*Р· ~ 12(1-й2)ДЗ ’

где п—число полуволн в поперечном сечении искривившейся трубы. При наименьшем значении п=2 сечение трубы принимает эллиптич. форму. Соответствующее этому случаю критич. давление п - ^Eh3

Чкр- 4(1__ва)ДЗ *

Эта формула хорошо согласуется с опытами и по ней можно проверять на У. длинные трубы. Та же труба длиной I с закрепленными концами при искривлении принимает волнообразный характер. По Мизесу Eh

Я-κρ. 2(п2 —1 )NR

+ («-^ι-^υψ^!)

Eh³

12(1-6*) R*⁹

где Ν — 1 + η—число полуволн по окруж ности искривившейся трубы. При подсчетах по этой формуле п надо подобрать так, чтобы q_Kp^ имело наименьшее значение. Несколько таких значений п для стальных труб дано в таблице 2.

Таблица 2.—Значения п для стальных труб.

Отношение 1 : R	Значения R : h
	250	100	50	25
СО	2	2	2	2
10	4	3	2	2
5	5	4	3	3
2	8	6	5	4

Чем короче труба, тем больше полуволн появляется на ней. Опыты хорошо согласуются с теорией. Для трубы кругового сечения, сжимаемой силами, равномерно распределенны-о ми по торцам и направленны ми вдоль оси трубы (фигура 11), критич. напряжение в случае деформации, симметричной относительно оси, равно

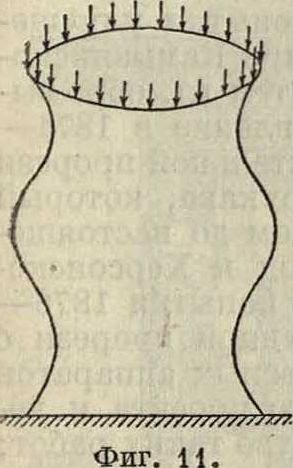
V кр. =

Eh

R V3(1-й²)

то есть р„_Р не зависит от длины трубы, а только от ее диаметрами толщины стенки h. Такой же тип деформации, но с одной полуволной имеет первая искривленная форма при коротких трубах; при длинных же могут появляться и другие более сложные типы деформации, несимметричные относительно оси. Для них

___ _Eh_ η² - 1

^P,:p r Vs(i-а») ^яа+¹ ’

где п—число полуволн, появившихся в поперечном сечении трубы. В этом случае р_к?ч меньше, чем при деформации, симметричной относительно оси. Если труба изгибается как одно целое, то критич. сила р _2n*ER«h.

критич. напряжения найдутся делением P_hrна площадь сечения 2 πΒ,ίι. Критич. сдвигающее напряжение при кручении тонкостенной трубки приближенно (по Э. Шверину) равно г_кр= 0,248E (1 + 0,45-|) (А)·.

кр.

По этой формуле можно проверять па У. тонкостенные трубчатые валы. Для сферич. оболочки радиуса В при действии гидростатич. давления q в случае деформации, симметричной относительно одного из диаметров, по Schwerin’у и Zoell’io критич. напряжение _ 2 Eh²

^3кр H²V з (i—

Устойчивость вращающихся валов. Для случая вала кругового сечения, вращающегося около своей оси с угловой скоростью (о, с увеличением со прямолинейная форма вала может оказаться неустойчивой и вал изогнется. Соответствующая скорость называется критич. скоростью ω_κρ_ (смотрите СкЬрость критическая).

Лит·: Основные исследования: Euler, De curvis elasticis, 1744; Lagrange, Sur la figure des colonnes,

P., 1757; В r i a n &., «Proc. CambridgePhilosoph. Society», Cambridge, 1888, 1899: Тимошенко С., Об устойчивости упругих систем, Киев, 1910. История: Т о t-huntera. Pearson, History of the Theory of Elasticity a. Strength of Materials, v. 1—2, Cambridge, 1886—1893; Тимошенко С., Сопротивление материалов, М,—Л., 1930; Timoschenko S., Strength of Materials, N. Y., 1930; Mayer R., Knickfestigkeit, B., 1921; Love A., Theory of Elasticity, Cambridge, 1927; Timoschenko S., Stabilitatsprobleme der Elastizitat, Hndb. d. physikalischen u. technischen Me-chanik, hrsg. v. F. Auerbach u. W. Hort, Band 4, T. 1, Lpz., 1929; Geekeler J., Stabilitatserscheinungen, Handbuch der Physik, hrsg. von H. Geiger und K. Scheel, B. 6, B., 1928; F 0 p p 1 A., Drang u. Zwang, 2 Aufl., B. 2, Mch., 1928. А. Динник.