Фаза

Фаза, в широком смысле слова—определенная стадия какого-либо переменного явления. В этом смысле термин применяется в различных отраслях знания, например в химии растворов (смотрите Правило фаз), в теории плавления (смотрите), в астрономии (Ф. луны, планет) и т. д. В более узком смысле термин Ф. применяется в теории колебаний, причем Ф. гармонич. колебательного движения точки называется линейная, 1-й степени ф-ия от времени ί, синус или косинус которой пропорционален расстоянию от данного положения точки до равновесного ее положения (смотрите Колебательное движение). Если обозначить последнее расстояние через х, амплитуду колебания через а, промежуток времени, истекший от начального до данного момента, через i, то гармонич. синусоидальное колебательное движение будет аналитически выражено равенством:

x=asin(kt + α₀). (1)

Выражение

α= Ы + а₀, (2)

где к и а₀—нек-рые определенные постоянные, и будет Ф. колебательного движения в момент t. Из вышесказанного следует, что каждому моменту впемени ί соответствует своя определенная Ф. При ί=ΟΦ.α=α₀, поэтому а называется начальной Ф. Т. к. полный период Т колебания равен а частота ν колебания, то есть число полных колебаний, совершаемых л единицу времени, равна

τό Ф. колебания в момент ί м. б. представлена, еще и сл. обр.:

^а —ψ i + ^αο> (5}

или

α= 2 nvt + а„. (6).

Изменение Ф. на величину +2 ηπ, где п—целое число, не изменяет ни положения точки ни направления ее движения. Поэтому Ф., отличающиеся друг от друга на i 2 ηπ, часто считаются за одинаковые Ф.

Фазы, отличающиеся на ±(2»ι + 1)π, дают против о п о л о ж и ы е Ф.

Графически Ф. гармонии. хсолебания м. б. представлена сл. обр.: пусть имеется точка, перемещающаяся по окружности радиуса г с постоянной угловой скоростью (смотрите) ω. Допустим, что начало отсчета дуговых расстояний находится в точке С (фигура 1), а начальное положение движущейся точки в А₀. Если в момент ί точка находится в положении А, то дуга АС, или соответствующий центральный угол, будет

Ψ=o)t + <р„, (7)

где <р₀= и. А₀ОС. Спроектируем точку А на прямую хх, проходящую через центр окружности

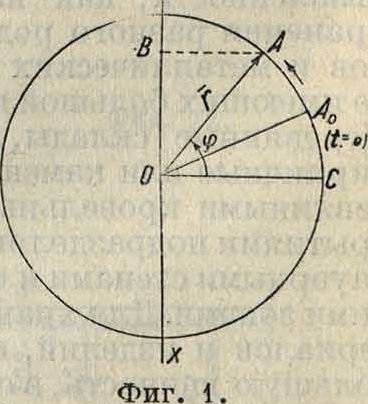
О перпендикулярно к ОС. Проекция В точки А будет находиться от О на расстоянии

ОВ=Х=Г sin φ (ωί + φ₀). (8)

Сопоставляя (8) и (1), видим, что точка В будет совершать по прямой х гармонич. колебание с частотой ν=~. Ф. колебания точки В в

2 л момент t будет определяться равенством (7), то есть углом НОС. Вместо точки А, движущейся по окружности, можно представить себе, что радиус-вектор г= О А вращается равномерно около своего начала О и проектируется на неподвижную прямую хх. Угол, образованный прямой ОС, перпендикулярной к прямой хх, и данным положением радиуса-вектора, и будет представлять собой Ф. в момент f. Вместо радиуса-вектора г можно взять также окружность с диаметром АО (фигура 2), которая очевидно

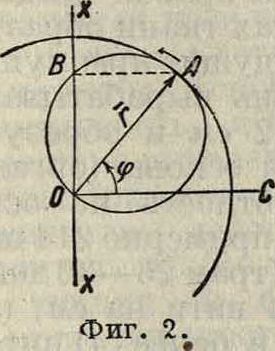
будет проходить через В. Если вращать эту окружность с угловой скоростью <о около точки О, то она будет пересекать неподвижную прямую хх в точке В, которая будет совершать гармонич. колебание; угол, образованный диаметром этой окружности с прямой ОС, и будет графически представлять собой Ф. колебания точки В. Можно наконец окружность диаметра АО=г закрепить, а вращать прямую хх в противоположном направлении; результаты получаются те же. Пусть имеются две точки В и В, которые совершают два гармонич. колебательных движения, определяемых ур-иями:

x=r sin(cof + φ₀), (9)

x’= r sin (со< + φ„). (10)

•Φ. колебания этих двух точек в один и тот же момент t будут соответственно равны:

Ψ=(ot + Ψο, (11)

φ= a>t + φ₀. (12)

Абсолютно значение разности Φ. φ и φ в один и тот же момент называется сдвигом Ф. в тот же момент. Т. о. сдвиг Φ. | Δφ | в момент < колебаний (11) и (12) будет равен:

Δρ I=|?» - φ I=I (ωί + <Pt>) - (ωί + <Po) I · (13) Из (13) видно, что в общем случае сдвиг Ф. колебательных движений изменяется с течением времени. Если в частности оба колебательных движения имеют одну и ту же частоту, то со=со, и в этом случае имеем из (13)

[>¥> I=I φ₀ — φ₀ I=Const, (14)

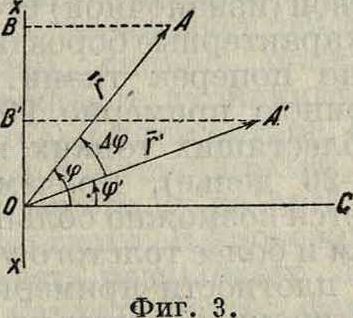
то есть если два гармонич. колебательных движения происходят с одной и той же частотой, то сдвиг Ф. есть величина постоянная, равная начальному с щигуФ. Графически сдвиг Ф. представлен очевидно углом между радиусами-векторами г=ОА и г=ОА, осуществляющими своими проекциями на прямую хх при вращении около О данные гармонич. колебания (фигура 3). Если взять две декартовы оси координат и по оси абсцисс откладывать значения от резков времени t, а по оси ординат расстояния х, то гармонические колебательные движения (9) и (10) будут представлены синусоидальными кривыми С₀С_хСзС₃. и Со С{ С₃ С₃. (фигура 4). При точке С_гх=0, т. ч. ОС_х=t_x определяется из равенства

sin (ωί_χ + φ₀) - О, (15У

откуда t_x=— —. Аналогичным образом имеем!

для отрезка ОС,=t[ величину t[= — ~, откуда

C_xCi~ti-t 1=£-58. (16)

В частности, если оба колебания происходят с одной и той же частотой, то со=го, и в этом случае имеем

C Ci=^V-°-J°· (17)

Из (17) видно, что в рассматриваемом частном случае отрезок С_гС{ пропорционален сдвигу Φ. Δ?> и при соответствующем выборе масштаба м. б. взят в качестве величины, определяющей сдвиг Ф.

В нек-рых отделах теоретич. физики термину Ф. придается часто несколько более общее понятие, чем > указанное выше, что имеет место напримерв теории ко-. лебания струны.

Если струна, за- ^с° крепленная своими концами, со- Фигура 4.

вершает плоское движение, то смещение ν в момент t точки, находящейся на расстоянии х от точки закрепления, определяется ф-лой:

η=со

Σ су cos [[τ^ ⁺ τ)^{2π + θη}] “

η=со

- Д ^С» ^cos [(ту - f) + β.]. (18)

причем правая часть последнего равенства представляет собой совокупность бесконечного множества попарно равных, противоположных, чисто периодических, т. ы. парциальных, волн с периодами, равными Т„, и длинами, равными λ_η. Выражения в квадратных скобках называются Ф. колебания соответствующих пан-циальных волн, а постоянные величины θ_ηназываются фазовыми постоянными данного плоского колебания струны.

Сказанное выше о соотношениях между величинами ж и ί, предопределяющими собой понятие Ф., справедливо также и для аналогичных соотношений между любыми другими величинами, что бы собой эти величины ни представляли, нано, сила тока, напряжение поля и тому подобное. (смотрите Сдтг фаз)

Лит.:×вольсон О., Курс физики, т. 1, Берлин, 1923; Эйхенвальд А., Теоретическая физика, ч. 2, М.—Л., 1932. М. Серебренников.