> Техника, страница 89 > Фермы

Фермы

Фермы, сооружения, состоящие из отдельных материальных стержней или дисков, взаимно соединенных между собой в систему, геометрически неизменяемую, в которой замена реальных узловых соединений шарнирами без трения не обращает ее в подвижный механизм (смотрите Неизменяемость геометрическая). Изготовляются Ф. из металла, дерева и реже из железобетона. Способы соединения стержней в узлах зависят от материала Ф. и выполняются в настоящее время в виде заклепочных, свар- ψ ных и болтовых сое-динений в металлич.

Ф., помощью врубок, нагелей, болтов и специального вида вкладышей в деревянных Ф. и помощью взаимосвязывающей арматуры в железобетонных Ф. (фигура

1а и 16). Особенностью Ф. как сооружения является работа ее прямолинейных элементов при узловых нагрузках преимущественно на продольную силу Ν, что отличает Ф. от прочих систем, в которых составные элементы как правило подвергаются сложному воздействию. По характеру образования и работы в сооружениях Ф. разделяются на плоскостные и пространственные .Ф. плоскостные имеют составные элементы, расположенные в одной плоскости, обладают плоскостной геометрической неизменяемостью и способны

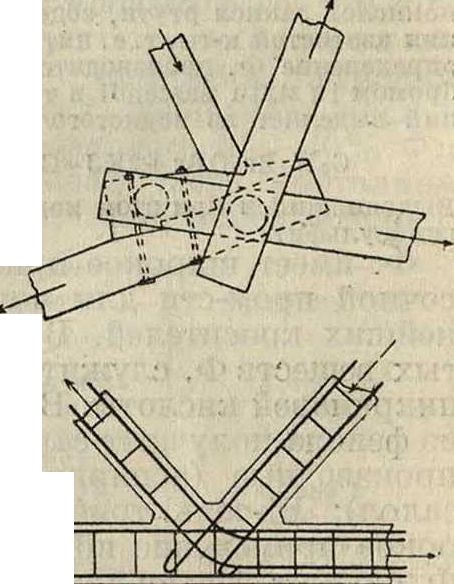
Фигура 1а.

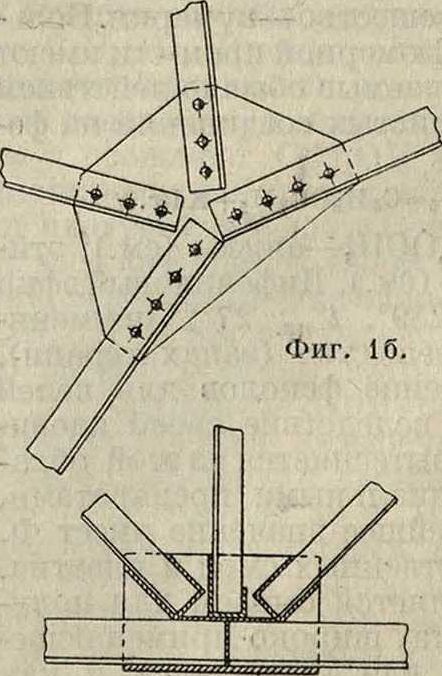
воспринимать на себя нагрузки, лежащие только в той же плоскости. Ферма плоскостная самостоятельно, в виде сооружения, встречается редко (краны, кронштейны), а употребляется гл. обр. как составная часть сооружения, особенно отчетливо выявляясь во всевозможных покрытиях гражданских и промышленных зданий, в мостах, гидротехнич. сооружениях и т. π. Ф. пространственные имеют элементы, пространственно расположенные, способны воспринимать на себя нагрузки любых направлений. Они в отличие от плоскостных Ф. представляют обычно законченные самостоятельные сооружения, в состав которых м. б. включены отдельные плоскостные Ф. Пространственные фермы в практике употребляются в качестве купольных, шатровых перекрытий, в кранах, в дирижаблях и других инженерных сооружениях (фигура 2). Изучение работы Ф. в сооружениях, необходимое для определения усилий и деформаций в элементах Ф. вне зависимости от узловых соединений, связано с понятием теоретической Ф., которая и рассматривается в курсах строительной механики. Ф. теоретическая представляет схему реальной Ф., в которой материальные стержни заменены линиями, а узловые соединения—теоретическими (в плоскостных Ф.—цилиндрическими, в пространственных—шаровыми) шарнирами без трения. Как показывают опытные исследования, теоре-тич. Ф. обладает свойствами, достаточно близкими к свойствам реальных Ф., почему во многих случаях практики довольствуются произведенным расчетом теоретич. Ф. без учета дополнительных факторов. Образование теоретич. Ф. как системы подчинено всем правилам образования сочлененных систем (смотрите Система).

Определение усилий в Ф. Статический расчет Ф. заключается в определении усилий ее элементов и упругой деформации самой Ф. По характеру действия нагрузки различают расчет на неподвижную и подвижную нагрузку. Расчет на подвижную нагрузку кроме непосредственного определения усилий или деформаций требует еще анализа опасного ее положения. Последнее обстоятельство связано с построением законов изменения определяемых факторов в зависимости от положения груза на Ф., т. н. линий влияния, или инфлюентных линий. Линии влияния позволяют определять опасное положение подвижной нагрузки и величину вызываемого ей усилия или деформации (смотрите Линии влияния). Расчет Ф. производится на Ф. теоретических по их схемам до деформаций, что практически точно в виду относительно малых упругих искажений Ф. В целях уточнения расчета, а также и по эксплуатон-ным соображениям Ф. иногда придают в процессе постройки т. н. строительный подъем— искажение Ф. в сторону, обратную возможным ее деформациям, с тем чтобы во время нагрузки схема Ф. отвечала расчетной. Однако такой прием в значительной степени усложняет вопросы конструирования Ф.,не давая значитель ного эффекта в приближении предположений к действительности. Все приемы расчетов Ф. основаны на приложениях к ним законов механики твердых и упругих тел. При определении усилий в статически определимых Ф. пользуются только законами механики твердых систем, а при определении деформаций и усилий в «лишних стержнях» статически неопределимых ферм—дополнительно законами упругих тел. Принципиальных различий расчетов пространственных и плоскостных Ф. нет, и можно лишь различать их по сложности или малой разработанности выполнения. Сложность расчета пространственных Ф. обусловлена гл. образом пользованием пространственной системой координат и законами пространственных материальных систем вместо плоскостных. Методика расчетов статически определимых Ф. зависит прежде всего от тех отделов механики, которые кладутся в основу расчета. Так, использование законов равновесия твердых тел дает статич. метод, а использование законов равновесия подвижных кинематич. цепей дает кине-матич. метод. Указанные два метода являются общими и в настоящее время достаточно разработанными, особенно в области плоскостных Ф. Они имеют свои достоинства и недостатки, и целесообразность применения каждого из них в разных случаях обусловливается схемой Ф. В начале расчета оба метода объединены одной общей идеей превращения определяемого внутреннего усилия элемента Ф. в силу внешнюю, что необходимо для приложения законов механики материальных систем. Достигается это разрезом или выбрасыванием, что одно и то же, элемента и заменой действия его на узлы, согласно свойствам теоретич. Ф., продольными силами, по величине равными усилию элемента. Превращение внутреннего усилия в силу внешнюю по отношению к Ф. или части ее дает возможность включать его в ур-ия, характеризующие условия равновесия системы, из которых и определять как неизвестное. Направление внутреннего усилия условно считается положительным, то есть растягивающим, действующим от узла, знак же, получаемый в результате решения, определяет истинное направление усилия. Статич. метод расчета основан на идее расчленения Ф. разрезами на две или большее количество частей и приложения к каждой из них условий статич. равновесия. Идея кинематич. метода заключается в том, что с вырезом элемента из Ф., последняя обращается в подвижную кинематич. цепь (механизм), которая под действием заданной нагрузки и усилия разрезанного элемента должна находиться в статич. состоянии. Применяя различные приемы исследования равновесного состояния кинематич. цепи, тем самым можно написать его условие, к-рое и определяет неизвестное усилие разрезанного элемента. В статически неопределимых Ф. прежде всего определяют усилия в лишних стержнях на основании анализа возможной деформации Ф. с лишними стержнями. Затем может прилагаться любой метод расчета статически определимых Ф., причем кроме заданной нагрузки нагрузкой же будут служить определенные выше усилия лишних стержней.

Расчет плоскостных статически определимых Ф. по статич. методу заключается в приложении ур-ия плоскостной статики котдельным сечениям Ф. в их аналитич. и графич. виде. При аналитич. решении в зависимости от вида ур-ия различают следующие способы расчета: 1) спо-

qo6 моментных точек (Риттера) по условию, что -сумма моментов всех внешних сил и рассеченных внутренних усилий относительно любой точки плоскости равна нулю, 2) способ проекций по условию, что проекция на ось всех внешних сил и рассеченных внутренних усилий равна нулю. Последний способ в нек-рых задачах является частным случаем первого. Располагая свободным выбором моментной точки 7с и направлением оси, следует их выбирать с расчетом упрощения задачи. Способ моментных

Фигура 4.

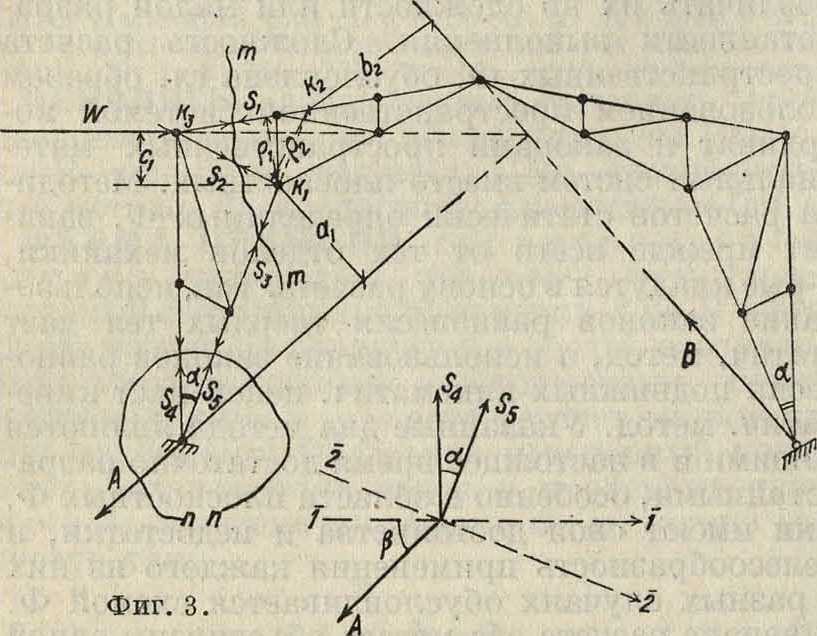
точек м. б. приложен при любых сечениях Ф. за исключением вырезания только одного узла, способ же проекций приложим и в этом последнем частном случае. Сечения Ф. для расчета м. б. проведены различным путем и как угодно, чем и следует пользоваться для упрощения задачи. Так например, особенно просто определяются усилия при рассечении Ф., проводимом через 3 стержня (на фигура 3 сечение т—т), и вырезанием узла с двумя стержнями (на фигура 3 сечение п—п). По первому из них для определения усилия Sx точку моментов следует взять на пересечении усилий 8 2 и $₃, то есть точку 7с_1; и рассмотреть равновесие левой или правой части Ф. Для равновесия левой части ур-ие моментов будет

— Λ(Χχ -)- Wei -f- SxQi=О,

откуда

<ς< Αθ-i -f- Wcj

Для определения силы <S₂ точка моментов будет 7сг. Равновесие правой части от сил, к ней приложенных, напишется:

= — ВЬ% -(- $202 ⁼ О*

Для определения усилий $₄ и S₅ при вырезании узла следует направление осей выбрать так, чтобы на каждую из них одно из неизвестных усилий $₄ и $₅ проектировалось в нуль. Этому условию удовлетворяют оси 1—1 и 2—2 (фигура 3). Проектируя на каждую из них, получаем два ур-ия, определяющих $₄ и $₅. Вид ур-ия будет:

— A cos β + $5 sin α=О — A cos (α + β) — $₄ sin a=0.

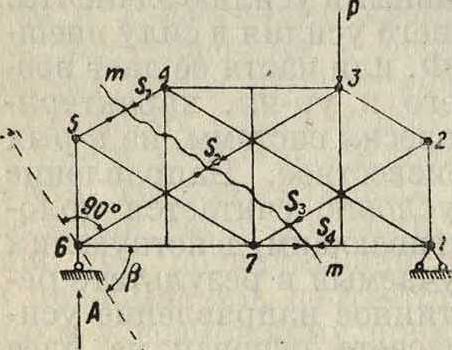
Использование способа проекций при разрезе т—т показано на фигуре 4, где за ось проекций взята ось 1—1. Ур-ие, определяющее $₄ из равновесия левой части, будет

— A cos (90° — β) + $4 cos β=0.

Когда в разрезе трех стержней два параллельны, то определение усилия третьего возможно только способом /„

проекций, т. к. точ- * ⁷

ка моментов в этом случае удаляется в бесконечность (фигура

5). Следует иметь в виду, что не во всякой Ф. можно провести сечение через три стержня или вырезать узел с двумя стержнями; но и в этих случаях задача решается тем же путем, только усложняется процесс расчета.Обычно это встречается в преобразованных Ф., в которых следует

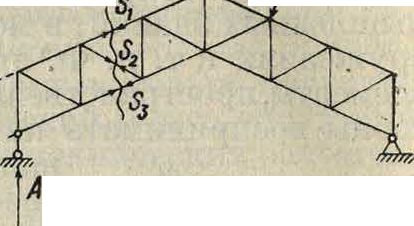
Фиг.

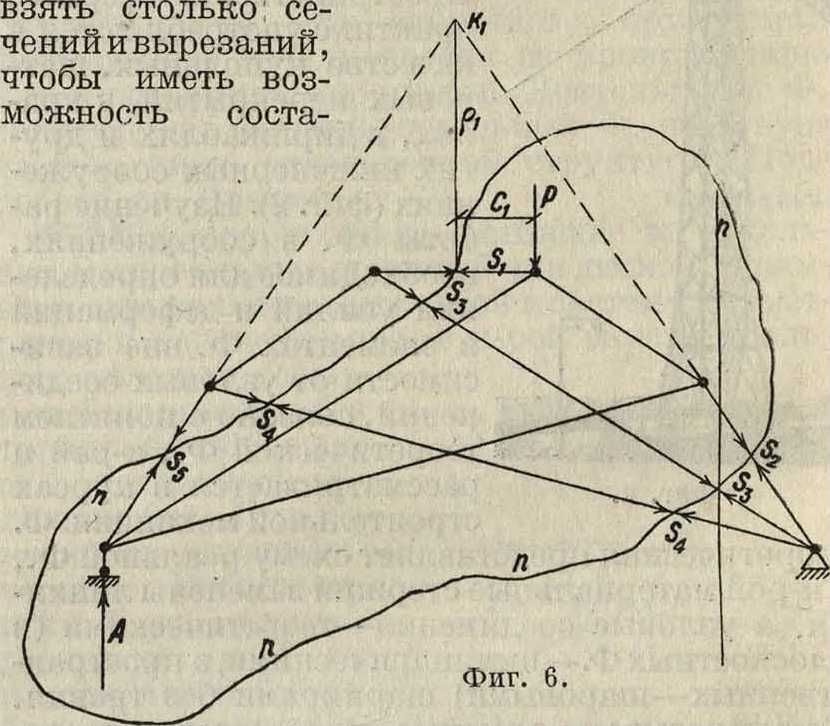
вить необходимое количество ур-ий. Успех расчета с наименьшей затратой будет зависеть от удачно выбранных сечений, которые иногда расчленяют систему ур-ий на отдельные самостоя-

зом (и—п) и написанием ур-ия моментов относительно точки 7с_х, а именно:

= А - + Ροχ + SiQx=0.

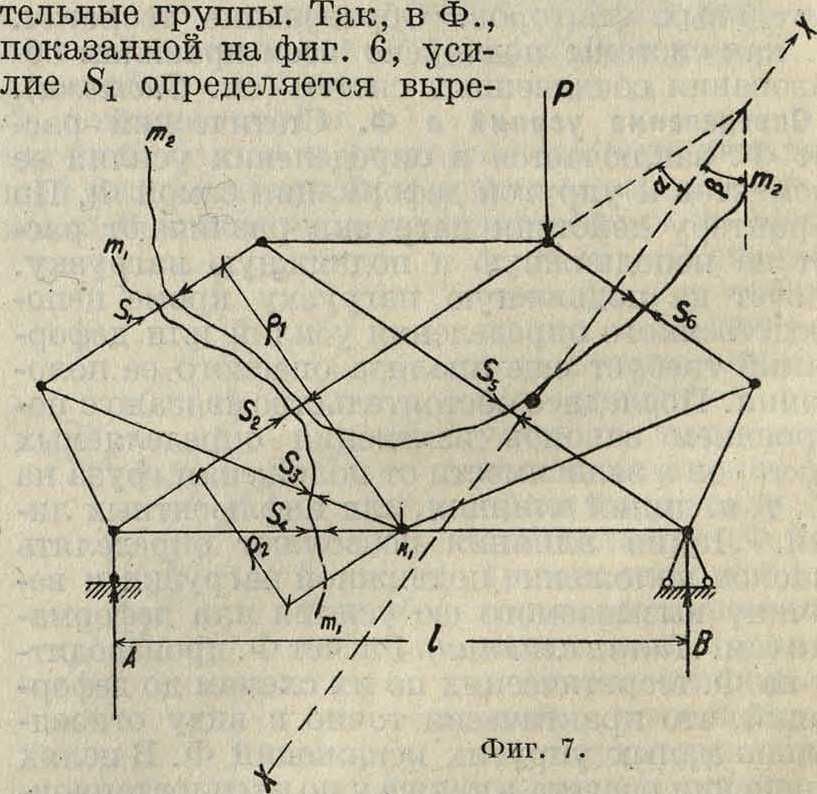
В Ф. на фигуре 7 усилия $₄ и $₂ определяются моментом по разрезу т_г—относительно точки fcj, а также проекцией по разрезу т₂—т₂

на ось X—X. Ур-ия, определяющиеусилия, напишутся так: по разрезу т₁—т₁ равновесие левой части:

= А - 8γ()χ -j- S-zQi=0;

по разрезу т_г—т., равновесие верхней части как сумма проекций на ось X—X

— S_x COS a — S₂ COS a2 — -P COS β=0.

Наряду с аналитич. приемами статич. ме-тода^расчета существуют и графические, основанные на общеизвестных положениях графо-статики, что всякая сила м. б. разложена на два любых направления, пересекающихся с ней в одной точке, и на три любых направления, не пересекающихся с силой в одной точке. Они возможны как по разрезам (способ Кульма-на-Циммермана), так и по вырезанию узлов (диаграмма Максвелла-Кремоны). Из названных способов наиболее совершенным и распространенным является диаграмма Максвелла-Кремоны. Диаграмма основана на построении замкнутых силовых мн-ков усилий и нагрузки

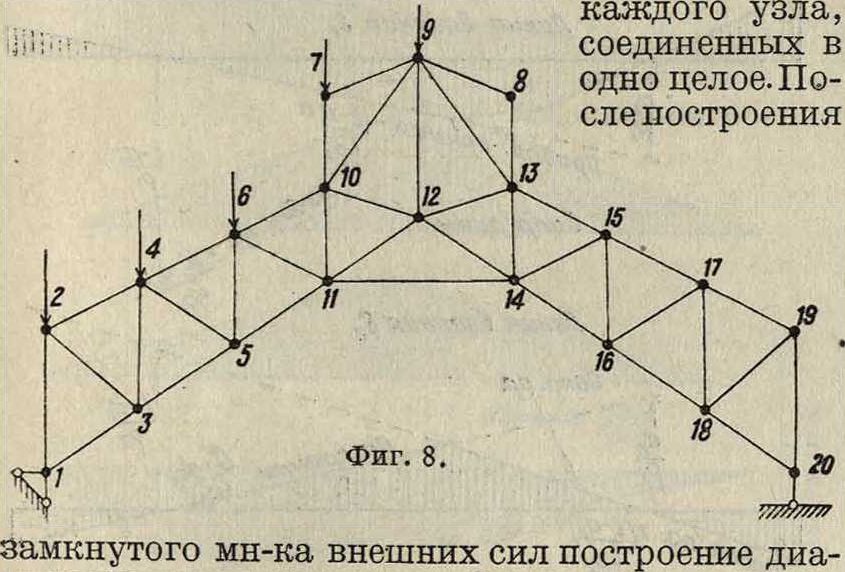
граммы заключается в обходе каждого узла по или против часовой стрелки, начиная с узла, где сходятся два элемента, на направления которых может быть разложена равнодействующая сил, приложенных в этом узле. Затем переходят к новому, часто соседнему, узлу, в к-ром м. б. и три стержня, но усилие одного узла известно, и т. д. При обходе каждого узла обязательно требуется не более двух неизвестных усилий, иначе построение силового мн-ка невозможно. На фигуре 8 показан номерами возможный порядок обхода узлов. Техника выполнения диаграммы проста, но требует тщательной чертежной работы (смотрите Графическое определение усилий). В том случае, если нет узла с двумя стержнями в начале или узла с двумя неизвестными в процессе построения,

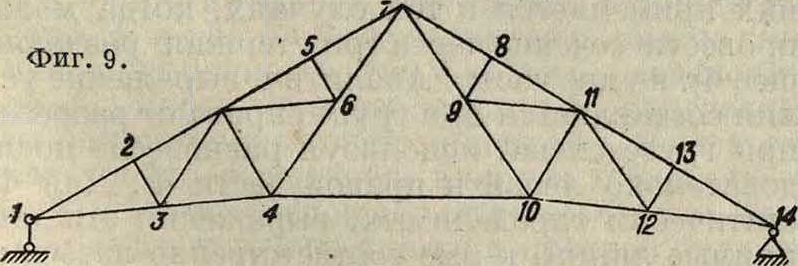
приходится усилия нек-рых элементов определять аналитически, после чего дальнейшее построение диаграмм будет возможно. Так, для фигура 4 построение возможно только после определения усилия какого-либо стержня, например 6₄, и тогда порядок вырезания узлов легко намечается. Так же для перехода к узлу 4 (фигура 9) необходимо определить сначала аналитически усилия Si, после чего становится возможным дальнейшее, построение диаграммы.

Кинематйч. метод расчета плоскостных, статически определимых Ф. заключается в приложениях к исследованию условий равновесия кинематич. цепей начала возможных перемеще

ний в его непосредственном виде или в виде диаграммы скоростей. Расчет этим методом проводится на основе составления ур-ия возможной работы сил, приложенных к механизму, полученному из Ф. при удалении стержня разрезом его и с заменой его действия на узлы усилием. Выбор возможных бесконечно малых перемещений м. б. вполне произволен, если свя-•зевые условия заменить силами, чем можно пользоваться при упрощениях решений. Так,

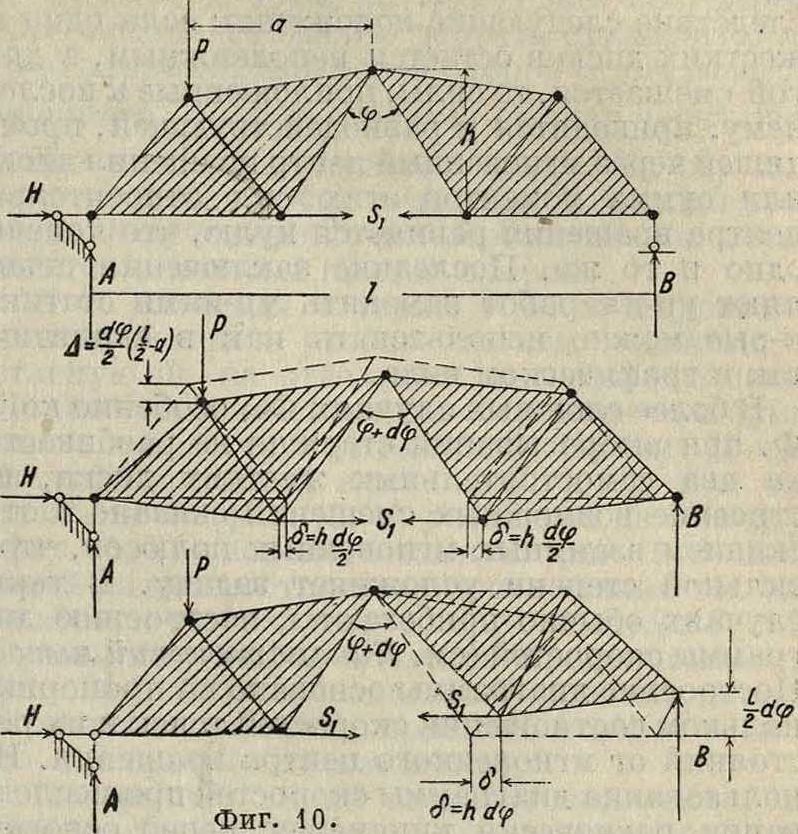
Ф., показанная на фигуре 10, превращена для определения усилия в механизм и дано два варианта возможных смещений. Ур-ия работ для них соответственно будут

^Р ΊΓ ~ о) - Szh^-S_th~=°

И

в d<p - Sjh άφ=0.

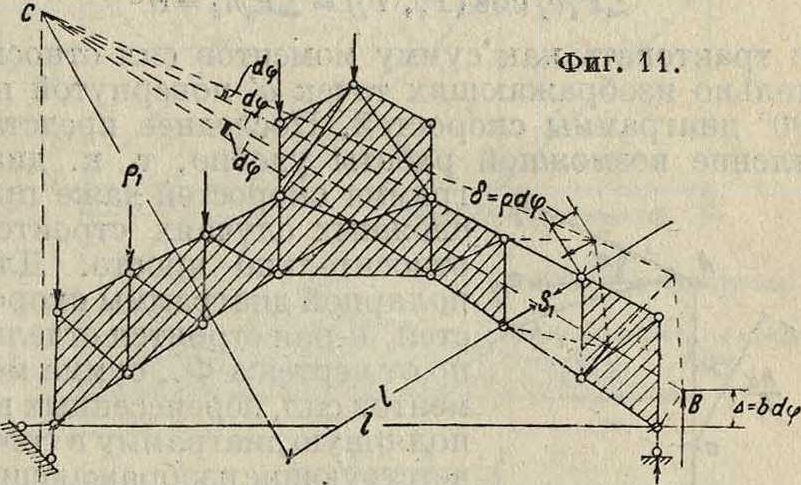
В первом варианте исключены из работы реактивные силы А,Н и В, а во втором Р, А,Н. Если первый вариант естественнее в смысле возможных перемещений с учетом опорных связей, то второй удобнее в процессе вычислений. Когда Ф. при выбрасывании элемента разбивается на два жестких диска, имеющих возможность взаимного смещения, удобнее принимать один из дисков неподвижным. Напр. для фигура 11 усилие Sj. определится заданным возможным смещением пра-

вого диска вокруг мгновенного полюса с. Ур-ие работ этого смещения имеет простой вид:

Вb d<p — S-lQ άφ=0.

Из самого смысла ур-ия работ вытекают как следствие следующие положения: если один из жестких дисков остается неподвижным, а другой смещается, то силы, приложенные к последнему, приводятся к равнодействующей, проходящей через мгновенный центр вращения диска, или сумма моментов этих сил относительно центра вращения равняется нулю, что конечно одно и то же. Последние заключения позволяют ур-ия работ заменить ур-иями статики, которые можно использовать как в аналитич., так и графическом виде.

В более сложных случаях Ф., особенно когда Ф. при выбрасывании стержня не разбивается на два самостоятельных жестких диска, построение возможных смещений связано с отысканием взаимных мгновенных полюсов, что в сильной степени усложняет задачу. В таких случаях обычно прибегают к построению диаграммы скоростей (смотрите Кинематический метод). Построение диаграммы основано на пропорциональном соотношении скоростей точек и их расстояний от мгновенного центра вращения. Использование диаграммы скоростей при исследовании равновесия кинематич. цепей основано на преобразовании ур-ия виртуальных работ в следующую форму:

ΣΡί dsg cos (Р_г- ds₍)=ΣΡ,νι dt cos (Р_{, т_г)=0 или

ΣΡΐ»ί cos (Р_г, Vi)=0.

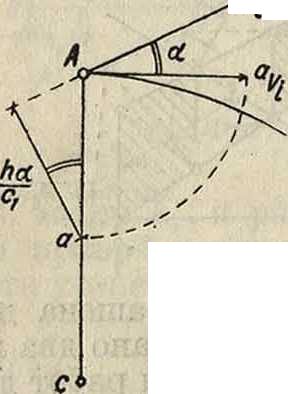
Если теперь для каждой точки полученную скорость (фигура 12) Аа отложить цо радиусу вращения Аа, то есть повернуть скорость на 90°, то последнее равенство можно записать в виде

Фигура 12.

ΣΡ,ν, cos (P_it ν_{)=ΣΡΧ=0

и трактовать как сумму моментов сил относительно изображающих точек а повернутой на 90° диаграммы скоростей. Последнее представление возможной работы удобно, т. к. диа-_яр. грамма скоростей даже при * сложных случаях строится относительно просто. Для полярной диаграммы скоростей, которая строится отдельно от чертежа Ф., сумма моментов сил, перенесенных на полярную диаграмму в соответствующие изображающие точки, относительно центра ее должна равняться нулю. Для неполярной же диаграммы силы, перенесенные в изображающие точки, должны также находиться в равновесии, т. к. перенос сил сопровождается дополнительным результирующим моментом, который в этом случае равен нулю.

Сравнивая между собой статич. и кинематич. методы при неподвижной нагрузке, можно отметить следующее: а) во всех простейших случаях статич. метод оказывается проще и быстрее ведет к цели, особенно через диаграмму Макс-велла-Кремоны; б) в случаях сложных, когда нельзя провести разреза через три стержня, часто кинематич. способ оказывается удобнее и проще; в этих случаях применение его вполне уместно хотя бы для определения усилия нескольких стержней, позволяющих далее перейти к диаграмме Кремоны.

Определение усилий в Ф. от действия подвижной нагрузки производится при помощи линий влияния (инфлюентных линий). Построение линий влияния, как и аналитич. расчет Ф., может быть сделано также статич. или кинематич. методами. Построение линий влияния по статич. методу заключается в составлении

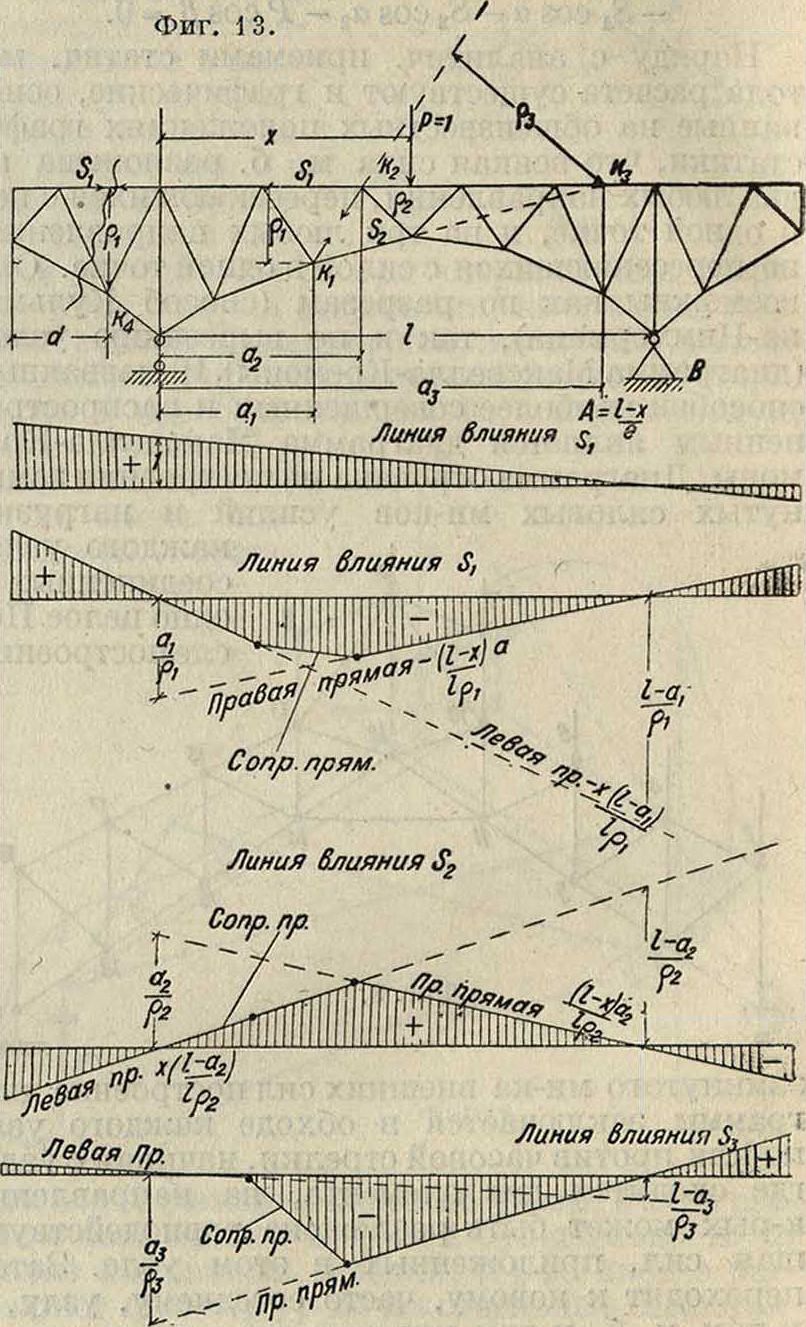
.Левая пр.

Сопр.пр.

Линия влияния S₄ (на нансоли) Правая прям._

аналитич. выражения усилия элемента от груза р=1, расположенного произвольно на текущей координате х, различными приемами этого метода. Наиболее часто встречаются два приема построения линий влияния: 1) прием сечения или рассечения и 2) вырезания узла. Первый из них применяется в тех случаях, когда можно провести сечение через три стержня, разделяющее Ф. на две части. Аналитич. выражение усилия составляется при грузе справа от разреза и при грузе слева, используя равновесие последовательно левой и правой части Ф. Для Ф., статически определимых, выражения эти дают прямые линии, которые соответственно называют правой и левой прямой. На фигуре 13 показано построение по законам статики линии влияния для нескольких характерных элементов консольной Ф. Ур-ия линий влияния усилий обычно выражаются в зависимости от величины опорных закреплений, почему часто последние называют основными линиями влияния. Ур-ия правой и левой прямой получаются из рассмотрения равновесия левой и правой части. Характерной особенностью построения правой и левой прямой является точка их взаимного пересечения; она лежит всегда на вертикали под точкой моментов. Пригодность правой (или левой) прямой благодаря узловой передаче нагрузки на Ф. ограничена соответственно первым правым (или левым) узлом от разреза по ездовому полотну.

Для Ф. с иными видами опорных закреплений (наклонными опорами, арочными) принцип

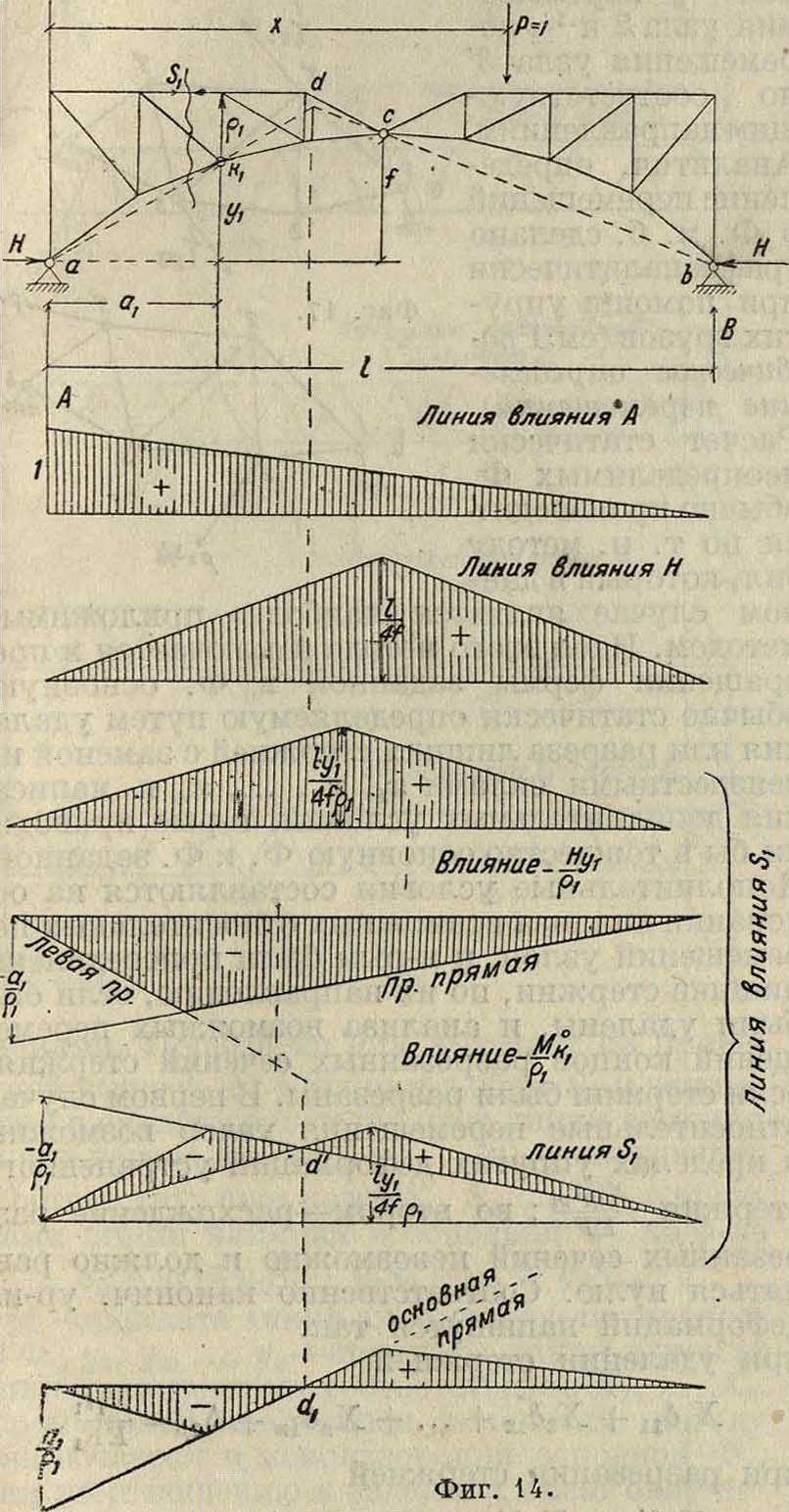
построения линии влияния сохраняется. Для арочных Ф. (фигура 14) следует в качестве основной линии построить еще линию влияния распора Н, которая будет представлять линию влияния двухопорной балки в точке с разделенную на /. Линия влияния усилия S_x определится из рассмотрения точки момента /с_х. В этом случае удобно расчленить влияние основных линий, выделив распор И в отдельный член. Тогда 1иВ дают линию влияния простой балочной Ф. с правой и левой прямой по общему выра-м°

жению —, где М°—линия влияния момента для точки Риттера в простой балке. Выражение для St можно написать в виде:

S|=-

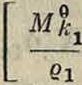
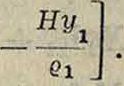
Влияние отдельных членов и суммарная линия S_x построены на фигуре 14. Из анализа выражения для Sx легко доказать важное свойство суммарной линии влияния. Нулевая точка в ней будет лежать под точкой пересечения линий оb через· два правых шарнира и ак_х через левый шарнир и моментную точку fcj. Последнее обстоятельство позволяет быстро чертить суммарную линию влияния. Под левой опорой откладывается ордината °¹ и проводится прямая через известное положение нулевой точки. На эту прямую сносятся точка моментов и средний шарнир. Полученные точки соответственно соединяются с левой и правой опорой.

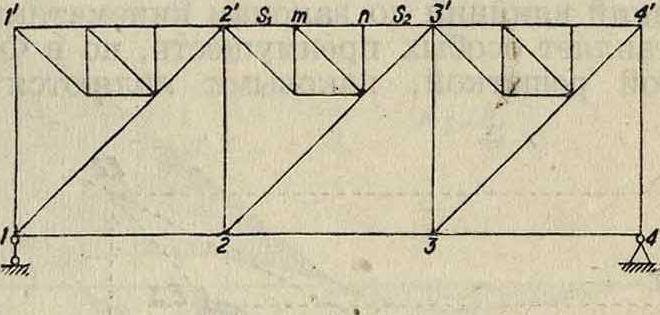
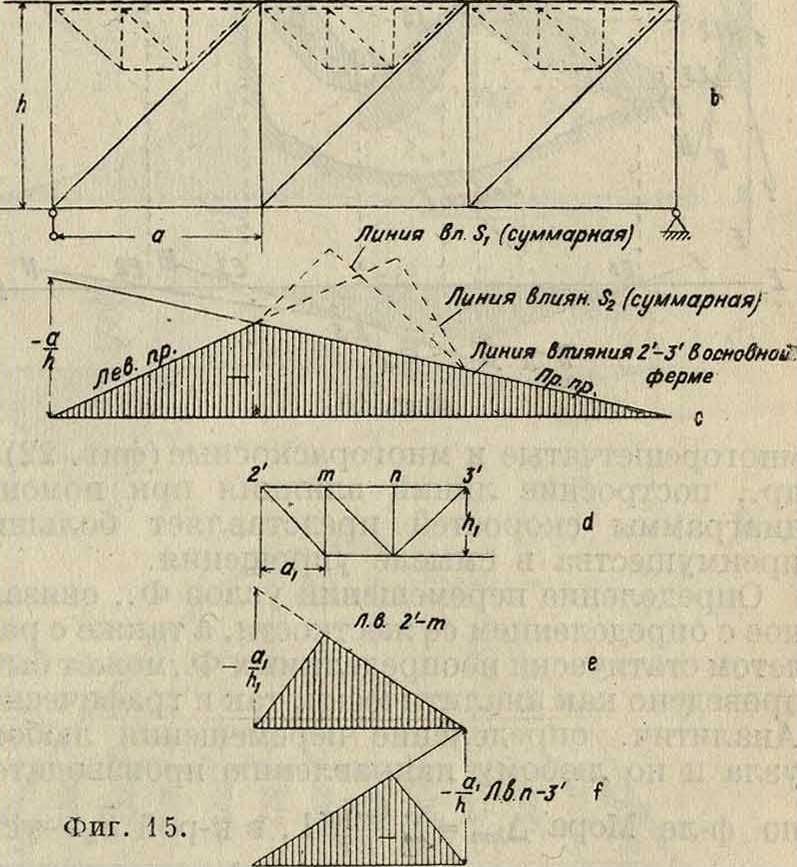
В Ф. сложных, а также в Ф. со шпренгелем линии влияния удобно строить, разлагая составную Ф. на отдельные ее составные части. Линия влияния элементов строится как сумма отдельных составных влияний. На фигуре 15 дано построение линий влияния Sx и S₂, для чего сложная Ф. (фигура 15, а) разделена на основную (фигура 15, Ь) и вспомогательную (фигура 15, d). В каждой из них построены линии влияния тех элементов, которые входят в состав элементов Sx и £₂. Суммарные линии влияния представлены на фигуре 15, с. В более сложных Ф. принципиальная сторона изложенных приемов остается в силе, но сам процесс осложняется.

Построение линий влияния кинематич. методом есть наиболее красивое приложение ки

нематики к расчету Ф., позволяющее быстро представить фигуру искомой линии влияния, пользуясь ее моделью—эпюрой смещения кинематич. цепи. Построение возможно как при непосредственном приложении начала возможных перемещений, так и в виде диаграммы скоростей. При непосредственном приложении начала возможных перемещений следует брать, возможные перемещения, исключающие работу связей опорных реакций. В этом случае работа будет выражаться всегда двучленами: работой груза р=1 и работой определяемого усилия S разрезанного стержня в виде Βδ, + 1-y-O.

Написанное равенство дает ключ к представлению эпюры смещений как модели линии влияния, стоит только определить из него усилие S,

к-рое будет равно — j. Числитель у есть проекция перемещения грузовой линии на направление груза р=1, а знаменатель—величина постоянная. Следовательно эпюра смещения грузовой линии по направлению груза определяет форму линии влияния и является непосредственно ей в масштабе <5_S=1. Эпюры проекций взаимных смещений отдельных элементов или дисков подвижного механизма дают прямые линии с нулевой ординатой под взаимными мгновенными центрами вращения, что непосредственно вытекает из рассмотрения движения отдельного диска, как поворота вокруг мгновенного центра. Свойства эпюры смещений следующие: 1) эпюра смещения отдельного диска дает прямую линию, 2) эпюра смещений не будет зависеть от расположения грузовой линии по диску,

3) на эпюре смещений линии, обозначающие смещения отдельных дисков, пересекаются между собой под взаимными мгновенными центрами вращения (фигура 16). В простых Ф. построение линий влияния по законам кинематики не представляет особых преимуществ, но в Ф. со сложной решеткой, каковыми являются Ф.

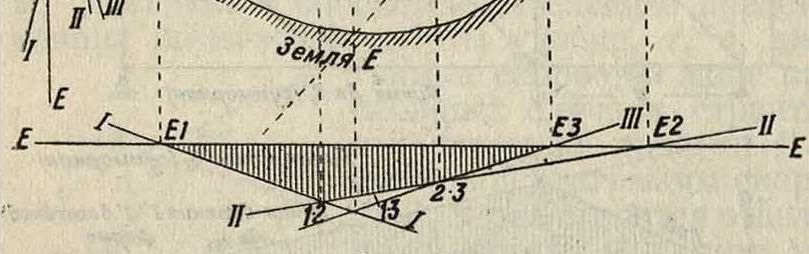
Фигура 16.

многорешетчатые и многораскосные (фигура 22) и др., построение линий влияния при помощи диаграммы скоростей представляет большие преимущества в смысле упрощения.

Определение перемещений узлов Ф., связанное с определением ее жесткости, а также с расчетом статически неопределимых Ф.,может быть проведено как аналитически, так и графически. Аналитич. определение перемещения любого узла и ио любому направлению производится по формуле Мора А_кт=Σ I, в которой Б_к— усилия элементов от силы р=;1 фиктивного состояния по направлению исследуемого перемещения, S_m—усилия от действующей нагрузки, F—площадь сечения и I—длина каждого элемента Ф. Темп-рные перемещения узлов определяются ф-лой Мора следующего вида Ам=SS_Aai · I.

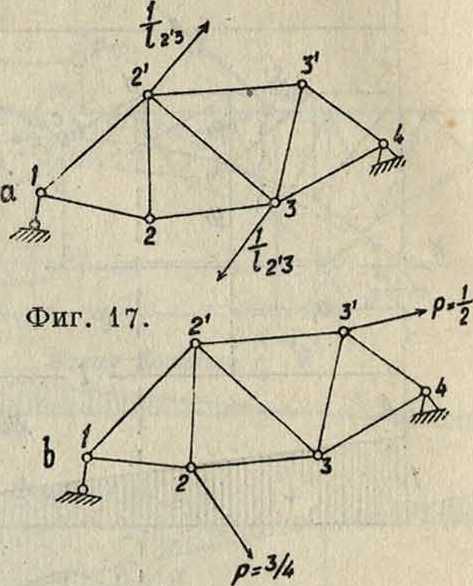
При определении угловых перемещений стержня, что связано с определением относительных перемещений его концов, виды ф-л сохраняют ся; только S_k будет усилие от сил р_к=приложенных к концам стержня длиной 1_к и составляющих между собой пару (фигура 17, а). Ф-ла Мора также дает возможность определять групповые суммарные перемещения, стоит только фиктивное состояние назначить сообразно требованиям поставленной задачи. Так, фигура 17, b дает групповое суммарное перемещение, причем ³/₄ перемещения узла 2 и Va перемещения узла 3 по соответствующим направлениям.

Аналитич. определение перемещений в Ф. м. б. сделано графоаналитически при помощи упругих грузов (смотрите Графическое определение перемещений).

Расчет статически неопределимых Ф. обычно производит^ ся по т. н. методу сил, который в данном случае является наиболее приложимым методом. Идея этого метода заключается в превращении фермы заданной в Ф. основную, обычно статически определяемую путем удаления или разреза лишних стержней с заменой их неизвестными силами ас, х_г, ., х_п и написания дополнительных условий, которые приводили бы в тождество основную Ф. к Ф. заданной. Дополнительные условия составляются на основании анализа возможных относительных перемещений узлов, к которым были присоединены лишние стержни, по их направлению, если они были удалены, и анализа возможных перемещений концов разрезанных сечений стержня, если стержни были разрезаны. В первом случае относительные перемещения узлов возможны в пределах упругих деформаций устраненного стержня -^Х£р^Щ ; во втором—расхождение разрезанных сечений невозможно и должно равняться нулю. Соответственно канонич. ур-ия деформаций напишутся так: при удалении стержней

XAl + ΆΑ2 + ·· + XJ_ln + Ар =

при разрезании стержней

-ХАг + -ААз + ··· + -Х?Аи + Ар ⁼ О-Между написанными канонич. ур-иями нет никакой разницы, ибо δ(j=<5_n + -А—. Входящие единичные перемещения 8_кт определяются ф-лой Мора (смотрите выше). После определения неизвестных×усилие любого стержня определяется ф-лой

А - А! + Χβι + ХА +. X_nS_n, где S, ., S_n — усилия в стержне от =

= Ζ₂=.=Ϊ„=1.

Процесс расчета статически неопределимой Ф. показан на фигуре 18. Канонич. ур-ия для этого случая будут:

*Αι + Х-2А2 + **Аз + Ар=- ;

-Х1А1 + Χιδ₂₂ + .Х3А3 + Δ_2ρ=0;

ΆΑι + Х-2 Аз + ХА? + А®= 0·

Отмечаем, что в статически неопределимых системах определение неизвестных связано с знанием наперед площадей поперечных сечений. Линии влияния усилий в элементах статически неопределимых Ф. могут быть построены двумя

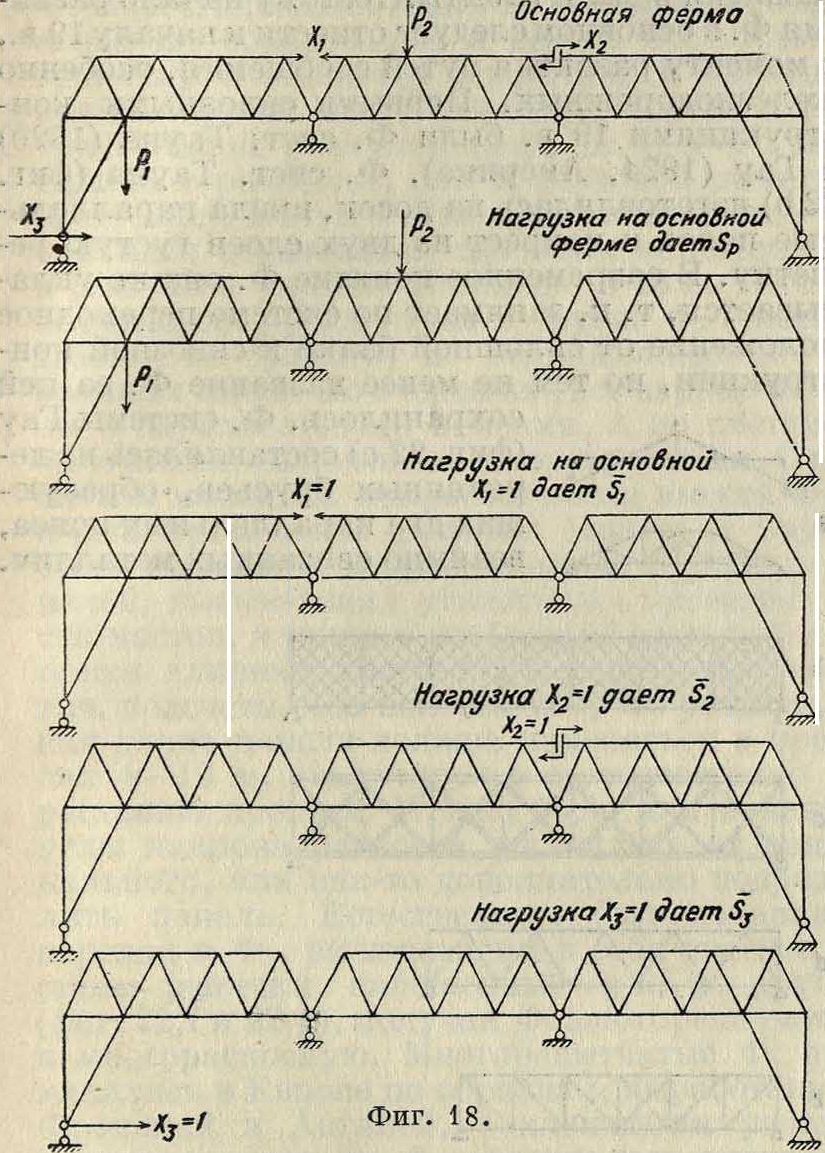
приемами. Первый из них вытекает^ из приведенной выше ф-лы усилия в любом и заключается в суммировании ординат линии влияния лишних неизвестных у_1г у₂,^.,у_п, умноженных на соответствующие коэф. S_u S₂, ., S_n, с ординатами линии влияния в основной Ф. по формуле S*=у% + ?/ι®ι + y₂S₂ +. + y_nS_n, где у %—ордината линии влияния усилия в основной Ф., Ух, у₂, ·, у_п—ординаты линии влияния лишних неизвестных соответственно .-Хи-

Второй прием аналогичен кинематич. методу и заключается в использовании основной Ф., которая по отношению к заданной имеет одну неопределимость, только того усилия, для которого строится линия влияния. При грузе р=1 кано-нич. ур-ие в этом случае будет:

^тпРтт "Ь З_тр О,

откуда

С___ ^тУ

— s

°тш.

или по принципу Максвелла

8

т ~

iVM..

Ьупт

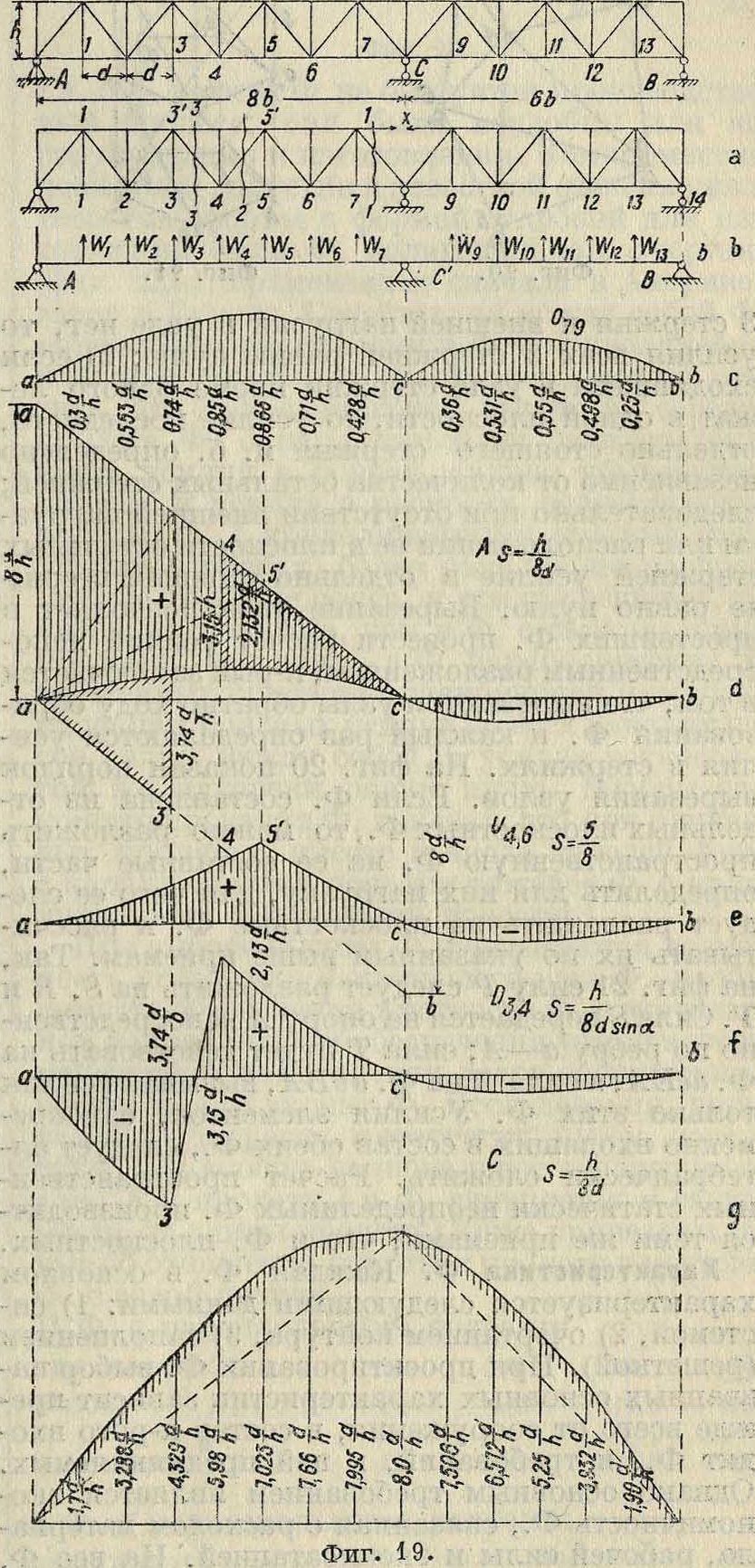
Числитель последнего равенства д_рт можно рассматривать как перемещение (прогиб) грузовой линии по направлению р=1 от силы S_m=1, приложенной к основной системе, а д_тт — собственное перемещение по направлению самого неизвестного. Как следствие можно сказать, что перемещение грузовой линии (прогиб от действия Х_т=1) есть модель искомой линии влияния и есть сама линия влияния в масштабе <5_тот=1. Последний прием связан с постро ением линйи прогибов узлов грузовой линии, что может быть проведено по указанным выше соображениям о перемещениях (фигура 19).

В расчете пространственных Ф. принципиально нового нет. Все приемы расчетов плоскостных Ф. приложимы и к Ф. пространственнвш, только здесь они принимают несколько иное оформление в связи с пользованием пространственной статикой и кинематикой. Следует отметить, что кинематические приемы расчетов для пространственных Ф. недостаточно еще разработаны и пока уступают статич. приемам. Статич. приемы расчета пространственных Ф. следующие: 1) прием произвольного сечения Ф.

U t Z j ** о ϋ 8 9’ ш П‘ ιέ А?" 14‘

на две части, аналогичный рассечению плоских Ф., 2) прием вырезания отдельных узлов, 3) способ Генеберга, к-рый является наиболее общим, идея которого изложена в курсах строительной механики. В виду большого разнообразия пространственных Ф. нет возможности указать, в каком случае применять тот или иной прием. Первые два обычно являются нераздельными, ибо по существу между ними разницы нет.

26

Т. Э. τη. XXIV.

В общем случае вырезанием узла можно пользоваться, когда в узле не более 3 неизвестных усилий, определяемых из ΣΧ=О, ΣΓ=О, ΣΖ=О, а в сечении не более 6 неизвестных, определяемых из условий:

ΣΧ=0; ΣΓ=0; ΣΖ=0; ΣΜ_χ=0; ΣΜ_ν=0; ΣΜ_Ζ=0. При расчете полезно иметь в виду следующие положения, вытекающие из пространственной статики: 1) если в узле Ф. сходятся только

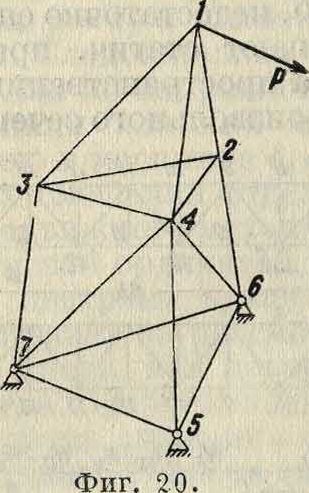
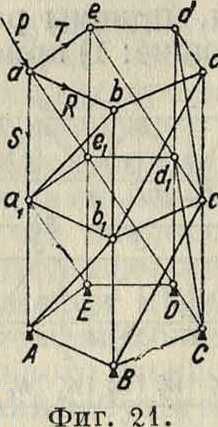
3 стержня и внешней нагрузки в узле нет, то усилия всех 3 стержней равны нулю; 2) если сходящиеся в узле стержни кроме одного лежат в одной плоскости, то усилие последнего, отдельно стоящего стержня м. б. определено независимо от количества остальных стержней; следовательно при отсутствии внешней нагрузки или расположении ее в плоскости остальных стержней усилие в отдельно стоящем стержне равно нулю. Вырезание узла позволяет в простейших Ф. провести расчет усилий непосредственным разложением, к-рый заключается в том, что вырезаются узлы обратно ходу образования Ф. и каждый раз определяются усилия в стержнях. На фигуре 20 показан порядок вырезания узлов. Если Ф. составлена из отдельных плоскостных Ф., то можно разложить пространственную Ф. на ее составные части, определить для них нагрузку, для чего ее следует разложить на плоскостные Ф. и рассчитывать их по указанным выше приемам. Так, на фигуре 21 силу Р следует разложить на S, R и Т. Сила S передается на опору А непосредственно по ребру а—А; сила Т будет действовать на Ф. аеЕА, а сила R на Ф. аbВА, вызывая усилия только этих Ф. Усилия элементов, одновременно входящих в состав обеих Ф., следует алгебраически сложить. Расчет пространственных статически неопределимых Ф. производится теми же приемами, что и Ф. плоскостных.

Характеристика Ф. Каждая Ф. в основном характеризуется следующими данными: 1) системой, 2) очертанием контура, 3) заполнением (решеткой). При проектировании Ф. выбор названных основных характеристик зависит прежде всего от сооружения, в состав которого входит Ф., и требований, к ней предъявляемых. Однако основным требованием является экономичность Ф., связанная с расходом материала, рабочей силы и эксплуатей. На вес Ф. оказывают сильное влияние система и очертание контура и в меньшей мере—заполнение (решетка). Очертание контура в Ф. специального назначения определяется характером сооружения (стропильные Ф.), а иногда и эстетич. соображениями (городские мосты). Первые плоскостные системы, применявшиеся для стропильных и мостовых покрытий, получившие четкое оформление Ф., были Ф. итальянского инж. Палладио (16 в.), выполняемые из дерева с металлич. поковками (фигура 22,а). По причинам трудности узловых сопряжений при переменных усилиях элементов и за отсутствием способов расчета Ф. эти не получили должного развития и были забыты. Поэтому начало развития Ф. в основном следует отнести к началу 19 в., к моменту развития путей сообщения, особенно железнодорожных. Первыми сквозными конструкциями 19 в были Ф. сист. Тауна (1820) и Гау (1824, Америка). Ф. сист. Тауна (фигура 22,Ь) изготовлялась из досок, имела параллельные пояса и накрест из двух слоев густую, решетку. В современное понятие Ф. она не укладывается, т. к. занимает по системе переходное положение от сплошной балки к сквозной конструкции, но тем не менее название Ф. за ней сохранилось. Ф. системы Гау (фигура 22,с) составлялась из деревянных брусьев, образую-щих два параллельных пояса, взаимно связанных металлич.

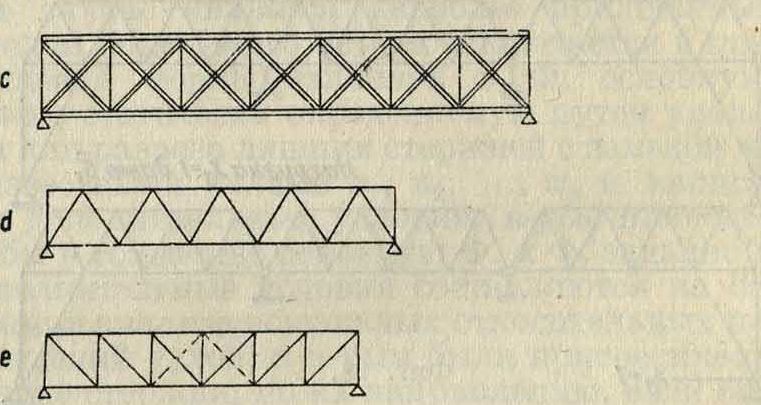
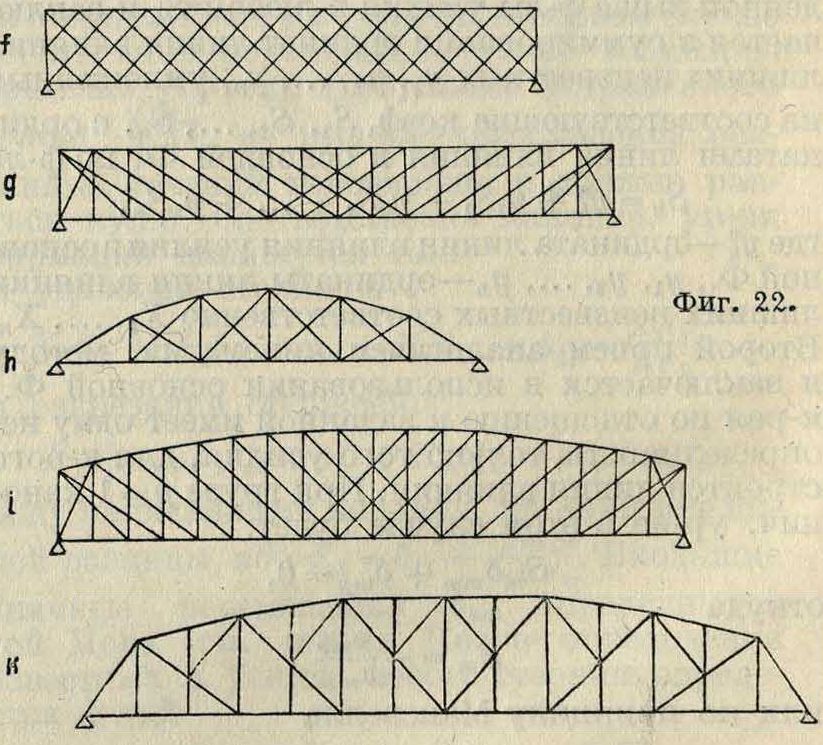
тяжами, между которыми помещаются деревянные перекрещивающиеся раскосы. С появлением массового изготовления металла и его прокатки многорешетчатая Ф. сист.Тауна была перенесена и в область металлич. сооружений (1850—60 гг.), в которых доски решетки заменялись вначале полосовым, а затем угловым и тавровым железом. Этим наметился в основном переход в металле от сплошной клепаной конструкции, которая была применена в мостах, к сквозной. Переход этот вызывался необходимостью перекрытия больших пролетов, в к-рых сплошная балка оказывалась экономически невыгодной. Сплошная стенка была заменена сквозной, но вследствие недостаточно развитой теории была оставлена густая решетка, которая не давала отчетливых представлений о работе Ф. В шестидесятых годах 19 в появились более ясные по образованию и работе Ф., которые по существу и являются основными в настоящее время. Это Ф. сист. Невиля и Варена с т. н. треугольной решеткой (фигура 22,d) и Ф. сист. Пратта с раскосной или N-образной решеткой (фигура 22,е). В этих Ф. сказалось повторение четкой идеи образования сквозных конструкций, которая была указана Палладио в 16 в В то же время были предложены и другие Ф. (системы Поста), по существу не отличающиеся от названных выше. По очертанию все первые Ф. были с параллельными поясами, а по системе— балочными, разрезными и неразрезными. С развитием масштаба покрытия росла высота Ф., в которых применение решетки Пратта и Варена было связано с необходимостью больших панелей, вызывающих утяжеление проезжей части мостов, а также с необходимостью проектировки длинных сжимаемых стержней. Теоре-тич. подсчеты веса показывают, что рациональная длина панели должна изменяться в пределах 4—10 м, увеличиваясь соответственно нарастанию пролета. Нужно было или изменять углы наклона раскосов, уклоняясь от рационального, или как-то дополнительно подразделять панель. Естественным был начальный переход к Ф., включающим в себя две-три системы решетки, наложенные одна на другую (фигура 22,f и 22,g), получая Ф. многорешетчатую и многораскосную. Многорешетчатые Ф. применялись в Европе по образцам, выработанным Францией и Англией, с клепаными узлами; многораскосная же Ф. развивалась вначале в Америке и с болтовыми соединениями.

Первые Ф. имели форму бруса с двумя параллельными поясами. Искание рациональных форм очертаний Ф. относится ко 2-й половине 19 в В области балочно-разрезных Ф. эти искания привели прежде всего к увеличению высоты по середине пролета в сравнении с опорами, что вытекает из анализа балочной системы, в которой усилия в поясах зависят от момента и высоты Ф. (S=M : h). Т. к. момент растет к середине пролета, то для сохранения постоянных усилий (й=Const) необходимо увеличивать высоту h. При равномерной нагрузке, точно следуя указанному правилу, была получена т. и. параболич. Ф. с постоянным усилием прямого пояса (фигура 22,h). Так как при равномерной нагрузке то

Ч1_Х_ qXJ

Sconst Sconst

дает семейство парабол в зависимости от^о,^. Конструктивные неудобства чисто параболич. Ф. привели к Ф. полупараболической—очертание, часто применявшееся в Ф. большого пролета (фигура 22,i). Стремление создать усилия, постоянные в обоих поясах, привели к Ф. сист. Паули, которая распространения не получила. Шведлером (1867) была создана Ф., в которой при любом положении подвижной нагрузки усилия в раскосах положительны (фигура 23). Идея ее заключается в том, что растягивающие усилия от постоянной нагрузки р более возможных сжи мающих усилий от временной нагрузки к.Очертание Ф. зависит от соотношения нагрузок к яр. Ради конструктивных удобств и эстетич. соображений вдавленный верхний пояс обычно выпрямлялся. Названные выше Ф., теоретически имеющие определенный смысл, особого развития не получили, ибо их форма не оказалась вкупе совершенной, т. к. она искалась только из нек-рых предпосылок, не учитывая во взаимосвязи всех обстоятельств, влияющих на изготовление в практике Ф. и их эксплуатю.

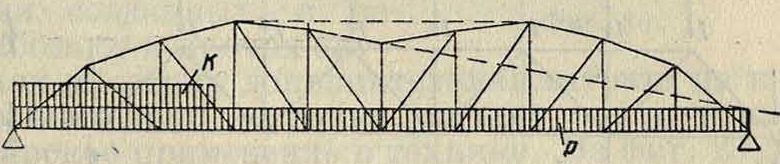
Фигура 23.

Гл. обр. во всех Ф. не был учтен пооизводствен-ный процесс; они были неудобны для конструирования и изготовления. Компромиссным решением, допустив в известной степени увязку теоретич. формы с формой, удобной для изготовления, были Ф. полигонального очертания (фигура 22,к), примененные сначала в Америке, а затем в Европе. Сопоставляя между собой Ф. с параллельными поясами и Ф. с криволинейным или полигональным очертанием, можно отметить, что при одинаковой высоте по середине пролета Ф. с параллельными поясами будет иметь усилия в поясах, сильно убывающие к опорам, и усилия в раскосах, возрастающие к опорам; Ф. с криволинейными поясами имеют усилия в поясах, более равномерно распределенные по длине пояса, и усилия решетки, значительно меньшие, чем вФ.с параллельными поясами. Так наир., в Ф. параболических, нагруженных сплошной равномерной нагрузкой, проекции поясных усилий во всех панелях поясов равны между собой, а усилия раскосов от той же нагрузки равны нулю. Вообще опыт конструирования Ф. показал, что при одинаковых пролетах, высоте и числе панелей фермы с параллельными поясами тяжелее Ф. с криволинейными и ломаными поясами.

При выборе высоты Ф. учитываются возможность получения наименьшего веса Ф., необходимость обеспечения жесткости Ф. в вертикальном направлении и обеспечения устойчивости в поперечном направлении всего сооружения, в состав которого входит Ф. Исследования, произведенные теоретич. и статистич. путем, показывают, что вообще рациональное отношение высоты h к пролету I в Ф. изменяется в зависимости от длины пролета. Ниже приведены данные об отношении высоты к пролету в мостовых Ф. с ездой понизу.

В Ф. с параллельными поясами: при пролетах I, м. зо 40

в СССР А. 1/4 1/5

в Америке. 1/4 1/4,5

в Ф. с полигональными поясами:

при пролетах I, м. 50 во 90 130 150

в ссср. ι/e ι/e 1/6 1/3,3 1/6,6

в Америке. 1/5,2 1/5,4 1/6 1/6,2 1/6,4

В стропильных Ф. выбор высоты Ф. часто зависит от конструктивных требований, предъявляемых к скату кровли. Проф. Стрелецкий характеризует зависимость изменения отношения h : I в стропильных Ф. графиком, показан-

50 60

1/6,0 1/6,1

1/8,6 1/6,0

ным на фигуре 24, в котором кривая Ϊ относится к ферме с параллельными поясами и раскосной решеткой; кривая 2 относится к ферме с параллельными поясами и треугольной решеткой;

1.	, 1,		,	1		1	, 1
		d	n?d =1 --»

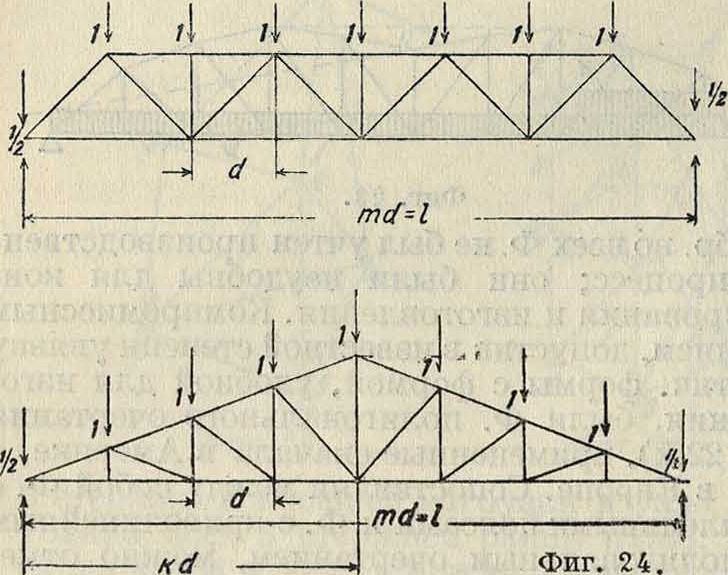
тельно; вес Ф. с треугольной решеткой и дополнительными стойками и подвесками близок к весу Ф. с простой треугольной решеткой.

Постепенное завоевание Ф. области больших пролетов, в которых собственный вес конструкции балочной системы становился все более и более чувствительным, проходило через стадии исканий новых форм. Эти искания были направлены по линии совершенствования системы как таковой и по линии

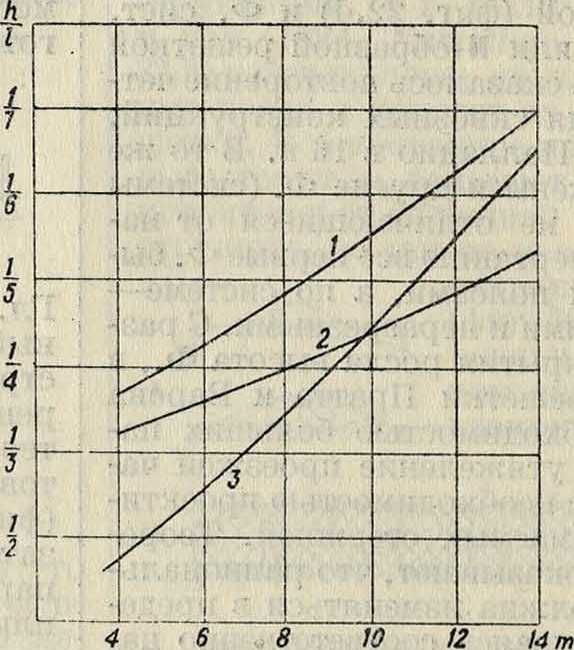
кривая 3 относится к ферме треугольного очертания и с раскосной решеткой.

Переходя к характеристике различных систем решеток, применяемых в Ф., надо прежде всего отметить, что величина и знак усилия решетки очень сильно зависят от контура поясов Ф. Так, в Ф. с параллельными поясами раскосы, нисходящие к месту наибольшего момента, работают на растяжение, в Ф. стропильного типа раскосы, нисходящие к месту наибольшего момента, работают на сжатие, в параболических Ф., контур которых является средним между указанными, раскосы не работают от постоянной очертания поясов и заполнения решетки Ф. Как новые системы были выдвинуты консольные и арочные Ф. Консольные Ф.,часто называемые Ф. сист. Гербера, по существу системы напоминают неразрезную, которая применялась уже раньше и к которой относились недоверчиво, имея в виду чувствительности этой Ф. как статически неопределимой системы к дополнительным напряжениям от осадки опор и Г. В консольных Ф., являющихся результатом преобразования

нагрузки. Все указанные свойства решетки относятся к постоянной нагрузке и нарушаются при действии подвижной, вызывающей своим движением по Ф. знакопеременное усилие в решетке, как это легко видеть.по-линиям влияния. Сама решетка обладает тем свойством, что знак усилия в ней меняется с переходом от раскоса к стойке в раскосных системах и от раскоса к раскосу в треугольных системах. Исследования показывают, что наименьший вес решетки имеет место при наклоне раскосов под углом 45—55° к горизонту. Сравнительные подсчеты веса Ф. при одинаковом очертании поясов, одинаковом пролете, высоте Ф., числе панелей и одинаковой нагрузке показали, что действительный вес Ф. с треугольной решеткой всегда меньше веса раскосной Ф., но незначи

Фигура 26.

неразрезных Ф. в статически определимые, уничтожен этот недостаток, а вместе с ним уничтожена и плавность упругой линии—ценнейшее качество неразрезных ферм в эксплуатонном отношении. Статич. смысл их заключается в том, что нагрузка, располагаемая на консолях и подвесных Ф., разгружает между-опорную часть, снижая вес Ф. Консольные Ф. легче балочных и могут перекрывать ббльшие пролеты. Однако чувствительная разница в весе сказывается лишь при пролетах более 120 метров Консольные Ф. кроме того представляют известные удобства сборки их и компановки сооружения. Из балочных систем за последнее время все больше и больше в практике вновь появляется система неразрезная, что связано с теоретическими достижениями в области регулирования дополнительных напряжений. Имея большие

положительные качества: жесткость, плавность упругой линии, экономичность и другие, неразрезная ферма несомненно займет надлежащее ей место среди перекрытий больших пролетов,

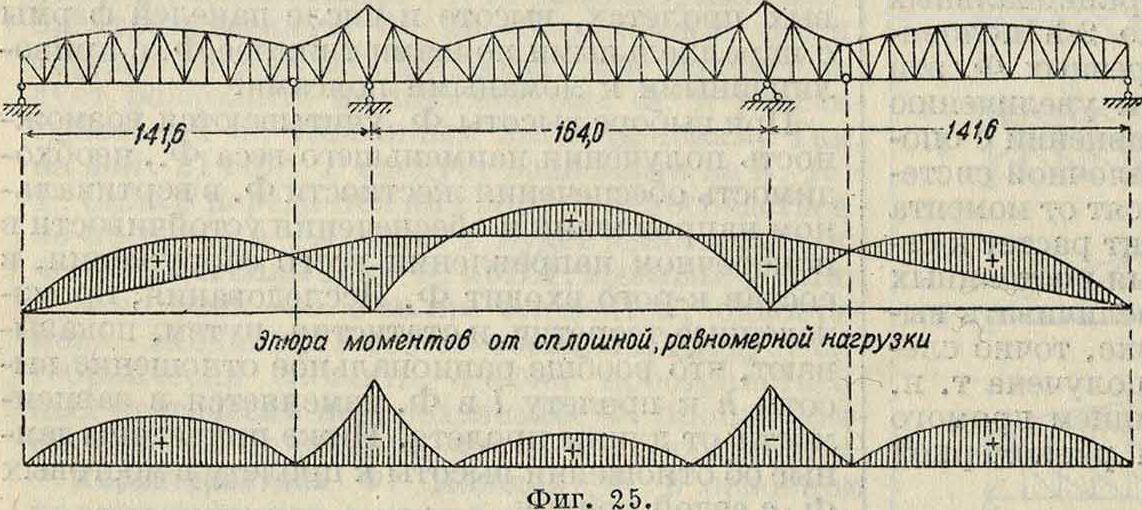
Прием очертания пояса по эпюре моментов от равномерной нагрузки был использован также в применении к балочно-консольным и- неразрезным фермам. На фигуре 25 даны сопоставления эпюры моментов и очертания пояса Ф. Подобное стремление иногда приводило к созданию не

красивых Ф. В практике последних лет поли-гональность очертания консольных Ф. значительно упрощается, т. к. производственные процессы все более и более накладывают отпечаток на форму сооружения, заставляя в Ф. консольных и неразрезных переходить к Ф. с параллельными поясами. Последние Ф. просты в конструктивном отношении и позволяют широко развить принципы стандартизации в процессе изготовления отдельных элементов, что ведет к быстроте изготовления фермы и к экономическому эффекту. При выявлении схемы консольных Ф. существенное значение имеет выбор длины консолей, влияющей как на вес бесшарнирного пролета, так и на вес подвесных ферм. Основываясь на исследовании ряда авторов, можно дать сл. характеристики отношения длины а консоли

Фигура 29.

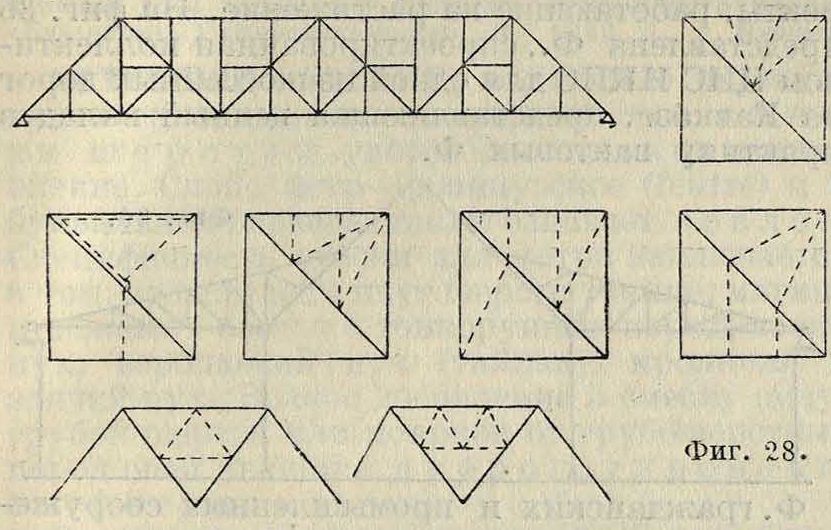
но зато растет количество узлов, что делает ее более тяжелой, чем шпренгельные Ф. Особенного внимания заслуживает прием введения в основную Ф. малых фер-мочек-шпренгелей, дающих дополнительные узловые точки (фигура 28).

Элементы таких фер-мочек работают исключительно при нагрузке дополнительных узлов, ими созданных, и не работают в прочих случаях. Поэтому дополнительная затрата на них сравнительно невелика, почему они и нашли широкое применение в технике. На фигуре 28 даны некоторые варианты шпренгельных включений, что конечно не исчерпывает все разнообразие примененных и могущих быть применен

ными в дальнейшем. Наличие шпренгелей в составе раскосов уменьшает свободную длину последних, снижая вес сжатых элементов. Решетка оказывает значительное влияние на развитие дополнительных напряжений в Ф. от жесткости узловых соединений. Подсчеты, производившиеся рядом специалистов, и опытные изучения Ф. показали, что наименьшие допол

к длине I пролета: при выпуклом очертании консолей as 0,15 Ϊ, при параллельных поясах as0,201, при вогнутом очертании α= 0,221.

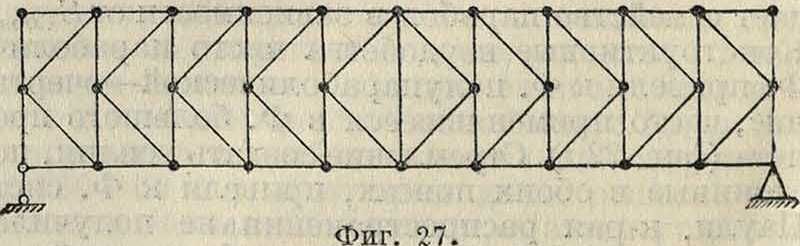
Обращаясь теперь к вопросу заполнения Ф., нужно отметить стремление, направленное к исканию простых форм с меньшими значениями дополнительных напряжений от жесткости узлов. Для раскосов выработался рациональный угол ок. 45—55°, причем треугольная решетка оказалась рациональнее N-образной. Деление панелей производилось введением дополнительных элементов, а не наложением решеток (фигура 26 и 22,к). Тех же целей достигает полураскосная Ф. (фигура 27), в которой свободная длина раскосов сокращается вдвое,

нительные напряжения имеют место в Ф. с раскосной простой треугольной, шпренгельной и полураскосной решетками; большие дополнительные напряжения имеют место в системах двухраскосной и двухрешетчатой и треугольной с подвесками. Что касается жесткости Ф. в смысле прогиба их, то здесь, наоборот, наибольшей жесткостью обладают Ф. с двухраскосной решеткой и двухрешетчатые и наименьшей жесткостью—Ф. со шпренгельной решеткой, К плоскостным балочным Ф. относят безрас-косную систему (фигура 29) и клепаную балку, называя их Ф., что не укладывается в понятие Ф.

Арочные Ф. в мостостроении появились вскоре после балочных и явились переходом от арочных чугунных мостов, которые к тому времени конструктивно оформились. Статич. отличие арочных Ф. от балочных заключается в

„		ggppP^/jj
-9	jmmmrniTTT.		rf

Фигура 3 5.

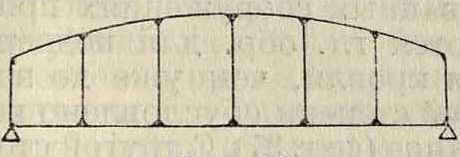
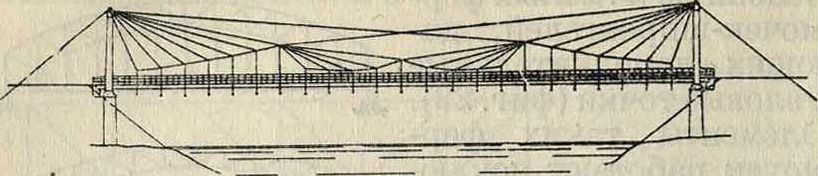
наличии горизонтальной составляющей опорных реакций (распора И), которая и дает разгрузку арки, создавая в пролете момент обратного знака. Распор в арочных Ф. неблагоприятен для опор, особенно высоких. И если арочные Ф. легче и более жестки, чем балочные, то опоры для них всегда массивнее. В неблагоприятных для опор случаях распор уничтожается введением затяжки (фигура 30), что дает уже комбинированные системы арки с затяжкой, к-рые второстепенного значения—в анты. Постепенное введение вант сгладило разницу между основными и второстепенными элементами висячего моста. Из вантовых Ф. широко применялись Ф. сист. Жискляра [фигура 35 (Франция)], дающие при любом положении нагрузки элементы, работающие на растяжение. На фигуре 36 представлена Ф., спроектированная коллективом ЦИС НКПС для одной из шоссейных дорог на е, представляющая ценный вклад в практику вантовых Ф.

Фигура 39.

Мевьш/пилон				ы}рМш палой
				I1
	£-	-800-	-1	] vitf

Ф. гражданских и промышленных сооружений, как отмечает практика, не представляют в своем развитии того широкого разнообразия, к-рое присуще фермам мостового типа. Это объясняется гл. обр. обстоятельствами, влияющими на характер работы Ф. промышленного и гражданского строительства. Ф. в названных сооружениях применяются гл. обр. для поддержания кровли, чем уже до некоторой степени обусловлено их

Фигура 36.

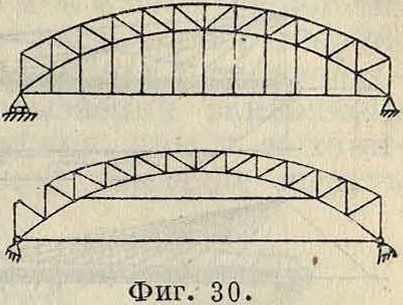
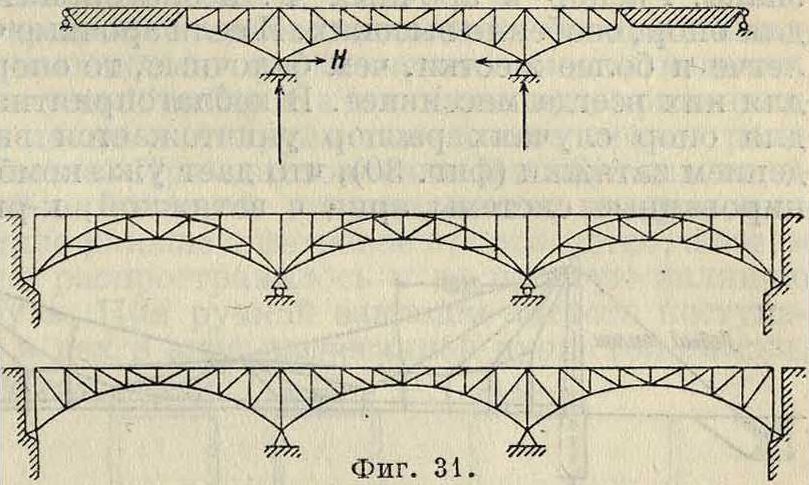
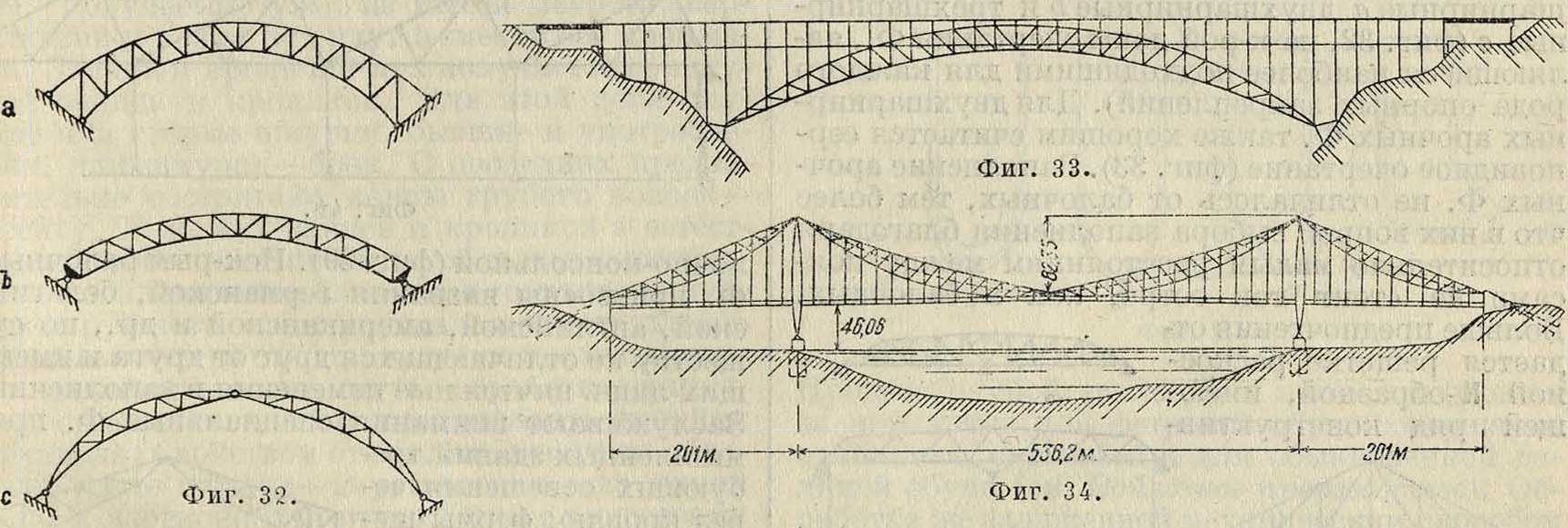
благодаря красивому их виду нашли широкое применение во всех странах света. Уменьшение влияния распора на опоры также было достигнуто применением консольных и неразрезных арок (фигура 31). Характер закрепления арок на опорах определяет название арочных Ф.: бес-шарнирные а, двухшарнирные Ь и трехшарнирные с (фигура 32, на которой даны очертания Ф., являющиеся наиболее подходящими для каждого рода опорных закреплений). Для двухшарнир-ных арочных Ф. также хорошим считается серповидное очертание (фигура 33). Заполнение арочных Ф. не отличалось от балочных, тем более что в них вопрос выбора заполнения благодаря относительно малым расстояниям между поясами не стоит так остро, как в балочных. Больше предпочтения от- _ л ^

дается решетке раскос- γΗ/Η>τ^

ной N-образной, имеющей ряд конструктив-

Фигура 37.

Фигура 38.

ных преимуществ при незначительной разнице в весе по сравнению с треугольной. В развитии висячих систем были также применены жесткие Ф. (фигура 34), которые по статич. смыслу одинаковы с аркой. Разница между ними только в направлении распора Н. В области висячих систем постепенное их развитие привело к т. н. вантовым гибким Ф., которые подходят под определение Ф. только в том случае, если все элементы Ф. растянуты. Они развились из висячих кабельных мостов, в которых для получения жесткости вводились дополнительные канаты роны, относительно малый масштаб перекрытий и легкость нагрузки по сравнению с сооружениями мостовыми не ставили острой, необходимости изыскания совершенных форм, и развитие их базировалось наразвитииФ. мостовых. В гражданских и промышленных зданиях Ф. была применена в системах: балочной (фигура 37), балочно-неразрезной (фигура 38) и ба-

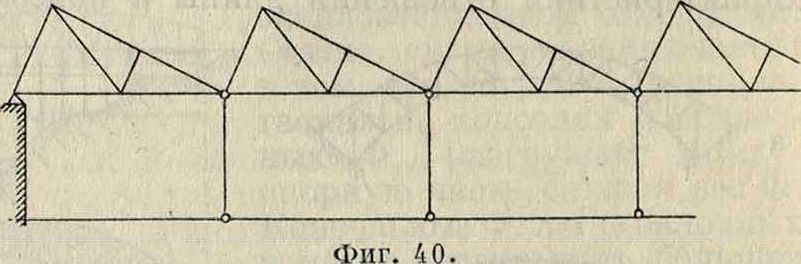
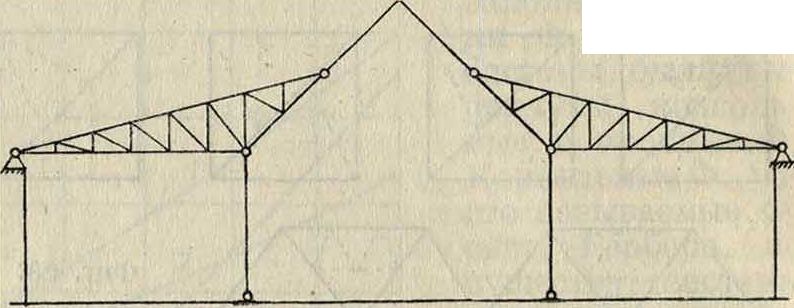
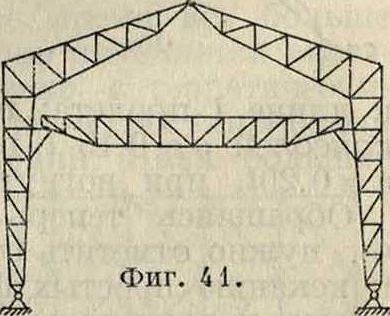
лочно-консолыюй (фигура 39). Нек-рым балочным Ф. присвоены названия германской, бельгийской, английской, американской и др., по существу не отличающихся друг от друга и имеющих лишь ничтожные изменения в заполнении. Заслуживают внимания специальные Ф. промышленных зданий,требующих освещения через кровлю: фермы ше-довые, или пилообразные (фигура 40). Фермы арочной системы употребляются как в промышленных сооружениях, так и особенно в перекрытиях вокзалов, платформ, выставочных и других общественных зданий (фигура 41), где они достигают значительных размеров. Особенного внимания заслуживает в настоящее время выполнение как балочных, так и арочных Ф. из дерева.

Лит.: Тимошенко С., Статика сооружений, ч. 1. 3 изд., Л., 1933; Прокофьев И., Теория сооружений, т. 1—2. М.—Л., 1 933; Симине кий К., Строительная механика, Киев, 1919; М ю л л е р-Б р е-

с л ay Г., Графическая статика, пер. с нем., СПБ, 1898; Подольский И., Пространственные фермы, М.—Л·, 1932; Патон и Горбунов, Стальные мосты, т. 1, Киев, 1930; Шухов В., Стропила, Изыскание рациональных типов прямолинейных стропильных ферм и теория арочных ферм, М., 1897; С т р е л е ц к и и Н., Законы изменения веса металлич. мостов,«Труды научно-техн. ком. НКПС», М., 1926, вып. 30; его же, Основы законов веса металла в промышленных конструкциях, «Бюллетень Гипростальмосты», М., 1932, 5. Киселев.